EE364A - Convex Optimization I
Lecture 9 - Complementary Slackness
-
Bookmarks
-
00:00:23
Complementary Slackness
-
00:04:28
Karush-Kuhn-Tucker (KKT) Conditions
-
00:06:52
KKT Conditions For Convex Problem
-
00:23:55
Perturbation And Sensitivity Analysis
-
00:29:39
Global Sensitivity Result
-
00:32:53
Local Sensitivity
-
00:47:50
Duality And Problem Reformulations
-
00:55:04
Introducing New Variables And Equality Constraints
-
01:01:45
Implicit Constraints
-
01:13:49
Semidefinite Program
-
00:00:23
Course Details
Show AllInstructor

Boyd, Stephen
Stephen P. Boyd is the Samsung Professor of Engineering, and Professor of Electrical Engineering in the Information Systems Laboratory at Stanford University. His current research focus is on convex optimization applications in control, signal processing, and circuit design.
Professor Boyd received an AB degree in Mathematics, summa cum laude, from Harvard University in 1980, and a PhD in EECS from U. C. Berkeley in 1985. In 1985 he joined the faculty of Stanford’s Electrical Engineering Department. He has held visiting Professor positions at Katholieke University (Leuven), McGill University (Montreal), Ecole Polytechnique Federale (Lausanne), Qinghua University (Beijing), Universite Paul Sabatier (Toulouse), Royal Institute of Technology (Stockholm), Kyoto University, and Harbin Institute of Technology. He holds an honorary doctorate from Royal Institute of Technology (KTH), Stockholm.
Professor Boyd is the author of many research articles and three books: Linear Controller Design: Limits of Performance (with Craig Barratt, 1991), Linear Matrix Inequalities in System and Control Theory (with L. El Ghaoui, E. Feron, and V. Balakrishnan, 1994), and Convex Optimization (with Lieven Vandenberghe, 2004).
Professor Boyd has received many awards and honors for his research in control systems engineering and optimization, including an ONR Young Investigator Award, a Presidential Young Investigator Award, and an IBM faculty development award. In 1992 he received the AACC Donald P. Eckman Award, which is given annually for the greatest contribution to the field of control engineering by someone under the age of 35. In 1993 he was elected Distinguished Lecturer of the IEEE Control Systems Society, and in 1999, he was elected Fellow of the IEEE, with citation: “For contributions to the design and analysis of control systems using convex optimization based CAD tools.” He has been invited to deliver more than 30 plenary and keynote lectures at major conferences in both control and optimization.
In addition to teaching large graduate courses on Linear Dynamical Systems, Nonlinear Feedback Systems, and Convex Optimization, Professor Boyd has regularly taught introductory undergraduate Electrical Engineering courses on Circuits, Signals and Systems, Digital Signal Processing, and Automatic Control. In 1994 he received the Perrin Award for Outstanding Undergraduate Teaching in the School of Engineering, and in 1991, an ASSU Graduate Teaching Award. In 2003, he received the AACC Ragazzini Education award, for contributions to control education, with citation: “For excellence in classroom teaching, textbook and monograph preparation, and undergraduate and graduate mentoring of students in the area of systems, control, and optimization.”
Handouts
Lecture Notes
| Introduction | Lecture 1 |
| Convex Sets | Lecture2 |
| Convex Functions | Lectures 3-4 |
| Convex Optimization Problems | Lectures 5-7 |
| Duality | Lectures 8-7 |
| Approximation and Fitting | Lecture 10 |
| Statistical Estimation | Lectures 11-12 |
| Geometric Problems | Lectures 12-13 |
| Numerical Linear Algebra Background | Lectures 13-14 |
| Unconstrained Minimization | Lectures 15-16 |
| Equality Constrained Minimization | Lectures 16-17 |
| Interior-point Methods | Lectures 17-19 |
| Conclusions | Lecture 19 |
Additional Lecture Notes:
| Convex Optimization Examples |
| Filter Design and Equalization |
| Disciplined Convex Programming and CVX |
Review Session Notes
| Review Session 1 | Lectures 1-2 |
| Review Session 2 | Lectures 3-4 |
| Review Session 3 | Lectures 5-6 |
| Review Session 4 | Lectures 7-8 |
| Review Session 5 | Lectures 9-10 |
| Review Session 6 | Lectures 11-13 |
| Review Session 7 | Lecture 14 |
| Review Session 8 | Lectures 15-16 |
| Review Session 9 | Lectures |
Assignments
Reading Assignments
Unless otherwise noted, all reading assignments are from the textbook. Copyright in this book is held by Cambridge University Press.
| Readings | Due Date |
|---|---|
| Chapters 1 and 2 | Lecture 4 |
| Chapters 3 and 4 | Lecture 6 |
| CVX Users' Guide | Lecture 8 |
| Chapter 5 | Lecture 10 |
| Chapters 6 and 7 | Lecture 12 |
| Chapter 8 and appendix C | Lecture 14 |
| Chapter 9 | Lecture 16 |
| Chapters 10 and 11 | Lecture 18 |
Homework Assignments
All numbered exercises are from the textbook. Copyright in this book is held by Cambridge University Press.
You will sometimes need to download Matlab files, see Software below.
| Assignment | Exercises | Solutions | Due Date |
|---|---|---|---|
| Homework 1 | 2.1, 2.2, 2.5, 2.7, 2.8, 2.11, 2.12, and 2.15 | Solutions | Lecture 4 |
| Homework 2 | 2.28, 2.33, 3.2, 3.5, 3.6, 3.15, 3.16(b-e), 3.18(b), 3.24(f-h), 3.36(a,d) Hint for 3.5: For each  , ,  is convex in is convex in  and thus and thus  is a convex function of is a convex function of 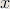 . . |
Solutions | Lecture 6 |
| Homework 3 | 3.42, 3.54, 3.57, 4.1, 4.4, 4.8(a-e), 4.17, and some additional exercises | Solutions | Lecture 8 |
| Homework 4 | 4.11, 4.16, 4.29, 4.30, 5.1, and some additional exercises Hint for 4.29: The condition is: There exists a feasible  for which for which  |
Solutions | Lecture 10 |
| Homework 5 | 4.15, 4.60, 5.13, 6.2, and some additional exercises | Solutions | Lecture 12 |
| Homework 6 | 6.9, and some additional exercises. You will also need to download flowgray.png Warning. Early printings of the book contain an error in the formulation of the A-optimal experiment design problem. See the book errata page |
Solutions | Lecture 14 |
| Homework 7 | 8.16, 9.30, 9.31 and some additional exercises (which include some hints for 9.30 and 9.31). | Solutions | Lecture 16 |
| Homework 8 | 9.8, 10.1a, 11.13, and some additional exercises | Solutions | Lecture 19 |
Course Sessions (19):
Show AllLecture 1
Lecture 2
| Watch Online: |
Download:
Right Click, and Save As
|
Duration: | |
| Watch Now | Download | 1 hr 17 min | |
| Topics: Guest Lecturer: Jacob Mattingley, Logistics, Agenda, Convex Set, Convex Cone, Polyhedra, Positive Semidefinite Cone, Operations That Preserve Convexity, Intersection, Affine Function, Generalized Inequalities, Minimum And Minimal Elements, Supporting Hyperlane Theorem, Minimum And Minimal Elements Via Dual Inequalities | |||
Transcripts
Lecture 3
| Watch Online: |
Download:
Right Click, and Save As
|
Duration: | |
| Watch Now | Download | 1 hr 17 min | |
| Topics: Logistics, Convex Functions, Examples, Restriction Of A Convex Function To A Line, First-Order Condition, Examples (FOC And SOC), Epigraph And Sublevel Set, Jensen’s Inequality, Operations That Preserve Convexity, Pointwise Maximum, Pointwise Maximum, Composition With Scalar Functions, Vector Composition | |||
Transcripts
Lecture 4
| Watch Online: |
Download:
Right Click, and Save As
|
Duration: | |
| Watch Now | Download | 1 hr 14 min | |
| Topics: Vector Composition, Perspective, The Conjugate Function, Quasiconvex Functions, Examples, Properties (Of Quasiconvex Functions), Log-Concave And Log-Convex Functions, Properties (Of Log-Concave And Log-Convex Functions), Examples (Of Log-Concave And Log-Convex Functions) | |||
Transcripts
Lecture 5
| Watch Online: |
Download:
Right Click, and Save As
|
Duration: | |
| Watch Now | Download | 1 hr 16 min | |
| Topics: Optimal And Locally Optimal Points, Feasibility Problem, Convex Optimization Problem, Local And Global Optima, Optimality Criterion For Differentiable F0, Equivalent Convex Problems, Quasiconvex Optimization, Problem Families, Linear Program | |||
Transcripts
Lecture 6
| Watch Online: |
Download:
Right Click, and Save As
|
Duration: | |
| Watch Now | Download | 1 hr 9 min | |
| Topics: (Generalized) Linear-Fractional Program, Quadratic Program (QP), Quadratically Constrained Quadratic Program (QCQP), Second-Order Cone Programming, Robust Linear Programming, Geometric Programming, Example (Design Of Cantilever Beam), GP Examples (Minimizing Spectral Radius Of Nonnegative Matrix) | |||
Transcripts
Lecture 7
| Watch Online: |
Download:
Right Click, and Save As
|
Duration: | |
| Watch Now | Download | 1 hr 15 min | |
| Topics: Generalized Inequality Constraints, Semidefinite Program (SDP), LP And SOCP As SDP, Eigenvalue Minimization, Matrix Norm Minimization, Vector Optimization, Optimal And Pareto Optimal Points, Multicriterion Optimization, Risk Return Trade-Off In Portfolio Optimization, Scalarization, Scalarization For Multicriterion Problems | |||
Transcripts
Lecture 8
| Watch Online: |
Download:
Right Click, and Save As
|
Duration: | |
| Watch Now | Download | 1 hr 16 min | |
| Topics: Lagrangian, Lagrange Dual Function, Least-Norm Solution Of Linear Equations, Standard Form LP, Two-Way Partitioning, Dual Problem, Weak And Strong Duality, Slater’s Constraint Qualification, Inequality Form LP, Quadratic Program, Complementary Slackness | |||
Transcripts
Lecture 10
| Watch Online: |
Download:
Right Click, and Save As
|
Duration: | |
| Watch Now | Download | 1 hr 18 min | |
| Topics: Applications Section Of The Course, Norm Approximation, Penalty Function Approximation, Least-Norm Problems, Regularized Approximation, Scalarized Problem, Signal Reconstruction, Robust Approximation, Stochastic Robust LS, Worst-Case Robust LS | |||
Transcripts
Lecture 11
Lecture 12
| Watch Online: |
Download:
Right Click, and Save As
|
Duration: | |
| Watch Now | Download | 1 hr 16 min | |
| Topics: Continue On Experiment Design, Geometric Problems, Minimum Volume Ellipsoid Around A Set, Maximum Volume Inscribed Ellipsoid, Efficiency Of Ellipsoidal Approximations, Centering, Analytic Center Of A Set Of Inequalities, Linear Discrimination | |||
Transcripts
Lecture 13
| Watch Online: |
Download:
Right Click, and Save As
|
Duration: | |
| Watch Now | Download | 1 hr 15 min | |
| Topics: Linear Discrimination (Cont.), Robust Linear Discrimination, Approximate Linear Separation Of Non-Separable Sets, Support Vector Classifier, Nonlinear Discrimination, Placement And Facility Location, Numerical Linear Algebra Background, Matrix Structure And Algorithm Complexity, Linear Equations That Are Easy To Solve, The Factor-Solve Method For Solving Ax = B, LU Factorization | |||
Transcripts
Lecture 14
| Watch Online: |
Download:
Right Click, and Save As
|
Duration: | |
| Watch Now | Download | 1 hr 10 min | |
| Topics: LU Factorization (Cont.), Sparse LU Factorization, Cholesky Factorization, Sparse Cholesky Factorization, LDLT Factorization, Equations With Structured Sub-Blocks, Dominant Terms In Flop Count, Structured Matrix Plus Low Rank Term | |||
Transcripts
Lecture 15
| Watch Online: |
Download:
Right Click, and Save As
|
Duration: | |
| Watch Now | Download | 1 hr 17 min | |
| Topics: Algorithm Section Of The Course, Unconstrained Minimization, Initial Point And Sublevel Set, Strong Convexity And Implications, Descent Methods, Gradient Descent Method, Steepest Descent Method, Newton Step, Newton’s Method, Classical Convergence Analysis, Examples | |||
Transcripts
Lecture 16
| Watch Online: |
Download:
Right Click, and Save As
|
Duration: | |
| Watch Now | Download | 1 hr 14 min | |
| Topics: Continue On Unconstrained Minimization, Self-Concordance, Convergence Analysis For Self-Concordant Functions, Implementation, Example Of Dense Newton System With Structure, Equality Constrained Minimization, Eliminating Equality Constraints, Newton Step, Newton’s Method With Equality Constraints | |||
Transcripts
Lecture 17
| Watch Online: |
Download:
Right Click, and Save As
|
Duration: | |
| Watch Now | Download | 1 hr 19 min | |
| Topics: Newton's Method (Cont.), Newton Step At Infeasible Points, Solving KKT Systems, Equality Constrained Analytic Centering, Complexity Per Iteration Of Three Methods Is Identical, Network Flow Optimization, Analytic Center Of Linear Matrix Inequality, Interior-Point Methods, Logarithmic Barrier | |||
Transcripts
Lecture 18
| Watch Online: |
Download:
Right Click, and Save As
|
Duration: | |
| Watch Now | Download | 1 hr 17 min | |
| Topics: Logarithmic Barrier, Central Path, Dual Points On Central Path, Interpretation Via KKT Conditions, Force Field Interpretation, Barrier Method, Convergence Analysis, Examples, Feasibility And Phase I Methods | |||
Transcripts
Lecture 19
| Watch Online: |
Download:
Right Click, and Save As
|
Duration: | |
| Watch Now | Download | 1 hr 15 min | |
| Topics: Interior-Point Methods (Cont.), Example, Barrier Method (Review), Complexity Analysis Via Self-Concordance, Total Number Of Newton Iterations, Generalized Inequalities, Logarithmic Barrier And Central Path, Barrier Method, Course Conclusion, Further Topics | |||