삼각 프리즘

균일 삼각 프리즘

유형	프리즘 균일 다면체
요소들	F = 5, E = 9 V = 6(수평 = 2)
옆얼굴	3{4}+2{3}
슐레플리 기호	t{2,3} 또는 {3}×{}
와이토프 기호	2 3 2
콕시터 다이어그램
대칭군	D_3h, [3,2], (*322), 주문 12
회전군	D₃, [3,2],⁺ (322), 주문 6
참조	U_76(a)
이중	삼각디피라미드
특성.	볼록하게 하다
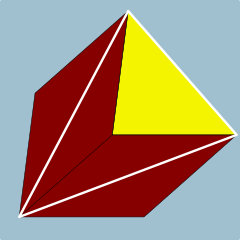정점수 4.4.3

삼각형 프리즘의 3D 모델

기하학에서 삼각 프리즘은 3면 프리즘으로, 삼각 베이스, 번역본, 3면이 해당 면을 접합하여 만든 다면체다. 오른쪽 삼각형 프리즘은 직사각형의 면이 있고, 그렇지 않으면 비스듬하다. 균일한 삼각형 프리즘은 정삼각형의 밑부분과 정사각형의 면을 가진 오른쪽 삼각형 프리즘이다.

동등하게, 그것은 두 면이 평행한 다면체인 반면, 다른 세 개의 표면 표준은 같은 평면에 있다(기초 평면에 반드시 평행하지 않다). 이 세 개의 얼굴은 평행사변형이다. 베이스 면에 평행한 모든 횡단은 동일한 삼각형이다.

반정형(또는 균일) 다면체로서

오른쪽 삼각형 프리즘은 반정형 또는 보다 일반적으로 밑면이 정삼각형이고 나머지 세 면은 정사각형인 경우 일률적인 다면체다. 잘린 삼각형 호소헤드론(Schléfli 기호 t{2,3})으로 볼 수 있다. 또는 삼각형과 선형의 카르테시안 상품으로 볼 수 있으며, 상품으로 대표되는 삼각형 프리즘의 이중은 삼각형 바이피라미드다.

삼각 베이스가 있는 오른쪽 3면 프리즘의 대칭 그룹은 순서 12의 D이다_3h. 회전 그룹은 순서 6의 D이다₃. 대칭 그룹은 역전을 포함하지 않는다.

볼륨

프리즘의 부피는 기지 면적과 두 베이스 사이의 거리의 산물이다. 이 경우 밑부분은 삼각형이기 때문에 삼각형의 면적을 계산하여 프리즘의 길이로 곱하면 된다.

V={\frac {bhl}{2}},

여기서 $b$ 는 삼각형의 한 면의 길이, $h$ 는 그 면으로 끌어당긴 고도의 길이, $l$ 는 삼각형 면 사이의 거리다.

잘린 삼각 프리즘

잘린 오른쪽 삼각형 프리즘은 비스듬히 하나의 삼각형 면이 잘려 있다(계획되어 있다.^[1]

기본 면적 A와 세 가지₁ 높이 h₂, h, h를₃ 가진 잘린 삼각 프리즘의 부피는 다음과^[2] 같이 결정된다.

V={\frac {A(h_{1}+h_{2}+h_{3}}}{3}}}.

면

삼각형 프리즘의 완전한_3h D 대칭 면은 2개가 있는데, 이 두 면 모두 6개의 이소셀 삼각형 면과 1개는 상하의 삼각형, 1개는 정사각형이다. 두_3v 개의 하부 C 대칭 면은 하나의 기본 삼각형, 세 개의 횡방향 교차 사각형 면, 세 개의 등각 삼각형 횡면을 가지고 있다.

볼록스	면
D_3h 대칭			C_3v 대칭

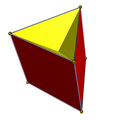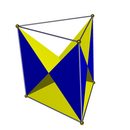2 {3} 3 {4}	3 {4} 6 ( ) v { }	2 {3} 6 ( ) v { }	1 {3} 3 t'{2} 6 ( ) v { }	1 {3} 3 t'{2} 3 ( ) v { }

관련 다면체 및 틸팅

일반 사면체 또는 사면체 분산체는 중앙 사각형으로 두 부분으로 나눌 수 있다. 각각의 절반은 위상학적 삼각 프리즘이다.

균일-곤 프리즘 계열
v
t
프리즘 이름	디조날 프리즘	(트리거) 삼각 프리즘	(Tetrangle) 사각 프리즘	오각형 프리즘	육각 프리즘	헵타곤 프리즘	팔각 프리즘	엔네오각 프리즘	십각형 프리즘	헨드각 프리즘	도십각 프리즘	...	아페이로곤 프리즘
다면체 이미지												...
구형 타일링 영상												평면 타일링 영상
정점 구성.	2.4.4	3.4.4	4.4.4	5.4.4	6.4.4	7.4.4	8.4.4	9.4.4	10.4.4	11.4.4	12.4.4	...	∞.4.4
콕시터 다이어그램												...

볼록 큐폴레과
v
t
n	2	3	4	5	6
이름	{2} t{2}	{3} t{3}	{4} t{4}	{5} t{5}	{6} t{6}
큐폴라	디조날 큐폴라	삼각 큐폴라	사각 큐폴라	오각형 큐폴라	육각 큐폴라 (플랫)
관련 획일적인 다면체	삼각 프리즘	큐복타- 헤드론	롬비- 큐방타- 헤드론	롬브- 이코시다데카- 헤드론	롬비- 삼헥사면의 타일링

대칭 돌연변이

이 다면체는 꼭지점 구성(3.2n.2n)과 [n,3] Coxeter 그룹 대칭성을 가진 균일한 절단 다면체의 일부로서 위상학적으로 관련이 있다.

*n32 잘린 틸팅의 대칭 돌연변이: t{n,3} v t
대칭 *n32 [n,3]	구면				유클리드	콤팩트 하이퍼브.		파라코.	비대칭 쌍곡선
대칭 *n32 [n,3]	*232 [2,3]	*332 [3,3]	*432 [4,3]	*532 [5,3]	*632 [6,3]	*732 [7,3]	*832 [8,3]...	*∞32 [∞,3]	[12i,3]	[9i,3]	[6i,3]
잘림 수치
기호	t{2,3}	t{3,3}	t{4,3}	t{5,3}	t{6,3}	t{7,3}	t{8,3}	t{{{propert,3}	t{12i,3}	t{9i,3}	t{6i,3}
트리아키스 수치
구성.	V3.4.4	V3.6.6	V3.8.8	V3.10.10	V3.12.12	V3.14.14	V3.16.16	V3.1987.1987

이 다면체는 꼭지점 수치(3.4.n.4)를 가진 칸막이가 있는 다면체의 일부로서 위상학적으로 연관되며 쌍곡면의 기울기로 계속된다. 이러한 정점 변환 수치는 반사 대칭(*n32)을 가진다.

*n32 확장 틸팅의 대칭 돌연변이: 3.4.n.4
대칭 *n32 [n,3]	구면				유클리드	콤팩트 하이퍼브.		파라콤.
대칭 *n32 [n,3]	*232 [2,3]	*332 [3,3]	*432 [4,3]	*532 [5,3]	*632 [6,3]	*732 [7,3]	*832 [8,3]...	*∞32 [∞,3]
피겨
구성.	3.4.2.4	3.4.3.4	3.4.4.4	3.4.5.4	3.4.6.4	3.4.7.4	3.4.8.4	3.4.∞.4

화합물

삼각 프리즘의 4가지 균일한 화합물이 있다.

4개의 삼각 프리즘의 혼합물, 8개의 삼각 프리즘의 혼합물, 10개의 삼각 프리즘의 혼합물, 20개의 삼각 프리즘의 혼합물.

허니컴스

삼각 프리즘 세포를 포함하는 9개의 균일한 꿀콤이 있다.

길쭉한 교대형 큐빅 벌집, 길쭉한 교대형 큐빅 벌집, 교대형 삼각 프리즘 벌집, 스너브 사각 프리즘 벌집, 삼각 프리즘 벌집, 삼각 프리즘 벌집, 잘린 육각형 프리즘 벌집, 스너브 삼각형 프리즘 벌집, 스너브 삼각형 프리즘 벌집c 벌집, 긴 삼각 프리즘 벌집

4차원 공간

삼각 프리즘은 다음을 포함한 다수의 4차원 균일한 4폴리토프의 세포로 존재한다.

삼각 프리즘이 있는 4차원 폴리탑
사면 프리즘	팔면 프리즘	큐폭타헤드랄 프리즘	이코사헤드랄 프리즘	이코시다데카헤드랄 프리즘	잘린두면 프리즘

롬브이코시다데코헤드랄 프리즘	Rhombi-cuboctaheadral 프리즘	잘린 입방 프리즘	스너브 도데카프리즘 프리즘	n-곤 항균 프리즘

캔터링 5세포	캔트런치 5-셀	런케이티드 5-셀	런시트드 5셀	캔터케이티드 테세락트	칸트룬칼로리테스락트	런케인테서락트	런티런탈테서락트

24-셀	캔트런던 24셀	런케이티드 24셀	24-셀 런시 셀	캔터레이티드 120셀	캔트런치 120셀	런케이티드 120 셀	120셀의 회전 속도

참고 항목

웨지(지오메트리)

참조

^ Kern, William F.; Bland, James R. (1938). Solid Mensuration with proofs. p. 81. OCLC 1035479.
^ "Volume of truncated prism". Mathematics Stack Exchange. Retrieved 9 July 2019.

[1] Kern, William F.; Bland, James R. (1938). Solid Mensuration with proofs. p. 81. OCLC 1035479.

[2] "Volume of truncated prism". Mathematics Stack Exchange. Retrieved 9 July 2019.

[1]

[2]

n차원의₂₁ k자
공간	유한한						유클리드 주	쌍곡선
E_n	3	4	5	6	7	8	9	10
콕시터 무리를 짓다	E₃=A₂A₁	E₄=A₄	E₅=D₅	E₆	E₇	E₈	E₉₈⁺ = ${\tilde {E}}_{8}$ ~ ${\tilde {E}}_{8}$ ${\$ ${\tilde {E}}_{8}$ = E	E₁₀ = ${\bar {T}}_{8}$ ${\$ ₈⁺⁺ $}}$ = E
콕시터 도표를 만들다
대칭	[3^−1,2,1]	[3^0,2,1]	[3^1,2,1]	[3^2,2,1]	[3^3,2,1]	[3^4,2,1]	[3^5,2,1]	[3^6,2,1]
주문	12	120	1,920	51,840	2,903,040	696,729,600	∞
그래프							-	-
이름	−1₂₁	0₂₁	1₂₁	2₂₁	3₂₁	4₂₁	5₂₁	6₂₁

Search