큐폴라(지오메트리)

큐폴레 세트
오각형 큐폴라(예)
슐레플리 기호	{n} t{n}
얼굴	ntriangles, nsquares, 1n-곤, 1 2n곤
가장자리	5n
정점	3n
대칭군	C_nv, [1,n], (*nn), 주문 2n
회전군	C_n, [1,n],⁺ (nn), 주문 n
이중	?
특성.	볼록하게 하다

기하학에서 큐폴라는 두 개의 폴리곤을 결합하여 형성된 고체로, 하나는 다른 하나는 두 배의 가장자리를 가지고 있고, 다른 하나는 이등변 삼각형과 직사각형의 교대 밴드에 의해 형성된다. 삼각형이 등각형이고 직사각형이 정사각형인 반면 밑면과 반대면이 일반 다각형이라면 삼각형, 사각형, 오각형 큐폴레는 모두 존슨 고형분 중 하나로 계산되며, 입체각형, 롬비큐옥타헤드론, 롬비코시도데코데카헤드론의 일부를 각각 떼어 형성할 수 있다.

큐폴라는 다른 정점을 합쳐서 폴리곤 중 하나가 반으로 무너진 프리즘으로 볼 수 있다.

큐폴라는 잘림, t{n} 또는 {2n}의 병렬로 연결된 일반 다각형 {n}을(를) 나타내는 확장된 Schléfli 기호 {n} t{n}을 부여할 수 있다.

큐폴레(Cupolae)는 프리즘토이드의 하위급이다.

그것의 이중은 면 사다리꼴의 절반과 양면 피라미드 사이의 일종의 용접 형태를 포함하고 있다.

예

볼록 큐폴레과
v
t
n	2	3	4	5	6
이름	{2} t{2}	{3} t{3}	{4} t{4}	{5} t{5}	{6} t{6}
큐폴라	디조날 큐폴라	삼각 큐폴라	사각 큐폴라	오각형 큐폴라	육각 큐폴라 (플랫)
관련 획일적인 다면체	삼각 프리즘	큐복타- 헤드론	롬비- 큐방타- 헤드론	롬브- 이코시다데카- 헤드론	롬비- 삼헥사면의 타일링

면 "헥스각형 큐폴레"

위에 언급한 3개의 다면체는 일반 얼굴을 가진 유일한 비삼면 볼록한 큐폴레이다. "헥사곤 큐폴라"는 평면 형상이며, 삼각 프리즘은 도 2의 "큐폴라"(선 구획과 사각형의 큐폴라)로 간주될 수 있다. 단, 고차 폴리곤의 큐폴레는 불규칙한 삼각형 및 직사각형 면으로 시공할 수 있다.

정점의 좌표

40면 큐폴라에는 40개의 이등변 삼각형(파란색), 40개의 직사각형(노란색), 상단의 40곤(빨간색), 하단의 80곤(숨겨진 색)이 있다.

큐폴라의 정의는 베이스(혹은 베이스 반대쪽, 위라고 할 수 있는 측면)를 일반 폴리곤으로 할 필요는 없지만 큐폴라의 최대 대칭인 C를_nv 갖는 경우를 생각해 보면 편리하다. 이 경우 상단은 일반 n곤이고, 하단은 일반 2n곤 또는 2n곤 중 하나로, 측면 길이가 서로 다른 2n곤과 교대하고 각도가 같다. 좌표계를 고정하여 기단이 xy 면에 놓이도록 하고, 상단은 xy 면에 평행하게 한다. z축은 n-폴드 축으로, 미러 평면은 z축을 통과하여 베이스의 측면을 이등분한다. 또한 그들은 상단 폴리곤의 옆면이나 각도를 이등분하거나 둘 다. (n이 짝수일 경우, 거울 평면의 반은 상단 폴리곤의 옆면을 이등분하고, 반면에 n이 홀수일 경우 각각의 거울 평면은 상단 폴리곤의 한쪽과 한쪽 각도를 이등분한다.) 베이스의 정점은 V에서₁ V까지_2n 지정할 수 있고, 상단 폴리곤의 정점은 V에서_3n V까지_2n+1 지정할 수 있다. 이러한 규약을 통해 정점의 좌표는 다음과 같이 기록할 수 있다.

V_2j−1: (r_b cos[2π(j − 1) / n + α], r_b sin[2π(j − 1) / n + α], 0)
V_2j: (r_b cos(2πj / n − α), r_b sin(2πj / n − α), 0)
V_2n+j: (r_t cos(πj / n), r_t sin(πj / n), h)

여기서 j = 1, 2, ..., n.

다각형 VVVV₁₂_2n+2_2n+1 등은 직사각형이기 때문에 r_b, r_t, α의 값에 제약을 가한다. VV의₁₂ 거리는

Rb{[코사인(2π/n− α)− 못 말리겠고 α]2+[죄(2π/n− α)− sin α]2}.mw-parser-output .sfrac{white-space:nowrap}.mw-parser-output.sfrac.tion,.mw-parser-output.sfrac .tion{디스플레이:inline-block, vertical-align:-0.5em, font-size:85%;text-align:센터}.mw-parser-output.sfrac .num,.mw-parser-output.sfrac .den{디스플레이:블록, line-height:1em, 마진:00.1em}.mw-pa.Rser-output.sfrac .den{border-top:1px 고체}.mw-parser-output .sr-only{국경:0;클립:rect(0,0,0,0), 높이:1px, 마진:-1px, 오버 플로: 숨어 있었다. 패딩:0;위치:절대, 너비:1px}1/2.

= r_b{{[cos²(2π / n - α) - 2cos(2π / n - α)cos α + cos² α] + [sin²(2π / n - α)] - 2sin(2 / / n - α)sin α + sin² α]}^1/2

= r_b{2[1] - cos(2π / n - α)cos α - sin(2π / n - α)sin α]}^1/2

= r_b{2[1 - cos(2( / n - 2α)]}^1/2

VV의_2n+1_2n+2 거리가 다음과 같을 때

r_t{[cos(cos) / n) - 1]² + sin²(sin(sin(sin) / n)}^1/2

= r_t{{[cos(cos²(ㄴ/n) - 2cos(ㄴ/n) + 1] + sin²(ㄴ/n)}^1/2

= r_t{2[1 - cos(cos(cos) / n)]}.^1/2

이것들은 같아야 하고, 만약 이 공통 가장자리가 s로 표시된다면,

r_b = s / {2[1 - cos(2( / n - 2α)]}^1/2

r_t = s / {2[1 - cos(cos)/n]}^1/2

이 값들은 앞에서 주어진 정점 좌표에 대한 표현식에 삽입되어야 한다.

별 큐폴레

별컵과
v
t
n/d	4	5	7	8
3	{4/3}	{5/3}	{7/3}	{8/3}
5	—	—	{7/5}	{8/5}

항성-cuploids 계열
v
t
½	3	5	7
2	교차 삼각 큐플로이드	펜타그램 큐플로이드	헵타그램 큐플로이드
4	—	교차 오각형 큐플로이드	교차 헵타그램 큐플로이드

스타 큐폴레는 모든 베이스 {n/d}에 존재한다. 여기서 ₅/ < _d6과 d는 홀수다. 한계에서 큐폴레는 평면 수치로 붕괴된다: 한계를 벗어나면 삼각형과 사각형은 더 이상 두 다각형 사이의 거리에 걸쳐 있을 수 없다(삼각형이나 사각형이 불규칙한 경우에도 만들 수 있다). d가 짝수일 때 하단 베이스 {2n/d}이 퇴화됨: 우리는 이 퇴화된 얼굴을 철회하고 대신 여기서 삼각형과 사각형이 서로 연결되도록 함으로써 큐플로이드나 세미푸폴라를 형성할 수 있다. 특히 테트라헤미헥사헤드론은 {3/2}-큐플로이드로 보일 수 있다. 큐폴레는 모두 방향을 잡을 수 있는 반면, 큐플로이드들은 모두 방향을 잡을 수 없다. cuploid에서 n/d > 2가 되면 삼각형과 사각형이 베이스 전체를 덮지 않고, 밑면에 작은 막이 남아 빈 공간을 간단하게 덮는다. 따라서 위에 그려진 {5/2} 및 {7/2} 큐플로이드는 막(채우지 않음)이 있는 반면, 위에 그려진 {5/4} 및 {7/4} 큐플로이드는 그렇지 않다.

한{n/d}-cupola 또는cuploid의 높이 h는 공식 h에 의해 1− 14죄 2⁡(π dn){\displaystyle h={\sqrt{1-{\frac{1}({\frac{\pi d}{n}})}}}}}. 특히 n/d의 한계점에서, h)06과 n/d)6/5, hn/d=2(그 삼각형을 똑바로 걷는 이는 삼각 프리즘,)에 극대화된다 주어진다.[1][2]

위의 이미지에서, 스타 큐폴레는 얼굴 식별을 돕기 위해 일관된 색상표가 제공되었다: 기저 n/d-곤은 빨간색, 기저 2n/d-곤은 노란색, 사각형은 파란색, 삼각형은 녹색이다. 큐플로이드는 다른 기지가 철수했기 때문에 베이스 n/d-곤 빨간색, 사각형 노란색, 삼각형 파란색이다.

안티큐폴라

안티쿠폴라 세트
오각형 예
슐레플리 기호	s{n} t{n}
얼굴	3ntriangles 1n-곤, 1 2n곤
가장자리	6n
정점	3n
대칭군	C_nv, [1,n], (*nn), 주문 2n
회전군	C_n, [1,n],⁺ (nn), 주문 n
이중	?
특성.	볼록하게 하다

n-곤 안티큐폴라는 일반 2n-곤 기반, 3n 삼각형 2종, 일반 n-곤 상단으로 구성된다. n = 2의 경우 상단 디건 면은 단일 가장자리로 축소된다. 상단 폴리곤의 정점은 하단 폴리곤의 정점과 정렬된다. 대칭은 C_nv, 순서 2n이다.

안티쿠폴라는 비록 어떤 것들은 규칙적으로 만들어질 수 있지만,^{[citation needed]} 모든 규칙적인 얼굴로 구성될 수는 없다. 상단 n-곤과 삼각형이 정규인 경우, 베이스 2n-곤은 평면적이고 정규적일 수 없다. 이러한 경우 n=6은 정육각형 및 주변 정육각형 삼각형을 생성하는데, 이 삼각형은 보다 큰 육각형 모양의 대칭 12곤과 함께 0볼륨 다각형으로 닫힐 수 있으며, 인접 쌍의 콜린어 가장자리가 있다.

두 개의 안티큐폴라는 그들의 베이스에 함께 생물학적으로 증강될 수 있다.

볼록항우울과
n	2	3	4	5	6...
이름	s{2} t{2}	s{3} t{3}	s{4} t{4}	s{5} t{5}	s{6} t{6}
이미지	디조날	삼각형	사각형	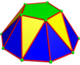오각형	육각형
투명
그물

과컵아과

다면 큐폴레 또는 다면 큐폴레(hypercupolae)는 볼록한 비통일성 폴리초라(여기서는 4차원 형상)로 큐폴라와 유사하다. 각자의 근거는 플라토닉 고체와 그 팽창이다.^[3]

이름	사면 큐폴라		큐빅 큐폴라		팔면 큐폴라		도데카헤드랄 큐폴라		육각 타일링 큐폴라
슐레플리 기호	{3,3} rr{3,3}		{4,3}r{4,3}		{3,4}r{3,4}		{5,3} rr{5,3}		{6,3}r{6,3}
세그먼트오코라 색인을^[3] 달다	K4.23		K4.71		K4.107		K4.152
만곡의	1		sqrt(3+sqrt(2)/2) = 1.485634		sqrt(2+sqrt(2) = 1.847759		3+sqrt(5) = 5.236068
이미지
캡셀
정점	16		32		30		80		∞
가장자리	42		84		84		210		∞
얼굴	42	24 {3} + 18 {4}	80	32 {3} + 48 {4}	82	40 {3} + 42 {4}	194	80 {3} + 90 {4} + 24 {5}	∞
세포	16	사면체 1개 삼각형 프리즘 4개 6 삼각 프리즘 4개의 삼각 피라미드 육면체 1개	28	정육면체 1개 6 제곱 프리즘 삼각 프리즘 12개 8개의 삼각 피라미드 롬비큐옥타헤드론 1개	28	팔면체 1개 8개의 삼각 프리즘 삼각 프리즘 12개 6개의 사각 피라미드 롬비큐옥타헤드론 1개	64	도데면체 1개 오각형 프리즘 12개 30 삼각 프리즘 삼각 피라미드 20개 롬비코시도데카헤드론 1개	∞	육각 타일링 1개 ∞ 육각 프리즘 ∞ 삼각 프리즘 ∞ 삼각 피라미드 1 rhombitrihexangle tiling
관련 획일적인 폴리초라	윤이 나는 5세포		윤활제 테세락트		윤택 24셀		재질의 120셀		육각형 타일링 벌집