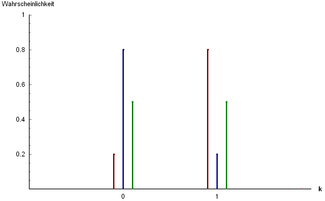
공정하지 않아도 되는 동전 던지기 확률 분포 모델링
확률 이론과 통계에서 확률과 확률 p{p\displaystyle}과 값 0q=1− p{\displaystyle q=1-p}로 1는 무작위 변수의, 베르누이 분포, 스위스의 수학자 제이콥 Bernoulli,[1]의 이름을 딴 것이 불연속 확률 분포. 덜 공식적으로 버틸 수 있다.oug 예-아니오 질문을 하는 단일 실험 의 가능한 결과 집합에 대한 모델로서 ht. 이러한 질문은 부울값 의 결과로 이어집니다 .즉, 값이 성공 /예 /참 /하나 이고 실패/아니오 /거짓/제로 (확률 q)인 단일 비트입니다. 1과 0이 각각 "앞면"과 "뒷면"을 나타내며 , p는 동전이 앞면에 착지할 확률이다(또는 반대로 1은 꼬리 , p는 뒷면의 확률). 특히, 부당한 동전은 p 1 / 2.\displaystyle \neq / 2 }
베르누이 분포는 단일 시행이 수행되는 이항 분포의 특수한 경우입니다(따라서 이러한 이항 분포의 경우 n은 1이 됩니다). 또한 2점 분포 의 특수한 경우로, 가능한 결과가 0과 1일 필요는 없습니다.
특성. X(\displaystyle ) 경우
PR ( X = 1 ) = p = 1 − PR ( X = 0 ) = 1 − q . \displaystyle \Pr(X=1)=p=1-\Pr(X=0)=1-q.} 가능한 결과 k에 대한 이 확률 displaystyle
f ( k ; p ) = { p 한다면 k = 1 , q = 1 − p 한다면 k = 0. {\displaystyle f(k;p)=cases}p&{\text{if}}k=1,\q=1-p&{\text{if}k=0. \end {case}} [2] 이것은 다음과 같이 표현될 수도 있다.
f ( k ; p ) = p k ( 1 − p ) 1 − k 위해서 k ∈ { 0 , 1 } {\displaystyle f(k;p)=p^{k}(1-p)^{1-k}\cisco {text{for}k\in\{0,1\}} 또는 로서
f ( k ; p ) = p k + ( 1 − p ) ( 1 − k ) 위해서 k ∈ { 0 , 1 } . {\displaystyle f(k;p)=syslog+(1-p)(1-k)\syslog{text{for}k\in\{0,1\}}. } 베르누이 분포는 n = . displaystyle =1} 분포 . } [3]
첨도는 p displaystyle ,} = 1 2 {displaystyle =1/2} 경우 첨도 가 낮습니다. 즉 -2입니다.
0 p 1 displaystyle leq leq 지수 패밀리를 형성합니다.
랜덤 표본에 기초한 p\style 최대우도 추정치 는 표본 평균입니다.
의미하다 베르누이 랜덤 변수 (\displaystyle ) 다음 과 같습니다.
E ( X ) = p \displaystyle \operatorname {E} \left(X\right)=p} 이는 Pr( X = = p displaystyle \Pr(X=1 p} Pr ( X = ) = q displaystyle \Pr(X=0 변수 displaystyle\ }
E [ X ] = PR ( X = 1 ) ⋅ 1 + PR ( X = 0 ) ⋅ 0 = p ⋅ 1 + q ⋅ 0 = p . \displaystyle \operatorname {E} [X]=\Pr(X=1)\cdot 1+\Pr(X=0)\cdot 0=p\cdot 1+q\cdot 0=p.} [2] 분산 Bernouli 분포 (\displaystyle ) 다음 과 같습니다.
변동 [ X ] = p q = p ( 1 − p ) {\displaystyle \operatorname {Var} [X]=pq=p(1-p)} 우선은
E [ X 2 ] = PR ( X = 1 ) ⋅ 1 2 + PR ( X = 0 ) ⋅ 0 2 = p ⋅ 1 2 + q ⋅ 0 2 = p = E [ X ] {\displaystyle \operatorname {E} [X^{2}]=\Pr(X=1)\Pr(X=0)\cdot 0^{2}=p\cdot 0^{2}+q\cdot 0^{2}=p=\operatorname {E}[X} 여기서부터
변동 [ X ] = E [ X 2 ] − E [ X ] 2 = E [ X ] − E [ X ] 2 = p − p 2 = p ( 1 − p ) = p q {\displaystyle \operatorname {Var} [X]=\operatorname {E}-\operatorname {E}[X]^{2}=\operatorname {E}[X]-\operatorname {E}[X]=p-{p}p=1p=1p} [2] 이 결과를 통해 Bernouli 분포에 대해 분산이 [0 , 1 4 ](\displaystyle [0, 1/4
왜도 왜도는 p q = 2 p q displaystyle ) = scfrac scfrt {pq}} 변수 E X Var display m 변수는 확률 q {\displaystyle {q} sqrt {pq }}} 얻고 q {\ displaystyle frac {p} {\sqrt }}}} 그러면
γ 1 = E [ ( X − E [ X ] 변동 [ X ] ) 3 ] = p ⋅ ( q p q ) 3 + q ⋅ ( − p p q ) 3 = 1 p q 3 ( p q 3 − q p 3 ) = p q p q 3 ( q − p ) = q − p p q . {\displaystyle {{1}\operatorname {E}\left[\left\frac {X-\operatorname {E}[X]}{\sqrt {Var}[X]}}\right)^{3}\light]\ \&=p\cdot \flac {q}{\flac {pq}}\오른쪽)^{3}+q\cdot \flac {p}{\flac {p}}\right}{3}\&=flac {1}{\flac {pq}^3}{p}}}}\left(p^{p}-3}) \&=sublicfrac {pq}{\sublicrt {pq}^{3}}(q-p)\&=sublicfrac {q-p}{\sublicrt {pq}}}}. \end { aligned}} 더 높은 모멘트와 누적률 1 displaystyle ^{k = 1 0 = 0 displaystyle ^{k 0 원시
E [ X k ] = PR ( X = 1 ) ⋅ 1 k + PR ( X = 0 ) ⋅ 0 k = p ⋅ 1 + q ⋅ 0 = p = E [ X ] . {\displaystyle \operatorname {E} [X^{k}]=\Pr(X=1)\Pr(X=0)\cdot 0^{k}=p\cdot 1+q\cdot 0=p=p=\operatorname {E}[X] } 명령어 k .
μ k = ( 1 − p ) ( − p ) k + p ( 1 − p ) k . {\displaystyle \mu _{k}=(1-p)(-p)^{k}+p(1-p)^{k}} 처음 6번의 중요한 순간은
μ 1 = 0 , μ 2 = p ( 1 − p ) , μ 3 = p ( 1 − p ) ( 1 − 2 p ) , μ 4 = p ( 1 − p ) ( 1 − 3 p ( 1 − p ) ) , μ 5 = p ( 1 − p ) ( 1 − 2 p ) ( 1 − 2 p ( 1 − p ) ) , μ 6 = p ( 1 − p ) ( 1 − 5 p ( 1 − p ) ( 1 − p ( 1 − p ) ) ) . {\displaystyle {style}\mu _{1}&=0,\mu _{2}&=p(1-p),\mu _{3}&=p(1-2p),\mu _{4}&=p(1-3p(1-p),\mu _5-p=p}(1-p) \end { aligned}} 중심 모멘트가 높을수록 μ2 ( 디스플레이 \mu {2}) 및 μ3 ( 디스플레이 \mu 3}) 보다
μ 4 = μ 2 ( 1 − 3 μ 2 ) , μ 5 = μ 3 ( 1 − 2 μ 2 ) , μ 6 = μ 2 ( 1 − 5 μ 2 ( 1 − μ 2 ) ) . ({displaystyle {argined}\mu _{4}&={2}(1-3\mu _{2}),\mu _{5}&={3}(1-2\mu _{2}),\mu _{6}&=_{2}(1-5\mu _{2})_{2}_{2}_\mu_{2}). \end { aligned}} 처음 6개의 누적액은
κ 1 = p , κ 2 = μ 2 , κ 3 = μ 3 , κ 4 = μ 2 ( 1 − 6 μ 2 ) , κ 5 = μ 3 ( 1 − 12 μ 2 ) , κ 6 = μ 2 ( 1 − 30 μ 2 ( 1 − 4 μ 2 ) ) . {\displaystyle {style } \kappa _{1} &=p,\kappa _{2} &=\mu _{3} &=,\kappa _{3} &= {2} (1-6\mu _{2}),\\\kappa _5\mu =_{1} & {} \end { aligned}} 관련 분포 X …, n displaystyle X_{1},\dots,X_{n}} 즉, X_ {n}) 랜덤 변수인 경우 성공 확률 p를 갖는 모든 Bernouli 시행은 n과 p 를 갖는 이항 분포에 따라 분배됩니다. k 1 k B [2] ( n displaystyle \sum k }^{n}X_{k}\sim \operatorname {B} n, p )} (표준분포 ) Bernouli 단순히 ( 1 p ){ displaystyle operatorname {B} 1, p) textstyle \mathrm {Bernouli} p) 표기 . } 범주형 분포는 이산값의 수가 일정한 변수에 대한 베르누이 분포의 일반화입니다.베타 분포 는 베르누이 분포 이전의 켤레 입니다.기하학적 분포 는 하나의 성공을 거두는 데 필요한 독립적이고 동일한 베르누이 시행 횟수를 모형화합니다.Y B e r n o l 1 textstyle sim mathrm Bernouli left frac {1 {2 right } 2 1 textstyle 2Y-1} Rademacher 분포 를 가집니다. 「 」를 참조해 주세요. 레퍼런스 ^ 제임스 빅터 유스펜스키: Mathemical Probability 소개 (McGraw-Hill, 뉴욕, 1937, 45페이지)^ a b c d Bertsekas, Dimitri P. (2002). Introduction to Probability . Tsitsiklis, John N. , Τσιτσικλής, Γιάννης Ν. Belmont, Mass.: Athena Scientific. ISBN 188652940X OCLC 51441829 .^ McCullagh, Peter ; Nelder, John (1989). Generalized Linear Models, Second Edition . Boca Raton: Chapman and Hall/CRC. Section 4.2.2. ISBN 0-412-31760-5
추가 정보 Johnson, N. L.; Kotz, S.; Kemp, A. (1993). Univariate Discrete Distributions (2nd ed.). Wiley. ISBN 0-471-54897-9 Peatman, John G. (1963). Introduction to Applied Statistics . New York: Harper & Row. pp. 162–171. 외부 링크 Wikimedia Commons에는 Bernouli
디스크리트 일변량
계속되는 일변량
에서 지원되는 유계 구간 에서 지원되는 반신반의 간격 서포트되고 있다 대체로 실선 지지와 함께 종류가 다른
혼재 일변량
다변량 (공동) 방향성 퇴화 단수 가족들












![{\displaystyle {\begin{cases}0&{\text{if }}p<1/2\\\left[0,1\right]&{\text{if }}p=1/2\\1&{\text{if }}p>1/2\end{cases}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/482cc0f5f8c739e3fe2462d72ee5b9f1f7b5d5a4)











 이 분포의 랜덤 변수인
이 분포의 랜덤 변수인 





 높은 값과 낮은 값의 무한대로 이동하지만 p
높은 값과 낮은 값의 무한대로 이동하지만 p 


 베르누이 분포 랜덤
베르누이 분포 랜덤 ![{\displaystyle \operatorname {E} [X]=\Pr(X=1)\cdot 1+\Pr(X=0)\cdot 0=p\cdot 1+q\cdot 0=p.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5011326253761bfe33bc3d51773a83268b8a56b7)
![\operatorname {Var} [X]=pq=p(1-p)](https://wikimedia.org/api/rest_v1/media/math/render/svg/2d4e26d8a1fdfb90e91a2fafd5fb3841de88f1fb)
![{\displaystyle \operatorname {E} [X^{2}]=\Pr(X=1)\cdot 1^{2}+\Pr(X=0)\cdot 0^{2}=p\cdot 1^{2}+q\cdot 0^{2}=p=\operatorname {E} [X]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1bf32718a7a52087297a46d9ebc177ee0c80df07)
![{\displaystyle \operatorname {Var} [X]=\operatorname {E} [X^{2}]-\operatorname {E} [X]^{2}=\operatorname {E} [X]-\operatorname {E} [X]^{2}=p-p^{2}=p(1-p)=pq}](https://wikimedia.org/api/rest_v1/media/math/render/svg/41972e4aade1430eb47d46a91051f00a583e0c45)
![{\displaystyle [0,1/4]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/604604d2122dc1c25141a841483b889d6832f261)




![{\displaystyle {\begin{aligned}\gamma _{1}&=\operatorname {E} \left[\left({\frac {X-\operatorname {E} [X]}{\sqrt {\operatorname {Var} [X]}}}\right)^{3}\right]\\&=p\cdot \left({\frac {q}{\sqrt {pq}}}\right)^{3}+q\cdot \left(-{\frac {p}{\sqrt {pq}}}\right)^{3}\\&={\frac {1}{{\sqrt {pq}}^{3}}}\left(pq^{3}-qp^{3}\right)\\&={\frac {pq}{{\sqrt {pq}}^{3}}}(q-p)\\&={\frac {q-p}{\sqrt {pq}}}.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2f5c4b867e768adc821f038408b00a6c8bdce2e4)


![{\displaystyle \operatorname {E} [X^{k}]=\Pr(X=1)\cdot 1^{k}+\Pr(X=0)\cdot 0^{k}=p\cdot 1+q\cdot 0=p=\operatorname {E} [X].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5cbafd464e73d482dc6c32d1c4f3eaedd5539952)






 독립적이고 동일한 분포(
독립적이고 동일한 분포(






