확률 이론 과 방향 통계 에서 래핑된 Cauchy 분포 는 단위 원 을 둘러싼 Cauchy 분포 의 "래핑"에서 비롯되는 래핑된 확률 분포 다.카우치 분포는 때때로 로렌츠 분포로 알려져 있으며, 포장된 카우치 분포는 때때로 래핑된 로렌츠 분포로 언급될 수 있다. null
포장된 Cauchy 분포는 종종 회절 패턴을 분석하는 데 사용되는 분광학 분야에서 발견된다(예: Fabry-Pérot interferometer 참조). null
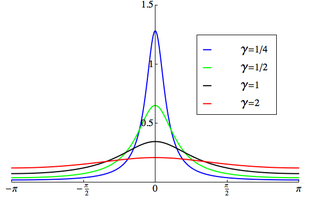
설명 포장된 Cauchy 분포 의 확률밀도함수 는 다음과 같다.[1]
f W C ( θ ; μ , γ ) = ∑ n = − ∞ ∞ γ π ( γ 2 + ( θ − μ + 2 π n ) 2 ) − π < θ < π f_{\displaystyle f_{ WC}(\theta ;\mu ,\gamma )=\sum _{n=-\infit }^{\frac {\\gamma }{\pi (\theta -\mu +2\pi n)^{2}}}}}}\quad -\pi <ta <\pi }}} 여기서 γ {\displaystyle \gamma } μ {\displaystyle \mu } 위의 PDF를 Cauchy 분포 수율의 특성 함수 로 표현 :
f W C ( θ ; μ , γ ) = 1 2 π ∑ n = − ∞ ∞ e i n ( θ − μ ) − n γ = 1 2 π 징징거리다 γ 코쉬 γ − cas ( θ − μ ) f_{\displaystyle f_{ WC}(\theta ;\mu ,\gamma )={\frac {1}{2\pi }}\sum _{n=-\infty }^{\infty }e^{in(\theta -\mu )- n \gamma }={\frac {1}{2\pi }}\,\,{\frac {\sinh \gamma }{\cosh \gamma -\cos(\theta -\mu )}}} PDF는 원형 변수 z = e iθ parameter = e 로도i (μ +iγ )
f W C ( z ; ζ ) = 1 2 π 1 − ζ 2 z − ζ 2 {\displaystyle f_{WC}(z;\zeta )={\frac {1}{2\pi }\\,\,\\frac {1- \zeta ^{2}}:00} 여기서, 아래와 같이 ζ = ⟨z ⟩. null
원형 변수 z e θ {\ displaystyle z=e^{i\theta }}}}}
⟨ z n ⟩ = ∫ Γ e i n θ f W C ( θ ; μ , γ ) d θ = e i n μ − n γ . \displaystyle \langle z^{n}\angle =\int_{\\\\\\\\\\\\\\n_{\\\\\\\\\\\\\\\\}\\\\\{\\\\\\ WC}(\theta ;\mu ,\gamma )\,d\d\theta =e^{in\mu - n \gamma }} 여기서 γ {\ displaystyle \Gamma \,} 2 π [\displaystyle 2\pi } . z 의 평균 값이다.
⟨ z ⟩ = e i μ − γ {\displaystyle \langle z\angle =e^{i\mu -\mu}}}} 평균각은
⟨ θ ⟩ = A r g ⟨ z ⟩ = μ \displaystyle \langle \theta \angle =\mathrm {Arg} \langle z\angle =\mu } 평균 결과물의 길이는
R = ⟨ z ⟩ = e − γ {\displaystyle R=\langle z\angle =e^{-\gamma }}} 1 - R 의 원형 분산을 산출한다.
모수 추정 포장된 Cauchy 일련 의 N 측정 z e in {\ displaystyle z_{n}=e^{i\theta_{n}} 영상 시리즈 '{\ displaystyle overline{z}}
z ¯ = 1 N ∑ n = 1 N z n {\displaystyle {\overline{z}={\frac {1}{{N}\sum _{n=1}^{N}z_{n}}}} 그리고 그 기대 가치는 단지 첫 순간일 것이다.
⟨ z ¯ ⟩ = e i μ − γ {\displaystyle \langle {\langle{z}\rangle =e^{i\mu -\cHB}}} 즉, z {\ displaystyle overline{z}} 피크 위치 μ {\ displaystyle \mu } ( π π ){\displaystyle [-\pi ,\pi )} (z ){\displaystystyle({\overline{z})} μ .
z displaystyle z_{n ( R {\ displaystyle {\overline{R}^{2}}
R ¯ 2 = z ¯ z ∗ ¯ = ( 1 N ∑ n = 1 N cas θ n ) 2 + ( 1 N ∑ n = 1 N 죄를 짓다 θ n ) 2 {\displaystyle {\overline {R}}^{2}={\overline {z}}\,{\overline {z^{*}}}=\left({\frac {1}{N}}\sum _{n=1}^{N}\cos \theta _{n}\right)^{2}+\left({\frac {1}{N}}\sum _{n=1}^{N}\sin \theta _{n}\right)^{2}} 그리고 그 기대치는
⟨ R ¯ 2 ⟩ = 1 N + N − 1 N e − 2 γ . {\displaystyle \langle {\overline{R}^{2}\angle ={\frac {1}{{N}+{\frac{{N-1}{N}e^{-2\gamma}}}}} 즉, 통계는
R e 2 = N N − 1 ( R ¯ 2 − 1 N ) {\displaystyle R_{e}^{2}={\frac {N}{{N:1}}\좌측({\overline{R}}^{{\frac {1}{N}\우측)}} e 2 γ {\ displaystyle ^{-2\gamma }}, ln ( 1 e 2 {\displaystyle \ln(1 / R_{e}^{2}}/2}/} displaysty \gamma } .
엔트로피 포장된 Cauchy 분포의 정보 엔트로피 는 다음과 같이 정의된다.[1]
H = − ∫ Γ f W C ( θ ; μ , γ ) ln ( f W C ( θ ; μ , γ ) ) d θ {\displaystyle H=--\int _{\Gamma }f_{ WC}(\theta ;\mu ,\gamma )\,\ln(f_{ WC}(\theta ;\mu ,\gamma )\,d\theta } 여기서 γ {\displaystyle \Gamma} 2π {\displaystyle 2\pi } . θ {\ displaystyle \teta \,}:
ln ( f W C ( θ ; μ , γ ) ) = c 0 + 2 ∑ m = 1 ∞ c m cas ( m θ ) {\displaystyle \ln(f_{ WC}(\theta ;\mu ,\gamma )=c_{0}+2\sum _{m=1}^{\inful }c_{m}\cos(m\theta )} 어디에
c m = 1 2 π ∫ Γ ln ( 징징거리다 γ 2 π ( 코쉬 γ − cas θ ) ) cas ( m θ ) d θ {\displaystyle c_{m}={\frac {1}{2\pi}\int_{\\\\\\ln \좌({\frac {\sinh \sinh \gamma }}{2\pi(\cos \gamma -\cos \ta )}\cos(m\,d\ta }). 산출되는 결과:
c 0 = ln ( 1 − e − 2 γ 2 π ) {\displaystyle c_{0}=\ln \left\frac {1-e^{-2\pi }}{2\pi }\오른쪽)} (c.f. Gradshteyn 및 Ryzhik [2]
c m = e − m γ m f o r m > 0 {\displaystyle c_{m}={\frac {e^{-m\filency }}{m}}}{{m}}\qquad \matrm {for}\m>0} (c.f. Gradshteyn과 Ryzhik [2] 적분 왼쪽의 래핑된 Cauchy 분포에 대한 특성 함수 표현은 다음과 같다.
f W C ( θ ; μ , γ ) = 1 2 π ( 1 + 2 ∑ n = 1 ∞ ϕ n cas ( n θ ) ) f_{\displaystyle f_{ WC}(\theta ;\mu ,\gamma )={\frac {1}{2\pi }}\좌측(1+2\sum _{n=1}^{\n}\phi _{n}\cos(n\theta )\right)}} 여기서 ϕn e n γ {\ displaystyle \phi _{n}=e^{- \gamma }}}}}.
H = − c 0 − 2 ∑ m = 1 ∞ ϕ m c m = − ln ( 1 − e − 2 γ 2 π ) − 2 ∑ m = 1 ∞ e − 2 n γ n {\displaystyle H=-c_{0}-2\sum _{m=1}^{\infty }\phi _{m}c_{m}=-\ln \left({\frac {1-e^{-2\gamma }}{2\pi }}\right)-2\sum _{m=1}^{\infty }{\frac {e^{-2n\gamma }}{n}}} 시리즈는 1 e 2 γ ) 테일러 확장 같이 폐쇄적인 형태 로 작성될 수 있다.
H = ln ( 2 π ( 1 − e − 2 γ ) ) {\displaystyle H=\ln(2\pi(1-e^{-2\gamma })\,} 원형 카우치 분포 X 가 중위수 μ와 척도 모수 μ로 분포된 Cauchy일 경우 복합 변수
Z = X − i X + i {\displaystyle Z={\frac {X-i}{X+i}}} 단위 계수를 가지며 밀도와 함께 단위 원에 분포한다.[3]
f C C ( θ , μ , γ ) = 1 2 π 1 − ζ 2 e i θ − ζ 2 {\displaystyle f_{CC}(\theta ,\mu ,\gamma )={\frac {1}{2\pi }}{\frac {1- \zeta ^{2}}:{ e^{i\theta }-\zeta ^{2}}: 어디에
ζ = ψ − i ψ + i {\displaystyle \zeta ={\frac {\fract -i}{\reason +i}} 및 ψ는 x 에 대한 관련 선형 Cauchy 분포의 두 가지 매개변수를 복합 숫자로 표현한다.
ψ = μ + i γ \displaystyle \cHB =\mu +i\cHB \,} 원형 Cauchy 분포는 z 와 ζ의 포장된WC Cauchy 분포와 동일한 기능 형태를 가지고 있음을 알 수 있다(즉, f(z,,)). 원형 Cauchy 분포는 재결정된 포장 Cauchy 분포:
f C C ( θ , m , γ ) = f W C ( e i θ , m + i γ − i m + i γ + i ) {\displaystyle f_{CC}(\theta ,m,\gamma )=f_{{ WC}\왼쪽(e^{i\theta },\,{\frac {m+i\gamma -i}{m+i\gamma +i}\오른쪽)} The distribution f C C ( θ ; μ , γ ) {\displaystyle f_{CC}(\theta ;\mu ,\gamma )} [3] [4] [3] McCullagh's parametrization of the Cauchy distributions and Poisson kernel for related concepts.) null
복잡한 형태로 표현된 원형 코치 분포는 모든 주문의 모멘트가 유한하다.
E [ Z n ] = ζ n , E [ Z ¯ n ] = ζ ¯ n {\displaystyle \operatorname {E}[Z^{n}]=\zeta ^{n},\quad \operatorname {E}[{\bar {Z}^{n}]={\bar {\zeta }^{n}}}}}}}}}} 정수 n ≥ 1의 경우.φ < 1의 경우, 변환
U ( z , ϕ ) = z − ϕ 1 − ϕ ¯ z {\displaystyle U(z,\phi )={\frac {z-\phi }{1-{\bar{\pa{\phi }}}}} 단위 디스크에서 홀로모르픽이며 , 변환 변수 U(Z , φ)는 파라미터 U(ζ, φ)와 함께 복합 Cauchy로 분포한다. null
표본 z 1 , ..., z 의n 크기 가 n > 2인 경우 최대우도 방정식
n − 1 U ( z , ζ ^ ) = n − 1 ∑ U ( z j , ζ ^ ) = 0 {\displaystyle n^{-1}U\왼쪽(z,{\hat {\zeta }}\오른쪽)=n^{-1}\sum U\left(z_{j},{\hat {\zeta }}\오른쪽)=0} 간단한 고정 포인트 반복으로 해결할 수 있다.
ζ ( r + 1 ) = U ( n − 1 U ( z , ζ ( r ) ) , − ζ ( r ) ) {\displaystyle \zeta ^{(r+1)}= U\왼쪽(n^{-1}U(z,\제타 ^{(r)}),\,-\제타 ^{(r)}\,} ζ(0) = 0으로 시작한다. 우도 값의 순서는 감소하지 않으며, 세 개 이상의 구별되는 값을 포함하는 표본에 대해 해법이 고유하다.[5] null
실제 Cauchy 샘플의 중위수(μ^ {\ displaystyle {\hat {\\mu}}}) γ )
μ ^ ± i γ ^ = i 1 + ζ ^ 1 − ζ ^ . {\displaystyle{\hat{\mu}}\pm i{\hat{\mu}}}}=i{\frac {1+{\hat{\zeta}}}{1-{\hat{\zeta}}}}}}}. } n ≤ 4의 경우 닫힌 형식 표현은 ζ ^ {\ displaystyle {\hat {\\zeta }} . [6] 단위 디스크의 t 에서 최대 우도 추정기의 밀도는 반드시 다음과 같은 형식이다.
1 4 π p n ( χ ( t , ζ ) ) ( 1 − t 2 ) 2 , {\displaystyle {\frac {1}{4\pi }{\frac {p_{n}(\chi(t,\zeta )}{{2}^{2}}}}} 어디에
χ t ζ ζ 4 1 t {\ displaystyle \chi (t,\zeta )={\frac t-\\zeta 2}}:{4(1- })(1- \zeta }}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}). p 와3 p 에4 대한 공식을 구할 수 있다.[7] null
참고 항목 참조 ^ a b Mardia, Kantilal ; Jupp, Peter E. (1999). Directional Statistics . Wiley. ISBN 978-0-471-95333-3 ^ a b Gradshteyn, Izrail Solomonovich ; Ryzhik, Iosif Moiseevich ; Geronimus, Yuri Veniaminovich ; Tseytlin, Michail Yulyevich (February 2007). Jeffrey, Alan; Zwillinger, Daniel (eds.). Table of Integrals, Series, and Products Academic Press, Inc. ISBN 0-12-373637-4 LCCN 2010481177 .^ a b c McCullagh, Peter (June 1992). "Conditional inference and Cauchy models" (PDF) . Biometrika . 79 (2): 247–259. doi :10.1093/biomet/79.2.247 . Retrieved 26 January 2016 . ^ K.V. Mardia (1972). Statistics of Directional Data . Academic Press . [페이지 필요 ^ J. Copas (1975). "On the unimodality of the likelihood function for the Cauchy distribution". Biometrika . 62 (3): 701–704. doi :10.1093/biomet/62.3.701 . ^ Ferguson, Thomas S. (1978). "Maximum Likelihood Estimates of the Parameters of the Cauchy Distribution for Samples of Size 3 and 4". Journal of the American Statistical Association . 73 (361): 211–213. doi :10.1080/01621459.1978.10480031 . JSTOR 2286549 .^ P. McCullagh (1996). "Möbius transformation and Cauchy parameter estimation". Annals of Statistics . 24 (2): 786–808. JSTOR 2242674 .
이산형 일변도의
연속 일변도의
의 지지를 받고 있는. 경계 간격 의 지지를 받고 있는. 반무한 간격을 두고 지지의 대체로 실선 지지하여 누구의 타입이 다른가.
혼합 일변도의
다변량 (공동) 방향 퇴보하다 그리고 단수 가족들










 (는) 스케일 팩터,
(는) 스케일 팩터, 






















 (는) 길이
(는) 길이 















![{\displaystyle \operatorname {E} [Z^{n}]=\zeta ^{n},\quad \operatorname {E} [{\bar {Z}}^{n}]={\bar {\zeta }}^{n}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/25350520804357a0441a4b661dd4141f49daa1de)