바이올린 음향학

다음에 대한 시리즈 일부
피들 앤 바이올린
바이올린 음향학
피들러
바이올린의 역사
루티어스
음악 스타일
바이올린 제작 및 유지 보수
바이올린 기법
바이올린 구성
바이올린 계열
바이올리니스트
v t

바이올린 음향학은 바이올린의 여러 부분들 간의 상호작용의 결과로서 바이올린의 소리가 어떻게 만들어지는가에 관한 음악적 음향학 내의 연구 영역이다.이러한 음향적 특성은 비올라와 같은 바이올린 계열의 다른 멤버들과 비슷하다.

진동하는 현의 에너지는 다리를 통해 바이올린의 몸체로 전달되어 소리가 주변 공기로 발산될 수 있게 한다.바이올린 줄의 양쪽 끝이 효과적으로 정지해 있어 서 있는 파도의 생성을 가능하게 한다.동시에 생성되는 다양한 고조파들은 음색에 각각 영향을 미치지만, 기본 주파수만 들린다.노트의 주파수는 문자열의 장력을 증가시키거나 문자열의 길이 또는 질량을 감소시킴으로써 상승될 수 있다.음조에 존재하는 고조파 수를 줄일 수 있으며, 예를 들어 를 사용하여 문자열 길이를 단축할 수 있다.각각의 현악기의 음색과 음색은 같지 않고, 사용되는 소재는 음질과 발음의 용이성에 영향을 미친다.바이올린 현은 원래 고양이굿으로 만들어졌지만 지금은 보통 강철이나 합성 물질로 만들어진다.대부분의 끈은 과도한 두께를 피하면서 질량을 증가시키기 위해 금속으로 감겨 있다.

활쏘기 중에는 끈의 장력이 돌아오게 할 때까지 끈을 당기고, 그 후에 활로부터 다시 에너지를 받는다.바이올린 연주자는 활의 속도, 사용하는 힘, 현상의 활의 위치, 현에 닿는 머리카락의 양 등을 조절할 수 있다.다리에서 작용하는 정적 힘, 즉 다리에서 작용하는 동적인 힘은 다리에서 작용하여 앞뒤로 흔들리게 하여 현에서 발생하는 진동이 전달되게 하는 큰 힘이다.바이올린의 몸은 현악기의 장력에 저항할 만큼 강하지만, 또한 적절하게 진동할 수 있을 만큼 가볍다.옆구리에 갈비뼈가 있는 아치형 목판 2개로 제작되었으며, 다리 양쪽에 f홀이 2개 있다.주변의 공기에 현악의 진동을 결합하는 사운드박스 역할을 하는데, 신체의 각기 다른 부분이 연주되는 음에 모두 다르게 반응하며, 모든 부분(내부에 숨겨져 있는 베이스바 포함)이 바이올린의 특색 있는 소리에 기여한다.끈을 숙일 때와 비교하면 뽑은 끈이 더 빨리 축축해진다.

바이올린 계열의 다른 멤버들은 다르지만 비슷한 시간대를 가지고 있다.비올라와 더블 베이스의 특성은 열린 현악기의 음정에 대응하는 최적의 치수를 가짐으로써 불리하게 영향을 받지 않는 첼로(비올론첼로)와는 대조적으로 오케스트라에서 솔로 악기로 덜 쓰이게 하는 데 기여한다.

역사적 배경

진동현의 성질은 고대 이오니아 그리스 철학자 피타고라스에 의해 연구되었는데, 그는 진동하는 현들의 길이와 그들이 내는 자음 소리 사이의 관계를 최초로 관찰한 것으로 생각된다.^[1][2]16세기에 이탈리아의 루테니스트 겸 작곡가 빈첸초 갈릴레이는 루트 현을 이용하여 늘어진 현을 체계적으로 시험하고 측정하는 것을 개척하였다.그는 간격의 비율이 줄의 길이에 비례하지만, 장력의 제곱근에 정비례한다는 것을 발견했다.그의 아들 갈릴레오 갈릴레이는 <두 개의 새로운 과학> (1638)에서 빈도, 길이, 긴장, 지름의 관계를 발표했다.^[3][4]초창기 바이올린 제작자들은 비록 매우 숙련된 기술이었지만 현악기의 음향에 대한 과학적인 지식은 전혀 발전시키지 못했다.^[5]

19세기 동안, 굽은 끈에서 나오는 다화음 소리는 프랑스 물리학자 펠릭스 사바트에 의해 처음으로 자세히 연구되었다.^[1][6]독일의 물리학자 헤르만 폰 헬름홀츠는 뽑은 끈의 물리학을 조사하여,^[7] 굽은 끈이 일정한 속도로 정점이 움직이는 삼각형 모양으로 이동한다는 것을 보여주었다.^[8]

바이올린의 진동 방식은 1930년대 독일에서 헤르만 백하우스와 그의 제자 헤르만 마이넬에 의해 연구되었는데, 그의 연구에는 바이올린의 주파수 응답에 대한 조사가 포함되어 있었다.비올린의 음향 특성에 대한 이해는 F.A.에 의해 개발되었다.1930년대와 40년대 선더스, 손더스와 그의 조수 칼린 허친스, 그리고 베르너 로테모서, 위르겐 마이어, 시몬 사코니에 의해 그 후 수십 년 동안 계속되었던 작품.^[9]허친스의 작품은 1960년대 이후 20년 동안 바이올린 음향 분야를 지배했으며, 음향학자 조지 비신저에 따르면 "바이올린의 음향학을 이해하는 데 매우 중요한" 기술인 모달 분석의 사용으로 대체되었다.^[10]

줄들

바이올린의 열린 현은 다리에서 바이올린 너트까지의 길이는 같지만 단위 길이마다 질량이 달라 음조가 다양하다.^[11][12]바이올린 현의 양쪽 끝은 진동할 때 기본적으로 정지되어 있어 두 개의 사인파가 서로 지나쳐 이동하는 중첩에 의해 발생하는 입자파(유전자파)가 생성될 수 있다.^[13][14]

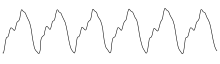
진동하는 문자열은 단일 주파수를 생성하지 않는다.그 소리는 음색이라고 알려진 악기에 개별적인 음질을 가지도록 하는 기본적인 주파수와 그 오버톤의 조합으로 설명될 수 있다.^[16]음색은 톤으로 존재하는 오버톤(조화학)의 수와 비교 강도에 의해 영향을 받는다.동시에 생성되더라도 진폭이 가장 큰 기본 주파수만 들린다.^[17]바이올린은 인간의 청각 상한을 넘어서는 주파수를 만들어 낸다는 점에서 특이하다.^[18]

그 결과 발생하는 소리의 기본 주파수와 오버톤은 스트링의 재료 특성인 장력, 길이,^[3] 질량뿐만 아니라 댐핑 효과와^[12] 스트링의 강성에 따라 달라진다.^[19]바이올린 연주자들은 왼손 손가락 끝으로 줄을 멈추며 연주 길이를 줄인다.대부분 바이올린의 핑거보드에 기대어 끈을 멈추는 경우가 많으나, 손가락 끝으로 가볍게 만지는 끈이면 충분하여 인위적인 하모닉이 만들어지는 경우도 있다.끈을 더 짧은 길이로 멈추면 피치가 올라가는 효과가 있으며, 핑거보드가 풀렸기 때문에 끈 길이에 어떤 주파수도 가능하다.^[14][20]손가락이 존재하는 고조파 수를 줄이기 위해 작용하기 때문에 '열린' 현에서 만든 음과 왼손 손가락을 현에 올려서 만든 음의 차이가 있다.^[21]게다가 네 줄의 음색과 음색은 같지 않다.^[22]

특정 간격의 운지 위치는 문자열의 진동 부분 길이에 따라 달라진다.바이올린의 경우, 열린 문자열의 전체 톤 간격이 대략1+1⁄4 인치(31.8 mm)—줄의 다른 쪽 끝에서, 같은 간격은 이 크기의 3분의 1 미만이다.비올라, 첼로(바이올론첼로), 더블 베이스의 경우 등가수가 연속적으로 더 크다.^[23]

바이올리니스트가 현(이탈리아 피치카토)을 뽑도록 지시하면, 만들어진 소리는 빠르게 사라지거나, 축축해진다: 축축한 것은 크기가 작기 때문에 바이올린 계열의 다른 멤버들에 비해 바이올린에 비해 더 두드러지며, 열린 현을 뽑으면 효과가 더 크다.^[24]피치카토 음을 내는 동안, 쇠퇴하고 있는 높은 고조파는 낮은 고조파보다 더 빨리 감소한다.^[25]

바이올린에 대한 바이브라토 효과는 팔, 손, 손목의 근육이 음의 음을 진동시킬 때 달성된다.^[26]일반적인 비브라토는 6Hz의 주파수를 가지고 있고 음조가 1/4 톤만큼 변화하게 한다.^[27]

텐션

늘어난 문자열의 장력(T)은 다음과 같이 주어진다.

${\displaystyle T=ES{\frac {{\Delta }L}{L}}}$

여기서 E는 영의 계량형, S는 단면형, ΔL은 연장형, L은 끈 길이형이다.진폭이 큰 진동의 경우 장력이 일정하지 않다.^[28]문자열의 장력을 증가시키면 주파수 노트가 더 높아진다:^[12] 장력의 제곱근에 정비례하는 진동 문자열의 주파수는 다음과 같은 방정식으로 나타낼 수 있다.^[3]

${\displaystyle f={1 \over 2}{\sqrt {\frac {T}{LM}}}$

여기서 f는 문자열의 기본 주파수, F는 장력, M은 질량이다.^[14]

바이올린의 현은 조절 가능한 튜닝 페그와 (일부 현으로) 더 미세한 튜너에 부착되어 있다.각 스트링의 튜닝은 원하는 피치에 도달할 때까지 느슨하게 하거나 조임으로써 이루어진다.^[29]바이올린 현의 장력은 8.7파운드에서 18.7파운드힘(39~83N)이다.^[30]

길이

속도 v로 이동하는 모든 파동, 한 시간 T에서 거리 λ을 이동하는 경우,

v= λ T ${\$ }$\over T$

주파수 f의 경우

${\displaystyle f={\frac {1}{T}}={\frac {v}{\lambda }}}$

바이올린에서 진동하는 현악의 기본 주파수를 위해 현악 길이는1/2 ,, 여기서 λ은 관련 파장이다, 그래서

${\$$L}}$ .^[14]

자재

현악 재료는 오버론 혼합에 영향을 미치고 음질에 영향을 미친다.^[31]반응과 관절의 용이성 또한 끈 재료의 선택에 의해 영향을 받는다.^[31]

바이올린 현은 원래 캣굿으로 만들어졌는데, 비록 다른 재료로 만든 현은 만드는 데 비용이 적게 들고 온도에 민감하지 않지만,^[32] 여전히 사용 가능하고 일부 전문 음악가들이 사용한다.^[31]현대의 현은 강철코어, 좌초된 강철코어 또는 펄론 같은 합성 물질로 만들어진다.^[31]바이올린 현(대부분의 E 스트링 제외)은 그 밀도와 비용을 위해 선택된 금속으로 나선형으로 감겨 있다.끈의 구불구불한 감촉은 끈의 질량을 증가시키고, 톤(생성된 소리의 질)을 변화시켜 더 밝고 따뜻한 소리가 나도록 하며, 반응에 영향을 준다.^[33]강줄은 강철이 쉽게 뾰족한 모양으로 변형되지 않고 그만큼 많은 고주파 고조파를 생성하지 않기 때문에 내장으로 만들어진 것보다 더 둔하게 들린다.^[25]

다리

사운드보드가 가장 높은 바이올린 몸체 상단에 놓인 다리는 현악기의 한 쪽 끝을 지탱한다.^[34]다리에서 작용하는 정적인 힘은 크며, 끈의 장력에 따라 달라진다:^[35] 50 lb_f(220 N)의 끈의 장력으로 인해_f 20 lb(89 N)가 다리를 통과한다.^[36]다리를 가로지르는 끈에 의해 만들어진 'break' 각도는 하방력에 영향을 미치며, 일반적으로 수평에 13~15°^[37]

그 다리는 현악기에서 바이올린 몸체로 에너지를 전달한다.^[35]첫 번째 근사치로서, 그것은 노드의 역할을 하는 것으로 간주된다. 그렇지 않으면 음을 재생할 때 기본 주파수와 관련 고조파들은 지속되지 않을 것이다. 그러나 그 동작은 에너지가 문자열에서 몸으로 어떻게 전달되는지, 그리고 문자열 자체의 행동을 결정하는 데 중요하다.^[13]그것의 움직임의 한 요소는 끈과 함께 움직일 때 좌우로 흔드는 것이다.^[38]그것은 소리의 음색을 필터링하고 형상화하는 기계적 필터 또는 질량과 "스프링"의 배열로 유용하게 볼 수 있다.^[39]이 다리는 약 3000Hz로 가수의 조형물을 강조하기 위해 만들어졌다.^[40]

1980년대 초부터 고품질 바이올린이 교량의 공명 특성에 기인하는 효과 때문에 2-3kHz의 주파수에서 더 잘 진동한 것으로 알려져 왔으며, 현재는 '교량 힐' 효과로 언급되고 있다.^[39]

교량 위에 클립을 장착하여 기기 본체에 전달되는 에너지의 일부를 흡수함으로써 돌연변이를 달성한다.음의 강도의 감소와 다른 음색이 모두 생산되기 때문에 음악가들에게는 음소거의 사용이 더 조용히 연주하고 싶을 때 사용하는 주요 방법으로 보이지 않는다.^[41]

활

바이올린은 절하는 과정에 의해 음조를 유지할 수 있는데, 마찰로 인해 현악의 장력에 의해 야기되는 반대 세력이 현악의 뒤로 미끄러질 정도로 커질 때까지 현악이 활에 의해 옆으로 당겨지게 된다.끈은 평형 위치로 돌아온 다음 이 위치를 지나 옆으로 움직이며, 그 후 움직이는 활로부터 다시 에너지를 받는다.^[42]활은 막대기의 끝 사이에 늘어뜨린 평행한 말털의 납작한 리본으로 구성되는데, 일반적으로는 펄남부코 나무로 만들어지는데, 그 특유의 탄성성이 있기 때문에 사용된다.^[26][43]머리카락에 로진을 입혀 끈과 직각으로 움직이면서 조절된 '스틱-슬립 진동'을 제공한다.^[44]2004년, 케임브리지 대학의 짐 우드하우스와 폴 갈루조는 활로 끈의 움직임을 "합리적으로 잘 이해되는 유일한 스틱 슬립 진동"^[45]이라고 묘사했다.

현대 활의 길이, 무게, 균형점을 표준화한다.선수들은 이러한 매개변수뿐만 아니라 강직성과 관성 모멘트에 기초하여 활에서 활까지 소리와 취급의 변화를 알아차릴 수 있다.바이올리니스트나 비올리스트는 지렛대가 더 크기 때문에 자연스럽게 현을 가로질러 활을 밀 때 더 크게 연주하는 경향이 있다('업보우').^[46]가장 조용할 때, 이 악기는 0.0000038와트의 힘을 가지고 있는데, 작은 오케스트라의 경우 0.09와트의 힘을 가지고 있다: 이 악기의 음압 수준은 25 - 30dB이다.^[47]

활의 물리학

바이올린 연주자들은 일반적으로 다리와 손가락판 사이에서 절하며, 활을 현에 수직으로 유지하도록 훈련받는다.고개를 숙일 때 선수의 즉각적인 통제 아래 가장 두드러지는 세 가지 요인은 활의 속도, 힘, 그리고 머리카락이 끈을 가로지르는 장소('소리 나는 지점')이다. 길이가 짧은 진동 스트링은 소리 나는 지점을 다리 가까이 위치시킨다.또한 선수는 보 스틱을 다리로부터 약간 더 멀리 기울임으로써 끈과 접촉하는 머리카락의 양을 변경할 수 있다.^[48]줄이 구부러질수록 꼬여 파형에 '리플'이 추가되는데, 이는 스트링이 더 크면 이 효과가 늘어난다는 것이다.^[49]

핑거보드 바로 위에서 절을 하면(이탈리아 술라 맛에라) 20세기 미국 작곡가 겸 작가 월터 피스톤이 설명한 "매우 부드럽고 유동적인 품질"로, 끈이 더 큰 진폭으로 진동하도록 강요되어 야기된다.^[50]Sul ponticello - 활을 다리 가까이에서 연주할 때, 반대되는 기법이며, 피스톤이 "유리하고 금속적인" 소리라고 설명한 것을 생산하는데, 이는 일반적으로 들리지 않는 고조파들이 음색에 영향을 줄 수 있기 때문이다.^[51]

헬름홀츠 운동

바이올린의 물리학에 대한 현대적인 연구는 헬름홀츠로부터 시작되었는데, 그는 고개를 숙일 때의 끈의 모양이 일정한 속도로 줄의 주요 부분을 따라 움직이는 꼭지점('헬름홀츠 코너'로 알려져 있다)과 함께 'V'의 형태임을 보여주었다.여기서 활과 끈의 마찰의 성질이 변하며, 모서리 부분이 움직이는 방향에 따라 미끄러지거나 고착되는 현상이 발생한다.^[44][52]생성된 파동은 헬름홀츠 모서리 부분이 뽑은 줄을 따라 움직이면서 회전하는 평면이 핑거보드에 평행하지 않을 때 감소된 에너지가 브리지로 전달되는 원인이 된다.활이 활 털에 비스듬히 있는 모든 진동(예: 초보 선수에 의해 고르지 않은 활 압력이 가해질 경우)을 감소시키는 효과가 있기 때문에, 끈을 구부렸을 때 더 적은 에너지가 공급된다.^[25]

인도의 물리학자 C. V. 라만은 1918년 자신의 연구 결과를 발표하면서 가장 먼저 활로 끈의 역학을 기술하는 정확한 모델을 얻었다.그의 모델은 헬름홀츠(요즘 헬름홀츠 모션으로 알려져 있다)가 설명한 동작을 예측할 수 있었지만, 진동하는 스트링이 완벽하게 유연하다고 가정해야 했고,^[13][53] 활 속도에 의존하는 반사계수로 파동이 반사되면 에너지를 잃었다.라만의 모델은 후에 수학자 조셉 켈러와 F.G. 프리드랜더에 의해 개발되었다.^[53]

헬름홀츠와 라만은 날카로운 코너링 파동을 포함하는 모델을 제작했다: 부드러운 코너에 대한 연구는 1968년에 크레머와 라자루스에 의해 수행되었다. 그는 정상적인 활력이 가해져야만 상당한 평활이 일어난다는 것을 보여주었다(즉, 고조파 수가 적다).이 이론은 1970년대와 1980년대에 더욱 발전하여 활의 속도의 복잡한 관계 행동과 존재하는 마찰력을 바탕으로 디지털 도파관 모델을 제작하였다.^[54]모델은 헬름홀츠 운동(더 큰 힘에 의해 발생하는 운동의 '플랫텐딩' 효과를 포함)을 시뮬레이션하는 데 성공했으며, 이후 스트링의 휨강성, 비틀림 운동, 그리고 신체진동의 끈에 미치는 영향과 활털의 왜곡 등을 고려하여 확장되었다.^[55]그러나 모델은 로진으로 인한 마찰계수는 활의 속도에 의해서만 결정된다고 가정하고, 다른 변수에 의존할 수 있는 가능성을 무시했다.2000년대 초반까지 활의 로신에 마찰로 공급되는 에너지, 활의 작용에 대한 선수의 투입 등 변수의 중요성이 인식되어 개선된 모델이 필요하다는 것을 보여주었다.^[56]

본문입니다.

바이올린의 몸체는 타원형이고 속이 비어 있으며, 다리 양쪽에 사운드홀이라고 불리는 f자 모양의 구멍이 두 개 있다.^[57]몸은 끈에서 나오는 긴장을 지탱할 수 있을 만큼 튼튼해야 하지만, 또한 제대로 진동할 수 있을 만큼 가볍고 얇아야 한다.^[36]그것은 배와 등판으로 알려진 두 개의 아치형 목판으로 만들어졌으며, 옆면은 가늘고 구부러진 갈비뼈에 의해 형성된다.끈의 진동을 주위 공기에 결합시켜 소리가 나게 하는 사운드박스 역할을 한다.이에 비해 거의 공기가 통하지 않는 현은 침묵하고 있다.^[16][58]

값비싼 바이올린의 존재는 값싼 바이올린의 존재에 비해 물리적 행동의 작은 차이점에 달려 있다.^[59]그들의 구조, 특히 배와 뒷판의 아치는 악기의 전반적인 음질에 지대한 영향을 미치며,^[60] 그 많은 다른 공명 주파수는 목조 구조물의 성질에 의해 발생한다.비록 고품질의 악기에서는 낮은 주파수 범위에 걸쳐 균일한 반응이 나오지만 칼린 허친스가 '목재 공명'^[1]이라고 표현한 것을 나타내면서 연주되는 노트에 각기 다른 부분이 모두 다르게 반응한다.^[20]끈의 반응은 진동 자기장에 놓였을 때 금속 줄을 통해 전류에 의해 생성되는 움직임을 감지하여 테스트할 수 있다.^[13]그러한 시험에서 최적의 '주목공명'(주파수가 가장 낮은 목재공명)은 392~494Hz 사이에서 발생하며, 이는₄ A 이하와 그 이상에 해당하는 톤에 해당한다.^[61]

늑골은 가장자리에 라이닝 스트립으로 보강되어 플레이트가 부착된 곳에 접착면을 추가로 제공한다.^[36]나무 구조물은 바이올린의 특징적인 소리에 기여하는 재료를 사용하여 채워지고, 접착되고, 니스를 칠한다.^[62]몸 안의 공기는 또한 바이올린의 공명하는 성질을 향상시키는 작용을 하는데, 이는 밀폐된 공기의 부피와 f홀의 크기에 영향을 받는다.^[63]

배와 뒷판은 특정 주파수에서 진동을 강요할 때 진동 모드를 표시할 수 있다.존재하는 여러 가지 모드는 바이올린 모양의 판 표면에 뿌려진 미세먼지나 모래를 이용해 찾을 수 있다.모드가 발견되면 (스테이션) 노드에서 먼지가 누적된다. 플레이트의 다른 곳에서 진동이 일어나면 먼지가 나타나지 않는다.생산된 문양은 이 실험 기법을 처음 개발한 독일의 물리학자 에른스트 클라드니의 이름을 따서 붙여졌다.^[16]

현대의 연구는 측정할 바이올린 표면의 움직임의 분석을 가능하게 하는 홀로그래피 간섭측정법, 1960년대 과학자들에 의해 처음 개발된 방법, 바이올린의 이산부분을 정확한 시뮬레이션을 구성하기 위해 연구하는 유한요소법 등 정교한 기법을 사용해 왔다.영국의 물리학자 버나드 리처드슨은 이런 기법을 이용해 가상 바이올린을 만들었다.^[16]이스트캐롤라이나 대학에서는 미국의 음향학자 조지 비싱어가 레이저 기술을 이용해 주파수 응답을 만들어내 바이올린 진동의 효율과 감쇠가 주파수에 어떻게 의존하는지를 판단하는 데 도움을 주었다.^[16]모달 분석이라고 알려진 또 다른 기법은 새로운 기기와 오래된 기구를 비교하기 위해 오래된 기구의 '톤컬 카피'를 사용하는 것이다.새로운 바이올린을 가장 작은 방법으로 바꾸는 효과는 구식 모델의 톤 반응을 복제하는 것을 목적으로 하여 확인할 수 있다.^[64]

베이스 바와 사운드 포스트

베이스 바와 사운드 포스트는 모두 바이올린의 뒷면에 소리를 전달하는 데 도움이 되며, 사운드 포스트도 구조를 지탱하는 역할을 한다.베이스 바는 상단 하단에 접착되어 있고, 사운드 포스트는 마찰에 의해 제자리에 고정되어 있다.베이스 바는 구조를 강화하기 위해 발명되었으며, 다리 한쪽 발 바로 아래에 위치해 있다.^[36][65]다리 발치 근처, 그러나 바로 아래는 아닌 소리 기둥이다.^[66]

교량이 현으로부터 에너지를 받으면, 그것은 흔들리게 되는데, 사운드 포스트는 피벗 역할을 하고 베이스 바는 지렛대의 결과로서 플레이트와 함께 움직인다.이러한 행동은 바이올린 음질을 향상시킨다: 사운드 포스트의 위치를 조정하거나 그것에 작용하는 힘이 바뀌면 바이올린이 만들어내는 소리에 악영향을 줄 수 있다.^[36]그들은 함께 바이올린 몸체의 모양을 비대칭적으로 만들어 서로 다른 진동이 일어나게 하고 음색을 더욱 복잡하게 만든다.^[16]

신체 구조의 정상적인 모드 외에도, 몸 안의 밀폐된 공기는 그것이 진동할 때 헬름홀츠 공명 모드를 나타낸다.^[67]

울프톤스

활은 주기적인 힘이 없기 때문에 강제적인 주파수가 아니라 시스템의 자연적인 주파수에서 최대 증폭이 일어나는 공명의 예다.^[68]늑대의 어조는 다리의 움직임에 의해 야기되는 기본 주파수의 작은 변화가 너무 커져서 음이 불안정해 질 때 생성된다.^[13]첼로의 몸(그리고 가끔 비올라나 바이올린)에서 나오는 날카로운 공명 반응은 늑대의 음색, 즉 불만족스러운 소리가 반복적으로 나타나고 사라진다.올바른 위치에 있는 억제기는 다른 주파수에서 기기 소리를 감쇠시키지 않고 해당 주파수에서 공명을 감소시킴으로써 음조를 제거할 수 있다.^[69]

바이올린 계열의 다른 멤버와의 비교

비올라의 물리학은 바이올린의 물리학과 같으며 첼로와 더블 베이스의 구성과 음향도 비슷하다.^[70]

비올라는 바이올린의 더 큰 버전이며, 평균적으로 총 몸 길이는 27+1⁄4 인치(69.2 cm)이며, 현은 바이올린보다 5분의 1 이하로 튜닝되어 있다(길이 약 23+3⁄8 인치(59.4 cm).비올라의 큰 사이즈는 현악기가 있는 그대로 연주되는 현악기에 상응할 정도로 비례적으로 크지 않아 음색이 다른 데 기여한다.비올리스트들은 손가락질도 편하게 할 수 있을 만큼 큰 손을 가져야 한다.C 현악기는 피스톤에 의해 "힘이 있고 특색 있는 음색을 가지고 있다"^[71]고 설명되어 왔지만, 아마도 부분적으로 그것이 만들어내는 소리가 쉽게 가려지기 때문에 비올라는 오케스트라에서 독주악기로 그리 자주 쓰이지 않기 때문일 것이다.^[72]미국의 물리학자 존 리그든에 따르면 비올라(첼로, 더블베이스와 함께)의 낮은 음은 힘과 질에 시달린다고 한다.비올라의 전형적인 공명 주파수는 중간 개방 문자열의 자연 주파수 사이에 위치하며, 하위 문자열의 주파수를 보강하기에는 너무 높기 때문이다.이 문제를 바로잡기 위해 리든은 비올라는 바이올린을 켜는 데 절반의 길이의 줄이 다시 필요하게 되어 악기를 연주하는 데 불편할 것이라고 계산했다.^[73]

전체 길이가 48인치(121.9cm)인 첼로는 비올라 아래로 한 옥타브를 던진다.몸의 두께가 비례적으로 크다는 것은 비올라의 경우처럼 음색이 열린 현의 음에 해당하지 않는 치수를 가짐으로써 부정적인 영향을 받지 않는다는 것을 의미한다.^[74]

이중 베이스는 다른 가족 구성원에 비해 배가 목으로 연결되는 부분이 더 뾰족해 끈의 장력에 의한 긴장을 보충하기 위한 것일 수 있으며, 끈을 조율하기 위한 톱니바퀴가 장착되어 있다.^[75][76]관현악 베이스의 평균 전체 길이는 74인치(188.0cm)이다.^[76]등을 아치형으로 하거나 납작하게 만들 수 있다.베이시스트의 손가락은 첼리스트의 손가락보다 두 배 더 멀리 뻗어야 하며, 손가락 판에 대고 누르기 위해서는 더 큰 힘이 필요하다.진동의 속도가 느려 '농축'하는 피치카토 톤은 관련 하모니가 어느 쪽이 더 우세한가에 따라 변화할 수 있다.더블 베이스의 기술 역량은 한정되어 있다.빠른 구절은 그것을 위해 쓰여지는 경우가 거의 없다; 그것들은 현이 진동하는 데 필요한 시간 때문에 명확성이 부족하다.더블 베이스는 오케스트라 전체의 기초가 되기 때문에 음악적으로 매우 중요하다.^[75]존 리그든에 따르면, 이중 베이스는 오케스트라에서 들을 수 있을 만큼 충분히 강력한 소리를 내기 위해 현재의 크기보다 두 배 더 커야 한다.^[77]

메모들

참고 문헌 목록

• Beament, James (1997). The Violin Explained: Components, Mechanism, and Sound. Oxford, New York: Oxford University Press. ISBN 978-0-19-816739-6.
• Bucur, Voichita (2018). Handbook of Materials for String Musical Instruments. AG Switzerland: Cham Springer International Publishing. ISBN 978-3-319-81191-8.
• Chisholm, Hugh, ed. (1886). "Double bass" . Dictionary of National Biography. Vol. 8. London: Smith, Elder & Co.
• Farga, Franz (1969). Violins and Violinists. New York: F. A. Praeger. OCLC 68030679.
• Galilei, Galileo (1914) [1638]. Dialogues Concerning Two New Sciences. Translated by Crew, Henry; de Salvio, Alfonso. New York: Dover Publications Inc. OCLC 708455337.
• Hutchins, Carleen Maley (1978). The Physics of Music. San Francisco: W.H. Fremman and Company. ISBN 978-0-7167-0095-1. (필요한 경우)
• Helmholtz, Hermann L. F. von (1895). Ellis, Alexander J. (ed.). On the Sensations of Tone as a Physiological basis for the Theory of Music (translation of the 1877 German edition) (3rd ed.). London, New York: Longmans, Green and Co. OCLC 1453852.
• Hutchins, Carleen Maley 바이올린 판의 음향.과학계 미국인, 제245권, 제4호.1981년 10월
• Olson, Harry F. (1967). Music, physics and engineering. New York: Dover Publications. ISBN 978-0-486-31702-1. (필요한 경우)
• Piston, Walter (1976). Orchestration (7th ed.). London: Victor Gollancz Ltd. OCLC 1016330383.
• Rigden, John S (1977). Physics and the sound of music. New York: Wiley. ISBN 978-0-471-87412-6.
• Siminoff, Roger H. (2002). The Luthier's Handbook: A Guide to Building Great Tone in Acoustic Stringed Instruments. Milwaukee: Hal Leonard Corp. ISBN 978-0-634-01468-0.
• Rossing, Thomas, ed. (2014). Springer Handbook of Acoustics. New York: Springer. ISBN 978-0-387-30446-5.
• Wishart, Trevor (1996). Emmerson, Simon (ed.). On Sonic Art. Amsterdam: OPA. ISBN 978-3-7186-5847-3.
• Wood, Alexander (1944). The Physics of Music. London: Methuen & Co. Ltd. OCLC 640010938.
• Woodhouse, J.; Galluzzo, P.M. (2004). "The Bowed String As We Know It Today" (PDF). Acta Acustica. 90: 579–589. Retrieved 11 May 2020.

추가 읽기

• Askenfelt, A. (1995). "Observations on the violin bow and the interaction with the string" (PDF). STL-QPSR. 36 (2–3): 23–42. S2CID 17812511. Archived from the original (PDF) on 2019-03-07.
• Bissinger, George (2006). "The violin bridge as filter". The Journal of the Acoustical Society of America. 120 (1): 482–491. Bibcode:2006ASAJ..120..482B. doi:10.1121/1.2207576. PMID 16875244.
• Cremer, Lothar (1984). Physics of the Violin (translation of Physik der Geige by John S. Allen). Cambridge, Massachusetts: MIT Press. ISBN 978-0-262-03102-8.
• Raman, C.V. (1918). "On the mechanical theory of vibrations of bowed strings and of musical instruments of the violin family". Indian Association of the Cultivation of Science.

• 1부(pp. 1-276).
• 2부 (pp. 277-331).
• 3부(pp. 332-389)

• 1937년 10월(F.A., Sunders)미국음향학회지 제9권 제2호 81~98편(2020년 5월)의 "바이올린의 기계적 작용"
• Savart, Félix (1819). Mémoire sur la construction des instrumens à cordes et à archets. Paris: Librairie Encyclopédique de Roret. OCLC 24148967. (프랑스어로)
• Schelleng, John C (January 1973). "The bowed string and the player". The Journal of the Acoustical Society of America. 53 (1): 26–41. Bibcode:1973ASAJ...53...26S. doi:10.1121/1.1913322. (등록 필요)(2020년 5월)

외부 링크

• 바이올린은 어떻게 작동하는가? 뉴사우스웨일스 대학교에서 발간한 바이올린 음향학 소개
• 숲을 통과하는 길 - 역사적 악기를 검사할 때 의학 이미징의 사용 이탈리아 악기를 현대 악기에서 음향을 복제하기 위해 컴퓨터 보조 단층 촬영(CT 스캐닝)을 사용하여 위대한 이탈리아 악기를 검사했다.
• 모달 애니메이션 - 보먼 비올린으로부터 다양한 주파수에서 플레이트가 진동하는 방식을 보여주는 비올린의 애니메이션.
• 다양한 고유모드 주파수에서 1712 스트라디바리 바이올린의 와이어프레임 애니메이션
• 피아스트라 디 클라드니: 비올리노(violino)는 밀라노 대학 물리학부(이탈리아어로 된 텍스트)가 올린 바이올린 모양의 클라드니 판에서 생산한 무늬를 유투브 영상이다.