스넬의 법칙

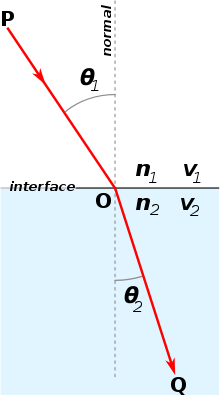
스넬의 법칙(Snell-Descartes law, Ibn-Sahl law, 굴절의 법칙)은 빛이나 다른 파동이 물, 유리, 공기와 같은 두 등방성 매질 사이의 경계를 통과할 때 입사각과 굴절 사이의 관계를 설명하는 데 사용되는 공식입니다. 광학에서 이 법칙은 입사각이나 굴절각을 계산하기 위한 광선 추적과 물질의 굴절률을 찾기 위한 실험 광학에서 사용됩니다. 이 법칙은 음의 굴절률로 빛을 음의 굴절각으로 "뒤로" 구부릴 수 있는 메타 물질에서도 만족됩니다.

법에 따르면, 주어진 한 쌍의 미디어에 대해 입사각$($θ 1 ${\displaystyle \theta$_{1}})과 $($θ 2 ${\displaystyle$\theta _{2}})의 비율은 첫 번째$(n$ 21 $displaystyle$ n_{21})에 대한 두 번째 매질의 굴절률과 동일하고 굴절률의 비율(n)과 동일합니다.2 n 1 ${\$ 또는 이와 동등하게 두 매체의 위상 속도의 비율(v 1 v 2 ${\$을 표시합니다.^[1]

${\displaystyle {\frac {\sin \theta _{1}}{\sin \theta _{2}}}=n_{21}={\frac {n_{2}}{n_{1}}}={\frac {v_{1}}{v_{2}}}}$

이 법칙은 페르마의 최소 시간의 원리를 따르며, 다시 빛이 파동으로 전파되는 것으로부터 이어집니다.

역사

이집트 알렉산드리아의 프톨레마이오스는 굴절각에 관한 관계를 발견했지만 ^[2]작지 않은 각도에 대해서는 부정확했습니다. 프톨레마이오스는 자신의 데이터를 이론에 맞게 약간 변경한 결과로 정확한 경험 법칙을 발견했다고 확신했습니다.^[3]

이 법칙은 마침내 스넬의 이름을 따서 지어졌지만, 984년 바그다드 법원에서 페르시아 과학자 이븐 살에 의해 처음 발견되었습니다.^[5][6][7] 불타고 있는 거울과 렌즈에 관한 원고에서 Sahl은 기하학적인 수차 없이 빛에 초점을 맞추는 렌즈 모양을 도출하기 위해 이 법칙을 사용했습니다.^[8]

알하젠은 그의 《광학의 책》(1021)에서 굴절의 법칙을 재발견하는 데 근접했지만, 그는 이 단계를 밟지 않았습니다.^[9]

이 법칙은 1602년 토마스 해리엇에 의해 재발견되었지만,^[10] 그는 바로 이 주제에 대해 케플러와 서신을 주고받았지만 그의 결과를 발표하지 않았습니다. 1621년, 네덜란드의 천문학자 빌레브로드 스넬리우스(1580–1626)는 수학적으로 동등한 형태를 도출했는데, 그의 일생 동안 출판되지 않은 채 남아있었습니다. 르네 데카르트는 1637년 자신의 에세이 디옵트리케에서 사인의 관점에서 휴리스틱 운동량 보존 논거를 사용하여 독자적으로 법칙을 도출하고, 이를 이용하여 다양한 광학 문제를 해결했습니다. 피에르 드 페르마는 데카르트의 해결책을 거부하고 오직 최소 시간의 원리만을 바탕으로 같은 해결책에 도달했습니다. 데카르트는 빛의 속도가 무한하다고 가정했지만, 스넬의 법칙을 유도할 때 그는 매질의 밀도가 높을수록 빛의 속도가 증가한다고 가정했습니다. 페르마는 반대되는 가정을 지지했습니다. 즉, 빛의 속도는 유한하고, 그의 유도는 밀도가 높은 매질에서 빛의 속도가 더 느리다는 것에 달려 있었습니다.^[11][12] 페르마의 유도는 또한 미분적분학과 동등한 수학적 절차인 적정성을 그의 발명을 극대, 극소, 접선을 구하는 데 활용했습니다.^[13][14]

데카르트는 그의 영향력 있는 수학 책 기하학에서 페르가의 아폴로니오스와 알렉산드리아의 파푸스가 작업한 문제를 풀었습니다. 각 선 위에 n개의 선 L과 점 P(L)이 주어지면 선분 QP(L)의 길이가 특정 조건을 만족하도록 점 Q의 궤적을 구합니다. 예를 들어, n = 4일 때, 선 a, b, c, d와 a, b 등의 점 A가 주어졌을 때, 곱 QA*QB가 곱 QC*QD와 같도록 점 Q의 위치를 구합니다. 선들이 모두 평행하지 않을 때, 파푸스는 유전자좌가 원뿔형이라는 것을 보여주었지만, 데카르트가 더 큰 n을 고려할 때, 그는 입방 곡선과 더 높은 도 곡선을 얻었습니다. 입체 곡선이 흥미롭다는 것을 보여주기 위해, 그는 그것들이 스넬의 법칙으로부터 광학적으로 자연적으로 생겨났다는 것을 보여주었습니다.^[15]

Dijksterhuis에 따르면,^[16] "데나투라 루시스 외 소유주 (1662)에서 아이작 보시우스는 데카르트가 스넬의 논문을 보고 자신의 증거를 만들었다고 말했습니다. 우리는 지금 이 요금이 부당하다는 것을 알고 있지만 그 이후로 여러 번 채택되었습니다." 데카르트가 스넬을 모방했다는 이 비난은 페르마와 하위헌스 모두에게 되풀이되었습니다. 프랑스어로 스넬의 법칙은 때때로 "laoi de Descartes" 또는 더 자주 "loi de Snell-Descartes"라고 불립니다.

1678년 Christiaan Huygens는 그의 Traité de la Lumière에서 어떻게 우리가 Huygens-Fresnel 원리라고 부르게 된 것을 사용하여 빛의 파동성에 의해 스넬의 사인 법칙이 설명되거나 그로부터 유도될 수 있는지를 보여주었습니다.

현대의 광학 이론과 전자기 이론이 발전하면서 고대 스넬의 법칙은 새로운 단계로 접어들었습니다. 1962년, Bloembergen은 비선형 매질의 경계에서 스넬의 법칙이 일반적인 형태로 쓰여져야 한다는 것을 보여주었습니다.^[17] 2008년과 2011년에는 플라즈모닉 메타 표면이 빛의 반사 및 굴절 방향을 변화시키는 것을 시연하기도 했습니다.^[18][19]

설명.

스넬의 법칙은 굴절률이 다양한 굴절 매질을 통해 광선의 방향을 결정하는 데 사용됩니다. 빛의 속도가 진공에서의 속도에 비해 유리나 물과 같은 굴절 매질을 통과할 때 감소하는 비율은 n1 ${\$ n2 ${\$ 등으로 표시된 매질의 굴절률에 의해 표시됩니다.

두 매질의 상대 굴절률에 따라 빛이 매질 사이의 경계를 통과할 때 빛은 더 작은 각도로 굴절되거나 더 큰 각도로 굴절됩니다. 이 각도는 경계에 수직으로 표시되는 정규 선에 대해 측정됩니다. 빛이 공기에서 물로 이동하는 경우, 빛은 물에서 속도가 느려지기 때문에 수직선 쪽으로 굴절됩니다. 물에서 공기로 이동하는 빛은 수직선에서 멀리 굴절됩니다.

두 표면 사이의 굴절을 가역이라고도 하는데, 모든 조건이 같다면 반대 방향으로 진행하는 빛에 대해서도 각도가 같기 때문입니다.

스넬의 법칙은 일반적으로 등방성 또는 정반사 매질(유리와 같은)에 대해서만 성립합니다. 일부 결정과 같은 이방성 매체에서 복굴절은 굴절된 광선을 두 개의 광선으로 분할할 수 있습니다. 즉, 스넬의 법칙을 따르는 일반 광선 또는 광선, 그리고 입사 광선과 동일 평면이 아닐 수 있는 다른 특수 광선 또는 전자 광선입니다.

관련된 빛이나 다른 파동이 단색일 때, 즉 단일 주파수의 경우, 스넬의 법칙은 두 매질, 즉λ 1 {\displaystyle$\lambda$ _{1}}와λ 2 {\displaystyle \lambda _{2}:

${\displaystyle {\frac {\sin \theta _{1}}{\sin \theta _{2}}={\frac {v_{1}}{v_{2}}={\frac {\lambda _{1}}{\lambda _{2}}}$

도함수와 공식

스넬의 법칙은 다양하게 도출될 수 있습니다.

페르마의 원리로부터 유도

스넬의 법칙은 빛이 가장 적은 시간이 걸리는 경로를 이동한다는 페르마의 원리로부터 유도될 수 있습니다. 광경로 길이의 도함수를 취함으로써 빛이 택한 경로를 제공하는 정지점이 발견됩니다. (구면 거울에서 반사하는 것처럼 빛이 가장 적은 시간 경로를 택하지 않음으로써 페르마의 원리를 위반하는 경우도 있습니다.) 전형적인 비유로, 굴절률이 낮은 지역은 해변으로, 굴절률이 높은 지역은 바다로 대체되며, 해변에 있는 구조자가 바다에 빠진 사람에게 가장 빨리 도달하는 방법은 스넬의 법칙을 따르는 길을 따라 달리는 것입니다.

오른쪽 그림과 같이 매체 1과 매체 2의 굴절률을 각각 n 1 ${\$과 n 2 ${\$라고 가정합니다. 빛은 매체 1에서 지점 O를 거쳐 매체 2로 들어갑니다.

$θ$ 1 ${\$$displaystyle$\theta _${$1}}는 입사각이고, θ 2 {\displaystyle \theta _{2}는 법선에 대한 굴절각입니다.

매질 1과 매질 2에서 빛의 위상 속도는

v 1 = c/ n 1 {\displaystyle v_{1} = c/n_{1}} 및

v2 = c/ n2 {\displaystyle v_{2} = c/n_{2}} 각각입니다.

$c {\displaystyle$ c$}$는 진공에서의 빛의 속도입니다.

빛이 Q점에서 O점을 거쳐 P점까지 이동하는 데 필요한 시간을 T라고 하자.

${\displaystyle T={\frac {\sqrt {x^{2}+a^{2}}}{v_{1}}}+{\frac {\sqrt {b^{2}+(l-x)^{2}}}{v_{2}}}={\frac {\sqrt {x^{2}+a^{2}}}{v_{1}}}+{\frac {\sqrt {b^{2}+l^{2}-2lx+x^{2}}}{v_{2}}}$

여기서 a, b, l 및 x는 오른쪽 그림에 표시된 대로 x는 변동 파라미터입니다.

이를 최소화하기 위해 다음을 구분할 수 있습니다.

$x$$}}}}}+{\frac {-(l-x)}{v_{2}{\sqrt {(l-x)^{2}+b^{2$}}}}}$=0}$ (정지점)

x x 2+ a 2 = sin ⁡ θ 1 {\displaystyle${\frac$ {x$}{\sqrt$ {x^{2}+a^{2$}}}}=\sin \theta _{1}}$

그리고 l- x(l- x) 2+ b 2 = sin⁡ θ 2 {\displaystyle ${\frac$ {l-x}{\sqrt ${(l-x)^{2$}+b^{2$}}}}=\sin \theta _{2}}$

그러므로,

${\displaystyle {\frac {dT}{dx}}={\frac {\sin \theta _{1}}{v_{1}}}-{\frac {\sin \theta _{2}}{v_{2}}}=0}$

${\displaystyle {\frac {\sin \theta _{1}}{v_{1}}={\frac {\sin \theta _{2}}{v_{2}}}$

${\displaystyle {\frac {n_{1}\sin \theta _{1}}{c}}={\frac {n_{2}\sin \theta _{2}{c}}$

${\displaystyle n_{1}\sin \theta_{1}=n_{2}\sin \theta_{2}}$

호이겐스의 원리로부터 유도

또는 소스에서 관찰자까지의 모든 가능한 광파 경로의 간섭을 사용하여 스넬의 법칙을 유도할 수 있으며, 이는 실제 경로가 되는 위상의 극한(간섭이 건설적인 경우)을 제외한 모든 곳에서 파괴적인 간섭을 초래합니다.

맥스웰 방정식에서 유도

스넬의 법칙을 유도하는 또 다른 방법은 전자기 복사와 유도에 대한 맥스웰 방정식의 일반적인 경계 조건을 적용하는 것입니다.

에너지와 운동량의 보존으로부터 유도

스넬의 법칙을 유도하는 또 다른 방법은 번역 대칭성을 고려하는 것입니다.^[20] 예를 들어 z 방향에 수직인 균일한 표면은 가로 운동량을 변경할 수 없습니다. 전파 벡터 k → {\$displaystyle$ ${\vec {k}}$은 광자의 운동량에 비례하므로 가로 전파 방향(k x, ky, 0) ${\displaystyle (k_{x}, k_{y}, 0)}$은 두 영역에서 동일하게 유지되어야 합니다. 일반성의 손실 없이 z, x ${\displaystyle$ z$,x}$ 평면 k x 영역 1 = k x 영역2 {\displaystyle k_{x{\text{Region}_{1}}=k_{x{\text{Region}_{2}}의 입사면을 가정합니다. 매질의 굴절률에 대한 파수의 잘 알려진 의존성을 사용하여 즉시 스넬의 법칙을 도출합니다.

${\displaystyle k_{x{\text{Region}_{1}}=k_{x{\text{Region}_{2}\,}$

${\displaystyle n_{1}k_{0}\sin \theta _{1}=n_{2}k_{0}\sin \theta _{2}\,}$

${\displaystyle n_{1}\sin \theta_{1}=n_{2}\sin \theta_{2}\,}$

여기서 k 0 = 2π λ 0 = ω c {\displaystyle k_{0} = {\frac {2\pi} {\lambda _{0}} = {\frac {\omega} {c}}는 진공에서의 파수입니다. 원자 규모에서는 어떤 표면도 진정으로 균질하지 않지만, 광파장 규모에서 지역이 균질할 때마다 완전한 병진 대칭은 훌륭한 근사치입니다.

벡터형태

정규화된 광 벡터 l → ${\$$displaystyle$ ${\vec${l}}(광원에서 표면 쪽으로 pointing) 및 정규화된 평면 정규 벡터 n → {\displaystyle {\vec {n}}이 주어지면 정규화된 반사 및 굴절 광선을 계산할 수 있습니다. 사인 값이나 삼각 함수 또는 각도를 명시적으로 사용하지 않고 입사각θ 1 ${\displaystyle \theta$ _{1}} 및굴절각 θ 2 ${\displaystyle$ \theta _{2}}의 코사인을 통해:

${\displaystyle \cos \theta _{1}=-{\vec {n}}\cdot {\vec {l}}$

참고: cos⁡ θ 1 {\displaystyle $\$$costheta _${1}}이 양수여야 합니다. n → {\displaystyle {\vec {n}}이 지표면에서 빛이 들어오는 쪽을 가리키는 정상 벡터이며, 인덱스가 n이 {\displaystyle n_{1}인 영역입니다. cos⁡ θ 1 {\displaystyle \costheta $_${1}}이 음수이면 n → {\displaystyle {\vec {n}}이(가) 불빛이 없는 쪽을 가리키므로 n → {\displaystyle {\vec {n}}이(가) 음수로 대체된 상태에서 다시 시작합니다.

${\displaystyle {\v}_{\mathrm {reflect}} = {\vec {l}+2\cos \theta _{1}{\vec {n}}$

이 반사된 방향 벡터는 빛이 나온 표면의 측면을 다시 향합니다.

이제 스넬의 법칙을 사인의 비율에 적용하여 굴절 광선의 방향 벡터에 대한 공식을 유도합니다.

${\displaystyle \sin \theta _{2}=\left ({\frac {n_{1}}\right)\sin \theta _{1}=\left ({\frac {n_{1}}\right){\sqrt {1-\left(\cos \theta _{1}\right)^{2}}}$

${\displaystyle \cos \theta _{2}={\sqrt {1-(\sin \theta _{2})^{2}}={\sqrt {1-\left ({\frac {n_{1}}\right)^{2}\left(1-\left(\cos \theta _{1}\right)^{2}\right)}}}$

${\displaystyle {\v}_{\mathrm {refract}} =\left ({\frac {n_{1}}{n_{2}}\right){\vec {l}}+\left({\frac {n_{1}}{n_{2}}}\cos \theta _{1}-\cos \theta _{2}\right){\vec {n}}$

공식은 이름이 바뀐 단순 값 r = n 1/ n 2 $displaystyle$ r = $n_${1}/n_{2}} 및 c = - n → ⋅ l → {\displaystyle c =-{\vec {n}}\cdot {\vec {l}}의 관점에서 더 단순하게 나타날 수 있으며, 이는 트리 함수 이름이나 각도 이름이 나타나지 않도록 합니다.

${\displaystyle {\v}_{\mathrm {refract} =r{\vc {l}}+\left(rc-{\sqrt {1-r^{2}\left(1-c^{2}\right)}\right)}{\vec {n}}$

예제:

${\displaystyle {\vec {l}}=\{0.707107,-0.707107\},~{\vec {n}}=\{0,1\},~r={\frac {n_{1}}{n_{2}}}=0.9}$

${\displaystyle c=\cos \theta _{1}=0.707107,~{\sqrt {1-r^{2}\left(1-c^{2}\right)}}=\cos \theta _{2}=0.771362}$

${\displaystyle {\vec {v}}_{\mathrm {reflect} }=\{0.707107,0.707107\},~{\vec {v}}_{\mathrm {refract} }=\{0.636396,-0.771362\}}$

코사인 값은 결과적인 광선의 세기를 계산하기 위한 프레넬 방정식에 저장되어 사용될 수 있습니다.

내부 전반사는 cos⁡ θ 2 {\displaystyle $\$$costheta _${2}}의 식에서 음의 라디칼로 표시되며, 이는 저밀도 매질(n 2 < n 1 {\displaystyle n_{2}< n_{1})로 통과하는 광선에만 발생할 수 있습니다.

내부 전반사 및 임계각

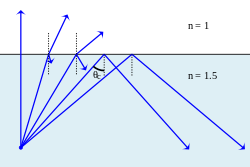
빛이 굴절률이 높은 매질에서 굴절률이 낮은 매질로 진행할 때, 스넬의 법칙은 어떤 경우에는 굴절각의 사인이 1보다 클 것을 요구하는 것처럼 보입니다. 물론 이것은 불가능하며, 이러한 경우의 빛은 경계에 의해 완전히 반사되는데, 이 현상을 전반사라고 합니다. 여전히 굴절된 광선을 발생시키는 가장 큰 입사각을 임계각이라고 합니다. 이 경우 굴절된 광선은 두 매질 사이의 경계를 따라 이동합니다.

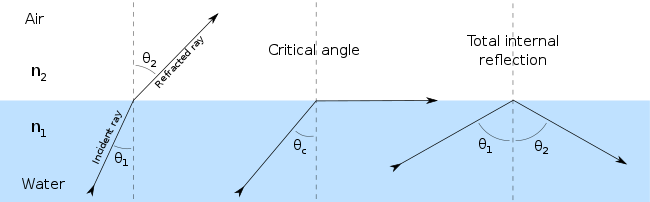
예를 들어, 입사각이 50°인 물에서 공기로 이동하는 한 줄기 빛을 생각해 보세요. 물과 공기의 굴절률은 각각 약 1.333과 1이므로, 스넬의 법칙은 우리에게 다음 관계를 제공합니다.

${\displaystyle \sin \theta _{2}={\frac {n_{1}}{n_{2}}}\sin \theta _{1}={\frac {1.333}{1}}\cdot \sin \left(50^{\circ }\right)=1.333\cdot 0.766=1.021,}$

그것은 만족시킬 수 없습니다. 임계 각도 θ은 θ가 90°인 θ의 값입니다.

${\displaystyle \theta _{\text{crit}}=\arcsin \left ({\frac {n_{2}}{n_{1}}}\sin \theta _{2}\right)=\arcsin {\frac {n_{2}}{n_{1}}=48.6^{\circ}}$

분산

많은 파동 전파 매체에서 파동 속도는 파동의 진동수나 파장에 따라 변합니다. 이것은 진공이 아닌 대부분의 투명한 물질에서 빛의 전파에 해당합니다. 이러한 매체를 분산이라고 합니다. 그 결과 스넬의 법칙에 의해 결정되는 각도도 주파수나 파장에 따라 달라지므로 백색광과 같은 혼합 파장의 광선이 퍼지거나 분산됩니다. 유리나 물 속의 이러한 빛의 분산은 서로 다른 파장이 서로 다른 색으로 나타나는 무지개와 다른 광학 현상의 근원이 됩니다.

광학 기기에서 분산은 색수차로 이어집니다. 때로는 해상도 제한 효과인 색 의존적인 흐림입니다. 특히 무채색 대물렌즈가 발명되기 전 굴절 망원경에서는 더욱 그러했습니다.

매체의 손실, 흡수 또는 전도

전도성 매체에서 유전율과 굴절률은 복소 값입니다. 결과적으로 굴절각과 파동벡터도 마찬가지입니다. 이것은 일정한 실제 위상의 표면들이 경계면의 법선과 굴절각이 같은 각도를 이루는 평면들인 반면, 반대로 일정한 진폭의 표면들은 경계면 자체와 평행한 평면들이라는 것을 의미합니다. 이 두 평면은 일반적으로 서로 일치하지 않기 때문에 파동이 불균일하다고 합니다.^[22] 굴절파는 지수 함수적으로 감쇠되며 지수는 굴절률의 허수 성분에 비례합니다.^[23][24]

참고 항목

• 굴절률 목록
• 빛의 굴절률 대 파장 – 굴절률과 파장의 경험적 관계
• 소멸파 – 전자파 에너지의 순 흐름이 0인 필드 유형 방향 전환 대상에 대한 짧은 설명을 표시하는 페이지
• 반사(물리학) – 인터페이스에서 파동의 "돌파"
• 스넬의 창 – 스넬의 법칙에 의한 수중현상
• 변분 미적분학 – 함수공간에 대한 미분적분학
• 브라키스토크론 곡선 – Jacob Bernoulli의 간단한 증명을 위해 마찰이 없는 가장 빠른 곡선 하강
• 해밀턴 광학
• 대기 중 전파 감쇄량 계산
• N-슬릿 간섭방정식

참고문헌

외부 링크

• 이븐 살과 스넬의 법칙
• 굴절법칙의 발견
• Wolfram 데모 프로젝트, Todd Rowland의 스넬의 굴절 법칙 (파면)
• 레이던 시내 벽에 대한 스넬의 법칙 2018-04-27 웨이백 머신에서 아카이브됨
• 해안선 효과