이코사곤

일반 이코사곤
규칙적인 이코사곤
유형	정규 다각형
모서리 및 정점	20
슐레플리 기호	{20}, t{10}, tt{5}
콕시터-딘킨 도표
대칭군	디헤드랄(D20), 2×20 주문
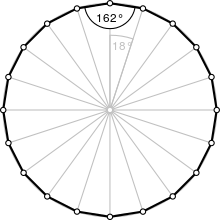
내부 각도(도)	162°
특성.	볼록, 주기, 등변, 이등변, 동위원소

기하학에서 이코사곤 또는 20곤은 20면 다각형이다. 어떤 이코사곤의 내부 각도의 합은 3240도 입니다.

일반 이코사곤

일반 이코사곤은 Schléfli 기호 {20}을(를) 가지며 잘린 데카곤, t{10} 또는 두 번 잘린 오각형 tt{5}로도 구성할 수 있다.

일반 이코사곤의 내부 각도는 162°로, 외부 각도가 18°임을 의미한다.

가장자리 길이 t를 가진 일반 이코사곤의 면적은

${\displaystyle A={5}t^{2}(1+{\sqrt{5}}}}+{\sqrt{5}}}}{\sqrt{5}})\simeq 31.5687t^{2}.}$

원곡선의 반경 R에 있어, 면적은 다음과 같다.

${\displaystyle A={\frac {5R^{2}}({\sqrt{5}-1);}$

원의 면적은 is R 2,${\displaystyle \pi R^{2}}}$이므로 일반 이코사곤은 원형의 약 98.36%를 채운다.

사용하다

미국의 인기 게임쇼인 "The Price Is Right"의 Big Wheel은 반각형의 단면을 가지고 있다.

윌리엄 셰익스피어의 연기회사가 사용하던 야외극장 글로브는 1989년 부분 발굴이 이뤄졌을 때 고각형 토대 위에 세워진 것으로 밝혀졌다.^[1]

고글리곤 길로서 스와스티카는 불규칙한 이코사곤으로 간주된다.^[2]

정사각형, 오각형, 이코사곤은 평면 꼭지점을 완전히 채울 수 있다.

건설

20 = 2² × 5로, 일반 아이코사곤은 나침반과 직선자를 사용하거나, 일반 디카곤의 가장자리 분리를 사용하거나, 두 번 검출된 정규 오각형을 사용하여 구성할 수 있다.

일반 이코사곤의 시공

일반 데카곤의 시공

이코사곤의 황금 비율

• 주어진 측면 길이의 구조에서 반경 CD가 있는 C 주위의 원형 호는 황금 비율의 세그먼트 EF를₂₀ 공유한다.

${\displaystyle {\frac {\overline {E_{20}E_{1}}{\overline {E_{1}}{\overline {E_{1}}}{\overline {1}}}}}}={\frac {\frac {E_{20}F}{\overline {E_{20}E_{1}:{1}:{\frac {{1+{\sqrt{5}}}{2}}=\varphi \1.618}}}$

대칭

일반 이코사곤은 Dih₂₀ 대칭, 순서 40이다. (Dih, Dih₁₀₅, Dih, Dih)와₄₂ (Dih, Dih, Dih₁), (Z, Z₂₀₁₀, Z₅)와 (Z₄, Z₂, Z, Z₁)의 5개의 부분군 분음 대칭이 있다.

이 10개의 대칭은 정점이나 가장자리를 통과할 수 있기 때문에 더 큰 숫자인 16개의 뚜렷한 대칭으로 볼 수 있다. 존 콘웨이는 편지와 단체 주문으로 이것들에 라벨을 붙였다.^[3] 정규형식의 완전한 대칭은 r40이며 어떤 대칭도 a1로 표기되지 않는다. 이음 대칭은 정점(대각의 경우 d) 또는 가장자리(직각의 경우 p)를 통과하는지와 반사선이 양쪽 가장자리와 정점을 통과했을 때 i에 따라 구분된다. 중앙 열의 주기적 대칭은 중심 교량 순서에 대해 g로 표시된다.

각 부분군 대칭은 불규칙한 형태에 대해 하나 이상의 자유도를 허용한다. g20 부분군만 자유도는 없지만 지시된 가장자리로 볼 수 있다.

가장 높은 대칭 불규칙한 이코사곤은 d20으로, 긴 가장자리와 짧은 가장자리를 교대할 수 있는 10개의 거울로 구성된 이등분 이코사곤과 가장자리 길이가 같지만 정점이 두 개의 내부 각도를 교대시키는 동위원소 이코사곤이다. 이 두 형태는 서로 이중으로 되어 있으며, 일반 이코사곤의 대칭 순서의 절반을 가지고 있다.

해부

광이 180나 되는 20곤

정칙의

동위원소

Coxeter는 모든 조노곤(상대방이 평행하고 길이가 같은 2m-곤)을 m(m-1)/2 평행그램으로 해부할 수 있다고 명시하고 있다.^[4] 특히 면적이 고르게 많은 일반 다각형의 경우, 이 경우 평행사변형은 모두 rhombi이다. 이코사곤의 경우 m=10이며, 45:5 제곱과 10 롬 4 세트로 나눌 수 있다. 이 분해는 페트리 폴리곤 투영법에 기초한 것으로, 11520면 중 45면이다. OEIS: A006245 목록에는 최대 20배의 회전과 치랄 형태를 반영하여 18,410,581,880개의 솔루션 수가 열거되어 있다.

45개의 롬으로 해부한다.

10시 30분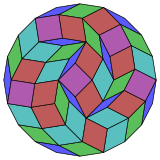

관련 다각형

아이코사그램은 기호 {20/n}로 표현되는 20면 별 다각형이다. 슐래플리 기호가 주는 정규 형태는 3가지로, 즉 {20/3}, {20/7}, {20/9}이다. 또한 동일한 꼭지점 배열을 사용하는 5개의 정규 별자리(축척)가 있다: 2{10, 4{5}, 5{4}, 2{10/3}, 4{5/2}, 10{2}.

n	1	2	3	4	5
형태	볼록 폴리곤	화합물	별 폴리곤	화합물
이미지	{20/1} = {20}	{20/2} = 2{10}	{20/3}	{20/4} = 4{5}	{20/5} = 5{4}
실내각	162°	144°	126°	108°	90°
n	6	7	8	9	10
형태	화합물	별 폴리곤	화합물	별 폴리곤	화합물
이미지	{20/6} = 2{10/3}	{20/7}	{20/8} = 4{5/2}	{20/9}	{20/10} = 10{2}
실내각	72°	54°	36°	18°	0°

일반 데카곤과 디카그램의 더 깊은 자르기는 정점과 두 개의 가장자리 길이의 등각형 중간 아이코사그램 형태를 생성할 수 있다.^[5]

일반 아이코사그램, {20/9}은(는) quasitrunculated decagon, t{10/9}={20/9}로 볼 수 있다. 마찬가지로 디카그램 {10/3}에는 quasitruncation t{10/7}={20/7}이 있으며, 마지막으로 디카그램의 단순한 잘라내기에서는 t{10/3}={20/3}이 부여된다.

일반 디카곤 및 디카그램의 잘라내기로서의 ICosagram, {10}, {10/3}

퀘이레굴라속					퀘이레굴라속
t{10}={20}					t{10/9}={20/9}
t{10/3}={20/3}					t{10/7}={20/7}

페트리 폴리곤

일반 이코사곤은 Coxeter 평면의 직교 투영에서 볼 수 있는 여러 가지 고차원 다상체에 대한 Petrie 폴리곤이다.

A을19	B10		D11	E8	H4	½2H2	2H2
19세기	십중팔구	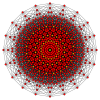10시 30분	11데미큐브	(421)	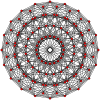600셀	대항미주의	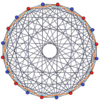10-10 듀오피라미드	10-10 듀오프리즘

또한 이등면 120셀, 소형면 120셀, 대이등면 120셀, 대이등면 120셀을 위한 페트리 폴리곤이다.

참조

외부 링크

• 폴리곤 및 폴리헤드라 명명
• 이코사곤