이중공간
Dual space수학에서 벡터 공간 V은는) V 의 모든 선형 형태와 함께 점 추가 및 상수별 스칼라 곱셈의 벡터 공간 구조로 구성된 해당하는 이중 벡터 공간(또는 단지 짧은 이중 공간)을 갖는다.
위에서 정의한 이중공간은 모든 벡터공간에 대해 정의되며, 모호성을 피하기 위해 대수적 이중공간이라고도 할 수 있다. 위상 벡터 공간에 대해 정의했을 때, 연속 이중 공간이라 불리는 연속 선형 함수에 해당하는 이중 공간의 하위 공간이 있다.
이중 벡터 공간은 유한차원 벡터 공간을 가진 텐서 분석과 같이 벡터 공간을 사용하는 수학의 많은 가지에서 응용을 찾는다. 함수의 벡터 공간(일반적으로 무한 차원)에 적용할 때 이중 공간을 사용하여 측정, 분포 및 힐버트 공간을 설명한다. 따라서 이중공간은 기능분석에서 중요한 개념이다.
이중의 초기 용어로는 폴러 라움[Han 1927], 에스페이스 커플게[Espace coupgué], 부선 공간[Alaoglu 1940], 트랜스폰더 라움[Schauder 1930], [Banach 1932] 등이 있다. 이중이라는 용어는 부르바키 1938년에 기인한다.[1]
대수 이중공간
밭 F{F\displaystyle}에 대한 벡터 공간 V{V\displaystyle}, V∗{\displaystyle V^{*}}[2](대신으로 V∨에 의해 표시된{\displaystyle V^{\lor}}[3]또는 V′{V'}\displaystyle[4][5])[nb 1]일부 선형 지도 φ의 집합으로 정의되어 있는(대수)이중 공간 V→ F{\displaysty.르 \varphi:V\to F선형 함수). 선형 지도가 벡터 공간 동형성이기 때문에 이중 공간은 , ) 으로 표기될 수 있다[6] 이중 V{{\ V 그 자체는 다음과 같은 만족스러운 추가와 스칼라 곱을 F{\에 대한 벡터 공간이 된다.
모든 , ∈ V {\ \ V F
대수학적 이중공간 V의 원소를 코브터 또는 원폼이라고 부르기도 한다.
V{V\displaystyle}의 이중 공간에 기능적인 φ{\displaystyle \varphi}V∗{\displaystyle V^{*}}의 짝 짓기 및 요소){\displaystyle)}은 가끔 브래킷:φ()))[x, φ]{\displaystyle \varphi())[x,\varphi]}[7]또는φ()))⟨에 의해,φ ⟩{\displaystyle \varph 표시됩니다.나는( [8] 이 쌍은 자연 쌍이라고 불리는 비degenerate 이선형 매핑[nb 2]mapping : V → :를 정의한다.
유한차원 케이스
V가 유한한 차원일 경우∗ V는 V와 동일한 차원을 갖는다. V에서 {e1, ..., en}의 근거를 제시하면, V에서∗ 특정 기준을 구성할 수 있으며, 이중 기준이라고 한다. 이 이중 기준은 V의 선형 함수 집합 {e1, ..., en}이며, 관계에 의해 정의된다.
계수 ci ∆ F. 특히 각 계수가 1과 같고 다른 계수가 0이 되도록 하면 방정식의 계수가 된다.
여기서 는 Kronecker 델타 기호다. 이 속성을 이직성 속성이라고 한다.
예를 들어, V가2 R이면 그 기초를 {e1 = (1/2, 1/2), e2 = (0, 1)}(으)로 선택하도록 한다. 기본 벡터는 서로 직교하지 않는다. 그런1 다음 e와12 e는 e(e1) = 11, e(e2) = 0, e2(e1) = 0, e2(e2) = 1과 같은 단일 형태(벡터를 스칼라에 매핑하는 기능)이다. (참고: 여기서 위첨자는 지수가 아니라 지수)이다. 이 방정식 체계는 행렬 표기를 사용하여 다음과 같이 표현할 수 있다.
이 방정식을 풀면 이중 기준이 {e1 = (2, 0), e2 = (-1, 1)}인 것을 알 수 있다. e와1 e는2 함수이기 때문에 e1(x, y) = 2x, e2(x, y) = -x + y로 다시 쓸 수 있다. 일반적으로 V가 R일n 때 E = (e1, ..., en)가 기본 벡터인 행렬이고 EE = (e1n, ..., e)가 이중 기본 벡터인 행렬인 경우
여기서 나는n 순서 n의 정체성 행렬이다. 이 두 가지 기본 세트의 생체역학 특성은 어떤 점 x ∈ V도 다음과 같이 나타낼 수 있도록 한다.
기본 벡터가 서로 직교하지 않을 때에도. 엄밀히 말하면, § Bilinar 제품과 이중 공간에 아래에 설명된 바와 같이, 위 문장은 내부 제품인{,{, {, \,\과 해당 이중성 쌍이 소개된 후에만 타당하다.
특히 R은n n개의 실수의 열공간으로 해석할 수 있으며, 이중공간은 일반적으로 n개의 실수의 행공간으로 표기된다. 그러한 행은 R에n 일반적인 행렬 곱셈에 의한 선형 함수로서 작용한다. 이것은 기능적 기능이 모든 n-벡터 x를 실제 숫자 y로 매핑하기 때문이다. 그 다음, 이 기능을 매트릭스 M, x, y, n × 1 매트릭스와 1 × 1 매트릭스(삼각형, 실수)로 보고, Mx = y이면 치수상 M은 반드시 1 × n 매트릭스여야 한다. 즉, M은 행 벡터여야 한다.
V가 평면에 있는 기하학적 벡터의 공간으로 구성되는 경우 V∗ 요소의 레벨 곡선은 범위가 1차원이기 때문에 V의 평행선 패밀리를 형성하여 범위의 모든 점이 0이 아닌 원소의 배수가 되도록 한다. 그래서 V의∗ 요소는 직감적으로 비행기를 덮고 있는 특정 평행선 계열로 생각할 수 있다. 주어진 벡터에서 함수 값을 계산하려면 벡터가 어느 선에 놓여 있는지 결정하기에 충분하다. 비공식적으로 이 "카운트"는 벡터가 몇 개의 선을 교차하는지 계산한다. 보다 일반적으로 V가 어떤 차원의 벡터 공간이라면 V에서∗ 선형 기능의 레벨 세트는 V에서 병렬 하이퍼플레인이며, 벡터에 대한 선형 기능의 작용을 이러한 하이퍼플레인의 관점에서 시각화할 수 있다.[9]
무한차원 케이스
V가 유한차원이 아니라 무한 집합 A에 의해 지수화된α 기초를[nb 3] 가지고 있다면, 유한차원의 경우와 동일한 구조는 이중 공간의 선형 독립요소 eα(α α α A)를 산출하지만, 그것들은 기초를 형성하지는 않을 것이다.
예를 들어, 요소인∞ 공간 R은 자연수 N: i for N에 대해 색인화된i 근거를 가진 0이 아닌 많은 항목만을 포함하는 실제 숫자의 시퀀스로서 i번째 위치인 1을 제외한 모든 0으로 구성된 시퀀스다. R의∞ 이중공간은 실수의 모든 시퀀스들의 공간인 (이형적 to) R이다N. 각 실제 시퀀스 (an)는 R의∞ 요소 (xn)가 숫자로 전송되는 함수를 정의한다.
0이 아닌 x가n 아주 많으므로 유한한 합이다. R의∞ 치수는 셀 수 없이 무한하지만, R은N 셀 수 있는 기초를 가지고 있지 않다.
이 관찰은 모든 필드 F에 걸쳐 무한[nb 3] 차원 벡터 공간 V로 일반화된다: 기준 {eα : α 0α A}의 선택은 f : f = fA(α)가 미세하게 많은 α α α A에 대해서만 0이 아닌 것으로 V를 식별한다. 여기서 그러한α 함수 f는 벡터로 식별된다.
V에서 (합계는 f에 대한 가정에 의해 유한하며, 모든 v ∈ V는 기초의 정의에 의해 이러한 방식으로 쓰여질 수 있다.)
그런 다음 V의 이중 공간은 A에서 F까지의 모든 기능의A 공간 F로 식별할 수 있다: V의 선형 기능 T는 V에 기초하여 취하는 값α = = T(eα)에 의해 고유하게 결정되며, 모든 함수 : : A → F (α(α) = θα)는 V의 선형 기능 T를 정의한다.
다시 말하지만 f는α 미세하게 많은 α에 대해서만 0이 아니기 때문에 합은 유한하다.
집합(FA)0은 A에 의해 색인화된 무한히 많은 F 복사본(자체 위에 1차원 벡터 공간으로 표시됨)의 직접적인 합으로 식별할 수 있다(본질적으로 정의에 의해). 즉, 선형 이형성이 있다.
반면 F는A (정의에 따라) A에 의해 지수화된 F의 무한히 많은 사본의 직접 생산물이며, 따라서 식별이 가능하다.
직접 제품과 직접 합계와 관련된 일반적인 결과의 특별한 경우.
여기서 절대값으로 표시된 기수 숫자를 고려하면, 무한 기초 A를 갖는 F-벡터 공간 V에 대한 값을 갖는다.
이는 벡터 공간이 유한한 차원이 아닌 경우, 선택 공리는 대수적 이중 공간이 원래 벡터 공간보다 항상 더 큰 차원(기수로서)이라는 것을 암시한다(두 베이스가 동일한 카디널리티를 갖는 경우, 스팬 벡터 공간은 동일한 카디널리티를 가지기 때문이다). 이는 아래에서 논하는 연속적인 이중 공간의 경우와는 대조적인 것으로, 후자가 무한 차원이라 하더라도 원래의 벡터 공간과 이형성이 있을 수 있다.
이선형 제품 및 이중 공간
V가 유한한 차원이라면 V는 V에∗ 대해 이형성이다. 그러나 이 두 공간 사이에는 일반적으로 자연 이형성이 존재하지 않는다.[10] V에 있는 모든 이선형 형태 ⟨··⟩은 V의 이중 공간에 V의 매핑을 제공한다.
여기서 우측은 각 w ∈ V에서 wv까지, w⟩까지 V의 기능으로 정의된다. 즉, 이선형 형태는 선형 매핑을 결정한다.
에 의해 정의된.
만약 이선형태가 비탈진형이라면, 이것은∗ V의 하위공간에 대한 이형성이다. 만약 V가 유한한 차원이라면, 이것은 모든 V에∗ 대한 이형성이다. 반대로 V에서 V의∗ 하위 공간(resp, V가 유한한 경우 모든∗ V)까지 모든 이형성 은(는) 고유한 비degenerate 이선형 형식form , ⟩ \ \ \ \ \\ )을 정의한다.V에 Phi by
따라서 V의 이형성과 V의 (resp, 모든) V의∗ 하위 공간과 V의 비데이지형 이선형 사이에 일대일 연관성이 있다.
벡터 공간 V가 복잡한 필드 위에 있다면, 때로는 이선형 대신 sesquilinar 형태를 고려하는 것이 더 자연스럽다. 그 경우 주어진 sesquilinar 형식인 ⟨··⟩은 이중 공간의 복합적 결합으로 V의 이형성을 결정한다.
이중 공간 의 결합은 모든 가법 복합 가치 함수 f : V → C의 집합으로 식별할 수 있다.
이중 이중 주입
에서 이중 V ={: = { ∗ : V → : l l l l ee e e { {} {\, defined by for all . In other words, if is the evaluation map defined by , then is defined as the map . 이 지도 }은([11]는) 항상 주입식이며,[nb 3] }이(가) 유한한 차원일 경우에만 이형성이다. 실제로 이중 이중성이 있는 유한차원 벡터 공간의 이소모르퍼시즘은 자연 이소모르퍼시즘의 원형적 예다. 무한 차원 힐버트 공간은 대수학적 이중 이중의 공간이 아니라 연속적인 이중 이중 이중의 이형성이기 때문에 이것에 대한 백과사례가 아니다.
선형 지도의 전치
f : V → W가 선형 지도인 경우 transpose (또는 이중) f∗ : W → V는∗ 다음에∗ 의해 정의된다.
W {\ W {\ 의 결과 f은 를 따라의 풀백이라고 한다.
다음 ID는 모든 및 에 대해 유지됨
여기서 왼쪽의 브래킷 [···]은 V의 이중 공간과 V의 자연적인 쌍이며, 오른쪽의 브래킷은 W의 이중 공간과의 자연적인 쌍이다. 이 정체는 전치체의 특징을 나타내며,[12] 정식으로 조정의 정의와 유사하다.
할당 f ↦ f는∗ V에서 W로 가는 선형 연산자의 공간과∗ W에서 V로∗ 가는 선형 연산자의 공간 사이에 주입식 선형 지도를 생성한다. 이 동형성은 W가 유한 차원일 경우에만 이형성이다. V = W이면 선형 지도의 공간은 사실 지도 구성상 대수학이고, 그 다음에는 (fg)∗ = gf라는 뜻의∗∗ 알헤브라의 반호몰피즘이다. 범주 이론의 언어에서 벡터 공간의 이중과 선형 지도의 전이를 취하는 것은 그러므로 F를 통한 벡터 공간의 범주에서 그 자체로 역행하는 펑터(francravariant functor이다. 이중 듀얼에 자연주사를 사용하여 f와 (f∗)∗를 식별할 수 있다.
선형 지도 f가 V와 W의 두 베이스에 대해 매트릭스 A로 표현되는 경우∗, f는∗ W와∗ V의 이중 베이스에 대해 전치T 매트릭스 A로 표현되며, 따라서 명칭은 다음과 같다. 또는, f는 컬럼 벡터의 왼쪽에 작용하는 A로 표현되므로, f는∗ 행 벡터의 오른쪽에 작용하는 동일한 행렬로 표현된다. 이러한 관점은 R의n 표준 내측 제품에 의해 관련되는데, 이는 행 벡터의 이중 공간을 가진 컬럼 벡터의 공간을 식별한다.
지수 공간 및 전멸기
S를 V의 하위 집합으로 합시다. 여기서∗ S로0 표시된 V의 S의 전멸기는 모든 s에 대해 [f, s] = 0인 선형 함수 f f V의∗ 집합이다. 즉, S는0 모든 선형 함수 f : V → F로 구성되며, S에 대한 제한은 f = 0으로 사라진다. 유한 치수 벡터 공간 내에서, 전멸기는 직교 보완물에 이중으로(이형성에 대해)된다.
서브셋의 섬멸자는 그 자체가 벡터 공간이다. 제로 벡터의 전멸기는 전체 이중 공간:{ 0= 전체 공간의 전멸기는 단지 제로 코브터일 뿐이다. ={ } V 더 나아가 V 포함의 하위 집합에 전멸기를 할당하여 S ⊆ T if V if V if if if if V if V.
A와 B가 V의 두 하위 집합이라면
그리고 균등보유 V는 유한한 차원이다. A가i 일부 인덱스 세트 I에 속한 i에 의해 인덱싱된 V 하위 세트 제품군인 경우
특히 A와 B가 V의 서브 스페이스라면
V가 유한한 차원이고 W가 벡터 서브공간이라면
이중 이중 이형성 이형성 V ≈ V∗∗ 하의 두 번째 이중 공간에서 W의 이미지로 식별한 후. 특히 전멸기 형성은 유한차원 벡터 공간의 서브셋 격자에 있는 갈루아 연결이다.
W가 V의 서브스페이스라면, 몫 공간 V/W는 그 자체로 벡터 공간이며, 따라서 이중 공간도 있다. 첫 번째 이형성 정리에서는 W가 f의 커널에 있는 경우에만 기능 f : V → F 인자를 V/W를 통한 V/W로 한다. 그러므로 이형성이 있다.
특히 V가 두 개의 서브 스페이스 A와 B의 직접 합이라면 V는∗ A와0 B의0 직접 합이다.
연속 이중공간
위상 벡터 공간을 다룰 때 기준 F= C R 에 이르는 공간의 연속 선형 함수가 특히 중요하다. 이로써 "지속적 이중공간" 또는 "지속적 이중공간"의 개념이 생기게 되는데, 공간은 대수학적 이중공간 V로 표기되며 V 유클리드 n-공간과 같은 모든 유한차원 규범적 벡터공간 또는 위상적 벡터 공간이다. 대수 이중 일치 그러나 이것은 불연속 선형 지도의 예에서 보듯이 무한 차원 규범된 공간에 대해서는 거짓이다. 그럼에도 불구하고 위상 벡터 공간 이론에서 "지속적인 이중 공간"과 "위상학적 이중 공간"은 종종 "이중 공간"으로 대체된다.
위상적인 벡터 공간 동안 V(위상 벡터 공간의 이론의 의미에서)그것의 지속적인 이중 space,[13]이나 위상 이중 space,[14]거나 이중 space[13][14][15][16]{V\displaystyle}V′{\displaystyle V'}은 정의하는 우주의 모든 연속 선형 functionals φ:V→ F{\displaystyle \varphi.:V\to{\mathbb{F}}}.
특성.
X가 Hausdorff 위상 벡터 공간(TV)이라면 X의 연속 이중 공간은 X의 완성의 연속 이중 공간과 동일하다.[1]
이중 토폴로지
위상학적 벡터 V{\}의 이중 V {\V'}에 토폴로지를 도입하기 위한 표준 구성이 있다 의 경계 하위 집합 {을(를) 수정하십시오 이렇게 하면 Unif의 V {\displaystytype V에 토폴로 토폴로 토폴로드가 제공된다. 수렴 A , 또는 동일한 것, 폼의 세미노름에 의해 생성된 위상
여기서 은(는) V 에서 연속적인 선형 함수이며, 은(는) A. 에서 실행된다.
, 함수 의 net of functionals i {\\varphi 이(가) V V의 함수 } displaysty}을(가)하는 경향이 있는 경우.
일반적으로(그러나 반드시 그렇지는 않음) 클래스 은(는) 다음 조건을 충족해야 한다.
- 의 각 포인트 은(는) 에 속하며
- 각 두 세트 및 A 은(는) C 에 포함되어 있다
- 스칼라에 의한 곱셈 작업 시 이(가) 닫힘:
이러한 요구 사항이 충족되면 의 해당 토폴로지는 Hausdorff이며 세트는
그 지방의 기지를 이루다
여기 가장 중요한 세 가지 특별 사례가 있다.
이(가) 표준 벡터 공간(예: Banach 공간 또는 Hilbert 공간)인 경우, {{\ V의 강력한 위상(사실 스칼라 필드가 완료된 경우 Banach 공간)과 함께 표준으로 규범화된다.
- 의 고정관념 토폴로지는 의 전체 경계 집합에 대한 균일한 수렴의 토폴로지다(따라서 서 A{\{\
- 의 약한 토폴로지는 의 유한 부분 집합에 대한 균일한 수렴의 토폴로지다(따라서 서 A{\{\는 V V의 모든 유한 부분 집합 클래스로 선택할 수 있다).
의 위상 세 가지 선택은 위상 벡터 공간에 대한 반사율 속성의 변형으로 이어진다.
- 에 강력한 위상이 부여되면 그에 상응하는 반사성의 개념은 표준적인 개념으로, 이러한 의미에서 반사적인 공간을 반사적인 공간이라고 부른다.[17]
- 에 고정관념 이중 토폴로지를 부여하면 그에 상응하는 반사성이 고정관념 공간 이론에 제시되는데, 이러한 의미에서 반사적인 공간을 고정관념이라고 한다.
- V에 약한 위상이 부여된 경우, 해당 반사율이 이중 쌍 이론에 제시된다:[18] 이러한 의미에서 반사하는 공간은 위상이 약한 임의(Hausdorff)[19] 국소 볼록 공간이다.
예
1 < p < ∞을 실제 숫자로 하고 Banach 공간 ℓ을 모든 p 시퀀스 a = (an)에 대해 고려한다.
숫자 q by 1/p + 1/q = 1을 정의하십시오. 그리고 ℓ의 연속 이중 자연스럽게ℓ q로:를 주어진 요소 φ ∈(pℓ)′{\displaystyle \varphi \in(\ell ^{p})의}, ℓ q의 해당 요소 시퀀스(φ(en)){\displaystyle(\varphi({\mathbf{e}}_{n}))}이 en{\displaystyle{\mathbf{e}}_{n}}은을 나타내는 식별됩니다. sequen번째 임기는 1이고 다른 모든 임기는 0이다. 반대로 요소 a = (an) ∈ ℓ에 q 따라 ℓ에 p 해당하는 연속 선형 함수 은(는) 다음에 의해 정의된다.
모든 b = (bn) ∈ ℓ p (Hölder의 불평등 참조).
이와 비슷한 방법으로 1 continuous의 연속적인 이중은 ∞ bound(경계된 시퀀스의 공간)과 자연스럽게 동일시된다. 나아가 바나흐 공간 c(모든 수렴 시퀀스의 정합성, 최상 규범)와 c(영0(0으로 수렴되는 시퀀스)의 연속적인 이중은 모두 ℓ과 1 자연스럽게 동일시된다.
리에즈 표현 정리(Riesz presentation organization)에 의해 힐베르트 공간의 연속적인 이중화는 다시 원래의 공간에 대한 반 이질성인 힐베르트 공간이다. 이것은 물리학자들이 양자역학의 수학적 공식화에 사용하는 브라켓 표기법을 만들어낸다.
리에츠-마르코프-카쿠타니 표현 정리에서는, 연속함수의 특정 공간의 연속적인 이중화를 측정을 이용하여 설명할 수 있다.
연속 선형 지도의 전치
T : V → W가 두 위상 벡터 공간 사이의 연속적인 선형 지도라면, (연속) T trans : W → → V′는 이전과 같은 공식으로 정의된다.
결과 기능 T′(φ)은 V′에 있다. 할당 T → T′는 V에서 W로 이어지는 연속 선형 지도의 공간과 W에서 V로 이어지는 선형 지도의 공간 사이에 선형 지도가 생성된다. T와 U가 합성 가능한 연속 선형 맵인 경우
V와 W가 정규화된 공간일 때, L(W′, V′)에서의 전치 표준은 L(V, W)의 전치 표준과 동일하다. 전치되는 몇 가지 성질은 한-바나흐의 정리에 의존한다. 예를 들어, 경계가 있는 선형 지도 T는 전치 T가 주입식인 경우에만 밀도 범위가 있다.
T가 두 바나흐 공간 V와 W 사이의 콤팩트한 선형 지도일 때 transpose T′는 콤팩트하다. 이것은 아르젤라-아스콜리 정리를 이용하여 증명할 수 있다.
V가 힐버트 공간일 때, V로부터 그것의 연속적인 이중 V ′에 반선형 이형성 i가V 있다. V의 모든 경계 선형 지도 T에 대해 전치 및 부선 연산자는 다음을 통해 연결된다.
When T is a continuous linear map between two topological vector spaces V and W, then the transpose T′ is continuous when W′ and V′ are equipped with"compatible" topologies: for example, when for X = V and X = W, both duals X′ have the strong topology β(X′, X) of uniform convergence on bounded sets of X, or both have the weak-∗ topology σ(X′, X) of X에 대한 점적 수렴 전치 T′은 β(W′, W)에서 β(V′, V)까지 또는 σ(W′, W)에서 σ(V′, V)까지 연속된다.
섬멸자
W가 정규 공간 V의 닫힌 선형 하위 공간이라고 가정하고, V and에서 W의 전멸기를 고려한다.
Then, the dual of the quotient V / W can be identified with W⊥, and the dual of W can be identified with the quotient V′ / W⊥.[20] Indeed, let P denote the canonical surjection from V onto the quotient V / W ; then, the transpose P′ is an isometric isomorphism from (V / W )′ into V′, with range equal to W⊥. j가 W에서 V로 주입 지도를 나타내는 경우 transpose j of의 커널은 W:의 전멸기다.
그리고 j′이 등축 이형성 V′ / W → W를⊥ 유도하는 것은 한-바나흐의 정리로부터 따른다.
추가 속성
정규화된 공간 V의 이중성이 분리 가능한 경우 공간 V 그 자체도 분리할 수 있다. 그 반대는 사실이 아니다: 예를 들어, 공간 ℓ은 1 분리할 수 있지만, 그것의 이중 ℓ은 ∞ 분리할 수 없다.
더블 듀얼
In analogy with the case of the algebraic double dual, there is always a naturally defined continuous linear operator Ψ : V → V′′ from a normed space V into its continuous double dual V′′, defined by
As a consequence of the Hahn–Banach theorem, this map is in fact an isometry, meaning ‖ Ψ(x) ‖ = ‖ x ‖ for all x ∈ V. Normed spaces for which the map Ψ is a bijection are called reflexive.
When V is a topological vector space then Ψ(x) can still be defined by the same formula, for every x ∈ V, however several difficulties arise. First, when V is not locally convex, the continuous dual may be equal to { 0 } and the map Ψ trivial. However, if V is Hausdorff and locally convex, the map Ψ is injective from V to the algebraic dual V′∗ of the continuous dual, again as a consequence of the Hahn–Banach theorem.[nb 4]
Second, even in the locally convex setting, several natural vector space topologies can be defined on the continuous dual V′, so that the continuous double dual V′′ is not uniquely defined as a set. Saying that Ψ maps from V to V′′, or in other words, that Ψ(x) is continuous on V′ for every x ∈ V, is a reasonable minimal requirement on the topology of V′, namely that the evaluation mappings
be continuous for the chosen topology on V′. Further, there is still a choice of a topology on V′′, and continuity of Ψ depends upon this choice. As a consequence, defining reflexivity in this framework is more involved than in the normed case.
See also
- Covariance and contravariance of vectors
- Dual module
- Dual norm
- Duality (mathematics)
- Duality (projective geometry)
- Pontryagin duality
- Reciprocal lattice – dual space basis, in crystallography
Notes
- ^ For used in this way, see An Introduction to Manifolds (Tu 2011, p. 19). This notation is sometimes used when is reserved for some other meaning. For instance, in the above text, is frequently used to denote the codifferential of , so that represents the pullback of the form . Halmos (1974, p. 20) uses to denote the algebraic dual of . However, other authors use for the continuous dual, while reserving for the algebraic dual (Trèves 2006, p. 35).
- ^ 양자역학과 같은 많은 영역에서 ⟨··⟩은 V × V에 정의된 sesquilinar 형식을 위해 유보된다.
- ^ a b c 이 글의 몇 가지 주장에는 정당성을 위한 선택의 공리가 필요하다. 임의 벡터 공간에 근거가 있다는 것을 보여주기 위해 선택의 공리가 필요하다: 특히 R에N 근거가 있다는 것을 보여줄 필요가 있다. 또한 무한차원 벡터 공간 V의 이중은 0이 아니므로 V에서 이중으로 이어지는 자연지도가 주입성이라는 것을 보여줄 필요가 있다.
- ^ V가 로컬 볼록하지만 하우스도르프가 아닌 경우, of의 커널은 {0}을(를) 포함하는 가장 작은 닫힌 하위 공간이다.
참조
- ^ a b 나리치 & 베켄슈타인 2011, 225-273페이지.
- ^ 캣즈넬슨 & 캣즈넬슨(2008) 페이지 37, §2.1.3
- ^ Tu(2011) 페이지 19, §3.1
- ^ 액슬러(2015) 페이지 101, §3.94
- ^ 할모스(1974년) 페이지 20, §13
- ^ Tu(2011) 페이지 19, §3.1
- ^ 할모스(1974년) 페이지 21, §14
- ^ 미스너, 쏘른 & 휠러 1973
- ^ 미스너, Thorne & Wheeler 1973, §2.5
- ^ 맥 레인 & 비르호프 1999, §VI.4
- ^ 할모스(1974년) 페이지 25, 28
- ^ 할모스(1974년) §44
- ^ a b 로버트슨 & 로버트슨 1964, II.2
- ^ a b 샤이퍼 1966, II.4
- ^ 루딘 1973, 3.1
- ^ 부르바키 2003, II.42
- ^ 샤이퍼 1966, IV.5.5
- ^ 샤이퍼 1966, IV.1
- ^ 샤이퍼 1966, IV.1.2
- ^ 루딘 1991년 제4장
참고 문헌 목록
- Axler, Sheldon Jay (2015). Linear Algebra Done Right (3rd ed.). Springer. ISBN 978-3-319-11079-0.
- Bourbaki, Nicolas (1989). Elements of mathematics, Algebra I. Springer-Verlag. ISBN 3-540-64243-9.
- Bourbaki, Nicolas (2003). Elements of mathematics, Topological vector spaces. Springer-Verlag.
- Halmos, Paul Richard (1974) [1958]. Finite-Dimensional Vector Spaces (2nd ed.). Springer. ISBN 0-387-90093-4.
- Katznelson, Yitzhak; Katznelson, Yonatan R. (2008). A (Terse) Introduction to Linear Algebra. American Mathematical Society. ISBN 978-0-8218-4419-9.
- Lang, Serge (2002), Algebra, Graduate Texts in Mathematics, 211 (Revised third ed.), New York: Springer-Verlag, ISBN 978-0-387-95385-4, MR 1878556, Zbl 0984.00001
- Tu, Loring W. (2011). An Introduction to Manifolds (2nd ed.). Springer. ISBN 978-0-8218-4419-9.
- Mac Lane, Saunders; Birkhoff, Garrett (1999). Algebra (3rd ed.). AMS Chelsea Publishing. ISBN 0-8218-1646-2..
- Misner, Charles W.; Thorne, Kip S.; Wheeler, John A. (1973). Gravitation. W. H. Freeman. ISBN 0-7167-0344-0.
- Narici, Lawrence; Beckenstein, Edward (2011). Topological Vector Spaces. Pure and applied mathematics (Second ed.). Boca Raton, FL: CRC Press. ISBN 978-1584888666. OCLC 144216834.
- Rudin, Walter (1973). Functional Analysis. International Series in Pure and Applied Mathematics. 25 (First ed.). New York, NY: McGraw-Hill Science/Engineering/Math. ISBN 9780070542259.
- Rudin, Walter (1991). Functional Analysis. International Series in Pure and Applied Mathematics. 8 (Second ed.). New York, NY: McGraw-Hill Science/Engineering/Math. ISBN 978-0-07-054236-5. OCLC 21163277.
- Robertson, A.P.; Robertson, W. (1964). Topological vector spaces. Cambridge University Press.
- Schaefer, Helmut H. (1966). Topological vector spaces. New York: The Macmillan Company.
- Schaefer, Helmut H.; Wolff, Manfred P. (1999). Topological Vector Spaces. GTM. 8 (Second ed.). New York, NY: Springer New York Imprint Springer. ISBN 978-1-4612-7155-0. OCLC 840278135.
- Trèves, François (2006) [1967]. Topological Vector Spaces, Distributions and Kernels. Mineola, N.Y.: Dover Publications. ISBN 978-0-486-45352-1. OCLC 853623322.

















 해당 이중성 쌍이 소개된 후에만 타당하다.
해당 이중성 쌍이 소개된 후에만 타당하다. 







![{\displaystyle \left[\Phi _{\langle \cdot ,\cdot \rangle }(v),w\right]=\langle v,w\rangle .}](https://wikimedia.org/api/rest_v1/media/math/render/svg/34f7e65aa80831f2103766c54ee6500fdc69cada)
 V의∗ 하위 공간(resp, V가 유한한 경우 모든∗ V)까지 모든 이형성
V의∗ 하위 공간(resp, V가 유한한 경우 모든∗ V)까지 모든 이형성 
![{\displaystyle \langle v,w\rangle _{\Phi }=(\Phi (v))(w)=[\Phi (v),w].\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f781bcee4a5f3ff513ef4f3b594e40b3d0f87184)



 이중
이중








 결과
결과 


![[f^*(\varphi),\, v] = [\varphi,\, f(v)],](https://wikimedia.org/api/rest_v1/media/math/render/svg/7fc543f6edb35635a9ad838b0832d22b6d411b7f)


















 각 포인트
각 포인트 














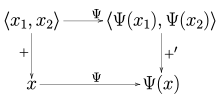
=\varphi (x_{1}+x_{2})=\varphi (x)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/700cff34675c74be68a626464650afe6fea57541)










