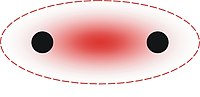
전하 이동 결합
Charge-shift bond전하-시프트 결합은 [1][2]각각 전자가 공유 또는 전달되는 친숙한 공유 결합, 이온 결합 및 금속 결합의 세 종류와 함께 존재하는 새로운 종류의 화학 결합으로 제안되었습니다.전하 이동 결합은 종종 결합된 원자 사이에 전자 밀도를 갖는 것으로 묘사되는 전자의 공유가 아닌 이온 형태의 공명으로부터 안정성을 얻습니다.전하 시프트 결합의 특징은 결합 원자 간의 예측 전자 밀도가 낮다는 것이다.결합된 원자 사이에 전하가 축적되는 것이 반드시 공유 [3]결합의 특징은 아니라는 것은 오랫동안 실험을 통해 알려져 왔다.실험적으로 발견된 낮은 전자 밀도를 설명하기 위해 전하 이동 결합이 사용된 예는 [1.1.1]프로펠란의 역 사면체 탄소 사이의 중심 결합이다.분자 범위에 대한 이론적 계산 결과 전하 이동 결합이 존재함을 알 수 있으며, 대표적인 예로 불소2, F가 있으며, 이는 일반적으로 전형적인 [2]공유 결합을 갖는 것으로 묘사됩니다.전하 시프트 본드(CSB)는 프로틱 이온 액체(PIL)[4]의 양이온-음이온 인터페이스에도 존재하는 것으로 나타났습니다.저자들은 또한 PIL의 CSB 특성이 물리화학적 특성과 어떻게 관련이 있는지를 보여주었다.
밸런스 채권 설명
폴링의 연구로 인한 화학적 결합의 원자가 결합의 관점은 전부는 아니더라도 많은 화학자들에게 친숙합니다.폴링의 화학적 결합에 대한 설명의 근거는 전자쌍 결합이 하나의 공유가와 두 개의 이온 구조의 혼합과 공명을 수반한다는 것입니다.같은 원소의 두 원자 사이의 결합, 즉 동핵 결합에서 폴링은 이온 구조가 전체적인 결합에 주목할 만한 기여를 하지 않는다고 가정했다.이 가정은 1933년 와인바움과 제임스, 쿨리지에[5] 의해 발표된 수소 분자에 대한 계산으로부터 이어졌으며, 이는 이온 형태의 기여가 H-H 결합 에너지의 작은 비율에 불과하다는 것을 보여주었다.헤테로핵결합의 경우, A-X, 폴링은 결합 해리 에너지에 대한 공유가 기여도를 동핵 A-A 및 X-X 결합의 결합 해리 에너지의 평균으로 추정했다.평균과 관측된 결합 에너지 사이의 차이는 이온성 기여에 의한 것으로 가정했다.HCl의 계산은 다음과 같습니다.[5]
| 실제 H-H | 실제 Cl-Cl | H-Clcov 공유 결합 에너지 H-Cl, 산술평균(H-H) 및 (Cl-Cl) | H−Clact 실제 H-Cl | "이온적 기여" H−Clact – H−Clcov | |
|---|---|---|---|---|---|
| 결합 해리 에너지(kcal−1 mol) | 103.5 | 57.8 | 80.6 | 102.7 | 22.1 |
전체 결합 해리 에너지에 대한 이온적 기여는 A와 X 사이의 전기 음성의 차이에서 기인했으며, 이러한 차이는 원소의 개별 전기 음성에 대한 폴링의 계산의 출발점이 되었다.전하 이동 결합의 지지자들은 이온 형태가 동핵 결합의 전체적인 결합 해리 에너지에 주목할 만한 기여를 하지 않는다는 폴링의 가정의 타당성을 재조사했다.그들이 현대 원자가 결합법을 사용하여 발견한 것은 어떤 경우 이온 형태의 기여가 유의하다는 것이다. 가장 주목할 만한 예는 F2, 불소이다. F-F 결합의 결합 에너지는 전적으로 이온의 [2]기여에 기인한다는 것을 그들의 계산이 보여준다.
계산된 결합 에너지
이온 공명 구조의 기여는 전하 이동 공명 에너지(REcs)라고 불리며,[2] 다음과 같은 단일 결합의 수가 계산되었습니다.
| 공유기여금 kcal−1 몰 | 재생cs kcal−1 몰 | % REcs 투고 | |
|---|---|---|---|
| H−H | 95.8 | 9.2 | 8.8 |
| 리튬 | 18.2 | 2.8 | 13.1 |
| H3C−CH3 | 63.9 | 27.2 | 30.2 |
| H2N−NH2 | 22.8 | 43.8 | 65.7 |
| 호오 | –7.1 | 56.9 | 114.3 |
| F−F | –28.4 | 62.2 | 183.9 |
| Cl-클론 | –9.4 | 48.7 | 124.1 |
| H−F | 33.2 | 90.8 | 73.2 |
| H−Cl | 57.1 | 34.9 | 37.9 |
| H3C−Cl | 34.0 | 45.9 | 57.4 |
| H3Si−Cl | 37.0 | 65.1 | 63.8 |
결과는 동핵 결합의 경우 전하 이동 공명 에너지가 유의할 수 있으며, F와2 Cl의 경우2 공명 에너지가 매력적인 성분인 반면 공유 기여는 거부감을 나타낸다.결합축 밀도를 따라 감소된 밀도는 전자 [2][6]밀도를 결정하기 위한 도구인 전자 국재 함수인 ELF를 사용하여 확인할 수 있습니다.
브릿지는 프로펠러로 접합되어 있다.
대체 [1.1.1] 프로펠란의 교두부 결합(교두부 원자 사이의 3주기에 공통적인 반전 결합)을 [7]실험적으로 검토하였다.[1.1.1] 프로펠란에 대한 이론적 연구는 프로펠란이 상당한cs RE 안정화 에너지를 [8]가지고 있다는 것을 보여주었다.
전하 시프트 본딩의 원인
전하 이동 공명 에너지가 유의한 여러 화합물의 분석 결과, 많은 경우 높은 전기 음성도를 가진 원소들이 관여하고 있으며, 이것들은 작은 궤도들을 가지고 있고 단일 쌍으로 풍부하다는 것을 알 수 있다.결합 에너지에 대한 공유가 기여도를 감소시키는 요인으로는 결합 궤도의 중첩이 낮고 Pauli 배타 원리에 의한 반발이 주요 [2]요인인 단일 쌍 결합 약화 효과가 있다.로Pauling 결합 모델에서 하지만, REcs과 그들의 electronegativities이 고립 전자 쌍 결합 무기력하게 하는 부분이 차지할 수 있는 합 사이에 세계적인 상관 관계가 있다고 예상할 수 있는charge−shift 공명 에너지 REcs고 보세의 원자 electronegativities의 차이를 사이에 아무런 상관 관계가 있다.에서g [2]효과[1.1.1]프로펠란에서 반전 결합의 전하 이동 특성은 인접한 "날개" 결합이 공유 기여도를 불안정하게 하기 때문에 Pauli 반발에 기인한다.
전하 이동 결합에 대한 실험적 증거
분자에서 실험적으로 결정된 전자 밀도의 해석은 종종 AIM 이론을 사용한다.이 때 결합경로를 따른 원자핵 간의 전자밀도를 계산하고 밀도가 최소인 결합임계점을 구한다.화학적 결합의 유형을 결정하는 요인은 결합 임계점의 라플라시안 및 전자 밀도입니다.결합 임계점에서 일반적인 공유 결합은 유의한 밀도와 큰 음의 라플라시안을 가진다.반대로 이온 결합에서와 같은 "닫힌 껍질" 상호작용은 작은 전자 밀도와 양의 라플라시안을 [2]가진다.전하 시프트 본드는 양의 라플라시안 또는 작은 라플라시안이어야 합니다.제한된 수의 실험 측정만 이루어졌으며, 양성의 라플라시안 결합을 가진 화합물은 고체24 [9][10]NO의 N-N 결합 및 (Mg-Mg)2+ 이원자 [11][disputed ]구조이다.
레퍼런스
- ^ Sini, Gjergji; Maitre, Philippe; Hiberty, Philippe C.; Shaik, Sason S. (1991). "Covalent, ionic and resonating single bonds". Journal of Molecular Structure: THEOCHEM. 229: 163–188. doi:10.1016/0166-1280(91)90144-9. ISSN 0166-1280.
- ^ a b c d e f g h Shaik, Sason; Danovitch, David; Wei, Wu & Hiberty, Phillippe.C. (2014) [1st. Pub. 2014]. "Chapter 5: The Valence Bond Perspective of the Chemical Bond". In Frenking, Gernod & Shaik, Sason (eds.). The Chemical Bond. Wiley-VCH.
- ^ Dunitz, Jack D.; Seiler, Paul (1983). "The absence of bonding electron density in certain covalent bonds as revealed by x-ray analysis". Journal of the American Chemical Society. 105 (24): 7056–7058. doi:10.1021/ja00362a007. ISSN 0002-7863.
- ^ Patil, Amol Baliram; Bhanage, Bhalchandra Mahadeo (2016). "Modern ab initio valence bond theory calculations reveal charge shift bonding in protic ionic liquids". Physical Chemistry Chemical Physics. 18: 15783–15790. doi:10.1039/C6CP02819E.
- ^ a b 화학적 결합의 본질, L. Pauling, 1940, 2d판, 49-59페이지, 옥스포드 대학 출판부
- ^ Shaik, Sason; Danovich, David; Silvi, Bernard; Lauvergnat, David L.; Hiberty, Philippe C. (2005). "Charge−Shift Bonding—A Class of Electron-Pair Bonds That Emerges from Valence Bond Theory and Is Supported by the Electron Localization Function Approach". Chemistry: A European Journal. 11 (21): 6358–6371. doi:10.1002/chem.200500265. ISSN 0947-6539. PMID 16086335.
- ^ Messerschmidt, Marc; Scheins, Stephan; Grubert, Lutz; Pätzel, Michael; Szeimies, Günter; Paulmann, Carsten; Luger, Peter (2005). "Electron Density and Bonding at Inverted Carbon Atoms: An Experimental Study of a [1.1.1]Propellane Derivative". Angewandte Chemie International Edition. 44 (25): 3925–3928. doi:10.1002/anie.200500169. ISSN 1433-7851.
- ^ Shaik, Sason; Danovich, David; Wu, Wei; Hiberty, Philippe C. (2009). "Charge-shift bonding and its manifestations in chemistry". Nature Chemistry. 1 (6): 443–449. Bibcode:2009NatCh...1..443S. doi:10.1038/nchem.327. ISSN 1755-4330.
- ^ Messerschmidt, Marc; Wagner, Armin; Wong, Ming Wah; Luger, Peter (2002). "Atomic Properties of N2O4 Based on Its Experimental Charge Density". Journal of the American Chemical Society. 124 (5): 732–733. doi:10.1021/ja011802c. ISSN 0002-7863.
- ^ Tsirelson, Vladimir G.; Shishkina, Anastasia V.; Stash, Adam I.; Parsons, Simon (2009). "The experimental and theoretical QTAIMC study of the atomic and molecular interactions in dinitrogen tetroxide" (PDF). Acta Crystallographica Section B. 65 (5): 647–658. doi:10.1107/S0108768109028821. hdl:20.500.11820/5fa0a31e-7a10-466e-a0f3-239f685217e6. ISSN 0108-7681.
- ^ Platts, James A.; Overgaard, Jacob; Jones, Cameron; Iversen, Bo B.; Stasch, Andreas (2011). "First Experimental Characterization of a Non-nuclear Attractor in a Dimeric Magnesium(I) Compound". The Journal of Physical Chemistry A. 115 (2): 194–200. Bibcode:2011JPCA..115..194P. doi:10.1021/jp109547w. ISSN 1089-5639. PMID 21158464.