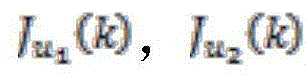CN113788008B - 一种基于纳什-mpc的集成底盘轨迹跟踪控制方法 - Google Patents
一种基于纳什-mpc的集成底盘轨迹跟踪控制方法 Download PDFInfo
- Publication number
- CN113788008B CN113788008B CN202110818448.4A CN202110818448A CN113788008B CN 113788008 B CN113788008 B CN 113788008B CN 202110818448 A CN202110818448 A CN 202110818448A CN 113788008 B CN113788008 B CN 113788008B
- Authority
- CN
- China
- Prior art keywords
- vehicle
- control
- model
- nash
- front wheel
- Prior art date
- Legal status (The legal status is an assumption and is not a legal conclusion. Google has not performed a legal analysis and makes no representation as to the accuracy of the status listed.)
- Active
Links
- 238000000034 method Methods 0.000 title claims abstract description 30
- 238000005457 optimization Methods 0.000 claims abstract description 10
- 239000011159 matrix material Substances 0.000 claims description 6
- 238000006243 chemical reaction Methods 0.000 claims description 3
- 238000005312 nonlinear dynamic Methods 0.000 claims description 3
- 238000005070 sampling Methods 0.000 claims description 3
- 230000000694 effects Effects 0.000 abstract description 6
- 230000008878 coupling Effects 0.000 abstract description 5
- 238000010168 coupling process Methods 0.000 abstract description 5
- 238000005859 coupling reaction Methods 0.000 abstract description 5
- 238000012986 modification Methods 0.000 description 2
- 230000004048 modification Effects 0.000 description 2
- 230000003044 adaptive effect Effects 0.000 description 1
- 238000013528 artificial neural network Methods 0.000 description 1
- 230000009286 beneficial effect Effects 0.000 description 1
- 230000001808 coupling effect Effects 0.000 description 1
- 230000007547 defect Effects 0.000 description 1
Images
Classifications
-
- B—PERFORMING OPERATIONS; TRANSPORTING
- B60—VEHICLES IN GENERAL
- B60W—CONJOINT CONTROL OF VEHICLE SUB-UNITS OF DIFFERENT TYPE OR DIFFERENT FUNCTION; CONTROL SYSTEMS SPECIALLY ADAPTED FOR HYBRID VEHICLES; ROAD VEHICLE DRIVE CONTROL SYSTEMS FOR PURPOSES NOT RELATED TO THE CONTROL OF A PARTICULAR SUB-UNIT
- B60W30/00—Purposes of road vehicle drive control systems not related to the control of a particular sub-unit, e.g. of systems using conjoint control of vehicle sub-units
- B60W30/02—Control of vehicle driving stability
-
- B—PERFORMING OPERATIONS; TRANSPORTING
- B60—VEHICLES IN GENERAL
- B60W—CONJOINT CONTROL OF VEHICLE SUB-UNITS OF DIFFERENT TYPE OR DIFFERENT FUNCTION; CONTROL SYSTEMS SPECIALLY ADAPTED FOR HYBRID VEHICLES; ROAD VEHICLE DRIVE CONTROL SYSTEMS FOR PURPOSES NOT RELATED TO THE CONTROL OF A PARTICULAR SUB-UNIT
- B60W40/00—Estimation or calculation of non-directly measurable driving parameters for road vehicle drive control systems not related to the control of a particular sub unit, e.g. by using mathematical models
- B60W40/10—Estimation or calculation of non-directly measurable driving parameters for road vehicle drive control systems not related to the control of a particular sub unit, e.g. by using mathematical models related to vehicle motion
-
- Y—GENERAL TAGGING OF NEW TECHNOLOGICAL DEVELOPMENTS; GENERAL TAGGING OF CROSS-SECTIONAL TECHNOLOGIES SPANNING OVER SEVERAL SECTIONS OF THE IPC; TECHNICAL SUBJECTS COVERED BY FORMER USPC CROSS-REFERENCE ART COLLECTIONS [XRACs] AND DIGESTS
- Y02—TECHNOLOGIES OR APPLICATIONS FOR MITIGATION OR ADAPTATION AGAINST CLIMATE CHANGE
- Y02T—CLIMATE CHANGE MITIGATION TECHNOLOGIES RELATED TO TRANSPORTATION
- Y02T10/00—Road transport of goods or passengers
- Y02T10/10—Internal combustion engine [ICE] based vehicles
- Y02T10/40—Engine management systems
Landscapes
- Engineering & Computer Science (AREA)
- Automation & Control Theory (AREA)
- Transportation (AREA)
- Mechanical Engineering (AREA)
- Physics & Mathematics (AREA)
- Mathematical Physics (AREA)
- Steering Control In Accordance With Driving Conditions (AREA)
- Control Of Driving Devices And Active Controlling Of Vehicle (AREA)
Abstract
本发明公开了一种基于纳什‑MPC的集成底盘轨迹跟踪控制方法,包括以下步骤获取上层决策模块规划的参考轨迹和参考速度;建立车辆动力学非线性模型;对车辆动力学模型进行线性化,然后再对线性车辆模型进行离散化;分别以前轮转角和车辆速度为控制量建立控制目标函数,并设置两个控制量和控制量增量的约束条件;建立两个控制目标函数间的纳什均衡方程,将控制问题转化为纳什优化问题进行求解。本发明考虑集成底盘车辆纵向和横向运动的耦合关系,对车辆前轮转角和车辆速度进行协同控制,通过将纳什均衡理论和MPC控制结合,建立前轮转角和车辆速度的纳什‑MPC优化模型,能够提高车辆纵向和横向的跟踪控制效果。
Description
技术领域
本发明属于集成底盘、轨迹跟踪技术领域,具体为一种基于纳什-MPC的集成底盘轨迹跟踪控制方法
背景技术
随着汽车工业的发展,如何控制车辆很好地跟踪给的目标转角和目标车速十分重要。目前车辆的控制主要分为车辆的纵向控制和横向控制。车辆纵向控制的主要控制参数为车辆的速度,车辆的速度由集成底盘的驱动与制动系统决定。车辆横向控制的主要控制参数为车辆的前轮转角,前轮转角由底盘的转向系统决定。现有的控制方法通常将纵向控制和横向控制分开,单独对纵向或者横向进行控制。CN107942679A--基于模糊免疫神经网络算法的全向底盘控制方法,其只是提供一种简单的底板控制方法。然而,车辆的纵向运动和横向运动存在较强的耦合作用,单独对两者进行控制往往无法取得较好的控制效果。在纵向控制方面,自适应巡航控制应用十分广泛,但其只适用于简单的跟车或直线行驶场景,无法适用于换道工况。模型预测控制(MPC)是常用的横向控制方法,但其往往认为车辆速度保持不变,无法达到最佳的控制效果。因此,考虑车辆纵横向耦合,同时对前轮转角和车辆速度进行控制能够提高车辆的整体控制性能。
发明内容
针对上述现有技术的不足,本发明的目的在于提供一种基于纳什-MPC的集成底盘轨迹跟踪控制方法,以解决集成底盘车辆纵横向耦合的问题,同时对前轮转角和车辆速度进行优化控制,实现车辆更好的跟踪控制效果。
为达到上述目的,本发明采用的技术方案如下:
一种基于纳什-MPC的集成底盘轨迹跟踪控制方法,包括以下步骤:
步骤1:获取上层决策模块规划的参考轨迹和参考速度;
步骤2:建立车辆动力学非线性模型;
步骤3:对车辆动力学模型进行线性化,然后再对线性车辆模型进行离散化;
步骤4:分别以前轮转角和车辆速度为控制量建立控制目标函数,并设置两个控制量和控制量增量的约束条件;
步骤5:建立两个控制目标函数间的纳什均衡方程,将控制问题转化为纳什优化问题进行求解。
作为优选,所述步骤2)的车辆动力学模型包括车辆单轨模型和轮胎模型,具体为:
2.1)车辆单轨模型具体为:
式中,m为车辆质量,x,y分别为车辆在车辆坐标系下的纵向和横向位置,为车辆的横摆角,a,b分别为质心到前后轴的距离,Iz为车辆绕z轴的转动惯量,Fxf,Fxr为前后轮在x方向受到的合力,Fyf,Fyr为前后轮在y方向受到的合力。前后路在x和y方向上受到的合力与纵、侧向力的转换关系为:
Fxf=Flfcosδf-Fcfsinδf
Fxr=Flrcosδr-Fcrsinδr
Fyf=Flfcosδf+Fcfsinδf
Fyr=Flrcosδr+Fcrsinδr
式中,Flf,Fcf为前轮的侧向力和纵向力,Flr,Fcr为后轮的侧向力和纵向力,δf为前轮转角;
2.2)轮胎模型为魔术公式经验模型,具体为:
y(x)=Dsin{C arctan[Bx-E(Bx-arctan(Bx))]}
式中,y(x)代表侧偏力、回正力矩等;x代表轮胎侧偏角或滑移率;D代表峰值因子;C代表曲线形状因子;B代表刚度因子;E代表曲线曲率因子。
2.3)根据小角度假设,即cosθ≈1,sinθ≈θ,tanθ≈θ,可以得到前后轮胎的侧向力和纵向力:
Flf=Clfsf
Flr=Clrsr
式中,Ccf,Ccr,Clf,Clr分别为前轮侧偏刚度、后轮侧偏刚度、前轮纵向刚度和后轮纵向刚度,sf,sr分别为前、后轮滑移率。通过车辆单轨模型和轮胎模型,得到最终的车辆动力学非线性模型:
式中,X,Y分别为车辆在大地坐标系下的纵向和横向位置。
作为优选,所述步骤3)具体包括:
3.1)线性化车辆动力学模型:
3.2)采用一阶差商的方法对线性时变方程进行离散化处理,得到离散的状态空间表达式:
ξdyn(t+1)=Adyn(k)ξdyn(k)+Bdyn(k)udyn(k)
式中,Adyn(k)=I+TAdyn(t),Bdyn(k)=TBdyn(t),I为单位矩阵,T为采样时间。
作为优选,所述步骤4)具体包括:
4.1)所建立的目标函数要能保证车辆快速且平稳地追踪期望轨迹,需要加入对系统状态量和控制量地优化,分别建立前轮转角和车辆速度的控制目标函数,具体为:
式中,分别为前轮转角和车辆速度的目标函数,ΔU1,ΔU2分别为前轮转角增量和速度增量,Np为预测时域,Nc为控制时域,Q,R为权重矩阵,u1,ref,u2,ref分别为参考前轮转角和参考车辆速度,ρ1,ε1为目标函数/>权重系数和松弛因子,ρ2,ε2为目标函数/>权重系数和松弛因子;
4.2)分别建立两个控制量以及控制增量的约束条件:
u1min(t+k)≤u1(t+k)≤u1max(t+k)
u2min(t+k)≤u1(t+k)≤u2max(t+k)
ΔU1min(t+k)≤ΔU1(t+k)≤ΔU1max(t+k)
ΔU2min(t+k)≤ΔU2(t+k)≤ΔU2max(t+k)
k=0,1,…,Nc-1
式中,Δumin,Δumax,ΔUmin,ΔUmax分别为控制量和控制量增量的最小和最大值。
作为优选,所述步骤5)具体为:
建立两个目标函数的纳什均衡,将其转化为纳什优化问题:
s.t.u1min(t+k)≤u1(t+k)≤u1max(t+k)
u2min(t+k)≤u1(t+k)≤u2max(t+k)
ΔU1min(t+k)≤ΔU1(t+k)≤ΔU1max(t+k)
ΔU2min(t+k)≤ΔU2(t+k)≤ΔU2max(t+k)
通过求解上式所示的问题,得到最优的前轮转角和车辆速度。
本发明的有益效果:
本发明考虑集成底盘车辆纵向和横向运动的耦合关系,对车辆前轮转角和车辆速度进行协同控制,通过将纳什均衡理论和MPC控制结合,建立前轮转角和车辆速度的纳什-MPC优化模型,能够提高车辆纵向和横向的跟踪控制效果。
附图说明
图1为车辆动力学非线性模型。
图2为本发明纳什-MPC控制方法流程。
具体实施方式
下面结合附图与实施例对本发明作进一步详细描述。
实施例1
一种基于纳什-MPC的集成底盘轨迹跟踪控制方法,包括以下步骤:
步骤1:获取上层决策模块规划的参考轨迹和参考速度;
步骤2:建立车辆动力学非线性模型;
步骤3:对车辆动力学模型进行线性化,然后再对线性车辆模型进行离散化;
步骤4:分别以前轮转角和车辆速度为控制量建立控制目标函数,并设置两个控制量和控制量增量的约束条件;
步骤5:建立两个控制目标函数间的纳什均衡方程,将控制问题转化为纳什优化问题进行求解。
本实施例中,所述步骤2)的车辆动力学模型包括车辆单轨模型和轮胎模型,具体为:
2.1)车辆单轨模型具体为:
式中,m为车辆质量,x,y分别为车辆在车辆坐标系下的纵向和横向位置,为车辆的横摆角,a,b分别为质心到前后轴的距离,Iz为车辆绕z轴的转动惯量,Fxf,Fxr为前后轮在x方向受到的合力,Fyf,Fyr为前后轮在y方向受到的合力。前后路在x和y方向上受到的合力与纵、侧向力的转换关系为:
Fxf=Flfcosδf-Fcfsinδf
Fxr=Flrcosδr-Fcrsinδr
Fyf=Flfcosδf+Fcfsinδf
Fyr=Flrcosδr+Fcrsinδr
式中,Flf,Fcf为前轮的侧向力和纵向力,Flr,Fcr为后轮的侧向力和纵向力,δf为前轮转角;
2.2)轮胎模型为魔术公式经验模型,具体为:
y(x)=Dsin{C arctan[Bx-E(Bx-arctan(Bx))]}
式中,y(x)代表侧偏力、回正力矩等;x代表轮胎侧偏角或滑移率;D代表峰值因子;C代表曲线形状因子;B代表刚度因子;E代表曲线曲率因子。
2.3)根据小角度假设,即cosθ≈1,sinθ≈θ,tanθ≈θ,可以得到前后轮胎的侧向力和纵向力:
Flf=Clfsf
Flr=Clrsr
式中,Ccf,Ccr,Clf,Clr分别为前轮侧偏刚度、后轮侧偏刚度、前轮纵向刚度和后轮纵向刚度,sf,sr分别为前、后轮滑移率。通过车辆单轨模型和轮胎模型,得到最终的车辆动力学非线性模型:
式中,X,Y分别为车辆在大地坐标系下的纵向和横向位置。
作为优选,所述步骤3)具体包括:
3.1)线性化车辆动力学模型:
3.2)采用一阶差商的方法对线性时变方程进行离散化处理,得到离散的状态空间表达式:
ξdyn(k+1)=Adyn(k)ξdyn(k)+Bdyn(k)udyn(k)
式中,Adyn(k)=I+TAdyn(t),Bdyn(k)=TBdyn(t),I为单位矩阵,T为采样时间。
作为优选,所述步骤4)具体包括:
4.1)所建立的目标函数要能保证车辆快速且平稳地追踪期望轨迹,需要加入对系统状态量和控制量地优化,分别建立前轮转角和车辆速度的控制目标函数,具体为:
式中,分别为前轮转角和车辆速度的目标函数,ΔU1,ΔU2分别为前轮转角增量和速度增量,Np为预测时域,Nc为控制时域,Q,R为权重矩阵,u1,ref,u2,ref分别为参考前轮转角和参考车辆速度,ρ1,ε1为目标函数/>权重系数和松弛因子,ρ2,ε2为目标函数/>权重系数和松弛因子;
4.2)分别建立两个控制量以及控制增量的约束条件:
u1min(t+k)≤u1(t+k)≤u1max(t+k)
u2min(t+k)≤u1(t+k)≤u2max(t+k)
ΔU1min(t+k)≤ΔU1(t+k)≤ΔU1max(t+k)
ΔU2min(t+k)≤ΔU2(t+k)≤ΔU2max(t+k)
k=0,1,…,Nc-1
式中,Δumin,Δumax,ΔUmin,ΔUmax分别为控制量和控制量增量的最小和最大值。
作为优选,所述步骤5)具体为:
建立两个目标函数的纳什均衡,将其转化为纳什优化问题:
s.t.u1min(t+k)≤u1(t+k)≤u1max(t+k)
u2min(t+k)≤u1(t+k)≤u2max(t+k)
ΔU1min(t+k)≤ΔU1(t+k)≤ΔU1max(t+k)
ΔU2min(t+k)≤ΔU2(t+k)≤ΔU2max(t+k)
通过求解上式所示的问题,得到最优的前轮转角和车辆速度。从而为车辆提供可靠的参数数据,保证车辆控制更加精准。
本发明考虑集成底盘车辆纵向和横向运动的耦合关系,对车辆前轮转角和车辆速度进行协同控制,通过将纳什均衡理论和MPC控制结合,建立前轮转角和车辆速度的纳什-MPC优化模型,能够提高车辆纵向和横向的跟踪控制效果。
本发明具体应用途径很多,以上所述仅是本发明的优选实施方式,应当指出,对于本技术领域的普通技术人员来说,在不脱离本发明原理的前提下,还可以作出若干改进,这些改进也应视为本发明的保护范围。
Claims (2)
1.一种基于纳什-MPC的集成底盘轨迹跟踪控制方法,其特征在于:包括以下步骤:
步骤1:获取上层决策模块规划的参考轨迹和参考速度;
步骤2:建立车辆动力学非线性模型;
步骤3:对车辆动力学模型进行线性化,然后再对线性车辆模型进行离散化;
步骤4:分别以前轮转角和车辆速度为控制量建立控制目标函数,并设置两个控制量和控制量增量的约束条件;
步骤5:建立两个控制目标函数间的纳什均衡方程,将控制问题转化为纳什优化问题进行求解;所述步骤2)的车辆动力学模型包括车辆单轨模型和轮胎模型,具体为:
2.1)车辆单轨模型具体为:
式中,m为车辆质量,x,y分别为车辆在车辆坐标系下的纵向和横向位置,为车辆的横摆角,a,b分别为质心到前后轴的距离,Iz为车辆绕z轴的转动惯量,Fxf,Fxr为前后轮在x方向受到的合力,Fyf,Fyr为前后轮在y方向受到的合力,前后轮在x和y方向上受到的合力与纵、侧向力的转换关系为:
Fxf=Flfcosδf-Fefsinδf
Fxr=Flrcosδr-Fcrsinδr
Fyf=Flfcosδf+Fcfsinδf
Fyr=Flrcosδr+Fersinδr
式中,Flf,Fcf为前轮的侧向力和纵向力,Flr,Fcr为后轮的侧向力和纵向力,δf为前轮转角;
2.2)轮胎模型为魔术公式经验模型,具体为:
y(x)=D sin{C arctan[Bx-E(Bx-arctan(Bx))]}
式中,y(x)代表侧偏力、回正力矩等;x代表轮胎侧偏角或滑移率;D代表峰值因子;C代表曲线形状因子;B代表刚度因子;E代表曲线曲率因子;
2.3)根据小角度假设,即cosθ≈1,sinθ≈θ,tanθ≈θ,可以得到前后轮胎的侧向力和纵向力:
Flf=Clfsf
Flr=Clrsr
式中,Ccf,Ccr,Clf,Clr分别为前轮侧偏刚度、后轮侧偏刚度、前轮纵向刚度和后轮纵向刚度,sf,sr分别为前、后轮滑移率;通过车辆单轨模型和轮胎模型,得到最终的车辆动力学非线性模型:
式中,X,Y分别为车辆在大地坐标系下的纵向和横向位置;所述步骤3)具体包括:
3.1)线性化车辆动力学模型:
3.2)采用一阶差商的方法对线性时变方程进行离散化处理,得到离散的状态空间表达式:
ξdyn(k+1)=Adyn(k)ξdyn(k)+Bdyn(k)udyn(k)
式中,Adyn(k)=I+TAdyn(t),Bdyn(k)=TBdyn(t),I为单位矩阵,T为采样时间;所述步骤4)具体包括:
4.1)所建立的目标函数要能保证车辆快速且平稳地追踪期望轨迹,需要加入对系统状态量和控制量地优化,分别建立前轮转角和车辆速度的控制目标函数,具体为:
式中,分别为前轮转角和车辆速度的目标函数,ΔU1,ΔU2分别为前轮转角增量和速度增量,Np为预测时域,Nc为控制时域,Q,R为权重矩阵,u1,ref,u2,ref分别为参考前轮转角和参考车辆速度,ρ1,ε1为目标函数/>权重系数和松弛因子,ρ2,ε2为目标函数权重系数和松弛因子;
4.2)分别建立两个控制量以及控制增量的约束条件:
u1min(t+k)≤u1(t+k)≤u1max(t+k)
u2min(t+k)≤u1(t+k)≤u2max(t+k)
ΔU1min(t+k)≤ΔU1(t+k)≤ΔU1max(t+k)
ΔU2min(t+k)≤ΔU2(t+k)≤ΔU2max(t+k)
k=0,1,…,Ne-1
式中,Δumin,Δumax,ΔUmin,ΔUmax分别为控制量和控制量增量的最小和最大值。
Priority Applications (1)
| Application Number | Priority Date | Filing Date | Title |
|---|---|---|---|
| CN202110818448.4A CN113788008B (zh) | 2021-07-20 | 2021-07-20 | 一种基于纳什-mpc的集成底盘轨迹跟踪控制方法 |
Applications Claiming Priority (1)
| Application Number | Priority Date | Filing Date | Title |
|---|---|---|---|
| CN202110818448.4A CN113788008B (zh) | 2021-07-20 | 2021-07-20 | 一种基于纳什-mpc的集成底盘轨迹跟踪控制方法 |
Publications (2)
| Publication Number | Publication Date |
|---|---|
| CN113788008A CN113788008A (zh) | 2021-12-14 |
| CN113788008B true CN113788008B (zh) | 2023-06-27 |
Family
ID=79181149
Family Applications (1)
| Application Number | Title | Priority Date | Filing Date |
|---|---|---|---|
| CN202110818448.4A Active CN113788008B (zh) | 2021-07-20 | 2021-07-20 | 一种基于纳什-mpc的集成底盘轨迹跟踪控制方法 |
Country Status (1)
| Country | Link |
|---|---|
| CN (1) | CN113788008B (zh) |
Families Citing this family (3)
| Publication number | Priority date | Publication date | Assignee | Title |
|---|---|---|---|---|
| CN114987604B (zh) * | 2022-06-07 | 2023-04-04 | 南京航空航天大学 | 一种多源耦合滑板底盘系统及其多目标集成控制方法 |
| CN115230720A (zh) * | 2022-07-22 | 2022-10-25 | 江苏大学 | 基于深度拉格朗日神经网络的自动驾驶车辆控制系统及方法 |
| CN115158292A (zh) * | 2022-07-22 | 2022-10-11 | 江苏大学 | 一种自动驾驶商用车载荷与道路自适应控制系统及方法 |
Citations (2)
| Publication number | Priority date | Publication date | Assignee | Title |
|---|---|---|---|---|
| CN111897344A (zh) * | 2020-08-14 | 2020-11-06 | 清华大学 | 一种兼顾稳定性的自动驾驶汽车路径跟踪控制方法 |
| DE102020130387A1 (de) * | 2019-11-19 | 2021-05-20 | Ford Global Technologies, Llc | Fahrzeugwegplanung |
Family Cites Families (6)
| Publication number | Priority date | Publication date | Assignee | Title |
|---|---|---|---|---|
| FR3017095B1 (fr) * | 2014-02-03 | 2017-05-12 | Renault Sas | Procede de suivi de trajectoire d'un vehicule automobile et vehicule associe |
| CN107521496B (zh) * | 2017-09-08 | 2018-11-13 | 吉林大学 | 一种无人车辆的横纵向协调控制轨迹跟随控制方法 |
| CN108454623B (zh) * | 2018-01-22 | 2019-10-29 | 大连理工大学 | 一种四轮独立驱动无人驾驶电动车辆轨迹跟踪控制方法 |
| CN109799828B (zh) * | 2019-02-28 | 2022-05-24 | 北京智行者科技有限公司 | 自动驾驶车辆横纵向协调控制方法 |
| CN110588633B (zh) * | 2019-08-21 | 2021-07-20 | 江苏大学 | 一种智能汽车极限工况下路径跟踪与稳定控制方法 |
| CN111258323B (zh) * | 2020-03-30 | 2021-10-26 | 华南理工大学 | 一种智能车辆轨迹规划与跟踪的联合控制方法 |
-
2021
- 2021-07-20 CN CN202110818448.4A patent/CN113788008B/zh active Active
Patent Citations (2)
| Publication number | Priority date | Publication date | Assignee | Title |
|---|---|---|---|---|
| DE102020130387A1 (de) * | 2019-11-19 | 2021-05-20 | Ford Global Technologies, Llc | Fahrzeugwegplanung |
| CN111897344A (zh) * | 2020-08-14 | 2020-11-06 | 清华大学 | 一种兼顾稳定性的自动驾驶汽车路径跟踪控制方法 |
Also Published As
| Publication number | Publication date |
|---|---|
| CN113788008A (zh) | 2021-12-14 |
Similar Documents
| Publication | Publication Date | Title |
|---|---|---|
| CN113788008B (zh) | 一种基于纳什-mpc的集成底盘轨迹跟踪控制方法 | |
| CN112092815B (zh) | 一种基于模型预测的车辆换道轨迹跟踪控制方法 | |
| CN110329255B (zh) | 一种基于人机协同策略的车道偏离辅助控制方法 | |
| CN107042841B (zh) | 一种轮毂电机驱动电动汽车差动助力转向稳定性控制方法 | |
| CN111240187B (zh) | 一种基于车辆误差模型的车辆轨迹跟踪控制算法 | |
| CN109976159A (zh) | 基于安全可控域的智能车辆横向控制方法 | |
| CN110588633B (zh) | 一种智能汽车极限工况下路径跟踪与稳定控制方法 | |
| CN109969183A (zh) | 基于安全可控域的弯道跟车控制方法 | |
| CN110481343A (zh) | 四轮轮毂电机驱动汽车力矩补偿的组合二阶滑模控制方法 | |
| CN108107732A (zh) | 主动前轮转向和直接横摆力矩联合的汽车稳定性控制方法 | |
| CN110696793A (zh) | 一种四轮转向联合差动制动的智能车辆分层控制方法 | |
| CN108107731A (zh) | 一种基于轮胎非线性特性的汽车稳定性控制方法 | |
| CN108732921A (zh) | 一种自动驾驶汽车横向可拓预瞄切换控制方法 | |
| CN108973769A (zh) | 一种全线控电动汽车路径跟踪控制方法 | |
| CN113460088A (zh) | 基于非线性轮胎和驾驶员模型的无人车路径跟踪控制方法 | |
| CN116872910A (zh) | 无人驾驶车辆轨迹跟踪与横摆稳定性控制方法及系统 | |
| Zhang et al. | Development of an active front steering (AFS) system with QFT control | |
| Chen et al. | Path tracking control of four-wheel independent steering electric vehicles based on optimal control | |
| Li et al. | Adaptive sliding mode control of lateral stability of four wheel hub electric vehicles | |
| CN116834754A (zh) | 一种自动驾驶车辆自适应调速的横纵协同控制方法 | |
| CN115675459A (zh) | 一种智能车辆及其路径跟踪的控制方法、装置和存储介质 | |
| Yih et al. | Steer-by-wire for vehicle state estimation and control | |
| CN116691668A (zh) | 一种大型智能车辆的横向控制方法 | |
| CN114896694B (zh) | 一种基于两点预瞄的路径跟踪控制方法 | |
| CN114044003B (zh) | 前后双轴转向车辆的循迹控制方法 |
Legal Events
| Date | Code | Title | Description |
|---|---|---|---|
| PB01 | Publication | ||
| PB01 | Publication | ||
| SE01 | Entry into force of request for substantive examination | ||
| SE01 | Entry into force of request for substantive examination | ||
| GR01 | Patent grant | ||
| GR01 | Patent grant |