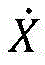CN112092815B - 一种基于模型预测的车辆换道轨迹跟踪控制方法 - Google Patents
一种基于模型预测的车辆换道轨迹跟踪控制方法 Download PDFInfo
- Publication number
- CN112092815B CN112092815B CN202010909744.0A CN202010909744A CN112092815B CN 112092815 B CN112092815 B CN 112092815B CN 202010909744 A CN202010909744 A CN 202010909744A CN 112092815 B CN112092815 B CN 112092815B
- Authority
- CN
- China
- Prior art keywords
- vehicle
- lane
- time
- changing
- expected
- Prior art date
- Legal status (The legal status is an assumption and is not a legal conclusion. Google has not performed a legal analysis and makes no representation as to the accuracy of the status listed.)
- Active
Links
- 238000000034 method Methods 0.000 title claims abstract description 44
- 230000001133 acceleration Effects 0.000 claims abstract description 28
- 238000004458 analytical method Methods 0.000 claims abstract description 6
- 239000011159 matrix material Substances 0.000 claims description 18
- 238000006073 displacement reaction Methods 0.000 claims description 9
- 238000005457 optimization Methods 0.000 claims description 9
- 238000005096 rolling process Methods 0.000 claims description 3
- 238000005070 sampling Methods 0.000 claims description 3
- 230000003190 augmentative effect Effects 0.000 claims description 2
- 230000010354 integration Effects 0.000 claims description 2
- 230000017105 transposition Effects 0.000 claims description 2
- 230000003247 decreasing effect Effects 0.000 claims 1
- 238000004364 calculation method Methods 0.000 description 4
- 230000006399 behavior Effects 0.000 description 3
- 238000013461 design Methods 0.000 description 3
- 238000010586 diagram Methods 0.000 description 2
- 238000005312 nonlinear dynamic Methods 0.000 description 2
- 238000011160 research Methods 0.000 description 2
- 238000004088 simulation Methods 0.000 description 2
- 238000012795 verification Methods 0.000 description 2
- 241000287196 Asthenes Species 0.000 description 1
- 241000218691 Cupressaceae Species 0.000 description 1
- 206010063385 Intellectualisation Diseases 0.000 description 1
- 230000003044 adaptive effect Effects 0.000 description 1
- 238000004422 calculation algorithm Methods 0.000 description 1
- 238000012937 correction Methods 0.000 description 1
- 230000001419 dependent effect Effects 0.000 description 1
- 238000011161 development Methods 0.000 description 1
- 230000018109 developmental process Effects 0.000 description 1
- 238000005516 engineering process Methods 0.000 description 1
- 230000007613 environmental effect Effects 0.000 description 1
- 238000012886 linear function Methods 0.000 description 1
- 238000002620 method output Methods 0.000 description 1
- 230000011218 segmentation Effects 0.000 description 1
- 230000006641 stabilisation Effects 0.000 description 1
- 238000011105 stabilization Methods 0.000 description 1
- 230000001131 transforming effect Effects 0.000 description 1
Images
Classifications
-
- B—PERFORMING OPERATIONS; TRANSPORTING
- B60—VEHICLES IN GENERAL
- B60W—CONJOINT CONTROL OF VEHICLE SUB-UNITS OF DIFFERENT TYPE OR DIFFERENT FUNCTION; CONTROL SYSTEMS SPECIALLY ADAPTED FOR HYBRID VEHICLES; ROAD VEHICLE DRIVE CONTROL SYSTEMS FOR PURPOSES NOT RELATED TO THE CONTROL OF A PARTICULAR SUB-UNIT
- B60W30/00—Purposes of road vehicle drive control systems not related to the control of a particular sub-unit, e.g. of systems using conjoint control of vehicle sub-units
- B60W30/18—Propelling the vehicle
- B60W30/18009—Propelling the vehicle related to particular drive situations
- B60W30/18163—Lane change; Overtaking manoeuvres
-
- B—PERFORMING OPERATIONS; TRANSPORTING
- B60—VEHICLES IN GENERAL
- B60W—CONJOINT CONTROL OF VEHICLE SUB-UNITS OF DIFFERENT TYPE OR DIFFERENT FUNCTION; CONTROL SYSTEMS SPECIALLY ADAPTED FOR HYBRID VEHICLES; ROAD VEHICLE DRIVE CONTROL SYSTEMS FOR PURPOSES NOT RELATED TO THE CONTROL OF A PARTICULAR SUB-UNIT
- B60W50/00—Details of control systems for road vehicle drive control not related to the control of a particular sub-unit, e.g. process diagnostic or vehicle driver interfaces
-
- B—PERFORMING OPERATIONS; TRANSPORTING
- B60—VEHICLES IN GENERAL
- B60W—CONJOINT CONTROL OF VEHICLE SUB-UNITS OF DIFFERENT TYPE OR DIFFERENT FUNCTION; CONTROL SYSTEMS SPECIALLY ADAPTED FOR HYBRID VEHICLES; ROAD VEHICLE DRIVE CONTROL SYSTEMS FOR PURPOSES NOT RELATED TO THE CONTROL OF A PARTICULAR SUB-UNIT
- B60W50/00—Details of control systems for road vehicle drive control not related to the control of a particular sub-unit, e.g. process diagnostic or vehicle driver interfaces
- B60W2050/0001—Details of the control system
- B60W2050/0019—Control system elements or transfer functions
- B60W2050/0028—Mathematical models, e.g. for simulation
- B60W2050/0031—Mathematical model of the vehicle
- B60W2050/0034—Multiple-track, 2D vehicle model, e.g. four-wheel model
Landscapes
- Engineering & Computer Science (AREA)
- Automation & Control Theory (AREA)
- Transportation (AREA)
- Mechanical Engineering (AREA)
- Human Computer Interaction (AREA)
- Control Of Driving Devices And Active Controlling Of Vehicle (AREA)
- Steering Control In Accordance With Driving Conditions (AREA)
Abstract
本发明公开了一种基于模型预测的车辆换道轨迹跟踪控制方法,属于智能车辆控制技术领域。本发明应用在车辆高级驾驶辅助系统上,包括:建立基于正反梯形横摆角加速度的换道期望轨迹模型;对换道车辆进行受力分析,建立三自由度车辆动力学模型;将非线性的三自由度车辆动力学模型转化为离散线性预测模型,设计模型预测控制器的目标函数和约束条件,根据期望轨迹来计算输出控制车辆运动的物理量。本发明规划的换道期望轨迹提高了驾驶员舒适性,控制量包括汽车行驶的驱动力和前轮转角,满足横向换道需求的同时,可保证较高精度的车速控制,控制跟踪的鲁棒性较强,控制精度较高,可有效减小横向跟踪误差。
Description
技术领域
本发明涉及一种车辆换道轨迹跟踪控制方法,具体涉及智能车辆在换道行驶中对换道轨迹的规划和控制方法,属于智能车辆控制技术领域。
背景技术
近年来,随着人们对车辆智能化、安全化的要求越来越高,传统车辆已经不再满足驾驶员的需求。高级驾驶辅助系统(ADAS)通过传感器采集环境信息,通过计算与分析,可以提醒驾驶员潜在的危险和辅助驾驶员进行驾驶,显著提高了行车安全性和舒适性。近年来,针对ADAS的研究与应用也越来越广泛。
在智能车辆的行驶过程中,车辆跟驰和换道是两种不同的行为,车辆跟驰是通过调整车辆的速度和加速度,控制自身与前车保持一定安全距离,使车辆达到安全行驶的目的。针对跟驰的驾驶辅助系统——自适应巡航控制(ACC)已经应用于市场中的车型中。车辆换道是通过调整车辆的速度和前轮转角从初始车道沿着期望轨迹行驶到目标车道,且过程中不和两条车道上正常行驶的车辆发生碰撞。换道行为较为复杂,涉及规划,决策和控制等,换道辅助系统的设计和研究还远远不如跟驰辅助系统。
目前大多数换道辅助系统根据换道初始时刻和结束时刻的位姿、速度约束条件来计算期望换道轨迹,并没有考虑换道过程中的速度变化和横摆角变化要求,如参考文件1(柏海舰,申剑峰,卫立阳.无人车“三阶段”换道轨迹规划过程分析[J].合肥工业大学学报(自然科学版),2019,42(05):577-584+676)。
轨迹跟踪方面更多地考虑横向跟踪,不考虑换道车辆的纵向速度跟踪,不能保证对期望换道轨迹的纵向跟踪精度,如参考文件2(白成盼,惠飞,景首才.基于微分平坦与MPC的智能车换道控制算法[J].计算机技术与发展,2020,30(05):16-20)。
发明内容
本发明针对目前车辆换道轨迹规划中,对换道过程中乘车舒适性约束考虑不足,忽略换道过程中的纵向速度控制等问题,提供了一种基于模型预测的车辆换道轨迹跟踪控制方法。
本发明提出的一种基于模型预测的车辆换道轨迹跟踪控制方法,包括如下步骤:
步骤一、建立基于正反梯形横摆角加速度的换道期望换道轨迹模型,然后利用期望总换道横向位移,期望横摆角加速度曲线,得到期望换道轨迹参数,再对期望换道轨迹拟合成高阶多项式;
所述的期望总换道横向位移为车道宽度;所述的期望横摆角加速度曲线是将车辆换道过程中的期望横摆角加速度表示为随时间呈正反梯形变化规律的曲线,其中,正梯形或反梯形的下底对应的值为0,上底对应的值为期望横摆角加速度最大值或最小值为未知参数;所述的期望换道轨迹参数包括
步骤二、对换道车辆进行受力分析,建立三自由度车辆动力学模型;
步骤三、将非线性的三自由度车辆动力学模型转化为离散线性预测模型,建立模型预测控制器的目标函数和约束条件,以控制车辆跟踪期望轨迹的偏差尽可能小。控制器在根据步骤一的期望换道轨迹获得预测时刻的车辆质心坐标后,计算输出控制车辆运动的物理量。
所述的离散线性预测模型中,设置状态变量为控制变量为u=[δf,Fxf]T,输出变量为设换道车辆坐标系为oxyz,地面坐标系为OXYZ,X、Y分别为换道车辆质心在地面坐标系下的X坐标和Y坐标,分别为换道车辆横摆角和横摆角速度,分别为换道车辆质心绝对速度的x轴分量和y轴分量,δf为换道车辆前轮转角,Fxf为换道车辆的前轮驱动力在x轴上的分量,上角标T表示转置。
所述的模型预测控制器用于计算控制变量增量序列,所述的目标函数是求取控制变量的增量序列,使得车辆跟踪期望轨迹的偏差最小;所述的约束条件包括为控制变量增量设置上下界,设置变道车辆的前轮胎和后轮胎的侧偏角尽可能小,不超过设置的阈值。
本发明的车辆换道轨迹跟踪控制方法与现有技术相比,具有以下优点:
(1)本发明规划的换道期望轨迹,考虑了横摆角加速度,建立的换道期望轨迹充分考虑了乘车的舒适性和安全性。
(2)本发明选取的控制变量包括汽车行驶的驱动力和前轮转角,在满足横向换道需求的同时,可保证较高精度的车速控制;在进行车辆换道时,采用模型预测控制器来控制换道车辆跟踪期望换道轨迹,控制跟踪的鲁棒性较强,控制精度较高,从而可有效减小横向跟踪误差。
附图说明
图1是本发明的单向直线双车道车辆换道参考轨迹示意图;
图2是本发明的换道横摆角加速度参考模型;
图3是本发明的三自由度车辆动力学模型;
图4是本发明的MPC轨迹跟踪控制原理框图。
具体实施方式
为了便于本领域普通技术人员理解和实施本发明,下面结合附图对本发明作进一步的详细和深入描述。
本发明应用在车辆高级驾驶辅助系统(ADAS)上,规划了一种考虑驾驶员舒适性的基于模型预测的车辆换道轨迹跟踪控制方法。在ADAS中,当接收到决策层发出的换道指令后,规划模块按照本发明方法规划换道轨迹,将计算出的期望轨迹发送给控制模块,控制模块根据期望轨迹控制车辆换道。本发明的基于模型预测的车辆换道轨迹跟踪控制方法,主要包括三个步骤:步骤一、建立基于正反梯形的横摆角加速度的换道期望轨迹模型,求解换道期望轨迹;步骤二、对换道车辆进行受力分析,建立三自由度车辆动力学模型;步骤三、将非线性三自由度车辆动力学模型转化为离散线性预测模型,设计模型预测控制器的目标函数和约束条件,以使得控制车辆跟踪期望轨迹的偏差尽可能小。本发明方法输出符合驾驶员舒适性要求的换道轨迹和控制车辆车轮驱动力矩和前轮转角,使得车辆沿规划轨迹行驶。下面对三个步骤进行具体说明。
步骤一,建立含参数的正反梯形约束的横摆角加速度参考模型,和对时间积分得到含时间参数的期望换道轨迹模型,结合已知的总换道横向位移确定参数,再对期望换道轨迹进行高阶多项式拟合。
步骤11,建立含时间参数的期望换道轨迹模型。
如图1所示,在地面坐标系XOY下分析单向直线双车道车辆换道参考轨迹,OX轴正向为车辆行驶方向;OY轴与车道垂直,正向为指向目标车道中心线。换道车辆M从初始车道中心线上坐标为(X(0),Y(0))的A点开始换道,t时刻的质心坐标为(X(t),Y(t))的B点,行驶到C点时质心到达目标车道中心线,曲线ABC表示换道过程中车辆质心的运动轨迹,d为换道过程总横向位移,即车道宽度。
其中,X(t)、Y(t)分别表示换道过程t时刻车辆质心在地面坐标系XOY下的X坐标和Y坐标。
步骤12,建立换道横摆角加速度参考模型。
为了保证换道行为的安全性和乘车的舒适性,换道轨迹应连续且光滑,考虑车辆换道过程中的期望横摆角加速度随时间呈正反梯形变化规律,如图2所示。本发明实施例中,期望横摆角加速度曲线包括两个正的等腰梯形曲线和一个反的等腰梯形曲线,三个梯形的底角相等,正梯形或反梯形的下底对应的值为0,上底对应的值为期望横摆角加速度最大值或最小值。
图2中,表示换道过程中期望横摆角加速度最大值,在这里为未知参数。ti(i=1,2…12)表示换道过程中的时刻值,可根据驾驶员需求自行设定,这里取t2-t1=t4-t3=t5-t4=t7-t6=t9-t8=t10-t9=t12-t11=T1=0.2s,t3-t2=t6-t5=t8-t7=t11-t10=T2=0.9s。由图2得到换道过程中期望横摆角加速度关于时间的表达式为:
步骤13,将期望换道轨迹进行高阶多项式拟合。
利用公式(2)对时间进行两次分段积分得到换道过程中期望横摆角关于时间的表达式。结合公式(1)、公式(2)期望换道横摆角和已知的总换道横向位移,利用MATLAB可以求解出待定参数进而确定期望换道轨迹表达式。为方便轨迹跟踪,将求得的期望换道轨迹进行高阶多项式拟合。
在得到期望换道轨迹的高阶多项式表达后,可获得预测时刻的车辆质心坐标,输出给下面步骤三中进行控制变量的获取。
步骤二,分析换道车辆所受的驱动力和基本阻力,根据牛顿第二运动定律,利用非线性连续微分方程组建立三自由度换道车辆动力学模型。
如图3所示,表示满足平面假设的单轨三自由度车辆动力学模型。本发明中的坐标系oxyz为其原点与换道车辆质心重合的换道车辆坐标系,z轴为垂直xoy平面的轴。坐标系OXYZ为地面坐标系,Z轴为正向垂直地面向上的轴。设m为换道车辆的质量,a和b分别为换道车辆质心至其前轴的距离和至其后轴的距离,Iz为换道车辆绕z轴的转动惯量。设Flf,Flr分别为地面给换道车辆前后轮的纵向力,Fcf,Fcr分别为地面给换道车辆前后轮的侧向力;Fxf,Fxr分别为地面给换道车辆前后轮合力在x轴上的分量,Fyf,Fyr分别为地面给换道车辆前后轮合力在y轴上的分量。和分别为换道车辆质心绝对速度的x轴分量和y轴分量。ax和ay为换道车辆质心加速度的x轴分量和y轴分量。为换道车辆横摆角,wr和分别为换道车辆横摆角速度和横摆角加速度。δf为换道车辆前轮转角,sf和sr分别为换道车辆前轮和后轮的纵向滑移率,αf和αr分别为换道车辆前轮和后轮的侧偏角。
三自由度车辆动力学模型在x轴和y轴上的力平衡方程式和绕z轴上的力矩平衡方程如公式(3)如下:
质心加速度某一瞬时在换道车辆坐标系x轴和y轴上的分量可表示为:
结合换道车辆坐标系与地面坐标系之间的变化关系,前轮轮胎所受的力在x轴和y轴上的分量与前轮轮胎所受的力在纵向上和横向上的分量关系如下:
在侧偏角及纵向滑移率较小时,轮胎受力可以用线性函数近似表示。即在侧偏角α≤5°和纵向滑移率s≤0.2时,对常规前、后轮轮胎具有如式(6)的拟合公式:
其中,Clf,Clr分别为换道车辆的前、后轮胎的纵向刚度,Ccf,Ccr分别为换道车辆前、后轮胎的侧偏刚度,刚度随垂向载荷变化而变化。
根据换道车辆坐标系oxyz的规定,换道车辆前后轮侧偏角αf,αr分别为:
将公式(4)~公式(7)代入公式(3)中,结合δf较小,sinδf≈δf,cosδf≈1,略去小量后得公式(8)如下:
公式(8)表示非线性车辆动力学模型,其为模型预测控制提供了基础。
步骤三,将步骤二建立的非线性动力学模型转换为离散线性定常预测模型,考虑轨迹跟踪控制器的设计目的和实际执行约束,建立模型预测控制器的优化目标函数和约束条件,通过MATLAB/Simulink对轨迹跟踪控制器进行仿真验证。
步骤31,将非线性动力学模型转换为离散线性预测模型。
组合得到描述基于小角度假设的公式(8)和线性轮胎假设的三自由度车辆动力学模型的公式(9)非线性时变方程组如下:
令状态变量 表示横摆角速度,控制变量u=[δf,Fxf]T,考虑到控制器控制换道车辆对换道过程中的纵向速度、横向位移和横摆角进行跟踪,定义输出变量为上角标T表示转置,则公式(10)表示的非线性动力学模型可以抽象为非线性状态空间方程,如公式(11)所示:
由于车辆换道行驶过程中车速较高,对控制器实时性有较高要求,上述非线性状态空间方程求解迭代计算量大,无法满足实时性要求,故需对非线性状态空间方程线性化。在初始时刻t0的(ξ(t0),u(t0))处对函数f进行一阶泰勒展开,忽略高次项,得线性时变预测模型如下:
其中,Jf(ξ(t0))为f相对于ξ的雅克比矩阵在ξ(t0)处的值,Jf(ξ(u0))为f相对于u的雅克比矩阵在u(t0)处的值。
在一个采样周期内,运用一阶差商法得到离散线性时变状态空间方程形式如下:
ξ(t+1|t)=A(t|t)ξ(t|t)+B(t|t)u(t|t)+ξe(t+1|t) (13)
其中,A(t|t)和B(t|t)分别为t时刻的系统状态系数矩阵和系统控制系数矩阵,ξ(t|t)和u(t|t)分别为t时刻的实际状态变量和控制变量,ξ(t+1|t)表示(t+1)时刻的实际状态变量,ξe(t+1|t)表示(t+1)时刻的实际状态量与通过线性模型预测得到的状态量差值,可以通过非线性微分方程组求解的精确预测状态量与通过线性预测模型得到的近似预测状态量作差得到。
输出变量与状态变量之间的关系式为:
η(t|t)=Cξ(t|t) (14)
其中,C表示系统输出系数矩阵,η(t|t)表示t时刻的实际输出变量。
故可将公式(13)和式(14)进行反复迭代,预测时域[t+1,t+Np]内输出变量序列Y(t),可以通过当前状态变量值ξ(t|t),控制时域[t,t+Nc-1]内的控制变量序列ΔU(t)和预测时域内的预测状态变量偏差来表示,如公式(15)所示,Np表示预测时域长度,Nc表示控制时域长度。即得到换道过程t时刻车辆质心在地面坐标系XOY下的Y坐标的关系式如下:
其中,Ψ、Θ分别表示增广后的状态系数矩阵和控制系数矩阵。
各矩阵值为:
其中,Y(t)表示预测时域内的t∈[t+1,t+NP]的输出变量序列,η(t+1|t)表示在t时刻预测的t+1时刻的输出变量;ΔU(t)表示控制时域内的控制变量序列,Δu(t+1|t)表示在t时刻计算的t+1时刻的控制变量的增量;表示预测时域内的预测状态变量偏差序列,表示预测时刻的状态变量与实际状态变量的误差,因为各误差值相差不大,此处为了加快计算,在计算出第一个值后,将其作为后面所有矩阵元素中的值。
步骤32,为预测模型控制器建立约束条件。
换道车辆在高速换道过程中,存在动力学上的约束和附着率约束,因此需要在轨迹跟踪控制器求解控制量时加入约束。
首先考虑为保证换道过程中控制量变化平稳,若变化过大容易造成控制系统不稳定,给控制变量增量设置上下界约束如下:
其中,Δδf表示前轮转角增量,ΔFxf表示前轮驱动力增量。
此外,考虑到预测模型建立在小角度假设和线性轮胎模型上,为了保证预测模型计算结果的精确性,要求前、后轮胎侧偏角αf,αr应尽量小,因此应添加如下约束:
步骤33,建立预测模型控制器的目标函数。
实际上,预测模型控制器中,控制时域内的控制变量序列ΔU(t)是待求量,需要先设定合适的优化目标函数,然后通过求解使优化目标函数取最小值时的控制增量序列ΔU(t),再根据ΔU(t)确定控制规律,下面进行优化目标函数的建立过程。
期望换道轨迹跟踪控制器的设计目的是为了保证跟踪参考期望换道轨迹的纵横向偏差尽量小,同时也需要考虑控制变量变化应平稳,即控制增量应当受到约束,以确保换道车辆能够尽快且平稳地跟踪上期望换道轨迹,因此,建立综合考虑跟踪误差和控制增量的目标函数如下:
其中:η(t+i|t)表示在t+i时刻的实际输出量,ηref(t+i|t)表示在t+i时刻的期望输出量,Δu(t+i|t)表示在t+i时刻的控制变量增量;Q为反映跟踪偏差项的权重矩阵,R为反映控制增量的权重矩阵,Q和R一般定义为正定或半正定的对角矩阵;ρ为反映约束松弛项的权重系数,ε为约束松弛因子。
利用步骤一的期望换道轨迹的高阶多项式,来获得期望的换道车辆质心坐标,然后再利用预测模型控制器在约束条件下计算控制变量增量,最后输出控制车辆运动的控制变量。
本发明实施例利用MATLAB/Simulink搭建本发明的车辆动力学模型和预测模型控制器,进行仿真验证,求解最优输出转矩序列,实现对换道车辆跟踪期望轨迹的控制。
模型预测控制(MPC)是在每一个采样周期内通过求解有限时域开环最优控制问题而获得当前最优控制量。主要由预测模型,滚动优化和反馈校正三个环节组成。与传统最优控制的根本区别是,本发明模型预测控制采用控制时域内滚动优化的方式求解控制量,即在线反复优化求局部最优解。模型预测控制问题是求解使设定优化目标取最优值时的控制时域内的控制序列,一般主要将其转化为带约束的在线序列二次规划问题。
如图4所示,本发明方法应用MPC进行轨迹跟踪控制的原理框图,其中利用Simulink建立车辆动力学模型,MPC控制器即本发明的预测模型控制器。在MPC控制器中利用MATLAB求解上述带约束的优化目标,得到控制时域内的最优控制增量序列,将第一个控制量输出给车辆动力学的Simulink模型,根据动力学模型,将状态变量输入给模型预测控制器,从而完成对换道车辆的闭环反馈控制。
Claims (6)
1.一种基于模型预测的车辆换道轨迹跟踪控制方法,其特征在于,包括:
步骤一、建立基于正反梯形横摆角加速度的换道期望换道轨迹模型,然后利用期望总换道横向位移,期望横摆角加速度曲线,得到期望换道轨迹参数,再对期望换道轨迹拟合成高阶多项式;
所述的期望总换道横向位移为车道宽度;所述的期望横摆角加速度曲线是将车辆换道过程中的期望横摆角加速度表示为随时间呈正反梯形变化规律的曲线,其中,正梯形或反梯形的下底对应的值为0,上底对应的值为期望横摆角加速度最大值或最小值 为未知参数;所述的期望换道轨迹参数包括
建立的期望横摆角加速度随时间的曲线,包括正等腰梯形曲线和反等腰梯形曲线,梯形的底角都相等;处于梯形的腰的时间段时,期望横摆角加速度均匀增加到最大值或均匀减少到最小值,处于梯形的底的时间段时,期望横摆角加速度保持在最大值或最小值;
步骤二、对换道车辆进行受力分析,建立三自由度车辆动力学模型;
步骤三、将非线性的三自由度车辆动力学模型转化为离散线性预测模型,建立模型预测控制器的目标函数和约束条件,在根据步骤一的期望换道轨迹获得预测时刻的车辆质心坐标后,计算输出控制车辆运动的控制变量;
所述的离散线性预测模型中,设置状态变量为控制变量为u=[δf,Fxf]T,输出变量为设换道车辆坐标系为oxyz,地面坐标系为OXYZ,X、Y分别为换道车辆质心在地面坐标系下的X坐标和Y坐标,分别为换道车辆横摆角和横摆角速度,分别为换道车辆质心绝对速度的x轴分量和y轴分量,δf为换道车辆前轮转角,Fxf为换道车辆的前轮驱动力在x轴上的分量,上角标T表示转置;
所述的模型预测控制器用于计算控制变量增量序列,所述的目标函数是求取控制变量的增量序列,使得车辆跟踪期望轨迹的偏差最小;所述的约束条件包括为控制变量增量设置上下界,设置变道车辆的前轮胎和后轮胎的侧偏角不超过阈值。
3.根据权利要求1所述的方法,其特征在于,所述的步骤三中,将非线性的三自由度车辆动力学模型转化为离散线性预测模型,如下:
将步骤二建立的三自由度车辆动力学模型的换道车辆坐标系oxyz下的速度变换为地面坐标系OXYZ下的速度,得到三自由度车辆动力学模型的非线性时变方程组如下:
其中,和分别为换道车辆质心绝对速度的x轴分量和y轴分量,和分别是和的一阶导数;wr和分别为换道车辆横摆角速度和横摆角加速度;m为换道车辆的质量;a和b分别为换道车辆质心至其前轴的距离和至其后轴的距离;Ccf,Ccr分别为换道车辆前、后轮胎的侧偏刚度;Clf,Clr分别为换道车辆前、后轮胎的纵向刚度;sf和sr分别为换道车辆前轮和后轮的纵向滑移率;Iz为换道车辆绕z轴的转动惯量;和分别为换道车辆质心速度在地面坐标系的X轴分量和Y轴分量;
将所述的三自由度车辆动力学模型抽象为非线性状态空间方程,表示如下:
对所述的非线性状态空间方程在初始t0时刻处对函数f进行一阶泰勒展开,忽略高次项,得线性时变预测模型如下:
其中,Jf(ξ(t0))为f相对于ξ的雅克比矩阵在ξ(t0)处的值,Jf(ξ(u0))为f相对于u的雅克比矩阵在u(t0)处的值;
在一个采样周期内,运用一阶差商法得到离散线性时变状态空间方程,如下:
ξ(t+1|t)=A(t|t)ξ(t|t)+B(t|t)u(t|t)+ξe(t+1|t)
其中,A(t|t)和B(t|t)分别为t时刻的状态系数矩阵和控制系数矩阵,ξ(t|t)和u(t|t)分别为t时刻的实际状态变量和控制变量,ξ(t+1|t)表示(t+1)时刻的实际状态变量,ξe(t+1|t)表示(t+1)时刻的实际状态变量与通过线性模型预测得到的状态变量的差值;
输出变量与状态变量之间的关系式为η(t|t)=Cξ(t|t);C表示输出系数矩阵,η(t|t)表示t时刻的实际输出变量;
利用离散线性时变状态空间方程对η(t|t)进行反复迭代计算,预测时域[t+1,t+Np]内输出变量序列Y(t),利用当前状态变量值ξ(t|t)、控制时域[t,t+Nc-1]内的控制变量增量序列ΔU(t)和预测时域内的预测状态变量偏差序列来表示,Np表示预测时域长度,Nc表示控制时域长度;
其中,Ψ、Θ分别表示增广后的状态系数矩阵和控制系数矩阵。
6.根据权利要求4所述的方法,其特征在于,所述的步骤三中,模型预测控制器采用控制时域内滚动优化的方式求解控制变量增量序列。
Priority Applications (1)
| Application Number | Priority Date | Filing Date | Title |
|---|---|---|---|
| CN202010909744.0A CN112092815B (zh) | 2020-09-02 | 2020-09-02 | 一种基于模型预测的车辆换道轨迹跟踪控制方法 |
Applications Claiming Priority (1)
| Application Number | Priority Date | Filing Date | Title |
|---|---|---|---|
| CN202010909744.0A CN112092815B (zh) | 2020-09-02 | 2020-09-02 | 一种基于模型预测的车辆换道轨迹跟踪控制方法 |
Publications (2)
| Publication Number | Publication Date |
|---|---|
| CN112092815A CN112092815A (zh) | 2020-12-18 |
| CN112092815B true CN112092815B (zh) | 2021-07-16 |
Family
ID=73757526
Family Applications (1)
| Application Number | Title | Priority Date | Filing Date |
|---|---|---|---|
| CN202010909744.0A Active CN112092815B (zh) | 2020-09-02 | 2020-09-02 | 一种基于模型预测的车辆换道轨迹跟踪控制方法 |
Country Status (1)
| Country | Link |
|---|---|
| CN (1) | CN112092815B (zh) |
Families Citing this family (13)
| Publication number | Priority date | Publication date | Assignee | Title |
|---|---|---|---|---|
| CN112904849A (zh) * | 2021-01-18 | 2021-06-04 | 北京科技大学 | 一体式自动驾驶汽车换道轨迹规划和跟踪控制方法及系统 |
| CN112918478B (zh) * | 2021-02-25 | 2022-04-01 | 中南大学 | 一种车辆变道的预测方法、装置及计算机存储介质 |
| CN112989499B (zh) * | 2021-04-22 | 2024-07-02 | 中国人民解放军国防科技大学 | 一种无人车数据驱动控制方法和装置 |
| CN113867330B (zh) * | 2021-05-11 | 2023-05-02 | 吉林大学 | 一种基于多自由度预测模型在任意路径下实现车辆漂移的控制方法 |
| CN113704902B (zh) * | 2021-07-26 | 2024-04-09 | 兰州大学 | 一种基于梯度投影神经动力学的门式起重机模型预测最优控制方法 |
| CN113515038B (zh) * | 2021-09-07 | 2021-11-26 | 西南交通大学 | 一种车辆换道方法、装置、设备及可读存储介质 |
| CN113771884B (zh) * | 2021-11-09 | 2022-02-08 | 清华大学 | 基于侧向量化平衡指标的智能汽车拟人化轨迹规划方法 |
| CN114220262B (zh) * | 2021-11-19 | 2023-06-23 | 东南大学 | 一种基于交通仿真的车辆换道轨迹偏差计算方法 |
| CN114379583B (zh) * | 2021-12-10 | 2024-05-14 | 江苏大学 | 一种基于神经网络动力学模型的自动驾驶车辆轨迹跟踪系统及方法 |
| CN114291092B (zh) * | 2022-01-26 | 2023-05-16 | 中国联合网络通信集团有限公司 | 车辆换道控制方法、装置、电子控制单元及存储介质 |
| CN114475596B (zh) * | 2022-02-22 | 2023-06-20 | 青岛德智汽车科技有限公司 | 一种换道场景下保证安全的智能网联队列鲁棒控制方法 |
| CN115171414B (zh) * | 2022-06-10 | 2023-07-14 | 哈尔滨工业大学重庆研究院 | 一种基于Frenet坐标系的CACC跟驰车流控制系统 |
| CN115285138B (zh) * | 2022-08-31 | 2024-02-27 | 浙江工业大学 | 一种基于紧约束的无人车鲁棒预测控制方法 |
Family Cites Families (7)
| Publication number | Priority date | Publication date | Assignee | Title |
|---|---|---|---|---|
| KR101294059B1 (ko) * | 2011-07-28 | 2013-08-08 | 현대자동차주식회사 | 인휠 시스템을 이용한 차선 유지 보조 시스템 |
| JP2017081421A (ja) * | 2015-10-28 | 2017-05-18 | 本田技研工業株式会社 | 車両制御装置、車両制御方法、および車両制御プログラム |
| CN105488485B (zh) * | 2015-12-07 | 2019-01-22 | 北京航空航天大学 | 基于车辆轨迹的车道线自动提取方法 |
| CN105644566B (zh) * | 2016-03-02 | 2017-12-19 | 厦门大学 | 一种基于车联网的电动汽车辅助换道轨迹的跟踪方法 |
| CN110286681B (zh) * | 2019-07-05 | 2022-01-28 | 西南交通大学 | 一种变曲率弯道的动态自动驾驶换道轨迹规划方法 |
| CN111413990A (zh) * | 2020-05-07 | 2020-07-14 | 吉林大学 | 一种车道变更轨迹规划系统 |
| CN111598069B (zh) * | 2020-07-27 | 2020-11-06 | 之江实验室 | 一种基于深度学习的高速公路车辆换道区域分析方法 |
-
2020
- 2020-09-02 CN CN202010909744.0A patent/CN112092815B/zh active Active
Also Published As
| Publication number | Publication date |
|---|---|
| CN112092815A (zh) | 2020-12-18 |
Similar Documents
| Publication | Publication Date | Title |
|---|---|---|
| CN112092815B (zh) | 一种基于模型预测的车辆换道轨迹跟踪控制方法 | |
| CN109318905B (zh) | 一种智能汽车路径跟踪混合控制方法 | |
| Tang et al. | An improved kinematic model predictive control for high-speed path tracking of autonomous vehicles | |
| CN111258323B (zh) | 一种智能车辆轨迹规划与跟踪的联合控制方法 | |
| CN112622903B (zh) | 一种车辆跟随驾驶环境下自主车辆的纵向和横向控制方法 | |
| Xie et al. | Coordinated control based path following of distributed drive autonomous electric vehicles with yaw-moment control | |
| Sentouh et al. | A sensorimotor driver model for steering control | |
| CN107867290B (zh) | 一种考虑运动障碍物的汽车紧急避撞分层式控制方法 | |
| JP4699465B2 (ja) | 車両の制御装置 | |
| CN108646763A (zh) | 一种自主行驶轨迹跟踪控制方法 | |
| CN111923908A (zh) | 一种融合稳定性的智能汽车路径跟踪控制方法 | |
| CN108674414A (zh) | 一种极限工况的智能汽车轨迹跟踪控制方法 | |
| CN110262229B (zh) | 基于mpc的车辆自适应路径追踪方法 | |
| CN111959527B (zh) | 一种基于转角优化序列的汽车路径跟踪控制方法 | |
| CN112947469A (zh) | 汽车换道轨迹规划与动态轨迹跟踪控制方法 | |
| CN113433942B (zh) | 一种基于最优航向角的长轴车辆路径跟踪控制方法 | |
| Chen et al. | Path tracking control of four-wheel independent steering electric vehicles based on optimal control | |
| CN116834754A (zh) | 一种自动驾驶车辆自适应调速的横纵协同控制方法 | |
| CN115675459A (zh) | 一种智能车辆及其路径跟踪的控制方法、装置和存储介质 | |
| CN114802200B (zh) | 一种智能汽车极限工况下轨迹跟踪和稳定性控制方法 | |
| CN116520700A (zh) | 一种欠驱动自动驾驶车辆的路径跟踪控制方法 | |
| Li et al. | Path tracking control based on the prediction of tire state stiffness using the optimized steering sequence | |
| CN113867330B (zh) | 一种基于多自由度预测模型在任意路径下实现车辆漂移的控制方法 | |
| CN114896694B (zh) | 一种基于两点预瞄的路径跟踪控制方法 | |
| CN115384529A (zh) | 一种应对极限工况的三轴商用车双阶段漂移控制方法及安全辅助系统 |
Legal Events
| Date | Code | Title | Description |
|---|---|---|---|
| PB01 | Publication | ||
| PB01 | Publication | ||
| SE01 | Entry into force of request for substantive examination | ||
| SE01 | Entry into force of request for substantive examination | ||
| GR01 | Patent grant | ||
| GR01 | Patent grant |