편상관

확률론과 통계학에서 편상관은 제어 랜덤 변수 집합의 효과가 제거된 상태에서 두 랜덤 변수 간의 연관성을 측정합니다.두 관심 변수 사이에 어느 정도 수치적 관계가 있는지 찾는 데 관심이 있는 경우, 두 관심 변수 모두에 수치적으로 관련된 또 다른 교란 요인이 있는 경우 이들의 상관 계수를 사용하면 잘못된 결과를 얻을 수 있다.이러한 오해의 소지가 있는 정보는 편상관계수를 계산하여 이루어지는 교란변수를 제어함으로써 회피할 수 있다.이것은 다른 오른쪽 변수를 다중 회귀 분석에서 포함하는 정확한 동기이다. 그러나 다중 회귀 분석에서는 효과 크기에 대해 편향되지 않은 결과를 제공하지만, 두 변수 사이의 관계 강도에 대한 수치 값은 제공하지 않는다.

예를 들어, 우리가 다양한 개인의 소비, 소득, 부에 대한 경제 데이터를 가지고 있고 우리는 소비와 소득 사이에 관계가 있는지 확인하고자 한다면, 소비와 소득 사이의 상관 계수를 계산할 때 부를 통제하지 못하면 소득이 수치적으로 관계될 수 있기 때문에 잘못된 결과를 초래할 수 있다.소비와 수치적으로 관련될 수 있는 ted to 부(富); 소비와 소득 사이의 측정된 상관관계는 실제로 이러한 다른 상관관계에 의해 오염될 수 있다.편상관을 사용하면 이 문제를 피할 수 있습니다.

상관 계수와 마찬가지로 편상관 계수는 –1 ~ 1 범위의 값을 취합니다.값 -1은 일부 변수에 대해 완벽한 음의 상관 제어(즉, 한 변수의 값이 높을수록 다른 변수의 값이 낮을수록 정확한 선형 관계)를 전달하고 값 1은 완벽한 양의 선형 관계를 전달하며 값 0은 선형 관계가 없음을 나타냅니다.

랜덤 변수가 다변량 정규, 기타 타원, 다변량 하이퍼기하, 다변량 음의 하이퍼기하, 다항식 또는 디리클레 분포로 함께 분포되어 있으면 편상관은 조건부 상관 관계와 일치하지만,^[1] 그렇지 않으면 일반적이지 않습니다.

형식적 정의

공식적으로_XY·Z, N개의 제어 변수 Z = {Z₁, Z₂, ..., Z_n}가 주어졌을 때 X와 Y 사이의 편상관은 각각 Z와 Y의 선형 회귀에서 생성된 잔차_X e와_Y e 사이의 상관 관계이다.1차 편상관(즉, n = 1)은 상관 관계와 제거 상관의 곱을 제거 상관의 소외 계수의 곱으로 나눈 값이다.이간계수와 상관관계를 통한 관절분산과의 관계는 길포드(1973년, 페이지 344–345년)^[2]에서 구할 수 있다.

계산

선형 회귀 분석 사용

일부 데이터에 대한 표본 편상관을 계산하는 간단한 방법은 연관된 두 선형 회귀 문제를 풀고 잔차를 가져온 다음 잔차 간의 상관 관계를 계산하는 것입니다.위와 같이 X와 Y를 실수값을 취하는 랜덤변수로 하고 Z를 n차원 벡터값 랜덤변수로 한다.회귀에서 일정한 항을 허용하기 위해 z가 1로 증가하여 실제 랜덤_i 변수 X, Y 및 Z에 대한 일부 공동 확률 분포에서 N.i.d. 관측치의 ith를 나타내기 위해 x, y_i 및 z를_i 쓴다_i.선형 회귀 문제를 해결하려면 다음과 같은 (n+1) 차원 회귀 계수 $\mathbf {w} _{X}^{*}$ $\mathbf {w} _{X}^{*}$ ${\$ {\ $displaystyle \mathbf {w} _{X}^*}$ 및 $\mathbf {w} _{Y}^{*}$ ${\$ {\ $displaystyle \mathbf {w}$ _ ${Y}^*}$ 를 $\mathbf {w} _{X}^{*}$ $\mathbf {w} _{Y}^{*}$ 찾아야 합니다.

\mathbf {w} _{X}^*}=\arg \min _{\sum _{i=1}^{N}(x_{i}-\langle \mathbf {w},\mathbf {z}_{i}\rangle }^{2}\right}

\mathbf {w} _{Y}^*}=\arg \min _{\sum _{i=1}^{N}(y_{i}-\langle \mathbf {w},\mathbf {z} _{i}\rangle }^2}\}\}}\right

N은 관측치 수이고 $\langle \mathbf {w} ,\mathbf {v} \rangle$ w는 벡터 w와 v 사이의 스칼라 곱인 v $\langle \mathbf {w} ,\mathbf {v} \rangle$ †(\ $displaystyle \langle \mathbf {w},\mathbf {v}$ \ $rangle)$ 이다 $\langle \mathbf {w} ,\mathbf {v} \rangle$ .

그러면 잔차는 다음과 같습니다.

\displaystyle e_{X,i}=x_{i}-\langle \mathbf {w}_{X}^*},\mathbf {z}_{i}\rangle }

\displaystyle e_{Y,i}=y_{i}-\langle \mathbf {w}_{Y}^{*},\mathbf {z}_{i}\rangle }

표본 부분 상관은 표본 상관을 위한 일반적인 공식에 의해 제시되지만, 이러한 새로운 파생 값 사이에 제시됩니다.

{\displaystyle\begin{aligned\hat\rho}_{X}Y\cdot \mathbf{Z}}&={\frac{N\sum_{i=1}^{N}e_{X,i}e_{Y,i}-\sum _{i=1}^{N}e_{X,i}\sum _{i=1}^{N}e_{Y,i}}{{\sqrt{N\sum_{i=1}(\sum_{i=1}^{N}e_{X,i}\right)^{2}}}~ᆺ^ᆻe_ᆼ^ᆽ-\left(\sum_{i=1}^{N}e_{Y,i}\right)^{2}}}}}\\&, ={\frac{N\sum_{i=1}^{N}e_{X,i}e_{Y,i}}{{\sqrt{N\sum_{i=1}^{N}e_{X,i}^{2.}}}일{\sqrt {N\sum _{i=1}^{N}e_{Y,i}^2}}}}.\end { aligned}}

첫 번째 식에서는 각각에 정규 최소 제곱법의 잔차 합계가 포함되어 있으므로 마이너스 기호 뒤에 있는 세 개의 항은 모두 0이 됩니다.

예

X, Y 및 Z의 세 변수에 대한 다음과 같은 데이터가 있다고 가정합니다.

X	Y	Z
2	1	0
4	2	0
15	3	1
20	4	1

변수 X와 Y 사이의 Pearson 상관 계수를 계산하면 결과가 약 0.970이지만 위의 공식을 사용하여 X와 Y 사이의 편상관 계수를 계산하면 0.919의 편상관 계수를 찾을 수 있습니다.계산은 다음 코드와 함께 R을 사용하여 수행되었습니다.

>X <-> c(2,4,15,20) >Y <-> c(1,2,3,4) >Z <-> c(0,0,1,1) >mm1 <-> lm(X~Z) >리셋 1 <-> mm1$잔차 >mm2 <-> lm(Y~Z) >리즈2 <-> mm2$잔차 >코(리셋 1,리즈2) [1] 0.919145 >코(X,Y) [1] 0.9695016 >제너럴코어::다량(카바인드(X,Y,Z))                   namij partij partji rijMrji [1,] 'X' 'Y' '0.8844' '1' '-0.1156' [2,] 'X' 'Z' '0.1581' '1' '-0.8419'

위 코드의 하부는 0.8844로 Z의 비선형 효과를 제거한 후 X와 Y 사이의 일반화 비선형 편상관 계수를 보고한다.또한 Y의 비선형 효과를 제거한 후의 X와 Z 사이의 일반화 편상관 계수는 0.1581이다.상세한 것에 대하여는, R패키지 「generalCorr」와 그 vignett를 참조해 주세요.시뮬레이션 및 기타 세부사항은 Vinod(2017) "개발 경제 분야 애플리케이션과의 일반화 상관관계 및 커널 인과관계", 통계 분야 커뮤니케이션 - 시뮬레이션 및 계산, vol. 46, [4513, 4534], 온라인: 2015년 12월 29일 URL https://doi.org/10.1080/03610918.2015.1122048에서 확인할 수 있다.

재귀 공식 사용

선형 회귀 문제를 해결하려면 계산 비용이 많이 들 수 있습니다.실제로 n차 편상관(즉, Z = n)은 3차 편상관으로부터 쉽게 계산할 수 있다.0차 편상관θ는_XY·Ø 정규 상관계수θ로_XY 정의된다.

$Z_{0}\in \mathbf {Z} ,$ 의 $Z_{0}\in \mathbf {Z} ,$ Z에 대해 다음과 같은 값이 유지됩니다 $.\$ $displaystyle Z_{0}\in$ \ $mathbf {Z$ ^{[citation needed]} $}$

{\displaystyle\rho_{X}Y\cdot \mathbf {Z} = frac {rho _ {X }Y\cdot \mathbf {Z} \setminus \{Z_{0}\}-\rho _{XZ_{0}\cdot \mathbf {Z} \setminus \{Z_{0}\}\rho _{Z_{0}Y\cdot \mathbfZ} \set {set} \{Z} \{{set} \{set}\} \{{{set}\}\}\rho}\{{{{{set}\}\}\}\}\}}

이 계산을 재귀 알고리즘으로 구현하면 시간이 기하급수적으로 복잡해집니다.단, 이 계산에는 중복되는 서브 문제가 있어 동적 프로그래밍을 사용하거나 재귀 콜의 결과를 캐싱하는 것만으로 복잡도가 O $n$ 3 $)\$ style ${O}(n^{3$ 가 됩니다.

Z가 단일 변수인 경우 다음과 ^{[citation needed]}같이 감소합니다.

{\displaystyle\rho_{X}Y\cdot Z=cdfrac {rho _{XY}-\rho _{XZ}\rho _{Z}Y}}{\sqrt {1-\rho _{XZ}^{2}}{\sqrt {1-\rho _{Z}Y}^{2}}}}}}}:

행렬 반전 사용

우리는 또한 부분적 상관관계를 결합 정밀도 행렬로 쓸 수 있다.카디널리티 n의 랜덤 $V={X_{1},\dots X_{n}}$ 인 V $=$ $V={X_{1},\dots X_{n}}$ 1, … $V={X_{1},\dots X_{n}}$ n({ $displaystyle$ V $={X_{$ 1},\ $dots$ X_ ${n}})$ $V={X_{1},\dots X_{n}}$ 를 $V={X_{1},\dots X_{n}}$ 고려합니다.다른 모든 $\mathbf {V} \setminus \{X_{i},X_{j}\}$ X와_j X 사이의 부분적 상관관계를 원합니다. 즉, V $\mathbf {V} \setminus \{X_{i},X_{j}\}$ { $\mathbf {V} \setminus \{X_{i},X_{j}\}$ i , $\mathbf {V} \setminus \{X_{i},X_{j}\}$ j $}$ { $displaystyle$ \ $mathbf$ { $V }$ \ $setminus$ \ { X $_$ { $i$ } , $X$ _ { $j$ } \ $\mathbf {V} \setminus \{X_{i},X_{j}\}$ 。 (공동/ $\Sigma =(\sigma _{ij})$ ) 공분산 행렬 $\Sigma =(\sigma _{ij})$ ( $표시$ jigma $\Sigma =(\sigma _{ij})$ \ sigma )정밀 행렬 $\Omega =(p_{ij})=\Sigma ^{-1}$ $\Omega =(p_{ij})=\Sigma ^{-1}$ ( $\Omega =(p_{ij})=\Sigma ^{-1}$ $\Omega =(p_{ij})=\Sigma ^{-1}$ ) $\Omega =(p_{ij})=\Sigma ^{-1}$ - $\Omega =(p_{ij})=\Sigma ^{-1}$ { $displaystyle \Omega =$ ( $p_{ij$ }) = $\Sigma$ ^{- $1$ 다음으로 다음이 있습니다.

\displaystyle \rho _ {X_{i}\cdot \mathbf {V} \setminus \ {X_{i},X_{j}\}=-{\frac {p_{ij}{\frac {p_i}p_{j}}}}}.}

이를 계산하려면 O ${\mathcal {O}}(n^{3})$ ( ${\mathcal {O}}(n^{3})$ 3 ${\mathcal {O}}(n^{3})$ ) ${{displaystyle$ { $O}}(n^{$ 3}) ${\mathcal {O}}(n^{3})$ 으로 ${\mathcal {O}}(n^{3})$ 되는 ${\mathcal {O}}(n^{3})$ 공분산 행렬 $\Sigma$ { $displaystyle \Sigma$ $}$ 을 $\Sigma$ (를) 반전시켜야 합니다(샘플 공분산 행렬을 사용하여 샘플 편상관 관계를 얻음).V{\ $displaystyle$ V $V$ 에서 변수 쌍 간의 모든 부분 상관 관계를 제공하기 위해 필요한 매트릭스 반전은 1개뿐입니다.

, 우리가 우리의 이전 표기법(즉 X, Y, Z↔ X나는, Xj, VX명확히 설명, Xj{\displaystyle X,Y,Z\leftrightarrow X_{나는},X_{j},V_{X_{나는},X_{j}}})and로 되돌아가 봅시다 그 정의를. 나머지 사이에 ρXY·Z은 상관 eX과 eY X의 Z과 선형 회귀, Y의 Z, respec과 결과 이 증명하기 위해tively.

따라서 선형 회귀 적합 계수가 $\beta ,\gamma$ , ${\$ { $displaystyle \beta$ , \ $gamma$ 라고 가정합니다.

\displaystyle =\operatorname {displaymin} _{\mathbb {E} \ X-\beta ^{T}Z\^{2}

\displaystyle =\operatorname {displaymin} _{\mathbb {E} \ Y - \ gamma ^ { T }Z \^ {2}

벡터 $(X,Y,Z^{T})^{T}$ ( $(X,Y,Z^{T})^{T}$ $(X,Y,Z^{T})^{T}$ $(X,Y,Z^{T})^{T}$ T $(X,Y,Z^{T})^{T}$ {\ $displaystyle (X, Y$ , $Z^{T})^$ 에 대한 공동 공분산 행렬을 쓰자. ${T$ 로서

\displaystyle \Sigma = sigma begin{bmatrix}\Sigma _{X}&\Sigma _{X}Y}&\Sigma_{XZ}\\Sigma_{YX}&\Sigma_{YY}&\Sigma_{YZ}\\Sigma_{ZX}&\Sigma_{Z}Y}&\Sigma _{ZZ}\end{bmatrix}=begin{bmatrix}C_{11}&C_{12}\C_{21}&C_{22}\\end{bmatrix}}

어디에

C_{11}=sigma begin{bmatrix}\Sigma _{X}&\Sigma _{X}Y}\\Sigma_{YX}&\Sigma_{YY}\end{bmatrix},\qquad C_{12}=sigma_{XZ}\\Sigma_{YZ}\end{bmatrix},\qad C_{21}=sigma{bmatrix}\Sigma_{X}Y}\end{bmatrix},\qquad C_{22}=\Sigma _{ZZ}

그런 다음 선형 회귀 분석의 표준 공식은 다음과 같습니다.

\signa =\left(\Sigma _{ZZ}\오른쪽)^{-1}\Sigma _{ZX}

따라서 우리는 잔차를 쓸 수 있다.

R_{X}=X-\beta ^{T}Z=X-\Sigma_{XZ}\left(\Sigma_{Z}\오른쪽)^{-1}Z

가로채기 용어를Z(\ $displaystyle$ Z $Z$ 에 포함시켰기 때문에 $R_{X}$ X $(\$ $displaystyle$ $R_{X})$ 의 $R_{X}$ 기대치는 0입니다.이제 다음을 계산할 수 있습니다.

\operatorname {Cov}(R_{X},R_{Y})=\dots=\Sigma_{XY}-\Sigma_{Z}\left(\Sigma_{Z}^{오른쪽)Y}

다음으로 정밀행렬 $\Omega =\Sigma ^{-1}$ $\Omega =\Sigma ^{-1}$ - $\Omega =\Sigma ^{-1}$ 1 \ $displaystyle$ \ $Omega$ = \ $Sigma$ ^ { - $1$ } 을 이와 유사한 블록 형태로 적습니다.

\displaystyle \Omega = begin{bmatrix}\Omega _{X}&\Omega _{X}Y}&\Omega_{XZ}\\Omega_{YX}&\Omega_{YY}&\Omega_{YZ}\\Omega_{ZX}&\Omega_{Z}Y}&\Omega_{ZZ}\end{bmatrix}=begin{bmatrix}P_{11}&P_{12}\P_{211}&P_{22}\\end {bmatrix}}

그리고 블록 매트릭스 반전에 대한 슈어의 공식에 의해 우리는

P_{11}^{-1}=C_{11}-C_{12}C_{22}^{-1}C_{214

우측 행렬의 입력이 정확히 우리가 계산한 공분산인지, 즉, 쉽게 확인할 수 있다.

({displaystyle P_{11}^{-1}=bgin{bmatrix}\operatorname {Cov}(R_{X},R_{X})&\operatorname {Cov}(R_{Y})}

2x2 행렬의 역식에 따라 다음과 같은 식을 얻을 수 있습니다.

P_{11}^{-1}=biginfrac {1}{\text{det}P_{11}}{\begin{pmatrix}[P_{11}_{22}&-[P_{11}_{12}\\-[P_{11}_{21)&[P_{11}_{11}\\end{pmatrix}=http frac {1}{\text{det}P_{11}{begin{p}_p}YY}&-p_{X}Y}\\-p_{YX}&p_{XX}\\end{pmatrix}

그래서 실제로 부분적 상관관계는

{\displaystyle\rho_{X}Y\cdot Z=parac {operatorname {Cov}(R_{X},R_{Y})}{\sqrt {operatorname {Cov}(R_{X},R_{X})\operatorname {Cov}(R_{Y}})Y}}{\sqrt {{\text{det}}P_{11}}p_{X}{\text{det}P_{11}}p_{\text{det}P_{11}}}YY}}}}}=-{\frac {p_{X}Y}}{\sqrt {p_{XX}p_{YY}}}}}}}}

주장대로.

해석

N = 3개의 관측치와 그에 따른 2차원 초평면의 경우에 대한 편상관 기하학적 해석

기하학적

세 변수 X, Y, Z(여기서 Z는 "관리" 또는 "추가 변수")를 n개의 변수 V에 대한 공동 확률 분포에서 선택하도록 합니다.또한 V에 대한 공동 확률 분포에서 얻은 N n차원 i.i.d. 관측치 v, 1 µi µ N으로_i 한다.그런 다음 N차원 벡터 x(관측치에 대한 X의 연속 값으로 형성), y(Y의 값으로 형성) 및 z(Z의 값으로 형성)를 고려한다.

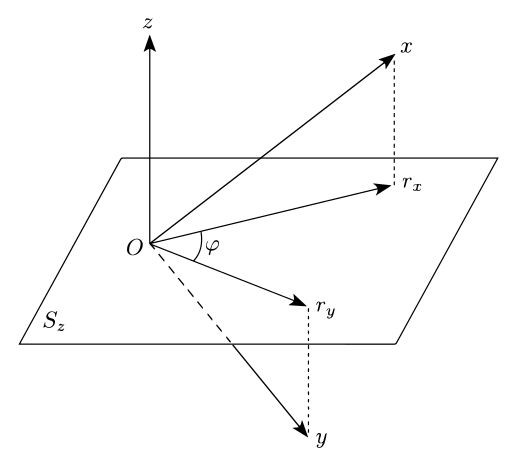
X on Z의 선형 회귀에서 오는 잔차_X,i e는 N차원 벡터_X e(첨부 그래프에서 r을_X 나타냄)로도 간주될 경우 Z에 의해 생성된 벡터 z의 0 스칼라 곱을 갖는다는 것을 보여줄 수 있다.즉, 잔차 벡터는 z에 수직인 (N–1)차원 초평면_z S에 놓여 있습니다.

벡터_Y e를 생성하는 잔차_Y,i e에도 동일하게 적용됩니다.원하는 편상관은 ^[3]^{: ch. 7}z에 수직인 하이퍼플레인 상의 투영 e와_X_Y x 및 y의 e와 e 사이의 각도 θ의 코사인입니다.

조건부 독립성 테스트로서

관련된 모든 변수가 다변량 가우스라고 가정할 때, X가 주어진 ^[1]Z로부터 조건적으로 독립적인 경우에만 편상관 θ는_XY·Z 0이다.이 속성은 일반적인 경우에는 사용할 수 없습니다.

${\hat {\rho }}_{XY\cdot \mathbf {Z} }$ 편상관 ${\hat {\rho }}_{XY\cdot \mathbf {Z} }$ ${\hat {\rho }}_{XY\cdot \mathbf {Z} }$ Y ${\hat {\rho }}_{XY\cdot \mathbf {Z} }$ Z ${\hat {\rho }}_{XY\cdot \mathbf {Z} }$ \ $displaystyle \ hat$ \ $rho$ } $_$ { $X$ } a if if if 。 $Y\cdot \mathbf {Z} }}$ 는 ${\hat {\rho }}_{XY\cdot \mathbf {Z} }$ 참 모집단 편상관 관계가 0과 다르다는 것을 의미하며, 편상관 z 변환을 사용할 수 있습니다.

z(\hat {rho }}_{X})Y\cdot \mathbf {Z} = flac {1}{2}}\ln \leftfac {1+{\hat {rho }}_{X}Y\cdot \mathbf {Z}}}{1-{\hat {rho }}_{X}Y\cdot \mathbf {Z}}}\right).

귀무 가설은 $H_{0}:\rho _{XY\cdot \mathbf {Z} }=0$ 0 : $H_{0}:\rho _{XY\cdot \mathbf {Z} }=0$ X $H_{0}:\rho _{XY\cdot \mathbf {Z} }=0$ Z $H_{0}:\rho _{XY\cdot \mathbf {Z} }=0$ { $displaystyle H_{0$ : \ $rho$ _ { $X$ }입니다. $Y\cdot \mathbf {Z} =0$ 양 꼬리 $H_{A}:\rho _{XY\cdot \mathbf {Z} }\neq 0$ $H_{A}:\rho _{XY\cdot \mathbf {Z} }\neq 0$ $H_{A}:\rho _{XY\cdot \mathbf {Z} }\neq 0$ X $H_{A}:\rho _{XY\cdot \mathbf {Z} }\neq 0$ Z $H_{A}:\rho _{XY\cdot \mathbf {Z} }\neq 0$ 0 { $displaystyle H_{A:\rho_{X$ }에 대해 테스트합니다. $Y\cdot \mathbf {Z}$ }\ $neq$ 0 $H_{A}:\rho _{XY\cdot \mathbf {Z} }\neq 0$ 다음 경우 유의 수준α의 H를 거부합니다₀.

{N-\mathbf {Z}-3}\cdot z({\hat {rho }}}_{X})Y\cdot \mathbf {Z} >\Phi ^{-1}(1-\alpha /2)

여기서 δ(·)는 평균 및 단위 표준 편차가 0인 가우스 분포의 누적 분포 함수이며, N은 표본 크기입니다.이 z 변환은 근사치이며 표본(부분) 상관 계수의 실제 분포가 간단하지 않습니다.그러나 편 회귀 계수, 편 상관 계수 및 편 분산의 조합을 기반으로 하는 정확한 t-검정을 사용할 ^[4]수 있습니다.

표본 편상관 분포는 ^[5]Fisher에 의해 설명되었다.

반부분 상관(부품 상관)

반부분(또는 부분) 상관 통계량은 편상관 통계량과 유사합니다.두 변수 모두 특정 요인이 제어된 후 두 변수의 변동을 비교하지만 반부분 상관 관계를 계산하기 위해 하나는 X 또는 Y에 대해 세 번째 변수 상수를 유지하고, 편상관에는 ^[6]두 변수 모두에 대해 세 번째 변수 상수를 유지합니다.반부분 상관 관계에서는 한 변수의 고유 변동(Z 변수와 관련된 변동 제거)을 필터링되지 않은 다른 변수의 변동과 비교하는 반면, 편상관에서는 한 변수의 고유 변동을 다른 변수의 고유 변동과 비교합니다.

반부분적(또는 부분) 상관관계는 "의존적(반응) 변수의 전체 변동성에 비례하여 조정되기 때문에" 보다 실질적으로 관련이 있는 것으로 볼 수 있다.^[7] 반대로, 독립 변수의 고유한 기여의 역할에 대해 덜 정확하기 때문에 이론적으로 덜 유용하다.

X와 Y의 반소수 상관의 절대값은 항상 X와 Y의 편상관보다 작거나 같습니다.이유는 다음과 같습니다.X와 Z의 상관 관계가 X에서 제거되어 잔차 벡터_x e가 주어졌다고 가정합니다. 반부분 상관 관계를 계산할 때 Y는 여전히 Z와의 연관성으로 인해 고유한 분산과 분산을 포함합니다.그러나_x e는 Z와 상관관계가 없기 때문에 Y 분산의 고유한 부분만 설명할 수 있고 Z와 관련된 부분은 설명할 수 없습니다.반면 편상관에서는 e(Z와 무관한 Y 분산의 부분)만_y 설명되므로 e가 설명할 수 없는_x 유형의 분산이 적습니다.

시계열 분석에 사용

시계열 분석에서 시계열의 편 자기 상관 함수(때로는 "부분 상관 함수")는 다음과 같이 지연 h에 대해 정의됩니다.

\displaystyle \varphi (h)=\rho _{X_{0}X_{h},\cdot \,\{X_{1},\dots \,X_{h-1}\}}.}

이 함수는 자동 복귀에 대한 적절한 지연 길이를 결정하는 데 사용됩니다.

「」를 참조해 주세요.

레퍼런스

^ ^a ^b Baba, Kunihiro; Ritei Shibata; Masaaki Sibuya (2004). "Partial correlation and conditional correlation as measures of conditional independence". Australian and New Zealand Journal of Statistics. 46 (4): 657–664. doi:10.1111/j.1467-842X.2004.00360.x. S2CID 123130024.
^ Guilford J. P., Fruchter B. (1973). Fundamental statistics in psychology and education. Tokyo: McGraw-Hill Kogakusha, LTD.
^ Rummel, R. J. (1976). "Understanding Correlation".
^ Kendall MG, Stuart A.(1973) The Advanced Theory of Statistics, 제2권 (제3판), ISBN 0-85264-215-6, 섹션 27.22
^ Fisher, R.A. (1924). "The distribution of the partial correlation coefficient". Metron. 3 (3–4): 329–332.
^ https://web.archive.org/web/20140206182503/https://luna.cas.usf.edu/~mbrannic/files/regression/Partial.html. Archived from the original on 2014-02-06. {{cite web}}:누락 또는 비어 있음 title=(도움말)
^ StatSoft, Inc. (2010)"반부분(또는 부분) 상관", 전자 통계 교재.Tulsa, OK: StatSoft, 2011년 1월 15일에 접속.

외부 링크

Prokhorov, A.V. (2001) [1994], "Partial correlation coefficient", Encyclopedia of Mathematics, EMS Press
IMSL 수치 라이브러리 PCORR 루틴의 "Description" 섹션의 수학 공식
3가지 변수 예시

[Baba-1] Baba, Kunihiro; Ritei Shibata; Masaaki Sibuya (2004). "Partial correlation and conditional correlation as measures of conditional independence". Australian and New Zealand Journal of Statistics. 46 (4): 657–664. doi:10.1111/j.1467-842X.2004.00360.x. S2CID 123130024.

[2] Guilford J. P., Fruchter B. (1973). Fundamental statistics in psychology and education. Tokyo: McGraw-Hill Kogakusha, LTD.

[3] Rummel, R. J. (1976). "Understanding Correlation".

[4] Kendall MG, Stuart A.(1973) The Advanced Theory of Statistics, 제2권 (제3판), ISBN 0-85264-215-6, 섹션 27.22

[5] Fisher, R.A. (1924). "The distribution of the partial correlation coefficient". Metron. 3 (3–4): 329–332.

[6] ttps://web.archive.org/web/20140206182503/https://luna.cas.usf.edu/~mbrannic/files/regression/Partial.html. Archived from the original on 2014-02-06. {{cite web}}:누락 또는 비어 있음 title=(도움말)

[7] StatSoft, Inc. (2010)"반부분(또는 부분) 상관", 전자 통계 교재.Tulsa, OK: StatSoft, 2011년 1월 15일에 접속.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

Search

편상관

네임스페이스

더

목차

형식적 정의

계산

선형 회귀 분석 사용

예

재귀 공식 사용

행렬 반전 사용

해석

기하학적

조건부 독립성 테스트로서

반부분 상관(부품 상관)

시계열 분석에 사용

「」를 참조해 주세요.

레퍼런스

외부 링크

Search

편상관

형식적 정의

계산

선형 회귀 분석 사용

예

재귀 공식 사용

행렬 반전 사용

해석

기하학적

조건부 독립성 테스트로서

반부분 상관(부품 상관)

시계열 분석에 사용

「 」를 참조해 주세요.

레퍼런스

외부 링크

「」를 참조해 주세요.