원자 궤도 선형 조합
Linear combination of atomic orbitals원자 궤도 또는 LCAO의 선형 결합은 원자 궤도의 양자 중첩이며 양자 화학에서 분자 궤도를 계산하는 기법이다.[1] 양자역학에서 원자의 전자적 구성은 파동기능으로 설명된다. 수학적 의미에서 이러한 파동함수는 주어진 원자의 전자를 기술하는 기본함수인 기본함수의 집합이다. 화학 반응에서 궤도 파동 기능은 화학 결합에 참여하는 원자의 유형에 따라 변형된다. 즉, 전자 구름 모양이 변화한다.
1929년 존 레나드 존스에 의해 주기율표의 첫 번째 주계열의 이원자 분자에 결합에 대한 설명과 함께 도입되었지만, 일찍이 리누스 폴링이2+ H를 위해 사용한 적이 있었다.[2][3]
수학적 설명
초기 가정은 분자 궤도의 수가 선형 확장에 포함된 원자 궤도의 수와 같다는 것이다. 어떤 의미에서는 n개의 원자 궤도가 결합하여 n개의 분자 궤도를 형성하는데, 이는 i = 1에서 n까지 번호가 매겨질 수 있고 모두 같지 않을 수도 있다. 분자 궤도 i th 분자 궤도에 대한 표현(선형 팽창)은 다음과 같을 것이다.
또는
여기서 는 n개의 원자 궤도 합계로 대표되는 분자 궤도 r 각각 해당 계수 r(1~n)를 곱하면 용어에 어떤 원자 궤도 합이 결합되어 있는지를 나타낸다. 계수는 분자궤도에 대한 n 원자궤도의 기여의 가중치다. 하트리-Fock 방법은 팽창 계수를 구하는 데 사용된다. 따라서 궤도는 기본 함수의 선형 결합으로 표현되며, 기본 함수는 분자의 성분 원자의 핵에 중심을 둘 수도 있고 아닐 수도 있는 단일 전자 함수다. 어느 경우든 기본 함수는 대개 원자 궤도(전자의 경우만 이 이름이 적절한 것 같음에도 불구하고)라고도 한다. 원자 궤도는 분석적으로 알려져 있기 때문에 일반적으로 수소 같은 원자의 것이다. 슬레이터형 궤도(slater-type orbitals) 그러나 표준 기준 집합의 가우스 함수 또는 평면파 유사성(philotentials)의 유사 원자 궤도(pseud-ater형 궤도(slater-type orbitals)
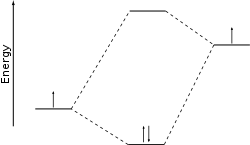
시스템의 총 에너지를 최소화함으로써, 선형 조합의 적절한 계수 집합을 결정한다. 이 양적 접근법은 현재 하트리-로 알려져 있다.포크 방식. 그러나 계산 화학의 발달 이후 LCAO 방법은 파동 함수의 실제 최적화가 아니라 보다 현대적인 방법을 통해 얻은 결과를 예측하고 합리화하는 데 매우 유용한 정성적 토론을 가리키는 경우가 많다. 이 경우 분자 궤도의 모양과 각각의 에너지는 개별 원자(또는 분자 조각)의 원자 궤도의 에너지를 비교하고 레벨 반발 등으로 알려진 몇 가지 레시피를 적용하여 대략 추론한다. 이 논의를 보다 명확하게 하기 위해 표시된 그래프를 상관 도표라고 한다. 필요한 원자 궤도 에너지는 계산에서 나올 수도 있고, 구피만스의 정리를 통한 실험에서 직접 나올 수도 있다.
이는 본딩에 관여하는 분자와 궤도의 대칭을 이용하여 이루어지며, 따라서 대칭적응 선형결합(SALC)이라고도 한다. 이 과정의 첫 번째 단계는 분자에 점 그룹을 할당하는 것이다. 점 그룹의 각 연산은 분자에 대해 수행된다. 움직이지 않는 채권의 수는 그 작전의 특성이다. 이 축소 가능한 표현은 되돌릴 수 없는 표현들의 합으로 분해된다. 이러한 돌이킬 수 없는 표현은 관련 궤도의 대칭에 해당한다.
분자 궤도 다이어그램은 간단한 질적 LCAO 처리를 제공한다. 후켈법, 확장 후켈법, 파리에르-파르-폴플법 등은 몇 가지 양적 이론을 제공한다.
참고 항목
외부 링크
- LCAO @ chemistry.umeche.maine.edu 링크
참조
- ^ 후히이, 제임스. 무기 화학:구조와 반응성의 원리
- ^ 프리드리히 헌드와 화학, 베르너 쿠첼니그, 헌트의 100번째 생일인 안젤완테 케미(35, 572–586, (1996) 도이: 10.1002/anie.199605721
- ^ Mulliken, Robert S. (1967-07-07). "Spectroscopy, Molecular Orbitals, and Chemical Bonding". Science. American Association for the Advancement of Science (AAAS). 157 (3784): 13–24. doi:10.1126/science.157.3784.13. ISSN 0036-8075.



 n개의
n개의