카타파야디 제도

이 글에는 인디케이터 텍스트가 포함되어 있다.적절한 렌더링 지원이 없으면 물음표나 상자, 잘못 배치된 모음 또는 결벽이 인디케이터 텍스트 대신 나타날 수 있다.

숫자 표기법(Devanagari: कटपयाािि)) 체계(일명 Paralppruru, Malayalam: രല്പ്പപ്്്്))는 숫자에 대한 글자를 단어나 구절로 쉽게 기억하기 위해 묘사하는 고대 인도의 알파셀라브 수 체계다.한 숫자에 두 개 이상의 문자를 할당하고 특정 다른 문자를 무능력자로 무효화함으로써, 이 시스템은 쉽게 기억될 수 있는 숫자 중에서 의미 있는 단어를 형성할 수 있는 유연성을 제공한다.

역사

카사파야디(산스크리트어: कटयाद system) 제도의 이용에 대한 가장 오래된 증거는 683년 하리다타에 의한 그라하카라시반다하나에서 나온 것이다.^[1]CE 869년에 by카라·나랴야가 쓴 《라후·바스카르ya야·비바라ṇa》에 사용되어 왔다.^[2]

일부 사람들은 이 제도가 바라루치에서 시작되었다고 주장한다.^[3]케랄라 행성 위치에서 인기 있는 몇몇 천문학적 문헌에는 카사파야디 계통에 암호화되어 있었다.그러한 첫 번째 작품은 전통적으로 4세기 CE에 배속된 바라루치의 찬드라바키니로 여겨진다.따라서, 첫 천년 초기의 어느 시기에 카자파야디 제도의 기원에 대한 합리적인 추정치가 된다.^[4]

아리아브하타는 그의 논문 '아리야·바하ya야'에서 천문학적인 숫자를 나타내기 위해 유사하고 더 복잡한 시스템을 사용한 것으로 알려져 있다.Ka-ṭa-pa-ya-di 체계가 랴바하수에서 비롯되었는지에 대한 명확한 증거는 없다.^[5]

용도의 지리적 확산

Ka-ṭa-pa-ya-di 시스템의 사용에 대한 거의 모든 증거는 인도 남부, 특히 케랄라에서 온 것이다.북인도에서의 사용에 대해서는 별로 알려져 있지 않다.그러나 인도 북부에서 발견된 산스크리트어 아스트롤라베에는 고도가 카자파야디 계통에 표시되어 있다.바라나시 삼푸르난드 산스크리트 대학의 사라스바티 바반 도서관에 보존되어 있다.^[6]

Ka-ya-pa-ya-di 시스템은 인도에만 국한되지 않는다.버마에서 Ka-ṭa-pa-ya-di 체계에 기초한 Pali 크로노그램이 발견되었다.^[7]

규칙 및 관행

챠우카라바르만의 사드라타나말라에서 발견된 다음 구절은 이 계통의 메커니즘을 설명한다.^[8][9]

नञावचश्च शून्यानि संख्या: कटपयादय:।
मिश्रे तूपान्त्यहल् संख्या न च चिन्त्यो हलस्वर:॥

전이성:

nanyavacaśca ūyanni saṃkhyaḥ kaṭapayadayaḥ
Miśre tupntyahal saṃkhyaha na cintyo halasvaraḥ.

번역: na (न), nya (ञ), a (अ)-s, 즉 모음은 0을 나타낸다.9개의 정수는 ka, ṭa, pa, ya로 시작하는 자음 그룹으로 표현된다.결막음에서는 마지막 자음만 셀 것이다.모음 없는 자음은 무시한다.

설명:숫자에 대한 글자 배정은 다음과 같다(각각 데바나가리, 칸나다, 텔루구, 말라얄람).

1	2	3	4	5	6	7	8	9	0
Ka क ಕ ക ക	Kha ख ಖ ఖ ഖ	가 ग ಗ ഗ ഗ	gha घ ಘ ఘ ഘ	nga ङ ಙ జ ఞ ങ ങ ങ	Ca च ಚ చ ച	차 छ ಛ ఛ ഛ	쟈 ಜ జ ജ ജ	쟈 झ ಝ ఝ ഝ	냐 ञ ಞ ఞ ഞ
ṭa ट ಟ ട ട	ṭha ठ ಠ ഠ ഠ	ḍa ड ಡ ഡ ഡ	ḍha ढ ಢ ഢ ഢ	ṇa ण ಣ ണ ണ	ta ತ త త ത ത	Tha थ ಥ థ ഥ	다 द ದ ద ദ	dha ध ಧ ధ ധ	나 न ನ న ന
파 प ಪ ప പ	파 फ ಫ ఫ ഫ	바 ब బ ബ	바하 भ ಭ భ ഭ	ma म ಮ మ മ	–	–	–	–	–
야 य ಯ య യ	라 र ರ ర ര ര	라 ल ల ల ല	va व ವ വ വ	śha श ಶ ശ ശ	샤 ष ಷ ష ഷ	사 स ಸ స സ	하 ह ಹ హ ഹ	–	–

• 자음에는 위의 표에 따라 숫자가 할당되어 있다.예를 들어 ba ( ()는 항상 3인 반면, 5는 nga ( () 또는 ṇa (ण) 또는 ma (म) 또는 śha (श)로 나타낼 수 있다.
• a(अ)와 ((ऋ)와 같은 모든 독립 모음은 0에 할당된다.
• 결막의 경우, 비보울에 부착된 자음은 무용지물이 된다.예를 들어 kya(क्)는 k(क्) + y(य) + a(अ)로 형성된다.모음과 함께 서 있는 유일한 자음은 ya( ()따라서 kya에 해당하는 숫자는 1이 될 것이다.
• 계통에서 소수 구분자를 나타내는 방법은 없다.
• 인도인들은 힌두-아랍 숫자 체계를 번호 매기기 위해 사용했는데, 전통적으로 왼쪽에서 오른쪽으로 위치 값을 증가시키는 방식으로 쓰여졌다.This is as per the rule "अङ्कानां वामतो गतिः" which means numbers go from right to left.

변형

• 자음인 ḷ(말레이아람: ള, 데바나가르ā: ळ, 칸나다: ಳ)은 마다바의 사인표와 같이 카아파야아디 시스템을 이용한 작품에 채용된다.
• 중세 말기의 실무자들은 독립형 모음을 0으로 매핑하지 않는다.하지만, 때때로 그것은 무용지물로 여겨지기도 한다.

사용법

수학과 천문학

• 14세기 사가마·그라마의 케랄라 수학자-아스트로노머 마드하바(Madhava)가 만든 마드하바의 사인표는 각도의 삼각계 시네(sines)를 얻기 위해 카사파야아디(kaṭapayaiadi) 시스템을 채용한다.
• 15세기에 쓰여진 카라샤·파다티에는 파이의 가치에 대한 다음과 같은 śloka가 있다(π).

അനൂനനൂന്നാനനനുന്നനിത്യൈ-

സ്സമാഹതാശ്ചക്രകലാവിഭക്താഃ

ചണ്ഡാംശുചന്ദ്രാധമകുംഭിപാലൈര്-

വ്യാസസ്തദര്ദ്ധം ത്രിഭമൗര്വിക സ്യാത്

반투명

아누나누나누나누나니티

스마하타하타카크라칼라비바쿠토

카아후칸드라다마쿠바흐파라이어

vyāsastadarddhaṃ tribhamaurvika syāt

It gives the circumference of a circle of diameter, anūnanūnnānananunnanityai (10,000,000,000) as caṇḍāṃśucandrādhamakuṃbhipālair (31415926536).

• ś카라·바르만의 사드·라트나·말라는 카사파야디 시스템을 사용한다.사담·라트나·말라의 제4장 제1절은 다음과 같은 선으로 끝난다.^[10]

(स्याद्) भद्राम्बुधिसिद्धजन्मगणितश्रद्धा स्म यद् भूपगी:

반투명

(syd) Badrabudhisddajanmagaṇita śraddhah sma yad bhupagīḥ

관련 구절의 자음을 나누면 다음과 같다.

भ bha	द् d	라	म् m	bu bu	द् d	धि dhi	si 시	द् d	ध dha	ja자	न्n	ma	ग가	णि i	त ta	श् ś	rara	द् d	다	स् s	ma	य야	द् d	भू bhu	प파	गी gī
4	–	2	–	3	–	9	7	–	9	8	–	5	3	5	6	–	2	–	9	–	5	1	–	4	1	3

소수점 이하 내림차순의 현대적 사용으로 숫자를 거꾸로 하면 파이 값인 314159265358979324가 소수점 17자리까지 나오고 마지막 자릿수는 4자리까지 반올림할 수 있다.

• 이 시는 소수점 이하 31자리까지의 파이(pi) 값을 암호화한다.

गोपीभाग्यमधुव्रात-शृङ्गिशोदधिसन्धिग॥  खलजीवितखाताव गलहालारसंधर॥

ಗೋಪೀಭಾಗ್ಯಮಧುವ್ರಾತ-ಶೃಂಗಿಶೋದಧಿಸಂಧಿಗ     ಖಲಜೀವಿತಖಾತಾವ ಗಲಹಾಲಾರಸಂಧರ

이 구절은 파이와 10: pi/10 = 0.314159265358979979323846433832792로 나눈 십진수 등가물을 직접 산출한다.

గోపీభాగ్యమధువ్రాత-శృంగిశోదధిసంధిగ    ఖలజీవితఖాతావ గలహాలారసంధర

전통적으로 카타파야디 시스템에서는 자릿수 순서를 거꾸로 하여 숫자를 형성한다.이 규칙은 이 슬록에서 위반된다.

카르나틱 음악

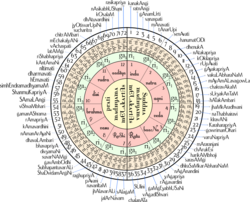
• 카르나틱 음악의 멜라카르타 라가스는 그 이름의 처음 두 음절이 그 번호를 주도록 이름 지어졌다.이 시스템은 때때로 카타파야디 산키야라고 불린다.스와라스 '사'와 '파'는 고정되어 있으며, 여기 멜라카르타 수에서 다른 스와라를 얻는 방법이 있다.

1. 멜라카르타스 1에서 36까지는 Ma1이 있고 37에서 72까지가 Ma2가 있다.
2. 다른 음은 멜라카르타 수보다 한 개 적은 음을 6으로 나눌 때 (의 통합 부분) 지수를 기록함으로써 도출된다.멜라카르타 수가 36보다 크면 이 단계를 수행하기 전에 멜라카르타 수에서 36을 빼십시오.
3. '리' 및 '가' 위치: 라가는 다음을 가질 것이다.
   • 몫이 0인 경우 Ri1 및 Ga1
   • 몫이 1일 경우 Ri1과 Ga2
   • 몫이 2인 경우 Ri1과 Ga3
   • Ri2와 Ga2가 3인 경우
   • Ri2와 Ga3가 4인 경우
   • Ri3와 Ga3가 5인 경우
4. '다' 및 '니' 위치: 라가는 다음을 가질 것이다.
   • 나머지가 0인 경우 Da1 및 Ni1
   • 나머지가 1인 경우 Da1 및 Ni2
   • 나머지가 2인 경우 Da1 및 Ni3
   • Da2 및 Ni2(잔량이 3인 경우)
   • 나머지가 4인 경우 Da2 및 Ni3
   • 나머지가 5인 경우 Da3 및 Ni3

• 위의 표기법에 대한 자세한 내용은 카르나틱 음악에서 스와라를 참조하십시오.

라가 데이라산카라바라바라바남

카타파야디 제도는 dha$£{\displaystyle \leftrightarrow}}$와 la$£{\displaystyle \leftrightarrow}}$를 연관지으며, 따라서 라가의 멜라카르타 번호는 29(92번 역)이다.이제 29$≤[\displaystyle \leq }$ 36, 따라서 드헤라산카라바라바남에는 Ma1이 있다.28(29점 이하 1점)을 6점으로 나누면, 몫은 4점, 나머지는 4점이다.따라서 이 라가는 리2, 가3, 다2, 니3, 다2, 니3를 가지고 있다.따라서 이 라가의 스케일은 사리2 가3 마1 파 다2 니3 SA이다.

라가 메차칼랴니

코드 체계 Ma £ ${\displaystyle \좌우타로우 }$ 5, Cha £ ${\displaystyle \좌우타로우 }$ 6.따라서 라가의 멜라카르타 수는 65(56역)이다.65는 36보다 크다.그래서 MechaKalyani는 Ma2를 가지고 있다.라가의 숫자는 36보다 크므로, 그것으로부터 36을 빼기 때문이다. 65–36=29. 28(29보다 작음)을 6: 몫=4, 나머지는 4로 나눈다.Ri2 Ga3가 발생한다.Da2 Ni3가 발생한다.그래서 MechaKalyani는 Sa Ri2 Ga3 Ma2 Pa Da2 Ni3 SA를 가지고 있다.

Simendramadhyamam에 대한 예외

위의 계산에 따르면, 우리는 Sa £{\$displaystyle \좌우타로우$} 7, Ha£{\$displaystyle \좌우타로우$} 8을 받아야 하며, 심헨드라마디함 에서는 57이 아니라 87이 되어야 한다.이것은 이상적으로 Sa £ ${\displaystyle \leftrightarrow}$ 7, Ma £ ${\displaystyle \leftrightarrow}$ 5가 되어야 하며, 숫자 57이 표시되어야 한다.그래서 명칭은 Sihmendramadhyam(산스크리트어로 브라흐마나의 경우처럼)으로 표기해야 한다고 생각된다.

날짜 표시

중요한 날짜는 카자파야디 시스템을 사용하여 변환함으로써 기억되었다.이러한 날짜는 일반적으로 칼리 유가가 시작된 이후의 일수로 표현된다.그것은 때때로 칼리디나 산키야라고 불린다.

• 칼라바르샴(Malayalam: :കല്വവരരരരംംംംംം))으로 알려진 말레이알람 달력은 825 CE부터 케랄라에서 채택되어 일부 달력을 개편하였다.이 날짜는 Ka yugapayadi를 사용하여 칼리 유가가 시작된 이후 1434160일로 변환된 ā랴 vagbhada로 기억된다.^[11]
• Narayaniyam, written by Melpathur Narayana Bhattathiri, ends with the line, āyurārogyasaukhyam (ആയുരാരോഗ്യസൌഖ്യം) which means long-life, health and happiness.^[12]

인말랄람	ആയുരാരോഗ്യസൌഖ്യം
데바나가리	आयुरारोग्यसौख्यम्
IAST에서	아로 갸사우크히암
Kaṭapayadi에 따른 값	1712210

이 숫자는 말레이알람 달력에 따라 칼리 유가가 시작된 이후 일수로 표현되는 작업을 완료한 시간이다.

다른이들

• 어떤 사람들은 신생아들의 이름을 짓는데 Kaṭapayadi 시스템을 사용한다.^[13][14]
• 코두알루르 쿠니크쿠안 타우푸란(Koduṅalur Kunikkuṭan Taṃpuran)이 카자파야디(Kaṭapayadi)를 이용하여 말레이알람에서 편찬한 다음 구절은 그레고리력으로 월의 일수다.

പലഹാരേ പാലു നല്ലൂ, പുലര്ന്നാലോ കലക്കിലാം

ഇല്ലാ പാലെന്നു ഗോപാലന് – ആംഗ്ലമാസദിനം ക്രമാല്

전이

팔라흐레 팔루 날루, 팔라흐르날루 칼라크킬라

Ila Palennu Gophalan – alagamamasadinaam Kramal.

번역:우유는 아침식사에 가장 좋으며, 아침이 되면 휘저어야 한다.그러나 고팔란은 순서에 따라 영어 월의 일수인 우유가 없다고 말한다.

Converting pairs of letters using Kaṭapayādi yields – pala (പല) is 31, hāre (ഹാരേ) is 28, pālu പാലു = 31, nallū (നല്ലൂ) is 30, pular (പുലര്) is 31, nnālo (ന്നാലോ) is 30, kala (കല) is 31, kkilāṃ (ക്കിലാം) is 31, illā (ഇല്ലാ) is 30, pāle (പാലെ) is 31, nnu go (ന്നു ഗോ) is 30, pālan (പാലന്) is 31.

참고 항목

참조

추가 읽기

• A.A. Hattangadi, 수학탐사, 대학 출판부 (인도) Pvt. Ltd, Hyderabad(2001) ISBN 81-7371-387-1 [3]