암시면

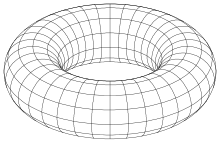
수학에서, 암묵적 표면(implicit surface)은 유클리드 공간에서 방정식으로 정의되는 표면입니다.

F(x,y,z)=0.

암묵적 표면은 세 변수의 함수에 대한 0의 집합입니다. 암묵적이란 방정식이 $x$ $또는$ $y$ 또는 z에 대해 풀리지 않는다는 것을 의미합니다.

함수의 그래프는 일반적으로 방정식 $z=f(x,y)$ = $z=f(x,y)$ $z=f(x,y)$ x $,$ y) {\displaystyle z = f (x, y)}로 설명되며 명시적 표현이라고 합니다. 표면의 세 번째 필수 설명은 매개 변수입니다. ( $(x(s,t),y(s,t),z(s,t))$ ( $(x(s,t),y(s,t),z(s,t))$ $(x(s,t),y(s,t),z(s,t))$ $(x(s,t),y(s,t),z(s,t))$ ( $(x(s,t),y(s,t),z(s,t))$ $(x(s,t),y(s,t),z(s,t))$ z $(x(s,t),y(s,t),z(s,t))$ ( $(x(s,t),y(s,t),z(s,t))$ t $(x(s,t),y(s,t),z(s,t))$ ) ${\displaystyle ($ x $(s,$ t $),$ y ( $s, t),$ z ( $s,$ t $)}.$ 여기서 표면 점의 $x$ , y, $t$ $x(s,t)\,,y(s,t)\,,z(s,t)$ z $x(s,t)\,,y(s,t)\,,z(s,t)$ 는 x ( $s$ t $x(s,t)\,,y(s,t)\,,z(s,t)$ $x(s,t)\,,y(s,t)\,,z(s,t)$ ( $x(s,t)\,,y(s,t)\,,z(s,t)$ $x(s,t)\,,y(s,t)\,,z(s,t)$ $x(s,t)\,,y(s,t)\,,z(s,t)$ ( $x(s,t)\,,y(s,t)\,,z(s,t)$ t $x(s,t)\,,y(s,t)\,,z(s,t)$ ) ${\displaystyle$ x( $s,$ t)\, $y(s,$ t $)\,z(s$ , t $),$ $t)}$ depending on common parameters $s,t$ . Generally the change of representations is simple only when the explicit representation $z=f(x,y)$ is given: $z-f(x,y)=0$ (implicit), ${\displaystyle (s,t,f(s,$ $t))}($ 모수).

예:

평면 $x+2y-3z+1=0.$ + $x+2y-3z+1=0.$ $x+2y-3z+1=0.$ - $x+2y-3z+1=0.$ $x+2y-3z+1=0.$ + $x+2y-3z+1=0.$ = 0 $x+2y-3z+1=0.$ {\displaystyle x+2 y - 3z + 1 = 0.}
구 $x^{2}+y^{2}+z^{2}-4=0.$ $x^{2}+y^{2}+z^{2}-4=0.$ + $x^{2}+y^{2}+z^{2}-4=0.$ $x^{2}+y^{2}+z^{2}-4=0.$ + $x^{2}+y^{2}+z^{2}-4=0.$ $x^{2}+y^{2}+z^{2}-4=0.$ - $x^{2}+y^{2}+z^{2}-4=0.$ = $.{\$ displaystyle x^{2}+y^{2}+z^{2}-4=0.}
토러스 $(x^{2}+y^{2}+z^{2}+R^{2}-a^{2})^{2}-4R^{2}(x^{2}+y^{2})=0.$ $(x^{2}+y^{2}+z^{2}+R^{2}-a^{2})^{2}-4R^{2}(x^{2}+y^{2})=0.$ + $(x^{2}+y^{2}+z^{2}+R^{2}-a^{2})^{2}-4R^{2}(x^{2}+y^{2})=0.$ 2 $(x^{2}+y^{2}+z^{2}+R^{2}-a^{2})^{2}-4R^{2}(x^{2}+y^{2})=0.$ + $(x^{2}+y^{2}+z^{2}+R^{2}-a^{2})^{2}-4R^{2}(x^{2}+y^{2})=0.$ $(x^{2}+y^{2}+z^{2}+R^{2}-a^{2})^{2}-4R^{2}(x^{2}+y^{2})=0.$ + R $(x^{2}+y^{2}+z^{2}+R^{2}-a^{2})^{2}-4R^{2}(x^{2}+y^{2})=0.$ - $(x^{2}+y^{2}+z^{2}+R^{2}-a^{2})^{2}-4R^{2}(x^{2}+y^{2})=0.$ $(x^{2}+y^{2}+z^{2}+R^{2}-a^{2})^{2}-4R^{2}(x^{2}+y^{2})=0.$ $(x^{2}+y^{2}+z^{2}+R^{2}-a^{2})^{2}-4R^{2}(x^{2}+y^{2})=0.$ - 4 $(x^{2}+y^{2}+z^{2}+R^{2}-a^{2})^{2}-4R^{2}(x^{2}+y^{2})=0.$ 2 $(x^{2}+y^{2}+z^{2}+R^{2}-a^{2})^{2}-4R^{2}(x^{2}+y^{2})=0.$ 2 $(x^{2}+y^{2}+z^{2}+R^{2}-a^{2})^{2}-4R^{2}(x^{2}+y^{2})=0.$ + $(x^{2}+y^{2}+z^{2}+R^{2}-a^{2})^{2}-4R^{2}(x^{2}+y^{2})=0.$ $(x^{2}+y^{2}+z^{2}+R^{2}-a^{2})^{2}-4R^{2}(x^{2}+y^{2})=0.$ ) = $.{\$ displaystyle(x^{2}+y^{2}+z^{2}+R^{2}-a^{2)^{2}-4R^{2}(x^{2}+y^{2)= $0.}$
속 2: $2y(y^{2}-3x^{2})(1-z^{2})+(x^{2}+y^{2})^{2}-(9z^{2}-1)(1-z^{2})=0$ $2y(y^{2}-3x^{2})(1-z^{2})+(x^{2}+y^{2})^{2}-(9z^{2}-1)(1-z^{2})=0$ $2y(y^{2}-3x^{2})(1-z^{2})+(x^{2}+y^{2})^{2}-(9z^{2}-1)(1-z^{2})=0$ $2y(y^{2}-3x^{2})(1-z^{2})+(x^{2}+y^{2})^{2}-(9z^{2}-1)(1-z^{2})=0$ - $2y(y^{2}-3x^{2})(1-z^{2})+(x^{2}+y^{2})^{2}-(9z^{2}-1)(1-z^{2})=0$ $2y(y^{2}-3x^{2})(1-z^{2})+(x^{2}+y^{2})^{2}-(9z^{2}-1)(1-z^{2})=0$ $2y(y^{2}-3x^{2})(1-z^{2})+(x^{2}+y^{2})^{2}-(9z^{2}-1)(1-z^{2})=0$ ) $2y(y^{2}-3x^{2})(1-z^{2})+(x^{2}+y^{2})^{2}-(9z^{2}-1)(1-z^{2})=0$ ( $2y(y^{2}-3x^{2})(1-z^{2})+(x^{2}+y^{2})^{2}-(9z^{2}-1)(1-z^{2})=0$ - $2y(y^{2}-3x^{2})(1-z^{2})+(x^{2}+y^{2})^{2}-(9z^{2}-1)(1-z^{2})=0$ $2y(y^{2}-3x^{2})(1-z^{2})+(x^{2}+y^{2})^{2}-(9z^{2}-1)(1-z^{2})=0$ ) $2y(y^{2}-3x^{2})(1-z^{2})+(x^{2}+y^{2})^{2}-(9z^{2}-1)(1-z^{2})=0$ + $2y(y^{2}-3x^{2})(1-z^{2})+(x^{2}+y^{2})^{2}-(9z^{2}-1)(1-z^{2})=0$ ( $2y(y^{2}-3x^{2})(1-z^{2})+(x^{2}+y^{2})^{2}-(9z^{2}-1)(1-z^{2})=0$ 2 $2y(y^{2}-3x^{2})(1-z^{2})+(x^{2}+y^{2})^{2}-(9z^{2}-1)(1-z^{2})=0$ + $2y(y^{2}-3x^{2})(1-z^{2})+(x^{2}+y^{2})^{2}-(9z^{2}-1)(1-z^{2})=0$ 2 $2y(y^{2}-3x^{2})(1-z^{2})+(x^{2}+y^{2})^{2}-(9z^{2}-1)(1-z^{2})=0$ ) 2 $2y(y^{2}-3x^{2})(1-z^{2})+(x^{2}+y^{2})^{2}-(9z^{2}-1)(1-z^{2})=0$ - $2y(y^{2}-3x^{2})(1-z^{2})+(x^{2}+y^{2})^{2}-(9z^{2}-1)(1-z^{2})=0$ ( $2y(y^{2}-3x^{2})(1-z^{2})+(x^{2}+y^{2})^{2}-(9z^{2}-1)(1-z^{2})=0$ $2y(y^{2}-3x^{2})(1-z^{2})+(x^{2}+y^{2})^{2}-(9z^{2}-1)(1-z^{2})=0$ $2y(y^{2}-3x^{2})(1-z^{2})+(x^{2}+y^{2})^{2}-(9z^{2}-1)(1-z^{2})=0$ - 1 $2y(y^{2}-3x^{2})(1-z^{2})+(x^{2}+y^{2})^{2}-(9z^{2}-1)(1-z^{2})=0$ ) $2y(y^{2}-3x^{2})(1-z^{2})+(x^{2}+y^{2})^{2}-(9z^{2}-1)(1-z^{2})=0$ ( $2y(y^{2}-3x^{2})(1-z^{2})+(x^{2}+y^{2})^{2}-(9z^{2}-1)(1-z^{2})=0$ - $2y(y^{2}-3x^{2})(1-z^{2})+(x^{2}+y^{2})^{2}-(9z^{2}-1)(1-z^{2})=0$ $2y(y^{2}-3x^{2})(1-z^{2})+(x^{2}+y^{2})^{2}-(9z^{2}-1)(1-z^{2})=0$ ) = ${\$ displaystyle 2y (y^{2}-3x^{2}) (1-z^{2) + (x^{2)^{2) - (9z^{2) - (1-z^{2) = 0.
레볼루션 $x^{2}+y^{2}-(\ln(z+3.2))^{2}-0.02=0$ $x^{2}+y^{2}-(\ln(z+3.2))^{2}-0.02=0$ + y $x^{2}+y^{2}-(\ln(z+3.2))^{2}-0.02=0$ - $x^{2}+y^{2}-(\ln(z+3.2))^{2}-0.02=0$ ( $x^{2}+y^{2}-(\ln(z+3.2))^{2}-0.02=0$ ⁡ $x^{2}+y^{2}-(\ln(z+3.2))^{2}-0.02=0$ + $x^{2}+y^{2}-(\ln(z+3.2))^{2}-0.02=0$ . $x^{2}+y^{2}-(\ln(z+3.2))^{2}-0.02=0$ 2 - $x^{2}+y^{2}-(\ln(z+3.2))^{2}-0.02=0$ . $02$ = 0 ${\displaystyle$ x^{ $2}$ + $y^{2}$ - (\ $ln($ z + 3.2)) $^{2}-0.02=0}$ (도면 와인잔 참조).

평면, 구 및 원환체의 경우 간단한 모수 표현이 있습니다. 네 번째 예에서는 그렇지 않습니다.

암묵적 함수 정리는 $F(x,y,z)=0$ $F(x,y,z)=0$ ( $F(x,y,z)=0$ y $F(x,y,z)=0$ z $F(x,y,z)=0$ ) = 0 ${\$ displaystyle F (x, y, $F(x,y,z)=0$ ) = 0}이 x, y 또는 z에 대해 (적어도 암묵적으로) 해결될 수 있는 조건을 설명합니다. 그러나 일반적으로 해결책은 명시적으로 제시되지 않을 수 있습니다. 이 정리는 접평면, 표면 정규, 곡률(아래 참조)과 같은 표면의 필수 기하학적 특징을 계산하는 열쇠입니다. 그러나 그들은 시각화가 어렵다는 본질적인 단점이 있습니다.

$F(x,y,z)$ ( $F(x,y,z)$ $F(x,y,z)$ $F(x,y,z)$ ) ${\displaystyle F(x,$ y, z $)}$ 가 $F(x,y,z)$ $x$ , $y$ , $z$ 에서 다항식이면 표면을 대수적이라고 합니다. 예 5는 대수적이지 않습니다.

시각화의 어려움에도 불구하고 암시적 표면은 이론적으로(예: 스타이너 표면) 그리고 실질적으로(아래 참조) 흥미로운 표면을 생성하는 비교적 간단한 기술을 제공합니다.

수식

다음 고려 사항에서 암시적 표면은 함수 F {\displaystyle F}가 미분 가능성의 필요 조건을 충족하는 방정식 $F(x,y,z)=0$ $F(x,y,z)=0$ $F(x,y,z)=0$ ) = $F(x,y,z)=0$ ${\$ displaystyle F(x, y, z) = 0}으로 표시됩니다. $F {\displaystyle$ F $}$ 의 부분 도함수는 $F_{x},F_{y},F_{z},F_{xx},\ldots$ $F_{x},F_{y},F_{z},F_{xx},\ldots$ $F_{x},F_{y},F_{z},F_{xx},\ldots$ $F_{x},F_{y},F_{z},F_{xx},\ldots$ $F_{x},F_{y},F_{z},F_{xx},\ldots$ … $F_{x$ 입니다 $F$ . $F_{y},F_{z},F_{xx},\ldots }$ .

접평면과 법선벡터

A surface point $(x_{0},y_{0},z_{0})$ is called regular if and only if the gradient of $F$ at $(x_{0},y_{0},z_{0})$ is not the zero vector $(0,0,0)$ , meaning

{\displaystyle (F_{x

F_{y}(x_{0},y_{0},z_{0}),

F_{z}(x_{0},y_{0},z_{0})\n

eq (0,0,0

표면 점 $(x_{0},y_{0},z_{0})$ $(x_{0},y_{0},z_{0})$ $(x_{0},y_{0},z_{0})$ 0 $(x_{0},y_{0},z_{0})$ $(x_{0},y_{0},z_{0})$ $(x_{0},y_{0},z_{0})$ ${\displaystyle(x_{0}, y_{0}, z_{0})}$ 가 $(x_{0},y_{0},z_{0})$ 규칙적이지 않으면 단수라고 합니다.

정칙점 $(x_{0},y_{0},z_{0})$ $(x_{0},y_{0},z_{0})$ $(x_{0},y_{0},z_{0})$ 0 $(x_{0},y_{0},z_{0})$ $(x_{0},y_{0},z_{0})$ $(x_{0},y_{0},z_{0})$ {\ $displaystyle(x_{0}, y_{0}, z_{0})}$ 에서의 접평면 방정식은 $(x_{0},y_{0},z_{0})$

F_{x}(x_{0},y_{0},z_{0})(x-x_{0})+F_{y}(x_{0},y_{0},z_{0})(y-y_{0})+F_{z}(x_{0},y_{0},z_{0})(z-z_{0})=0,

그리고 정규 벡터는

{\displaystyle \mathbf {n} (x_{0},y_{0},z_{0})=(F_{x}(x_{0},y_{0},z_{0}),F_{y}(x_{0},y_{0},z_{0}),F_{z}(x_{0},y_{0},z_{0})^{T}.

법선곡률

공식을 단순하게 유지하기 위해 $(x_{0},y_{0},z_{0})$ ( $(x_{0},y_{0},z_{0})$ 0 $(x_{0},y_{0},z_{0})$ $(x_{0},y_{0},z_{0})$ $(x_{0},y_{0},z_{0})$ z $(x_{0},y_{0},z_{0})$ ) ${\displaystyle$ ( $x_{0}, y_{0}, z_{0}}$ 인수는 생략됩니다 $(x_{0},y_{0},z_{0})$ .

\kappa_{n}={\frac {\mathbf {v} ^{\top}H_{F}\mathbf {v}{\ \operatorname {grad} F\}

는 단위 접선 $\mathbf {v}$ v ${\$ 에 대한 정칙점에서의 표면의 법선 곡률입니다 $\mathbf {v}$ $H_{F}$ $H_{F}$ ${\$ 는 $H_{F}$ F ${\displaystyle F}($ 이차 도함수의 행렬)의 헤센 행렬입니다.

이 공식의 증명은 (묵시 곡선의 경우와 마찬가지로) 매개변수 표면의 정규 곡률에 대한 암묵적 함수 정리와 공식에 의존합니다.

암시적 표면의 응용

암시적 곡선의 경우와 마찬가지로 단순 프리미티브에 대수 연산( 덧셈, 곱셈)을 적용하여 원하는 모양의 암시적 표면을 생성하는 것은 쉬운 작업입니다.

점전하의 등전위면

$\mathbf {p} _{i}=(x_{i},y_{i},z_{i})$ $\mathbf {p} _{i}=(x_{i},y_{i},z_{i})$ = $\mathbf {p} _{i}=(x_{i},y_{i},z_{i})$ ( $,$ $y,$ zi) {\displaystyle $q_{i}}$ 에서 점전하 $q_{i}$ ${\displaystyle$ q_{i}}의 전위가 점 p = (x, y, z) {\displaystyle \mathbf {p} = (x, $\mathbf {p} =(x,y,z)$ , z)}에서 전위(물리 상수 생략)를 생성합니다.

F_{i}(x,y,z)={\frac {q_{i}}{\ \mathbf {p} -\mathbf {p} _{i}\ }}.

전위 값 $c$ ${\displaystyle$ c $}$ 의 등전위 표면은 암시적 표면 $F_{i}(x,y,z)-c=0$ ( $F_{i}(x,y,z)-c=0$ y $F_{i}(x,y,z)-c=0$ $F_{i}(x,y,z)-c=0$ ) $F_{i}(x,y,z)-c=0$ - $F_{i}(x,y,z)-c=0$ = $F_{i}(x,y,z)-c=0$ ${\$ displaystyle F_ ${i$ }(x, y, z) - c = 0}이며, 이는 p {\displaystyle \mathbf {p} _{i} 지점에 중심이 있는 구입니다.

$4$ $4$ 포인트 $4$ 전하의 전위는 다음과 같이 표시됩니다.

F(x,y,z)={\frac {q_{1}}{\ \mathbf {p} -\mathbf {p} _{1}\ }}+{\frac {q_{2}}{\ \mathbf {p} -\mathbf {p} _{2}\ }}+{\frac {q_{3}}{\ \mathbf {p} -\mathbf {p} _{3}\ }}+{\frac {q_{4}}{\ \mathbf {p} -\mathbf {p} _{4}\ }}.

그림의 경우 4개의 전하가 1과 같고 지점 $(\pm 1,\pm 1,0)$ $(\pm 1,\pm 1,0)$ ± $(\pm 1,\pm 1,0)$ 0 $(\pm 1,\pm 1,0)$ ${\displaystyle(\pm$ 1 $,\pm$ 1, 0 $)}$ 에 위치합니다 $(\pm 1,\pm 1,0)$ 표시되는 표면은 등전위 표면(implicit 표면) F $F(x,y,z)-2.8=0$ y $F(x,y,z)-2.8=0$ z $F(x,y,z)-2.8=0$ ) $F(x,y,z)-2.8=0$ - 2. $F(x,y,z)-2.8=0$ = ${\displaystyle$ F(x, y, $F(x,y,z)-2.8=0$ ) - $F(x,y,z)-2.8=0$ 2.8 = 0}입니다.

등거리 상품면

카시니 타원은 주어진 두 점까지의 거리의 곱이 일정한 점 집합으로 정의할 수 있습니다(반대로 타원의 경우 합이 일정합니다). 비슷한 방법으로 암시적 표면은 여러 고정점에 대한 일정한 거리 곱에 의해 정의될 수 있습니다.

왼쪽 상단 표면이 변형되는 다이어그램에서 이 규칙에 의해 생성됩니다. 와 함께

{\begin{aligned}F(x,y,z)={}&{\Big (}{\sqrt {(x-1)^{2}+y^{2}+z^{2}}}\cdot {\sqrt {(x+1)^{2}+y^{2}+z^{2}}}\\&\qquad \cdot {\sqrt {x^{2}+(y-1)^{2}+z^{2}}}\cdot {\sqrt {x^{2}+(y+1)^{2}+z^{2}}}{\big )}\end{align}}

등거리 제품 표면 F(x $F(x,y,z)-1.1=0$ $F(x,y,z)-1.1=0$ $F(x,y,z)-1.1=0$ ) $F(x,y,z)-1.1=0$ - 1 $F(x,y,z)-1.1=0$ = ${\$ displaystyle F( $F(x,y,z)-1.1=0$ , y, z) - 1.1 = 0} 가 표시됩니다.

토러스와 일정한 거리 곱 표면이라는 두 개의 암시적 표면 사이에서 변형됩니다.

암시적 표면의 변성

새로운 암시적 표면을 생성하는 더 간단한 방법은 암시적 표면의 변형이라고 합니다.

두 개의 암시적 표면 $F_{1}(x,y,z)=0,F_{2}(x,y,z)=0$ $F_{1}(x,y,z)=0,F_{2}(x,y,z)=0$ ( $F_{1}(x,y,z)=0,F_{2}(x,y,z)=0$ y $F_{1}(x,y,z)=0,F_{2}(x,y,z)=0$ $F_{1}(x,y,z)=0,F_{2}(x,y,z)=0$ ) = $F_{1}(x,y,z)=0,F_{2}(x,y,z)=0$ $F_{1}(x,y,z)=0,F_{2}(x,y,z)=0$ 2 $F_{1}(x,y,z)=0,F_{2}(x,y,z)=0$ (x, $y,$ z ) = 0 {\displaystyle F_{1}(x, y, z) = 0,F_{2}(x, y, z) = 0}(도해: 일정한 거리의 곱 표면과 토러스)에 대해 설계 매개 변수 μ ∈ [0, 1] {\displaystyle \mu \in [0, 1]}을 사용하여 새 표면을 정의합니다.

F(x,y,z)=\mu F_{1}(x,y,z)+(1-\mu )F_{2}(x,y,z)=0

다이어그램에서 설계 모수는 $\mu =0,\,0.33,\,0.66,\,1$ 으로 μ = $\mu =0,\,0.33,\,0.66,\,1$ 0 $.33$ , 0.66, 1 {\displaystyle \mu = 0,\,0.33,\,0.66,\,1}입니다.

여러 내포 표면의 매끄러운 근사

$π {\$ displaystyle \Pi} - 표면은 R3 {\displaystyle R^{3}에서 주어진 매끄럽고 경계가 있는 물체의 근사화에 사용될 수 있으며, 표면은 보조 다항식의 곱으로 단일 다항식으로 정의됩니다. 즉, 우리는 어떤 매끄러운 물체라도 하나의 대수적 표면으로 설계할 수 있습니다. $f_{i}\in \mathbb {R} [x_{1},\ldots ,x_{n}](i=1,\ldots ,k)$ 다항식을 \mathbb {R} [x $f_{i}\in \mathbb {R} [x_{1},\ldots ,x_{n}](i=1,\ldots ,k)$ , $f_{i}\in \mathbb {R} [x_{1},\ldots ,x_{n}](i=1,\ldots ,k)$ x $f_{i}\in \mathbb {R} [x_{1},\ldots ,x_{n}](i=1,\ldots ,k)$ ] ( $f_{i}\in \mathbb {R} [x_{1},\ldots ,x_{n}](i=1,\ldots ,k)$ = 1 $…,$ k) {\displaystyle f_{i}\in \mathbb {R} [x_{1},\ldots,x_{n}] (i= $f_{i}\in \mathbb {R} [x_{1},\ldots ,x_{n}](i=1,\ldots ,k)$ ,\ldots,k)}에서 f ∈ $f_{i}\in \mathbb {R} [x_{1},\ldots ,x_{n}](i=1,\ldots ,k)$ R로 표기하자. 그러면 근사 대상은 다항식으로 정의됩니다.

F(x,y,z)=\prod _{i}f_{i}(x,y,z)-r

^[1]

$r\in \mathbb {R}$ 서 $r$ ∈ R ${\display r\in \mathbb$ {R}은 근사 오차를 제어하는 혼합 파라미터를 나타냅니다.

암시적 곡선을 사용하는 매끄러운 근사와 유사하게 방정식

F(x,y,z)=F_{1}(x,y,z)\cdot F_{2}(x,y,z)\cdot F_{3}(x,y,z)-r=0

는 적합한 $매개변수$ c{\ $displaystyle$ c $}$ 를 나타냅니다. 3개의 교차하는 토리의 $c$ 매끄러운 근사값은 방정식으로 표현됩니다.

{\begin{aligned}F_{1}=(x^{2}+y^{2}+z^{2}+R^{2}-a^{2})^{2}-4R^{2}(x^{2}+y^{2})=0,\\[3pt]F_{2}=(x^{2}+y^{2}+z^{2}+R^{2}-a^{2})^{2}-4R^{2}(x^{2}+z^{2})=0,\\[3pt]F_{3}=(x^{2}+y^{2}+z^{2}+R^{2}-a^{2})^{2}-4R^{2}(y^{2}+z^{2})=0.\end{align}}

(그림에서 모수는 $R=1,\,a=0.2,\,r=0.01.$ = $R=1,\,a=0.2,\,r=0.01.$ a $R=1,\,a=0.2,\,r=0.01.$ = $R=1,\,a=0.2,\,r=0.01.$ r = 0 $R=1,\,a=0.2,\,r=0.01.$ 입니다. ${\displaystyle R=1,\,a=0.2,\,r=0.01.$ $}$ )

POV-Ray 영상: 구와 일정한 거리의 제품 표면(6점) 사이에서 변형됩니다.

암시적 표면의 시각화

마칭 큐브 알고리즘을 ^[2]포함하여 암시적 표면을 렌더링하는 다양한 알고리즘이 있습니다.^[3] 기본적으로 암시적 표면을 시각화하기 위한 두 가지 아이디어가 있습니다. 하나는 가시화된 다각형의 그물을 생성하고(표면 삼각측량 참조), 두 번째는 표면과의 광선의 교차점을 결정하는 광선 추적에 의존합니다.^[4] 교차점은 표면까지의 거리를 찾기 위해 부호화된 거리 함수를 사용하여 구면 추적으로 근사화할 수 있습니다.^[5]

참고 항목

암시곡선

참고문헌

^ ^a ^b Adriano N. Raposo; Abel J.P. Gomes (2019). "Pi-surfaces: products of implicit surfaces towards constructive composition of 3D objects". WSCG 2019 27. International Conference in Central Europe on Computer Graphics, Visualization and Computer Vision. arXiv:1906.06751.
^ Jules Bloomenthal; Chandrajit Bajaj; Brian Wyvill (15 August 1997). Introduction to Implicit Surfaces. Morgan Kaufmann. ISBN 978-1-55860-233-5.
^ Ian Stephenson (1 December 2004). Production Rendering: Design and Implementation. Springer Science & Business Media. ISBN 978-1-85233-821-3.
^ 에릭 헤인즈, 토마스 아케닌 몰러: 레이 트레이싱 젬즈, 스프링어, 2019, ISBN 978-1-4842-4427-2
^ Hardy, Alexandre; Steeb, Willi-Hans (2008). Mathematical Tools in Computer Graphics with C# Implementations. World Scientific. ISBN 978-981-279-102-3.

v t 치수
치수공간	벡터공간 유클리드 공간 아핀 공간 사영공간 프리모듈 다양체 대수다양성 시공간
기타 치수	크룰 레베그 피복 귀납적 하우스도르프 민코프스키 프랙탈 자유도
다각형 및 도형	초평면 초표면 하이퍼큐브 초직각 데미하이퍼큐브 초구 크로스 폴리토프 심플렉스 하이퍼피라미드
숫자별 치수	영 하나. 두명 세개 네개 다섯개 여섯개 일곱개 8 n차원
참고 항목	초공간 코디멘션
카테고리

Search

암시면

네임스페이스

더

목차

수식