쌍곡선 나선형

쌍곡선 나선은 평면 곡선으로, 방정식으로 극좌표로 설명할 수 있다.

${\displaystyle r={\frac {a}{\barphi }}}$

쌍곡선의 그것은 아르키메데스 나선형의 원 반대로 생성될 수 있기 때문에, 상호주의 나선형이라고도 불린다.^[1][2]

피에르 바리뇽은 1704년에 처음으로 곡선을 연구했다.^[2] 후에 요한 베르누이와 로저 코테스도 곡선에서 일했다.

데카르트 좌표

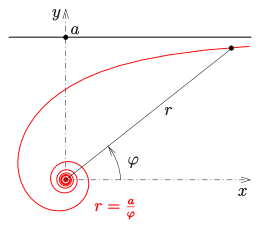
극 방정식이 있는 쌍곡선 나선형

${\displaystyle r={\frac {a}{\\varphi }},\cHB\varphi \neq 0}$

다음과 같이 데카르트 좌표(x = r cos φ, y = r sin φ)로 나타낼 수 있다.

${\displaystyle x=a{\frac {\cos \varphi }{\barphi }},\qquad y=a{\fraci {\sin \varphi },\barphi \barphi \neq.}$

하이퍼볼라는 좌표 축을 rφ-평면에 점근으로 가지고 있다. 쌍곡선 완화곡선(xy-plane에서)은 asy → ±3으로 원점에 점근한다. φ → ±0의 경우 곡선에 점근선이 있다(다음 섹션 참조).

극지방의 방정식과 φ부터).mw-parser-output .sfrac{white-space:nowrap}.mw-parser-output.sfrac.tion,.mw-parser-output.sfrac .tion{디스플레이:inline-block, vertical-align:-0.5em, font-size:85%;text-align:센터}.mw-parser-output.sfrac.num,.mw-parser-output.sfrac .den{디스플레이:블록, line-height:1em, 마진:00.1em}.mw-parser-output.sfrac .den{.Border-top:1px 고체}.mw-parser-output .sr-only{국경:0;클립:rect(0,0,0,0), 높이:1px, 마진:-1px, 오버 플로: 숨어 있었다. 패딩:0;위치:절대, 너비:1px}a/r, r)√x2+한 y2:방정식에 의한 표현을 가져옵니다.

${\displaystyle {\frac {y}{x}}=\tan \left\frac {a}{\sqrt {x^{2}+y^{2}}}}}\오른쪽).}$

기하학적 특성

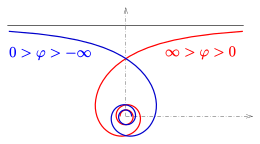
점근균류

왜냐하면

${\displaystyle \lim _{\varphi \to 0}x=a\lim _{\varphi \to 0}{\frac {\cos \varphi }{\varphi }}=\infty ,\qquad \lim _{\varphi \to 0}y=a\lim _{\varphi \to 0}{\frac {\sin \varphi }{\varphi }}=a}$

곡선에는 등식 y = a를 갖는 점근법이 있다.

극지경사

극좌표계의 벡터 미적분학으로부터 극경사에 대한 황갈색 α = r r/r 공식과 곡선의 탄젠트와 해당 극원의 탄젠트 사이의 각도 α를 얻는다.

쌍곡선 완화곡선 r = a/sv의 경우 극 기울기는

${\displaystyle \tan \cHB =-{\frac {1}{\varphi }}.}$

곡률

극성 방정식 r = r(φ)을 갖는 곡선의 곡률은

${\displaystyle \kappa ={\frac {r^{2}+2(r')^{2}-r\,r"{\좌측(r^{2}+(r')^{2}\오른쪽)^{\frac {3}{2}}}.}$

r = a/properties 및 파생 r′ = -a/properties² 및 r″ = 2a/properties에서³ 쌍곡선 완화곡선을 구한다.

${\displaystyle \kappa(\varphi )={\frac {\varphi ^{4}{a\좌(\varphi ^{2}+1\우)^{\frac {3}}}}}.}$

호 길이

(r₁( spiral), φ₁(φ)과 (r₂), φ₂) 사이의 쌍곡선 완화곡선의 호 길이는 다음 적분으로 계산할 수 있다.

${\displaystyle {\reasoned}L&, =\int _{\varphi_{1}}^{\varphi_{2}}{\sqrt{\left(r^{\prime}(\varphi)\right)^{2}(\varphi)}}\,d\varphi =\cdots, =a\int _{\varphi_{1}}^{\varphi_{2}}{\frac{\sqrt{1+\varphi ^{2}}}{\varphi ^{2}}}\,d\varphi \\&, =a\left[-{\frac{\sqrt{1+\varphi ^{2}}}{\varphi}}+\ln \left(\varphi+{\sqrt{1+\varphi ^{2}}}\right)\right]_{\varph \\&.나는 _{1}}^{\varphi _{2}}.\end{정렬}}}$

섹터 영역

등식 r = a/scal을 갖는 쌍곡선 완화곡선의 섹터(위 다이어그램 참조) 영역은 다음과 같다.

${\displaystyle {\reasoned}A&={\frac {1}{2}}\int _{\varphi _{1}}^{\varphi _{2}}r(\varphi )^{2}\,d\varphi \\&={\frac {1}{2}}\int _{\varphi _{1}}^{\varphi _{2}}{\frac {a^{2}}{\varphi ^{2}}}\,d\varphi \\&={\frac {a}{2}}\left({\frac {a}{\varphi _{1}}}-{\frac {a}{\varphi _{2}}}\right)\\&={\frac{a}{2}}:\bigl (}r(\varphi _{1})-r(\varphi _{2}}{\bigr )}.\end{정렬}}}$

반전

단위 원의 반전에는 (r, φ) ↦ (1/r, φ)의 간단한 설명이 극좌표 안에 있다.

원 역전이 있는 아르키메데스 나선형 r = φ/a의 이미지는 방정식 r = a/φ을 갖는 쌍곡선 나선형이다. φ = 두 곡선이 단위 원의 고정점에서 교차한다.

원점에서 아르키메데스 나선형 r = φ/a의 오스카 원은 반지름 ρ₀ = 1/2a(아키메데스 나선형 참조)와 중심(0, ρ₀)을 가진다. 이 원의 이미지는 y = a 선입니다(원 반전 참조). 따라서 아르키메데스 나선형의 역행과 함께 쌍곡선 나선형의 점증상(premptote)은 원점에서 아르키메데스 나선형의 오스카 원이다.

예: 도표에는 a = π이 있는 예가 나와 있다.

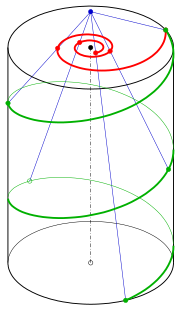
나선형의 중심 투영

C₀ = (0, 0, d) 지점에서 영상 평면 z = 0으로 중앙 투영을 고려하십시오. 이렇게 하면 점(x, y, z)을 d/d - z(x, y) 지점에 매핑한다.

파라메트릭 표현을 사용한 나선형 투영 아래의 이미지

$(r\displaystyle)(r\cos t,r\sin t,ct),\caps c\neq 0,}$

커브다

${\displaystyle {\frac {dr}{d-ct}(\cos t,\sin t)}$

극 방정식으로

${\displaystyle \rho ={\frac {dr}{d-ct},}$

쌍곡선 나선형을 묘사하고 있지

매개변수 t₀ = d/c의 경우 쌍곡선 나선은 극을 가지며 나선은 점 V에서₀ 평면 z = d를 교차한다. 나선이 V에₀ 가까워질 때의 이미지가 쌍곡선 나선형의 점증상임을 계산해 확인할 수 있다.

참조

• 한스-조헨 바트슈, 마이클 삭스: 태셴부치 수학자 포멜른 퓌르 인제네셔 und Naturwissenschaftler, Carl Hanser Verlag, 2018, ISBN 34464570, 9783446457072, S. 410.
• 긴코 쓰지, 스테판 C. 뮐러: 나선형 및 보르티스: 문화, 자연, 과학에서 스프링거, 2019년 ISBN 3030057984, 9783030057985, S. 96.
• 피에르 바리뇽: 누벨형성 de Spirales – 예 II, Mémoires de l'Academie des science de l'Institut de France, 1704, 페이지 94–103.
• 프리드리히 그렐레: 베라크 F. 브레케, 1861년 하이퍼볼리스케 스피랄레, S. 215.
• Jakob Philip Kulik: Lehrbuch der Höurn Analysis, Band 2, In Commiss. 1844년 스피랄리니엔, S. 222년

외부 링크

• Weisstein, Eric W. "Hyperbolic Spiral". MathWorld.
• JSXGraph(JavaScript)를 이용한 온라인 탐색
• 2d곡선 "곡선 완화곡선" 페이지