동적 평형

화학에서 동적 평형은 일단 가역 반응이 일어나면 존재한다.물질은 반응물과 생성물 간에 동일한 속도로 이동하므로 순변화가 없습니다.반응물 및 생성물은 어느 농도도 변하지 않는 속도로 형성된다.이것은 안정된 상태에 있는 시스템의 특별한 예입니다.

열역학에서, 닫힌 계는 혼합물의 구성이 시간에 따라 변하지 않는 속도로 반응이 일어날 때 열역학적 평형 상태에 있다.사실 반응은 때때로 격렬하게 일어나지만, 성분의 변화를 관찰할 수 없을 정도로 일어난다.평형 상수는 가역 반응에 대한 속도 상수로 표현될 수 있다.

예

새로운 탄산음료 병에서는 액상의 이산화탄소 농도가 특정 값을 가진다.액체의 절반을 붓고 병을 밀봉하면 이산화탄소는 액상을 점점 감소시키는 속도로 벗어나 평형에 이를 때까지 기체상의 이산화탄소의 부분압력이 높아진다.그 시점에서 열운동으로 인해 CO 분자가₂ 액체상을 떠날 수 있지만, 매우 짧은 시간 내에 또 다른 CO₂ 분자가 기체에서 액체로, 그리고 그 반대도 마찬가지입니다.평형상태에서 기체에서 액상으로의 CO₂ 전달 속도는 액체에서 기체로의 속도와 같다.이 경우, 액체 내 CO의₂ 평형 농도는 액체 내 가스의 용해도가 액체 ^[1]위 가스의 부분 압력에 정비례한다는 헨리의 법칙에 의해 주어진다.이 관계는 다음과 같이 기술됩니다.

${\displaystyle c=KP}$

여기서 K는 온도에 의존하는 상수, P는 부분 압력, c는 액체에 용해된 가스의 농도이다.따라서 Henry의 법칙이 준수될 때까지 기체 중 CO의₂ 부분 압력이 증가했습니다.액체 속의 이산화탄소 농도가 낮아졌고 음료는 거품을 조금 잃었다.

헨리의 법칙은 두 단계의 이산화탄소의 화학적 잠재성을 서로 동등하게 설정함으로써 도출될 수 있다.화학적 전위의 평등은 화학적 평형을 정의한다.상변화를 수반하는 동적 평형의 다른 상수로는 분할 계수 및 용해도 곱이 있다.라울트의 법칙은 이상적인 용액의 평형 증기압을 정의한다.

동적 평형은 단상 시스템에서도 존재할 수 있습니다.간단한 예는 수용액에서 아세트산의 해리와 같은 산염기 평형과 함께 발생한다.

$(\displaystyle {CH3COOH <=> CH3COOH- + H+})$

평형상태에서 산 해리상수인 농도상수 K는 일정하다(일부 조건에 따라 다름).

${\displaystyle K_{c}=\mathrm {\frac}[CH_{3}CO_{2}^{-}][H^{+}}{[CH_{3}CO_{2}H]}}}}}$

이 경우 전방 반응은 아세트산 분자로부터 일부 양성자를 해방시키는 것을 포함하며, 후방 반응은 아세트산 이온이 양성자를 받아들일 때 아세트산 분자의 형성을 포함한다.평형은 평형식의 왼쪽에 있는 종의 화학적 전위 합계가 오른쪽에 있는 종의 화학적 전위 합계와 같을 때 달성된다.동시에 전달과 역방향의 반응 속도는 동일합니다.화학적 복합체의 형성과 관련된 평형 또한 동적 평형이며, 농도는 복합체의 안정성 상수에 의해 제어된다.

동적 평형은 예를 들어 이산화질소가 이량화되었을 때와 같이 기체상에서도 발생할 수 있다.

$displaystyle {2$$NO2 <$=> $N2O4$ Kp = [ N2O4 ][ NO2]2{ $displaystyle K_{p$ } = \ $mathrm${ [ $N$_ { $2 }$} { [ ]$NO_{2}]^{2}}} }$

기체상에서는 대괄호는 부분압력을 나타냅니다.또는 물질의 분압을 P(물질)^[2]로 표기해도 된다.

평형과 속도 상수 간의 관계

이성질화와 같은 간단한 반응에서:

$({displaystyle {A <=> B})$

고려해야 할 두 가지 반응이 있는데, A종이 B로 변환되는 전진 반응과 B종이 A로 변환되는 후진 반응이다.만약 두 반응이 모두 기본 반응이라면, 반응 속도는 다음과 같이 주어진다^[3].

${\displaystyle {d[\ce {A}}}{dt}}=-k_{f}[{\ce {A}}_{t}+k_{b}[{\ce {B}}_{t}}}$

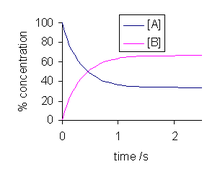
여기서_f k는 순방향 반응의 속도 상수이고_b k는 역방향 반응의 속도 상수이고, 대괄호 [..]는 농도를 나타낸다. 만약 A만 처음에 존재한다면, 시간 t=0, 두 농도 [A]_0t와 [B]_t의 합은 시간 t에서 [A]₀와 같다.

${\displaystyle {d[\ce {A}}}{dt}=-k_{f}[{\ce {A}}_{b}\left([\ce {A}}_{0}-[\ce {A}}}_{t}\right})$

이 미분 방정식의 해답은

$\displaystyle [ { \ce { A } ] _ { t } = specfrac { k _ { b } + k _ { f } + k _ { b } ^ { - \ left ( k _ { f } + k _ { b } } ] _ { 0 }$

우측에 표시되어 있습니다.시간이 무한대로 흐를수록 [A]_t와 [B]_t의 농도는 일정한 값으로 흐릅니다.위의 식에서 t가 무한대에 접근하도록 하자. 즉, t→colony이다.

${displaystyle [{\ce {A}}_{\infty }=param frac {k_{b}}{k_{f}+k_{b}}}[{\ce {A}}}_{0};[\infty }=param frac {k_{f}_{k}_{b}}}{ce}}$

실제로 t10 10 kf + kb {\$textstyle$ t$\gtrapprox {frac {10}$ {$k_{f}+k_{b$ 후에는 농도 변화를 측정할 수 없습니다. 그 후 농도는 변하지 않으므로 정의상 평형 농도로 정의됩니다.이제, 반응에 대한 평형 상수는 다음과 같이 정의된다.

${\displaystyle K=syslogfrac {{\ce {B}}}_{\text {eq}}}{{\ce {A}}}_{\text {eq}}}}$

따라서 평형 상수는 속도 상수의 몫과 수치적으로 동일하다.

${{displaystyle K=frac {k_{f}}{k_{f}+k_{b}}{\ce {A}}_{0}}{\frac {k_{f}}{\ce {A}}+k_{b}}}{\f}=frac {k_{k}}}{f}}$

일반적으로 그것들은 하나 이상의 전진 반응과 둘 이상의 후진 반응일 수 있다.앳킨스는^[4] 일반적인 반응의 경우, 전체적인 평형 상수는 다음과 같은 기본 반응의 속도 상수와 관련이 있다고 말한다.

${\displaystyle K=\left({\frac {k_{b}}\right)_{1}\times \lefts\frac {k_{f}}\right)_{2}\times \cdots }$

「 」를 참조해 주세요.

• 평형화학
• 기계적 평형
• 화학적 평형
• 방사 평형

레퍼런스

Atkins, P.W.; de Paula, J. (2006). Physical Chemistry (8th. ed.). Oxford University Press. ISBN 0-19-870072-5.

외부 링크

• https://demonstrations.wolfram.com/DynamicEquilibriumExample/