위상 규칙

열역학에서 위상 규칙은 "pVT" 시스템(즉, 열역학적 평형에서 변수 압력( $p$ ), 체적( $V$ ), 온도( $T$ )에 의해 상태가 완전히 설명되는 시스템)을 지배하는 일반적인 원칙이다. $F$ 가 자유도 수인 $경우$ C는 성분 수, $P$ 는 단계 수인 경우^[1]^[2]

F=C-P+2.}

그것은 미국의 물리학자 조시아 윌러드 깁스가 1875년에서 1878년 사이에 일부에 걸쳐 발표한 그의 획기적인 논문 "이질적인 물질의 평형성에 관한 것"에서 도출한 것이다.^[3] 규칙은 그 요소들이 서로 반응하지 않는다고 가정한다.

자유도는 독립적인 집중 변수의 수, 즉 온도나 압력 같은 열역학적 매개변수가 서로 결정하지 않고 동시에 임의로 변화할 수 있는 수가 가장 많은 것이다. 1성분 시스템의 예로는 순수 화학 물질 1개를 포함하는 시스템을 들 수 있으며, 물과 에탄올의 혼합물 등 2성분 시스템은 화학적으로 독립된 2성분 등을 가지고 있다. 대표적인 위상은 고체, 액체, 기체다.

파운데이션

위상은 화학적 구성과 물리적 상태에 있어서 동질적인 물질의 형태다. 대표적인 위상은 고체, 액체, 기체다. 구별되는 경계로 분리된 두 개의 불활성 액체(또는 다른 구성을 가진 액체 혼합물)는 두 개의 불활성 고형물과 마찬가지로 두 개의 상으로 계산된다.
성분 수(C)는 화학적으로 시스템의 독립적인 성분 수, 즉 시스템의 모든 단계의 구성을 정의하는 데 필요한 최소 독립 종의 수입니다.^[2] 예제는 성분(열역학)을 참조하십시오.
이 맥락에서 자유도(F)의 수는 서로 독립적인 집중 변수의 수입니다.

규칙(Atkins and de Paula,^[2] 정당성 6.1)의 근거는 단계 간의 평형이 집약적 변수에 제약을 가한다는 것이다. 보다 엄밀하게 말하면, 위상이 서로 열역학적 평형 상태에 있기 때문에 위상의 화학적 전위는 같아야 한다. 평등 관계의 수가 자유의 정도를 결정한다. 예를 들어, 액체와 액체의 증기의 화학적 전위가 온도(T)와 압력(p)에 따라 달라지는 경우, 화학적 전위의 동일성은 각 변수가 다른 변수에 종속된다는 것을 의미할 것이다. 수학적으로 μ_liq(T, p) = μ_vap(T, p) = μ(t, p) 등식은 온도를 압력의 함수로 정의하거나 그 반대로 정의한다.(주의: p = 압력과 P = 위상의 수를 혼동하지 않는다)

좀 더 구체적으로 말하면, 각 위상의 구성은 각 위상의 C - 1 집약 변수( 몰 분율 등)에 의해 결정된다. 총 변수 수는 (C - 1)P + 2이며, 여기서 나머지 두 변수는 온도 T와 압력 p이다. 각 성분의 화학적 전위는 모든 단계에서 같아야 하기 때문에 제약조건의 수는 C(P - 1)이다. 변수 개수에서 제약조건 수를 빼서 자유도를 F = (C - 1)P + 2 - C(P - 1) = C - P + 2로 구한다.

위상 간의 평형이 중력, 전기 또는 자력 또는 표면적에 의해 영향을 받지 않고 온도, 압력, 농도에 의해서만 영향을 받는다면 이 규칙은 유효하다.

결과 및 예

순수물질(성분 1개)

순수 물질 C = 1에 대해 F = 3 - P. 순수 성분 시스템의 단일 위상(P = 1) 조건에서는 온도, 압력 등 두 변수(F = 2)를 독립적으로 선택하여 위상과 일치하는 값의 쌍이 될 수 있다. 그러나 온도와 압력 조합이 순수 성분이 2상(P = 2)으로 분리를 거치는 지점까지 이어진다면 F는 2에서 1로 감소한다. 시스템이 2상 영역으로 들어가면 더 이상 독립적으로 온도와 압력을 제어할 수 없게 된다.

이산화탄소의 3중점과 임계점을 나타낸 이산화탄소 압력 온도 위상도

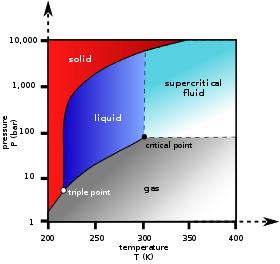
오른쪽 위상 다이어그램에서 액체와 가스 영역 사이의 경계 곡선은 단일 구성요소 시스템이 평형 상태에서 액체와 가스 단계로 분리되었을 때 온도와 압력 사이의 구속조건을 나타낸다. 2상 라인에서 압력을 높이는 유일한 방법은 온도를 높이는 것이다. 냉각으로 온도가 낮아지면 가스의 일부가 응축되어 압력이 낮아진다. 두 공정에서 온도와 압력은 증발이나 응축에 의해 한 상이 완전히 소비되지 않는 한 또는 임계점에 도달하지 않는 한 이 경계 곡선에 의해 표시된 관계를 유지한다. 두 개의 위상이 있는 한, 위상 경계 곡선을 따라 있는 위치에 해당하는 자유도는 한 가지에 불과하다.

중요한 점은 액체-가스 경계 끝의 검은 점이다. 이 지점이 다가옴에 따라, 액체와 가스 단계는 점점 더 유사해지고, 결정적인 지점에서 더 이상 두 단계로 분리되지 않게 된다. 임계점 이상과 위상 경계 곡선에서 떨어져 있는 F = 2 및 온도와 압력을 독립적으로 제어할 수 있다. 따라서 단 하나의 위상이 있을 뿐이며, 그것은 밀도가 높은 기체의 물리적 성질을 가지고 있지만, 초임계 유체라고도 한다.

다른 두 경계 곡선 중 하나는 이 두 단계 사이의 평형 조건을 나타내는 고체-액체 경계 또는 용융점 곡선이고, 다른 하나는 낮은 온도와 압력에서의 고체-가스 경계다.

순수한 물질이라도 고체, 액체, 증기 등 3상이 평형(P = 3)에서 함께 존재할 수 있다. 성분이 하나만 있는 경우 3상일 때 자유도(F = 0)가 없다. 따라서 단성분계에서는 이 3상 혼합물이 단온과 압력에서만 존재할 수 있는데, 이를 삼중점이라고 한다. 여기에는 두 개의 방정식 μ_sol(T, p) = μ_liq(T, p) = μ_vap(T, p)가 있는데, 이 두 변수 T와 p를 결정하기에 충분하다. CO₂ 다이어그램에서 3중 지점은 고체, 액체 및 가스 단계가 5.2bar와 217K로 조합되는 지점이다. 다른 상들의 세트가 트리플 포인트를 형성하는 것도 가능하다. 예를 들어 물 시스템에는 얼음 I, 얼음 III, 액체가 공존할 수 있는 트리플 포인트가 있다.

순수 물질의 4상(P = 4)이 평형 상태라면 위상 규칙은 F = -1 독립 변수가 있을 수 없으므로 의미가 없다. 이것은 순수 물질의 4상(얼음 I, 얼음 III, 액체 물, 수증기 등)이 어떤 온도와 압력에서도 평형상태에서 발견되지 않는다는 사실을 설명한다. 화학적 전위성의 관점에서 보면, 일반적으로 두 변수 T와 p의 어떤 값으로도 만족할 수 없는 세 개의 방정식이 존재하는데, 비록 원칙적으로 하나의 방정식이 다른 두 변수에 수학적으로 의존하는 특수한 경우에 풀릴 수 있다. 그러나 실제로는 단계 규칙이 허용하는 것보다 더 많은 단계가 공존한다는 것은 일반적으로 단계가 모두 진정한 평형 상태에 있지 않다는 것을 의미한다.

2성분계

화학적으로 독립된 두 성분의 이항 혼합물의 경우, C = 2가 F = 4 - P가 되도록 한다. 온도와 압력 외에 다른 자유도는 각 단계의 구성으로, 종종 한 성분의 몰 분율 또는 질량 분율로 표현된다.

비등점 다이어그램

예를 들어, 톨루엔과 벤젠과 같은 완전히 잘못 작동되는 두 액체의 계통을 그들의 증기와 평형상태로 생각해 보자. 이 시스템은 (고정 압력에서) 온도의 함수로 평형상태에서 두 단계의 구성(몰레 분율)을 보여주는 비등점 도표로 설명할 수 있다.

시스템을 설명할 수 있는 4개의 열역학 변수로는 온도(T), 압력(p), 액체 위상(x_1L)의 성분 1(톨루엔) 몰 분율, 증기 위상(x_1V)의 성분 1 몰 분율이 있다. 그러나 평형에는 2상(P = 2)이 있으므로 이 변수들 중 2개만 독립적일 수 있다(F = 2). 왜냐하면 네 가지 변수는 액체 톨루엔과 톨루엔 증기의 화학적 잠재력의 평등과 그에 상응하는 벤젠의 평등이라는 두 가지 관계에 의해 구속되기 때문이다.

주어진 T와 p의 경우, 시스템의 전체 구성(시스템 포인트)이 두 곡선 사이에 있을 때 평형 상태에서 두 단계가 있을 것이다. 수평선(기타선 또는 동점선)은 그러한 시스템 점을 통해 그려질 수 있으며, 평형 구성에서 각 위상에 대한 곡선을 교차한다. 각 위상의 수량은 레버 규칙(X축에 해당하는 변수, 여기 몰 분율)에 의해 주어진다.

분수 증류 분석의 경우, 두 개의 독립 변수는 대신 액체 위상 구성(x_1L)과 압력인 것으로 간주된다. 이 경우 위상 규칙은 평형 온도(끓는점)와 증기 위상 조성이 결정된다는 것을 의미한다.

다른 시스템의 액체-바퍼 위상 다이어그램은 구성 곡선에 아조트로프(최대 또는 최소)가 있을 수 있지만 위상 규칙의 적용은 변경되지 않는다. 유일한 차이점은 두 단계의 구성이 항등방성 구성에서 정확히 같다는 것이다.

일정한 압력에서의 위상 규칙

서로 다른 고체 구조들 사이의 위상 변화를 다루는 재료 과학에서의 적용의 경우, 압력은 일정하다고 상상되는 경우가 많으며(예를 들어 한 대기에서) 자유도로 무시되기 때문에 규칙이 되는 것이다.

F = C - P + 1

이것은 오해의 소지가 있는 "응축 단계 규칙"이라고 부르기도 하지만, 이러한 압력의 영향이 중요할 수 있기 때문에 (예를 들어 지질학에서) 고압의 영향을 받는 응축된 시스템에는 적용되지 않는다.

참조

^ Smith, Joe Mauk (2018). Introduction to chemical engineering thermodynamics. United States of America: McGraw-Hill Education. p. 422. ISBN 978-1-259-69652-7.
^ ^a ^b ^c Atkins, Peter; Paula, Julio De; Keeler, James (2018). Atkins' Physical chemistry (Eleventh ed.). Oxford University Press. pp. 123–125. ISBN 9780198769866.
^ Gibbs, J. W. (1961), Scientific Papers, Dover, New York

추가 읽기

모그, 데이비드: 교육 단계인 평형주의. 깁스의 단계 규칙: 모든 것이 시작되는 곳(지질학의 단계 규칙)
Predel, Bruno; Hoch, Michael J. R.; Pool, Monte (14 September 2004). Phase Diagrams and Heterogeneous Equilibria : A Practical Introduction. Springer. ISBN 3-540-14011-5.
White, Mary Anne (1999). Properties of Materials. Oxford University Press (1999). ISBN 0-19-511331-4. 제9장. 열역학적으로 안정성에 관한 연구

[1] Smith, Joe Mauk (2018). Introduction to chemical engineering thermodynamics. United States of America: McGraw-Hill Education. p. 422. ISBN 978-1-259-69652-7.

[Atkins-2] Atkins, Peter; Paula, Julio De; Keeler, James (2018). Atkins' Physical chemistry (Eleventh ed.). Oxford University Press. pp. 123–125. ISBN 9780198769866.

[3] Gibbs, J. W. (1961), Scientific Papers, Dover, New York

[1]

[2]

[3]

Search