사이클로믹스

사이클로매틱 복잡성은 프로그램의 복잡성을 나타내기 위해 사용되는 소프트웨어 메트릭이다. 프로그램의 소스 코드를 통해 선형 독립 경로의 수를 정량적으로 측정하는 것이다. 그것은 1976년 토마스 J. 매카브 Sr.에 의해 개발되었다.

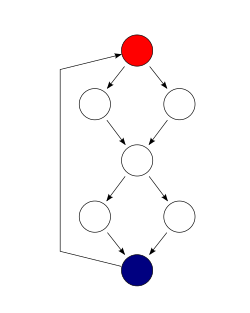
사이클로매틱 복잡성은 프로그램의 제어 흐름 그래프를 사용하여 계산된다: 그래프의 노드는 프로그램의 분리할 수 없는 명령 그룹에 해당하며, 두 번째 명령이 첫 번째 명령 직후 실행될 수 있는 경우 방향 에지는 두 개의 노드를 연결한다. 또한 프로그램 내의 개별 기능, 모듈, 방법 또는 등급에도 사이클로 인한 복잡성이 적용될 수 있다.

처음 그것을 제안한 McCabe에 의해 기본 경로 테스트라고 불리는 하나의 테스트 전략은 프로그램을 통해 각각의 선형 독립 경로를 테스트하는 것이다. 이 경우, 테스트 사례의 수는 프로그램의 사이클로성 복잡성과 동일할 것이다.^[1]

설명

정의

단순 프로그램의 제어 흐름 그래프. 프로그램은 빨간색 노드에서 실행을 시작한 다음, 루프(빨간 노드 바로 아래의 3개 노드로 구성된 그룹)로 들어간다. 루프를 종료할 때 조건문(루프 아래 그룹)이 있고, 마지막으로 프로그램이 블루노드에서 종료된다. 이 그래프는 9개의 가장자리, 8개의 노드, 1개의 연결된 구성요소를 가지고 있어 프로그램의 사이클로믹스 복잡도는 9 - 8 + 2*1 = 3이다.

소스 코드 섹션의 주기적 복잡성은 그 안에 있는 선형 독립 경로의 수입니다. 즉, 에지 집합의 대칭적 차이가 비어 있는 하나 이상의 경로의 하위 집합이 있는 경우 일련의 경로가 선형적으로 종속된다. 예를 들어, 소스 코드에 제어 흐름 문(조건 또는 결정 지점)이 없는 경우, 코드를 통과하는 단일 경로만 존재하기 때문에 복잡성은 1이 될 것이다. 코드에 하나의 단일 조건 IF 문이 있다면, IF 문이 TRUE로 평가되는 경로와 FALSE로 평가되는 경로의 두 가지가 있을 것이므로 복잡성은 2가 될 것이다. 두 개의 중첩된 단일 조건 IF 또는 두 개의 조건을 가진 하나의 IF는 3의 복잡성을 야기할 것이다.

수학적으로, 구조화된 프로그램의^[a] 사이클로메틱 복잡성은 프로그램의 제어 흐름 그래프를 참조하여 정의된다. 프로그램의 기본 블록을 포함하는 방향 그래프로서, 제1차에서 제2차까지 통제가 통과될 수 있는 경우 두 개의 기본 블록 사이에 에지가 있다. 그런 다음 복잡도 M을^[2] 다음과 같이 정의된다.

M = E − N + 2P,

어디에

E = 그래프의 가장자리 수입니다.

N = 그래프의 노드 수입니다.

P = 연결된 구성 요소의 수입니다.

각 출구점이 진입점에 다시 연결되는 대체 제형을 사용하여 표현되는 위와 동일한 기능. 이 그래프는 10개의 가장자리, 8개의 노드, 1개의 연결된 구성요소를 가지며, 대체 제형(10 - 8 + 1 = 3)을 사용하여 3의 사이클로믹스를 유발하기도 한다.

대안 공식은 각 출구점이 진입점에 다시 연결되는 그래프를 사용하는 것이다. 이 경우, 그래프는 강하게 연결되고 프로그램의 사이클로믹 복잡성은 그 그래프의 사이클로믹 수(첫 번째 베티 번호라고도 함)와 같으며, 이 숫자는 다음과^[2] 같이 정의된다.

M = E - N + P

이는 그래프에 존재하는 선형 독립 사이클의 수, 즉 그 안에 다른 사이클을 포함하지 않는 사이클의 수를 계산하는 것으로 볼 수 있다. 각 출구점은 다시 진입점으로 루프되기 때문에 각 출구 지점에 대해 적어도 하나의 사이클이 있다는 점에 유의하십시오.

단일 프로그램(또는 서브루틴 또는 메서드)의 경우 P는 항상 1과 같다. 그래서 단일 서브루틴에 대한 간단한 공식은

M = E - N + ^[3]2

그러나 사이클로메틱 복잡성은 여러 프로그램이나 하위 프로그램(예: 클래스의 모든 방법에 적용)에 동시에 적용될 수 있으며, 이 경우 P는 각 하위 프로그램이 그래프의 분리된 하위 집합으로 나타나기 때문에 해당 프로그램의 수와 동일할 것이다.

McCabe는 하나의 진입점과 하나의 출구점만을 가진 구조화된 프로그램의 사이클로매틱한 복잡성이 그 프로그램에 포함된 결정점 수(즉, "if" 문 또는 조건부 루프)와 같다는 것을 보여주었다. 그러나 이는 가장 낮은 기계 수준의 지시사항으로 계산된 결정점에 대해서만 적용된다.^[4] 다음과 같은 고급 언어에서 발견되는 복합 술어와 관련된 결정 IF cond1 AND cond2 THEN ... 관련된 술어 변수의 측면에서 계수되어야 한다. 즉, 이 예에서는 두 개의 결정 지점을 계수해야 한다. 왜냐하면 기계 수준에서 결정 지점은 다음과 같기 때문이다. IF cond1 THEN IF cond2 THEN ....^[2]^[5]

사이클로성 복잡성은 다중 출구점이 있는 프로그램으로 확장될 수 있다. 이 경우 다음과 같다.

π - s + 2

여기서 π은 프로그램의 결정 포인트의 수, s는 출구 포인트의 수입니다.^[5]^[6]

대수적 위상에 대한 설명

그래프의 짝수 서브그래프(Ulerian subgraph라고도 한다)는 모든 꼭지점이 짝수 수의 가장자리와 충돌하는 것이다. 그러한 서브그래프는 사이클과 분리된 정점들의 결합이다. 아래에서는 서브그래프조차 에지 집합으로 식별되는데, 이는 전체 그래프의 모든 정점을 포함하는 서브그래프만 고려하는 것과 같다.

그래프의 모든 짝수 하위 그래프의 집합은 대칭 차이에 의해 닫히고, 따라서 GF(2)를 통한 벡터 공간으로 볼 수 있다. 이 벡터 공간을 그래프의 사이클 공간이라고 한다. 그래프의 사이클로메틱 수는 이 공간의 치수로 정의된다. GF(2)는 2개의 원소를 가지며, 사이클 공간은 반드시 유한하므로 사이클 공간 내 원소 수의 2-로그람과도 같다.

사이클 공간의 기초는 먼저 그래프의 스패닝 포리스트를 고친 다음, 포리스트가 아닌 한 에지에 의해 형성된 사이클과 그 에지의 끝점을 연결하는 포리스트의 경로를 고려함으로써 쉽게 구성된다. 이러한 사이클은 사이클 공간의 기초가 된다. 따라서, 사이클로메틱 수는 또한 그래프의 최대 스패닝 포리스트에 있지 않은 가장자리 수와 같다. 그래프의 최대 스패닝 포리스트에 있는 에지 수는 정점의 개수에서 성분 수를 뺀 값과 같기 $E-N+P$ 에 $E-N+P$ $E-N+P$ 의 E - $E-N+P$ N + P {\ $displaystyle E-N$ +P} 공식은 사이클로메틱 수에 대해 다음과 같다.^[7]

보다 위상적으로 기울어진, 사이클로믹 복잡성은 상대적 베티 번호로, 상대적 호몰로지 그룹의 크기로서 대안으로 정의될 수 있다.

M:=b_{1}(G,t):=\operatorname {rank} H_{1}(G,t),

이는 "단자 노드 t에 상대적인 그래프 G의 첫 번째 호몰로지 그룹의 순위"로 읽힌다. 이것은 "입구에서 출구까지의 흐름 그래프를 통한 선형 독립 경로의 수"라고 기술하는 방법이다. 여기서 다음과 같다.

"선형적으로 독립적"은 호몰로지(homology)에 해당하며, 역추적을 이중으로 계산하지 않는 것을 의미한다.
"경로"는 첫 번째 호몰로지(homology)에 해당하며, 경로는 1차원 객체임.
"경로"는 경로가 진입점 또는 출구 지점에서 시작하고 끝나야 함을 의미한다.

이는 사이클로메틱 복잡성의 직관적 개념에 해당하며, 위와 같이 계산할 수 있다.

반면 절대 베티 수(절대 상동 – 아니라 상대적)를 통해 점에( 새로운 증강 그래프 G일{\displaystyle{\tilde{G}}}은-LSB- cla 요구하고 주어진 구성 요소(또는 동등하게, 입구에 두 출구를 연결하는 길을 그리)에 모든 터미널 노드(함께 접착)를 식별함으로써 이 계산할 수 있다.rification), 불쌍히 여겼고, 해결을 필요한ne gets

M=b_{1}({\tilde{G}})=\operatorname {rank}H_{1}({\tilde {G}).

그것은 또한 호모토피를 통해 계산될 수 있다. 제어 흐름 그래프를 $X$ ${\displaystyle$ X $X$ 라고 하는 1차원 CW 콤플렉스로 간주할 경우 $X$ {\ $displaystyle X$ }의 기본 그룹은 $\pi _{1}(X)=\mathbb {Z} ^{n}$ 1 $\pi _{1}(X)=\mathbb {Z} ^{n}$ $\pi _{1}(X)=\mathbb {Z} ^{n}$ ) = $\pi _{1}(X)=\mathbb {Z} ^{n}$ $\pi _{1}(X)=\mathbb {Z} ^{n}$ ${\$ ^{ $n}}$ 이 된다 $X$ $\pi _{1}(X)=\mathbb {Z} ^{n}$ $n+1$ + $n+1$ $n+1$ 의 값은 사이클로믹 복잡성이다 $n+1$ . 기본 그룹은 그래프를 통해 최대 호모토피까지 얼마나 많은 루프가 있는지 계산하고, 따라서 우리가 직관적으로 기대하는 것과 일치한다.

이는 "루프 수 + 구성요소 수"라는 사이클로믹 복잡성의 특성화에 해당한다.

해석

Tom McCabe는 국토안보부를 위한 '위험을 식별하는 소프트웨어 품질 지표'^[8] 프레젠테이션에서 사이클로매틱 복잡성을 해석하기 위해 다음과 같은 범주화를 소개한다.

1 - 10 간단한 절차, 위험은 거의 없음
11 - 20 더 복잡하고 적당한 위험
21 - 50 복합체, 고위험
> 50 측정불가 코드, 매우 높은 위험

적용들

개발 중 복잡성 제한

McCabe의 원래 응용 프로그램 중 하나는 프로그램 개발 중에 루틴의 복잡성을 제한하는 것이었다. 그는 프로그래머들이 개발 중인 모듈의 복잡성을 세어보고 모듈의 사이클로믹스 복잡성이 10을 초과할 때마다 더 작은 모듈로 나누라고 권고했다.^[2] 이 관행은 McCabe의 최초 간행물 이후 10의 수치는 상당한 확증 증거를 제공받았지만, 어떤 상황에서는 15까지 복잡도가 높은 모듈의 제한과 허용을 완화하는 것이 적절할 수 있다는 관찰과 함께 NIST 구조화 시험 방법론에 의해 채택되었다. 방법론은 합의된 한도를 벗어나는 이유가 가끔 있음을 인정하면서 "각 모듈에 대해 사이클로 복잡성을 [약정된 한도]로 제한하거나 왜 한도가 초과되었는지에 대한 서면 설명을 제공하라"^[9]고 권고안을 표현했다.

프로그램의 "구조" 측정

McCabe의 1976년 논문의 섹션 6은 구조화되지 않은 프로그램의 제어 흐름 그래프(CFG)가 그들의 하위 그래프에서 어떻게 보이는지 결정하는 것과 관련이 있다. 이것은 McCabe가 식별한다. (그 부분에 대한 자세한 내용은 구조화된 프로그램 정리를 참조한다.) McCabe는 주어진 프로그램에 얼마나 가까운 구조화된 프로그래밍, 즉 McCabe의 신학주의를 사용한 "구조화"에 대한 수치적 측정을 제안함으로써 이 부분을 결론짓는다. McCabe는 그가 이 목적을 위해 고안한 조치들을 본질적인 복잡성이라고 불렀다.^[2]

이 측정치를 계산하기 위해, 단일 입력점과 단일 출구점을 갖는 서브그래프를 식별하여 원래의 CFG를 반복적으로 감소시킨 다음, 단일 노드로 대체한다. 이 감소는 더 큰 코드 조각에서 서브루틴을 추출했을 때 인간이 할 수 있는 것과 일치한다. (요즘은 그러한 과정이 리팩토링이라는 포괄적 용어에 해당된다.) 맥케이브의 감량법은 후에 일부 교과서에서는 응축법으로 불렸는데, 이는 그래프 이론에 사용된 구성요소에 대한 응축의 일반화로 보여졌기 때문이다.^[10] 프로그램이 구조화된 경우, McCabe의 감소/응축 프로세스는 그것을 단일 CFG 노드로 감소시킨다. 이와는 대조적으로 프로그램이 구조화되지 않은 경우, 반복적인 프로세스는 되돌릴 수 없는 부분을 식별한다. McCabe가 정의한 본질적인 복잡성 측정은 단순히 이 수정 불가능한 그래프의 사이클로적인 복잡성일 뿐이므로, 모든 구조화된 프로그램에는 정확하게 1이 될 것이지만, 구조화되지 않은 프로그램에는 1보다 클 것이다.^[9]^{: 80}

소프트웨어 테스트에 대한 의미

또 다른 주기적 복잡성의 적용은 특정 모듈의 철저한 시험 적용범위를 달성하기 위해 필요한 시험 사례의 수를 결정하는 데 있다.

특정 모듈에 대한 사이클로매틱 복잡성의 두 가지 특성인 M 때문에 유용하다.

M은 완전한 분기 커버리지 달성에 필요한 시험 사례의 수에 대한 상한이다.
M은 제어 흐름 그래프(CFG)를 통과하는 경로 수에 대한 하한이다. 각 시험 사례가 하나의 경로를 취한다고 가정할 때, 경로 적용범위를 달성하는데 필요한 경우의 수는 실제로 취할 수 있는 경로의 수와 동일하다. 그러나 일부 경로는 불가능할 수 있기 때문에 CFG를 통과하는 경로의 수가 경로 적용에 필요한 시험 사례의 수에 대한 상한선이 분명하지만, 이 (가능한 경로 중) 후자의 수는 때때로 M보다 작다.

위의 세 숫자는 모두 같을 수 있다: 분기 범위 $\leq$ $\leq$ 사이클 $\leq$ 복잡성 $\leq$ complexity $\leq$ 경로 수입니다 $\leq$ .

예를 들어, if-ten-else 문 두 개로 구성된 프로그램을 고려해 보십시오.

만일 (c1())     f1(); 다른     f2();  만일 (c2())     f3(); 다른     f4();

위의 소스 코드에 대한 제어 흐름 그래프. 빨간색 원은 함수의 진입점이고 파란색 원은 출구점이다. 출구는 출구에 연결되어 그래프를 강하게 연결했다.

이 예에서, 완전한 분기 커버리지를 달성하기에 두 가지 테스트 사례로 충분한 반면, 완전한 경로 커버리지를 위해서는 네 가지가 필요하다. 프로그램의 사이클로메틱 복잡도는 3이다(프로그램에 대해 강하게 연결된 그래프는 에지 9개, 노드 7개, 연결된 구성 요소 1개를 포함하고 있기 때문에).(9 - 7 + 1)

일반적으로 모듈을 완전히 테스트하기 위해서는 모듈을 통과하는 모든 실행 경로를 연습해야 한다. 이는 복잡도 수가 높은 모듈이 값이 낮은 모듈보다 더 많은 테스트 노력을 요구한다는 것을 의미한다. 왜냐하면 복잡도 수가 높을수록 코드를 통과하는 경로가 더 많음을 나타내기 때문이다. 이것은 또한 프로그래머가 다른 경로와 그 경로의 결과를 이해해야 하기 때문에 프로그래머가 복잡성이 높은 모듈을 이해하기가 더 어렵다는 것을 의미한다.

안타깝게도, 프로그램을 통해 가능한 모든 경로를 테스트하는 것이 항상 실용적인 것은 아니다. 위의 예를 고려할 때 if-ten-else 문장이 추가될 때마다 가능한 경로의 수는 2배씩 증가한다. 프로그램이 이러한 방식으로 성장함에 따라 모든 경로를 테스트하는 것이 비현실적으로 되는 지경에 빠르게 도달한다.

예를 들어 NIST 구조화 시험 방법론에 의해 제시된 한 가지 일반적인 시험 전략은 모듈의 주기적인 복잡성을 이용하여 모듈의 충분한 적용범위를 얻기 위해 필요한 화이트 박스 시험의 수를 결정하는 것이다. 거의 모든 경우에, 그러한 방법론에 따르면, 모듈은 적어도 사이클로적인 복잡성만큼 많은 시험을 가져야 한다. 대부분의 경우, 이 시험의 수는 기능의 모든 관련 경로를 행사하기에 충분하다.^[9]

정확한 테스트를 위해 단순히 분기 이상의 커버리지가 필요한 기능의 예로서 위의 기능을 다시 고려하되, 버그가 발생하지 않도록 하려면 f1() 또는 f3() 중 하나를 호출하는 코드도 다른 코드와 통화해야 한다고 가정한다.^[b] c1()과 c2()의 결과가 독립적이라고 가정하면, 그것은 위에서 제시한 함수에 버그가 포함되어 있다는 것을 의미한다. 분기 커버리지는 단 두 번의 테스트만으로 방법을 테스트할 수 있도록 하며, 가능한 테스트 세트는 다음과 같은 경우를 테스트할 수 있다.

c1() 진실로 돌아오다 c2() 진실로 돌아오다
c1() 거짓으로 돌려주다. c2() 거짓으로 돌려주다

이 두 경우 모두 버그를 노출시키지 않는다. 그러나, 만약 우리가 필요한 시험의 수를 나타내기 위해 사이클로믹 복잡성을 사용한다면, 그 수는 3으로 증가한다. 따라서 다음 경로 중 하나를 테스트해야 한다.

c1() 진실로 돌아오다 c2() 거짓으로 돌려주다
c1() 거짓으로 돌려주다. c2() 진실로 돌아오다

이 테스트들 중 어느 것이든 버그를 노출시킬 것이다.

결점 수에 대한 상관 관계

많은 연구가 McCabe의 사이클로믹스 수치와 함수나 방법에서 발생하는 결함의 빈도 사이의 상관관계를 조사했다.^[11] 일부 연구는^[12] 사이클로믹스 복잡성과 결함 사이에 긍정적인 상관관계를 발견한다: 가장 복잡성이 높은 기능과 방법 또한 가장 많은 결함을 포함하고 있는 경향이 있다. 그러나, 사이클로매틱 복잡성과 프로그램 크기 사이의 상관관계(일반적으로 코드 선으로 측정)는 여러 번 입증되었다. 레스 해튼은 복잡성이 코드 라인과 동일한 예측 능력을 가지고 있다고 주장했다^[13]. 프로그램 크기에 대해 통제된 연구(즉, 복잡성은 다르지만 비슷한 크기의 모듈을 비교하는 연구)는 일반적으로 결정성이 떨어지는 반면, 많은 연구들은 유의미한 상관관계가 없다는 것을 발견하는 반면, 다른 연구들은 상관관계를 발견한다. 이 분야를 연구한 일부 연구자들은 아무런 상관관계가 없는 연구들이 사용한 방법의 타당성에 의문을 제기한다.^[14] 비록 이 관계가 아마도 사실일지라도, 쉽게 활용할 수 있는 것은 아니다.^[15] 프로그램 크기는 상업용 소프트웨어의 관리 가능한 기능이 아니기 때문에, McCabes 번호의 유용성에 의문이 제기되었다.^[11] 이 관찰의 본질은 큰 프로그램이 더 복잡하고 결점이 더 많은 경향이 있다는 것이다. 코드의 주기적인 복잡성을 줄이는 것은 그 코드의 오류나 버그 수를 줄이는 것으로 증명되지 않는다. 그러나 ISO 26262와 같은 국제 안전 표준은 낮은 코드 복잡성을 강제하는 코딩 지침을 의무화한다.^[16]

인공지능

인공지능 프로그램의 의미적 복잡성 평가에도 사이클로메틱 복잡성이 이용될 수 있다.^[17]

초경량 위상

사이클로메틱 복잡성은 초경량 거리 그래프에서 구현될 수 있다는 것이 입증된 후 지리적, 경관적 생태학적 분석에 유용하다는 것이 입증되었다.^[18]

참고 항목

메모들

^ 여기서 "구조화"는 특히 "함수별로 하나의 출구(반환명세서)를 갖는" 것을 의미한다.
^ 이것은 꽤 흔한 유형의 조건이다; f1이 f3가 방출하는 일부 자원을 할당하는 가능성을 고려하라.

참조

^ A J Sobey. "Basis Path Testing".
^ ^a ^b ^c ^d ^e McCabe (December 1976). "A Complexity Measure". IEEE Transactions on Software Engineering. SE-2 (4): 308–320. doi:10.1109/tse.1976.233837. S2CID 9116234.
^ Philip A. Laplante (25 April 2007). What Every Engineer Should Know about Software Engineering. CRC Press. p. 176. ISBN 978-1-4200-0674-2.
^ Fricker, Sébastien (April 2018). "What exactly is cyclomatic complexity?". froglogic GmbH. Retrieved October 27, 2018. To compute a graph representation of code, we can simply disassemble its assembly code and create a graph following the rules: ...
^ ^a ^b Belzer, Kent, Holzman and Williams (1992). Encyclopedia of Computer Science and Technology. CRC Press. pp. 367–368.{{cite book}}: CS1 maint : 복수이름 : 작성자 목록(링크)
^ Harrison (October 1984). "Applying Mccabe's complexity measure to multiple-exit programs". Software: Practice and Experience. 14 (10): 1004–1007. doi:10.1002/spe.4380141009. S2CID 62422337.
^ Diestel, Reinhard (2000). Graph theory. Graduate texts in mathematics 173 (2 ed.). New York: Springer. ISBN 978-0-387-98976-1.
^ https://www.mccabe.com/ppt/SoftwareQualityMetricsToIdentifyRisk.ppt
^ ^a ^b ^c Arthur H. Watson; Thomas J. McCabe (1996). "Structured Testing: A Testing Methodology Using the Cyclomatic Complexity Metric" (PDF). NIST Special Publication 500-235.
^ Paul C. Jorgensen (2002). Software Testing: A Craftsman's Approach, Second Edition (2nd ed.). CRC Press. pp. 150–153. ISBN 978-0-8493-0809-3.
^ ^a ^b Norman E Fenton; Martin Neil (1999). "A Critique of Software Defect Prediction Models" (PDF). IEEE Transactions on Software Engineering. 25 (3): 675–689. CiteSeerX 10.1.1.548.2998. doi:10.1109/32.815326.
^ Schroeder, Mark (1999). "A Practical guide to object-oriented metrics". IT Professional. 1 (6): 30–36. doi:10.1109/6294.806902. S2CID 14945518.
^ Les Hatton (2008). "The role of empiricism in improving the reliability of future software". version 1.1.
^ Kan (2003). Metrics and Models in Software Quality Engineering. Addison-Wesley. pp. 316–317. ISBN 978-0-201-72915-3.
^ G.S. Cherf (1992). "An Investigation of the Maintenance and Support Characteristics of Commercial Software". Journal of Software Quality. 1 (3): 147–158. doi:10.1007/bf01720922. ISSN 1573-1367. S2CID 37274091.
^ ISO 26262-3:2011(en) Road vehicles — Functional safety — Part 3: Concept phase. International Standardization Organization.
^ Papadimitriou, Fivos (2012). "Artificial Intelligence in modelling the complexity of Mediterranean landscape transformations". Computers and Electronics in Agriculture. 81: 87–96. doi:10.1016/j.compag.2011.11.009.
^ Papadimitriou, Fivos (2013). "Mathematical modelling of land use and landscape complexity with ultrametric topology". Journal of Land Use Science. 8 (2): 234–254. doi:10.1080/1747423X.2011.637136. S2CID 121927387.

외부 링크

[2] 여기서 "구조화"는 특히 "함수별로 하나의 출구(반환명세서)를 갖는" 것을 의미한다.

[12] 이것은 꽤 흔한 유형의 조건이다; f1이 f3가 방출하는 일부 자원을 할당하는 가능성을 고려하라.

[1] A J Sobey. "Basis Path Testing".

[mccabe76-3] McCabe (December 1976). "A Complexity Measure". IEEE Transactions on Software Engineering. SE-2 (4): 308–320. doi:10.1109/tse.1976.233837. S2CID 9116234.

[Laplante2007-4] Philip A. Laplante (25 April 2007). What Every Engineer Should Know about Software Engineering. CRC Press. p. 176. ISBN 978-1-4200-0674-2.

[5] Fricker, Sébastien (April 2018). "What exactly is cyclomatic complexity?". froglogic GmbH. Retrieved October 27, 2018. To compute a graph representation of code, we can simply disassemble its assembly code and create a graph following the rules: ...

[ecst-6] Belzer, Kent, Holzman and Williams (1992). Encyclopedia of Computer Science and Technology. CRC Press. pp. 367–368.{{cite book}}: CS1 maint : 복수이름 : 작성자 목록(링크)

[harrison-7] Harrison (October 1984). "Applying Mccabe's complexity measure to multiple-exit programs". Software: Practice and Experience. 14 (10): 1004–1007. doi:10.1002/spe.4380141009. S2CID 62422337.

[8] Diestel, Reinhard (2000). Graph theory. Graduate texts in mathematics 173 (2 ed.). New York: Springer. ISBN 978-0-387-98976-1.

[9] ttps://www.mccabe.com/ppt/SoftwareQualityMetricsToIdentifyRisk.ppt

[nist-10] Arthur H. Watson; Thomas J. McCabe (1996). "Structured Testing: A Testing Methodology Using the Cyclomatic Complexity Metric" (PDF). NIST Special Publication 500-235.

[11] Paul C. Jorgensen (2002). Software Testing: A Craftsman's Approach, Second Edition (2nd ed.). CRC Press. pp. 150–153. ISBN 978-0-8493-0809-3.

[fenton-13] Norman E Fenton; Martin Neil (1999). "A Critique of Software Defect Prediction Models" (PDF). IEEE Transactions on Software Engineering. 25 (3): 675–689. CiteSeerX 10.1.1.548.2998. doi:10.1109/32.815326.

[schroeder99-14] Schroeder, Mark (1999). "A Practical guide to object-oriented metrics". IT Professional. 1 (6): 30–36. doi:10.1109/6294.806902. S2CID 14945518.

[taic-15] Les Hatton (2008). "The role of empiricism in improving the reliability of future software". version 1.1.

[kan-16] Kan (2003). Metrics and Models in Software Quality Engineering. Addison-Wesley. pp. 316–317. ISBN 978-0-201-72915-3.

[cherf-17] G.S. Cherf (1992). "An Investigation of the Maintenance and Support Characteristics of Commercial Software". Journal of Software Quality. 1 (3): 147–158. doi:10.1007/bf01720922. ISSN 1573-1367. S2CID 37274091.

[ISO26262Part3-18] ISO 26262-3:2011(en) Road vehicles — Functional safety — Part 3: Concept phase. International Standardization Organization.

[19] Papadimitriou, Fivos (2012). "Artificial Intelligence in modelling the complexity of Mediterranean landscape transformations". Computers and Electronics in Agriculture. 81: 87–96. doi:10.1016/j.compag.2011.11.009.

[20] Papadimitriou, Fivos (2013). "Mathematical modelling of land use and landscape complexity with ultrametric topology". Journal of Land Use Science. 8 (2): 234–254. doi:10.1080/1747423X.2011.637136. S2CID 121927387.

[1]

[a]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[b]

[11]

[12]

[13]

[14]

[15]

[16]

[17]

[18]

Search