흑체

Black body
열평형 상태의 흑체로부터의 방사선에 대해서는, 흑체 방사선을 참조해 주세요.캐나다 단편 영화의 경우 Black Bodies(영화)를 참조하십시오.
A physical approximation of a black body radiator model constitutes of a heated pyrographite chamber and peripheral devices which ensure temperature stability.
폴란드의 CARLO 연구소에서 사용되는 검은색 바디 라디에이터입니다.이는 스펙트럼 방사조도 표준으로 사용되는 플랑크의 법칙에 의해 기술된 모델의 근사치이다.
흑체의 온도가 낮아지면 강도도 낮아지고 피크는 더 긴 파장으로 이동한다.비교를 위해 보여지는 것은 고전적인 레일리-진스 법칙과 그 자외선 재앙이다.

흑체 또는 흑체는 주파수나 입사 각도에 관계없이 모든 입사 전자파를 흡수하는 이상적인 물체입니다."검은 몸체"라는 이름은 그것이 모든 색의 빛을 흡수하기 때문에 붙여졌습니다.검은 물체는 또한 검은 물체의 방사선을 방출한다.반면 흰색 물체는 "모든 입사 광선을 모든 [1]방향으로 완전히 균일하게 반사하는 거친 표면"을 가진 물체이다.

열평형 상태의 흑체는 (즉, 일정한 온도에서) 전자파 흑체 방사선을 방출한다.방사선은 플랑크의 법칙에 따라 방출되는데, 이는 물체의 모양이나 조성이 아닌 온도만으로 결정되는 스펙트럼(오른쪽 그림 참조)을 가지고 있다는 것을 의미한다.

열평형 상태에 있는 이상적인 흑체에는 두 가지 [2]주요 특성이 있습니다.

  1. 이상적인 이미터입니다.모든 주파수에서 동일한 온도에서 다른 물체만큼 또는 그 이상의 열복사에너지를 방출합니다.
  2. 이는 확산 이미터입니다. 방향에 수직인 단위 면적당 측정되며, 에너지는 방향에 관계없이 등방적으로 방사됩니다.

검은 표면의 대략적인 구현은 큰 절연 인클로저(예: 오븐)의 벽에 있는 구멍입니다.구멍에 들어오는 모든 빛은 차체 내부 표면에서 반사되거나 흡수되며, 다시 반사되지 않기 때문에 구멍은 거의 완벽한 흡수체 역할을 합니다.그러한 인클로저에 갇힌 방사선이 열평형 상태에 있을 때, 구멍에서 방출되는 방사선은 평형 [further explanation needed]온도의 다른 물체에서 방출되는 방사선만큼 커진다.

실제 물질은 흑체 에너지 수준의 극히 일부(방사율이라고 함)의 에너지를 방출합니다.정의상 열평형 상태의 흑체는 방사율이 θ = 1이다. 주파수와 무관하게 낮은 방사율을 가진 선원을 흔히 [3][4]회색체라고 한다.방사율이 가능한 한 1에 가까운 흑체를 만드는 것은 현재도 여전히 [5]관심의 대상이다.

천문학에서, 별과 행성으로부터의 방사선은 때때로 전자파 에너지의 총 플럭스를 방출할 수 있는 흑체의 온도인 유효 온도의 관점에서 특징지어진다.

정의.

흑체에 대한 아이디어는 1860년 구스타프 키르히호프에 의해 처음 소개되었습니다.

무한히 작은 두께로 입사 광선을 완전히 흡수하고 반사도 투과도 하지 않는 신체를 상상할 수 있다는 가정입니다.나는 그런 시체들을 완벽한 흑인이라 부르겠다, 더 간단히 말하면 [6]흑인이라 부르겠다.

보다 현대적인 정의에서는 "무한히 작은 두께"[7]에 대한 참조가 사라집니다.

이제 흑체라고 불리는 이상적인 물체가 정의되었다.흑체는 모든 입사 방사선을 통과시키고(반사 에너지 없음) 입사 방사선을 내부적으로 흡수합니다(신체를 통해 전달되는 에너지 없음).이것은 모든 파장과 모든 입사 각도의 방사선에 적용된다.따라서 흑체는 모든 입사 [8]방사선의 완벽한 흡수체이다.

이상화

이 섹션에서는 흑체와 관련하여 개발된 몇 가지 개념을 설명합니다.

절연 인클로저의 작은 구멍으로 흑체를 대략 실현

구멍이 있는 공동

검은 표면에서 널리 사용되는 모델은 [8]방사선에 불투명한 벽이 있는 공동에 있는 작은 구멍입니다.구멍에 입사한 방사선은 캐비티로 전달되며, 캐비티가 클 경우 재방출될 가능성이 매우 낮습니다.이 구멍은 매우 완벽한 검은 표면이 아닙니다. 특히 입사 방사선의 파장이 구멍의 지름보다 클 경우 일부가 반사됩니다.마찬가지로, 완전한 열평형 상태에서도 유한 크기의 캐비티 내부의 방사선은 [9]캐비티 크기와 동등하거나 더 큰 파장에 대해 이상적인 플랑크 스펙트럼을 가지지 못할 것이다.

캐비티가 고정 온도 T로 유지되고 인클로저 내부에 갇힌 방사선이 인클로저와 열 평형 상태라고 가정합니다.인클로저의 구멍에 의해 방사선이 방출됩니다.홀이 작을 경우 홀을 드나드는 방사선이 캐비티 내 방사선의 평형에 미치는 영향은 미미하다.이 누출 방사선은 온도 T의 에너지 특성 분포를 나타내며, 적어도 구멍 [9]크기보다 작은 파장에서는 공동이나 구멍의 특성에 의존하지 않는 흑체 방사선에 근접합니다.E = 에너지, h = 플랑크의 상수, f = 주파수인 E = hf 등식으로 방사 에너지와 관련된 방사 주파수의 함수로 스펙트럼 소개 그림을 참조한다.

언제든지 공동 내 방사선이 열평형 상태가 아닐 수 있지만, 열역학 제2법칙은 방해를 받지 않고 그대로 두면 결국 [10]평형에 도달하지만, 그렇게 하는 데 시간이 매우 [11]오래 걸릴 수 있다.일반적으로 평형은 공동이나 [12][13][14][15]벽의 물질에 의한 방사선의 지속적인 흡수 및 방출에 의해 달성된다.공동에 들어가는 방사선은 이 메커니즘에 의해 "열화"됩니다. 즉, 광자의 앙상블이 플랑크 분포를 이룰 때까지 에너지가 재분배됩니다.열화에 걸리는 시간은 희박한 가스 같은 희박한 물질보다 응축 물질이 존재할 때 훨씬 더 빠릅니다.수십억 켈빈 이하의 온도에서,[17] 직접 광자-광자 상호작용은[16] 물질과의 상호작용에 비해 보통 무시할 수 있다.광자는 상호작용하는 보손 [18]가스의 한 예이며,[19] H-이론으로 설명되었듯이, 매우 일반적인 조건에서는 상호작용하는 보손 가스는 열 평형에 접근합니다.

투과, 흡수, 반사

열복사에 대한 물체의 거동은 투과θ, 흡수α, 반사θ로 특징지어진다.

물체의 경계는 주위와의 계면을 형성하며, 이 계면은 거칠거나 매끄러울 수 있다.부드러운 계면에 대한 플레넬 방정식에 의해 제어되는 반사 및 굴절의 법칙은 재료와 그 주변의 굴절률이 [20]다를 때 반사선을 필요로 하기 때문에 굴절률이 다른 비반사 계면을 분리하는 영역은 거칠어야 한다.몇 가지 이상적인 동작 유형에는 특정 이름이 지정됩니다.

불투명한 물체는 [21][22]일부 반사될 수도 있지만 도달하는 방사선을 전혀 전달하지 않는 물체입니다.즉, θ = 0 및 α + θ = 1이다.

투명한 물체는 도달하는 모든 방사선을 전달하는 물체이다.즉, θ = 1 및 α = θ = 0이다.

회색체는 모든 파장에 대해 α, θ, θ가 일정한 것을 말한다.이 용어는 α가 온도와 파장에 의존하지 않는 물체를 의미하기도 한다.

백색체는 모든 입사 방사선이 모든 방향으로 균일하게 반사되는 물체이다. 즉, θ = 0, α = 0, θ = 1이다.

흑체의 경우, θ = 0, α = 1, θ = 0이다. 플랑크는 완벽하게 검은 물체에 대한 이론적인 모델을 제공하는데, 그는 이것이 자연에는 존재하지 않는다고 언급했다. 즉, 불투명한 내부 외에, 그것들은 완벽하게 전달되고 [23]반사되지 않는 인터페이스를 가지고 있다.

키르히호프의 완벽한 검은 몸

1860년 키르히호프는 무한히 작은 두께의 완전히 흡수하는 표면층을 가진 완벽한 검은 물체의 이론적인 개념을 도입했지만, 플랑크는 이 아이디어에 몇 가지 심각한 제한을 두었다.플랑크는 흑체에 대한 세 가지 요건에 주목했다. 즉, (i) 방사선이 들어오되 반사되지 않아야 하며, (ii) 입사 방사선을 흡수하고 재방사를 방지하기에 충분한 최소 두께를 가져야 하며, (iii) 방사선이 들어오고 다시 튀어 나오는 것을 방지하기 위해 산란 시 엄격한 한계를 충족해야 한다.그 결과 자신에게 떨어지는 모든 방사선을 흡수하는 키르히호프의 완벽한 흑체는 무한히 얇은 표면층으로는 실현될 수 없고,[24][25] 만족하기 어려운 흑체 내 빛의 산란 조건을 붙인다.

실현

흑체의 실현은 현실세계, 물리적인 실시형태에 관한 것이다.여기 몇 가지 있습니다.

구멍이 있는 공동

1898년 오토 루머와 페르디난드 쿨바움은 공동 방사선원에 [26]대한 설명을 발표했다.그 설계는 오늘날까지 방사선 측정에 거의 변경되지 않고 사용되고 있다.그것은 백금 상자 벽에 난 구멍으로, 다이어프램으로 나누어져 있었고, 내부가 산화철로 검게 칠해져 있었다.그것은 플랑크의 [27][28]법칙을 발견하게 된 점진적으로 개선된 측정의 중요한 요소였다.1901년에 기술된 버전은 크롬,[29] 니켈, 코발트 산화물의 혼합물로 내부를 검게 만들었다.Hollraum도 참조하십시오.

검정색에 가까운 소재

위장용 흑체 물질과 레이더 [30][31]비투명용 레이더 흡수 물질에 관심이 있다.그들은 또한 태양 에너지 수집기, 적외선 열 감지기로도 응용되고 있다.방사선의 완벽한 방출자로서, 특히 대류 가열을 [32]사용할 수 없는 공간이나 진공에서 검은 물체 거동을 가진 뜨거운 물질은 효율적인 적외선 히터를 만들 것이다.그것들은 또한 망원경과 카메라에서 유영을 줄이기 위한 반사 방지 표면으로 유용하며, 흑체 같은 물질들이 잘못된 소스에서 나오는 빛을 흡수하는 고대비 영역에 있는 물체에 대한 정보를 수집합니다.

램프 블랙 코팅이 차체를 거의 검은색으로 만든다는 것은 오래전부터 알려져 왔다.제조된 카본나노튜브에서 램프블랙의 개량점이 발견되었다.나노 다공질 재료는 진공에 가까운 굴절률을 달성할 수 있으며, 한 가지 경우 0.045%[5][33]의 평균 반사율을 얻을 수 있습니다.2009년, 일본 과학자 팀은 수직으로 정렬된 단일 벽의 탄소 나노튜브에 기초하여 이상적인 흑체에 가까운 나노블랙이라는 물질을 만들었다.이는 자외선에서 원적외선 [32]영역까지 스펙트럼 범위에서 들어오는 빛의 98~99%를 흡수한다.

거의 완벽한 검은색 재료의 다른 예로는 니켈-인 합금,[34] 수직으로 정렬된 카본 나노튜브 어레이(VantaBlack) 및 플라워 카본 나노 [35]구조를 화학적으로 식각하여 만든 슈퍼 블랙이 있습니다. 모두 99.9% 이상의 빛을 흡수합니다.

별과 행성

UBV 색상 색인에 대한 자세한 내용은 광도계를 참조하십시오.
별의 단면을 이상화한 뷰입니다.광구는 거의 열평형 상태에 있는 빛의 광자를 포함하고 있으며, 일부는 거의 흑체 방사선으로 우주로 빠져나간다.

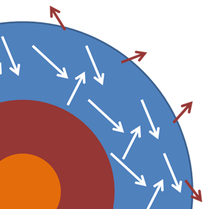
별이나 행성은 종종 검은 물체로 모델링되고 이러한 물체에서 방출되는 전자파 방사선은 검은 물체 방사선으로 모델링됩니다.그림은 아이디어를 설명하기 위한 매우 도식화된 단면을 보여준다.방출된 빛이 발생하는 별의 광구는 빛의 광자가 광구 내의 물질과 상호작용하여 장기간에 걸쳐 유지되는 공통 온도 T에 도달하는 층으로 이상화된다.일부 광자는 탈출하여 우주로 방출되지만, 그들이 운반하는 에너지는 별 안에서 나오는 에너지로 대체되어 광구의 온도는 거의 안정적입니다.노심의 변화는 광구에 대한 에너지 공급의 변화로 이어지지만, 이러한 변화는 이곳의 관심 시간 척도로 볼 때 느립니다.이러한 상황이 실현될 수 있다고 가정할 때, 별의 바깥쪽 층은 작은 구멍이 있는 외함의 예와 다소 유사하며, 이 구멍은 광구 바깥쪽의 제한된 우주로의 전송으로 대체된다.이 모든 가정 하에 이 별은 [36]광구의 온도에서 흑체 복사를 방출한다.

색채도라고 불리는 주계열성 및 초거성의 B-V 및 U-B 색지수와 비교한 흑체의 유효 온도.[37]

이 모델을 사용하여 별의 유효 온도를 추정하며, 이는 별과 동일한 표면 에너지 플럭스를 생성하는 검은 물체의 온도로 정의됩니다.만약 별이 흑체라면, 스펙트럼의 어느 영역에서나 같은 유효 온도가 발생할 것이다.예를 들어, B(파란색) 또는 V(가시적) 범위의 비교는 소위 B-V 색 지수로 이어지며, 이는 태양의 색 지수가 +0.648 ± 0.[39]006인 상태에서 별이 [38]붉을수록 증가합니다.U(자외선)와 B지수를 합치면 U-B지수가 나오는데, U-B지수는 별이 뜨거울수록 더 음수가 되고 자외선 복사가 많아진다.태양이 G2 V형 별이라고 가정하면 U-B 지수는 +0.[40]12입니다.가장 일반적인 두 가지 유형의 별 배열에 대한 두 가지 지수는 그림(그림)에서 별이 완벽한 흑체일 경우 유효 표면 온도와 비교된다.대략적인 상관관계가 있다.예를 들어 특정 B-V 지수 측정의 경우 가장 일반적인 별의 배열(주계열과 초거성) 곡선은 자외선 스펙트럼을 포함하는 대응하는 흑체 U-B 지수 아래에 있으며, 이는 두 별의 그룹이 동일한 B-V 지수를 가진 흑체보다 적은 자외선을 방출한다는 것을 보여준다.별들의 [41]깊이가 서로 다른 온도들을 가지고 있다는 것을 고려하면, 그들이 흑체 곡선에 잘 맞는다는 것은 아마도 놀라운 일일 것이다.예를 들어, 태양의 유효 온도는 5780 [42]K로 광구(빛을 발생시키는 영역)의 온도와 비교할 수 있으며, 광구(빛을 발생시키는 영역)는 채층과의 외부 경계에서 약 5000 K에서 약 500 km(310 mi) [43]깊이의 대류 구역과의 내부 경계에서 약 9500 K에 이른다.

블랙홀

다음 항목도 참조하십시오.호킹 복사

블랙홀은 아무것도 빠져나가지 않는 시공간 영역입니다.블랙홀 주위에는 돌아오지 않는 지점을 표시하는 사건의 지평선이라고 불리는 수학적으로 정의된 표면이 있습니다.그것은 지평선에 닿는 모든 빛을 흡수하고 아무것도 반사하지 않기 때문에 "검은색"이라고 불리며, 거의 이상적인 흑체이다[44].[45]물리학자들은 외부 관찰자들에게 블랙홀은 0이 아닌 온도를 가지고 있으며, 흑체 방사선을 방출하고, 거의 완벽한 흑체 스펙트럼을 가진 방사선을 방출하며, 궁극적으로 [46]증발한다고 믿고 있다.이 방출의 메커니즘은 가상 한 쌍의 입자가 구멍의 중력에 의해 분리되어 한쪽 부재가 구멍 안으로 빨려 들어가고 다른 한쪽 부재가 [47]방출되는 진공 변동과 관련이 있습니다.방출의 에너지 분포는 플랑크의 법칙에 의해 온도 T:

여기서 c는 빛의 속도, θ는 환원된 플랑크 상수, k는B 볼츠만 상수, G는 중력 상수, M은 블랙홀의 [48]질량이다.이러한 예측은 아직 관찰적 또는 [49]실험적으로 테스트되지 않았다.

우주 마이크로파 배경 복사

다음 항목도 참조하십시오.빅뱅 및 우주 마이크로파 배경 복사

빅뱅 이론은 우주가 대규모로 균질하고 등방성이라는 우주론적 원리에 기초하고 있다.이론에 따르면, 우주는 형성된 지 약 1초 후에 10K 이상의10 온도에서 열평형 상태에 있는 거의 이상적인 흑체였다.우주가 팽창하고 그 안에 있는 물질과 방사선이 식으면서 온도는 낮아졌다.오늘날 관측된 우주 마이크로파 배경 복사는 "자연에서 측정된 것 중 가장 완벽한 흑체"[50]이다.이것은 약 2.7 K의 온도에서 거의 이상적인 플랑크 스펙트럼을 가지고 있다.그것은 하늘의 각도에 따라 10만분의 1 정도만 변하는 관측된 이방성에 의한 진정한 흑체 복사의 완벽한 등방성에서 출발한다.

복사 냉각

피크 방출 파장 및 복사 이탈 대 흑체 온도의 로그 로그 그래프 – 빨간색 화살표는 5780K 흑체의 피크 파장이 501nm이고 63.3MW2/m임을 나타낸다. 복사 이탈
참고 항목: 복사 냉각 및 방사선(열전달)

모든 주파수에 대한 플랑크의 법칙의 통합은 온도 T에서 유지되는 흑체에 의해 방사되는 표면적의 단위당 시간 단위당 총 에너지를 제공하며, 스테판-볼츠만 법칙으로 알려져 있다.

여기서 θ는 스테판-볼츠만 상수, θ 5.67×10−8 W wmkK−2−4[51] 일정한 온도 T에서 열 평형을 유지하기 위해 흑체는 주어진 영역 A에 걸쳐 이 양의 전력 P를 흡수하거나 내부적으로 생성해야 한다.

열 복사에 의한 물체의 냉각은 종종 스테판-볼츠만 법칙에 의해 "물체" 방사율 δ 1(P/A = δT4)을 보충하여 근사치를 구한다.방출체의 온도 저하율은 방사된 전력과 인체의 열 [52]용량으로 추정할 수 있다.이 접근방식은 열이 식는 동안 체내에서 발생하는 열 재배포 메커니즘(구성 변화, 상전 또는 신체 재구성을 포함할 수 있음)의 세부 사항을 무시하고, 각 순간에 신체가 단일 온도에 의해 특징지어진다고 가정하는 단순화이다.또한 온도와 [53][54]방사율의 변화, 그리고 중성미자와 같은 [55]입자의 방출과 같은 다른 형태의 에너지 방출의 역할과 같은 다른 가능한 합병증도 무시합니다.

열방출체가 스테판-볼츠만의 법칙을 따른다고 가정하고 그 전력방출 P와 온도 T를 알고 있는 경우, 이 법칙을 사용하여 총 방출 전력이 방출 표면의 면적에 비례하기 때문에 방출 물체의 치수를 추정할 수 있다.이런 방식으로 천문학자들이 관측한 X선 폭발은 원래 [56]추측했던 블랙홀이 아니라 반지름이 약 10km인 중성자 별에서 발생한다는 것이 밝혀졌다.정확한 크기 추정을 위해서는 방사율, 특히 스펙트럼과 [57]각도의존성에 대한 지식이 필요하다.

「 」를 참조해 주세요.

레퍼런스

인용문

  1. ^ 플랑크 1914, 9-10페이지
  2. ^ Mahmoud Massoud (2005). "§2.1 Blackbody radiation". Engineering thermofluids: thermodynamics, fluid mechanics, and heat transfer. Springer. p. 568. ISBN 978-3-540-22292-7.
  3. ^ 표면의 방사율은 원칙적으로 주파수, 시야각 및 온도에 따라 달라집니다.그러나 회색 물체로부터의 복사는 같은 온도에서 단순히 흑체의 복사에 비례하기 때문에 방사율은 주파수(또는 동등한 파장)에 의존하지 않는다.참고 지도자인 마수드 Kaviany(2002년)."그림 4.3(b):비틀 림보 강재의 회색( 없파장 의존), 미만성(무지향성의. 의존)와 불투명한(가 포함되지 않)표면".열 전달의 원리Wiley-IEEE. 페이지의 주 381. 아이 에스비엔 978-0-471-43463-4., 로널드 G.Driggers(2003년).백과 사전 광학 공학의 볼륨 3.CRC프레스. p. 2303.아이 에스비엔 978-0-8247-4252-2.
  4. ^ 일부 저자는 방사율이 약 0.99보다 큰 적외선 선원을 흑체로 설명한다.참조
  5. ^ a b Chun, Ai Lin (2008). "Blacker than black". Nature Nanotechnology. doi:10.1038/nnano.2008.29.
  6. ^ F번역Annalen der Physik의 Guthrie: 109, 275-301(1860):
  7. ^ 무한히 얇은 층의 개념은 플랑크에 의해 폐기되었다.플랑크 1914, 페이지 10, 각주 2 참조.
  8. ^ a b Siegel, Robert; Howell, John R. (2002). Thermal Radiation Heat Transfer; Volume 1 (4th ed.). Taylor & Francis. p. 7. ISBN 978-1-56032-839-1.
  9. ^ a b 스펙트럼 보정은 벽, 곡률 및 토폴로지의 경계 조건, 특히 공동 치수와 유사한 파장에 대해 발생한다.
  10. ^ Clement John Adkins (1983). "§4.1 The function of the second law". Equilibrium thermodynamics (3rd ed.). Cambridge University Press. p. 50. ISBN 978-0-521-27456-2.
  11. ^ 단순한 경우에서 균형에 대한 접근은 이완 시간에 의해 통제된다.Adkins(1983)(10페이지)에서 설명한 바와 같이, 다른 경우에는 시스템이 준안정 상태에서 '끊길' 수 있습니다.다른 예에 대해서는, 을 참조해 주세요.
  12. ^ 빈 공간 안에 방사능의 열 평형 상태에 대한 접근 문제의 작은 조각에 몰입해서 모든 주파수에서 방열할 수를 첨가하여 높여야 할 수 있다.피터 시어도어 Landsberg(1990년)을 참조하십시오.열역학과 통계 역학(옥스포드 대학 출판부 1978년 교육의 Reprint.).택배 도버 출판물. 우편 209.아이 에스비엔 978-0-486-66493-4.
  13. ^ 플랑크 1914년 페이지의 주 44, §52.
  14. ^ 루던. 2000년 제1장
  15. ^ 만델&울프 1995년 제13장.
  16. ^ 로버트 Karplus*와 마유 라이스 노이만,"그 발생하는 비산 빛의 라이트에 의해", Phys.목사 83776–784(1951년)
  17. ^ Ludwig Bergmann; Clemens Schaefer; Heinz Niedrig (1999). Optics of waves and particles. Walter de Gruyter. p. 595. ISBN 978-3-11-014318-8. Because the interaction of the photons with each other is negligible, a small amount of matter is necessary to establish thermodynamic equilibrium of heat radiation.
  18. ^ 그 근본 보손은 광자, 약한 상호 작용, 글루온의 벡터 보손, 그리고 graviton.;D. 앨런 그리핀을 참조하십시오WSnoke.S.Stringari(1996년).보즈-아인슈타인 서림.캠브리지 대학 출판부. p. 4. 아이 에스비엔 978-0-521-58990-1.
  19. ^ Richard Chace Tolman (2010). "§103: Change of H with time as a result of collisions". The principles of statistical mechanics (Reprint of 1938 Oxford University Press ed.). Dover Publications. pp. 455 ff. ISBN 978-0-486-63896-6. ...we can define a suitable quantity H to characterize the condition of a gas which [will exhibit] a tendency to decrease with time as a result of collisions, unless the distribution of the molecules [is already that of] equilibrium. (p. 458)
  20. ^ Paul A. Tipler (1999). "Relative intensity of reflected and transmitted light". Physics for Scientists and Engineers, Parts 1-35; Part 39 (4th ed.). Macmillan. p. 1044. ISBN 978-0-7167-3821-3.
  21. ^ Massoud Kaviany (2002). "Figure 4.3(b) Radiation properties of an opaque surface". Principles of heat transfer. Wiley-IEEE. p. 381. ISBN 978-0-471-43463-4.
  22. ^ BA Venkanna (2010). "§10.3.4 Absorptivity, reflectivity, and transmissivity". Fundamentals of heat and mass transfer. PHI Learning Pvt. Ltd. pp. 385–386. ISBN 978-81-203-4031-2.
  23. ^ 플랑크 1914년 페이지의 주 10
  24. ^ 플랑크 1914년,를 대신하여 서명함. 9–10, §10.
  25. ^ Kirchhoff1860c
  26. ^ 독일의 물리학자&Kurlbaum 1898년
  27. ^ 광범한 역사적 토론 Mehra, 자그디시;Rechenberg, 헬무트(2000년)에서 발견된다.양자 이론의 역사적 발전.스프링거.를 대신하여 서명함. 39페이지와 그 다음.아이 에스비엔 978-0-387-95174-4.
  28. ^ Kangro 1976년,p. 159
  29. ^ 독일의 물리학자&Kurlbaum 1901년
  30. ^ CF Lewis (June 1988). "Materials keep a low profile" (PDF). Mech. Eng.: 37–41.[영구 데드링크]
  31. ^ Bradley Quinn (2010). Textile Futures. Berg. p. 68. ISBN 978-1-84520-807-3.
  32. ^ a b K. Mizuno; et al. (2009). "A black body absorber from vertically aligned single-walled carbon nanotubes". Proceedings of the National Academy of Sciences. 106 (15): 6044–6077. Bibcode:2009PNAS..106.6044M. doi:10.1073/pnas.0900155106. PMC 2669394. PMID 19339498.
  33. ^ Zu-Po Yang; et al. (2008). "Experimental observation of an extremely dark material made by a low-density nanotube array". Nano Letters. 8 (2): 446–451. Bibcode:2008NanoL...8..446Y. doi:10.1021/nl072369t. PMID 18181658. S2CID 7412160.
  34. ^ 영국 국립 물리 연구소의 Richard Brown과 그의 동료들의 작업에 대한 설명을 참조하십시오.
  35. ^ Ghai, Viney; Singh, Harpreet; Agnihotri, Prabhat K. (2019). "Dandelion-Like Carbon Nanotubes for Near-Perfect Black Surfaces". ACS Applied Nano Materials. 2 (12): 7951–7956. doi:10.1021/acsanm.9b01950.
  36. ^ Simon F. Green; Mark H. Jones; S. Jocelyn Burnell (2004). An introduction to the sun and stars. Cambridge University Press. pp. 21–22, 53. ISBN 978-0-521-54622-5. A source in which photons are much more likely to interact with the material within the source than to escape is a condition for the formation of a black-body spectrum
  37. ^ 본떠 만든 그림
  38. ^ David H. Kelley; Eugene F. Milone; Anthony F. (FRW) Aveni (2011). Exploring Ancient Skies: A Survey of Ancient and Cultural Astronomy (2nd ed.). Springer. p. 52. ISBN 978-1-4419-7623-9.
  39. ^ David F Gray (February 1995). "Comparing the sun with other stars along the temperature coordinate". Publications of the Astronomical Society of the Pacific. 107: 120–123. Bibcode:1995PASP..107..120G. doi:10.1086/133525.
  40. ^ M Golay (1974). "Table IX: U-B Indices". Introduction to astronomical photometry. Springer. p. 82. ISBN 978-90-277-0428-3.
  41. ^ Lawrence Hugh Aller (1991). Atoms, stars, and nebulae (3rd ed.). Cambridge University Press. p. 61. ISBN 978-0-521-31040-6.
  42. ^ Kenneth R. Lang (2006). Astrophysical formulae, Volume 1 (3rd ed.). Birkhäuser. p. 23. ISBN 978-3-540-29692-8.
  43. ^ B. Bertotti; Paolo Farinella; David Vokrouhlický (2003). "Figure 9.2: The temperature profile in the solar atmosphere". New Views of the Solar System. Springer. p. 248. ISBN 978-1-4020-1428-4.
  44. ^ Schutz, Bernard (2004). Gravity From the Group Up: An Introductory Guide to Gravity and General Relativity (1st ed.). Cambridge University Press. p. 304. ISBN 978-0-521-45506-0.
  45. ^ PCW Davies (1978). "Thermodynamics of black holes" (PDF). Rep Prog Phys. 41 (8): 1313–1355. Bibcode:1978RPPh...41.1313D. doi:10.1088/0034-4885/41/8/004. Archived from the original (PDF) on 10 May 2013.
  46. ^ Robert M Wald (2005). "The thermodynamics of black holes". In Andrés Gomberoff; Donald Marolf (eds.). Lectures on quantum gravity. Springer Science & Business Media. pp. 1–38. ISBN 978-0-387-23995-8.
  47. ^ Bernard J Carr & Steven B Giddings (2008). "Chapter 6: Quantum black holes". Beyond Extreme Physics: Cutting-edge science. Rosen Publishing Group, Scientific American (COR). p. 30. ISBN 978-1-4042-1402-6.
  48. ^ Valeri P. Frolov; Andrei Zelnikov (2011). "Equation 9.7.1". Introduction to Black Hole Physics. Oxford University Press. p. 321. ISBN 978-0-19-969229-3.
  49. ^ Robert M Wald (2005). "The thermodynamics of black holes (pp. 1–38)". In Andrés Gomberoff; Donald Marolf (eds.). Lectures on Quantum Gravity. Springer Science & Business Media. p. 28. ISBN 978-0-387-23995-8. ... no results on black hole thermodynamics have been subject to any experimental or observational tests ...
  50. ^ White, M. (1999). "Anisotropies in the CMB" (PDF). Proceedings of the Los Angeles Meeting, DPF 99. UCLA. arXive.org 도 참조해 주세요.
  51. ^ "2018 CODATA Value: Stefan–Boltzmann constant". The NIST Reference on Constants, Units, and Uncertainty. NIST. 20 May 2019. Retrieved 20 May 2019.
  52. ^ 간단한 예를 다음에 나타냅니다.
  53. ^ M Vollmer; K-P Mõllmann (2011). "Figure 1.38: Some examples for temperature dependence of emissivity for different materials". Infrared Thermal Imaging: Fundamentals, Research and Applications. John Wiley & Sons. p. 45. ISBN 978-3-527-63087-5.
  54. ^ Robert Osiander; M. Ann Garrison Darrin; John Champion (2006). MEMS and Microstructures in aerospace applications. CRC Press. p. 187. ISBN 978-0-8247-2637-9.
  55. ^ Krishna Rajagopal; Frank Wilczek (2001). "6.2 Coling by Neutrino Emissions (pp. 2135-2136) – The Condensed Matter Physics of QCD". In Mikhail A. Shifman (ed.). At The Frontier of Particle Physics: Handbook of QCD (On the occasion of the 75th birthday of Professor Boris Ioffe). Vol. 3. Singapore: World Scientific. pp. 2061–2151. arXiv:hep-ph/0011333v2. CiteSeerX 10.1.1.344.2269. doi:10.1142/9789812810458_0043. ISBN 978-981-02-4969-4. S2CID 13606600. For the first 105–6 years of its life, the cooling of a neutron star is governed by the balance between heat capacity and the loss of heat by neutrino emission. ... Both the specific heat CV and the neutrino emission rate Lν are dominated by physics within T of the Fermi surface. ... The star will cool rapidly until its interior temperature is T < Tc ~ ∆, at which time the quark matter core will become inert and the further cooling history will be dominated by neutrino emission from the nuclear matter fraction of the star.
  56. ^ Walter Lewin; Warren Goldstein (2011). "X-ray bursters!". For the love of physics. Simon and Schuster. pp. 251 ff. ISBN 978-1-4391-0827-7.
  57. ^ TE Strohmayer (2006). "Neutron star structure and fundamental physics". In John W. Mason (ed.). Astrophysics update, Volume 2. Birkhäuser. p. 41. ISBN 978-3-540-30312-1.

참고 문헌

외부 링크

  • Keesey, Lori J. (12 December 2010). "Blacker than black". NASA. Engineers now developing a blacker-than pitch material that will help scientists gather hard-to-obtain scientific measurements... nanotech-based material now being developed by a team of 10 technologists at the NASA Goddard Space Flight Center