공기역학
Aerodynamics
공기역학(Aerodynamics, 고대 그리스어: ἀήρ aero (공기) + 고대 그리스어: δυναμ ική (역학)은 특히 비행기 날개와 같은 고체 물체의 영향을 받을 때 공기의 움직임을 연구하는 학문입니다. 유체 역학 분야와 기체 역학의 하위 분야에서 다루는 주제를 포함하며, 항공학에서 중요한 연구 분야입니다. 공기 역학이라는 용어는 종종 기체 역학과 동의어로 사용되며, 차이점은 "기체 역학"이 모든 기체의 운동에 대한 연구에 적용되며 공기에만 국한되지 않는다는 것입니다. 공기역학에 대한 공식적인 연구는 18세기에 현대적인 의미에서 시작되었지만, 공기역학적 항력과 같은 기본 개념에 대한 관찰은 훨씬 이전에 기록되었습니다. 공기역학의 초기 노력의 대부분은 1891년 오토 릴리엔탈(Otto Lilienthal)에 의해 처음으로 입증된 공중보다 무거운 비행을 달성하는 것을 목표로 했습니다.[2] 이후 수학적 분석, 경험적 근사치, 풍동실험, 컴퓨터 시뮬레이션 등을 통한 공기역학의 활용은 공중보다 무거운 비행을 비롯한 여러 기술 개발의 합리적 기반을 형성했습니다. 최근 공기역학 연구는 압축성 흐름, 난류 및 경계층과 관련된 문제에 초점을 맞추고 있으며 본질적으로 점점 더 계산적이 되고 있습니다.
역사
현대의 공기역학은 17세기까지만 거슬러 올라가지만, 공기역학적 힘은 수천 년 동안 돛단배와 풍차에서 인간에 의해 활용되어 왔으며,[3] 고대 그리스의 전설인 이카루스와 다이달로스와 [4]같은 기록된 역사 전반에 걸쳐 비행에 대한 이미지와 이야기가 등장합니다.[5] 아리스토텔레스와 아르키메데스의 작품에는 연속체, 항력, 압력 구배의 기본 개념이 등장합니다.[6]
1726년, 아이작 뉴턴 경은 공기 저항 이론을 최초로 개발한 사람이 되었고,[7] 그를 최초의 공기역학자 중 한 명으로 만들었습니다. 네덜란드계 스위스인 수학자 다니엘 베르누이는 1738년에 하이드로다이나믹을 사용하여 오늘날 베르누이의 원리로 알려진 비압축성 흐름에 대한 압력, 밀도 및 유속 사이의 근본적인 관계를 설명했으며, 이는 공기역학적 양력을 계산하는 한 가지 방법을 제공합니다.[8] 1757년 레온하르트 오일러는 압축성 흐름과 비압축성 흐름 모두에 적용될 수 있는 보다 일반적인 오일러 방정식을 발표했습니다. 오일러 방정식은 1800년대 전반에 점도의 영향을 통합하기 위해 확장되었고, 그 결과 나비에가 탄생했습니다.– 스톡 방정식.[9][10] 나비에– 스톡 방정식은 유체 흐름의 가장 일반적인 지배 방정식이지만 가장 단순한 형태를 제외한 모든 흐름에 대해 해결하기가 어렵습니다.

1799년, 조지 케일리 경은 비행의 네 가지 공기역학적 힘(무게, 양력, 항력, 추력)과 그들 사이의 관계를 처음으로 확인한 사람이 되었고,[11][12] 그렇게 함으로써 다음 세기 동안 공중보다 무거운 비행을 달성하기 위한 길을 개략적으로 설명했습니다. 1871년 프란시스 허버트 웬햄은 공기역학적 힘을 정밀하게 측정할 수 있는 최초의 풍동을 건설했습니다. 항력 이론은 Jean le Rond'Allebert,[13] Gustav Kirchhoff,[14] 그리고 Lord Rayleigh에 의해 개발되었습니다.[15] 1889년, 프랑스의 항공공학자인 찰스 레나르는 지속적인 비행에 필요한 힘을 합리적으로 예측한 최초의 사람이 되었습니다.[16] 글라이더 비행으로 크게 성공한 최초의 사람인 오토 릴리엔탈(Otto Lilienthal)은 또한 높은 양력과 낮은 항력을 생산하는 얇고 구부러진 에어포일을 최초로 제안했습니다. 1903년 12월 17일, 라이트 형제는 자신들의 풍동에서 수행된 연구뿐만 아니라 이러한 발전을 바탕으로 최초의 동력 비행기를 날렸습니다.
첫 비행이 진행되는 동안 프레드릭 W. 랜체스터,[17] 마틴 쿠타, 니콜라이 주코프스키는 각각 독립적으로 유체 흐름의 순환을 들어올리기로 연결하는 이론을 만들었습니다. 쿠타와 주코프스키는 2차원 날개 이론을 개발했습니다. Lancester의 연구를 확장한 Ludwig Prandtl은 얇은 에어포일과 리프팅 라인 이론의 배후에 있는 수학을[18] 개발하고 경계층을 연구한 것으로 인정받고 있습니다.
항공기 속도가 증가함에 따라 설계자들은 음속에 가까운 속도에서 공기 압축성과 관련된 문제에 직면하기 시작했습니다. 이러한 조건에서 공기 흐름의 차이는 항공기 제어의 문제, 충격파에 의한 항력 증가, 공기 탄성 플러터에 의한 구조적 고장의 위협으로 이어집니다. 음속에 대한 유속의 비율은 초음속 흐름의 특성을 처음으로 조사한 사람 중 한 명인 에른스트 마하의 이름을 따서 마하 수라고 이름 지었습니다. 맥콘 랭킨과 피에르 앙리 위고니오는 충격파 전후의 유동 특성에 대한 이론을 독립적으로 개발했고, 야콥 아케레는 초음속 에어포일의 양력과 항력을 계산하는 초기 작업을 주도했습니다.[19] 테오도르 폰 카르만과 휴 라티머 드라이든은 항력이 급격히 증가하는 임계 마하 수와 마하 1 사이의 유속을 설명하기 위해 트랜소닉이라는 용어를 도입했습니다. 이러한 항력의 급격한 증가는 공기역학자들과 비행사들로 하여금 1947년 벨 X-1 항공기를 사용하여 음향 장벽이 깨질 때까지 초음속 비행이 가능한지에 대해 의견이 엇갈리게 만들었습니다.
소리의 장벽이 깨질 무렵에는 아음속과 낮은 초음속 흐름에 대한 공기역학자들의 이해가 성숙해졌습니다. 냉전은 끊임없이 진화하는 고성능 항공기 라인의 디자인을 촉발시켰습니다. 컴퓨터 유체 역학은 복잡한 물체 주변의 흐름 특성을 해결하기 위한 노력으로 시작되어 컴퓨터 소프트웨어를 사용하여 전체 항공기를 설계할 수 있을 정도로 빠르게 성장했으며, 바람 터널 테스트에 이어 컴퓨터 예측을 확인하기 위한 비행 테스트가 이어졌습니다. 초음속 및 극초음속 공기역학에 대한 이해는 1960년대 이후 성숙되었으며, 공기역학자들의 목표는 유체 흐름의 거동에서 차량의 공학으로 이동하여 유체 흐름과 예측 가능하게 상호 작용합니다. 현재 항공기 및 추진 시스템의 공기역학적 효율을 향상시키고자 하는 욕구뿐만 아니라 초음속 및 극초음속 조건을 위한 항공기 설계는 공기역학 분야의 새로운 연구에 계속 동기를 부여하고 있습니다. 흐름 난류와 관련된 기본 공기역학 이론의 중요한 문제와 나비에에 대한 해석적 해결책의 존재 및 고유성에 대한 작업이 계속 수행되는 동안– 스톡 방정식.
기본개념
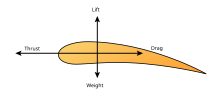
물체 주변의 공기의 움직임을 이해하면 물체에 작용하는 힘과 모멘트를 계산할 수 있습니다. 많은 공기역학 문제에서 관심의 힘은 비행의 기본적인 힘, 즉 양력, 항력, 추력 및 무게입니다. 이 중 양력과 항력은 공기역학적 힘, 즉 고체 물체 위의 공기 흐름으로 인한 힘입니다. 이러한 양의 계산은 종종 흐름 필드가 연속체로서 동작한다는 가정에 기초합니다. 연속체 유동장은 위치와 시간의 함수일 수 있는 유속, 압력, 밀도 및 온도와 같은 특성을 특징으로 합니다. 이러한 특성은 공기역학 실험에서 직간접적으로 측정되거나 공기 흐름의 질량, 운동량 및 에너지 보존 방정식에서 시작하여 계산될 수 있습니다. 유동장 분류에는 밀도, 유속 및 추가 특성인 점도가 사용됩니다.
유동구분
유속은 속도 영역에 따라 흐름을 분류하는 데 사용됩니다. 아음속 흐름은 공기 속도 필드가 항상 로컬 음속보다 낮은 흐름 필드입니다. 트랜스오닉 흐름은 아음속 흐름의 영역과 국소 흐름 속도가 국소 음속보다 큰 영역을 모두 포함합니다. 초음속 흐름은 모든 곳에서 유속이 음속보다 큰 흐름으로 정의됩니다. 네 번째 분류인 극초음속 흐름은 유속이 음속보다 훨씬 큰 흐름을 말합니다. 공기역학자들은 극초음속 유동의 정확한 정의에 대해 의견이 다릅니다.
압축성 유동은 유동 내의 다양한 밀도를 설명합니다. 아음속 흐름은 종종 비압축성으로 이상화됩니다. 즉, 밀도는 일정하다고 가정됩니다. 초음속 및 초음속 흐름은 압축 가능하며, 이러한 흐름장의 밀도 변화를 무시하는 계산은 부정확한 결과를 산출합니다.
점도는 흐름의 마찰력과 관련이 있습니다. 일부 흐름장에서는 점성 효과가 매우 작으며, 근사해가 점성 효과를 안전하게 무시할 수 있습니다. 이러한 근사치를 비점형 흐름이라고 합니다. 점성이 무시되지 않는 흐름을 점성 흐름이라고 합니다. 마지막으로 공기역학적 문제도 흐름 환경에 따라 분류될 수 있습니다. 외부 공기역학은 다양한 모양의 고체 물체 주변(예: 비행기 날개 주변)의 흐름을 연구하는 반면, 내부 공기역학은 고체 물체 내부(예: 제트 엔진을 통한)의 통로를 통한 흐름을 연구하는 것입니다.
연속체 가정
액체나 고체와 달리 기체는 기체가 채우는 부피의 극히 일부만을 차지하는 이산 분자로 구성되어 있습니다. 분자 수준에서 유동장은 많은 개별 기체 분자가 고체 표면과 충돌하는 것으로 구성됩니다. 그러나 대부분의 공기역학 응용 분야에서 기체의 이산 분자 특성은 무시되며 유동장은 연속체로 작용하는 것으로 가정됩니다. 이 가정을 통해 밀도 및 유속과 같은 유체 특성을 흐름 내의 모든 곳에서 정의할 수 있습니다.
연속체 가정의 유효성은 가스의 밀도와 문제의 적용에 따라 달라집니다. 연속체 가정이 유효하려면 평균 자유 경로 길이가 해당 응용 프로그램의 길이 척도보다 훨씬 작아야 합니다. 예를 들어, 많은 공기역학 응용 프로그램은 평균 자유 경로 길이가 마이크로미터 정도이고 차체가 훨씬 큰 대기 조건에서 비행하는 항공기를 다룹니다. 이러한 경우 항공기의 길이 척도는 수 미터에서 수십 미터에 이르며, 이는 평균 자유 경로 길이보다 훨씬 큽니다. 이러한 애플리케이션의 경우 연속체 가정이 합리적입니다. 연속체 가정은 매우 높은 고도(예: 300,000ft/90km)[6]에 있는 차량이나 지구 저궤도에 있는 위성과 같은 극도로 밀도가 낮은 흐름에는 덜 유효합니다. 이러한 경우 통계역학은 연속체 공기역학보다 더 정확한 문제 해결 방법입니다. 크누센 수는 통계 역학과 공기 역학의 연속 공식 사이의 선택을 안내하는 데 사용될 수 있습니다.
보존법
유체 연속체의 가정을 통해 유체 역학 보존 법칙을 사용하여 공기 역학의 문제를 해결할 수 있습니다. 다음 세 가지 보존 원칙이 사용됩니다.
- 질량 보존
- 질량 보존을 위해서는 흐름 안에서 질량이 생성되거나 소멸되지 않아야 하는데, 이 원리를 수학적으로 공식화한 것을 질량 연속 방정식이라고 합니다.
- 운동량보존
- 이 원리를 수학적으로 공식화한 것은 뉴턴의 제2법칙을 적용한 것으로 볼 수 있습니다. 흐름 내의 운동량은 외부 힘에 의해서만 변경되며, 이는 점성(마찰) 힘과 같은 표면 힘과 무게와 같은 신체 힘을 모두 포함할 수 있습니다. 운동량 보존 원리는 벡터 방정식으로 표현되거나 세 개의 스칼라 방정식 집합(x,y,z 성분)으로 분리될 수 있습니다.
- 에너지 절약
- 에너지 보존 방정식은 흐름 내에서 에너지가 생성되지도 파괴되지도 않으며 흐름 내의 부피에 에너지를 가감하는 것은 열 전달 또는 관심 영역 안팎의 작업에 의해 발생한다고 말합니다.
이 방정식들은 함께 나비에(Navier)라고 알려져 있습니다.– Stocks 방정식, 일부 저자는 모멘텀 방정식만 포함하도록 용어를 정의합니다. 나비에– 스톡스 방정식은 알려진 분석 솔루션이 없으며 현대 공기역학에서 계산 기술을 사용하여 해결됩니다. 고속 컴퓨터를 이용한 계산 방법은 역사적으로 사용할 수 없었고 이러한 복잡한 방정식을 푸는 데 드는 높은 계산 비용이 이제는 사용할 수 있게 되었기 때문에 나비에의 단순화– 스톡 방정식은 사용되어 왔고 계속 사용되고 있습니다. 오일러 방정식은 점도를 무시하고 점도의 영향이 작을 것으로 예상되는 경우에 사용할 수 있는 유사한 보존 방정식의 집합입니다. 추가적인 단순화는 라플라스의 방정식과 잠재적 흐름 이론으로 이어집니다. 또한 베르누이의 방정식은 운동량과 에너지 보존 방정식 모두에 대한 1차원 해입니다.
이상 기체 법칙 또는 다른 상태 방정식은 종종 이러한 방정식과 함께 사용되어 미지의 변수에 대한 해를 허용하는 결정된 시스템을 형성합니다.[20]
공기역학과

공기역학적 문제는 유속, 압축성 및 점도를 포함한 유동 환경 또는 유동의 특성에 따라 분류됩니다. 외부 공기역학은 다양한 모양의 고체 물체 주변의 흐름을 연구하는 학문입니다. 외부 공기역학은 비행기의 양력이나 로켓의 코 앞에 형성되는 충격파를 평가하는 것입니다. 내부 공기역학은 고체 물체의 통로를 통한 흐름을 연구하는 학문입니다. 예를 들어, 내부 공기역학은 제트 엔진 또는 공조 파이프를 통한 공기 흐름에 대한 연구를 포함합니다.
공기역학적 문제는 유속이 음속 아래인지, 근처인지, 위인지에 따라 분류할 수도 있습니다. 문제의 모든 속도가 음속보다 작으면 아음속, 음속보다 아래와 위의 속도가 모두 존재하면(보통 특성 속도가 대략 음속일 때), 특성 흐름 속도가 음속보다 크면 초음속, 그리고 유속이 음속보다 훨씬 클 때 극초음속입니다. 공기역학자들은 극초음속 흐름에 대한 정확한 정의에 대해 의견을 달리합니다. 대략적인 정의는 마하 수가 5 이상인 흐름을 극초음속으로 간주합니다.[6]
점도가 흐름에 미치는 영향은 세 번째 분류를 지시합니다. 일부 문제는 매우 작은 점성 효과만 발생할 수 있으며, 이 경우 점도는 무시할 수 있는 것으로 간주될 수 있습니다. 이러한 문제에 대한 근사치를 비점성 흐름이라고 합니다. 점성을 무시할 수 없는 흐름을 점성 흐름이라고 합니다.
비압축성 공기역학
비압축성 흐름은 시간과 공간 모두에서 밀도가 일정한 흐름입니다. 모든 실제 유체는 압축 가능하지만 밀도 변화의 영향으로 인해 계산된 결과에 작은 변화만 생기는 경우 흐름이 압축 불가능한 것으로 추정되는 경우가 많습니다. 이것은 유속이 음속보다 현저히 낮을 때 더 사실일 가능성이 높습니다. 압축성의 영향은 음속에 가깝거나 그 이상의 속도에서 더 크게 나타납니다. 마하 수는 비압축성을 가정할 수 있는지 여부를 평가하는 데 사용되며, 그렇지 않으면 압축성의 영향이 포함되어야 합니다.
아음속 흐름
아음속(또는 저속) 공기역학은 흐름의 모든 곳에서 음속보다 훨씬 낮은 흐름에서 유체 운동을 설명합니다. 아음속 흐름에는 여러 가지 분기가 있지만 흐름이 비점형, 비압축성 및 비회전성일 때 한 가지 특별한 경우가 발생합니다. 이 경우를 전위 흐름이라고 하며, 흐름을 설명하는 미분 방정식을 유체 역학 방정식의 단순화된 버전으로 만들 수 있으므로 공기 역학자가 빠르고 쉬운 솔루션 범위를 사용할 수 있습니다.[21]
아음속 문제를 해결할 때 공기역학자가 결정해야 할 한 가지 사항은 압축성의 영향을 통합할 것인지 여부입니다. 압축성은 흐름의 밀도 변화량을 설명하는 것입니다. 용액에 대한 압축성의 영향이 작을 때 밀도가 일정하다는 가정을 할 수 있습니다. 문제는 비압축성 저속 공기역학 문제입니다. 밀도가 변화하도록 허용되면 흐름이 압축 가능하다고 합니다. 공기 중에서 압축성 효과는 일반적으로 흐름의 마하 수가 0.3(초당 약 335피트(102m) 또는 60°F(16°C)에서 시속 228마일(366km)을 초과하지 않을 때 무시됩니다. 마하 0.3 이상에서는 압축성 공기역학을 사용하여 문제 흐름을 설명해야 합니다.
압축공기역학
공기역학 이론에 따르면, 흐름은 유선형을 따라 밀도가 변하면 압축 가능한 것으로 간주됩니다. 이는 비압축성 흐름과는 달리 밀도의 변화를 고려한다는 것을 의미합니다. 일반적으로 흐름의 일부 또는 전부의 마하 수가 0.3을 초과하는 경우입니다. 마하 0.3 값은 다소 임의적이지만, 그 값보다 낮은 마하 수를 가진 가스 흐름은 5% 미만의 밀도 변화를 나타내기 때문에 사용됩니다. 또한, 최대 5%의 밀도 변화는 정체점(유속이 0인 물체 상의 지점)에서 발생하는 반면, 나머지 물체 주변의 밀도 변화는 현저히 낮아질 것입니다. 트랜소닉, 초음속 및 극초음속 흐름은 모두 압축 가능한 흐름입니다.
트랜소닉 플로우
트랜소닉(Transonic)이라는 용어는 국소 음속(일반적으로 마하 0.8–1.2로 간주됨) 바로 아래와 위의 유속 범위를 나타냅니다. 항공기 공기 흐름의 일부가 초음속이 될 때 임계 마하 수와 모든 공기 흐름이 초음속일 때 일반적으로 마하 1.2 근처의 더 높은 속도 사이의 속도 범위로 정의됩니다. 이 속도 사이에서 일부 공기 흐름은 초음속인 반면 일부 공기 흐름은 초음속이 아닙니다.
초음속 흐름
초음속 공기역학 문제는 음속보다 더 큰 유속과 관련된 문제입니다. 순항 중 콩코드 호의 양력을 계산하는 것은 초음속 공기역학적 문제의 예가 될 수 있습니다.
초음속 흐름은 아음속 흐름과 매우 다르게 행동합니다. 유체는 압력의 차이에 반응합니다; 압력 변화는 유체가 환경에 반응하도록 "알려지는" 방법입니다. 따라서 소리는 사실상 유체를 통해 전파되는 극소의 압력차이기 때문에 그 유체에서 음속은 흐름 속에서 '정보'가 이동할 수 있는 가장 빠른 속도라고 할 수 있습니다. 이 차이는 유체가 물체에 부딪히는 경우에 가장 명확하게 나타납니다. 그 물체 앞에서 유체는 물체와의 충격으로 움직이는 유체를 정지시킴에 따라 정체 압력을 형성합니다. 아음속으로 이동하는 유체에서 이 압력 교란은 상류로 전파되어 물체 앞의 흐름 패턴을 변화시키고, 유체가 겉보기에는 움직임을 조정하여 물체가 거기에 있다는 것을 "알고 있다"는 인상을 줍니다. 그러나 초음속 흐름에서는 압력 교란이 상류로 전파될 수 없습니다. 따라서 유체가 마침내 물체에 도달하면 유체는 물체에 부딪히고 유체는 충격파라고 불리는 극도로 격렬하고 비가역적인 방식으로 그 성질인 온도, 밀도, 압력, 마하 수를 변화시켜야 합니다. 높은 유속(레이놀즈 수 참조) 유체의 압축성 효과와 함께 충격파의 존재는 초음속과 아음속 공기역학 체제 사이의 중심적인 차이점입니다.
극초음속 흐름
공기역학에서 극초음속은 초음속이 높은 속도입니다. 1970년대에 이 용어는 일반적으로 마하 5 (음속의 5배) 이상의 속도를 나타냅니다. 극초음속 체제는 초음속 체제의 하위 집합입니다. 극초음속 흐름은 충격파 뒤의 고온 흐름, 점성 상호작용, 기체의 화학적 해리 등이 특징입니다.
관련 용어

비압축성 및 압축성 유동 체제는 경계층 및 난류와 같은 많은 관련 현상을 생성합니다.
경계층
경계층의 개념은 공기역학의 많은 문제에서 중요합니다. 공기 중의 점도와 유체 마찰은 이 얇은 층에서만 중요한 것으로 추정됩니다. 이 가정은 이러한 공기역학의 설명을 수학적으로 훨씬 더 다루기 쉽게 만듭니다.
난류
공기역학에서 난류는 흐름에 혼란스러운 특성 변화가 특징입니다. 여기에는 낮은 운동량 확산, 높은 운동량 대류, 시공간에서 압력과 유속의 급격한 변화가 포함됩니다. 난류가 아닌 흐름을 층류라고 합니다.
기타 분야의 공기역학
엔지니어링 디자인
공기역학은 차량 항력 계수를 줄이는 것이 주요 목표인 로드카와 트럭, 레이싱카를 포함한 차량 설계의 중요한 요소이며, 항력을 줄이는 것 외에도 전반적인 다운포스 수준을 높이는 것이 목표입니다.[21] 공기역학은 또한 항해하는 선박에 작용하는 힘과 모멘트를 예측하는 데 중요합니다. 하드 드라이브 헤드와 같은 기계 부품의 설계에 사용됩니다. 구조 엔지니어는 대형 건물, 교량 및 풍력 터빈의 설계에서 풍하중을 계산할 때 공기역학, 특히 공기 탄성에 의존합니다.
내부 통로의 공기역학은 가열/환기, 가스 배관 및 세부 흐름 패턴이 엔진의 성능에 강하게 영향을 미치는 자동차 엔진에서 중요합니다.
환경디자인
도시 공기역학은 도시 계획자와 설계자가 실외 공간의 편의성을 개선하거나 도시 오염의 영향을 줄이기 위해 도시 미세 기후를 만드는 데 연구합니다. 환경 공기역학 분야는 대기 순환과 비행 역학이 생태계에 영향을 미치는 방식을 설명합니다.
공기역학 방정식은 수치 기상 예측에 사용됩니다.
스포츠의 제구력
공기역학이 결정적으로 중요한 스포츠는 축구, 탁구, 크리켓, 야구, 골프 등으로 대부분의 선수가 '매그너스 효과'를 이용해 공의 궤적을 조절할 수 있습니다.
참고 항목
참고문헌
- ^ Wragg, David W. (1974). A Dictionary of Aviation (1st American ed.). New York: Frederick Fell, Inc. p. 8. ISBN 0-85045-163-9.
- ^ "How the Stork Inspired Human Flight". flyingmag.com.[영구 데드링크]
- ^ "Wind Power's Beginnings (1000 BC – 1300 AD) Illustrated History of Wind Power Development". Telosnet.com. Archived from the original on 2010-12-02. Retrieved 2011-08-24.
- ^ Berliner, Don (1997). Aviation: Reaching for the Sky. The Oliver Press, Inc. p. 128. ISBN 1-881508-33-1.
- ^ Ovid; Gregory, H. (2001). The Metamorphoses. Signet Classics. ISBN 0-451-52793-3. OCLC 45393471.
- ^ a b c Anderson, John David (1997). A History of Aerodynamics and its Impact on Flying Machines. New York, NY: Cambridge University Press. ISBN 0-521-45435-2.
- ^ Newton, I. (1726). Philosophiae Naturalis Principia Mathematica, Book II.
- ^ "Hydrodynamica". Britannica Online Encyclopedia. Retrieved 2008-10-30.
- ^ Navier, C. L. M. H. (1827). "Memoire Sur les Lois du Mouvement des fluides". Mémoires de l'Académie des Sciences. 6: 389–440.
- ^ Stokes, G. (1845). "On the Theories of the Internal Friction of Fluids in Motion". Transactions of the Cambridge Philosophical Society. 8: 287–305.
- ^ "U.S Centennial of Flight Commission – Sir George Cayley". Archived from the original on 20 September 2008. Retrieved 2008-09-10.
Sir George Cayley, born in 1773, is sometimes called the Father of Aviation. A pioneer in his field, he was the first to identify the four aerodynamic forces of flight – weight, lift, drag, and thrust and their relationship. He was also the first to build a successful human-carrying glider. Cayley described many of the concepts and elements of the modern airplane and was the first to understand and explain in engineering terms the concepts of lift and thrust.
- ^ d'Alembert, J. (1752). Essai d'une nouvelle theorie de la resistance des fluides.
- ^ Kirchhoff, G. (1869). "Zur Theorie freier Flussigkeitsstrahlen". Journal für die reine und angewandte Mathematik. 1869 (70): 289–298. doi:10.1515/crll.1869.70.289. S2CID 120541431.
- ^ Rayleigh, Lord (1876). "On the Resistance of Fluids". Philosophical Magazine. 2 (13): 430–441. doi:10.1080/14786447608639132.
- ^ Renard, C. (1889). "Nouvelles experiences sur la resistance de l'air". L'Aéronaute. 22: 73–81.
- ^ Lanchester, F. W. (1907). Aerodynamics.
- ^ Prandtl, L. (1919). Tragflügeltheorie. Göttinger Nachrichten, mathematischphysikalische Klasse, 451–477.
- ^ Ackeret, J. (1925). "Luftkrafte auf Flugel, die mit der grosser also Schallgeschwindigkeit bewegt werden". Zeitschrift für Flugtechnik und Motorluftschiffahrt. 16: 72–74.
- ^ "공기역학의 이해: 실제 물리학의 논쟁" 더그 맥린 존 와일리 & 손스, 2012 장 3.2 "NS 방정식을 구성하는 주요 관계는 질량, 운동량 및 에너지에 대한 기본 보존 법칙입니다. 완전한 방정식을 설정하려면 온도, 압력 및 밀도와 관련된 상태 방정식도 필요합니다.." https://play.google.com/books/reader?id=_DJuEgpmdr8C&printsec=frontcover&pg=GBS.PA191.w.0.0.0.151
- ^ a b Katz, Joseph (1991). Low-speed aerodynamics: From wing theory to panel methods. McGraw-Hill series in aeronautical and aerospace engineering. New York: McGraw-Hill. ISBN 0-07-050446-6. OCLC 21593499.
추가읽기
일반 공기역학
- Anderson, John D. (2007). Fundamentals of Aerodynamics (4th ed.). McGraw-Hill. ISBN 978-0-07-125408-3. OCLC 60589123.
- Bertin, J. J.; Smith, M. L. (2001). Aerodynamics for Engineers (4th ed.). Prentice Hall. ISBN 0-13-064633-4. OCLC 47297603.
- Smith, Hubert C. (1991). Illustrated Guide to Aerodynamics (2nd ed.). McGraw-Hill. ISBN 0-8306-3901-2. OCLC 24319048.
- Craig, Gale (2003). Introduction to Aerodynamics. Regenerative Press. ISBN 0-9646806-3-7. OCLC 53083897.
아음속 공기역학
- Katz, Joseph; Plotkin, Allen (2001). Low-Speed Aerodynamics (2nd ed.). Cambridge University Press. ISBN 0-521-66552-3. OCLC 43970751.
- 오버트, 에드 (2009). 구글 북스의 수송기의 공기역학적 설계. 델프트(Delft); 산업의 실용적인 공기역학과 항공기 설계에 미치는 영향에 대해. ISBN 978-1-58603-970-7.
트랜스오닉 공기역학
- Moulden, Trevor H. (1990). Fundamentals of Transonic Flow. Krieger Publishing Company. ISBN 0-89464-441-6. OCLC 20594163.
- Cole, Julian D; Cook, L. Pamela (1986). Transonic Aerodynamics. North-Holland. ISBN 0-444-87958-7. OCLC 13094084.
초음속 공기역학
- Ferri, Antonio (2005). Elements of Aerodynamics of Supersonic Flows (Phoenix ed.). Dover Publications. ISBN 0-486-44280-2. OCLC 58043501.
- Shapiro, Ascher H. (1953). The Dynamics and Thermodynamics of Compressible Fluid Flow, Volume 1. Ronald Press. ISBN 978-0-471-06691-0. OCLC 11404735.
- Anderson, John D. (2004). Modern Compressible Flow. McGraw-Hill. ISBN 0-07-124136-1. OCLC 71626491.
- Liepmann, H. W.; Roshko, A. (2002). Elements of Gasdynamics. Dover Publications. ISBN 0-486-41963-0. OCLC 47838319.
- von Mises, Richard (2004). Mathematical Theory of Compressible Fluid Flow. Dover Publications. ISBN 0-486-43941-0. OCLC 56033096.
- Hodge, B. K.; Koenig K. (1995). Compressible Fluid Dynamics with Personal Computer Applications. Prentice Hall. ISBN 0-13-308552-X. OCLC 31662199.
극초음속 공기역학
- Anderson, John D. (2006). Hypersonic and High Temperature Gas Dynamics (2nd ed.). AIAA. ISBN 1-56347-780-7. OCLC 68262944.
- Hayes, Wallace D.; Probstein, Ronald F. (2004). Hypersonic Inviscid Flow. Dover Publications. ISBN 0-486-43281-5. OCLC 53021584.
공기역학의 역사
- Chanute, Octave (1997). Progress in Flying Machines. Dover Publications. ISBN 0-486-29981-3. OCLC 37782926.
- von Karman, Theodore (2004). Aerodynamics: Selected Topics in the Light of Their Historical Development. Dover Publications. ISBN 0-486-43485-0. OCLC 53900531.
- Anderson, John D. (1997). A History of Aerodynamics: And Its Impact on Flying Machines. Cambridge University Press. ISBN 0-521-45435-2. OCLC 228667184.
공학 관련 공기역학
지상 차량
- Katz, Joseph (1995). Race Car Aerodynamics: Designing for Speed. Bentley Publishers. ISBN 0-8376-0142-8. OCLC 181644146.
- Barnard, R. H. (2001). Road Vehicle Aerodynamic Design (2nd ed.). Mechaero Publishing. ISBN 0-9540734-0-1. OCLC 47868546.
고정익 항공기
- Ashley, Holt; Landahl, Marten (1985). Aerodynamics of Wings and Bodies (2nd ed.). Dover Publications. ISBN 0-486-64899-0. OCLC 12021729.
- Abbott, Ira H.; von Doenhoff, A. E. (1959). Theory of Wing Sections: Including a Summary of Airfoil Data. Dover Publications. ISBN 0-486-60586-8. OCLC 171142119.
- Clancy, L.J. (1975). Aerodynamics. Pitman Publishing Limited. ISBN 0-273-01120-0. OCLC 16420565.
헬리콥터
- Leishman, J. Gordon (2006). Principles of Helicopter Aerodynamics (2nd ed.). Cambridge University Press. ISBN 0-521-85860-7. OCLC 224565656.
- Prouty, Raymond W. (2001). Helicopter Performance, Stability, and Control. Krieger Publishing Company Press. ISBN 1-57524-209-5. OCLC 212379050.
- Seddon, J.; Newman, Simon (2001). Basic Helicopter Aerodynamics: An Account of First Principles in the Fluid Mechanics and Flight Dynamics of the Single Rotor Helicopter. AIAA. ISBN 1-56347-510-3. OCLC 47623950.
미사일
- Nielson, Jack N. (1988). Missile Aerodynamics. AIAA. ISBN 0-9620629-0-1. OCLC 17981448.
모형 항공기
- Simons, Martin (1999). Model Aircraft Aerodynamics (4th ed.). Trans-Atlantic Publications, Inc. ISBN 1-85486-190-5. OCLC 43634314.
공기역학 관련 분야
공기열역학
- Hirschel, Ernst H. (2004). Basics of Aerothermodynamics. Springer. ISBN 3-540-22132-8. OCLC 228383296.
- Bertin, John J. (1993). Hypersonic Aerothermodynamics. AIAA. ISBN 1-56347-036-5. OCLC 28422796.
공기탄성
- Bisplinghoff, Raymond L.; Ashley, Holt; Halfman, Robert L. (1996). Aeroelasticity. Dover Publications. ISBN 0-486-69189-6. OCLC 34284560.
- Fung, Y. C. (2002). An Introduction to the Theory of Aeroelasticity (Phoenix ed.). Dover Publications. ISBN 0-486-49505-1. OCLC 55087733.
경계층
- Young, A. D. (1989). Boundary Layers. AIAA. ISBN 0-930403-57-6. OCLC 19981526.
- Rosenhead, L. (1988). Laminar Boundary Layers. Dover Publications. ISBN 0-486-65646-2. OCLC 17619090.
난류
- Tennekes, H.; Lumley, J. L. (1972). A First Course in Turbulence. The MIT Press. ISBN 0-262-20019-8. OCLC 281992.
- Pope, Stephen B. (2000). Turbulent Flows. Cambridge University Press. ISBN 0-521-59886-9. OCLC 174790280.
외부 링크
- 2012-07-15 Wayback Machine에 보관된 NASA 공기역학 입문 안내서
- 학생용 공기역학
- 조종사용 공기역학
- 공기역학 및 경주용 자동차 튜닝
- 2018-12-13 Wayback Machine에 보관된 공기역학 관련 프로젝트
- 유체 자전거 공기역학
- 화학식 1의 공기역학적 적용 (F1)
- 2009-12-06 Wayback Machine에 보관된 자동차 경주의 공기역학
- 2010-03-24 Wayback Machine에 보관된 조류의 공기역학
- NASA 공기역학 지수

