A
「A」の基本的な意味
「A」は英語などで使われるアルファベット(ラテン文字)の1番最初の文字にあたり、小文字は「a」と表記し共に「エイ」と読む。英単語としては主に「a book(1冊の本)」「a day(1日)」という具合に「1つ」であるということを表す不定冠詞として用いられる。また成績や等級などのように何か順序を付ける時には「A,B,C」という具合に「第1位」「最上位」という意味で用いられることもある(これは日本でもしばしばみられる)。また音楽においては英米やドイツでは「ラ」「シ」「ド」「レ」「ミ」「ファ」「ソ」の順に「A」「B」「C」「D」「E」「F」「G」の名称で音名を割り当てている(ドレミファソラシドはイタリア語 )。また「Q&A」などという言うように単体で「Answer(答え)」のことを表す他、「A/B testing(A/Bテスト)」などと言うように表/裏の2択ある状況での「表」を表すこともある。またトランプにおいてはace(エース)のことを「A」と表記する他、その際にエースの絵柄が最も役の高いカードとして使用されるようになったところから転じて、「サービスエース(テニス)」「エースパイロット」という具合に秀でていることを表すのに「エース」がしばしば用いられる。なお、日本では「A=キス」「B=ペッティング」という具合に、キスの隠語として使われることがあるが、英語圏では「X」がキスの隠語として一般的には用いられる。アー【(ドイツ)A/a】
エイ【A/a】
読み方:えい
⇒エー
エー【A/a】
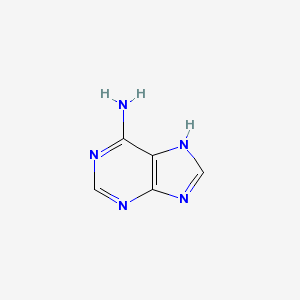
アデニン
| 化合物名や化合物に関係する事項: | アセトシリンゴン アセトン アゾ基 アデニン アデニンアラビノシド アデニンヌクレオチド アデニン環 |
A
ベンゾ(a)ピレン(C20H12)
A
出典: フリー百科事典『ウィキペディア(Wikipedia)』 (2025/01/02 16:17 UTC 版)
Aは、ラテン文字(アルファベット)の1番目の文字。小文字は「a」。
- 1 Aとは
- 2 Aの概要
A (阿部義晴のアルバム)
((A) から転送)
出典: フリー百科事典『ウィキペディア(Wikipedia)』 (2024/06/20 16:31 UTC 版)
『Ⓐ』は、阿部義晴(現・ABEDON)のソロ1枚目のアルバム。1994年11月2日にSony Recordsより発売された。
- 1 A (阿部義晴のアルバム)とは
- 2 A (阿部義晴のアルバム)の概要
- 3 概要
- 4 参考資料
A*
出典: フリー百科事典『ウィキペディア(Wikipedia)』 (2023/04/17 16:11 UTC 版)
A*(A-star、エースター)探索アルゴリズム(エースターたんさくアルゴリズム)は、グラフ探索アルゴリズムの一つ。 最良優先探索を拡張したZ*に、さらにf値として「現時点までの距離」g と「ゴールまでの推定値」h の和を採用したもの[1]。h は ヒューリスティック関数と呼ばれる。
概要
A* アルゴリズムは、「グラフ上でスタートからゴールまでの道を見つける」というグラフ探索問題において、 ヒューリスティック関数 h(n) という探索の道標となる関数を用いて探索を行うアルゴリズムである。h は各頂点 n からゴールまでの距離のある妥当な推定値を返す関数で、解くグラフ探索問題の種類に応じてさまざまな h を設計することが出来る。 例えば、カーナビなどで用いられる単純な二次元の地図での探索では、h としてユークリッド距離 を使うことができ、この値は道に沿った実際の距離のおおまかな予測になっている。しかし、高次元空間でのグラフ探索を効率的に行うためには、より高度に設計された関数を用いる必要がある。例えば、15パズルにおいてはマンハッタン距離やパターンデータベース、STRIPSプランニングにおいてはFFヒューリスティック[2]、Merge-and-Shrink[2]、Landmark-Cut[3] などがある。
A* アルゴリズムは、ダイクストラ法を推定値付きの場合に一般化したもので、h が恒等的に 0 である場合はもとのダイクストラ法に一致する。
A* の探索効率は h の正確さに左右される。 もしも h がまったくでたらめな値を返すならば、探索はゴールとはあさっての方向に進んでしまい、現実的な時間内(一時間、一週間、一年)では解を発見できない場合がある。しかし、いくらおかしな方向に探索が進んだとしても、いつかは必ず解を発見できる保証がある(完全性)。 一方、h が常に正しい値 h* を返す場合、計算機は「迷うこと無く=分岐をすること無く」グラフ上の最短経路を発見することができる。そのような h のことを、パーフェクト・ヒューリスティクスとよぶ[4]。 現実に用いられる有用な h は、これらの中間の位置にある。
歴史
A* アルゴリズムは1968年に Peter E. Hart、Nils J. Nilsson、Bertram Raphael の三人が発表した論文[5]の中で最初に記述された。A* というこの一風変わった名前は、この論文でスタートからゴールまでの最短経路を確実に見つけるアルゴリズムを許容的(英: admissible)と呼び、論文の数式中に 許容的なアルゴリズムの集合を A と表し、そのAの中でも評価回数が最適になる物を A* と表記していたためである[6]。
A*の考え方
スタートノードから、あるノード n を通って、ゴールノードまでたどり着くときの最短経路を考える。このときこの最短経路のコストを f* (n) とおくと、
- f* (n)= g* (n) + h* (n)
と置くことが出来る。ここで g* (n) はスタートノードから n までの最小コスト、h* (n) は n からゴールノードまでの最小コストである。もし g* (n) の値と h* (n)の値を知っていれば、全体の最短経路 f* (n) は容易に求まる。しかしながら実際には g* (n) と h* (n) をあらかじめ与えることは出来ない。そこで f* (n) を次のような推定値 f (n) に置き換えることを考える。
ここで g(n) はスタートノードから n までの最小コストの推定値、h(n) は n からゴールノードまでの最小コストの推定値である。この場合 g に関しては探索の過程で更新を加えることにより g* に近づけてゆくことができるが、h* は、実際にゴールに辿り着くまでは誰にもわからない。そこで、h(n) には人間が(ある程度妥当性を持つように)設計した推定値を与えることにする。このアルゴリズムを A*探索アルゴリズムといい、h (n) をヒューリスティック関数という。
アルゴリズムの流れ
A* のアルゴリズムの実装を以下に示す。この OPENリスト実装は後に述べるように遅いことを記しておく。
- スタートノード()を作成する。また計算中のノードを格納しておくための優先度付きキュー OPENリストと、計算済みのノードを格納しておくCLOSEリストを用意する。(名前は「リスト」だが、これらの実際のデータ構造は必ずしも連結リストである必要はない。)
- ゴールは必ずしも1つである必要はないので、ゴール条件を満たすノード集合を と呼ぶことにする。
- スタートノードを Openリストに追加する、このとき = であり = となる。また Closeリストは空にする。
- Openリストが空なら探索は失敗とする(スタートからゴールにたどり着くような経路が存在しなかったことになる)。
- Openリストに格納されているノードの内、最小の を持つノード を1つ取り出す。同じ を持つノードが複数ある場合、タイブレーク手法によりどれかのノードを選択する。
- であるなら探索を終了する。それ以外の場合は を Close リストに移す。
- に隣接している全てのノード(ここでは隣接ノードを とおく)に対して以下の操作を行う
- を計算する、ここで はノード n から m へ移動するときのコストである。また は で求めることができる。
- m の状態に応じて以下の操作を行う
- m が Openリストにも Closeリストにも含まれていない場合 とし m を Openリストに追加する。このとき m の親を n として記録する。
- m が Openリストにある場合、 であるなら、m を Open から削除し、 に置き換え、再び Open に挿入する(Open が正しくソートされていることを保証するため)。また、記録してある m の親を n に置き換える。
- m が Closeリストにある場合、 であるなら として m を Openリストに移動する。また記録してある m の親を n に置き換える。
- 3 以降を繰り返す。
- 探索終了後、発見されたゴール から親を順次たどっていくと S から ゴール までの最短経路が得られる。
以上の流れを見れば、アルゴリズムが手続き的で、並列化が非常に難しいことがわかる。しかし、近年では HDA*[7]、PBFS などの並列手法が開発され、特に HDA* は768コア以上の大規模並列計算環境にもスケールすることが実証されている。
実際に使われているOPEN/CLOSEリストの実装
OPEN/CLOSEリストに登録されているノードの数が多い場合、ノードの展開ごとに子ノード m をOPENから CLOSE へ移動(あるいは逆)するのは非常に高価な操作である。 たとえば、OPEN/CLOSEリストが2分探索木(赤黒木など)で実装されている場合、まずノードの探すのに かかり(ノードのIDで検索)、また削除にも かかる。配列の場合には削除により大きなコストがかかる。
しかし、データ構造を工夫することで、より効率よい実装を行うことが出来る。ノードを OPEN/CLOSEリスト間で行ったり来たりさせる代わりに、以下のように実装する[8]:
- それぞれのノードに、ノードの状態として OPEN, CLOSE の2種類のタグをもたせる。全てのノードは始めOPENである。
- ノードに一意な整数 ID をもたせる。
- また、ID からノードを で参照できるハッシュテーブルを用意する。
- OPEN にノードを追加する際には、m が Openリストに含まれているかは検証せず、重複を許して追加する。かつ、このときノードではなく ID のみを追加する。
- ID は整数1つ分なので、重複のオーバーヘッドを最小化出来る。
- OPEN からノードを pop する際、pop したノードの状態が OPEN であれば展開を行うが、CLOSE であれば単にスキップする。
- CLOSEリストは使用しない。
- f値による優先度付きキューは、辺のコストが1である場合には単にf値ごとの可変配列にしたほうが高速な操作が可能である。
- 辺のコストに大幅なばらつきがある場合には、ヒープとして実装したほうがよい。
性質
A* の性質は h の性質によって大きく左右される。
- A* はダイクストラの一般化であり、ダイクストラと同様、グラフに負のコストの辺があれば完全性を失う。その場合にはベルマン–フォード法を用いる。
- h(n) は常に非負でなくてはならない。
- あるヒューリスティクス h(n) が 全てのノード n について 真のゴール距離 h*(n) を上回らない場合、h は Admissible/許容的であると言う。
このとき、A*の返す経路は最適、つまり最短経路である。
- あるヒューリスティクス h(n) について、全てのノード n と、それに隣接しているノード m について である場合、その h はconsistent/無矛盾であるという。
- consistent な h は、常に admissible である[9]。
- ある2つのヒューリスティック関数 h1, h2 について、 が成り立つ時、 h2 は h1 を支配する (dominate) とよぶ。このとき、特に両者が許容的な場合、h2 を用いた探索はより効率的だろうと考えられている。しかし、いくつかのコーナーケースではこのことは成り立たない[10]。
このアルゴリズムはCPUの使用率、メモリの使用率など、計算負荷は高いが、問題に応じた適切なヒューリスティック関数を用いることにより、問題に対しての最適化が可能である。
部分問題に分割する場合
分割統治法のように、部分問題に分割したうえで全体問題を解いた方が効率的な問題もある。A* 同様の通常の状態遷移はどれかがゴールに到達すれば良いので OR と呼び、部分問題に分割する場合は全ての部分問題が解けないといけないので AND と呼ぶと、探索木が AND/OR 木になる。AND で状態を分割する際、ゴールも分割する必要がある。
同じ状態が2度出現した場合に1つのノードにまとめると AND/OR グラフになる。閉路のない AND/OR グラフに対する A* アルゴリズムに対応する物が1968年に開発され[11]、1980年に AO*アルゴリズム と命名された[6]。閉路のある AND/OR グラフに対する A* アルゴリズムに対応する A0アルゴリズム は1976年に開発された[12]。AND ノードのコストを「辺のコスト+部分問題のコストの最大値」や「辺のコスト+部分問題のコストの総和」などの単調非減少関数で定義すると[13]、ヒューリスティック関数が許容的であれば、A* 同様、最適解が求まる。なお、閉路のない AND/OR グラフは文脈自由文法(タイプ-2 文法)[14]、閉路のある AND/OR グラフは制限のない文法(タイプ-0 文法)に1対1対応することが証明されている。
関連項目
参照
- ^ Pearl, Judea (1984) (English). "Heuristics intelligent search strategies for computer problem solving". Addison-Wesley. ISBN 0201055945
- ^ a b Hoffmann, Jörg, and Bernhard Nebel. "The FF planning system: Fast plan generation through heuristic search." Journal of Artificial Intelligence Research (2001): 253-302.
- ^ Helmert, Malte, and Carmel Domshlak. "Landmarks, critical paths and abstractions: what's the difference anyway?." ICAPS. 2009.
- ^ How Good is Almost Perfect?. M Helmert, G Röger - AAAI, 2008
- ^ Peter E. Hart; Nils J. Nilsson; Bertram Raphael (July 1968). “A Formal Basis for the Heuristic Determination of Minimal Cost Paths”. IEEE Transactions on Systems Science and Cybernetics 4 (2): 100-107. doi:10.1109/TSSC.1968.300136. ISSN 0536-1567.
- ^ a b Nils J. Nilsson 著、白井良明, 辻井潤一, 佐藤泰介 訳『人工知能の原理』日本コンピュータ協会、1983年1月15日(原著1980年)。ISBN 4-88917-026-X。
- ^ Kishimoto, Akihiro, Alex S. Fukunaga, and Adi Botea. "Scalable, Parallel Best-First Search for Optimal Sequential Planning." ICAPS. 2009.
- ^ Burns, E. A., Hatem, M., Leighton, M. J., & Ruml, W. (2012, July). Implementing fast heuristic search code. In Fifth Annual Symposium on Combinatorial Search. https://www.aaai.org/ocs/index.php/SOCS/SOCS12/paper/view/5404/5173
- ^ Russel, Norvig, Artificial intelligence: a modern approach
- ^ Robert C. Holte. Common Misconceptions Concerning Heuristic Search, SoCS 2010
- ^ Nils J. Nilsson (August 1968). “Searching problem-solving and game-playing trees for minimal cost solutions”. Information Processing 68 : proceedings of IFIP Congress 1968 (Amsterdam : North-Holland) 2: 1556-1562.
- ^ Giorgio Levi; Franco Sirovich (January 1976). “Generalized and/or graphs”. Artificial Intelligence 7 (3): 243-259. doi:10.1016/0004-3702(76)90006-0.
- ^ Vipin Kumar; Dana S. Nau; Laveen N. Kanal (August 1985). A General Paradigm for AND/OR Graph and Game Tree Search.
- ^ Patrick A. V. Hall (July 1973). “Equivalence between AND/OR graphs and context-free grammars”. Communications of the ACM 16 (7): 444-445. doi:10.1145/362280.362302.
A+
α (欠性辞)
A(2013年-2015年)
出典: フリー百科事典『ウィキペディア(Wikipedia)』 (2021/04/07 22:31 UTC 版)
「ニコン COOLPIX」の記事における「A(2013年-2015年)」の解説
ニコンで初めてのDXフォーマットを搭載したハイエンド機種。後継機種が登場しないまま製造が終了した。 品名発売日撮像素子サイズ画素数外観解説A 2013年3月21日 DXフォーマット23.6×15.6mm 1616万画素 Coolpix初のDXフォーマットを搭載した機種。レンズは35ミリ換算で28mm相当の単焦点レンズを搭載。
※この「A(2013年-2015年)」の解説は、「ニコン COOLPIX」の解説の一部です。
「A(2013年-2015年)」を含む「ニコン COOLPIX」の記事については、「ニコン COOLPIX」の概要を参照ください。
「( ・A・)」の例文・使い方・用例・文例
- 彼女は今朝早く緊急虫垂切除(術)を受けた。
- 空中給油機は給油中に吹き流しの空中曳航(えいこう)標的をつるす。
- オルガスム(ス)の声をあげる
- その商社はターボプロップ(航空)機市場が拡大すると見込んでいる。
- アルコールの突然の摂取は無血管(性)壊死と呼ばれる状態をもたらす可能性がある。
- ヨム・キプル(ユダヤ教の贖罪の日)はショファーの音とともに終わってしまった。
- 4Pの要素は、売り手側の視点に基づいた製品(Product)、価格(Price)、販売促進(Promotion)、販売ルート(Place)である。
- タックマンモデルとは、チームビルディングにおける5段階、すなわち形成(Forming)、混乱(Storming)、統一(Norming)、機能(Performing)、散会(Adjourning)を示すモデルである。
- ヘッドアンドショルダーズは投資家にとって最も信頼度の高いフォーメーション(株価動向)のひとつだ。
- 典型的なマネジメントサイクルとしてPDCA (計画・実行・検証・改善)が有名です。
- マネジメントバイアウト(MBO)は一種のM&Aだ。
- マネー・マーケット・アカウント(MMA/金融市場預金口座)
- リフレレーション政策(リフレ政策:景気刺激策)
- エコノミック・ リベラリズム(経済自由主義)
- 銘柄コードやアイジンコードなどの証券コードは証券コード協議会(SICC)により付番されている。
- (表示を)よく確認していなかったため、目的地とは反対側の改札口から出てしまった。
- (私は)授業後、友人を待った。
- (私は)コーチにしごかれた。
- あなたの特別な日にキスとハグがあげられるように(私は)そこにいた
- 話を読みなさい。ページの下部にある「聴く(“listen”)」ボタンをクリックして話を聞きなさい。
Weblioカテゴリー/辞書と一致するものが見つかりました。
- M&A用語集 - 株式会社ストライク
(A)と同じ種類の言葉
固有名詞の分類
- (A)のページへのリンク