Multiplikasjon av naturlige tall er det samme som å addere dem (legge dem sammen) gjentatte ganger. Eksempel, som også vist i illustrasjon 1:
Dette regnestykket kan for eksempel knyttes til denne situasjonen: Fire barn har tre appelsiner hver. Hvor mange appelsiner har disse barna totalt?
I en multiplikasjon spiller det ingen rolle hvilken rekkefølge faktorene står i. 3·4 er det samme som 4·3. Det vil si at multiplikasjon oppfyller den kommutative loven. Dette uttrykkes ofte som at «Faktorenes orden er likegyldig». Se illustrasjon 2.
Faktoren 3 i eksempelet over kalles også for multiplikand, og faktoren 4 kalles multiplikator. Her er altså multiplikasjon definert slik at multiplikanden står først, og multiplikatoren står sist. Det er også mulig å definere multiplikasjon slik at multiplikatoren står først, og multiplikanden står sist. Da vil 3·4 være definert som 3 grupper av 4, i stedet for 4 grupper av 3. Begge variantene finnes i bruk, og begge variantene dukker også opp i vitenskapelige forsøk på å bygge opp matematikken fra grunnen (der multiplikasjon defineres som gjentatt addisjon).
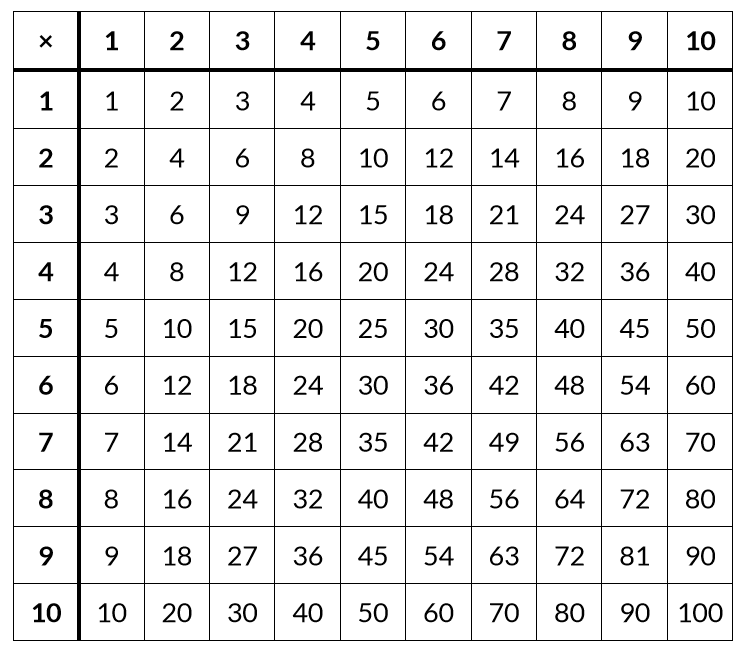
Den lille multiplikasjonstabellen (også kalt gangetabellen) inneholder alle produkter av to ensifrede tall. Tegnet × for multiplikasjon ble først brukt av William Oughtred.



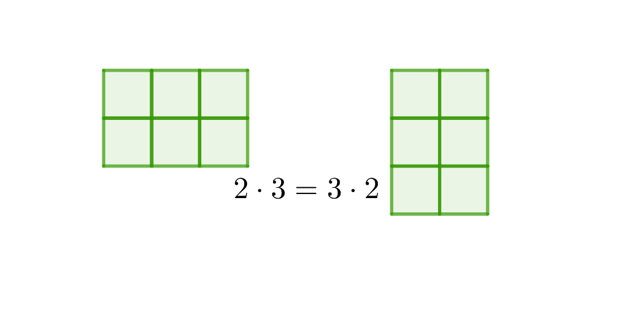


Kommentarer
Kommentarer til artikkelen blir synlig for alle. Ikke skriv inn sensitive opplysninger, for eksempel helseopplysninger. Fagansvarlig eller redaktør svarer når de kan. Det kan ta tid før du får svar.
Du må være logget inn for å kommentere.