Beispiele für Vektorräume
(320)
-
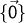 mit
mit  und
und  ist ein
ist ein  -Vektorraum.
-Vektorraum.
-
 ist ein
ist ein  -Vektorraum
-Vektorraum
- Analog ist
 ein
ein  -Vektorraum mit komponentenweiser Addition und
Skalarmultiplikation. Auch ist
-Vektorraum mit komponentenweiser Addition und
Skalarmultiplikation. Auch ist  ein
ein  -Vektorraum.
-Vektorraum.
- Sei
 eine nicht leere Menge, und sei
eine nicht leere Menge, und sei  die Menge
aller Abbildungen von
die Menge
aller Abbildungen von  mit Werten in
mit Werten in  . Definiere für
. Definiere für  und
und 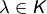

Dann wird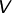 dadurch zu einem
dadurch zu einem  -Vektorraum.
-Vektorraum.
Das neutrale Element der Addition ist die Nullabbildung, die jedes Element aus auf
auf 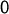 abbildet,
abbildet,
 .
.
Die zu inverse Abbildung ist
inverse Abbildung ist

Dass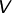 ein
ein  -Vektorraum ist, zeigt man durch Rückführung auf die
entsprechenden Vektorraumeigenschaften von
-Vektorraum ist, zeigt man durch Rückführung auf die
entsprechenden Vektorraumeigenschaften von  .
Wir nennen
.
Wir nennen  einen Funktionenraum mit Werten in
einen Funktionenraum mit Werten in
 und bezeichnen diesen Vektorraum auch als
und bezeichnen diesen Vektorraum auch als
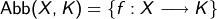
- Ist allgemeiner
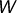 ein
ein  -Vektorraum und
-Vektorraum und 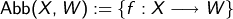
so ist analog wie oben ein
analog wie oben ein  -Vektorraum. Speziell nennen wir für
-Vektorraum. Speziell nennen wir für  und
und  den Vektorraum
den Vektorraum
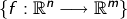 den Raum
der vektorwertigen
Funktionen in
den Raum
der vektorwertigen
Funktionen in  Veränderlichen.
Veränderlichen.
-
 ist ein
ist ein 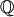 -Vektorraum, wie aus den Körpereigenschaften von
-Vektorraum, wie aus den Körpereigenschaften von  folgt. Ebenso ist
folgt. Ebenso ist 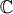 ein
ein  -Vektorraum und ein
-Vektorraum und ein 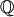 -Vektorraum.
Allgemein gilt: Ist
-Vektorraum.
Allgemein gilt: Ist  ein Körper, der
ein Körper, der  als "Teilkörper" enthält, so
ist
als "Teilkörper" enthält, so
ist  ein
ein  -Vektorraum.
-Vektorraum.