Untervektorräume
Definition.
Sei  ein
ein 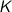 -Vektorraum.
Eine Teilmenge
-Vektorraum.
Eine Teilmenge  von
von  heißt Teilraum oder
Untervektorraum von
heißt Teilraum oder
Untervektorraum von  , wenn folgendes gilt:
, wenn folgendes gilt:
- (UV1)

 enthält mindestens ein Element
enthält mindestens ein Element
- (UV2)

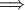

 ist abgeschlossen
gegenüber der Addition
ist abgeschlossen
gegenüber der Addition
- (UV3)
 und
und 
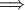

 ist abgeschlossen bezüglich der Skalarmultiplikation
ist abgeschlossen bezüglich der Skalarmultiplikation
Ein Teilraum  von
von  ist selbst ein
ist selbst ein 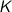 -Vektorraum.
-Vektorraum.
Beweis.
Wir müssen nur prüfen, dass  und dass mit
und dass mit  auch
auch
 ist. Alle anderen Vektorraumaxiome sind dann erfüllt, da sie in
ist. Alle anderen Vektorraumaxiome sind dann erfüllt, da sie in
 gelten.
gelten.
Nach (UV1) gibt es ein  und es folgt:
und es folgt:

Für beliebiges gilt:
gilt:

Für beliebiges