Definition und Rechenregeln
und zusätzlich ist eine
Skalarmultiplikation
gegeben derart, dass die folgenden Regeln gelten:
 -Vektorraumes nennen wir auch
Vektoren. Statt
-Vektorraumes nennen wir auch
Vektoren. Statt
 -Vektorraum sagen wir auch Vektorraum über
-Vektorraum sagen wir auch Vektorraum über
 .
.
- (SM1)
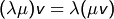 für alle
für alle  ,
,

- (SM2)
 für alle
für alle 
- (D1)
 für alle
für alle  ,
, 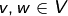
- (D2)
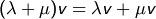 für alle
für alle 
Rechenregeln in Vektorräumen
Sei ein
ein  -Vektorraum. Das neutrale Element der Addition in
-Vektorraum. Das neutrale Element der Addition in  bezeichnen wir mit
bezeichnen wir mit  und nennen diesen Vektor den
Nullvektor.
Wir schreiben
und nennen diesen Vektor den
Nullvektor.
Wir schreiben  für das Inverse von
für das Inverse von  . Nach (G3) und Satz,
folgen
. Nach (G3) und Satz,
folgen
Sei
für alle 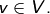 Es gilt ferner
Es gilt ferner
Es folgen die Regeln:
- Für das neutrale Element der Addition
 ist
ist 
-
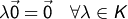
-

Beweis.
-
Es ist
 . Addition von
. Addition von 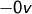 ergibt
ergibt  .
.
-
Es ist
 . Addition von
. Addition von  ergibt
ergibt
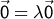 .
.
-
Es ist
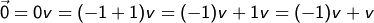 , also
, also
 .
.
Geometrische Anschauung
Sei und
und 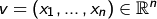 . Dann ist
. Dann ist
Sei

Für beliebiges 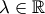 ist
ist  Ist
Ist  , so ist
, so ist  Beispiel in
Beispiel in  :
:  Ist
Ist  , so sind
, so sind  und
und  "linear abhängig". Ist
"linear abhängig". Ist  nur für
nur für  möglich, so
sind
möglich, so
sind  und
und  "linear unabhängig".
"linear unabhängig".