Syllogismi

Syllogismi (kreik. συλλογισμό, syllogismos ’johtopäätös, päätelmä’) on loogisen argumentin tyyppi, jossa kahdesta tai useammasta, todeksi oletetusta lauseesta johdetaan deduktiivisen päättelyn avulla niistä loogisesti seuraava johto­päätös.

Varhaisimmassa muodossaan, jonka määritteli Aristoteles, syllogismissa oli lähtö­kohtana yleinen lause (pääpremissi) ja merkitykseltään suppeampi lause (alipremissi), joista tehtiin päätelmä. Esimerkiksi kun tiedetään, että kaikki ihmiset ovat kuolevaisia (pääpremissi) ja että Sokrates on ihminen (alipremissi), voidaan pätevästi päätellä, että Sokrates on kuolevainen. Syllo­gisti­set päätelmät on tapana esittää kolmella allek­kai­sella rivillä seuraavaan tapaan; lauseiden lopusta jätetään tällöin usein pisteet pois:

Kaikki ihmiset ovat kuolevaisia

Sokrates on ihminen

Siis Sokrates on kuolevainen

Varhaishistoria

Antiikin aikana oli kaksi kilpailevaa syllogismien teoriaa: aristotelinen syllogis­tiikka ja stoalainen syllogis­tiikka. Aristoteles määritteli syllogismin "... päätelmäksi, jossa joistakin asetetuista väittämistä seuraa jotakin muuta kuin ne, koska ne ovat nämä."

Tästä hyvin yleisestä määritelmästä huolimatta Aristoteles rajoittuu teoksessaan Ensimmäinen analytiikka kategorisiin syllogismeihin, jotka muodostuvat kolmesta kategorisesta väittämästä. Näihin sisältyvät kategoriset modaaliset syllogismit.

Keskiajalta lähtien termejä kategorinen syllogismi ja syllogismi käytettiin yleensä samassa merkityksessä. Tämä artikkeli käsittelee syllogismeja vain tässä perinteisessä merkityksessä. Syllogismit muodostivat perinteisen deduk­tiivisen päättelyn ytimen, jossa tosi­asiat määritellään yhdistämällä jo olemassa olevia lauseita, päin­vastoin kuin induk­tiivisessa päättelyssä, jossa tosiasiat määritellään toistuvien havaintojen avulla.

Akateemisissa yhteyksissä syllogismin syrjäytti ensimmäisen asteen predikaatti­logiikka, jonka kehitti Gottlob Frege varsinkin teoksessaan Begriffsschrift (1879), mutta syllogismit ovat yhä hyödyllisiä joissakin yhteyksissä, ja niitä käytetään edelleen myös yleis­tajuisissa johdatuksissa logiikkaan.

Aristoteles

Pääartikkeli: Aristotelinen logiikka

Syllogismien käytön ymmärryksen apuvälineenä voidaan katsoa saaneen alkunsa Aristoteleen logiikkaa käsittelevistä tutkielmista. Ennen 1100-luvun puoliväliä keskiajan loogikot tunsivat vain osan Aristoteleen teoksista, muun muassa teokset Kategoriat ja Tulkinnasta, jotka vaikuttivat mitä suurimmassa määrin tuolloin vallinneeseen vanhaan logiikkaan ("logica vetus"). Uusi logiikka ("logica nova") sai alkunsa, kun teos Ensimmäinen analytiikka, jossa Aristoteles esitti syllogismien teoriansa, jälleen löydettiin.

Kun Ensimmäinen analytiikka jälleen löydettiin, loogikot alkoivat heti pitää sitä "alan suljettuna ja täydellisenä perus­teoksena", joka jätti aikakauden ajattelijoille kovin vähän väittelyn ja uudelleen­järjestelyn sijaa. Aristoteleen teoriaa väitelauseiden syllogismeista pidettiin erityisen merkittävänä, ja aikojen kuluessa siihen tehtiin vain vähän muutoksia. Teoriaa ei liitetty yleisempään seurausl­ogiikkaan ennen kuin 1300-luvun puoli­välissä, jolloin muun muassa Jean Buridan kehitti logiikkaa pidemmälle.

Aristoteleen Ensimmäiseen analytiikka ei kuitenkaan sisältänyt selvää modaalisia syllogismeja koskevaa teoriaa. Modaalinen syllogismi on päätelmä, jossa ainakin jompaan­kumpaan premissiin liittyy modaalinen määrite kuten mahdollisesti, välttämättä tai varmasti. Tältä osin Aristoteleen termino­logia oli puutteellinen ja varsin epäselvä ja osittain risti­riidassakin sen kanssa, mitä hän oli kirjoittanut teoksessaan Tulkinnasta. Mitä hän kirjoitti tästä aiheesta, antoi aihetta laajaan keskusteluun, jota kommentoijat ovat jatkaneet nykyaikaan saakka. Aristoteleen oppia modaalisista syllogismeista alettiinkin lopulta pitää käytäntöön soveltumattomana, ja sen ovat korvanneet kokonaan uudet teoriat.

Keskiajan oppineet

Boethius

Boethius (noin 475–526) yritti saattaa Aristoteleen logiikan laajempien piirien ulottuville. Hän käänsi Ensimmäisen analytiikan latinaksi, mutta tämä käännös jäi lähes tunte­matto­maksi 1100-luvulle saakka. Sen sijaan hänen omilla teoksillaan kategorisista syllogismeista oli keskeinen osuus aihetta käsittelevän keskustelun laajenemiseen. Boethiuksen merkitys logiikan alalla ei niinkään perustu hänen omiin tutkimuksiinsa vaan siihen, että hän tehokkaasti välitti varhaisemmat teoriat myöhemmille logiikoille sekä siihen, että hän hyvin selvästi ja oikein esitti Aristoteleen tulokset.

Peter Abelard

Toinen keskiaikaisen logiikan varhainen edustaja latinalaisessa lännessä oli Peter Abelard (1079–1142). Hän tutki syllogismin käsitettä ja siihen liittyvää teoriaa perusteellisesti teoksessaan Dialectica, minkä lisäksi hän käsitteli aihetta muissakin teoksissaan kuten Logica Ingredientibus. Abelard jakoi modaaliset lauseet de dicto- ja de re -tyyppisiin, mikä teki keskiajan loogikoille mahdolliseksi kehittää modaalisille syllogismeille parempi teoria kuin mihin Aristoteles oli päässyt.

Jean Buridan

Jean Buridan (noin 1300–1361), jota monet pitävät myöhäis­keski­ajan suurimpana loogikkona, laati kaksi merkittävää teosta: Tractatus de consequentiis ja Summulae de Dialectica, joissa hän käsitteli syllogismin käsitettä, sen komponentteja, tyyppejä ja tapoja, joilla sen loogista käyttö­mahdollisuutta voitaisiin laajentaa. Buridanin jälkeen syllogistiseen logiikkaan ei kahteen­sataan vuoteen lisätty juuri mitään. Logiikan historioitsijat ovat väittäneet, että keski­ajan jälkeisinä vuosi­satoina alalla ei tapahtunut muita muutoksia kuin että alku­peräis­lähteet tulivat laajemman yleisön ulottuville, logiikan hienouksia arvostettiin entistä vähemmän ja alaa tunnettiin yleisesti yhä huonommin, mille 1900-luvun alun loogikot usein naureskelivat.

Perusrakenne

Kategorisessa syllogismissa on kolme osaa:

• Pääpremissi
• Alipremissi
• Johtopäätös

Jokainen osa on kategorinen arvostelma, ja jokaisessa kategorisessa arvostelmassa on kaksi yleistä termiä. Aristoteleella kumpikin premissi on muotoa "Kaikki A:t ovat B", "Jotkut A:t ovat B", "Mikään A ei ole B" tai "Jotkut A:t eivät ole B", missä "A" ja "B" ovat joitakin asioita tarkoittavia termejä. Lauseita "Kaikki A:t ovat B" ja "Mikään A ei ole B" nimitetään "yleisiksi" (universaaleiksi) lauseiksi, lauseita "Jotkut A:t ovat B" ja "Jotkut A:t eivät ole B" taas "rajoittuneiksi" (partikulaarisiksi) lauseiksi. Uudemmassa logiikassa näistä esiintyy enemmän muunnelmia. Kummallakin premissillä toinen termeistä on yhteinen johto­päätöksen kanssa: pää­premississä tämä on päätermi (johto­päätöksen predikaatti, ali­premississä taas alitermi (johto­päätöksen subjekti. Esimerkiksi:

Pääpremissi: Kaikki ihmiset ovat kuolevaisia.

Alipremissi: Kaikki kreikkalaiset ovat ihmisiä.

Johtopäätös: Kaikki kreikkalaiset ovat kuolevaisia.

Näissä esiintyy yhteensä kolme termiä, joista kukin tarkoittaa jotakin luokkaa, tässä tapauksessa ihmiset, kuolevaiset ja kreikkalaiset. Kuolevaiset on päätermi, kreikkalaiset alitermi. Molemmilla termeillä on myös yksi yhteinen termi, jota sanotaan välitermiksi, tässä tapauksessa ihmisen. Tässä esimerkissä molemmat premissit ovat yleisiä eli universaalisia, samoin johtopäätös.

Polysyllogismi eli soriitti on argumentin tyyppi, jossa sarja epä­täydellisiä syllogismeja on järjestetty niin, että jokaisen premissin predikaatti on samalla seuraavan subjekti, kunnes ensimmäisen premissin subjekti yhdistetään viimeisen premissin predikaatin kanssa johto­päätökseksi. Jos esimerkiksi joku väittää, että tietty määrä hiekan­jyviä ei muodosta kasaa ja että yksi lisättykään hiekan­jyvä ei tee siitä kasaa, ja jos tästä päätellään, ettei mikään määrä hiekan­jyviä muodosta kasaa, on kyseessä soriittinen argumentti.

Syllogismien tyypit

Neljän lausetyypin väliset suhteet vastakohtaisuuksien neliössä.

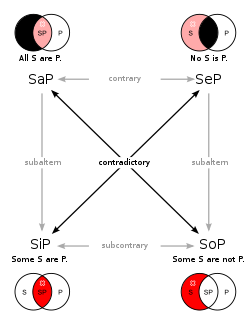
Mustat alueet ovat tyhjiä, punaiset alueet eivät.
Ylävasemmalla oleva kaavio tarkoittaa lausetta
"Kaikki S:t ovat P",
yläoikealla "Mikään S ei ole P",
alavasemmalla "jotkut S:t ovat P",
alaoikealla "Jotkut S:t eivät ole P".

Mahdollisia syllogismeja on äärettömän paljon, mutta niitä on vain 256 loogisesti erilaista tyyppiä, ja niistäkin vain jäljempänä lueteltavat 24 tyyppiä on päteviä. Syllogismi on muotoa

Pääpremissi: Kaikki M:t ovat P.

Alipremissi: Kaikki S:t ovat M.

Johtopäätös: Kaikki S:t ovat P.

(Huomautus: M – välijäsen, S – subjekti, P – predikaatti, selitetään tarkemmin jäljempänä.

Syllogismin premissit ja johtopäätös ovat jotakin neljästä tyypistä, joita merkitään kirjaimilla A, E, I ja O. Irving Copi arveli näiden olevan peräisin latinan sanoista "AffIrmo" ja "nEgO, joista edellinen tarkoittaa "Myönnän", jälkimmäinen "Kiellän"; kummassakin tapauksessa sanan ensimmäinen vokaali on tullut tarkoittamaan yleistä, toinen rajoitettua lausetta. Näiden kirjainsymbolien merkitykset osoittaa seuraava taulukko:

merkintä

kvanttori

subjekti

kopula

predikaatti

tyyppi

esimerkki

A

Kaikki

S:t

ovat

P

yleinen myöntävä lause

Kaikki ihmiset ovat kuolevaisia.

E

Mitkään (Ketkään)

S:t

eivät ole

P

yleinen kieltävä lause

Ketkään ihmiset eivät ole täydellisiä.

I

Jotkin (Jotkut)

S:t

ovat

P

rajoittunut myöntävä lause

Jotkut ihmiset ovat terveitä.

O

Jotkin (Jotkut)

S:t

eivät ole

P

rajoittunut kieltävä lause

Jotkut ihmiset eivät ole lahjakkaita.

Analytiikassaan Aristoteles käytti ei yleensä esittänyt konkreettisia esimerkkejä vaan käytti termien symboleina yleensä kreikkalaisia kirjaimia alfa, beeta ja gamma, jotka käännöksissä on korvattu vastaavilla latinalaisilla kirjaimilla A, B ja C. Tämä kirjainten käyttö paikan­varaajina oli Aristoteleen aikana uusi keksintö. On tullut tavaksi käyttää kirjaimia näiden välissä pieniä kirjaimia a, e, i ja o osoittamaan käsitteiden välisiä suhteita seuraavasti:

Muoto	Lyhenne
Kaikki A:t ovat B	AaB
Mitkään A:t eivät ole B	AeB
Jotkut A:t ovat B	AiB
Jotkut A:t eivät ole B	AoB

Kirjaimella S merkitään usein johto­päätöksen subjektia ja P:llä sen predikaattia, kun taas väli­termiä merkitään kirjaimella M. Tällöin pääpremissi yhdistää termit M ja P, alipremissi termit M ja S. väli­termi kuitenkin voi olla kummassakin premississä, jossa se esiintyy, yhtä hyvin subjektina kuin predikaattinakin. Sen perusteella, missä asemassa pää-, ali- ja väli­termi esiintyvät, syllogismit voidaan ryhmitellä myös neljään luokkaan, joita sanotaan kuvioiksi. Jos johto­päätöksen termit ovat aina S ja P, neljä kuviota ovat seuraavat:

		Kuvio 1		Kuvio 2		Kuvio 3		Kuvio 4
Pääpremissi:		M–P		P–M		M–P		P–M
Alipremissi:		S–M		S–M		M–S		M–S

Aristoteleen alkuperäiseen esitykseen ei neljäs kuvio sisältynyt, vaan sen lisäsi myöhemmin Theofrastus.. Myöhemminkään esimerkiksi Peter Abelard ja Jean Buridan eivät pitäneet sitä ensimmäisestä erotettavana kuviona.

Kaiken kaikkiaan on 256 mahdollista syllogismin tyyppiä (tai 512, jos pää- ja ali­premissi vaihdetaan keskenään, millä ei kuitenkaan logiikan kannalta ole merkitystä). Kumpikin premissi ja johto­päätös voivat olla tyyppiä A, E, I tai O, ja syllogismi voi olla neljästä kuviosta minkä tahansa mukainen. Syllogismi voidaan kuvata lyhyesti premissejä ja johto­päätöksiä vastaavilla kirjaimilla sekä kuvion numerolla. Esimerkiksi jäljempänä kuvattu Barbara-syllogismi on AAA-1 eli "A-A-A ensimmäisessä kuviossa". Suurin osa näin 256 mahdollisesta syllogismista on kuitenkin epä­päteviä, eli johto­päätös ei ole premissien looginen seuraus. Vain 24 syllogismia on päteviä. Niistäkin muutamat ovat päteviä vain, jos premisseillä katsotaan olevan eksistentiaalinen merkitys, toisin sanoen jos esimerkiksi lauseeseen "kaikki A:t ovat B" katsotaan sisältyvän, että on olemassa ainakin yksi A, tai jos tämä erikseen oletetaan (tarkemmin jäljempänä osissa "Eksis­tenti­aalinen merkitys"). Muussa tapauksessa ne voivat johtaa eksis­tenti­aaliseen virhe­päätelmään.

Pätevistä syllogismien muodoista käytetään keskiajan skolastikkojen antamia nimiä. Ne kehitettiin alkujaan muisti­säännöiksi siten, että niissä esiintyvät vokaalit A, E, I ja O vastaavat niissä olevien premissien ja johto­päätöksen yleistä myöntävää tai kieltävää tai rajoittunutta myöntävää tai kieltävää muotoa edellä esitetyllä tavalla. Esimerkiksi syllogismilla AAA on nimi "Barbara", tyypillä EAE nimi "Celarent" ja niin edelleen.

Seuraavassa taulukossa on lueteltu pätevien syllogismien muodot. Syllogismi­tyypit, jotka pätevät vain, jos premisseille oletetaan eksis­tenti­aalinen merkitys, on kursivoitu. Näistä kursivoiduista malleista muut paitsi neljä (felapton, darapti, fesapo ja bamalip) ovat heikennettyjä muotoja, toisin sanoen samoista premisseistä voidaan tehdä vahvempikin johtopäätös.

Kuvio 1	Kuvio 2	Kuvio 3	Kuvio 4
Barbara	Cesare	Datisi	Calemes
Celarent	Camestres	Disamis	Dimatis
Darii	Festino	Ferison	Fresison
Ferio	Baroco	Bocardo	Calemos
Barbari	Cesaro	Felapton	Fesapo
Celaront	Camestros	Darapti	Bamalip

Esimerkkejä

Seuraavassa taulukossa on lueteltu pätevien syllogismien eri tyypit esimerkkeineen. Jotkin näistäkin ovat keskenään yhtäpitäviä siinä mielessä, että niiden premissit ilmaisevat saman asian eri tavoin. Niinpä esimerkiksi lause "Jotkut lemmikit ovat kissanpoikia" (SiM Darii-syllogismissa AII-1) merkitsee itse asiassa samaa kuin "Jotkut kissanpojat ovat lemmikkejä" (MiS Datisi-syllogismissa AII-3).

Jokaisen premissin ja johtopäätöksen yhteydessä on lyhyt kuvaus lauseesta. Esimerkiksi syllogismissa AAI-3 premissi "Kaikki neliöt ovat suorakulmioita" on muotoa "MaP"; symbolit tarkoittavat, että ensimmäinen termi ("neliö") on välitermi, toinen termi ("suorakulmio") johtopäätöksen predikaatti ja näiden välistä suhdetta merkitään kirjaimella "a" (kaikki M:t ovat P).

Taulukossa eri syllogismeja myös havainnollistetaan Venn-diagrammeilla. Niissä on mustalla merkitty alueet, joihin kuuluvia kohteita ei premissien tai johto­päätöksen mukaan ole, punaisella alueet, joihin nimenomaan väitetään kuuluvan jotakin. Valkoisella merkityistä alueista nämä lauseet eivät sano mitään. Ylä­vasemmalla ja ylä­oikealla olevat, toisensa leikkaavat ympyrät tarkoittavat premissejä, alhaalla olevat johto­päätöstä. Niiden syllogismien kohdalla, joihin eksistentiaalisen virhe­päätelmän mahdollisuus liittyy, on lisäksi merkitty punainen ympyrä osoittamaan, että tarkoitettuja kohteita oletetaan olevan olemassa.

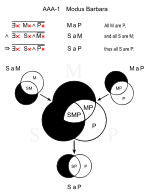
Barbara (AAA-1)

M:ihminen S:kreikkalainen   P:kuolevainen

   Kaikki ihmiset ovat kuolevaisia. (MaP)

   Kaikki kreikkalaiset ovat ihmisiä. (SaM)

∴] Kaikki kreikkalaiset ovat kuolevaisia. (SaP)

M:matelija S:käärme   P:turkki

Celarent (EAE-1)

Yhtäpitävä: Cesare (EAE-2)

   Millään matelijalla ei ole turkkia. (MeP)

   Kaikki käärmeet ovat matelijoita. (SaM)

∴ Millään käärmeellä ei ole turkkia . (SeP)

Calemes (AEE-4)
M:reptile S:fur   P:snake Calemes on kuten Celarent, mutta S ja P on vaihdettu keskenään. Yhtäpitävä: Camestres (AEE-2)    Kaikki käärmeet ovat matelijoita. (PaM)    Kaikki käärmeet ovat matelijoita. (MeS) ∴ Mikään eläin, jolla on turkki, ei ole käärme. (SeP)

M:kaniini S:lemmikki   P:turkki

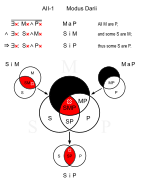
Darii (AII-1)

Yhtäpitävä: Datisi (AII-3)

   Kaikilla kaniineilla on turkki. (MaP)

   Jotkut lemmikit ovat kaniineja. (SiM)

∴ Joillakin lemmikeillä on turkki. (SiP)

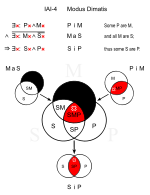
Dimatis (IAI-4)
M:kaniini S:turkki   P:lemmikki Dimatis on kuten Darii, mutta S ja P on vaihdettu. Samankaltainen: Disamis (IAI-3)    Jotkut lemmikit ovat kaniineja. (PiM)    Kaikilla kaniineilla on turkki. (MaS) ∴ Jotkin eläimet, joilla on turkki, ovat lemmikkejä. (SiP)

M:kotityö S:lukeminen   P:huvi

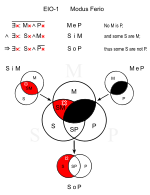
Ferio (EIO-1)

Samankaltainen: Festino (EIO-2), Ferison (EIO-3), Fresison (EIO-4)

   Mikään kotityö ei ole huvia. (MeP)

   Jokin lukeminen on kotityötä. (SiM)

∴ Jokin lukeminen ei ole huvia. (SoP)

M:antaa tietoa S:verkkosivu   P:hyödyllinen

Baroco (AOO-2)

   Kaikki, mikä antaa tietoa, on hyödyllistä. (PaM)

   Jotkin verkkosivut eivät ole hyödyllisiä. (SoM)

∴ Jotkin verkkosivut eivät anna tietoa. (SoP)

M:kissa S:nisäkäs   P:häntä

Bocardo (OAO-3)

   Joillakin kissoilla ei ole häntää. (MoP)

   Kaikki kissat ovat nisäkkäitä. (MaS)

∴ Joillakin nisäkkäillä ei ole häntää. (SoP)

---

M:ihminen S:kreikkalainen   P:kuolevainen

Barbari (AAI-1)

   Kaikki ihmiset ovat kuolevaisia. (MaP)

   Kaikki ihmiset ovat kreikkalaisia. (SaM)

∴ Jotkut kuolevaiset ovat kreikkalaisia. (SiP)

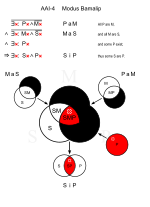
Bamalip (AAI-4)
M:ihminen S:kuolevainen   P:kreikkalainen Bamalip on kuten Barbari, mutta S ja P on vaihdettu keskenään:    Kaikki kreikkalaiset ovat ihmisiä. (PaM)    Kaikki ihmiset ovat kuolevaisia. (MaS) ∴ Jotkut kuolevaiset ovat kreikkalaisia. (SiP)

M:matelija S:käärme   P:turkki

Celaront (EAO-1)

Samankaltainen: Cesaro (EAO-2)

   Millään matelijoilla ei ole turkkia. (MeP)

   Kaikki käärmeet ovat matelijoita. (SaM)

∴ Joillakin käärmeillä ei ole turkkia. (SoP)

M:kaviot S:ihminen   P:hevonen

Camestros (AEO-2)

Samankaltainen: Calemos (AEO-4)

   Kaikilla hevosilla on kaviot. (PaM)

   Millään ihmisillä ei ole kavioita. (SeM)

∴ Jotkut ihmiset eivät ole hevosia. (SoP)

M:kukka S:kasvi   P:eläin

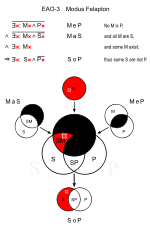
Felapton (EAO-3)

Samankaltainen: Fesapo (EAO-4)

   Mitkään kukat eivät ole eläimiä. (MeP)

   Kaikki kukat ovat kasveja. (MaS)

∴ Jotkin kasvit eivät ole eläimiä. (SoP)

M:neliö S:suunnikas   P:suorakulmio

Darapti (AAI-3)

   Kaikki neliöt ovat suorakulmioita. (MaP)

   Kaikki neliöt ovat suunnikkaita. (MaS)

∴ Jotkin suunnikkaat ovat suorakulmioita. (SiP)

Taulukko syllogismeista

Tässä taulukossa esitetään kaikki 24 pätevää syllogismia, joita kuvataan Venn-diagrammeilla. Samankaltaiset syllogismit on sijoitettu samaan sarakkeeseen, ja ne on yhdistetty premissien yhdistelmien mukaan. Reunukset vastaavat johtopäätöksiä. Ne, jotka edellyttävät eksistentiaalista oletusta, on ympäröity katkoviivoin.

figure	A ∧ A		A ∧ E				A ∧ I		A ∧ O		E ∧ I
1	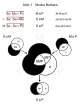Barbara	Barbari			Celarent	Celaront	Darii				Ferio
2			Camestres	Camestros	Cesare	Cesaro			Baroco		Festino
3		Darapti				Felapton	Datisi	Disamis		Bocardo	Ferison
4		Bamalip	Calemes	Calemos		Fesapo		Dimatis			Fresison

Yleiset ja erityiset termit, kategoriset syllogismit

Aristoteleen tavoin voidaan erottaa toisistaan erityiset termit kuten Sokrates ja yleiset termit kuten kreikkalaiset. Kieliopillisesti edelliset ovat yleensä erisnimiä. Aristoteles erotti lisäksi (a) termit, jotka voivat esiintyä vain subjekteina, ja (b) termit, jotka voivat esiintyä muuhun subjektiin kopulan on välityksellä liittyvänä predikaattina. Tällaista predikaattia sanotaan distributiiviseksi erotukseksi ei-distributiivisesta kuten kreikkalaiset ovat runsas­lukuisia. On selvää, että Aristoteleen syllogismit edellyttävät predikaattien olevan distribu­tiivisia, sillä esimerkiksi seuraava päätelmä ei ole pätevä: Kaikki kreikkalaiset ovat ihmisiä, ihmiset ovat runsas­lukuisia, siis kaikki kreikkalaiset ovat runsas­lukuisia. Aristoteleen mukaan erityiset termit ovat tyyppiä (a) ja yleiset termit tyyppiä (b). Siksi sana "ihminen" voi olla nimen "Sokrates" predikaattina ("Sokrates on ihminen"), mutta "Sokrates" ei voi olla minkään predikaattina. Sen vuoksi termit ovat vaihdettavissa keskenään vain, jos ne ovat yleisiä, niin sanottuja kategorisia termejä. Siksi syllogismeissa esiintyvien lauseiden olisi oltava kategorisia lauseita, joissa molemmat termit ovat yleisiä, ja ainoastaan kategorisia termejä sisältäviä syllogismia alettiin kutsua kategorisiksi syllogismeiksi.

On kuitenkin ilmeistä, ettei mikään estä erityistä termiä, siis erisnimeä esiintymästä syllogismissa, kunhan se on aina subjektin asemassa. Sellainen syllogismi ei kuitenkaan ole kategorinen, vaikka olisikin pätevä. Esimerkkinä voidaan mainita: "Sokrates on ihminen, kaikki ihmiset ovat kuolevaisia, siis Sokrates on kuolevainen." Intui­tiivi­sesti tämä on yhtä ilmeisen pätevä kuin "Kaikki kreikkalaiset ovat ihmisiä, kaikki ihmiset ovat kuolevaisia, siis kaikki kreikkalaiset ovat kuolevaisia." Aristoteles käsittikin muotoa "Sokrates on ihminen" olevat lauseet erikois­tapauksiksi muotoa "kaikki A:t ovat B" (AaB) olevista lauseista, missä tapauksessa edellä mainittu syllogismi kuuluisi Barbara-tyyppiin. Myöhemmät tutkijat kuten Bertrand Russell ovat kuitenkin pitäneet näitä oleellisesti erilaisina ja väittäneet, että niiden samastaminen on aikojen kuluessa aiheuttanut filosofiassa paljon sekaannusta, vaikka tämä syllogismi sinänsä onkin pätevä. Nykyaikaisen joukko-opin kannalta sen sijaan oleellinen ero näiden lauseiden välillä on siinä, että Sokrates on kaikkien ihmisten joukon alkio, kaikkien kreikkalaisten joukko taas saman joukon osajoukko.

Eksistentiaalinen merkitys

Kysymys lauseiden eksistentiaalisesta merkityksestä koskee sitä, voidaanko lauseiden katsoa edellyttävän, että niissä mainittuja kohteita on olemassa. Tavallisessa kielen­käytössä esimerkiksi muotoa "Kaikki A:t ovat B" olevan lauseen katsotaan yleensä edellyttävän, että kohteita A on olemassa. Jos lauseen tämän mukaisesti katsotaan olevan epätosi, mikäli termillä ei ole yhtään instanssia, sillä sanotaan olevan eksis­tenti­aalinen merkitys tämän termin suhteen. Ei kuitenkaan ole yksi­selitteisen selvää, sisältyykö lauseilla, joissa esiintyy sana "kaikki", aina myös tällainen merkitys. Toisin sanoen voidaan kysyä, onko lause "Kaikki A:t ovat B" tosi, epätosi tai edes merkityksellinen, jos kohteita A ei ole.

Tähän liittyvät seuraavat kysymykset:

(a) Onko lauseilla "Kaikki A:t ovat B", "Mitkään A:t eivät ole B", "Jotkut A:t ovat B" tai "Jotkut A:t eivät ole B" luonnollisessa kielessä eksistentiaalinen merkitys ja jos niin minkä termien suhteen?

(b) Millä niistä neljästä kategorisen lauseen muodosta (AaB, AeB, AiB ja AoB), joita syllogismeissa käytetään, on eksistentiaalinen merkitys ja minkä termien suhteen?

(c) Mitkä eksistentiaaliset merkitykset muodoilla AaB, AeB, AiB ja AoB on ajateltava olevan, jotta vasta­kohtaisuuksien neliö olisi voimassa?

(d) Mitkä eksistentiaaliset merkitykset muodoilla AaB, AeB, AiB ja AoB on ajateltava olevan, jotta aiemmin esitetyt, yleensä pätevinä pidetyt syllogismien muodot pysyisivät pätevinä?

(e) Ovatko ne eksistentiaaliset merkitykset, joita kohdassa (d) edellytetään, sellaisia, että muotoa AaB, AeB, AiB ja AoB olevila kategorisilla lauseilla on sama merkitys, joka muotoa "Kaikki A:t ovat B", "Mitkään A:t eivät ole B", "Jotkut A:t ovat B" ja "Jotkut A:t eivät ole B" olevilla lauseilla on tavan­omaisessa kielen­käytössä?

Jos esimerkiksi oletetaan, että AiB on epätosi, jos yhtään A:ta ei ole, ja ettei AaB voi olla tosi, ellei myös AiB ole (toisin sanoen AaB edellyttää lausetta AiB), lauseella AiB on eksistentiaalinen merkitys A:n kannalta, ja samoin AaB:llä. Jos lisäksi hyväksytään, että muodot AiB ja BiA ovat yhtäpitävät, lauseilla AiB ja AaB on eksis­tenti­aalinen merkitys myös B:n suhteen. Jos taas myös AoB on epätosi ellei yhtään A:ta ole, ja jos lisäksi AeB edellyttää lauseita AoB ja BeA joka vuorostaan edellyttää lausetta BoA), lauseilla AeB ja AoB on molemmilla eksis­tenti­aalinen merkitys sekä A:n että B:n kannalta. Tästä seuraa välittömästi, että kaikille yleisille kategorisille lauseille on oletettava eksis­tenti­aalinen merkitys molempien termien kannalta. Jos AaB ja AeB esittävät tavan­omaisen kielen lauseita "Kaikki A:t ovat B" ja "Mitkään A:t eivät ole B", edellä sanotusta seuraa kuitenkin paradoksaalisia johto­päätöksiä:

Lause "Kaikki lentävät hevoset ovat mytologisia" on epätosi, jos lentäviä hevosia ei ole.

Jos lause "Ketkään ihmiset eivät ole tulta syöviä kaniineja" on tosi, myös lause "On olemassa tulta syöviä kaniineja" on tosi ja niin edelleen.

Jos sovitaan, että yleisillä lauseilla ei ole eksistentiaalista merkitystä, vastakohtaisuuksien neliö ei tietyissä tapauksissa päde (esimerkiksi AaB ei edellytä, että myös AiB on tosi), ja muutamat edellä esitetyt syllogismit eivät päde (esimerkiksi Barbari, BaC, AaB->AiC).

Nämä ongelmat ja paradoksit tulevat vastaan sekä luonnollisen kielen lauseilla että syllogismin muodossa esitetyillä lauseilla, ellei ei ole selvää, edellyttääkö sana "kaikki", että sillä tarkoitettuja kohteita on. Jos joku esimerkiksi väittää, että kaikki hänen kirjoittamansa kirjat ovat saaneet Pulitzerin palkinnon, sisältyykö väitteeseen, että hän on kirjoittanut kirjoja? Ellei, onko lause tosi? Jos taas joku sanoo, että kukaan hänen ystävistään ei ole köyhä, onko lause tosi, jos hänellä ei ole yhtään ystävää?

Ensimmäisen asteen predikaattikalkyylissä tällaiset kaksiselitteisyydet vältetään sopimalla, että yleisillä lauseilla ei ole eksistentiaalista merkitystä. Kohteiden olemassaolo on erikseen eksplisiittisesti mainittava. Niinpä muotoa lauseet "Kaikki A:t ovat B", "Mitkään A:t eivät ole B" eivät sinänsä sisällä oletusta, että on yhtään A:ta.

Nykyaikaisessa matemaattisessa logiikassa lauseet, joihin sisältyy sana "kaikki", "jotkin" tai "ei mitkään", voidaan esittää joukko-opin termein. Jos kaikkien A:iden joukkoa merkitään s(A) ja vastaavasti kaikkien B:iden joukkoa s(B), niin:

• "Kaikki A:t ovat B" (AaB) merkitsee samaa kuin: "s(A) on s(B):n osajoukko", eli s(A) ⊆ s(B)
• "Mikään A ei ole B" (AeB) merkitsee samaa kuin: "Joukkojen s(A) ja s(B) leikkaus on tyhjä joukko, eli $s(A)\cap s(B)=\emptyset$
• "Jotkin A:t ovat B" (AiB) merkitsee samaa kuin: "Joukkojen s(A) ja s(B) leikkaus ei ole tyhjä joukko", eli $s(A)\cap s(B)\neq \emptyset$
• "Jotkin A:t eivät ole B" (AoB) merkitsee samaa kuin "s(A) ei ole s(B):n osajoukko".

Lisäksi määritellään, että tyhjä joukko on jokaisen joukon osajoukko. Tämän vuoksi nykyisessä matemaattisessa logiikassa käsitetään muotoa "Kaikki A:t ovat B" ja "Mikään A ei ole B" olevat lauseet aina tosiksi, muotoa "Jotkin A:t ovat B" ja "Jotkin A:t eivät ole B" sen sijaan aina epätosiksi, jos kohteita A ei ole. Tästä kuitenkin seuraa, että AaB (kaikki A:t ovat B) voi olla tosi, vaikka lause AiB (jotkin A:t ovat B) on epätosi, ja muutamat edellä esitetyt syllogismit eivät päde, jos yhtään A:ta ei ole.

Itse asiassa on kuitenkin mahdollista määritellä muodot AaB, AeB, AiB ja AoB eri tavoin niin, että millä tahansa niistä joko on eksistentiaalinen merkitys A:n, B:n, molempien tai ei kummankaan suhteen. Tällöin on myös mahdollista selvittää, voidaanko nämä määritelmät valita siten, että vastakohtaisuuksien neliö ja vanhastaan pätevinä pidettyjen syllogismien pätevyys säilyy. Galen Strawson on väittänyt, että merkitykset todella voidaan määritellä näin, mutta tulos on sellainen, että edellä esitettyyn kysymykseen (e) on vastattava kieltävästi.

Syllogismi logiikan historiassa

Pääartikkeli: Logiikan historia

Aristoteleen syllogismi­oppi hallitsi länsi­maista filosofista ajattelua monen vuosi­sadan ajan. Francis Bacon kuitenkin hylkäsi 1600-luvulla syllogismin parhaana keinona luontoa koskevien päätelmien tekoon. Sen sijaan hän suosi induktiivisempaa, kokeellista lähestymis­tapaa havaintojen tekemiseksi, mikä merkitsi kokeellista tutkimusta, jonka pohjalta voitaisiin tehdä yleisempiä päätelmiä.

1800-luvulla syllogismeista kehitettiin muunnelmia, joissa esiintyi myös disjunktiivisia ("A tai B") ja ehdollisia lauseita ("jos A niin B"). Kant väitti teoksessaan Logiikka (1800), että logiikka oli ainoa loppuun saakka kehitetty tiede ja että Aristoteleen logiikka sisälsi jo kaiken, mitkä logiikan alalta ylipäänsä voitiin tietää. Kuitenkin jopa Kantin omaa, hänen muissa teoksissaan esitettyä filosofiaa voidaan hyvällä syyllä pitää logiikankin kannalta merkittävinä uusina tuloksina. Vaikka muissa osissa maailmaa logiikkaa oli kehitetty itsenäisesti, esimerkiksi Avicennan ja intialainen logiikka, Kantin käsitys oli länsimaissa pitkälti vallitsevana vuoteen 1879 saakka, jolloin Frege julkaisi teoksensa Begriffsschrift. Siinä hän julkaisi uuden menelmän, lausekalkyylin, jolla niin syllogismeissa esiintyvät kategoriset kuin muunkinlaisetkin lauseet voitiin esittää kvanttorien ja muuttujien avulla.

Tästä sai alkunsa lause­logiikan ja ensimmäisen asteen predikaatti­logiikan kehitys. Jo 2000 vuotta käytössä ollut syllogistinen menetelmä menetti keskeisen merkityksensä, ja sitä alettiin yleisesti pitää vanhentuneena. Nykyisin Aristoteleen järjestelmää käsitellään opetuksessa pääasiassa vain johdantona sekä tieteenhistoriallisissa yhteyksissä.

Huomattavana poikkeuksena ovat kuitenkin katolinen Uskonopin kongregaatio, jonka virkamiehet yhä soveltavat Aristoteleen logiikkaa, sekä Rota Romanan apostolinen tuomioistuin, joka edelleen edellyttää asianajajien esittävän perustelunsa syllogistisessa muodossa.

Boole ja Aristoteleen logiikka

Logiikan historiaa tutkinut John Corcoran korosti George Boolen teoksen Laws of Thought uuteen painokseen liittämässään esipuheessa, että Boole epäröimättä hyväksyi Aristoteleen logiikan Corcoran myös vertaili kohta kohdalta Aristoteleen Ensimmäistä analytiikkaa ja Boolen teosta Laws of Thought.

Corcoranin mukaan Boole hyväksyi Aristoteleen logiikan täysin ja tuki sitä. Boolen tarkoituksena oli "edetä syvemmälle, korkeammalle ja pidemmälle" kuin Aristoteleen logiikka

1. muodostamalle sille yhtälöitä käyttävä matemaattinen perusta,
2. laajentamalla niiden probleemien luokkaa, jotka sillä voidaan ratkaista – yhtälöiden ratkaiseminen lisättiin niihin keinoihin, joilla päätelmien pätevyys voitiin selvittää, ja
3. laajentaa sen sovellusalaa vain kaksi termiä käsittävistä lauseista lauseisiin, joissa niitä voi olla kuinka monta tahansa.

Erityisesti Boole hyväksyi sen, mitä Aristoteles oli kirjoittanut. Hänen "erimielisyytensä", sikäli kuin sellaista oli, koski sitä, mistä Aristoteles ei ollut sanonut mitään.

Ensinnäkin, perusteiden osalta, Boole yhdisti Aristoteleen neljä lausemuotoa yhdeksi ainoaksi, yhtälöiden muotoon, mikä jo sinänsä oli vallankumouksellinen idea. Toiseksi, loogisten probleemojen osalta, se, että Boole yhdisti yhtälöiden ratkaisun logiikkaan, johti päätelmään, että Aristoteleen päättelysääntöjä oli täydennettävä yhtälöiden ratkaisemisella.

Kolmanneksi, sovellusten osalta, Boolen järjestelmällä voitiin käsitellä monen termin lauseita ja argumentteja, kun taas Aristoteles pystyi käsittelemään vain kahden termin muodostamia subjekti-predikaatti -lauseita. Esimerkiksi Aristoteleen järjestelmässä lausetta: "Mikään suorakulmio, joka ei ole neliö, ei ole nelikulmio olematta suunnikas" ei olisi voitu johtaa lauseista: "Mikään neliö, joka on suorakulmio, ei ole suunnikas, joka on suorakulmio" tai "Mikään suunnikas, joka on suorakulmio, ei ole neliö, joka on suorakulmio."

Syllogistiset virhepäätelmät

Syllogistisessa päättelyssä tehdään usein tietyn tyyppisiä virheitä.

Esimerkiksi premisseistä "Jotkut A:t ovat B" ja "Jotkut B:t ovat C" päätellään usein virheellisesti, että jotkut A:t ovat C. Tällainen syllogismin tyyppi (III-1) ei kuitenkaan ole pätevä, eikä johtopäätös seuraa premisseistä. Esimerkiksi vaikka jotkut kissat (A) ovat mustia (B) ja jotkut mustat eläimet (B) ovat korppeja (C), tästä ei seuraa, että jotkut kissat (A) olisivat korppeja (C). Tämä aiheutuu siitä, että kumpikaan premisseistä ei koske kaikkia välitermin tarkoittamia kohteita, ja tätä sanotaan "yleistymättömän välitermin virhepäätelmäksi".

Sen selvittämiseksi, mitkä syllogismit ovat päteviä, on kummastakin premissistä tutkittava, koskevatko ne kaikkia niissä mainituilla termeillä tarkoitettuja kohteita.

Yksin­kertaisista syllogistista muodoista monet ovat epäpäteviä. Ne voivat johtaa seuraaviin virhe­päätelmiin:

• Rajoitettu välitermi: kumpikaan premissi ei koske kaikkia välitermin tarkoittamia kohtia, minkä vuoksi tämä termi ei yhdistä pää- ja alipremissin termejä.
• Pääpremissin termin luvaton käsittely: Johtopäätös koskee kaikkia päätermin tarkoittamia kohteita (P — tarkoittaa, että lause on kielteinen); kuitenkaan pääpremissi ei koske niitä kaikkia (toisin sanoen P on siinä joko myönteinen predikaatti tai rajoittunut subjekti)
• Alipremissin termin luvaton käsittely: kuten edellä, mutta kohdistettuna alipremissiin ja sen termiin (S — tarkoittaa, että termi on yleinen) Tällöin S on joko rajoittunut subjekti tai myönteisen lauseen predikaatti.
• Poissulkevat premissit: Molemmat premissit ovat kielteisiä, jolloin pää- ja alitermin välille ei muodostu yhteyttä.
• Myönteinen johtopäätös kielteisestä premissistä: Jos ainakin jompikumpi premissi on kielteinen, vain kielteinen johtopäätös on mahdollinen.
• Kielteinen johtopäätös myönteisistä premisseistä: Jos molemmat premissit ovat myönteisiä, vain myönteinen johtopäätös on mahdollinen.
• Eksistentiaalinen virhepäätelmä, kiistanalaisempi. Jos molemmat premissit ovat yleisiä, toisin sanoen muotoa "kaikki" tai "ei mitkään", erään koulukunnan mukaan näistä ei seuraa, että termien tarkoittamia kohteita on olemassa. Silloin ei voida tehdä eksistentiaalista eli sanalla "jotkut" alkavaa johtopäätöstä. Toisen koulukunnan mukaan myönteiset lauseet, yleiset ja rajoittuneet, edellyttävät niissä tarkoitettuja kohteita olevan, kielteiset sen sijaan eivät.

Katso myös

• Aristotelinen logiikka

Lähteet

• ”Syllogism”, Oxford Dictionary of Philosophy. Oxford University Press, 1995. ISBN 0-19-283134-8
• Alexander Broadie: Introduction to Medieval Logic. Oxford University Press, 1993. ISBN 0-19-824026-0
• Completeness of an ancient logic. Journal of Symbolic Logic, 1972, nro 37, s. 696–702.
• The founding of logic. Modern interpretations of Aristotle's logic. Ancient Philosophy, 1994, nro 14, s. 9–24.
• George Englebretsen: The New Syllogistic. Bern: Peter Lang, 1987.
• Charles L. Hamblin: Fallacies. Lontoo: Methuen, 1970. ISBN 0-416-70070-5
• Jan Lukasiewicz: Aristotle's Syllogistic from the Standpoint of Modern Formal Logic. New York: Garland Publishers, 1987 (1957). ISBN 0-8240-6924-2
• Marko Malink: Aristotle's Modal Syllogistic. Harvard University Press, 2013.
• Günter Patzig: Aristotle's theory of the syllogism: a logico-philological study of Book A of the Prior Analytics. Dordrecht: Reidel, 1968.
• What is a syllogism? Journal of Philosophical Logic, 1973, nro 2, s. 136–154.
• Immediate propositions and Aristotle's proof theory. Ancient Philosophy, 1986, nro 6, s. 47–68.
• Paul Thom: The Syllogism. München: Philosophia, 1981. ISBN 3-88405-002-8

Aiheesta muualla

• Aristotle's Logic Robin Smith, Stanford Encyclopedia of Philosophy.
• The Traditional Square of Opposition Terence Parsons, Stanford Encyclopedia of Philosophy.
• Aristotle's Prior Analytics: the Theory of Categorical Syllogism an annotated bibliography on Aristotle's syllogistic
• The Figures of the Syllogism lyhyt taulukko syllogismen muodoista.
• Interactive Syllogistic Machine Web.pohjainen syllogistinen kone, jolla voi tutkia virhepäätelmiä, kuvioita ja syllogismityyppejä.
• CrystalTower – Esimerkkejä syllogismeista (Arkistoitu – Internet Archive)
• Development of Fuzzy Syllogistic Algorithms and Applications Distributed Reasoning Approaches (Arkistoitu – Internet Archive)
• Vertailua aristotelisten ja intialais-tiibetiläisten syllogismien välillä
• The Buddhist Philosophy of Universal Flux (Chapter XXIII - Members of a Syllogism (avayava))