Přeskočit na obsah

Samoopravný kód

Z Wikipedie, otevřené encyklopedie

Samoopravné kódy (anglicky Error Correction Code, Error Correcting Code, ECC) se ve výpočetní technice, telekomunikacích, teorii informace a v teorii kódování používají pro detekci a opravu chyb v datech přenesených nespolehlivými nebo zarušenými komunikačními kanály.[1][2] Ústřední myšlenkou je, že ke zprávě se přidají nadbytečné informace ve formě samoopravného kódu. Tato redundance umožňuje příjemci detekovat omezený počet chyb kdekoli ve zprávě, a obvykle tyto chyby i opravit bez opakování přenosu. Průkopníkem v tomto oboru byl ve 40. letech 20. století americký matematik Richard Hamming, který v roce 1950 sestrojil první samoopravný kód Hammingův kód (7,4).[2]

Samoopravné kódy se od kódů samodetekčních liší tím, že chyby, ke kterým dochází při přenosu, umějí nejen detekovat, ale i opravit. Díky tomu není nutný zpětný kanál, kterým se v případě chyby zasílají požadavky na opakování přenosu. Nevýhodou je nutnost přidávat ke zprávě další informace, takže je nutné přenášet větší objem dat. Samoopravné kódy se proto používají v situacích, kdy by opakované vysílání bylo drahé nebo nemožné, jako jsou jednosměrné komunikační spoje a při přenosu na více přijímačů při multicastu. Jsou také vhodné u spojení s velkou latencí; v případě sondy obíhající planetu Uran může opakování přenosu kvůli chybě způsobit zpoždění pěti hodin. Samoopravné kódy se obvykle používají v modemech, ale i ve velkokapacitních úložištích a v systémech s ECC pamětí.

Zpracování samoopravného kódu v přijímači může být aplikováno až na digitální bitový proud nebo již při demodulaci digitálně modulované nosné. Ve druhém případě jsou samoopravné kódy nedílnou součástí vstupního A/D převodníku v přijímači. Pro demodulaci digitálních dat z analogového signálu poškozeného šumem se obvykle používá Viterbiho dekodér, který implementuje algoritmus s měkkým rozhodováním. Mnoho kodérů/dekodérů samoopravných kódů také generuje BER signál, který je možné použít pro doladění analogové přijímací elektroniky.

Maximální podíl chyb nebo chybějících bitů, které lze opravit, je určen návrhem samoopravného kódu, v různých podmínkách jsou tedy vhodné různé samoopravné kódy. Silnější kódy mají obecně větší redundanci, kterou je potřeba přenést dostupnou přenosovou kapacitou, což snižuje efektivní přenosovou rychlost při zlepšování efektivního poměru signál/šum přijímaného signálu. Pro výpočet maximální dosažitelné komunikační rychlosti pro danou maximální přijatelnou pravděpodobnost chyby lze použít Shannonovu větu o kanálu, která určuje meze teoretické maximální rychlosti přenosu kanálem s určitou úrovní základního šumu. Důkaz však není konstruktivní, tedy neposkytuje návod, jak vytvořit kód blížící se kapacitě kanálu. Po letech výzkumu se některé pokročilé systémy samoopravných kódů od roku 2016[3] přibližují teoretickému maximu.

Dopředná oprava chyb

[editovat | editovat zdroj]

Dopředná oprava chyb (FEC) nebo kanálové kódování[4][3] je v telekomunikacích, teorii informace, a teorii kódování technika používaná pro detekci a opravu chyb při přenosu dat přes nespolehlivé nebo zarušené komunikační kanály. Ústřední myšlenkou je, že odesilatel kóduje zprávu nadbytečným způsobem, nejčastěji pomocí samoopravných kódů.

Redundance umožňuje příjemci detekovat omezený počet chyb, které se mohou objevit kdekoli ve zprávě, a často tyto chyby i opravit bez opakování přenosu. FEC dává příjemci schopnost opravit chyby bez potřeby zpětného kanálu, pomocí kterého by si vyžádal opakování přenosu dat, ale za cenu potřeby větší šířky pásma dopředného kanálu. FEC se proto používá v situacích, kdy opakované přenosy jsou drahé nebo nemožné, například na jednosměrných komunikačních spojích, při přenosu na více přijímačů při multicastu nebo když by opakování přenos způsobilo významnou latenci. Například při příjmu ze sondy obíhající kolem planety Uran by opakování přenosu kvůli chybám způsobilo zpoždění nejméně 5 hodin. FEC informace se používá také v modemech, kde opakování přenosu je možné, ale často neefektivní. Dalším použitím jsou paměti a velkokapacitní úložiště (s magnetickým, optickým nebo polovodičovým médiem) pro zotavení z poškozených dat.

Zpracování samoopravného kódu v přijímači může být aplikováno na digitální proud bitů nebo na demodulaci digitálně modulované nosné. Ve druhém případě je FEC nedílnou součástí počáteční A/D převodníku v přijímači. Viterbiho dekodér implementuje algoritmus s měkkým rozhodováním pro demodulaci digitálních dat z analogového signálu poškozeného šumem. Mnoho FEC kodérů také generuje BER signál, který může být používán jako zpětná vazba pro doladění analogové přijímací elektroniky.

Maximální podíl chyb nebo chybějících bitů, které lze opravit, je dán návrhem samoopravného kódu, proto jsou pro různé podmínky vhodné různé dopředné samoopravné kódy. Silnější kódy mají obecně větší redundanci, kterou je potřeba přenést dostupnou přenosovou kapacitou, což snižuje efektivní přenosovou rychlost při zlepšování efektivního poměru signál/šum přijímaného signálu. Pro výpočet maximální dosažitelné komunikační rychlosti pro danou maximální přijatelnou pravděpodobnost chyby lze použít Shannonovu větu o kanálu, která určuje meze teoretické maximální rychlosti přenosu kanálem s určitou úrovní základního šumu. Důkaz však není konstruktivní, tedy neposkytuje návod, jak vytvořit kód blížící se kapacitě kanálu. Po letech výzkumu se některé pokročilé systémy samoopravných kódů od roku 2016[3] přibližují teoretickému maximu za předpokladu nekonečné délky rámce.


Princip fungování

[editovat | editovat zdroj]

Pro opravu chyb se využívají redundantní informace přidané k přenášeným datům užitím nějakého algoritmu. Nadbytečné bity mohou být složitou funkcí mnoha původních informačních bitů. Původní informace se v zakódovaném výstupu může ale nemusí vyskytovat doslovně; kódy, u nichž je součástí výstupu neupravený vstup, jsou systematické; kódy, kde tomu tak není, jsou nesystematické.

Triviálním příkladem samoopravných kódů je vysílat každý datový bit třikrát, což se nazývá (3,1) opakovací kód. Na výstupu zarušeného kanálu se může objevit 8 verzí výstupu, viz tabulka níže.

Přijatá trojice Interpretováno jako
000 0 (bezchybný)
001 0
010 0
100 0
111 1 (bezchybný)
110 1
101 1
011 1

To umožňuje opravit chybu v jakémkoli ze tří vzorků „většinovým“ nebo „demokratickým hlasováním“. Opravná schopnost tohoto samoopravného kódu je:

  • až 1 chybný bit v trojici nebo
  • až 2 vynechané bity v trojici (případy nejsou uvedené v tabulce).

Přestože že tento kód jednoduché implementovat a je široce používaný, tato trojitá modulární redundance je poměrně neefektivní samoopravný kód. Lepší samoopravné kódy obvykle kontrolují posledních několik desítek nebo dokonce stovek přijatých bitů pro určení, jak dekódovat několik málo současných bitů (obvykle ve skupinách 2 až 8 bitů).

Průměrování šumu pro omezení chyb

[editovat | editovat zdroj]

Je možné říci, že samoopravné kódy využívají „průměrování šumu“; protože každý datový bit ovlivňuje mnoho přenášených symbolů, poškození některých symbolů šumem obvykle umožňuje získat původní uživatelská data z jiných přijatých, nepoškozených symbolů, které závisejí také na stejných uživatelských datech.

  • Kvůli tomuto efektu „hromadění rizika“ digitální komunikační systémy, které používají samoopravné kódy, inklinují k tomu, že fungují dobře nad určitým minimálním poměrem signálu a šumu a nefungují vůbec pod ním.
  • Tento sklon k výsledkům všechno nebo nic – efekt útesu – se projevuje tím silněji, čím silnější je kód, tedy především u kódů, které se blíží teoretickému Shannonovu limitu.
  • Tuto vlastnost všechno nebo nic může omezovat prokládání dat v případech, kdy mají kanálové chyby tendenci objevovat se ve shlucích. Ale i tato metoda má své limity; nejlépe funguje pro úzkopásmová data.

Většina telekomunikačních systémů používá pevný kanálový kód navržený tak, aby fungoval v očekávaném nejhorším případě BER, ale pokud je bitová chybovost horší, zcela selžou. Určité systémy se však mohou přizpůsobit podmínkám kanálových chyb: některé druhy hybridní zpětné vazby s automatickým opakováním používají metodu pevných samoopravných kódů, pokud samoopravné kódy stačí pro danou četnost chyb, a když četnost chyb začne být příliš vysoká, přepínají na zpětnou vazbu s automatickým opakováním; adaptivní modulace a kódování používá několik poměrů samoopravného kódu, při vyšší četnosti chyb v kanálu přidávají do paketu více opravných bitů; a méně, když nejsou potřebné.

Typy samoopravných kódů

[editovat | editovat zdroj]
Podrobnější informace naleznete v článcích Blokový kód a Konvoluční kód.
Blokový kód (konkrétně Hammingův kód), v němž se redundantní bity přidávají na konec původní zprávy.
Spojitý kód konvoluční kód, kde se redundantní bity přidávají do struktury kódového slova průběžně.
Stručná klasifikace samoopravných kódů

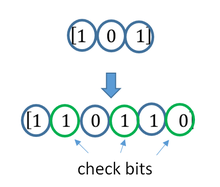
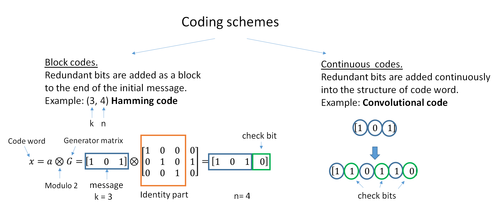
Samoopravné kódy lze rozdělit na kódy blokové a konvoluční.

  • Blokové kódy pracují na blocích (paketech) bitů nebo symbolů pevné, předem určené, velikosti. Praktické blokové kódy obecně mohou být pevně dekódovány v čase úměrném délce bloku.
  • Konvoluční kódy pracují na proudech bitů nebo symbolů libovolné délky. Obvykle používají měkký přístup k dekódování s použitím Viterbiho algoritmu, někdy se však používají i jiné algoritmy. Viterbiho dekódování umožňuje asymptoticky optimální dekódovací efektivitu s rostoucím omezením délky konvolučního kódu, ale na úkor exponenciálně rostoucí složitosti. Konvoluční kód, který je ukončený, je také 'blokový kód' v tom, že kóduje blok vstupních dat, ale velikost bloku konvolučního kódu je obecně libovolná, zatímco blokové kódy mají pevnou velikost vynucenou jejich algebraickou charakteristikou. Typy ukončení pro konvoluční kódy zahrnuje „useknutí konce“ a „bitový výplach“.

Existuje mnoho typů blokových kódů; Reedovy–Solomonovy kódy jsou významné pro své velké rozšíření na kompaktních discích, DVD, a pevných discích. Příkladem klasických blokových kódů jsou Golayův kód, BCH kód, vícerozměrný kód s kontrolou parity, a Hammingovy kódy.

Hammingův samoopravný kód se často používá pro opravu chyb ve flash pamětech.[5] To poskytuje opravu jednobitových chyb a detekci dvoubitových chyb. Hammingovy kódy jsou vhodné pouze pro spolehlivější (SLC) NAND s víceúrovňovými buňkami. hustější NAND s víceúrovňovými buňkami (MLC) mohou používat vícebitové samoopravné kódy, jako například BCH nebo Reed–Solomon.[6][7] Flash paměti NOR obvykle nepoužívají žádnou opravu chyb.[6]

Klasické blokové kódy se obvykle dekódují pomocí algoritmů s pevným rozhodováním,[8] což znamená, že pro každý vstupní a výstupní signál se provede pevné rozhodnutí, zda odpovídá jedničkovému nebo nulovému bitu. Naproti tomu konvoluční kódy se obvykle dekódují pomocí algoritmů s měkkým rozhodováním jako je Viterbiho algoritmus, MAP nebo algoritmus BCJR, které zpracovávají (diskretizované) analogové signály, a které poskytují mnohem vyšší výkonnost při opravách chyb než dekódování s pevným rozhodováním.

Téměř všechny klasické blokové kódy využívají algebraické vlastnosti konečných těles. Proto jsou klasické blokové kódy často označovány jako algebraické kódy.

V protikladu ke klasickým blokovým kódům, u nichž se často udává schopnost detekce nebo opravy chyb, mnoho moderních blokových kódů jako například Nízkohustotní kód s kontrolou parity takovou záruku postrádá. Místo toho se moderní kódy hodnotí podle jejich četnosti bitových chyb.

Většina kódů pro dopřednou opravu chyb opravuje pouze změny hodnot jednotlivých bitů, ne však vložení nebo výpadek bitu. V tomto případě je Hammingova vzdálenost vhodným způsobem, jak měřit BER. Několik málo dopředných samoopravných kódů, jako například Marker Kódy a Watermark kódy, je navrženo tak, aby byly schopné opravit vložení nebo vypouštění bitu. Při použití takových kódů je pro měření bitové chybovosti vhodnější Levenštejnova vzdálenost. [9]

Kódový poměr a kompromis mezi spolehlivostí a přenosovou rychlostí

[editovat | editovat zdroj]
Související informace naleznete také v článku Přenosová rychlost.

Základním principem samoopravného kódu je přidat nadbytečné bity, které pomáhají dekodéru najít původní zprávu, která byla zakódována vysílačem. Kódový poměr určitého samoopravného kódu se definuje jako poměr mezi počtem informačních bitů a celkovým počtem bitů (tj. informace plus redundance bity) v daném komunikačním paketu. Kódový poměr je tedy reálné číslo. Nízký kódový poměr blízký nule implikuje silný kód, které používá mnoho nadbytečných bitů pro dosažení dobré výkonnosti, zatímco velký kódový poměr blízký jedničce implikuje slabý kód.

Nadbytečné bity, které chrání informaci, se musí přenášet stejnými komunikačními prostředky jako užitečná data. Z toho plyne základní kompromis mezi spolehlivostí a přenosovou rychlostí.[10] Jedním extrémem je silný kód (s nízkým kódovým poměrem), který může způsobit významné zvýšení poměru signálu k šumu (SNR) v přijímači klesající bitovou chybovostí, za cenu omezení efektivní přenosové rychlosti. Opačným extrémem je nepoužívat žádný samoopravný kód (tj. kódový poměr roven 1), tj. používat celou kapacitu kanálu pro přenos informací, ale bez jakékoli ochrany dat proti poškození.

Zajímavou otázkou je, jak efektivní může být přenos informací s využitím samoopravného kódu, který má zanedbatelnou četnost chyb. Tuto otázku zodpověděl Claude Shannon ve své druhé větě, která říká, že kapacita kanálu je maximální přenosová rychlost dosažitelná takovým samoopravným kódem, jehož četnost chyb se blíží nule:[11] Její důkaz používá gaussovské náhodné kódování, které pro skutečné aplikace není vhodné. Horní mez daná Shannonovou prací inspirovala dlouhou historii navrhování samoopravných kódů, které se této výkonnostní hranici mohou blížit. Po roce 2000 je známo několik kódů, které mohou Shannonova limitu téměř dosáhnout. Implementace takových samoopravných kódů je však obvykle extrémně složitá.

Nejoblíbenější samoopravné kódy představují kompromis mezi výkonností a výpočetní složitostí. Jejich parametry obvykle udávají rozsah možných kódových poměrů, které lze optimalizovat podle použitého scénáře. Tato optimalizace se obvykle provádí pro dosažení nízké pravděpodobnosti dekódovacích chyb při minimalizaci vlivu na přenosovou rychlost. Jiným kritériem pro optimalizaci kódového poměru je vyvážit nízkou četnost chyb a počet opakování přenosu pro minimalizaci energetické náročnosti komunikace.[12]

Zřetězení samoopravných kódů pro zlepšení výkonnosti

[editovat | editovat zdroj]
Podrobnější informace naleznete v článku Concatenated error correction codes.

Klasické (algebraické) blokové kódy a konvoluční kódy se často kombinují do zřetězených kódovacích schémat, v nichž většinu práce zastane konvoluční kód malé omezené délky, který se dekóduje Viterbiho algoritmem, a blokový kód (obvykle Reedův–Solomonův) s větší délkou symbolu a délkou bloku „uklidí“ chyby způsobené konvolučním dekodérem. Velmi nízké četnosti chyb lze dosáhnout jediným průchodem dekodérem s touto rodinou samoopravných kódů, ale pro velký rozsah přenosových podmínek (jako jsou přenosy z kosmických sond) se doporučuje iterativní dekódování.

Zřetězené kódy byly standardní praxí pro satelitní komunikaci a komunikaci s kosmickými sondami od doby Voyageru 2, technika byla poprvé použita v roce 1986 pro přenos záznamů z Uranu. Sonda Galileo používala iterativní zřetězené kódy pro snížení velmi vysoké četnosti chyb způsobené selháním antény.

Nízkohustotní kontrolou parita (LDPC)

[editovat | editovat zdroj]
Podrobnější informace naleznete v článku Nízkohustotní kód s kontrolou parity.

Nízkohustotní kódy s kontrolou parity (LDPC) kódy jsou třídou vysoce efektivních lineárních blokových kódů vytvořených z mnoha kódů s jedinou kontrolou parity (anglicky single parity check, SPC). Mohou poskytovat výkonnost velmi blízkou kapacitě kanálu (teoretickému maximu) dekódovacím přístupem s opakovanými měkkými rozhodnutími, a časovou složitostí úměrnou délce bloku. Praktické implementace silně spoléhají na paralelní dekódování složkových SPC kódů.

LDPC kódy jako první popsal Robert G. Gallager ve své doktorské práci v roce 1960, ale kvůli výpočetní náročnosti kodéru a dekodéru a nasazení Reedových–Solomonových kódů byly až do 90. let téměř ignorovány.

LDPC kódy se nyní používají v mnoha moderních standardech vysokorychlostní komunikace, jako například DVB-S2, WiMAX (IEEE 802.16 standard pro mikrovlnnou komunikaci), Vysokorychlostní bezdrátové LAN (IEEE 802.11n),[13] 10GBase-T Ethernet (802.3an) a G.hn/G.9960 (ITU-T Standard pro přenos dat přes energetická vedení, telefonní linky a koaxiální kabely). Další LDPC kódy jsou součástí bezdrátových komunikačních standardů v 3GPP MBMS (viz Fountainovy kódy).

Turbokódy

[editovat | editovat zdroj]
Podrobnější informace naleznete v článku Turbo kód.

Turbokódy používají iterativní schéma s měkkým dekódováním; pro získání blokového kódu, který může fungovat zlomek decibelu od Shannonova limitu, se kombinují dva nebo více relativně jednoduchých konvolučních kódů s prokládáním. V praktických aplikacích se používaly před nízkohustotními kódy s kontrolou parity, a v současnosti poskytují podobnou výkonnost.

Jednou z prvních komerčních aplikací turbo kódování byla technologie používaná digitálními mobilními sítěmi CDMA2000 1x (TIA IS-2000), kterou vyvinula firma Qualcomm a prodávaly firmy Verizon Wireless, Sprint, a další mobilní operátoři. Používá se také ve standardu Evolution CDMA2000 1x pro přístup k Internetu jako 1xEV-DO (TIA IS-856). I tento standard vyvinula firma Qualcomm, a byl používán firmami Verizon Wireless (jako Broadband Access), Sprint (jako Power Vision příp. Mobile Broadband).

Lokální dekódování a testování kódů

[editovat | editovat zdroj]
Podrobnější informace naleznete v článcích Lokálně dekódovatelný kód a Lokálně testovatelný kód.

Někdy je nezbytné dekódovat pouze jednobitové zprávy nebo kontrolovat, zda je daný signál kódové slovo bez prohledávání celého signálu. Může to mít smysl při streamování, kde kódová slova jsou příliš velká na to, aby byla klasicky dekódována dostatečně rychle, a kde nás někdy zajímá jen málo bitů zprávy. Takové kódy začaly být také důležitým nástrojem v teorii složitosti, např. pro návrh pravděpodobnostně kontrolovatelný důkazy.

Lokálně dekódovatelné kódy jsou samoopravné kódy pro který jediný bity zprávy lze pravděpodobnostně získat pouze hledáním v malém (řekněme konstantním) počtu pozic kódového slova, dokonce když kódové slovo bylo poškozeno v nějaké konstantní části pozic. Lokálně testovatelné kódy jsou samoopravné kódy, pro něž lze pravděpodobnostně zkontrolovat, zda signál je blízký kódovému slovu zpracováním pouze malého počtu symbolů ze signálu.

Prokládání

[editovat | editovat zdroj]
Na tuto kapitolu jsou přesměrována hesla Interleaver, the fiber-optic device a optical interleaver.
Demonstrace významu prokládání

Prokládání se často používá v digitální komunikaci a pro ukládání dat, aby se zlepšila výkonnost dopředných samoopravných kódů. Mnoho komunikačních kanálů není bezpaměťových: chyby se obvykle objevují ve shlucích. Pokud počet chyb v kódovém slově překračuje funkčnost samoopravného kódu, získání původního kódového slova selže. Prokládání tento problém zmírňuje zamícháním zdrojových symbolů do několika kódových slov, s cílem dosáhnout rovnoměrnějšího rozdělení chyb.[14] Proto se prokládání často používá pro opravu shluků chyb.

Analýza moderních opakovaných kódů, jako jsou turbokódy a LDPC kódy, obvykle předpokládá nezávislé rozdělení chyb.[15] Systémy používající LDPC kódy proto obvykle využívají přídavné prokládání symbolů uvnitř kódového slova.[16]

Prokladač je integrální komponentou turbokódů a jeho patřičný návrh je kritický pro dosažení dobré výkonnosti.[14][17] Iterativní dekódovací algoritmus funguje nejlépe, když ve faktorgrafu, který reprezentuje dekodér, nejsou žádné krátké cykly; prokladač se proto konstruuje tak, aby neobsahoval krátké cykly.

Návrh prokladače zahrnuje:

  • pravoúhlé (nebo rovnoměrné) prokladače (podobné metodě používající skip faktory popsané výše)
  • konvoluční prokladače
  • náhodné prokladače (kde prokladač je známá náhodná permutace)
  • S-náhodné prokladač (kde prokladač je známá náhodná permutace taková, že žádné vstupní symboly do vzdálenosti S se neobjeví na výstupu do vzdálenosti S).[18]
  • bezkonfliktní kvadratický permutační polynom (QPP).[19] Příkladem jeho použití je mobilní komunikační standard Long Term Evolution.[20]

V komunikačních systémech s více nosnými se může používat prokládání mezi nosnými pro získání frekvenční diverzity, např. pro zmírnění kmitočtově závislého úniku nebo při úzkopásmovém rušení.[21]

Příklad

[editovat | editovat zdroj]

Přenos bez prokládání: 

Bezchybná zpráva:       aaaabbbbccccddddeeeeffffgggg
Přenos se shlukem chyb: aaaabbbbccc____deeeeffffgggg

Každá skupina stejných písmen zde reprezentuje čtyřbitové kódové slovo s jednobitovou informací pro opravu chyb. Zatímco kódové slovo cccc bylo změněno v jednom bitu a lze jej tedy opravit, kódové slovo dddd bylo změněno ve třech bitech, takže buď nemůže být vůbec dekódováno nebo bude dekódováno nesprávně.

S prokládáním: 

Původní kódová slova:                          aaaabbbbccccddddeeeeffffgggg
S prokládání:                                  abcdefgabcdefgabcdefgabcdefg
Přenos se shlukem chyb:                        abcdefgabcd____bcdefgabcdefg
Přijatá kódová slova po odstranění prokládání: aa_abbbbccccdddde_eef_ffg_gg

V každém z kódových slov „aaaa“, „eeee“, „ffff“, a „gggg“ je změněn pouze jeden bit, takže jednobitový samoopravný kód je všechna dekóduje správně.

Přenos bez prokládání: 

Původní přenášená věta:       ThisIsAnExampleOfInterleaving
Přijatý věta se shlukem chyb: ThisIs______pleOfInterleaving

Výraz „AnExample“ skončí téměř nesrozumitelný a je obtížné jej opravit.

S prokládáním: 

Přenášená věta:                        ThisIsAnExampleOfInterleaving...
Bezchybný přenos:                      TIEpfeaghsxlIrv.iAaenli.snmOten.
Přijatá věta se shlukem chyb:          TIEpfe______Irv.iAaenli.snmOten.
Přijatá věta po odstranění prokládání: T_isI_AnE_amp_eOfInterle_vin_...

Žádné slovo není úplně ztraceno, a chybějící písmena lze snadno uhodnout.

Nevýhody prokládání

[editovat | editovat zdroj]

Použití prokládání zvyšuje celkové zpoždění, protože pro dekódování paketu musí být přijat celý prokládaný blok.[22] Prokladače také skrývají strukturu chyb; pokročilejší dekódovací algoritmy mohou zohlednit strukturu chyb bez prokládání a dosáhnout spolehlivější komunikace než jednodušší dekodéry kombinované s prokladačem[zdroj?]. Příkladem takového algoritmu jsou struktury založené na neuronových sítích.[23]

Software pro samoopravné kódy

[editovat | editovat zdroj]

Při návrhu samoopravných kódů (ECCs) a pro jejich ověřování a zlepšování je běžnou praxí simulace jejich chování softwarem. Bezdrátový standard 5G vyvolává celou řadu aplikací pro softwarové samoopravné kódy v podobě cloudové rádiové přístupové sítě (C-RAN) s použitím softwarově definovaného rádia (SDR). Softwarové samoopravné kódy by se měly přímo používat při komunikaci. Například v 5G sítích by mohl být software zpracovávající samoopravné kódy umístěn v cloudu a signál z antén by se přímo zpracovával počítači: tímto způsobem by se zlepšila flexibilita komunikační sítě a zlepšila energetická efektivita systému.

V tomto kontextu existuje různě dostupný software s otevřeným zdrojovým textem uvedený níže (seznam není kompletní).

  • AFF3CT (A Fast Forward Error Correction Toolbox): kompletní komunikační řetěz v C++ (obsahuje mnoho podporovaných kódů jako Turbo, LDPC, polární kódy, atd.), velmi rychlý a specializovaný na kanálové kódování (může být použit jako program pro simulace nebo jako knihovna pro SDR).
  • IT++: C++ knihovna tříd a funkcí pro lineární algebru, numerické optimalizace, zpracování signálu, komunikaci a statistiku.
  • OpenAir: implementace 3GPP specifikací sítí Evolved Packet Core v jazyce C.

Seznam samoopravných kódů

[editovat | editovat zdroj]
Vzdálenost Kód
2 (detekce jedné chyby) parita
3 (oprava jedné chyby) trojitá modulární redundance
3 (oprava jedné chyby) perfektní Hammingův kód, např. Hammingův kód (7,4)
4 (Hammingův kód) rozšířený Hammingův kód
5 (oprava dvou chyb)
6 (oprava dvou chyb odhalení tří chyb) Nordstromův-Robinsonův kód
7 (oprava tří chyb) perfektní binární Golayův kód
8 (TECFED) rozšířený binární Golayův kód

Odkazy

[editovat | editovat zdroj]

Reference

[editovat | editovat zdroj]

V tomto článku byl použit překlad textu z článku Error correction code na anglické Wikipedii.

  1. ↑ GLOVER, Neal; DUDLEY, Trent. Practical Error Correction Design For Engineers. Revision 1.1, 2. vyd. CO, USA: Cirrus Logic, 1990. ISBN 0-927239-00-0. 
  2. ↑ a b HAMMING, Richard Wesley. Error Detecting and Error Correcting Codes. Bell System Technical Journal. USA: V&T, April 1950, roč. 29, čís. 2, s. 147–160. DOI 10.1002/j.1538-7305.1950.tb00463.x. S2CID 61141773. 
  3. ↑ a b c MAUNDER, Robert, 2016. Overview of Channel Coding [online]. 2016. Dostupné online. 
  4. ↑ Charles Wang; Dean Sklar; Diana Johnson. Forward Error-Correction Coding. Crosslink. The Aerospace Corporation, Winter 2001–2002, roč. 3, čís. 1. How Forward Error-Correcting Codes Work (Jak fungují samoopravné kódy)]. Dostupné v archivu pořízeném z originálu dne 2012-03-14.  Archivováno 14. 3. 2012 na Wayback Machine.
  5. ↑ “Hamming codes for NAND flash memory devices“ Archivováno 21. 8. 2016 na Wayback Machine.. EE Krát-Asia. Zdánlivě založený na “Micron Technical Note TN-29-08: Hamming Codes for NAND Flash Memory Devices“ Archivováno 29. 8. 2017 na Wayback Machine.. 2005. Oba říkají: „Hammingův algoritmus je průmyslově přijatá metoda detekce a opravy chyb v mnoha SLC NAND vycházející z flash aplikace.“
  6. ↑ a b , 2011. What Types of ECC Should Be Used on Flash Memory? [online]. Spansion, 2011. Jak Reedův–Solomonův algoritmus, tak BCH algoritmus jsou samoopravné kódy často používané pro MLC NAND flash. … Blokové kódy vycházející z Hammingových kódů jsou nejčastěji používané samoopravné kódy pro SLC… Jak Reedovy–Solomonovy kódy, tak BCH jsou schopny opravit více chyb a jsou velmi používané na MLC flash.. Dostupné online. 
  7. ↑ Jim Cooke. The Inconvenient Truths of NAND Flash Memory [online]. Srpen 2007. S. 28. Pro SLC je dostačující kód s opravným limitem 1. t=4 je nutné ... pro MLC.. Dostupné online. 
  8. ↑ BALDI, M.; CHIARALUCE, F., 2008. A Simple Scheme for Belief Propagation Decoding of BCH and RS Codes in Multimedia Transmissions. International Journal of Digital Multimedia Broadcasting. Roč. 2008, s. 1–12. DOI 10.1155/2008/957846. 
  9. ↑ SHAH, Gaurav; MOLINA, Andres; BLAZE, Matt, 2006. Keyboards and covert channels [online]. USENIX, 2006 [cit. 2018-12-20]. Dostupné online. 
  10. ↑ TSE, David; VISWANATH, Pramod, 2005. Fundamentals of Wireless Communication. [s.l.]: Cambridge University Press, UK. 
  11. ↑ SHANNON, C. E., 1948. A mathematical theory of communication. Bell System Technical Journal. Roč. 27, čís. 3–4, s. 379–423 & 623–656. Dostupné online. DOI 10.1002/j.1538-7305.1948.tb01338.x. 
  12. ↑ ROSAS, F.; BRANTE, G.; SOUZA, R. D., 2014. Optimizing the code rate for achieving energy-efficient wireless communications. In: Proceedings of the IEEE Wireless Communications and Networking Conference (WCNC). [s.l.]: [s.n.]. Dostupné online. ISBN 978-1-4799-3083-8. DOI 10.1109/WCNC.2014.6952166. S. 775–780.
  13. ↑ IEEE Standard, část 20.3.11.6 “802.11n-2009“ Archivováno 8. 9. 2017 na Wayback Machine., IEEE, 29. října 2009, datum přístupu: 21. března 2011.
  14. ↑ a b VUCETIC, B.; YUAN, J., 2000. Turbo codes: principles and applications. [s.l.]: Springer Verlag. ISBN 978-0-7923-7868-6. 
  15. ↑ LUBY, Michael; MITZENMACHER, M.; SHOKROLLAHI, A.; SPIELMAN, D.; STEMANN, V., 1997. Practical Loss-Resilient Codes. Proc. 29th Annual Association for Computing Machinery (ACM) Symposium on Theory of Computation. 
  16. ↑ Digital Video Broadcast (DVB); Second generation framing structure, channel coding and modulation systems for Broadcasting, Interactive Services, News Gathering and other satellite broadband applications (DVB-S2). En 302 307. Evropský ústav pro telekomunikační normy, duben 2009, čís. V1.2.1. 
  17. ↑ ANDREWS, K. S.; DIVSALAR, D.; DOLINAR, S.; HAMKINS, J.; JONES, C. R.; POLLARA, F. The Development of Turbo and LDPC Codes for Deep-Space Applications. Proceedings of IEEE. Listopad 2007, roč. 95, čís. 11, s. 2142–2156. DOI 10.1109/JPROC.2007.905132. S2CID 9289140. 
  18. ↑ DOLINAR, S.; DIVSALAR, D. Weight Distributions for Turbo Codes Using Random and Nonrandom Permutations. TDA Progress Report. 1995-08-15, roč. 122, s. 42–122. Bibcode 1995TDAPR.122...56D. 
  19. ↑ TAKESHITA, Oscar, 2006. Permutation Polynomial Interleavers: An Algebraic-Geometric Perspective. IEEE Transactions on Information Theory. Roč. 53, čís. 6, s. 2116–2132. DOI 10.1109/TIT.2007.896870. S2CID 660. Bibcode 2006cs........1048T. arXiv cs/0601048. 
  20. ↑ 3GPP TS 36.212, verze 8.8.0, stránka 14
  21. ↑ Digital Video Broadcast (DVB); Frame structure, channel coding and modulation for a second generation digital terrestrial television broadcasting system (DVB-T2). En 302 755. Evropský ústav pro telekomunikační normy, září 2009, čís. V1.1.1. 
  22. ↑ Techie. Explaining Interleaving [online]. W3 Techie Blog, 2010-06-03 [cit. 2010-06-03]. Dostupné online. 
  23. ↑ KRASTANOV, Stefan; JIANG, Liang. Deep Neural Network Probabilistic Decoder for Stabilizer Codes. Scientific Reports. 2017-09-08, roč. 7, čís. 1, s. 11003. DOI 10.1038/s41598-017-11266-1. PMID 28887480. Bibcode 2017NatSR...711003K. arXiv 1705.09334. 
  24. ↑ NORDSTROM, A.W.; ROBINSON, J.P. An optimum nonlinear code. Information and Control. 1967, roč. 11, čís. 5–6, s. 613–616. Dostupné online. DOI 10.1016/S0019-9958(67)90835-2. 
  25. ↑ PERRY, Jonathan; BALAKRISHNAN, Hari; SHAH, Devavrat. Rateless Spinal Codes. In: Proceedings of the 10th ACM Workshop on Hot Topics in Networks. [s.l.]: [s.n.], 2011. Dostupné online. ISBN 9781450310598. DOI 10.1145/2070562.2070568. S. 1–6.

Literatura

[editovat | editovat zdroj]

Související články

[editovat | editovat zdroj]

Externí odkazy

[editovat | editovat zdroj]
Citováno z „https://cs.wikipedia.org/w/index.php?title=Samoopravný_kód&oldid=24147457“