삼각 측량
Triangulation삼각측량학 및 기하학에서 삼각측량은 알려진 점으로부터 점으로 삼각형을 형성하여 점의 위치를 결정하는 과정입니다.
적용들
측량중
특히 측량에서는 삼각측정을 삼변측정과 같이 지점까지의 거리를 직접 측정하는 것이 아니라 알려진 지점에서의 각도 측정만 포함합니다. 각도와 거리 측정의 사용을 삼각측량이라고 합니다.
컴퓨터 비전
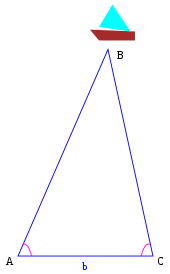
컴퓨터 스테레오 비전 및 광학 3D 측정 시스템은 이 원리를 사용하여 [2]물체의 공간적 치수와 형상을 결정합니다.기본적으로 구성은 항목을 감시하는 2개의 센서로 구성됩니다.센서 중 하나는 일반적으로 디지털 카메라 장치이고 다른 하나는 카메라나 조명 프로젝터일 수도 있습니다.센서의 투영 중심과 객체 표면의 고려점은 (공간) 삼각형을 정의합니다.이 삼각형 내에서 센서 사이의 거리는 베이스 b이며, 알고 있어야 합니다.센서의 투영광과 베이스의 각도를 결정함으로써 삼각관계로부터 교점, 즉 3D 좌표를 산출한다.
역사

오늘날 삼각측량은 측량, 항법, 도량형, 측성, 쌍안시, 모형 로켓, 그리고 군에서는 화력의 궤적과 분포를 포함한 많은 목적으로 사용된다.
거리를 추정하기 위해 삼각형을 사용한 것은 고대로 거슬러 올라간다.프톨레마이오스 왕조가 세워지기 약 250년 전인 기원전 6세기에 그리스 철학자 탈레스는 고대 이집트의 피라미드 높이를 추정하기 위해 비슷한 삼각형을 사용했다고 기록되었다.그는 피라미드의 그림자와 자신의 그림자의 길이를 동시에 측정하고, 그 비율을 자신의 키와 비교했다.[3]탈레스는 또한 알려진 추락에 대해 가시선이 가로지르는 수평 거리를 측정하고 [4]절벽 전체 높이까지 측정하여 절벽에서 본 배까지의 거리를 추정했다.그러한 기술은 고대 이집트인들에게 친숙했을 것이다.1000년 전의 린드 파피루스의 문제 57에서는 seqt 또는 seked를 경사면 상승에 대한 런의 비율, 즉 오늘날 측정된 구배 역수로 정의한다.기울기와 각도는 그리스인들이 디옵트라라고 불렀던 아라비안 알리데이의 전신인 조준봉을 사용하여 측정되었다.이 기구를 사용하여 먼 거리에서의 길이를 결정하기 위한 상세한 동시대의 건축 컬렉션은 아랍어 번역으로 살아남은 알렉산드리아 영웅의 디옵트라(서기 10-70년)로 알려져 있다.그러나 그 지식은 에라토스테네스의 작업 후 1615년 스넬리우스에 의해 유럽에서 상실되었다.지구의 둘레를 측정하기 위해 비워집니다.중국에서 페이슈(224~271)는 정확한 [5]거리 설정에 필요한 정확한 지도 제작의 여섯 가지 원칙 중 다섯 번째로 "직각과 예각 측정"을 확인하였고, 류후이(劉 (, c. 263)는 접근 불가능한 [6][7]장소의 수직 거리 측정에 대한 위의 계산 버전을 제시하였다.
「 」를 참조해 주세요.
- 방향 검색
- GSM 현지화
- 다변측정 - 다른 알려진 지점 간의 도착 시간 차이를 사용하여 점이 계산됩니다.
- 시차
- 절제(방향)
- 스테레오시스
- 테셀레이션, 다각형을 삼각형으로 덮습니다.
- Trig 점
- 무선 삼각 측량
레퍼런스
- ^ "מה בתמונה? (תשובה: נקודת טריאנגולציה)" [what is in the picture? (Answer: Triangulation Point)]. Jeepolog.com forums (in Hebrew). 2007-07-08.
- ^ Thomas Luhmann; Stuart Robson; Stephen Kyle; Jan Boehm (27 November 2013). Close-Range Photogrammetry and 3D Imaging. De Gruyter. ISBN 978-3-11-030278-3.
- ^ Diogenes Laërtius, "Life of Thales", The Lives and Opinions of Eminent Philosophers, I, 27, retrieved 2008-02-22
{{citation}}: CS1 유지보수: 위치(링크) - ^ 유클리뎀의 프로클로스
- ^ 조지프 니덤(1986년).중국의 과학과 문명: 제3권 수학과 천지의 과학.타이베이: 케이브북스 주식회사 539-540페이지
- ^ 류후이, 하이다오 쑤안징
- ^ Kurt Vogel(1983년; 1997년), 중국에서 파리로의 측량 문제, 중국에서 파리로의 이본 돌드-삼플로니우스(ed.)에서 1997년 7월 독일 오버울파흐의 Mathisches for Schungsinstitutt, Overwolfach에서 열린 회의의 속행.ISBN 3-515-08223-9.