총 변동 감소

수치적 방법에서 총변동감소(TVD)는 쌍곡 부분미분식을 해결하기 위해 사용되는 특정 탈색체계의 속성이다.이 방법의 가장 주목할 만한 적용은 계산 유체 역학이다.TVD의 개념은 아미 하텐에 의해 소개되었다.^[1]null

모형 방정식

다음과 같은 쌍곡선 부착 방정식과 같이 부분 미분 방정식으로 기술된 시스템에서는,

{\frac {\fract u}{\preason t}+a{\fract u}{\preason x}=0,

총 변화량(TV)은 다음에 의해 주어진다.

TV(u(\cdot ,t))=\int \왼쪽 {\frac {\frac {\reason u}{\\reason x}\right \mathrm {d} x,

이산형 케이스의 총 변동은

TV(u^{n}=TV(u(\cdot ,t^{n})=\sum _{j}\왼쪽 u_{j+1}^{n}-u_{j}^{n}\오른쪽 .

여기서 $u_{j}^{n}=u(x_{j},t^{n})$ $u_{j}^{n}=u(x_{j},t^{n})$ = $u_{j}^{n}=u(x_{j},t^{n})$ ( $u_{j}^{n}=u(x_{j},t^{n})$ j $u_{j}^{n}=u(x_{j},t^{n})$ , t $u_{j}^{n}=u(x_{j},t^{n})$ ) ${\displaystyle u_{j}^{n}=u(x_{j},t^{n}})$ .

수치적 방법은 다음과 같은 경우 총변동 감소(TVD)라고 한다.

[\displaystyle TV\left(u^{n+1}\오른쪽)\leq TV\left(u^{n}\오른쪽).}

특성.

숫자 체계는 다음과 같은 성질을 유지할 경우 보존하는 단조라고 한다.

$u^{n}$ $u^{n}$ ${\$ 이(가) 단조롭게 우주에서 증가(또는 감소)하고 $u^{n}$ 있다면 $u^{n+1}$ n + $u^{n+1}$ {\ $displaystyle u^{n+1$ }도 마찬가지다 $u^{n+1}$

Harten 1983은 숫자 체계에서 다음과 같은 속성을 증명했다.

단조로운 계획은 TVD이고,
TVD 계획은 단조로움을 보존하는 것이다.

CFD에서의 적용

Computing Fluid Dynamics에서는 필드 변수 " $\phi$ ${\displaystyle \phi$ $\phi$ 의 변동이 불연속적일 때 잘못된 진동 없이 더 날카로운 충격 예측을 포착하기 위해 TVD 방식을 사용한다.변동 미세 격자( $\Delta x$ x $\Delta x$ {\ $displaystyle \Delta$ x $}$ 매우 $\Delta x$ 작은 크기)를 캡처하려면 계산이 무거워지고 따라서 비경제적이 된다.중심 차이 계획, 역풍 계획, 혼합 차이 계획 및 동력 법칙 계획과 함께 거친 그리드를 사용하면 잘못된 충격 예측을 할 수 있다.TVD 체계는 거친 그리드에서 더 날카로운 충격 예측을 가능하게 하여 연산 시간을 절약할 수 있으며, 체계가 단조성을 보존하기 때문에 용액에 거짓 진동이 없다.null

디스레트화

정상 상태 1차원 대류 확산 방정식을 고려한다.

\nabla \cdot (\rho \mathbf {u} \phi )\,=\nabla \cdot (\Gamma \nabla \phi )+S_{\phi }\;

\nabla \cdot (\rho \mathbf {u} \phi )\,=\nabla \cdot (\Gamma \nabla \phi )+S_{\phi }\;

(

\nabla \cdot (\rho \mathbf {u} \phi )\,=\nabla \cdot (\Gamma \nabla \phi )+S_{\phi }\;

\nabla \cdot (\rho \mathbf {u} \phi )\,=\nabla \cdot (\Gamma \nabla \phi )+S_{\phi }\;

= ) =

\nabla \cdot (\rho \mathbf {u} \phi )\,=\nabla \cdot (\Gamma \nabla \phi )+S_{\phi }\;

\nabla \cdot (\rho \mathbf {u} \phi )\,=\nabla \cdot (\Gamma \nabla \phi )+S_{\phi }\;

(

\nabla \cdot (\rho \mathbf {u} \phi )\,=\nabla \cdot (\Gamma \nabla \phi )+S_{\phi }\;

∇

\nabla \cdot (\rho \mathbf {u} \phi )\,=\nabla \cdot (\Gamma \nabla \phi )+S_{\phi }\;

∇

\nabla \cdot (\rho \mathbf {u} \phi )\,=\nabla \cdot (\Gamma \nabla \phi )+S_{\phi }\;

) + S

\nabla \cdot (\rho \mathbf {u} \phi )\,=\nabla \cdot (\Gamma \nabla \phi )+S_{\phi }\;

\displaystyle

\

nabla \cdot (\rho \mathbf

{u} \

phi )\,=\nabla \cdot (\Gamma

\nabla \nabla \

nabla

\nabla \nabla

\pi

nabla

\nabla \nabla \

pi

)+

여기서 $\rho$ $\rho$ 은 $\rho$ 밀도, $\mathbf {u}$ ${\$ 은 ${\mathbf {u}}$ (는) 속도 벡터, $\Gamma$ ${\displaystyle \pi$ }은 $($ 는 $\phi$ $\Gamma$ $)$ 확산 계수, S $S_{\phi }$ ${\$ 은 생성을 담당하는 소스 용어다 $S_{\phi }$ . $\phi$ ▼ ${\displaystyle \phi$ $\phi$

우리가 얻은 통제량에 대해 이 성질의 유동성 균형을 맞추면

\int _{A}\mathbf {n} \cdot (\rho \mathbf {u} \phi )\,\mathrm {d} A=\int _{A}\mathbf {n} \cdot (\Gamma \nabla \phi )\,\mathrm {d} A+\int _{CV}S_{\phi }\,\mathrm {d} V

\;

여기서 $\mathbf {n}$ ${\$ 은 ${\mathbf {n}}$ $($ 는) 제어 볼륨 표면의 정상이다.null

소스 항을 무시하면 방정식은 다음과 같이 더욱 감소한다.

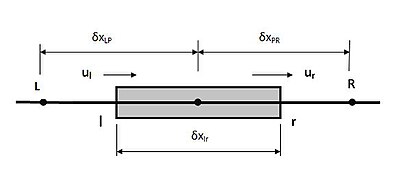
(\rho \mathbf {u} \phi A)_{r}-(\rho \mathbf {u} \phi A)_{l}=\left(\Gamma A{\frac {\partial \phi }{\partial x}}\right)_{r}-\left(\Gamma A{\frac {\partial \phi }{\partial x}}\right)_{l}

얼굴, 노드와 그 사이의 거리에 속도, 속도가 있는 제어 볼륨을 보여주는 그림이며, 여기서 'P'는 중앙에 있는 노드다.

가정하여

{\frac {\partial \phi }{\partial x}}={\frac {\delta \phi }{\delta x}}

x =

{\frac {\partial \phi }{\partial x}}={\frac {\delta \phi }{\delta x}}

{\frac {\partial \phi }{\partial x}}={\frac {\delta \phi }{\delta x}}

x

{\frac {\partial \phi }{\partial x}}={\frac {\delta \phi }{\delta x}}

x

{\frac {\partial \phi }{\partial x}}={\frac {\delta \phi }{\delta x}}

Δ x

{\frac

{\

partial \phi

}{\

partial

x

}={\partial

x}={\

fraca \delta

x

}}={\delta x}

및

{\frac {\partial \phi }{\partial x}}={\frac {\delta \phi }{\delta x}}

A

A_{r}=A_{l},

=

A_{r}=A_{l},

A_{r}=A_{l},

{\displaystystyle A_{r}=A_{l}},}}}}}}}}}}}}}}}

그 방정식은 로 감소한다.

(\rho \mathbf {u} \phi )_{r}-(\rho \mathbf {u} \phi )_{l}\,=\left({\frac {\Gamma }{\delta x}}\delta \phi \right)_{r}-\left({\frac {\Gamma }{\delta x}}\delta \phi \right)_{l}.

말해봐

F_{r}=(\rho \mathbf {u} )_{r};\qquad F_{l}=(\rho \mathbf {u} )_{l};

D_{l}=\왼쪽({\frac {\delta x}}\오른쪽)_{l};\qquad D_{r}=\left({\fracta }}{\delta x}\오른쪽)_{r};};

그림에서:

\delta \phi _{r}=\phi _{R}-\phi _{P};\qquad \delta x_{r}=x_{{{}}}}{{{{}}}}}}}{{{{}}}}}}}}}}}}}}}PR};}

\delta \phi _{L}=\phi _{P}-\phi _{L};\qquad \delta x_{L}=x_{{{}}}}{{{{}}}}}}}}{{{}}}}}}LP};

방정식은 다음과 같이 된다.

{\displaystyle F_{r}\phi _{r}-F_{l}\phi _{l}(\phi _{R}-\pi _{P}-D})(\phi _{P}-\pi _{L}).

연속성 방정식은 또한 이 문제에 대해 동등한 형태 중 하나로 충족되어야 한다.

{\displaystyle(\rho \mathbf {u} )_{r}-(\rho \mathbf {u}}\,=0\\ \Long 왼쪽 오른쪽 화살표 \ \ \ F_{r}-F_{l}=F_{l}.}

분산성이 균일한 특성 및 동일한 그리드 간격이라고 가정할 경우

\Gamma _{l}=\Gamma _{r};\qquad \delta x_{LP}=\delta x_{PR}=\delta x,

우리는 얻는다.

D_{l}=D_{r}=D.

이 방정식은 다음과 같이 더 감소한다.

{\displaystyle(\phi _{r}-\phi _{l})\cdot F=D\cdot(\phi _{R}-2\phi _{P}+\phi _{L}).}

위의 방정식은 다음과 같이 쓸 수 있다.

{\displaystyle(\phi _{r}-\phi _{l})\cdot P=(\phi _{R}-2\phi _{P}+\phi _{L}}}}}}

여기서

P

P

은

P

(는) Péclet 번호임

P={\frac {F}{D}}={\frac {\rho \mathbf {u} \delta x}{\Gamma }}}.

TVD 방식

총 변동 감소 체계는^[2]^[3] $\phi _{r}$ 과 같이 disc r ${\$ 및 $\phi _{r}$ $\phi _{l}$ $\phi _{l}$ ${\$ 의 값을 변위 방정식으로 대체한다고 $\phi _{l}$ 가정한다.

\phi _{r}\cdot P={\frac {1}{2}}(P+ P )[f_{r}^{+}\phi _{R}+(1-f_{r}^{+})\phi _{L}]+{\frac {1}{2}}(P- P )[f_{r}^{-}\phi _{P}+(1-f_{r}^{-})\phi _{RR}]

\phi _{l}\cdot P={\frac {1}{2}}(P+ P )[f_{l}^{+}\phi _{P}+(1-f_{l}^{+})\phi _{LL}]+{\frac {1}{2}}(P- P )[f_{l}^{-}\phi _{L}+(1-f_{l}^{-})\phi _{R}]

여기서 $P$ $P$ 은 $P$ (는) Péclet 번호이고 $f$ $f$ 은 $f$ (는) 확인할 체중 함수,

f=f\left({\frac {\phi _{U}-\pi _{{U}-\pi _{\pi _{UU}}{\pi _{D}-\pi _{{D}-\pi _{UU}}\오른쪽)

여기서 $U$ $U$ 은 $U$ 업스트림을, $U$ $U$ 은 $U$ U {\ $displaystyle$ U}의 $업스트림을,$ $D$ {\ $displaystyle$ D $}$ 은 다운스트림을 가리킨다 $UU$ $D$ .null

$f^{+}$ 로 f $f^{+}$ + ${\$ 는 $f^{+}$ 흐름이 양방향(즉, 왼쪽에서 오른쪽으로)일 때의 체중함수이고, $f^{-}$ - $f^{-}$ {\ $displaystyle f^{-}$ 는 $f^{-}$ 흐름이 오른쪽에서 왼쪽으로 음방향일 때의 체중함수라는 점에 유의한다.그렇게

{\displaystyle{\begin{정렬}&, f_{r}^{+}{의 \text{함수}}\leftᆪ,\\[10pt]&, f_{r}^{-}{의 \text{함수}}\leftᆫ,\\[10pt]&, f_{나는}^{+}{의 \text{함수}}\left({\dfrac{\phi_{나는}-\phi _{LL}}{\phi_{P}-\.phi_{LL}}})오른쪽),{\text{\text}\\[10pt]&f_{l}^{-}{-}{\text{{\dfrac {\phi _{P}-\{R}{R}pi _{L}-\ri}\right)의 함수다.\end{정렬}}}

If the flow is in positive direction then, Péclet number $P$ is positive and the term $(P- P )=0$ , so the function $f^{-}$ won’t play any role in the assumption of $\phi _{r}$ and $\phi _{l}$ . Likewise when the flow is in negative direction, $P$ is negative and the term $(P+ P )=0$ , so the function $f^{+}$ won’t play any role in the assumption of $\phi _{r}$ and $\phi _{r}$ .

따라서 흐름의 방향에 따른 속성 값을 고려하며 가중함수를 사용하면 용액에서 단조로움을 달성하여 가짜충격 없이 결과를 도출한다.null

제한 사항

단조로운 계획은 비물리적 해결책을 생산하지 않기 때문에 공학적이고 과학적인 문제를 해결하는데 매력적이다.고두노프의 정리는 단조로움을 보존하는 선형계획이 기껏해야 첫 번째 순서만 정확하다는 것을 증명한다.순서가 높은 선형 구조는 매끄러운 해결책을 위해 더 정확하지만 TVD는 아니며 불연속이나 충격이 발생하는 거짓 진동(위글)을 도입하는 경향이 있다.이러한 단점을 극복하기 위해 다양한 고해상도 비선형 기법이 개발되었으며, 플럭스/슬로프 제한기를 사용하는 경우가 많다.null

참고 항목

참조

^ Harten, Ami (1983), "High resolution schemes for hyperbolic conservation laws", J. Comput. Phys., 49 (2): 357–393, doi:10.1016/0021-9991(83)90136-5, hdl:2060/19830002586
^ Versteeg, H.K.; Malalasekera, W. (2007). An introduction to computational fluid dynamics : the finite volume method (2nd ed.). Harlow: Prentice Hall. ISBN 9780131274983.
^ Blazek, Jiri (2001). Computational fluid dynamics : Principles and Applications (1st ed.). London: Elsevier. ISBN 9780080430096.

추가 읽기

Hirsch, C. (1990), 내부 및 외부 흐름의 수치 연산, Vol 2, Wiley.
Laney, C. B. (1998), Cambridge University Press, Computing Gas Dynamics.
Toro, E. F. (1999), Riemann Solvers와 Springer-Verlag 유체 역학을 위한 수치적 방법.
Tannehill, J. C., Anderson, D. A., Pletcher, R. H. (1997), Computing Fluid Mechanics and Heat Transfer, 2 Edd, Taylor & Francis.
웨셀링, P.(2001) 스프링거-버락 계산 유체 역학의 원리.
캠브리지 대학 출판부의 Anil W. Date 소개 전산유체역학.

[1] Harten, Ami (1983), "High resolution schemes for hyperbolic conservation laws", J. Comput. Phys., 49 (2): 357–393, doi:10.1016/0021-9991(83)90136-5, hdl:2060/19830002586

[2] Versteeg, H.K.; Malalasekera, W. (2007). An introduction to computational fluid dynamics : the finite volume method (2nd ed.). Harlow: Prentice Hall. ISBN 9780131274983.

[3] Blazek, Jiri (2001). Computational fluid dynamics : Principles and Applications (1st ed.). London: Elsevier. ISBN 9780080430096.

[1]

[2]

[3]

Search