램지의 정리

결합 수학에서, 램지의 정리는, 그래프-이론적 형태 중 하나로, 충분히 큰 완전한 그래프의 어떤 가장자리 라벨링(색상)에서라도 단색 색상의 편협한 분열을 발견하게 될 것이라고 명시하고 있다.두 가지 색상(예: 파란색과 빨간색)에 대한 정리를 설명하려면 r과 s를 두 개의 양의 정수가 되도록 한다.^[1]램지의 정리는 R(r, s) 정점에 있는 전체 그래프의 모든 청색 적색 가장자리 색상이 r 정점의 청색 클라이크 또는 정점의 적색 클라이크를 포함하는 최소 양의 정수 R(r, s)이 존재한다고 말한다.(여기서 R(r, s)은 r과 s 모두에 의존하는 정수를 의미한다.)

램지의 정리는 조합학에서 기초적인 결과물이다.이 결과의 첫 번째 버전은 F. P. 램지에 의해 증명되었다.이것은 현재 램지 이론이라고 불리는 결합 이론을 시작했는데, 장애 속에서 규칙성을 추구한다: 규칙적인 성질을 가진 하부구조의 존재에 대한 일반적인 조건이다.이 애플리케이션에서 그것은 단색 하위 집합, 즉 단색의 연결된 가장자리의 하위 집합의 존재에 대한 질문이다.null

이 정리의 확장은 단지 두 가지 색상이 아닌, 어떤 한정된 수의 색상에 적용된다.더 자세하게, 정리 국가들은 색깔, c, 어느 정수 n1,..., nc의 어떤 주어진 번호를, 수, R(n1,..., nc), 만약 주문 R(n1,..., nc)의 완전한 그래프의 가장자리 c 다른 색깔로, 색이 그런 다음 몇가지 나는 1와 c사이에, 그 가장자리가 주문 ni의 완전한 부분 그래프 포함하고 있어야 한다 그런 것을 의미한다. 모든 colour i. 위의 특별한 경우는 c = 2 (그리고 n₁ = r 및 n = s₂)를 가진다.null

예

R(3, 3) = 6

6개의 꼭지점에 있는 전체 그래프의 가장자리가 빨간색과 파란색이라고 가정합시다.꼭지점 v를 선택한다. v에 입사하는 가장자리가 5개 있으므로 (비둘기홀 원리에 의해) 적어도 3개는 같은 색이어야 한다.일반성의 상실 없이 우리는 정점, v, 정점, r, s, t를 연결하는 이들 가장자리 중 적어도 3개가 파란색이라고 가정할 수 있다.(그렇지 않다면 다음에 나오는 것은 빨강과 파랑으로 교환한다.)만약 어떤 가장자리들, (r, s), (r, t), (s, t) 또한 파란색이라면, 우리는 완전히 파란색 삼각형을 가진다.만약 그렇지 않다면, 그 세 개의 가장자리는 모두 빨간색이고 우리는 완전히 빨간 삼각형을 가지고 있다.이 주장은 어떤 착색에도 통하기 때문에, 어떤₆ K도 단색 K를₃ 포함하고 있기 때문에, 따라서 R(3, 3) 6 6. 이것에 대한 인기 있는 버전은 친구나 낯선 사람에 대한 정리라고 불린다.null

대안적인 증거는 이중으로 세는 것으로 효과가 있다.그것은 다음과 같다.가장자리(xy), 가장자리(xy), 가장자리(yz)가 빨간색이고 가장자리(yz)가 파란색인 정점(x, y, z)의 순서 3배수를 세십시오.첫째, 주어진 정점은 0 × 5 = 0 (정점으로부터의 모든 가장자리는 동일한 색상), 1 × 4 = 4 (4는 동일한 색상, 1은 다른 색상), 또는 2 × 3 = 6 (3은 동일한 색상, 2는 다른 색상)의 중간이다.따라서 최대 6 × 6 = 36 그러한 세 배가 있다.둘째로, 어떤 단색 삼각형(xyz)에 대해서도 정확히 두 개의 그러한 세 쌍이 존재한다.따라서 단색 삼각형이 최대 18개까지 있다.따라서 K에₆ 있는 20개의 삼각형 중 적어도 2개는 단색이다.null

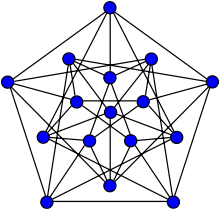
반대로 단색 K를₃ 생성하지 않고 K를₅ 2컬러링할 수 있어 R(3, 3) > 5를 나타낸다.유니크한^[2] 컬러링이 우측에 표시된다.따라서 R(3, 3) = 6.

R(3, 3) ≤ 6이 1953년 윌리엄 로웰 푸트남 수학 경시대회의 문제 중 하나였음을 증명해야 하는 과업은 1947년 헝가리 수학 올림피아드에서도 마찬가지였다.null

다중 색상 예제: R(3, 3, 3) = 17

멀티컬러 램지 번호는 3가지 이상의 색상을 사용하는 램지 번호다.(대칭까지) 정확한 값을 알 수 있는 비 멀티컬러 램지 번호는 R(3, 3, 3) = 17과 R(3, 3, 4) = 30 두 개뿐이다.^[3]null

빨간색, 녹색, 파란색 등 3가지 색상을 사용한 전체 그래프의 가장자리 색상이 있다고 가정해 보십시오.더 나아가 가장자리 색상에 단색 삼각형이 없다고 가정하자.정점 v를 선택하십시오. 정점 v에 빨간색 가장자리가 있는 정점 집합을 고려하십시오.이것은 v의 붉은 이웃이라고 불린다.v의 빨간색 인접 영역은 빨간색 가장자리를 포함할 수 없으며, 그렇지 않으면 빨간색 가장자리와 꼭지점 v의 두 끝점으로 구성된 빨간색 삼각형이 있을 수 있기 때문이다.따라서, v의 빨간색 인접 지역에서 유도된 가장자리 색상은 녹색과 청색의 두 가지 색상만 가진 가장자리 색상을 가진다.R(3, 3) = 6이므로 v의 빨간색 인접성은 최대 5개의 정점을 포함할 수 있다.마찬가지로, v의 녹색과 파란색 이웃은 각각 최대 5개의 꼭지점을 포함할 수 있다.v 자체를 제외한 모든 꼭지점은 v의 빨간색, 녹색 또는 파란색 인접 영역 중 하나에 있으므로 전체 그래프는 최대 1 + 5 + 5 + 5 = 16 정점을 가질 수 있다.그러므로 우리는 R(3, 3, 3) <= 17>을 가지고 있다.null

R(3, 3, 3) = 17을 보려면 단색 삼각형을 피하는 3가지 색상으로 16개의 정점에 전체 그래프에 에지 색상을 그리면 충분하다.K에는₁₆ 그러한 색상이 정확히 두 가지 있는데, 이른바 지지되지 않은 색상과 꼬인 색상이 있다.두 가지 색상은 모두 오른쪽 그림에서 나타나며, 윗부분에는 지지되지 않은 색상이, 아랫부분에는 꼬인 색상이 표시된다.null

우리가₁₆ K의 지지되지 않은 색이나 꼬인 색상의 어떤 색상을 선택하고, 가장자리가 정확히 지정된 색상의 가장자리인 그래프를 고려한다면, 우리는 Clebsch 그래프를 얻을 것이다.null

K에는₁₅ 단색 삼각형을 피하는 3가지 색상의 엣지 색상이 정확히 2가지로 알려져 있는데, 이는₁₆ K의 미부착 색상과 꼬임 색상에서 정점을 각각 삭제해 구성할 수 있다.null

색상의 순열에 의해 다른 에지 색상을 동일하다고 간주한다면 K에₁₄ 단색 삼각형을 피하는 3가지 색상의 에지 색상이 정확히 115개 있는 것으로 알려져 있다.null

증명

2개 케이스

2-색상 사례에 대한 정리는 r + s에 대한 유도를 통해 증명할 수 있다.^[4]모든 n에 대해 R(n, 2) = R(2, n) = n. 이것이 유도를 시작한다.우리는 R(r, s)이 존재한다는 것을 그것에 대한 명시적인 구속을 찾아냄으로써 증명한다.귀납 가설 R(r - 1, s)과 R(r, s - 1)이 존재한다.null

보조정리기 1. R(r, s) ≤ R(r - 1, s) + R(r, s - 1):

증명. 가장자리가 두 가지 색으로 색칠된 R(r - 1, s) + R(r, s - 1) 정점에 대한 전체 그래프를 고려한다.그래프에서 꼭지점 v를 선택하고 나머지 꼭지점을 두 세트 M과 N으로 분할하십시오. 즉, 모든 꼭지점 w에 대해 w는 (v, w) 파란색이면 M이고 w는 (v, w) 빨간색이면 N이다.그래프에는 R(r - 1, s) + R(r, s - 1) = M + N + 1 정점이 있으므로, M r R(r - 1, s) 또는 N r R(r, s - 1) 중 하나를 따른다.전자의 경우, 만약 M이 빨간색_s K를 가지고 있다면, 원본 그래프도 그렇게 되고 우리는 끝난다.그렇지 않으면 M은 파란색 K를_r−1 가지므로 M definition {v}은(는) M의 정의로 파란색 K를_r 갖는다.후자의 경우는 유사하다.따라서 그 주장은 사실이고 우리는 2가지 색에 대한 증거를 완성했다.null

이 2-색상 사례에서 R(r - 1, s)과 R(r, s - 1)이 모두 짝수인 경우 유도 불평등은 다음과 같이 강화될 수 있다.^[5]

R(r, s) ≤ R(r - 1, s) + R(r, s - 1) - 1

증명. p = R(r - 1, s)과 q = R(r, s - 1)이 모두 짝수라고 가정하자.t = p + q - 1로 하고 t 정점의 2색 그래프를 고려한다.d i ${\$${$$i}$이(가) 파란색 서브그래프에서i {\$displaystyle$ i} -th 꼭지점인 경우, 핸드셰이킹 보조정리법에 따르면ii = 1t di ${\$ 스타일 $\i=1}^{t}d_{i}}}$는 짝수다.t가 홀수임을 감안할 때 반드시 짝수 d i ${\$가 있어야 한다. d 1 ${\$}가 짝수라고 가정하면, M과 N은 각각 청색 및 적색 서브그래프에서 정점 1에 해당하는 정점이라고 한다.$그러면$ M= d 1 ${\$ M =$d_{1$}와 N= t- 1- d 1 ${\dplaystyle$N =$t-1-d_{$1}모두 짝수인 것이다.According to the Pigeonhole principle, either ${\displaystyle M \geq p-1}$, or ${\displaystyle N \geq q}$. Since ${\displaystyle M }$ is even, while ${\displaystyle p-1}$ is odd, the first inequality can be strengthened, so either ${\displaystyle M \geq$$p}$ or ${\displaystyle N \geq q}$. Suppose ${\displaystyle M \geq p=R(r-1,s)}$. Then either the M subgraph has a red ${\displaystyle K_{s}}$ and the proof is complete, or it has a blue ${\displaystyle K_{r-1}}$ which along with vertex 1 makes a blue Kr ${\$사례 N ≥ q= R( r, s- 1) ${\displaystyle$N$\geq=R(r,s-1)$도 이와 비슷하게 처리한다.null

색상이 더 많은 경우

보조정리 2.c>2일 경우 R(n₁, ..., n_c) ≤ R(n₁, ..., n), R_c−2(n_c−1, n_c)이다.null

증명. R(n₁, ..., n_c−2, R(n_c−1, n_c) 정점의 전체 그래프를 고려하고 그 가장자리에 c 색상을 입힌다.이제 '색맹'으로 가서 c - 1과 c가 같은 색인 척 하라.따라서 그래프는 이제 (c - 1) 색상이 된다.R(n₁, ..., n_c−2, R(n_c−1, n_c)의 정의로 인해, 그러한 그래프는 약 1 i i c c - 2의 색상 i를 가진 K 단색_ni 또는 '블러드 컬러'의 K-색상을_{R(nc − 1, nc)} 포함한다.전자의 경우 우리는 끝장이다.후자의 경우, 우리는 다시 시력을 회복하고 R_c−1(n_c, n)의 정의로부터 우리는 반드시 a(c - 1) 단색 K나_nc−1 c-단색 K를_nc 가져야 한다.어느 경우든 증거가 완전하다.null

보조정리법 1은 모든 R(r,s)이 유한하다는 것을 의미한다.Leemma 2의 불평등 우측은 더 적은 색상을 위한 Ramsey 숫자의 관점에서 c 색상의 Ramsey 숫자를 나타낸다.따라서 모든 R(n₁, ..., n_c)은 어떤 색상에도 유한하다.이것이 정리를 증명한다.null

램지 수

Ramsey의 정리에서 숫자 R(r, s)은 Ramsey 번호로 알려져 있다. (그리고 그것들의 세 가지 이상의 색상까지 확장됨).램지 번호 R(m, n)은 파티 문제에 대한 해결책을 제시하는데, R(m, n)은 적어도 m이 서로를 알거나 n이 서로를 알 수 없도록 초대해야 하는 최소 손님 R(m, n)을 요구한다.그래프 이론의 언어에서, Ramsey 번호는 순서 v의 모든 비방향 단순 그래프가 순서 m의 일렬 또는 독립된 순서 n을 포함하는 정점수 v = R(m, n)의 최소 수이다. Ramsey의 정리에는 그러한 숫자가 모든 m과 n에 대해 존재한다고 명시되어 있다.

대칭에 의해, R(m, n) = R(n, m)인 것은 사실이다.R(r, s)에 대한 상한은 정리 증명에서 추출할 수 있으며, 다른 주장은 하한을 부여한다.(첫 번째 지수 하한은 Paul Erdős가 확률론적 방법을 사용하여 얻었다.)그러나 가장 엄격한 하한과 가장 엄격한 상한 사이에는 엄청난 차이가 있다.또한 R(r, s)의 정확한 값을 알고 있는 r과 s의 숫자도 거의 없다.null

R(r, s)에 대한 하한 L을 계산하려면 일반적으로 파란색 K_r 하위 그래프와 빨간색 K_s 하위 그래프 없이 그래프 K의_L−1 파란색/빨간색 색상을 표시해야 한다.이런 백범례를 램지 그래프라고 한다.Brendan McKay는 알려진 Ramsey 그래프의 목록을 유지한다.^[6]상한은 종종 훨씬 더 설정하기가 어렵다. 백범 표본의 부재를 확인하기 위해 가능한 모든 색상을 검사하거나, 또는 그 부재의 수학적 주장을 제시하기 위해 검사해야 한다.null

계산 복잡성

에르디스는 우리에게 우리보다 훨씬 더 강력한 외계인이 지구에 상륙하여 R(5, 5)의 가치를 요구하지 않으면 우리 행성을 파괴할 것이라고 상상하라고 요구한다.그 경우에, 그는 우리가 모든 컴퓨터와 수학자들을 정리해서 그 가치를 찾도록 노력해야 한다고 주장한다.그러나 그들이 R(6, 6)을 요구한다고 가정해보자.그렇다면 외계인을 파괴하려고 시도해야 한다고 그는 믿고 있다.

— Joel Spencer^[7]

정교한 컴퓨터 프로그램은 모든 색상을 제거하기 위해 모든 색상을 개별적으로 볼 필요가 없다. 그럼에도 불구하고 그것은 기존 소프트웨어가 작은 크기에서만 관리할 수 있는 매우 어려운 계산 작업이다.각각의 완전 그래프 Kn{.sfrac{white-space:nowrap}.mw-parser-output.sfrac.tion,.mw-parser-output.sfrac .tion{디스플레이:inline-block, vertical-align:-0.5em, font-size:85%;text-align:센터}.mw-parser-output.sfrac.num,.mw-parser-output.sfrac .den{디스플레이:블록, line-height:1em, 마진:00.1em}.mw-parser-output.sfrac .den .mw-parser-output다.Border-top:1px 고체}.sr-onlyᆬ1(n− 1)가장자리 .mw-parser-output, cn(n− 1)/2 그래프 만약 폭력 사용된다(c색상을)을 통해 검색하기가 될 것이다.[8]따라서 가능한 모든 그래프를 (브루트 힘을 통해) 검색하는 복잡성은 c 색상과 최대 n개 노드에 대한 O(cⁿ²)이다.null

양자컴퓨터의 등장으로 상황이 나아질 것 같지 않다.가장 잘 알려진 알고리즘은^{[citation needed]} 클래식 컴퓨터에 비해 2차 속도 상승(c.f. Grover's algorithm)만 보여서 계산 시간은 여전히 노드 수에 있어서 기하급수적이다.^[9]null

알려진 값

As described above, R(3, 3) = 6. It is easy to prove that R(4, 2) = 4, and, more generally, that R(s, 2) = s for all s: a graph on s − 1 nodes with all edges coloured red serves as a counterexample and proves that R(s, 2) ≥ s; among colourings of a graph on s nodes, the colouring with all edges coloured red contains a s-node red subgraph, and all o이들의 색상은 2-노드 파란색 서브그래프(즉, 파란색 가장자리로 연결된 한 쌍의 노드)를 포함한다.null

유도불평등도를 이용하여 R(4, 3) r R(4, 2) + R(3, 3) - 1 = 9, 따라서 R(4, 4) r R(4, 3) + R(4, 4) 18 18)으로 결론지을 수 있다.16노드 그래프 6.4 × 10개의²² 서로 다른 2-색상 중 2개의 (4, 4, 16) 그래프(즉, 4-노드 빨강 또는 청색 전체 하위 그래프가 없는 16개 노드에 전체 그래프의 2-색상)만 있고, 2.46 × 10개의²⁶ 색상 중 1개의 (4, 4, 17개의 순서의 창백한 그래프) 그래프(순서 17)만 있다.^[6](이것은 1979년 에반스, 풀럼, 쉬한에 의해 증명되었다.)R(4, 4) = 18을 따른다.null

R(4, 5) = 25라는 사실은 1995년 브렌던 맥케이와 스타니스와프 라지즈쇼스키에 의해 처음 확립되었다.^[10]null

R(5, 5)의 정확한 값은 알 수 없지만 43(조프리 엑소(1989년)^[11]과 48(앙겔트베이트와 맥케이(2017년)^[12] 사이(포함) 사이인 것으로 알려져 있다.null

1997년 맥케이, 라지즈조스키, 엑소는 R(5, 5), 43을 추측하기 위해 컴퓨터 보조 그래프 생성 방법을 채용했다.그들은 정확히 656개의 (5, 5, 42) 그래프를 만들 수 있었고, 다른 경로를 통해 동일한 그래프 집합에 도달할 수 있었다.656개 그래프 중 어떤 그래프도 a(5, 5, 43) 그래프까지 확장할 수 없다.^[13]null

r(r, s)이 5 이상인 R(r, s)의 경우 약한 한계만 사용할 수 있다.R(6, 6)과 R(8, 8)의 하한선은 각각 1965년과 1972년 이후 개선되지 않았다.^[3]null

r(r, s)이 있는 R(r, s)은 아래 표와 같다.정확한 값을 알 수 없는 경우 표에는 가장 잘 알려진 한계가 나열되어 있다.r이 있는 R(r, s)은 s의 모든 값에 대해 R(1, s) = 1과 R(2, s) = s로 주어진다.

램지 번호 연구의 개발에 관한 표준 조사는 스타니스와프 라지즈쇼스키가 정기적으로 업데이트하는 <전자 결합기 저널>의 동적 조사 1이다.^[3]달리 인용되지 않은 경우, 아래 표의 기재사항은 2021년 1월호부터 취합한다.(R(r, s) = R(s, r)이기 때문에 대각선 전체에 사소한 대칭이 있다.)

Ramsey 번호 R(r, s)에 대한 값/알려진 경계 범위(OEIS의 시퀀스 A212954)

s r	1	2	3	4	5	6	7	8	9	10
1	1	1	1	1	1	1	1	1	1	1
2		2	3	4	5	6	7	8	9	10
3			6	9	14	18	23	28	36	40–42
4				18	25[10]	36–41	49–61	59[14]–84	73–115	92–149
5					43–48	58–87	80–143	101–216	133–316	149[14]–442
6						102–165	115[14]–298	134[14]–495	183–780	204–1171
7							205–540	219–1031	252–1713	292–2826
8								282–1870	329–3583	343–6090
9									565–6588	581–12677
10										798–23556

점증약학

부등식 R(r, s) r R(r - 1, s) + R(r, s - 1)을 인덕션 적용하여 다음을 증명할 수 있다.

${\displaystyle R(r,s)\leq {\binom {r+s-2}{r-1}}$

특히 이 결과는 Erdős와 Szekeres로 인해 r = s일 때

${\displaystyle R(s,s)\leq [1+o(1)]{\frac {4^{s-1}{\sqrt{\pi s}}.}$

지수 하한,

${\displaystyle R(s,s)\geq [1+o(1)]{\frac {s}{{\sqrt{2}}e}2}}^{s/2},}$

1947년에 Erdős에 의해 주어졌고 확률론적 방법의 도입에 중요한 역할을 했다.이 두 경계 사이에는 분명히 큰 차이가 있다. 예를 들어 s = 10과 같은 경우, 이것은 101㎛ R(10, 10) ≤ 48620을 준다.그럼에도 불구하고 두 한계 중 하나의 지수 성장 요인은 현재까지 개선되지 않고 있으며 각각 4와 √2에 있다.지수 하한을 생성하는 것으로 알려진 명시적 구조는 없다.대각선 Ramsey 번호에 대해 가장 잘 알려진 하한 및 상한은 현재 다음과 같다.

${\displaystyle [1+o(1)]{\frac {{\sqrt{2}}^{{e}2}}:{{2}}:\leq R(s)\leq s^{-(c\log s)/(\log \log s)}4^{s}}}}}$

각각 스펜서와 콘론 때문이지null

비대각 램지 번호 R(3, t)의 경우, t 2 loglog t {\$displaystyle {\$의 순서인 것으로 알려져 있다. 이는 n-vertex 삼각형이 없는 그래프에서 가능한 가장 작은 독립성 번호라고 동등하게 명시할 수 있다.

${\displaystyle \Theta \left({\sqrt{n\log n}}\오른쪽).}$

R(3, t)의 상한은 아제타이, 콤일로스, 스제메레디가 부여하고, 하한은 원래 킴이 획득한 것이고, 하한은 그리피스, 모리스, 피즈 폰티베로스, 보만과 키에바시가 삼각 프리 공정을 분석하여 개선하였다.보다 일반적으로, R(s, t)과 s가 고정되고 t가 커지는 비대각형 Ramsey 숫자의 경우, 가장 잘 알려진 한계는 다음과 같다.

${\displaystyle c'_{s}{\frac {t^{\frac {s+1}{2}}}{(\log t)^{{\frac {s+1}{2}}-{\frac {1}{s-2}}}}}\leq R(s,t)\leq c_{s}{\frac {t^{s-1}}{(\log t)^{s-2}}},}$

보만과 케바시와 아제타이, 콤일로스와 스제메레디 때문이다.null

유도 램지

유도 서브그래프를 위한 램지의 정리에는 덜 알려져 있지만 흥미로운 아날로그가 있다.대략적으로 말하면, 단색의 서브그래프를 찾는 대신에, 우리는 이제 단색의 유도 서브그래프를 찾아야 한다.이 변종에서는 완전한 서브그래프의 존재가 유도 서브그래프의 존재를 의미하지 않기 때문에 더 이상 그래프를 완성하기 위해 우리의 초점을 제한하는 것만으로는 충분하지 않다.다음 절의 정리에 대한 정성적 진술은 1970년대 에르드외스, 하지날과 포사, 드우버, 뢰들 등에 의해 독립적으로 처음으로 증명되었다.^[15][16][17] 그 이후로, 유도된 램지 숫자에 대한 좋은 한계를 얻기 위한 많은 연구가 있었다.null

성명서

H ${\displaystyle H}$을(를) n ${\displaystyle n}$ 정점에 대한 그래프로 표시하십시오.그런 다음 두 가지 색상을 사용하는 G ${\displaystyle G}$의 가장자리 색상은 H ${\displaystyle H}$의 단색 유도 사본(즉, G ${\displaystyle G}$의 유도 하위 그래프)을 포함하고 H ${\displaysty H}$에 이형이며 가장자리가 단색인 그래프 G ${\displaysty$ G$}$이 있다.matic. G ${\displaystyle G}$의 가능한 최소 정점 수는 유도 Ramsey number r ind (H) ${\displaystyle r_{\indext}}(H)}$이다.

때때로 우리는 문제의 비대칭 버전을 고려하기도 한다.빨간색 또는 파란색만 사용하는 G ${\displaystyle G}$ 가장자리의 모든 색상이 X ${\displaystyle X}$ 또는 Y의 파란색 유도 하위 그래픽을 포함하도록 r$,Y)$를 그래프 G ${\\displaystyle G}$의 가능한 최소 정점 수로 정의한다.$(\displaystyle$ Y})

역사와 경계

램지의 정리(Ramsey's Organization)와 마찬가지로 모든 그래프 H ${\displaystyle H}$에 대해 유도된 램지 숫자가 존재하는지는 선례가 불분명하다 1970년대 초 에르드예스, 하지날, 포사, 드우버, 뢰들 등이 독자적으로 증명했다.^[15][16][17] 그러나, 원래의 증거는 유도된 램지 숫자에 대해 끔찍한 한계(예: twos tows)를 주었다.더 나은 한계를 달성할 수 있는지 묻는 것은 흥미롭다.1974년, Erdös{\displaystyle c}가 k{k\displaystyle}vertices에 모든 그래프 H{H\displaystyle}가이었고 넌 결코 모르네ind(H)≤ 2ck{\displaystyle r_{\text{ind}}(H)\leq 2^{ck}}.[18]만약 이 추측이 사실이라면, 최적이 상수 c까지{\di이 지속적인 c가 존재한다고 그가 추측했다.spl전체 그래프가 이 형식의 하한을 달성하기 때문에(사실 램지 번호와 동일) $aystyle$ c$}.$그러나 이 추측은 현재로선 아직 미정이다.null

1984년 에르디스와 하지날은 바운드 rind(H)≤ 2 k 1 +o (1) ${\$ 2$^{2^{k^{1+o(1)}}}}}}}}$을 증명했다고 주장했지만, 그것은 에르데스의 지수적인 추측과는 여전히 거리가 멀었다.It was not until 1998 when a major breakthrough was achieved by Kohayakawa, Prőmel and Rődl, who proved the first almost-exponential bound of ${\displaystyle r_{\text{ind}}(H)\leq 2^{ck(\log k)^{2}}}$ for some constant ${\displaystyle c}$.이들의 접근방식은 투영 평면에 구성된 적절한 랜덤 그래프를 고려하고 0이 아닌 확률로 원하는 특성을 갖는다는 것을 보여주는 것이었다.투영 평면에 무작위 그래프를 사용하는 아이디어는 또한 정점 색상과 한계도 그래프 H ${\displaystyle H}$에 유도된 Ramsey 문제와 관련하여 Ramsey 속성을 연구하는데 이전에 사용되었다.^[20]

고하야카와, 프르멜, 르들 감독의 바운드는 10년 동안 최고의 바운드로 남아 있었다.2008년, 폭스사와 스다코프는 동일한 경계로 유도된 램지 번호에 대해 명시적인 구조를 제공했다.[21]사실, 그들은 G{G\displaystyle}-graph 작은λ와 적당한{\lambda\displaystyle}d{\displaystyle d}과 매주(n, d, λ){\displaystyle(n,d,\lambda)}G{\displayst의 가장자리가 조금도 수식에서 어떤 그래프의 k{k\displaystyle}vertices에 유도 단색이 들어 있는 것으로 나타났다.yle$두$ 가지 컬러로 G$}$특히, 일부 상수 c{\$displaystyle c$의 경우, n2 2 c log 2k k{\$displaystyle n\geq$2^{$ck\log ^{2}k$}} 정점의 모든 에지 색상이 모든 k ${\style k}$ -vertex 그래프의 유도 단색 카피를 포함하도록 되어 있다.null

2010년 콘론, 폭스, 수다코프는 rind (H ) ≤ 2 c 로그 ⁡ k ${\$에 대한 바인딩을 개선할 수 있었는데, 이는 일반 유도 Ramsey 번호에 대한 현재 최고 상한으로 남아 있다.[22]2008년 이전 작업과 비슷하게, 그들은 G{G\displaystyle}-graph 작은λ{\lambda\displaystyle}과 밀도 12{\displaystyle{\frac{1}{2}과 매주(n, d, λ){\displaystyle(n,d,\lambda)}}}모든 그래프의 k{k\displaystyle}가 있담에 유도 단색이 들어 있는 것으로 나타났다.rti어떤 엣지 컬러로든 두 가지 컬러로 쎄즈현재 r ind(H ) ≤ 2 c ${\$가 열린 채로 극단적 그래프 이론의 중요한 문제 중 하나라는 에르도스의 추측이 있다.null

하한에 대해서는 유도 램지 번호가 적어도 해당 램지 번호여야 한다는 사실을 제외하고는 일반적으로 잘 알려져 있지 않다.일부 특수 사례에 대해 일부 하한을 얻었다(특수 사례 참조).null

특수 케이스

유도된 Ramsey 숫자에 대한 일반적인 한계는 그래프의 크기가 지수적이지만, 그 행동은 특별한 등급의 그래프(특히 희박한 그래프)에서 크게 다르다.이 클래스들 중 많은 수가 정점 수에서 Ramsey number 다항식을 유도했다.null

H ${\displaystyle H}$이(가) k ${\displaystyle k}$ 정점의 주기, 경로 또는 별인 경우 r ind (H) ${\displaystyle r_{\text{ind}(H)$는 k ${\$displaysty k$}$에서 선형인 $것$으로 알려져 있다.

H ${\displaystyle H}$이(가) k ${\displaystyle k}$ 정점에 있는 트리인 경우, r ind( H )= O( k 2 log 2 ⁡ k$){\displaysty r_{\textind}(H)=$로 알려져 있다.$O(k^{2}\log ^{2}k)}$^[23].r($H$$){\displaystyle r_{\dext}}(H)}$이(가) 초선형(예: r ind(H )= $($ ) $displaystyle r_{\dext}}}=\omega(k)})$인 것으로도 알려져 있다.이는 일반적인 Ramsey 번호와 대조적인데, 여기서 Burr-Erdős 추측(현재 입증된)은 r($){\displaystyle r(H)}$이(나무는 1-degenate이기 때문에) 선형임을 알려준다.null

For graphs ${\displaystyle H}$ with number of vertices ${\displaystyle k}$ and bounded degree ${\displaystyle \Delta }$, it was conjectured that ${\displaystyle r_{\text{ind}}(H)\leq cn^{d(\Delta )}}$, for some constant ${\displaystyle d}$ depending only on ${\displaysty$$le \Delta }$. This result was first proven by Łuczak and Rödl in 1996, with ${\displaystyle d(\Delta )}$ growing as a tower of twos with height ${\displaystyle O(\Delta ^{2})}$.^[24] More reasonable bounds for ${\displaystyle d(\Delta )}$ were obtained since then.2013년 콘론, 폭스, 자오 등은 rind($H$)c c 2 Δ +${\$ind$}}\leq cn^{2$\Delta +$8}}$인 희소 유사 그래프에 계산 보조마사를 사용하는 것을 보여주었는데, 여기서 지수는 일정한 요인까지 가장 잘 가능하다.^[25]

일반화

Ramsey numbers와 유사하게, 우리는 Hamsey numbers를 hypergraphs와 multicolor settings로 유도한 Ramsey number의 개념을 일반화할 수 있다.null

더 많은 색상

유도된 램지의 정리를 다색 설정으로 일반화할 수도 있다.For graphs ${\displaystyle H_{1},H_{2},\cdots ,H_{r}}$, define ${\displaystyle r_{\text{ind}}(H_{1},H_{2},\cdots ,H_{r})}$ to be the minimum number of vertices in a graph ${\displaystyle G}$ such that any coloring of the edges of ${\displaystyl$$e G}$ into ${\displaystyle r}$ colors contain a induced subgraph isomorphic to ${\displaystyle H_{i}}$ where all edges are colored in the ${\displaystyle i}$-th color for some ${\displaystyle 1\leq i\leq r}$. Let ${\displaystyle r_{\text{ind}}(H;q$$}=r_{\text}}(H,H,\cdots,H)}}($Q{\$displaystyle q}$개의 H ${\displaystyle H}).$null

two-color case에 바운드를 반복적으로 적용함으로써 ~ log q${\displaystyle r_{\text{ind}(H;q)$의 약 2개의 타워인 r ind(H; \$displaystyle \sim$ \log $q)$에 대한 바운드를 도출할 수 있다.The current best known bound is due to Fox and Sudakov, which achieves ${\displaystyle r_{\text{ind}}(H;q)\leq 2^{ck^{3}}}$, where ${\displaystyle k}$ is the number of vertices of ${\displaystyle H}$ and ${\displaystyle c}$ is a constant depending only on ${\displaystyle q}$. ^[26]

하이퍼그래프

문장의 단어 그래프를 하이퍼그래프로 바꾸는 것만으로 유도된 램지 숫자의 정의를 d ${\displaystyle d}$ -uniform 하이퍼그래프로 확장할 수 있다.또한 이전 항과 동일한 방식으로 유도된 Ramsey 번호의 다중색 버전을 정의할 수 있다.null

H ${\displaystyle H}$을(를) k ${\displaystyle k}$ 정점이 있는 d ${\displaystyle d}$ - 균일형 하이퍼그래프로 한다.Define the tower function ${\displaystyle t_{r}(x)}$ by letting ${\displaystyle t_{1}(x)=x}$ and for ${\displaystyle i\geq 1}$, ${\displaystyle t_{i+1}(x)=2^{t_{i}(x)}}$. Using the hypergraph container method, Conlon, Dellamonica, La Fleur, Rödland Schacht were able to show that for ${\displaystyle d\geq 3,q\geq 2}$, ${\displaystyle r_{\text{ind}}(H;q)\leq t_{d}(ck)}$ for some constant ${\displaystyle c}$ depending on only ${\displaystyle d}$ and ${\displaystyle q}$. In particular, this result mirrorsd= 3 ${\displaystyle d=3}$일 때 일반적인 Ramsey 번호에 대해 가장 잘 알려진 바운드.

정리의 연장

무한 그래프

흔히 램지의 정리라고도 하는 추가 결과는 무한 그래프에 적용된다.유한 그래프도 논의되고 있는 상황에서 흔히 "무한 램지 정리"라고 부른다.유한 그래프에서 무한 그래프로 이동할 때 그래프의 그림 표현에 의해 제공되는 직관이 줄어들기 때문에, 이 영역의 이론들은 보통 이론적 용어로 표현된다.^[28]null

정리.X를 무한대 집합으로 하고 X의⁽ⁿ⁾ 요소(n 사이즈의 X 부분 집합)를 c 다른 색상으로 색칠한다.그 다음 X의 일부 무한 부분 집합 M이 존재하여 크기 n 부분 집합이 모두 동일한 색상을 갖는다.

증명: 그 증거는 하위 집합의 크기인 n에 의한 것이다.n = 1의 경우 이 문장은 무한 집합을 한정된 집합 수로 나누면 그 중 하나가 무한하다는 말과 같다.이것은 명백하다.정리가 n ≤ r에 대해 참이라고 가정하면 n = r + 1. X의 (r + 1)-element subset의 c-컬러링을 감안하여 a를₀ X의 요소가 되게 하고 Y = X \ {a₀}로 한다.그런 다음 각 r-element subset(r₀ + 1)-element subset(X의 (r + 1)-element subset)에 a를 추가함으로써 Y의 r-element subset의 c-컬러링을 유도한다.유도 가설에 의해 Y의 무한 부분 집합₁ Y가 존재하여 Y의₁ 모든 r-요소 부분 집합이 유도 착색에서 동일한 색상으로 색칠된다.따라서 원소 a와₀ 무한 부분집합₁ Y가 존재하여, Y의₁ a와₀ r 요소로 구성된 X의 모든 (r + 1) 요소 부분집합이 동일한 색상을 갖는다.동일한 인수에 의해 Y에₁ 원소₁ a가 있고 Y의₁ 무한 부분 집합₂ Y가 동일한 특성을 가지고 있다.결과적으로, 우리는 시퀀스 {a₀, a₁, a₂, ...를 얻는다.} i(1) < i(2) > ...< i(r + 1)가 있는 각 (r_i(1) + 1)-의 부분 집합(a, a_i(2), ..., a_{i(r + 1)})의 색상은 i(1)의 값에 따라서만 달라진다.또한 i(n)의 값이 무한히 많아 이 색상이 동일할 것이다.원하는 단색 세트를 얻으려면 이 a를_i(n) 사용하십시오.null

램지의 그래프에 대한 정리의 강하지만 불균형한 무한 형태인 Erdős-Dusnik-Miller 정리는 모든 무한 그래프에는 카운트다운 무한 독립 집합이나, 원본 그래프와 동일한 카디널리티의 무한 클릭이 포함되어 있다고 명시하고 있다.^[29]null

무한 버전은 유한성을 의미한다.

모순에 의한 증거에 의해 무한판으로부터 유한한 램지 정리를 추론할 수 있다.유한한 램지 정리가 거짓이라고 가정하자.그 다음, 모든 정수 k에 대해 크기 T의 단색 집합이 없는[k ]( n$){\$의 c-색상이 존재하는 정수 c, n, T가 있다.C는_k 크기 T의 단색 세트가 없는 [k ]( n) ${\$의 c-색상을 나타낸다.

모든 k에 대해, C에서_k+1[ k ]( n) ${\$k + 1을 포함하는 모든 세트의 색상을 무시함)까지 색칠을 제한하는 것은_k C의 색칠이다.C_k+1 k 1 ${\$1}을(를) C의_k 착색 제한으로 정의하십시오.C가_k+1 비어 있지 않기 때문에 C k 1 ${\$1}도 아니다.

마찬가지로, C k+ 1 1 ${\$1}의 모든 색상 제한은 C k 1 ${\$$1$}:{1$}:{$2$}}$을 $이러한$ 모든 제한집합, 비어 있지 않은 집합으로 정의할 수 있다.계속하여 모든 정수 m, k에 대해 C k m ${\$을 정의하십시오.

이제 모든 정수 k에 대해 C k ⊇ C 1 ⊇ C 2 ⊇ ⋯ ⋯ {{ {\$displaystyle C_{k}\supseteq C_{k}^{1}^{k}^{2}\supseteq \codots$ }}, 각 집합은 비어 있지 않다.더욱이 C는_k C k ≤ c k! n! (k- n)! ${\$로 유한하다!$}}}$. It follows that the intersection of all of these sets is non-empty, and let ${\displaystyle D_{k}=C_{k}\cap C_{k}^{1}\cap C_{k}^{2}\cap \cdots }$. Then every colouring in D_k is the restriction of a colouring in D_k+1.따라서 D의_k 색상을 D의_k+1 색상으로 제한하지 않고 계속 그렇게 함으로써 크기 T의 단색 세트 없이 N( n) ${\$의 색상을 구성한다.이것은 무한 램지 정리와는 상반된다.null

적절한 위상학적 관점을 취한다면, 이 주장은 정리의 무한한 버전이 유한한 버전을 내포하고 있음을 보여주는 표준 압축성 논거가 된다.^[30]null

하이퍼그래프

정리도 하이퍼그래프로 확장할 수 있다.m-하이퍼그래프는 "에지"가 m 정점 집합인 그래프를 의미한다. 일반 그래프에서 에지는 정점 집합 2이다.램지의 정리의 hypergraphs의 모든 진술은 어떤 정수 m, c, 그리고 어떤 정수 n1,..., nc에, 있습니다는 정수 R(n1,..., nc, c, m)등이 hyperedges의 완전한 m-hypergraph의 주문 R(n1,..., nc, c, m)은 유색인과 함께 c 다른 색깔, 그런 다음 어떤 나의 1퍼센트와 c, 하이퍼 그래프야 한다 포함한 compl.seteub-m-m-magraph of order n_i, hydography all color i.이 정리는 보통 그래프의 '하이퍼 네스(hyper-ness)'인 m에 유도로 증명된다.증명의 기본 케이스는 m = 2인데, 이것이 바로 위의 정리인 것이다.null

지시 그래프

지시된 그래프에 대해 Ramsey 숫자를 정의하는 것도 가능하다; 이것들은 P에 의해 소개되었다. 에르디스와 L.모세르(1964년).단일 방향 호("tournament"라고도 함)와 and Q 노드가 있는 완전한 그래프가 Acyclic("transitive"라고도 함) n-노드 하위 어쿠르나멘트를 포함하도록 R(n)을 최소 숫자 Q로 한다.null

이것은 (위)가 R(n, n; 2)이라고 불린 것의 지시-그래프 아날로그로서, ≥ Z 노드가 있는 완전한 비방향 그래프의 가장자리의 2-색상이 n 노드에 단색 완료 그래프를 포함하도록 최소 숫자 Z이다.(두 개의 가능한 호 색상의 방향 아날로그는 호의 두 방향이고, "단색색"의 아날로그는 "모든 호 화살표가 같은 방향을 가리키고", 즉 "아크로클릭"이다.)

우리는 R(0) = 0, R(1) = 1, R(2) = 2, R(3) = 4, R(4) = 8, R(5) = 14, R(6) = 28, 34 47 R(7) 47 47을 가지고 있다.^[31][32]

선택 공리에 대한 관계

역수학에서는 무한 그래프에 대한 램지의 정리 버전(사례 n = 2)과 무한 다중그래프(사례 n ≥ 3) 사이에 입증 강도에 상당한 차이가 있다.정리의 다중글 버전은 산술 이해 공리와 강도가 동등하여 역수학에서 빅5 서브시스템 중 하나인 2차 산술의 서브시스템 ACA의₀ 일부가 된다.이와는 대조적으로, 데이비드 세타푼의 정리로는, 정리의 그래프 버전이 ACA보다₀ 약하며, (세타푼의 결과를 다른 것과 결합) 큰 5개의 서브시스템 중 하나에 속하지 않는다.^[33]그러나 ZF를 넘어서는 그래프 버전은 고전적인 Kőnig의 보조정리기와 동등하다.^[34]null

참고 항목

• 램지 추기경
• 파리-해링턴 정리
• 심(연필게임)
• 무한 램지 이론
• 반데르 베르덴 수
• 램지 게임
• 에르데스-라도 정리

메모들

참조

• Ajtai, Miklós; Komlós, János; Szemerédi, Endre (1980), "A note on Ramsey numbers", J. Combin. Theory Ser. A, 29 (3): 354–360, doi:10.1016/0097-3165(80)90030-8.
• Bohman, Tom; Keevash, Peter (2010), "The early evolution of the H-free process", Invent. Math., 181 (2): 291–336, arXiv:0908.0429, Bibcode:2010InMat.181..291B, doi:10.1007/s00222-010-0247-x, S2CID 2429894
• Brualdi, Richard A. (2010), Introductory Combinatorics (5th ed.), Prentice-Hall, pp. 77–82, ISBN 978-0-13-602040-0
• Conlon, David (2009), "A new upper bound for diagonal Ramsey numbers", Annals of Mathematics, 170 (2): 941–960, arXiv:math/0607788v1, doi:10.4007/annals.2009.170.941, MR 2552114, S2CID 9238219.
• Erdős, Paul (1947), "Some remarks on the theory of graphs", Bull. Amer. Math. Soc., 53 (4): 292–294, doi:10.1090/S0002-9904-1947-08785-1.
• Erdős, P.; Moser, L. (1964), "On the representation of directed graphs as unions of orderings" (PDF), A Magyar Tudományos Akadémia, Matematikai Kutató Intézetének Közleményei, 9: 125–132, MR 0168494
• Erdős, Paul; Szekeres, George (1935), "A combinatorial problem in geometry" (PDF), Compositio Mathematica, 2: 463–470, doi:10.1007/978-0-8176-4842-8_3, ISBN 978-0-8176-4841-1.
• Exoo, G. (1989), "A lower bound for R(5,5)", Journal of Graph Theory, 13: 97–98, doi:10.1002/jgt.3190130113.
• Graham, R.; Rothschild, B.; Spencer, J. H. (1990), Ramsey Theory, New York: John Wiley and Sons.
• Gross, Jonathan L. (2008), Combinatorial Methods with Computer Applications, CRC Press, p. 458, ISBN 978-1-58488-743-0
• Harary, Frank (1972), Graph Theory, Addison-Wesley, pp. 16–17, ISBN 0-201-02787-9
• Ramsey, F. P. (1930), "On a problem of formal logic", Proceedings of the London Mathematical Society, 30: 264–286, doi:10.1112/plms/s2-30.1.264.
• Spencer, J. (1975), "Ramsey's theorem – a new lower bound", J. Combin. Theory Ser. A, 18: 108–115, doi:10.1016/0097-3165(75)90071-0.
• Bian, Zhengbing; Chudak, Fabian; Macready, William G.; Clark, Lane; Gaitan, Frank (2013), "Experimental determination of Ramsey numbers", Physical Review Letters, 111 (13): 130505, arXiv:1201.1842, Bibcode:2013PhRvL.111m0505B, doi:10.1103/PhysRevLett.111.130505, PMID 24116761, S2CID 1303361.

외부 링크

위키북 콤비네이터(Wikibook Combinatorics)에는 Ramsey numbers라는 주제에 관한 페이지가 있다.

• "Ramsey theorem", Encyclopedia of Mathematics, EMS Press, 2001 [1994]
• Ramsey@Home은 다양한 기법의 호스트를 이용하여 다양한 Ramsey 번호에 대한 새로운 하한을 찾기 위해 고안된 분산 컴퓨팅 프로젝트다.
• 전자 저널 콤비네이터ics의 소규모 Ramsey 번호 동적 조사 (Staniswow Radziszzowski)
• Ramsey 번호 – MathWorld(R(19, 19)까지 하한 및 상한 포함)
• 램지 번호 – 제프리 엑소 (R(5, 5 포함) > 방호 42개)