양자 비밀 공유

Quantum Secret Sharing(QSS; 양자비밀공유)은 단순한 양자키 배포를 넘어 안전한 통신을 위한 양자암호방식입니다.이는 양자 정보와 복제 금지 정리를 사용하여 통신에 대한 궁극적인 보안을 달성하기 위해 고전적인 비밀 공유(CSS) 방식을 수정합니다.

시크릿 공유 방식은, 수신측의 많은 부분이 함께 동작하는 경우에 한해, 시크릿이 완전하게 밝혀지도록, 복수의 수신측과 시크릿을 공유하려고 하는 송신측으로 구성됩니다.그러나 충분한 수신자가 힘을 합쳐 비밀을 밝히지 않으면 그 비밀은 전혀 알려지지 않은 채 남아 있다.

고전적인 계획은 1979년 Adi^[1] Shamir와 George Blakley에^[2] 의해 독립적으로 제안되었다.1998년 마크 힐러리, 블라디미르 부제크, 안드레 베르티아움은 양자 상태를 이용하여 고전 데이터를 ^[3]통해 비밀을 전달하는 데 사용될 수 있는 안전한 키를 설정하도록 이론을 확장했다.이후 몇 년 동안,^[4]^[5] 암호키를 확립하기 위해 양자 상태를 사용하는 것이 아니라 비밀로서 양자 정보를 전송하는 것으로 이론을 확장하기 위한 더 많은 작업이 이루어졌다.

QSS는 양자^[6] 머니뿐만 아니라 공동 당좌예금계좌, 양자네트워킹, 분산 양자컴퓨팅 등에서도 사용될 수 있도록 제안되어 왔다.

프로토콜

가장 간단한 경우: GHZ 상태

이 예는 1998년 Hillery 등이 그린버거를 사용한 원래의 계획을 따른다.Horne-Zeilinger(GHZ) 상태그 직후에 3개의 입자 상태 ^[7]대신 2개의 입자가 얽힌 상태를 사용하는 유사한 방식이 개발되었습니다.두 경우 모두 프로토콜은 본질적으로 양자 키 배포의 한 개가 아닌 두 개의 수신기로의 확장입니다.

일반적인 언어에 따라 송신자를 Alice로, 2개의 수신자를 Bob과 Charlie로 나타냅니다.Alice의 목표는 다음과 같은 방법으로 각 수신자에게 개인 키의 "공유"를 보내는 것입니다(실제로 양자 상태).

밥과 찰리의 공유에는 앨리스의 원래 메시지에 대한 정보가 포함되어 있지 않기 때문에 둘 다 스스로 비밀을 추출할 수 없습니다.
그 비밀은 오직 밥과 찰리가 함께 일해야만 추출할 수 있고, 이 경우 그 비밀은 완전히 드러난다.
외부 도청자 또는 부정 수신자(Bob 또는 Charlie 중 하나)의 존재는 비밀이 드러나지 않고 검출할 수 있습니다.

Alice는 Bob 및 Charlie와 각각 (표준) Z베이스의 GHz 트리플렛에서 하나의 입자를 공유하여 프로토콜을 시작합니다.

{\displaystyle \mathrm {Psi} \rangle _{GHZ}=sq frac {000\rangle + 111\rangle }{\sqrt {2}}},

$|\mathrm {0} \rangle$ 서 0 $|\mathrm {0} \rangle$ {\({ $displaystyle \mathrm {0}$ \ $rangle$ }) $|\mathrm {1} \rangle$ 1 $|\mathrm {1} \rangle$ ⟩({ $displaystyle \mathrm {1} \rangle$ })은 $|\mathrm {1} \rangle$ 임의의 힐베르트 공간에서 직교 모드입니다.

각 참가자는 X 베이스 또는 Y 베이스(임의로 선택)에서 입자를 측정한 후, 측정을 위해 사용한 기본을 공유한다. 결과 자체는 공유하지 않는다.측정 결과를 조합하면 밥과 찰리는 앨리스가 측정한 시간의 50%를 추론할 수 있습니다.이 과정을 여러 번 반복하고 작은 부분을 사용하여 악의적인 행위자가 존재하지 않음을 확인함으로써 3명의 참가자는 안전하게 통신하기 위한 공동 키를 확립할 수 있습니다.이 동작의 명확한 예에 대해서는, 다음을 고려해 주세요.

다음과 같은 표준 방법으로 x 및 y 고유 상태를 정의합니다.

\mathrm {+x} \rangle = specfrac {0\rangle + 1\rangle }, \mathrm {-x} \rangle = specfrac {0\rangle - 1\rangle }

|\mathrm {+y} \rangle ={\frac {|0\rangle +i|1\rangle }{\sqrt {2}}},|\mathrm {-y} \rangle ={\frac {|0\rangle -i|1\rangle }{\sqrt {2}}}

|\mathrm {+y} \rangle ={\frac {|0\rangle +i|1\rangle }{\sqrt {2}}},|\mathrm {-y} \rangle ={\frac {|0\rangle -i|1\rangle }{\sqrt {2}}}

|\mathrm {+y} \rangle ={\frac {|0\rangle +i|1\rangle }{\sqrt {2}}},|\mathrm {-y} \rangle ={\frac {|0\rangle -i|1\rangle }{\sqrt {2}}}

|\mathrm {+y} \rangle ={\frac {|0\rangle +i|1\rangle }{\sqrt {2}}},|\mathrm {-y} \rangle ={\frac {|0\rangle -i|1\rangle }{\sqrt {2}}}

|\mathrm {+y} \rangle ={\frac {|0\rangle +i|1\rangle }{\sqrt {2}}},|\mathrm {-y} \rangle ={\frac {|0\rangle -i|1\rangle }{\sqrt {2}}}

|\mathrm {+y} \rangle ={\frac {|0\rangle +i|1\rangle }{\sqrt {2}}},|\mathrm {-y} \rangle ={\frac {|0\rangle -i|1\rangle }{\sqrt {2}}}

+

|\mathrm {+y} \rangle ={\frac {|0\rangle +i|1\rangle }{\sqrt {2}}},|\mathrm {-y} \rangle ={\frac {|0\rangle -i|1\rangle }{\sqrt {2}}}

1

|\mathrm {+y} \rangle ={\frac {|0\rangle +i|1\rangle }{\sqrt {2}}},|\mathrm {-y} \rangle ={\frac {|0\rangle -i|1\rangle }{\sqrt {2}}}

, - y

|\mathrm {+y} \rangle ={\frac {|0\rangle +i|1\rangle }{\sqrt {2}}},|\mathrm {-y} \rangle ={\frac {|0\rangle -i|1\rangle }{\sqrt {2}}}

|\mathrm {+y} \rangle ={\frac {|0\rangle +i|1\rangle }{\sqrt {2}}},|\mathrm {-y} \rangle ={\frac {|0\rangle -i|1\rangle }{\sqrt {2}}}

|\mathrm {+y} \rangle ={\frac {|0\rangle +i|1\rangle }{\sqrt {2}}},|\mathrm {-y} \rangle ={\frac {|0\rangle -i|1\rangle }{\sqrt {2}}}

-

|\mathrm {+y} \rangle ={\frac {|0\rangle +i|1\rangle }{\sqrt {2}}},|\mathrm {-y} \rangle ={\frac {|0\rangle -i|1\rangle }{\sqrt {2}}}

1

2

|\mathrm {+y} \rangle ={\frac {|0\rangle +i|1\rangle }{\sqrt {2}}},|\mathrm {-y} \rangle ={\frac {|0\rangle -i|1\rangle }{\sqrt {2}}}

\

displaystyle

\

mathrm

{ +

y

} \

rangle =

0 \ rangle {

0

\

rangle

} , \

mathrm {

-

y

} \

rangle = frac

0 \

langle

{ \

langle }

그 후 GHZ 상태는 다음과 같이 고쳐 쓸 수 있습니다.

|\mathrm {\Psi } \rangle _{GHZ}={\frac {1}{2{\sqrt {2}}}}[({|+x\rangle _{a}|+x\rangle _{b}+|-x\rangle _{a}|-x\rangle _{b}})(|0\rangle _{c}+|1\rangle _{c})+({|+x\rangle _{a}|-x\rangle _{b}+|+x\rangle _{a}|-x\rangle _{b}})(|0\rangle _{c}-|1\rangle _{c})]

a}

+

x\rangle

_

{b}

+

-x\rangle

_{a}

-x\rangle _{b}) 0\rangle

_{

c} +({+x\rangle

_{

a} -x\rangle

_{b}

+x\rangle

_

{a} -x\rangle

_

{b})

0-{

c}

_

{c

})

여기서 (a, b, c)는 (Alice, Bob, Charlie)의 입자를 나타내며, Alice와 Bob의 상태는 X-basis에 기재되어 있습니다.이 형식을 사용하면 앨리스와 밥의 측정값과 찰리의 단일 입자 상태 사이에 상관 관계가 있음을 알 수 있습니다.

Alice와 Bob의 상관관계가 있는 경우 Charlie의 상태는 ${\frac {|0\rangle _{c}+|1\rangle _{c}}{\sqrt {2}}}$ ${\frac {|0\rangle _{c}+|1\rangle _{c}}{\sqrt {2}}}$ c ${\frac {|0\rangle _{c}+|1\rangle _{c}}{\sqrt {2}}}$ + ${\frac {|0\rangle _{c}+|1\rangle _{c}}{\sqrt {2}}}$ c 2 { ${\frac {|0\rangle _{c}+|1\rangle _{c}}{\sqrt {2}}}$ style \ $frac$ { $0$ \ $rangle$ $_$ { $c }$ { \ $sqrt {$ } } 、 Alice와 ${\frac {|0\rangle _{c}+|1\rangle _{c}}{\sqrt {2}}}$ Bob의 상관관계가 없는 경우 Charlie의 $상태$ 는 ${\frac {|0\rangle _{c}-|1\rangle _{c}}{\sqrt {2}}}$ c - 1 ${\frac {|0\rangle _{c}-|1\rangle _{c}}{\sqrt {2}}}$ c ${\frac {|0\rangle _{c}-|1\rangle _{c}}{\sqrt {2}}}$ + $1$ ${\frac {|0\rangle _{c}-|1\rangle _{c}}{\sqrt {2}}}$ c $2$ display { $frc$ }입니다 $.$ $gle$ _ ${c}}{\carrt$ {2 ${\frac {|0\rangle _{c}-|1\rangle _{c}}{\sqrt {2}}}$

앨리스와 밥의 측정값이 표준 GHZ 트리플렛에 대한 찰리의 상태에 미치는 영향입니다.

이러한 상관관계를 요약한 표를 보면 찰리는 앨리스와 밥의 측정기반을 알 수 있으므로 자신의 측정결과를 사용하여 앨리스와 밥의 결과가 같은지 반대의지를 추론할 수 있습니다.그러나 이 연산을 하기 위해서는 Charlie가 자신의 입자를 측정하기 위한 올바른 측정 기준을 선택해야 합니다.그는 무작위로 두 개의 비상근 베이스 중 하나를 선택하기 때문에 유용한 정보를 추출할 수 있는 시간은 절반에 불과하다.나머지 절반은 결과를 폐기해야 합니다.또한 표를 통해 앨리스와 밥의 결과가 상관 관계 또는 반상관 관계일 경우에만 찰리는 누가 무엇을 측정했는지 결정할 방법이 없음을 알 수 있습니다.따라서 찰리가 앨리스의 치수를 알아낼 수 있는 유일한 방법은 밥과 협력하여 결과를 공유하는 것입니다.이렇게 하면 측정마다 Alice의 결과를 추출하고 이 정보를 사용하여 자신만 아는 암호 키를 만들 수 있습니다.

(k,n) 임계값 방식

위의 간단한 케이스는 임계값 설정 방식을 통해 Shamir 및 Blakley가 CSS에서 수행한 경우와 동일하게 확장할 수 있습니다.(k,n) 임계값 스킴(양자 스킴을 나타내는 이중 괄호)에서 앨리스는 자신의 비밀 키(양자 상태)를 n개의 공유로 분할하여 완전한 정보를 추출하는데 k aren 공유가 필요하지만 k-1 이하의 공유는 앨리스의 키에 대한 정보를 추출할 수 없다.

비밀 추출에 필요한 사용자 수는 n/2<k≤n으로 제한됩니다.n22k의 경우, (k,n) 임계값 스킴이 n의 2개의 분리된 k 세트에 적용되면 앨리스의 비밀 복사본 2개를 재구성할 수 있다.이것은 당연히 복제 금지 정리에 위배되므로 n은 2k 미만이어야 합니다.

(k,n) 임계값 스킴이 존재하는 한 (k,n-1) 임계값 스킴은 공유 1개를 폐기하는 것만으로 구성할 수 있습니다.이 방법은 k=n까지 반복할 수 있습니다.

다음은 간단한 ((2,3) 임계값 ^[4]스킴의 개요이며, Alice가 원래 상태를 분할하는 공유 수를 늘리면 보다 복잡한 스킴을 생각할 수 있습니다.

단일 Qutrit 상태로 시작하는 Alice를 고려합니다.

\displaystyle \mathrm {Psi} \rangle _{a}=\alpha 0\rangle +\color 1\rangle +\color 2\rangle ,}

3개의 큐트릿에 매핑합니다.

\displaystyle \mathrm = \alpha ( 000 \rangle + 111 \rangle + 222 \rangle ) + \rangle ( 012 \rangle + 120 \rangle + 201 \rangle ) + \rangle ( 021 \rangle + 102 \rangle + 210 \rangle ) }

3개의 리시버 각각과 1개의 큐트릿을 공유합니다.각 공유가 최대 혼합 상태이기 때문에 단일 공유는 앨리스의 원래 상태에 대한 정보를 제공하지 않는 것이 분명합니다.그러나 앨리스의 원래 상태를 복원하기 위해 두 개의 공유를 사용할 수 있습니다.처음 두 주식이 주어졌다고 가정합니다.첫 번째 주식을 두 번째 주식(모듈로 3)에 추가한 후 두 번째 주식의 새 가치를 첫 번째 주식에 추가합니다.결과 상태는 다음과 같습니다.

\displaystyle \mathrm {psi} \rangle =(\alpha 0\rangle +\rangle 1\rangle +\rangle 2\rangle )(00\rangle + 12\rangle + 21\rangle )

여기서 첫 번째 큐트릿은 정확히 앨리스의 원래 상태입니다.이 방법을 통해 송신자의 원래 상태를 수신자의 입자 중 하나로 재구성할 수 있지만, 이 재구성 과정이나 양자 상태 내의 중첩이 붕괴되지 않도록 하는 것이 중요합니다.

보안.

QSS의 보안은 부정직한 사용자뿐만 아니라 잠재적인 도청자로부터 보호하기 위해 복제 금지 정리에 의존합니다.이 절에서는 위에서 ^[7]간략히 언급한 두 입자 얽힘 프로토콜을 채택합니다.

도청

QSS는 양자 키 배포와 동일한 방법으로 도청으로부터 보안을 보장합니다.QSS 프로토콜에서 사용되는 양자 상태를 완벽하게 구별하고 생성할 수 있는 것으로 가정되는 도청자 이브에 대해 생각해 보십시오.이브의 목표는 수취인 중 한 명(예를 들어 밥의 주식)을 가로채서 측정하여 주를 재작성하여 최초 의도된 누구에게나 보내는 것이다.이 방법의 문제는 이브가 측정할 기준을 무작위로 선택해야 하고, 그 중 절반은 잘못된 기준을 선택할 수 있다는 것입니다.올바른 기준을 선택하면 정확한 측정 결과를 확실하게 얻을 수 있으며, 측정했던 상태를 다시 만들어 밥에게 보낼 수 있습니다.하지만, 그녀가 잘못된 기준을 선택하면, 그녀는 결국 두 상태 중 하나를 잘못된 기준에서 보내게 될 것이다.밥은 그녀가 보낸 상태를 측정할 것이고, 그 시간의 절반은 올바른 검출이 될 것입니다.단, 잘못된 기준에서 나온 상태가 두 개의 상태가 올바른 기준에서 동등하게 중첩되기 때문입니다.따라서 이브가 잘못된 기준으로 측정하여 잘못된 상태를 보내는 시간의 절반은 밥이 잘못된 상태를 측정합니다.이브의 개입은 25%의 추가 재판에서 프로토콜 오류를 야기합니다.따라서 충분한 측정치가 있으면 이론에서 예측한 50% 확률 대신 75% 확률로 발생하는 프로토콜 오류를 놓치는 것이 거의 불가능하며, 따라서 통신 채널 내에 도청자가 있음을 알 수 있습니다.

ancilla 상태를 사용하여 보다 복잡한 도청 전략을 수행할 수 있지만, 도청자는 여전히 유사한 방법으로 탐지할 수 있습니다.

부정직한 참가자

이제 프로토콜의 참가자 중 한 명(예를 들어 밥)이 다른 참가자가 알지 못하는 사이에 비밀을 얻으려고 시도함으로써 악의적인 사용자로 행동하고 있는 경우를 생각해 보겠습니다.가능성을 분석하면서, 사람들은 밥과 찰리가 도청 테스트를 할 때 측정 기준과 결과를 공개하는 적절한 순서를 선택하는 것이 일어날 수 있는 부정행위를 탐지할 수 있다는 것을 알게 된다.올바른 순서는 다음과 같습니다.

수신기 1은 측정 결과를 발표합니다.
수신기 2는 측정 결과를 발표합니다.
수신기 2는 측정 기준을 릴리스합니다.
수신기 1은 측정 기준을 릴리스합니다.

리시버 2는 리시버 1이 어떤 기준을 사용했는지 아직 알 수 없기 때문에 이 순서에 의해 리시버 2는 다른 참가자를 속이기 위해 어떤 기준을 공유해야 하는지 알 수 없습니다.마찬가지로, 수신기 1은 먼저 결과를 발표해야 하므로, 사용된 베이스의 유효한 조합에 대해 측정이 상관되어야 하는지 또는 반상관되어야 하는지를 제어할 수 없다.이와 같이 부정하게 행동하면 부정직한 참가자가 리시버 1인지 리시버 2인지를 도청 테스트 국면에서 에러가 발생합니다.따라서 부정직한 사용자가 다른 참가자의 눈에 띄지 않고 비밀을 획득하지 않도록 데이터 공개 순서를 신중하게 선택해야 한다.

실험적인 실현

이 절은 양자 ^[8]광학 기술의 발전을 통해 가능해진 2001년 QSS의 첫 번째 실험 시연에 이은 것이다.

GHz 상태를 사용하는 QSS에 대한 원래 아이디어는 § $(\$ ^[9] $displaystyle \chi$ ^{ $3})$ 비선형성 $\chi ^{3}$ 또는 3광자 포지트로늄 소멸을 통한 하향 변환 프로세스를 통해 3 입자 상관관계를 생성하는 것이 어려웠기 때문에 구현하기가 더 어려웠다.대신, 원래의 실험은 표준 $\chi ^{2}$ 2(\ $displaystyle \chi ^{2})$ 자연 $\chi ^{2}$ 파라미터 다운 변환(SPDC) 프로세스를 사용하여 두 입자 체계를 통해 수행되었으며, 세 번째 관련 광자는 펌프 광자였다.

자발적 파라미터 다운컨버전(SPDC)을 통한 2광자 양자비밀공유(QSS) 셋업

실험 설정은 다음과 같이 동작합니다.

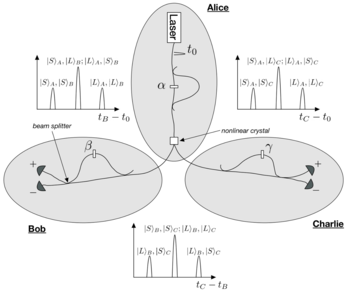
앨리스: 시간 $t_{0}$ 0 $({$ 에 $t_{{0}}$ 방출되는 펄스 레이저가 경로 길이가 다른 간섭계에 들어가 펌프가 동일한 진폭의 두 개의 서로 다른 시간 펄스로 분할됩니다.간섭계의 한쪽 암에는 두 $\alpha .$ 암의 위상차를 제어하는 위상 시프터가 포함되어 $\alpha .$ . α $.$ {\ $display$ \alpha $.}$ 펌프 $\alpha .$ 펄스는 SPDC를 통해 펌프 광자 중 일부가 광자 쌍으로 하향 변환되는 비선형 결정에 초점이 맞춰집니다.다음으로 SPDC 쌍이 분할되어 하나는 Bob에게, 다른 하나는 Charlie에게 전송됩니다.
밥과 찰리:두 리시버 모두 Alice가 사용한 것과 동일한 간섭계를 가지고 있어 두 암 사이의 시간차가 정확히 일치하며 Bob의 경우 β $(\displaystyle \beta$ ), Charlie의 경우 $\gamma$ (\ $displaystyle \gamma)$ 로 $\beta$ $\gamma$ 표시된 위상 시프트기가 있습니다.간섭계마다 가능한 궤적이 다르기 때문에 앨리스의 펌프 펄스가 방출되는 시점과 Bob 및 Charlie의 SPDC 광자가 감지되는 시점 사이에 세 가지 뚜렷한 시간 차이( $t_{B}$ t B ${\$ $t_{C}$ C {\ $displaystyle t_{C$ 가 발생합니다.밥과 찰리의 탐지기 각각에 배치되어 있어요

$|\mathrm {X} \rangle _{i},|\mathrm {Y} \rangle _{j}$ $|\mathrm {X} \rangle _{i},|\mathrm {Y} \rangle _{j}$ , $|\mathrm {X} \rangle _{i},|\mathrm {Y} \rangle _{j}$ Y $|\mathrm {X} \rangle _{i},|\mathrm {Y} \rangle _{j}$ j \ $displaystyle$ \ $mathrm$ { X } \ $rangle$ _ { $i$ } , \ $mathrm$ { Y $}$ \ $rangle$ _ ${j}$ 를 $|\mathrm {X} \rangle _{i},|\mathrm {Y} \rangle _{j}$ 사용합니다.여기서 X와 Y는 쇼트 패스의 경우 'S' 또는 롱 패스의 경우 'L'이며 i와 j는 참가자의 'A', 'B' 또는 'Cometer' 중 하나입니다.. S $|\mathrm {S} \rangle _{A},|\mathrm {L} \rangle _{j}$ $|\mathrm {S} \rangle _{A},|\mathrm {L} \rangle _{j}$ 、 $、$ j \ $displaystyle$ \ $mathrm$ { S } \ $rangle$ _ { $A$ } , \ $mathrm$ ${$ L } \ $rangle$ $|\mathrm {S} \rangle _{A},|\mathrm {L} \rangle _{j}$ _ { $j$ } 및 $|\mathrm {L} \rangle _{A},|\mathrm {S} \rangle _{j}$ $|\mathrm {L} \rangle _{A},|\mathrm {S} \rangle _{j}$ $、$ $|\mathrm {L} \rangle _{A},|\mathrm {S} \rangle _{j}$ \ $displaystyle$ \ $mathrm$ { L } \ $rangle _$ { A 、 \ rangle { $A$ } 중 $|\mathrm {S} \rangle _{A},|\mathrm {L} \rangle _{j}$ $|\mathrm {L} \rangle _{A},|\mathrm {S} \rangle _{j}$ 하나 입니다 $.$ e는 완전히 똑같다.S $|\mathrm {S} \rangle _{B},|\mathrm {S} \rangle _{C}$ B $|\mathrm {S} \rangle _{B},|\mathrm {S} \rangle _{C}$ 、 $|\mathrm {S} \rangle _{B},|\mathrm {S} \rangle _{C}$ C \ $displaystyle$ \ $mathrm { S$ } \ $rangle$ _ { $B$ $|\mathrm {L} \rangle _{B},|\mathrm {L} \rangle _{C}.$ $}$ , \ $mathrm$ { $S }$ \ $rangle$ _ { $C$ $|\mathrm {L} \rangle _{B},|\mathrm {L} \rangle _{C}.$ $|\mathrm {L} \rangle _{B},|\mathrm {L} \rangle _{C}.$ L . \ $displaystyle$ \ $mathrm$ { $L$ \ $rangle$ _ { $B }$ 、 \ $langle$ { $L }$ 。

\mathrm {psi } \rangle = {1} {\rangle {2}(L\rangle _ {A}, S\rangle _ {B} S\rangle _{C}+e^{i(\alpha +\lang +\langle )} S\rangle _{A}, L\rangle _{B

이는 "의사 GHZ 상태"로 간주될 수 있으며, 실제 GHZ 상태와의 차이점은 "의사 GHZ 상태"라고 생각할 수 있습니다.그럼에도 불구하고, 삼중 "사고"는 실제 GHZ 상태와 정확히 동일한 확률 함수로 설명할 수 있다.

(\displaystyle P_{i,j,k}=param frac {1}{8}}(1+ijk\cos(\alpha +\cos(\alpha +\cos +\clos)),})

QSS는 이 2개의 파티클 소스에 대해서도 동일하게 동작합니다.

위상α $\alpha ,\beta ,$ $\gamma$ $,$ \ $displaystyle$ \ $alpha,$ \ $beta$ $\gamma$ $,$ ${\$ \ $displaystyle \gamma$ } or or0 또는 $(\$ }{ $2})$ 로 ${\frac {\pi }{2}}$ 설정하면 이 설정이 3개의 입자에 대한 벨 타입의 부등식을 위반함을 알 수 있습니다.

S_{3}=|E(\alpha '+\beta +\gamma )+E(\alpha +\beta '+\gamma )+E(\alpha +\beta +\gamma ')-E(\alpha '+\beta '+\gamma ')|\leq {2}

3

S_{3}=|E(\alpha '+\beta +\gamma )+E(\alpha +\beta '+\gamma )+E(\alpha +\beta +\gamma ')-E(\alpha '+\beta '+\gamma ')|\leq {2}

(

S_{3}=|E(\alpha '+\beta +\gamma )+E(\alpha +\beta '+\gamma )+E(\alpha +\beta +\gamma ')-E(\alpha '+\beta '+\gamma ')|\leq {2}

+

S_{3}=|E(\alpha '+\beta +\gamma )+E(\alpha +\beta '+\gamma )+E(\alpha +\beta +\gamma ')-E(\alpha '+\beta '+\gamma ')|\leq {2}

β

S_{3}=|E(\alpha '+\beta +\gamma )+E(\alpha +\beta '+\gamma )+E(\alpha +\beta +\gamma ')-E(\alpha '+\beta '+\gamma ')|\leq {2}

+

S_{3}=|E(\alpha '+\beta +\gamma )+E(\alpha +\beta '+\gamma )+E(\alpha +\beta +\gamma ')-E(\alpha '+\beta '+\gamma ')|\leq {2}

+

S_{3}=|E(\alpha '+\beta +\gamma )+E(\alpha +\beta '+\gamma )+E(\alpha +\beta +\gamma ')-E(\alpha '+\beta '+\gamma ')|\leq {2}

)

S_{3}=|E(\alpha '+\beta +\gamma )+E(\alpha +\beta '+\gamma )+E(\alpha +\beta +\gamma ')-E(\alpha '+\beta '+\gamma ')|\leq {2}

+

S_{3}=|E(\alpha '+\beta +\gamma )+E(\alpha +\beta '+\gamma )+E(\alpha +\beta +\gamma ')-E(\alpha '+\beta '+\gamma ')|\leq {2}

(

S_{3}=|E(\alpha '+\beta +\gamma )+E(\alpha +\beta '+\gamma )+E(\alpha +\beta +\gamma ')-E(\alpha '+\beta '+\gamma ')|\leq {2}

S_{3}=|E(\alpha '+\beta +\gamma )+E(\alpha +\beta '+\gamma )+E(\alpha +\beta +\gamma ')-E(\alpha '+\beta '+\gamma ')|\leq {2}

β +

S_{3}=|E(\alpha '+\beta +\gamma )+E(\alpha +\beta '+\gamma )+E(\alpha +\beta +\gamma ')-E(\alpha '+\beta '+\gamma ')|\leq {2}

+

S_{3}=|E(\alpha '+\beta +\gamma )+E(\alpha +\beta '+\gamma )+E(\alpha +\beta +\gamma ')-E(\alpha '+\beta '+\gamma ')|\leq {2}

) -

S_{3}=|E(\alpha '+\beta +\gamma )+E(\alpha +\beta '+\gamma )+E(\alpha +\beta +\gamma ')-E(\alpha '+\beta '+\gamma ')|\leq {2}

( α

S_{3}=|E(\alpha '+\beta +\gamma )+E(\alpha +\beta '+\gamma )+E(\alpha +\beta +\gamma ')-E(\alpha '+\beta '+\gamma ')|\leq {2}

+ β +

S_{3}=|E(\alpha '+\beta +\gamma )+E(\alpha +\beta '+\gamma )+E(\alpha +\beta +\gamma ')-E(\alpha '+\beta '+\gamma ')|\leq {2}

)

S_{3}=|E(\alpha '+\beta +\gamma )+E(\alpha +\beta '+\gamma )+E(\alpha +\beta +\gamma ')-E(\alpha '+\beta '+\gamma ')|\leq {2}

S_{3}=|E(\alpha '+\beta +\gamma )+E(\alpha +\beta '+\gamma )+E(\alpha +\beta +\gamma ')-E(\alpha '+\beta '+\gamma ')|\leq {2}

E ( \

display style

S_

{3

} =

E

( \

alpha

' + \

display

style + \

β

+ β +

S_{3}=|E(\alpha '+\beta +\gamma )+E(\alpha +\beta '+\gamma )+E(\alpha +\beta +\gamma ')-E(\alpha '+\beta '+\gamma ')|\leq {2}

) + ′ ) + E ( \ α ' + s + \ ) + \ ) + s ) + s ) + s ) + s + s s ) s s s s s s

$E(\alpha +\beta +\gamma )$ 서 E $E(\alpha +\beta +\gamma )$ $E(\alpha +\beta +\gamma )$ β + $)$ {{ $displaystyle$ E $(\$ $S_{exp}=3.69$ $E(\alpha +\beta +\gamma )$ +\ $display +\displays})$ 는 $E(\alpha +\beta +\gamma )$ 위상 시프트 설정 $(\alpha ,\beta ,\gamma )$ β, $,$ δ) { $displaystyle(\alpha$ ,\displays $,\$ displays $(\alpha ,\beta ,\gamma )$ 의 일치 측정에 대한 기대치입니다. 이 실험에서 벨형 부등식은 S $(S)$ 에서 $S_{exp}=3.69$ 되었습니다.g 이 설정에 양자 논로컬리티가 있음을 나타냅니다.

이 중요한 실험은 이 설정의 양자 상관관계가 확률 $P_{i,j,k}.$ P $P_{i,j,k}.$ , $P_{i,j,k}.$ , $P_{i,j,k}.$ . { $displaystyle P_{i,j,k}$ 에 의해 실제로 $P_{i,j,k}.$ 설명된다는 것을 보여주었다. SPDC 소스의 단순성은 기존의 3광자 얽힘 소스에 비해 훨씬 높은 비율로 일치성을 허용하여 QSS를 보다 실용적으로 만들었다.이것은 QSS 프로토콜의 실현 가능성을 증명하는 첫 번째 실험이었다.

레퍼런스

^ Shamir, Adi (1 November 1979). "How to share a secret" (PDF). Communications of the ACM. 22 (11): 612–613. doi:10.1145/359168.359176. S2CID 16321225. Archived (PDF) from the original on 2017-08-10.
^ Blakley, G.R. (1979). "Safeguarding Cryptographic Keys" (PDF). Managing Requirements Knowledge, International Workshop on (AFIPS). 48: 313–317. doi:10.1109/AFIPS.1979.98. S2CID 38199738. Archived from the original (PDF) on 2018-06-28.
^ Hillery, Mark; Bužek, Vladimír; Berthiaume, André (1998). "Quantum Secret Sharing" (PDF). Physical Review A. 59 (3): 1829–1834. doi:10.1103/PhysRevA.59.1829. Retrieved 2021-12-14.
^ ^a ^b Cleve, Richard; Gottesman, Daniel; Lo, Hoi-Kwong (1999). "How to share a quantum secret" (PDF). Physical Review Letters. 83 (3): 648–651. doi:10.1103/PhysRevLett.83.648. Retrieved 14 December 2021.
^ Gottesman, Daniel (2000). "Theory of quantum secret sharing". Physical Review A. 61 (4): 042311. doi:10.1103/PhysRevA.61.042311. Retrieved 14 December 2021.
^ Wiesner, Stephen (January 1983). "Conjugate coding". ACM SIGACT News. 15 (1): 78–88. doi:10.1145/1008908.1008920. Retrieved 16 December 2021.
^ ^a ^b Karlsson, Anders; Koashi, Masato; Imoto, Nobuyuki (1999). "Quantum entanglement for secret sharing and secret splitting". Physical Review A. 59 (1): 162–168. doi:10.1103/PhysRevA.59.162. Retrieved 14 December 2021.
^ Tittel, W.; Zbinden, H.; Gisin, N. (2001). "Experimental demonstration of quantum secret sharing". Physical Review A. 63 (4): 042301. doi:10.1103/PhysRevA.63.042301. Retrieved 15 December 2021.
^ Żukowski, M.; Zeilinger, A.; Horne, M.A.; Weinfurter, H. (1998). "Quest for GHZ states" (PDF). Acta Physics Polonica A. 98 (1): 187–195. Retrieved 15 December 2021.

[shamir-1] Shamir, Adi (1 November 1979). "How to share a secret" (PDF). Communications of the ACM. 22 (11): 612–613. doi:10.1145/359168.359176. S2CID 16321225. Archived (PDF) from the original on 2017-08-10.

[blakley-2] Blakley, G.R. (1979). "Safeguarding Cryptographic Keys" (PDF). Managing Requirements Knowledge, International Workshop on (AFIPS). 48: 313–317. doi:10.1109/AFIPS.1979.98. S2CID 38199738. Archived from the original (PDF) on 2018-06-28.

[hillery-3] Hillery, Mark; Bužek, Vladimír; Berthiaume, André (1998). "Quantum Secret Sharing" (PDF). Physical Review A. 59 (3): 1829–1834. doi:10.1103/PhysRevA.59.1829. Retrieved 2021-12-14.

[cleve-4] Cleve, Richard; Gottesman, Daniel; Lo, Hoi-Kwong (1999). "How to share a quantum secret" (PDF). Physical Review Letters. 83 (3): 648–651. doi:10.1103/PhysRevLett.83.648. Retrieved 14 December 2021.

[gottesman-5] Gottesman, Daniel (2000). "Theory of quantum secret sharing". Physical Review A. 61 (4): 042311. doi:10.1103/PhysRevA.61.042311. Retrieved 14 December 2021.

[6] Wiesner, Stephen (January 1983). "Conjugate coding". ACM SIGACT News. 15 (1): 78–88. doi:10.1145/1008908.1008920. Retrieved 16 December 2021.

[karlsson-7] Karlsson, Anders; Koashi, Masato; Imoto, Nobuyuki (1999). "Quantum entanglement for secret sharing and secret splitting". Physical Review A. 59 (1): 162–168. doi:10.1103/PhysRevA.59.162. Retrieved 14 December 2021.

[8] Tittel, W.; Zbinden, H.; Gisin, N. (2001). "Experimental demonstration of quantum secret sharing". Physical Review A. 63 (4): 042301. doi:10.1103/PhysRevA.63.042301. Retrieved 15 December 2021.

[9] Żukowski, M.; Zeilinger, A.; Horne, M.A.; Weinfurter, H. (1998). "Quest for GHZ states" (PDF). Acta Physics Polonica A. 98 (1): 187–195. Retrieved 15 December 2021.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

Search