필요성과 충분성
Necessity and sufficiency논리학과 수학에서 필요성과 충분성은 두 진술 사이의 조건부 또는 함축적 관계를 설명하기 위해 사용되는 용어입니다.예를 들어 조건문 "If P then Q"에서는 Q의 진실은 P의 진실에 의해 보장되기 때문에 P에 Q가 필요합니다(따라서 [1]Q가 없으면 P를 가질 수 없습니다).마찬가지로 P가 true이면 항상 Q가 true임을 의미하지만 P가 true가 아니라고 해서 항상 Q가 [2]true가 아닌 것은 아니기 때문에 P는 Q에 대해 충분합니다.
일반적으로 필요한 조건은 다른 조건이 발생하기 위해 존재해야 하는 조건이며, 충분한 조건은 해당 조건을 [3]발생시키는 조건이다.진술이 다른 진술의 "필요하고 충분한" 조건이라는 주장은 전자의 진술이 사실일 경우에만 사실이라는 것을 의미한다.즉, 두 개의 문장은 동시에 참이거나 동시에 [4][5][6]거짓이어야 합니다.
일반 영어(또한 자연어)에서 "필요"와 "충분"은 진술이 아닌 조건이나 상황 사이의 관계를 나타냅니다.예를 들어, 남성이 되는 것은 형제가 되기 위한 필수 조건이지만, 충분하지는 않다. 반면 남성 형제가 되는 것은 형제가 되기 위한 필수적이고 충분한 조건이다.조건문은 하나 이상의 충분한 조건과 하나 이상의 필요한 조건으로 구성됩니다.
정의들
조건문에서는 S로 표현되는 식을 선행이라고 하고, N으로 표현되는 식을 결과라고 한다.이 조건부 문장은 "N if S", "S only if N", "S only if N", "S uny N", "N은 S에 의해 암시됨", "S → N, S † N 및 "N anywhere S"[7]와 같은 여러 가지 동등한 방법으로 작성될 수 있다.
이 경우 N은 S에 필요한 조건이라고 한다.일반적인 언어에서 이것은 조건부 진술이 참인 경우, 결과 N이 참이어야 한다고 말하는 것과 같다. S가 참인 경우(아래 "진실 표"의 세 번째 열 참조).즉, N이 참이 아니면 선행 S가 참이 될 수 없다.예를 들어, 누군가가 소크라테스라고 불리기 위해서는 그 누군가가 명명되어야 한다.마찬가지로 인간이 살기 위해서는 [8]공기가 있어야 한다.
이 경우 S는 N에 대해 충분한 조건이라고 할 수 있다(아래 진실표의 세 번째 열 참조).조건부 스테이트먼트가 true일 경우 S가 true이면 N이 true여야 하며 조건부 스테이트먼트가 true이고 N이 true이면 S가 true이거나 false일 수 있습니다.일반적으로 "S의 진실은 N의 진실을 보장한다"[8]는 것이다.예를 들어, 앞의 예로부터, 누군가가 소크라테스라고 불리는 것을 아는 것으로는 누군가가 이름을 가지고 있다는 것을 알기에 충분하다고 말할 수 있다.
필요충분조건은SN \ S \ N N \ S \ S( S N \ S \ N of of of of of of of of of ofof of of of of of of of of of of of of a a a a a a a a a a a a 。첫 번째 암시는 S가 N에 대해 충분한 조건임을 시사하고, 두 번째 암시는 S가 N에 대해 필요한 조건임을 시사한다.이는 "S is need and efficient for N", "S if and only if N" "S N\ S \ N으로 표시됩니다
| S | N | |||
|---|---|---|---|---|
| T | T | T | T | T |
| T | F | F | T | F |
| F | T | T | F | F |
| F | F | T | T | T |
필요성

P에 Q가 필요하다는 주장은 "Q가 참이 아니면 P가 참이 될 수 없다" 또는 "Q가 거짓이면 P가 거짓이다"[8][1]와 구어적으로 동등하다.반대로 말하면, 이것은 "P가 참이면 Q도 마찬가지"와 같습니다.
P와 Q의 논리관계는 "If P, then Q"로 표현되며 "P q Q"로 표기됩니다(P는 Q를 의미합니다).또한 "P only if Q", "Q, if P", "Q any P" 및 "Q when P" 중 하나로 표현될 수 있다.예를 들어 수학 산문에서는 예 5와 같이 충분한 조건(즉, 개별적으로 필요하고 공동으로[8] 충분한 조건)을 구성하는 몇 가지 필요한 조건을 종종 찾을 수 있다.
- 예 1
- '존은 독신이다'가 사실이기 위해서는 그가 독신이라는 것도 사실이어야 한다.
- 미혼,
- 남자,
- 어른들
- "존은 독신이다"라고 말하는 것은 존이 세 가지 술어를 각각 가지고 있다는 것을 의미하기 때문이다.
- 예 2
- 2보다 큰 정수의 경우, 홀수는 소수이기 때문에 홀수가 되어야 합니다. 왜냐하면 2는 짝수이자 소수이기 때문입니다.
- 예 3
- 번개에 의해 발생하는 소리인 천둥을 생각해 보자.번개는 천둥 없이는 일어나지 않기 때문에 번개는 번개에 필요하다고 말한다.번개가 칠 때마다 천둥소리가 나요.번개가 번개를 일으키는 것은 아니지만 번개는 항상 천둥과 함께 오기 때문에 번개는 번개에 필요하다고 말한다.
- 예 4
- 미국 상원에서 일하기 위해서는 적어도 30세가 되어야 한다.만약 당신이 30세 미만이라면, 상원의원이 되는 것은 불가능하다.즉, 만약 당신이 상원의원이라면, 당신은 적어도 30살이 되어야 한다.
- 예 5
- 대수학에서, 일부 집합 S와 연산 { }가 그룹을 형성하기 위해서는 { }가 연관성이 있어야 한다.또한 S의 모든 x에 대해 e \} 및 x \} 가 모두 x가 되도록 S에 특수 요소 e를 포함할 필요가 있다.또한 S의 모든 x에 대응하는 요소 x'가 존재해야 합니다.그러면 x displaystyle ' 와 x '\\star 가 모두 특수 요소 e 와 같아집니다.이 세 가지 필수 조건만으로는 충분하지 않지만, 이 세 가지 조건을 합치면 충분합니다.
충분.
P가 Q에 충분한 경우 P가 참임을 아는 것이 Q가 참임을 결론짓는 데 충분한 근거가 됩니다.단, P가 거짓임을 아는 것은 Q가 거짓이라고 결론짓는 최소한의 필요성을 충족시키지 못합니다.
논리관계는 이전과 같이 "If P, then Q" 또는 "P q Q"로 표현된다.이는 "P only if Q", "P incommends Q" 또는 다른 여러 변형으로 표현될 수도 있습니다.예 5에서 설명한 바와 같이, 여러 가지 충분한 조건을 함께 취했을 때, 단일 필수 조건(즉 개별적으로 충분하고 공동으로 필요한 조건)을 구성하는 경우가 있을 수 있다.
- 예 1
- "John is King"은 John이 남자라는 것을 암시한다.그래서 존이 왕이라는 것을 아는 것만으로 그가 남자라는 것을 알 수 있다.
- 예 2
- 4로 나눌 수 있는 숫자는 짝수가 되기에 충분하지만(필요하지는 않지만), 2로 나눌 수 있는 숫자는 짝수가 되기에 충분하고 필요한 숫자입니다.
- 예 3
- 천둥의 발생은 천둥을 듣고 명확하게 인식함으로써 번개가 있었다는 결론을 정당화한다는 점에서 번개가 발생하기 위한 충분한 조건이다.
- 예 4
- 미 의회가 법안을 통과시키면 대통령의 서명만으로도 충분히 법제화할 수 있다.대통령이 거부권을 행사하는 등 법안에 서명하지 않은 경우는 법안이 법이 되지 않았다는 것을 의미하지 않습니다(예를 들어, 의회의 재정의를 통해 법이 될 수도 있습니다).
- 예 5
- 플레이 카드의 중앙에 큰 스페이드(♠)를 1개 표시하면 카드가 에이스가 될 수 있습니다.카드 중앙에 다이아몬드(♦), 하트(♥) 또는 클럽(♣)이 하나 더 있는 다른 세 가지 조건이 있습니다.카드가 에이스가 되기 위해서는 이러한 조건 중 어느 것도 필요하지 않지만, 이러한 조건 중 적어도 하나를 충족시키지 않으면 카드가 에이스가 될 수 없기 때문에 이러한 조건의 해제는 필요하지 않습니다.
필요성과 충분성의 관계
조건은 필요하거나 충분할 수 있으며, 다른 조건이 될 필요는 없습니다.예를 들어 포유류(N)가 되는 것은 필요하지만 인간(S)이 되기에는 불충분하고 x)가 합리적(N)이면 충분하지만 숫자 x)가 실수(N)가 되기 는 필요하지 않다(합리적이지 않은 실수가 있기 때문에).
조건은 필요하고도 충분할 수 있습니다.예를 들어 현재 "오늘은 7월 4일"은 "오늘은 미국의 독립기념일"에 필요한 충분한 조건이다.마찬가지로 행렬 M의 가역성을 위해 필요하고 충분한 조건은 M이 0이 아닌 행렬식을 갖는 것입니다.
수학적으로 말하면, 필요성과 충분성은 서로 이중적이다.어떤 스테이트먼트 S와 N에 대해서도, "N은 S에 필요하다"는 주장은 "S는 N에 충분하다"는 주장과 같다.이 이중성의 또 다른 측면은 위에서 설명한 바와 같이 필요한 조건의 결합(및 사용)은 충분하고 충분한 조건의 분리(또는 사용)는 필요성에 도달할 수 있다는 것이다.세 번째 면에서는 N이 참인 객체, 이벤트 또는 스테이트먼트의 집합 T(N)로 모든 수학적 술어 N을 식별한다.그러면 S에 대한 N의 필요성을 주장하는 것은 T(S)의 슈퍼셋이라고 주장하는 것과 동등하지만, N에 대한 S의 충분성을 주장하는 것은 T(S)와 동등하다.
필요성과 충분성의 동시성
P가 Q에 필요하고 충분하다고 말하는 것은 다음 두 가지를 말하는 것입니다.
- P는 Q, PQ(\ P\왼쪽 Q에 필요하고 P는 Q, Q(\ P\오른쪽 Q에 충분합니다.
- 마찬가지로 P와 Q는 다른 쪽 Q QP p P \ P \ Q \ Q \ P에는 필요한 것으로 이해될 수 있으며, 각각은 서로 충분하거나 암시할 수도 있다.
PQ \ P \ Q、 P Q \ P\ Arrow P displaydisplaydisplaydisplaydisplay displaydisplaydisplaydisplaydisplaydisplaydisplaydisplaydisplaydisplaydisplaydisplaydisplay displaydisplaydisplaydisplay displaydisplaydisplaydisplay displaydisplaydisplaydisplaydisplaydisplaydisplaydisplay displaydisplaydisplaydisplaydisplaydisplaydisplaydisplaydisplaydisplaydisplaydisplaydisplaydisplaydisplay displaydisplaydisplaydisplaydisplaydisplaydisplaydisplaydisplaydisplaydisplaydisplay displaydisplaydisplaydisplaydisplaydisplaydisplaydisplaydisplaydisplaydisplaydisplaydisplaydisplay displaydisplaydisplaydisplaydisplaydisplaydisplaydisplay
예를 들어 그래프 이론에서 그래프 G는 G의 모든 가장자리가 각 색상의 끝점을 가지도록 각각의 정점에 검은색 또는 흰색으로 할당할 수 있는 경우 이분이라고 불립니다.그래프가 양분되기 위해서는 홀수 길이의 사이클을 포함하지 않는 것이 필수적이고 충분한 조건입니다.따라서 그래프가 홀수 주기를 가지고 있는지 여부를 발견하는 것은 그래프가 초당적인지, 그리고 그 반대로도 마찬가지인지 알 수 있다.철학자는[9] 이러한 상황을 다음과 같이 특징지을 수 있다: "초당과 홀수 주기의 부재의 개념은 의도에 따라 다르지만,[10] 그들은 동일한 확장을 가지고 있다.
수학에서 정리법은 종종 "P가 참인 경우 그리고 Q가 참인 경우에만"이라는 형식으로 언급된다.
앞의 항에서 설명한 바와 같이 다른 한쪽의 필요성은 첫 번째 한쪽의 필요성과 같기 때문에 예를 P Q \P \ Left Q is Q P p 、 Q p P \ , 、 P necessary P and and P and and and 、 P and P and and and and and and p p p p p p p p p p p p p p p for for for forfficientfficientfficientfficientfficientfficientfficientfficient fficientfficientfficientfficientfficientfficientfficientfficientfficient p p p pfficientfficientfficientfficientfficientfficientfficientfficientP Q QP { P \ left Q \ Q \ P} 라고 , 「Q가 true인 경우 및 P가 true인 경우에만 Q가 true」라고 하면 됩니다.
「 」를 참조해 주세요.
레퍼런스
- ^ a b "[M06] Necessity and sufficiency". philosophy.hku.hk. Retrieved 2019-12-02.
- ^ Bloch, Ethan D. (2011). Proofs and Fundamentals: A First Course in Abstract Mathematics. Springer. pp. 8–9. ISBN 978-1-4419-7126-5.
- ^ Confusion-of-Necessary (2019-05-15). "Confusion of Necessary with a Sufficient Condition". www.txstate.edu. Retrieved 2019-12-02.
- ^ Betz, Frederick (2011). Managing Science: Methodology and Organization of Research. New York: Springer. p. 247. ISBN 978-1-4419-7487-7.
- ^ Manktelow, K. I. (1999). Reasoning and Thinking. East Sussex, UK: Psychology Press. ISBN 0-86377-708-2.
- ^ Asnina, Erika; Osis, Janis & Jansone, Asnate (2013). "Formal Specification of Topological Relations". Databases and Information Systems VII. 249 (Databases and Information Systems VII): 175. doi:10.3233/978-1-61499-161-8-175.
- ^ Devlin, Keith (2004), Sets, Functions and Logic / An Introduction to Abstract Mathematics (3rd ed.), Chapman & Hall, pp. 22–23, ISBN 978-1-58488-449-1
- ^ a b c d "The Concept of Necessary Conditions and Sufficient Conditions". www.sfu.ca. Retrieved 2019-12-02.
- ^ 스탠포드 대학 입문서, 2006년.
- ^ "이런 의미에서 의미는 종종 인텐션(intensions)이라고 불리며 지정된 것을 확장이라고 합니다.확장이 중요한 콘텍스트는 당연히 확장이라고 불리지만 확장이 충분하지 않은 콘텍스트는 집중적입니다.수학은 일반적으로 전체적으로 확장됩니다."스탠포드 대학 입문서, 2006년.
외부 링크
- 비판적 사고 웹 튜토리얼:필요충분조건
- 사이먼 프레이저 대학교:예시를 포함한 개념






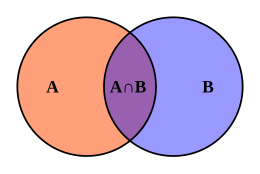
 합리적(N)이면 충분하지만 숫자 x
합리적(N)이면 충분하지만 숫자 x







