자기 쌍극자

전자기학에서 자기 쌍극자는 자기 모멘트를 일정하게 유지하면서 소스의 크기가 0으로 감소함에 따라 전류의 닫힌 루프 또는 한 쌍의 극의 한계이다.이것은 전기 쌍극자의 자기 유사체이지만, 유추는 완벽하지 않다.특히, 전하의 자기 유사체인 진정한 자기 모노폴은 자연에서 관찰된 적이 없습니다.그러나 자기 단극 준입자는 특정 응축 물질 ^[2]시스템의 출현 특성으로 관찰되었습니다.게다가, 자기 쌍극자 모멘트의 한 형태는 기본 양자 특성인 소립자의 스핀과 관련이 있다.

자기 단극이 존재하지 않기 때문에, 정적 자기원으로부터 먼 거리에 있는 자기장은 같은 쌍극자 모멘트를 가진 쌍극자의 장처럼 보입니다.다이폴 모멘트가 없는 고차 선원(예: 쿼드루폴)의 경우, 그 장은 다이폴 장보다 더 빠른 거리로 0을 향해 감소한다.

자기 쌍극자 모멘트에 의해 발생하는 외부 자기장

고전물리학에서 쌍극자의 자기장은 자기모멘트 m을 일정하게 유지하면서 소스가 한 점으로 축소됨에 따라 전류루프 또는 한 쌍의 전하의 한계로 계산된다.전류 루프의 경우 이 한계는 벡터 ^[3]전위로부터 가장 쉽게 도출됩니다.

${\displaystyle {\mathbf {A}({\mathbf {r}) = frac {\mathbf {m} {4\pi r^2}} {\frac {\mathbf {m} } } = frac {\mathbf {0} } {\f}$

여기서₀ μ는 진공 투과성 상수이고 4µr은² 반지름 r 구면의 표면이다.자속 밀도(B장의 강도)는 다음과 같습니다^[3].

$\displaystyle \mathbf {B}({\mathbf {r} } =\displayla \times {mathbf {A}} =times {mathbf {0} {4\pi }}} left[\frac {3\mathbf {r}(\mathbf {m} \cdot \mathbf {r} {r} {r} {r} {r} {r} {r} } {r} } } } {r} }}$

또는 먼저 자극 한계에서 스칼라 전위를 구할 수 있다.

$\displaystyle \psi({\mathbf {r} } = scdot {\mathbf {m} } {4\pi r^{3}} }$

따라서 자기장 강도(또는 H장의 강도)는

${\displaystyle {\mathbf {H}({\mathbf {r}) =\displayla \psi = scfff frac {1}{4\pi}}}\left[{\frac {3\mathbf {r}(\mathbf {m})\cdot \mathbf {r} {r} }}$

자기장 강도는 자기 모멘트 축을 중심으로 회전할 때 대칭입니다.구면 좌표에서 z^ = r^ cosθ -^ sin ⁡ displaydisplay $display$ \ style $\mathbf {hat$ {$r}$= \$mathbf {r}$ \$cos \theta -$ {\$boldsymbol$ {$hat }$ \sin \$theta }$ \$sin$\sin \theta }일 때 z축 강도와 같이 간단하게 표현할 수 있습니다.

$\displaystyle \mathbf {H}({\mathbf {r} } = sn frac {\mathbf {m} } {4\pi r^{3}}\left(2\cos \theta {r} +\sin \theta }, {\boldsymbol {\hat } } } } } {\ {\ {\ {\ {\ 。}$

다이폴 내부 자기장

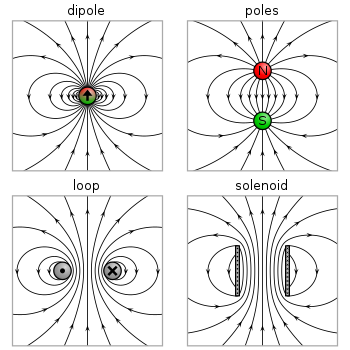
다이폴의 두 모델(전류 루프와 자극)은 소스에서 멀리 떨어진 자기장에 대해 동일한 예측을 제공합니다.그러나 소스 영역 내에서는 서로 다른 예측을 내놓습니다.극간 자기장은 자기 모멘트(음전하로부터 양전하를 가리키는 것)와 반대 방향이며 전류 루프 내에서는 같은 방향입니다(오른쪽 그림 참조).소스 크기가 0으로 줄어들기 때문에 이러한 필드의 제한도 달라야 합니다.이 구별은 자성 물질 내부의 필드를 계산하기 위해 쌍극자 한계를 사용하는 경우에만 문제가 됩니다.

전류 루프를 점점 더 작게 만들고 전류와 면적의 곱을 일정하게 유지함으로써 자기 쌍극자가 형성되면, 제한장은

${\displaystyle \mathbf {B}(\mathbf {r})=frac {0} {4\pi }}\left[\frac {3\mathbf {r}(\mathbf {r})\cdot \mathbf {m}-\mathbf {m} ^3}$

여기서 θ(r)는 3차원의 Dirac 델타 함수입니다.이전 섹션의 식과 달리 이 제한은 쌍극자의 내부 필드에 대해 정확합니다.

만약 자기 쌍극자가 "북극"과 "남극"을 취하여 형성되고, 이들을 점점 더 가깝게 하지만 자기극 전하와 거리의 곱을 일정하게 유지한다면, 한계장은 다음과 같다.

$(\displaystyle \mathbf {r})(\mathbf {r}) = spec frac {1}{4\pi }} \left [\frac {3\mathbf {r} (\mathbf {m}) - \mathbf {m} {\frac} ^3} } } }}$

이러한 필드는 B = μ₀(H + M)로 관련지어집니다.

$\displaystyle \mathbf {M}(\mathbf {r})=\mathbf {m} \displaystyle(\mathbf {r})}$

자화입니다.

두 개의 자기 쌍극자 사이의 힘

한 쌍극자 모멘트 m이 벡터 r에 의해 분리된 다른₂ m에₁ 가해지는 힘 F는 다음을 ^[4]사용하여 계산할 수 있다.

${\displaystyle \mathbf {F} =\displayla \left(\mathbf {m} _{2} \cdot \mathbf {B} _{1} \right),}$

또는

$\displaystyle \mathbf {F}(\mathbf {r},\mathbf {m},\mathbf {m},\mathbf {m},\mathbf {m},\pi r^{5}}},\left[(\mathbf {1}\cdot \mathbf {m}){r}} {r^{2}}\mathbf {r} \right],}$

여기서 r은 쌍극자 사이의 거리입니다.m에 작용하는₁ 힘은 반대 방향이다.

토크는 다음 공식에서 구할 수 있습니다.

${\displaystyle {\boldsymbol {\mathbf {m} _{2} \times \mathbf {B} _{1}.}$

유한원으로부터의 쌍극자장

유한한 소스에 의해 생성되지만 그 외부에 있는 자기 스칼라 전위는 다중극 확장에 의해 표현될 수 있습니다.팽창의 각 항은 소스로부터의 거리에 따라 특징적인 감소율을 갖는 특성 모멘트 및 전위와 관련지어진다.모노폴 모멘트는 r1/감소율, 다이폴 모멘트는 r²1/감소율, 4극 모멘트는 1/r³감소율 등이 있습니다.순서가 높을수록 잠재력이 더 빨리 떨어집니다.자기장에서 관측되는 가장 낮은 차수의 항이 쌍극자 항이기 때문에, 그것은 먼 거리에서 지배적이다.따라서, 먼 거리에서는 어떤 자기 소스도 같은 자기 모멘트의 쌍극자처럼 보입니다.

메모들

레퍼런스