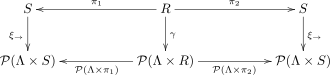비시뮬레이션

이 글은 검증을 위해 인용구가 추가로 필요하다. 신뢰할 수 있는 출처에 인용문을 추가하여 이 기사를 개선할 수 있도록 도와주십시오. 공급되지 않은 재료는 도전하여 제거할 수 있다. 출처 찾기: "Bisimulation" – 뉴스 · 신문 · 책 · 학자 · JSTOR (2017년 2월) (이 템플릿 메시지를 제거하는 방법과 시기 학습)

이론 컴퓨터 과학에서 이등분산이란 한 시스템이 다른 시스템을 시뮬레이션하고 그 반대도 시뮬레이션하는 동일한 방식으로 동작하는 시스템을 연관시키는 주 전환 시스템들 사이의 이진 관계다.

우리가 어떤 규칙에 따라 게임을 하는 것으로 간주한다고 가정할 때 직관적으로 두 시스템이 서로 다른 움직임을 일치시킨다면 두 시스템은 이등분한다.이런 의미에서 관찰자가 각 계통을 서로 구별할 수는 없다.

형식 정의

Given a labelled state transition system (${\displaystyle S}$, ${\displaystyle \Lambda }$, →), where ${\displaystyle S}$ is a set of states, ${\displaystyle \Lambda }$ is a set of labels and → is a set of labelled transitions (i.e., a subset of ${\displaystyle S\times \Lambda \times S}$), a bisimulation은 2진수 관계 R × S {\$displaystyle R\subseteq S\times$ S$}$이다. 즉, R ${\displaystyle$ $R$$}$과(와)의 역수 R T ${\$ R$^{T}$가 모두 시뮬레이션이다.이로부터 이등분석의 대칭적 폐쇄는 이등분법이며, 각 대칭 시뮬레이션은 이등분법이다.따라서 일부 저자들은 이등분석을 대칭 시뮬레이션으로 정의한다.^[1]

동등하게, R${\$$displaystyle R}$의 모든 상태(p ,q )${\displaystyle$ ($p,q)}$ 및 λ ${\displaystyle \Lambda }$의 모든 라벨 α인 경우에만 R {\displaystyle R$}$이 이등분법이다.

• if ${\displaystyle p\mathrel {\overset {\alpha }{\rightarrow }} p'}$, then there is ${\displaystyle q\mathrel {\overset {\alpha }{\rightarrow }} q'}$ such that ${\displaystyle (p',q')\in R}$;
• if ${\displaystyle q\mathrel {\overset {\alpha }{\rightarrow }} q'}$, then there is ${\displaystyle p\mathrel {\overset {\alpha }{\rightarrow }} p'}$ such that ${\displaystyle (p',q')\in R}$.

Given two states ${\displaystyle p}$ and ${\displaystyle q}$ in ${\displaystyle S}$, ${\displaystyle p}$ is bisimilar to ${\displaystyle q}$, written ${\displaystyle p\,\sim \,q}$, if and only if there is a bisimulation ${\displaystyle R}$ such that ${\displaystyle (p,$$q)\in R}$. This means that the bisimilarity relation ${\displaystyle \,\sim \,}$ is the union of all bisimulations: ${\displaystyle (p,q)\in \,\sim \,}$ precisely when ${\displaystyle (p,q)\in R}$ for some bisimulation ${\displaystyle R}$.

이등분들의 집합은 결합에 의해 폐쇄된다.^{[Note 1]} 따라서 이등분 관계는 그 자체로 이등분이다.모든 이등분들의 결합이기 때문에, 그것은 독특한 가장 큰 이등분이다.이등분할은 반사적, 대칭적, 전이적 닫힘에서도 닫히므로 가장 큰 이등분할은 반사적, 대칭적, 전이적이어야 한다.여기서부터 가장 큰 이등분율(이등분율)은 동등성 관계라는 것이다.^[2]

p ${\displaystyle p}$이(가) q ${\displaystyle q}$과(와) q ${\displaystyle q}$을(를) 시뮬레이션하는 경우 p ${\displaystyle$ p$}$이(가) 동일하지 않은 경우가 항상 있다는 점에 유의하십시오.For ${\displaystyle p}$ and ${\displaystyle q}$ to be bisimilar, the simulation between ${\displaystyle p}$ and ${\displaystyle q}$ must be the converse of the simulation between ${\displaystyle q}$ and ${\displaystyle p}$. Counter-example in CCS: ${\displaystyle \,M=a.b+a\,}$ aND M ′=. b ${\$은(는) 서로 시뮬레이션하지만 이등분할 수는 없다.

---

대체 정의

관계 정의

비시뮬레이션은 다음과 같은 관계 구성의 관점에서 정의할 수 있다.

Given a labelled state transition system ${\displaystyle (S,\Lambda ,\rightarrow )}$, a bisimulation relation is a binary relation ${\displaystyle R}$ over ${\displaystyle S}$ (i.e., ${\displaystyle R}$ ⊆ ${\displaystyle S}$ × ${\displaystyle S}$) such that ${\displaystyle \fo$$랄 \alpha \in \Lambda }$

${\displaystyle R\ ;\\\\overset {\alpha }{\오른쪽 화살표 }}\quad {\subseteq }\coverset {\alpha }{\오른쪽 화살표 }\\\\R}$

그리고

${\displaystyle R^{-1}\;\\\overset {\alpha }{\lapha }{\lapha }}\jubseteq }\quad{\nalpha }}}}}}\rightarrow{-1}$

관계 구성의 단조로움과 연속성으로부터는 즉시 이등분 집합이 결합(관계의 양태에 결합)되어 닫히는 것이 뒤따르며, 간단한 대수적 계산으로 이등분율의 관계인 모든 이등분들의 결합이 동등성 관계임을 알 수 있다.이 정의와 이등비례의 관련 치료는 어떤 비자발적인 퀀텀으로 해석될 수 있다.

픽스포인트 정의

이등유사성은 또한 질서-이론적 패션, 고정점 이론 측면에서도 아래에 정의된 특정 기능의 가장 큰 고정점으로서 더 정밀하게 정의될 수 있다.

Given a labelled state transition system (${\displaystyle S}$, Λ, →), define ${\displaystyle F:{\mathcal {P}}(S\times S)\to {\mathcal {P}}(S\times S)}$ to be a function from binary relations over ${\displaystyle S}$ to binary relations over ${\displaystyle S}$, as follows:

R ${\$$displaystyle$ $R}$을(를) S ${\displaystyle S}$에 대한 이항 관계가 되게 하라. F(R) ${\$$displaystyle$ $F(R)}$은(는$)$ 다음과 같이S {\$displaystystyle$ $S}$에서$모든$ 쌍$(p,$ q)의 집합으로 정의된다$.$

${\displaystyle \forall \alpha \in \Lambda .\,\forall p'\in S.\,p{\overset {\alpha }{\rightarrow }}p'\,\Rightarrow \,\exists q'\in S.\,q{\overset {\alpha }{\rightarrow }}q'\,{\textrm {and}}\,(p',q')\in R}$

그리고

${\displaystyle \forall \alpha \in \Lambda .\,\forall q'\in S.\,q{\overset {\alpha }{\rightarrow }}q'\,\Rightarrow \,\exists p'\in S.\,p{\overset {\alpha }{\rightarrow }}p'\,{\textrm {and}}\,(p',q')\in R}$

그런 다음 Bisimilarity는 F ${\displaystyle F}$의 가장 큰 고정점으로 정의된다.

에렌페우흐트-프레셰 게임 정의

비시뮬레이션은 공격수와 수비수라는 두 선수의 경기 측면에서도 생각할 수 있다.

"Attacker"가 먼저 진행되며 유효한 전환인 α ${\displaystyle \alpha }$에서 (p , q) ${\displaystyle (p,q)}$을(를) 선택할 수 있다. 예:

(p, q)→ α($p$,$q$q ){\$displaystyle$(p$,$q){\set${\p, q}}$ 또는 (p, q)→ α(p, $displaystystyle (p,q$){\$p, q')}}}$

그런 다음 "Defender"는 공격자의 이동에 따라α {\$displaystyle \alpha$ }(p ′ ,q) {\$displaystyle$($p$$',q$)}또는 (p,q $)$ {\$displaystyle$ ($p,q')$의 전환과 일치하도록 시도해야 한다.즉, 다음과 같은 α ${\displaystyle \alpha }$을(를) 찾아야 한다.

${\displaystyle (p',q){\overset {\alpha }{\rightarrow }}(p',q')}$ or ${\displaystyle (p,q'){\overset {\alpha }{\rightarrow }}(p',q')}$

공격자와 수비수는 다음과 같은 상황이 발생할 때까지 계속 교대한다.

• 수비수는 공격자의 움직임과 일치하는 유효한 전환을 찾을 수 없다.이 경우 공격자가 승리한다.
• 게임이 두 'dead' 상태(p, q) ${\displaystyle(p,q)}$에 도달함(즉, 어느 상태에서도 전환이 없음)이 경우 수비수가 이긴다.
• 경기는 영원히 계속되는데, 이 경우 수비수가 승리한다.
• 게임은 이미 방문한 상태(p ,q) ${\displaystyle(p,q)}$에 도달한다.이는 무한 플레이에 해당하며 수비수의 승리로 간주된다.

위의 정의에 따르면, 시스템은 수비수를 위한 승리 전략이 존재하는 경우에만 이등분할이다.

연골 정의

국가전환 시스템을 위한 이등분석은 공변력 발전기의 유형에 대한 결합형 이등분율의 특별한 경우다.Note that every state transition system ${\displaystyle (S,\Lambda ,\rightarrow )}$ is bijectively a function ${\displaystyle \xi _{\rightarrow }}$ from ${\displaystyle S}$ to the powerset of ${\displaystyle S}$ indexed by ${\displaystyle \Lambda }$ written as ${\displa$$ystyle {\mathcal{P}(\Lambda \time$ S)}에 의해 정의됨

${\displaystyle p\mapsto \{(\alpha ,q)\in \Lambda \time S:p{\overset {\alpha }{\alpha }{\rightarrow q\}}}}$

Let ${\displaystyle \pi _{i}\colon S\times S\to S}$ be ${\displaystyle i}$-th projection mapping ${\displaystyle (p,q)}$ to ${\displaystyle p}$ and ${\displaystyle q}$ respectively for ${\displaystyle i=1,2}$; and ${\displaystyle {\mathcal {$$P}(\Lambda \times \pi_{1$}}세 번째 구성 요소를 삭제하여 정의된 defined 1 ${\$}의 정방향 이미지

${\displaystyle P\mapsto \{(\alpha ,p)\in \Lambda \times S:\exists q.(\alpha ,p,q)\}}$

여기서 P ${\displaystyle P}$은(는) × S × S ${\displaystyle \lambda \times S}$의 하위 집합이다. 마찬가지로 P (λ × π 2) ${\displaystystyle {\mathcal}{P}(\Lambda \time \pi _{2$

Using the above notations, a relation ${\displaystyle R\subseteq S\times S}$ is a bisimulation on a transition system ${\displaystyle (S,\Lambda ,\rightarrow )}$ if and only if there exists a transition system ${\displaystyle \gamma \colon R\to {\mathcal {P}}(\Lambda \times R)}$ on t다이어그램과 같은 관계 R{\$displaystyle R}$

통근, 즉 i= 1,2 ${\displaystyle$ i$=1,2$ 방정식

${\displaystyle \xi _{\rightarrow }\circle \pi _{i}={\mathcal {P}(\Lambda \times \pi _{i}\circur \gamma }}}}$

여기서 hold→ ${\$은$($는){\$displaystyle$(S,\$Lambda ,\rightarrow )}$의 기능적 표현이다.

이등변형

특별한 맥락에서 이등분석의 개념은 때때로 추가 요구사항이나 제약조건을 추가함으로써 개선된다.예를 들어, 중간 상태가 시작 상태("스튜터")^[3]와 동일하다면 한 시스템의 한 전환이 다른 시스템의 여러 전환과 일치할 수 있는 말더듬이 이등분산이다.

상태 전환 시스템이 종종 τ ${\displaystyle \tau },$즉 외부 관찰자가 볼 수 없는 동작으로 표시되는 무성(또는 내부) 동작 개념을 포함하는 경우 다른 변형이 적용되며, 두 상태 p ${\displaystyle p$$}$ 및 q ${\st$.$yle q}$은(는) 이등분하며 p ${\displaystyle p}$에서 일부 상태 $\$ {\$displaystyle$ p$'}($으)로 이어지는 몇 가지 내부 작업이 q ${\displaystyle q}$에서 $}($으)로 이어지는 몇 가지 상태 ${\$$displaystystyty$}이(으)여야 한다.$tyle q'}$. A relation ${\displaystyle {\mathcal {R}}}$ on processes is a weak bisimulation if the following holds (with ${\displaystyle {\mathcal {S}}\in \{{\mathcal {R}},{\mathcal {R}}^{-1}\}}$, and ${\displaystyle a,\tau }$ being an observable and mute transition respectively):

${\displaystyle \ forall p,q.\quad (p,q)\in {\mathcal {S}\Rightarrow p{\stackrel {\tau}{\p'\Rightarrow \exists q'.\quad q{\stackrel{\tau ^{\}{\\}{\\오른쪽 화살표 }}}}\in {\mathcal {S}}$

${\displaystyle \ forall p,q.\quad (p,q)\in {\mathcal {S}\Rightarrow p{a}{\wrightarrow \exists q'.\quad q{\stackrel{\tau ^{\a\tau ^{\}}{\\n1}{\\wardge(p',q')\in {\mathcal {S}}$

이것은 관계까지의 이등분율과 밀접한 관련이 있다.

전형적으로, 국가 전환 시스템이 프로그래밍 언어의 운영 의미론을 제공한다면, 이등분산의 정확한 정의는 프로그래밍 언어의 제한에 특정될 것이다.따라서 일반적으로 문맥에 따라 둘 이상의 이등분, (이등분) 관계가 있을 수 있다.

이등분법과 모달 논리학

크립케 모델은 (라벨로 표시된) 국가 전환 시스템의 특별한 경우이기 때문에, 이등분산도 모달 논리학에서는 하나의 주제다.사실 모달논리는 이등분법(van Benthem의 정리) 하에서는 1차 논리 불변성의 단편이다.

알고리즘.

두 개의 유한 전환 시스템이 이등분인지 확인하는 작업은 다항식 시간에 수행할 수 있다.^[4]가장 빠른 알고리즘은 가장 강력한 파티션 문제를 줄여 파티션 미세화를 사용하는 선형 시간이다.

참고 항목

• 시뮬레이션 사전 주문
• 합치관계
• 확률론적 이등분

참조

추가 읽기

• Park, David (1981). "Concurrency and Automata on Infinite Sequences". In Deussen, Peter (ed.). Theoretical Computer Science. Proceedings of the 5th GI-Conference, Karlsruhe. Lecture Notes in Computer Science. Vol. 104. Springer-Verlag. pp. 167–183. doi:10.1007/BFb0017309. ISBN 978-3-540-10576-3.
• Milner, Robin (1989). Communication and Concurrency. Prentice Hall. ISBN 0-13-114984-9.
• 다비데 생요르기.(2011).비시뮬레이션과 코인전도 소개.케임브리지 대학 출판부.ISBN 9781107003637

외부 링크

소프트웨어 도구

• CADP: 다양한 이등분법에 따라 유한 상태 시스템을 최소화하고 비교하는 도구
• mCRL2: 다양한 이등분법에 따라 유한 상태 시스템을 최소화하고 비교하는 도구
• 비시뮬레이션 게임