Casing_Design(1).ppt
- 3. 1. To keep the hole open and to provide support for weak, vulnerable or fractured formations. In the latter case, if the hole is left uncased, the formation may cave in and re-drilling of the hole will then become necessary. . 2. To isolate porous media with different fluid/pressure regimes from contaminating the pay zone. This is basically achieved through the combined presence of cement and casing. Therefore, production from a specific zone can be achieved. 3. To prevent contamination of near-surface fresh water zones. 3
- 4. 4. To provide a passage for hydrocarbon fluids; most production operations are carried out through special tubing's which are run inside the casing. 5. To provide a suitable connection for the wellhead equipment and later the Christmas tree. The casing also serves to connect the blowout prevention equipment (BOPS) which is used to control the well while drilling. 6. To provide a hole of known diameter and depth to facilitate the running of testing and completion equipment. 4
- 5. 5 Casing Design Why run casing? 1. To prevent the hole from caving in 2. Onshore - to prevent contamination of fresh water sands 3. To prevent water migration to producing formation What is casing? Casing Cement
- 6. 6 Casing Design 4. To confine production to the wellbore 5. To control pressures during drilling 6. To provide an acceptable environment for subsurface equipment in producing wells 7. To enhance the probability of drilling to total depth (TD) e.g., you need 14 ppg mud to control a lower zone, but an upper zone will fracture at 12 lb/gal. What do you do?
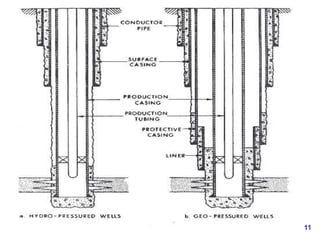
- 7. 7 Types of Strings of Casing 1. Drive pipe or structural pile {Gulf Coast and offshore only} 150’-300’ below mud line. 2. Conductor string. 100’ - 1,600’ 3. Surface pipe. 2,000’ - 4,000’ Diameter Example 16”-60” 30” 16”-48” 20” 8 5/8”-20” 13 3/8”
- 8. 8 Types of Strings of Casing 4. Intermediate String 5. Production String 6. Liner(s) 7. Tubing String(s) 7 5/8”-13 3/8” 9 5/8” Diameter Example 4 1/2”-9 5/8” 7”
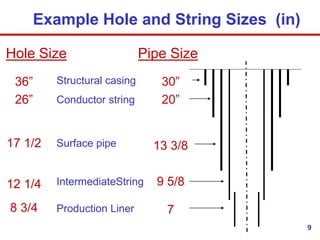
- 9. 9 Example Hole and String Sizes (in) Structural casing Conductor string Surface pipe IntermediateString Production Liner Hole Size 30” 20” 13 3/8 9 5/8 7 Pipe Size 36” 26” 17 1/2 12 1/4 8 3/4
- 10. 10 Example Hole and String Sizes (in) Structural casing Conductor string Surface pipe IntermediateString Production Liner 250’ 1,000’ 4,000’ Mudline
- 11. 11
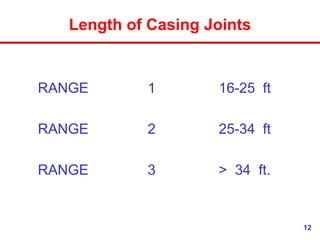
- 12. 12 Length of Casing Joints RANGE 1 16-25 ft RANGE 2 25-34 ft RANGE 3 > 34 ft.
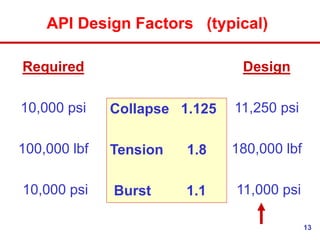
- 13. 13 API Design Factors (typical) Collapse 1.125 Tension 1.8 Burst 1.1 Required 10,000 psi 100,000 lbf 10,000 psi Design 11,250 psi 180,000 lbf 11,000 psi
- 14. 14 Burst Design for maximum pressure on the inside of the casing. API design recommendations call for the worst case scenario, which is the casing is empty, and no external pressure. The pressure to design for is the estimated formation pressure at TD for production casing, or estimated formation pressure at the next casing depth.
- 15. 15 Collapse API design recommendations call for worst case, where there is no pressure inside the casing, and we design for the maximum mud weight at the casing depth. We also allow for the reduction of the collapse rating from the weight of the casing hanging below the depth of interest.
- 16. 16 Tension API recommendations call for worst case, where there is no buoyancy effect. Design is based on the weight of the entire casing string.
- 17. 17 Normal Pore Pressure Abnormal Pore Pressure 0.433 - 0.465 psi/ft gp > normal Abnormal
- 19. 19 Casing Design Burst: Assume full reservoir pressure all along the wellbore. Collapse: Hydrostatic pressure increases with depth Tension: Tensile stress due to weight of string is highest at top STRESS Tension Burst Collapse Collapse Tension Depth Burst
- 20. 20 Casing Design - Burst Example 1 Design a 7” Csg. String to 10,000 ft. Pore pressure gradient = 0.5 psi/ft Design factor, Ni=1.1 Design for burst only.
- 21. 21 Burst Example 1. Calculate probable reservoir pressure. psi 000 , 5 ft 000 , 10 * ft psi 5 . 0 pres 2. Calculate required pipe internal yield pressure rating psi 500 , 5 1 . 1 * 000 , 5 N * p p i res i Ni = API Design Factor for BURST = 1.1
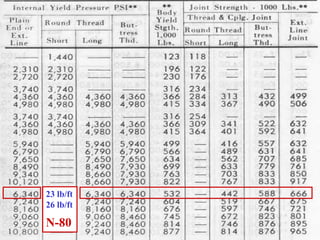
- 22. 22 Example 3. Select the appropriate csg. grade and wt. from the Halliburton Cementing tables: Burst Pressure required = 5,500 psi 7”, J-55, 26 lb/ft has BURST Rating of 4,980 psi 7”, N-80, 23 lb/ft has BURST Rating of 6,340 psi 7”, N-80, 26 lb/ft has BURST Rating of 7,249 psi Use N-80 Csg., 23 lb/ft
- 23. 23
- 25. 25 Collapse Pressure The following factors are important: The collapse pressure resistance of a pipe depends on the axial stress The API Design Factor
- 26. 26 Casing Design Collapse pressure - with axial stress 1. P A 2 / 1 2 P A P PA Y S 5 . 0 Y S 75 . 0 1 Y Y YPA = yield strength of axial stress equivalent grade, psi YP = minimum yield strength of pipe, psi SA = Axial stress, psi (tension is positive)
- 27. 27 Example 3 Determine the collapse strength for a 5 1/2” O.D., 14.00 #/ft, J-55 casing under axial load of 100,000 lbf The axial tension will reduce the collapse pressure as follows: P p A 2 p A PA Y Y S 5 . 0 Y S 75 . 0 1 Y psi Area F S A A 820 , 24 012 . 5 5 . 5 4 000 , 100 2 2
- 28. 28 Example 3 cont’d The axial tension will reduce the collapse pressure rating to: psi 216 , 38 000 , 55 000 , 55 820 , 24 5 . 0 000 , 55 820 , 24 75 . 0 1 Y 2 PA Here the axial load decreased the J-55 rating to an equivalent “J-38.2” rating P p A p A PA Y Y S Y S Y 5 . 0 75 . 0 1 2
- 29. 29 Example 3 - cont’d We shall be using API Tables to correct for the effect of axial tension on collapse strength of casing. The Halliburton Cementing Tables list the collapse resistance of 5 ½ -in, 14.00 lb/ft J-55 casing at 3,120 psi. The axial tension in this case would derate the collapse strength to about 2,550 psi.
- 30. 30
- 31. 31
- 32. 32 Casing Design Example Example Problem API Design Factors “Worst Possible Conditions” Effect of Axial Tension on Collapse Strength Iteration and Interpolation Design for Burst, Collapse and Tension
- 33. 33 Casing Design Example Design a 9 5/8-in., 8,000-ft combination casing string for a well where the mud wt. will be 12.5 ppg and the formation pore pressure is expected to be 6,000 psi. Only the grades and weights shown are available (N-80, all weights). Use API design factors. Design for “worst possible conditions.”
- 34. 34 Casing Design - Solution Before solving this problem is it necessary to understand what we mean by “Design Factors” and “worst possible conditions”. API Design Factors Design factors are essentially “safety factors” that allow us to design safe, reliable casing strings. Each operator may have his own set of design factors, based on his experience, and the condition of the pipe.
- 35. 35 Casing Design we’ll use the design factors recommended by the API unless otherwise specified. These are the API design Factors: Tension and Joint Strength: NT = 1.8 Collapse (from external pressure): Nc= 1.125 Burst (from internal pressure): Ni = 1.1
- 36. 36 Casing Design What this means is that, for example, if we need to design a string where the maximum tensile force is expected to be 100,000 lbf, we select pipe that can handle 100,000 * 1.8 = 180,000 lbf in tension. Note that the Halliburton Cementing Tables list actual pipe strengths, without safety factors built in.
- 37. 37 Casing Design Unless otherwise specified in a particular problem, we shall also assume the following: Worst Possible Conditions 1. For Collapse design, assume that the casing is empty on the inside (p = 0 psig) 2. For Burst design, assume no “backup” fluid on the outside of the casing (p = 0 psig)
- 38. 38 Casing Design Worst Possible Conditions, cont’d 3. For Tension design, assume no buoyancy effect 4. For Collapse design, assume no buoyancy effect The casing string must be designed to stand up to the expected conditions in burst, collapse and tension. Above conditions are quite conservative. They are also simplified for easier understanding of the basic concepts.
- 39. 39 Casing Design - Solution Burst Requirements (based on the expected pore pressure) The whole casing string must be capable of withstanding this internal pressure without failing in burst. psi 600 , 6 P 1 . 1 * psi 000 , 6 Factor Design * pressure pore P B B Depth Pressure
- 40. 40 Casing Design - Solution Collapse Requirements For collapse design, we start at the bottom of the string and work our way up. Our design criteria will be based on hydrostatic pressure resulting from the 12.5 ppg mud that will be in the hole when the casing string is run, prior to cementing.
- 41. 41 Casing Design Collapse Requirements, cont’d severe less are ts requiremen collapse the hole the up Further . bottom the at d ' req psi 850 , 5 P 125 . 1 * 000 , 8 * 5 . 12 * 052 . 0 factor design * depth * weight mud * 052 . 0 P c c Depth Pressure
- 42. 42 Casing Design Req’d: Burst: 6,600 psi Collapse: 5,850 psi
- 43. 43 Casing Design Note that two of the weights of N-80 casing meet the burst requirements, but only the 53.5 #/ft pipe can handle the collapse requirement at the bottom of the hole (5,850 psi). The 53.5 #/ft pipe could probably run all the way to the surface (would still have to check tension), but there may be a lower cost alternative.
- 44. 44 Casing Design To what depth might we be able to run N-80, 47 #/ft? The maximum annular pressure that this pipe may be exposed to, is: psi 231 , 4 125 . 1 760 , 4 factor design pipe of pressure Collapse Pc Depth Pressure
- 45. 45 Casing Design First Iteration At what depth do we see this pressure (4,231 psig) in a column of 12.5 #/gal mud? ft 509 , 6 5 . 12 * 052 . 0 231 , 4 5 . 12 * 052 . 0 P h h * 5 . 12 * 052 . 0 P c 1 1 c
- 46. 46 Casing Design This is the depth to which the pipe could be run if there were no axial stress in the pipe… But at 6,509’ we have (8,000 - 6,509) = 1,491’ of 53.5 #/ft pipe below us. The weight of this pipe will reduce the collapse resistance of the 47.0 #/ft pipe! 8,000’ 6,509’
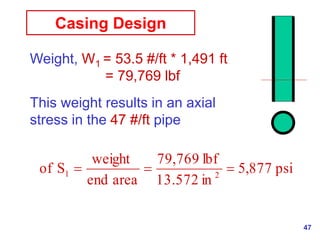
- 47. 47 Casing Design Weight, W1 = 53.5 #/ft * 1,491 ft = 79,769 lbf This weight results in an axial stress in the 47 #/ft pipe psi 877 , 5 in 13.572 lbf 769 , 79 area end weight S of 2 1
- 48. 48 Casing Design The API tables show that the above stress will reduce the collapse resistance from 4,760 to somewhere between 4,680 psi (with 5,000 psi stress) and 4,600 psi (with 10,000 psi stress)
- 49. 49 Casing Design Interpolation between these values shows that the collapse resistance at 5,877 psi axial stress is: psi 148 , 4 125 . 1 666 , 4 P psi 666 , 4 ) 600 , 4 680 , 4 ( * ) 000 , 5 000 , 10 ( ) 000 , 5 877 , 5 ( 680 , 4 P cc1 1 c With the design factor, 2 1 1 2 1 1 c1 P P P S S S S P
- 50. 50 Casing Design This (4,148 psig) is the pressure at a depth Which differs considerably from the initial depth of 6,509 ft, so a second iteration is required. ft 382 , 6 5 . 12 * 052 . 0 148 , 4 h2
- 51. 51
- 52. 52
- 53. 53 Casing Design Second Iteration Now consider running the 47 #/ft pipe to the new depth of 6,382 ft. psi 378 , 6 in 572 . 13 lbf 563 , 86 S lbf 563 , 86 5 . 53 * ) 382 , 6 000 , 8 ( W 2 2 2
- 54. 54 Casing Design Interpolating again, This is the pressure at a depth of psi pcc 140 , 4 600 , 4 680 , 4 * 5000 5000 378 , 6 680 , 4 125 . 1 1 2 ft 369 , 6 5 . 12 * 052 . 0 140 , 4 h3 2 1 1 2 1 1 c1 D.F. 1 P P P S S S S P
- 55. 55 Casing Design This is within 13 ft of the assumed value. If more accuracy is desired (generally not needed), proceed with the: Third Iteration psi 429 , 6 572 . 13 259 , 87 S lbf 259 , 87 5 . 53 * ) 369 , 6 000 , 8 ( W ' 369 , 6 h 3 3 3 Pcc3 = ?
- 56. 56 Casing Design Third Iteration, cont’d 2 3 140 , 4 ) 600 , 4 680 , 4 ( * 000 , 5 000 , 5 429 , 6 680 , 4 125 . 1 1 cc cc P psi P thus
- 57. 57 Casing Design Third Iteration, cont’d This is the answer we are looking for, i.e., we can run 47 #/ft N-80 pipe to a depth of 6,369 ft, and 53.5 #/ft pipe between 6,369 and 8,000 ft. Perhaps this string will run all the way to the surface (check tension), or perhaps an even more economical string would include some 43.5 #/ft pipe?
- 58. 58 Casing Design At some depth the 43.5 #/ft pipe would be able to handle the collapse requirements, but we have already determined that it will not meet burst requirements. ! NO
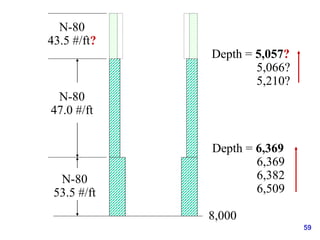
- 59. 59 N-80 53.5 #/ft N-80 47.0 #/ft N-80 43.5 #/ft? Depth = 5,057? 5,066? 5,210? Depth = 6,369 6,369 6,382 6,509 8,000
- 60. 60 Tension Check The weight on the top joint of casing would be With a design factor of 1.8 for tension, a pipe strength of weight actual 602 , 386 ) / # 5 . 53 * 631 , 1 ( ) / # 0 . 47 * 369 , 6 ( lbs ft ft ft ft required is lbf 080 , 695 602 , 386 * 8 . 1
- 61. 61 Tension Check The Halliburton cementing tables give a yield strength of 1,086,000 lbf for the pipe body and a joint strength of 905,000 lbf for LT & C. surface to OK is ft / # 0 . 47