Эволюта
Перейти к навигации
Перейти к поиску

Эволю́та (от лат. evolutus «развёрнутый») плоской кривой — геометрическое место точек, являющихся центрами кривизны исходной кривой[1].
Эволюта — огибающая нормалей, проведённых в каждой точке плоской кривой[2].
По отношению к своей эволюте любая кривая является эвольвентой.
Уравнения
[править | править код]Если линия задана параметрическими уравнениями , то её эволюта имеет уравнение:
В частности, если является натуральным параметром кривой , то её эволюта может быть задана[2] уравнением:
- ,
где — единичный вектор нормали кривой, направленный в сторону центра кривизны, — кривизна.
Примеры
[править | править код]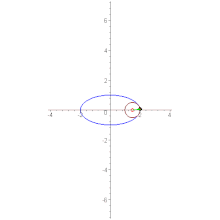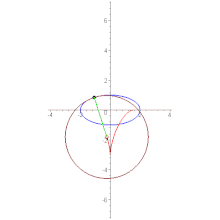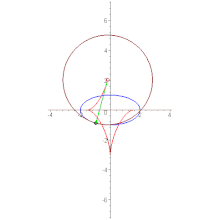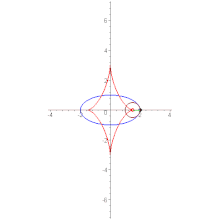
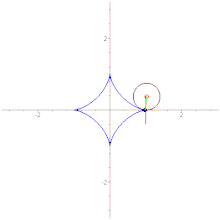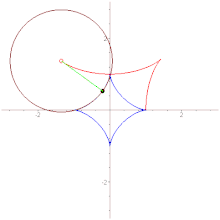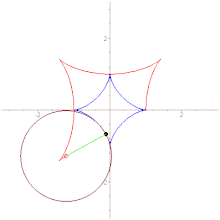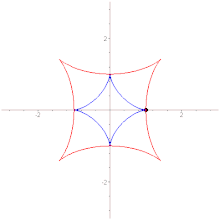
- Вытянутая астроида
- является эволютой эллипса
- .
- Эволюта астроиды подобна ей, но вдвое больше неё и повёрнута относительно неё на 45°.
- Эволюта циклоиды является циклоидой, конгруэнтной исходной и параллельно сдвинутой от исходной так, что вершины переходят в её каспы. Эти свойства открыты Христианом Гюйгенсом; они были им использованы при создании точных механических часов, собственная частота маятника в которых не зависит от амплитуды колебаний.
См. также
[править | править код]Примечания
[править | править код]- ↑ Эволюта, 1988.
- ↑ 1 2 Эволюта — статья из Математической энциклопедии. Д. Д. Соколов
Литература
[править | править код]- В. Бляшке. Диференциальная геометрия и геометрические основы теории относительности Эйнштейна / М. Я. Выгодский (перевод с немецкого). — М.: ОНТИ, 1935. — 331 с.
- Д. А. Граве. Дифференциальное исчисление // Энциклопедический словарь Брокгауза и Ефрона : в 86 т. (82 т. и 4 доп.). — СПб., 1890—1907.
- Эволюта // Математический энциклопедический словарь / Гл. ред. Ю. В. Прохоров; Ред. Кол.: С. И. Адян, Н. С. Бахвалов, В. И. Битюцков, А. П. Ершов, Л. Д. Кудрявцев, А. Л. Онищик, А. П. Юшкевич. М.: «Советская энциклопедия», 1988. 847 с., ил. С. 640—641.
В другом языковом разделе есть более полная статья Evolute (англ.). |









