Ciclo (teoria de grafos)
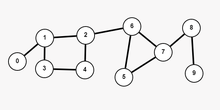
Um ciclo em teoria de grafos é um caminho em que o primeiro e o último vértice coincidem, mas nenhum outro vértice é repetido".[1] Um ciclo é uma cadeia simples e fechada.[2][3]
Em grafos não direcionados, para configurar um ciclo o caminho precisará de no mínimo três arestas, com o primeiro e último vértice se coincidindo e todos outros distintos. Em grafos direcionados precisa-se apenas de uma aresta para configurar um ciclo.[4][5]
O comprimento de um ciclo é o número de arestas que o caminho possui. Um ciclo com comprimento 1, é chamado de laço (loop).[4]
O termo ciclo pode também ser usado para se referir ao grafo que contém os vértices e arestas de um ciclo na definição acima.[1]
Definição matemática
[editar | editar código-fonte]Matematicamente: Seja G um grafo. Um ciclo em G é um caminho
- {v1, v2, . . ., vk, vk+1}
sendo
- v1 = vk+1, 3 ≤ k[6]
Referências
- ↑ a b SCHEINERMAN, Edward (2011). Matemática Discreta. Uma Introdução 2ª ed. São Paulo: Cengage Learning. p. 473
- ↑ FURTADO, Antonio Luz (1973). Teoria dos Grafos. Algoritmos. Rio de Janeiro, Guanabara: LTC/Editora da USP. p. 6. CDD 511.2076
- ↑ BOAVENTURA NETTO, Paulo Oswaldo (2001). Grafos. Teoria, Modelos Algoritmos. São Paulo: Edgard Blücher. p. 24. ISBN 85-212-0292-X
- ↑ a b «Caminhos e ciclos em grafos». www.ime.usp.br. Consultado em 11 de agosto de 2021
- ↑ Diestel, Reinhard (2000). Graph Theory. New York: Springer
- ↑ SZWARCFITER, Jayme Luiz (1988). Grafos e algoritmos computacionais. Rio de Janeiro: Campus. ISBN 85-7001-341-8
