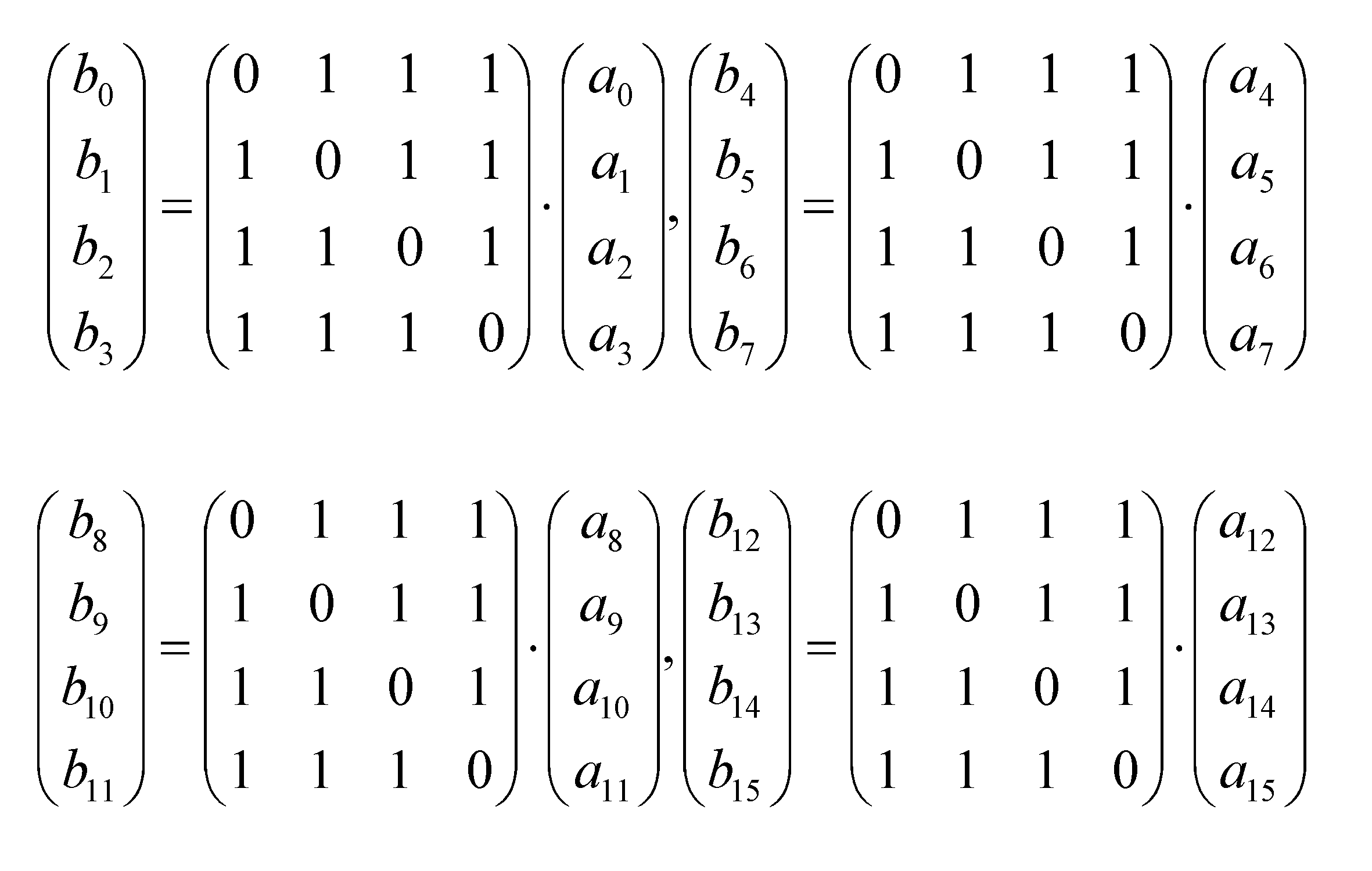WO2015146430A1 - 暗号処理装置、および暗号処理方法、並びにプログラム - Google Patents

暗号処理装置、および暗号処理方法、並びにプログラム Download PDF

Info

Publication number
WO2015146430A1
WO2015146430A1 PCT/JP2015/055280 JP2015055280W WO2015146430A1 WO 2015146430 A1 WO2015146430 A1 WO 2015146430A1 JP 2015055280 W JP2015055280 W JP 2015055280W WO 2015146430 A1 WO2015146430 A1 WO 2015146430A1
Authority
WO
WIPO (PCT)
Prior art keywords
key
conversion
round
function
cryptographic processing
Prior art date
Application number
PCT/JP2015/055280
Other languages
English (en)
French (fr)
Inventor
香士 渋谷
孝典 五十部
Original Assignee
ソニー株式会社
Priority date (The priority date is an assumption and is not a legal conclusion. Google has not performed a legal analysis and makes no representation as to the accuracy of the date listed.)
Filing date
Publication date
Application filed by ソニー株式会社 filed Critical ソニー株式会社
Publication of WO2015146430A1 publication Critical patent/WO2015146430A1/ja

Links

Images

Classifications

    • G—PHYSICS
    • G09—EDUCATION; CRYPTOGRAPHY; DISPLAY; ADVERTISING; SEALS
    • G09C—CIPHERING OR DECIPHERING APPARATUS FOR CRYPTOGRAPHIC OR OTHER PURPOSES INVOLVING THE NEED FOR SECRECY
    • G09C1/00—Apparatus or methods whereby a given sequence of signs, e.g. an intelligible text, is transformed into an unintelligible sequence of signs by transposing the signs or groups of signs or by replacing them by others according to a predetermined system
    • H—ELECTRICITY
    • H04—ELECTRIC COMMUNICATION TECHNIQUE
    • H04L—TRANSMISSION OF DIGITAL INFORMATION, e.g. TELEGRAPHIC COMMUNICATION
    • H04L9/00—Cryptographic mechanisms or cryptographic arrangements for secret or secure communications; Network security protocols
    • H04L9/06—Cryptographic mechanisms or cryptographic arrangements for secret or secure communications; Network security protocols the encryption apparatus using shift registers or memories for block-wise or stream coding, e.g. DES systems or RC4; Hash functions; Pseudorandom sequence generators
    • H04L9/0618—Block ciphers, i.e. encrypting groups of characters of a plain text message using fixed encryption transformation
    • H04L9/0625—Block ciphers, i.e. encrypting groups of characters of a plain text message using fixed encryption transformation with splitting of the data block into left and right halves, e.g. Feistel based algorithms, DES, FEAL, IDEA or KASUMI
    • H—ELECTRICITY
    • H04—ELECTRIC COMMUNICATION TECHNIQUE
    • H04L—TRANSMISSION OF DIGITAL INFORMATION, e.g. TELEGRAPHIC COMMUNICATION
    • H04L9/00—Cryptographic mechanisms or cryptographic arrangements for secret or secure communications; Network security protocols
    • H04L9/06—Cryptographic mechanisms or cryptographic arrangements for secret or secure communications; Network security protocols the encryption apparatus using shift registers or memories for block-wise or stream coding, e.g. DES systems or RC4; Hash functions; Pseudorandom sequence generators
    • H04L9/0618—Block ciphers, i.e. encrypting groups of characters of a plain text message using fixed encryption transformation
    • H04L9/0631—Substitution permutation network [SPN], i.e. cipher composed of a number of stages or rounds each involving linear and nonlinear transformations, e.g. AES algorithms
    • H—ELECTRICITY
    • H04—ELECTRIC COMMUNICATION TECHNIQUE
    • H04L—TRANSMISSION OF DIGITAL INFORMATION, e.g. TELEGRAPHIC COMMUNICATION
    • H04L2209/00—Additional information or applications relating to cryptographic mechanisms or cryptographic arrangements for secret or secure communication H04L9/00
    • H04L2209/12—Details relating to cryptographic hardware or logic circuitry
    • H—ELECTRICITY
    • H04—ELECTRIC COMMUNICATION TECHNIQUE
    • H04L—TRANSMISSION OF DIGITAL INFORMATION, e.g. TELEGRAPHIC COMMUNICATION
    • H04L2209/00—Additional information or applications relating to cryptographic mechanisms or cryptographic arrangements for secret or secure communication H04L9/00
    • H04L2209/24—Key scheduling, i.e. generating round keys or sub-keys for block encryption

Definitions

  • the present disclosure relates to a cryptographic processing device, a cryptographic processing method, and a program. More specifically, the present invention relates to a cryptographic processing apparatus, a cryptographic processing method, and a program that execute common key encryption.
  • common key block cipher There are various cryptographic processing algorithms, but one of the basic techniques is called common key block cipher.
  • the encryption key and the decryption key are common.
  • a plurality of keys are generated from the common key, and the data conversion process is repeatedly executed in a certain block unit, for example, a block data unit such as 64 bits, 128 bits, 256 bits.
  • DES Data Encryption Standard
  • AES Advanced Encryption Standard
  • CLEFIA proposed by Sony Corporation in 2007 is one of the common key block ciphers.
  • Patent Document 1 Japanese Patent Laid-Open No. 2012-215813.
  • Such a common key block cipher algorithm mainly includes an encryption processing unit having a round function execution unit that repeatedly executes conversion of input data, and a key schedule unit that generates a round key to be applied in each round of the round function unit. It is comprised by.
  • the key schedule unit first generates an extended key with an increased number of bits based on a master key (primary key) that is a secret key, and applies it to each round function unit of the cryptographic processing unit based on the generated extended key. Generate a round key (subkey).
  • a structure for repeatedly executing a round function having a linear conversion unit and a non-linear conversion unit is known.
  • typical structures include an SPN (Substitution-Permutation Network) structure, a Feistel structure, and an extended Feistel structure.
  • Cryptographic processing devices are required to have resistance to these various attacks, high-speed processing, or downsizing.
  • the present disclosure has been made in view of, for example, the above-described situation, and an encryption processing device that realizes improvements in various elements required for an encryption processing device, such as safety, high speed, and downsizing, and encryption processing It is an object to provide a method and a program.
  • the first aspect of the present disclosure is: An encryption processing unit that performs round operation on input data to generate output data; A key schedule unit that outputs a round key applied in a round operation in the cryptographic processing unit to the cryptographic processing unit;
  • the key schedule part A key register storing a secret key K;
  • a key conversion unit that generates a conversion key Kd by a conversion process in which a conversion function G is applied to the secret key K;
  • the secret key K and the conversion key Kd are configured to be a round key that is output to the encryption processing unit, or round key generation data.
  • the conversion function G is in a cryptographic processing device which is an involution function in which the inverse function G ⁇ 1 is the same function as the function G.
  • the second aspect of the present disclosure is: An encryption processing unit that performs round operation on input data to generate output data; A key schedule unit that outputs a round key applied in a round operation in the cryptographic processing unit to the cryptographic processing unit;
  • the key schedule part A key register storing a secret key K;
  • a key conversion unit that generates a conversion key Kd by a conversion process in which a conversion function G is applied to the secret key K;
  • the secret key K and the conversion key Kd are configured to be a round key that is output to the encryption processing unit, or round key generation data.
  • Each of the secret key K and the conversion key Kd is a state composed of m ⁇ n elements each having 1 bit or more
  • the conversion function G is in the cryptographic processing apparatus in which all the state elements of the secret key K are functions having full diffusion that affects all the state elements of the conversion key Kd.
  • the third aspect of the present disclosure is: A cryptographic processing method executed in the cryptographic processing device,
  • the cryptographic processing device includes: An encryption processing unit that performs round operation on input data to generate output data;
  • a key schedule unit that outputs a round key applied in a round operation in the cryptographic processing unit to the cryptographic processing unit;
  • the key schedule part A conversion key Kd is generated by a conversion process in which a conversion function G is applied to the secret key K stored in the key register, A process of setting the secret key K and the conversion key Kd as a round key to be output to the cryptographic processing unit or data for generating a round key;
  • the conversion function G is in a cryptographic processing method that is an involution function in which the inverse function G ⁇ 1 is the same function as the function G.
  • the fourth aspect of the present disclosure is: A cryptographic processing method executed in the cryptographic processing device,
  • the cryptographic processing device includes: An encryption processing unit that performs round operation on input data to generate output data;
  • a key schedule unit that outputs a round key applied in a round operation in the cryptographic processing unit to the cryptographic processing unit;
  • the key schedule part A conversion key Kd is generated by a conversion process in which a conversion function G is applied to the secret key K stored in the key register, A process of setting the secret key K and the conversion key Kd as a round key to be output to the cryptographic processing unit or data for generating a round key;
  • Each of the secret key K and the conversion key Kd is a state composed of m ⁇ n elements each having 1 bit or more,
  • the conversion function G is in a cryptographic processing method in which all the state elements of the secret key K are functions having full diffusion properties that affect all the state elements of the conversion key Kd.
  • the fifth aspect of the present disclosure is: A program for executing cryptographic processing in the cryptographic processing device,
  • the cryptographic processing device includes: An encryption processing unit that performs round operation on input data to generate output data; A key schedule unit that outputs a round key applied in a round operation in the cryptographic processing unit to the cryptographic processing unit;
  • the program is stored in the key schedule unit.
  • the conversion function G is in a program having an involution property in which the inverse function G ⁇ 1 is the same function as the function G.
  • the sixth aspect of the present disclosure is: A program for executing cryptographic processing in the cryptographic processing device,
  • the cryptographic processing device includes: An encryption processing unit that performs round operation on input data to generate output data; A key schedule unit that outputs a round key applied in a round operation in the cryptographic processing unit to the cryptographic processing unit;
  • the program is stored in the key schedule unit.
  • Each of the secret key K and the conversion key Kd is a state composed of m ⁇ n elements each having 1 bit or more,
  • the conversion function G is in a program in which all the state elements of the secret key K are functions having full diffusion that affects all the state elements of the conversion key Kd.
  • the program of the present disclosure is a program provided by, for example, a storage medium to an information processing apparatus or a computer system that can execute various program codes. By executing such a program by the program execution unit on the information processing apparatus or the computer system, processing according to the program is realized.
  • system is a logical set configuration of a plurality of devices, and is not limited to one in which the devices of each configuration are in the same casing.
  • a highly secure cryptographic processing configuration with improved resistance to various attacks has a cryptographic processing unit that repeats a round operation on input data to generate output data, and a key schedule unit that outputs a round key applied in the round operation in the cryptographic processing unit to the cryptographic processing unit.
  • the unit includes a key register that stores the secret key K, and a key conversion unit that generates a conversion key Kd by a conversion process in which the conversion function G is applied to the secret key K.
  • the secret key K and the conversion key Kd are The round key to be output to the encryption processing unit or round key generation data.
  • the conversion function G As the conversion function G, an involution property in which the inverse function G ⁇ 1 is the same function as the function G and a function having a full diffusion property are applied. With this configuration, diffusion characteristics are improved, and a highly secure cryptographic processing configuration with improved resistance to various attacks is realized. Note that the effects described in the present specification are merely examples and are not limited, and may have additional effects.
  • n bit common key block encryption algorithm corresponding to the key length of k bits. It is a figure explaining the decoding algorithm corresponding to the n bit common key block cipher algorithm corresponding to the key length of k bit shown in FIG. It is a figure explaining the relationship between a key schedule part and an encryption process part. It is a figure explaining the structural example of an encryption processing part. It is a figure explaining the example of the round function of a SPN structure. It is a figure explaining an example of the round function of a Feistel structure. It is a figure explaining an example of an extended Feistel structure. It is a figure explaining an example of an extended Feistel structure. It is a figure explaining the structural example of a nonlinear transformation part.
  • S box (S-box) of the nonlinear transformation part of an encryption processing part It is a figure explaining the structural example of S box (S-box) of the nonlinear transformation part of an encryption processing part. It is a figure explaining the structural example of S box (S-box) of the nonlinear transformation part of an encryption processing part. It is a figure explaining the structural example of S box (S-box) of the nonlinear transformation part of an encryption processing part. It is a figure explaining one structural example of a cryptographic processing apparatus. It is a figure which shows the structural example of IC module 700 as a cryptographic processing apparatus. It is a figure which shows the structural example of the smart phone which has an encryption process execution function.
  • the common key block cipher (hereinafter sometimes referred to as block cipher) refers to the one defined below.
  • the block cipher takes as input plaintext P and key K and outputs ciphertext C.
  • n can take an arbitrary integer value, it is usually a predetermined value for each block cipher algorithm.
  • a block cipher with a block length of n is sometimes called an n-bit block cipher.
  • the bit length of the key is represented by k.
  • the key can take any integer value.
  • Plaintext P n bits
  • Ciphertext C n bits
  • K k bits
  • FIG. 1 shows a diagram of an n-bit common key block cipher algorithm E corresponding to a key length of k bits.
  • the decryption algorithm D corresponding to the encryption algorithm E can be defined as the inverse function E ⁇ 1 of the encryption algorithm E, receives the ciphertext C and the key K as input, and outputs the plaintext P.
  • FIG. 2 shows a diagram of a decryption algorithm D corresponding to the encryption algorithm E shown in FIG.
  • Block ciphers can be considered in two parts.
  • One is the secret key K, and the “key schedule part” that outputs the round key to be applied in each round of the cryptographic processing part in a certain step.
  • the other is the round key from the plaintext P and the key schedule part.
  • it is a “cryptographic processing unit” that performs data conversion and outputs ciphertext C.
  • the relationship between the two parts is shown in FIG.
  • the encryption processing unit is configured to be able to execute decryption processing in which the ciphertext C is input and the plaintext P is output. Also in this case, the decryption process using the round key supplied from the key schedule unit is executed. The relationship between the two parts is shown in FIG.
  • the cryptographic processing unit used in the following embodiments can be divided into processing units called round functions.
  • the round function performs predetermined data conversion on input data and outputs converted data.
  • the input data for the round function is, for example, n-bit data being encrypted.
  • the output of the round function in one round is supplied as the input of the next round.
  • one configuration of the round function includes a calculation configuration with a round key generated based on the key output from the key schedule unit. Specifically, an exclusive OR operation is performed on the n-bit data being encrypted and the round key.
  • the total number of round functions is called the total number of rounds, and is a value determined in advance for each cryptographic algorithm.
  • Round function Depending on the block cipher algorithm, the round function can take various forms. Round functions can be classified according to the structure adopted by the cryptographic algorithm. As typical structures, an SPN (Substitution-Permutation Network) structure, a Feistel structure, and an extended Feistel structure are exemplified here.
  • SPN substitution-Permutation Network
  • Feistel structure Feistel structure
  • extended Feistel structure extended Feistel structure
  • a SPN (Substitution-Permutation Network) structure round function A configuration in which exclusive OR operation with a round key, nonlinear transformation, linear transformation processing, etc. are applied to all n-bit input data. The order of each operation is not particularly determined.
  • FIG. 5 shows an example of a round function having an SPN structure.
  • the linear conversion unit may be referred to as a P layer (Permutation-layer).
  • (A) Feistel structure The n-bit input data is divided into two n / 2-bit data.
  • a function (F function) having one of the data and the round key as inputs is applied, and the output is exclusively ORed with the other data. After that, the left and right data are exchanged as output data.
  • F function function having one of the data and the round key as inputs
  • the output is exclusively ORed with the other data.
  • the left and right data are exchanged as output data.
  • There are various types of internal structure of the F function but basically, it is realized by a combination of exclusive OR operation, non-linear operation, and linear transformation with round key data as in the SPN structure.
  • FIG. 6 shows an example of the round function of the Feistel structure.
  • the extended Feistel structure is an extended Feistel structure in which the number of data divisions is 2 and is divided into 3 or more. If the number of divisions is d, various extended Feistel structures can be defined by d. Since the input / output size of the F function is relatively small, it is said that it is suitable for small packaging.
  • Nonlinear conversion unit tends to increase the cost in mounting as the size of input data increases. In order to avoid this, it is often the case that the target data is divided into a plurality of units and nonlinear transformation is performed on each of the units. For example, the input size is set to ms bits, and these are divided into m pieces of data of s bits, and nonlinear conversion having s bits input / output is performed on each of them.
  • These non-linear conversion execution units in s bit units are called S-boxes. An example of the S box (S-box) is shown in FIG.
  • the input data consisting of ms bits is divided into m s-bit data, and each divided data is input to m S-boxes that execute s-bit nonlinear conversion processing,
  • the output of each S box is concatenated to obtain an ms-bit nonlinear conversion result.
  • the linear conversion unit can be defined as a matrix due to its nature.
  • the matrix elements can be expressed in various ways, such as a body element of the extension field GF (2 8 ) or an element of GF (2).
  • FIG. 10 shows an example of a linear conversion unit having an ms-bit input / output and defined by an m ⁇ m matrix defined on GF (2 s ).
  • FIG. 11 shows an example in which input data is represented as A, output data after data conversion for input data A is represented as B, and input data A and output data B are represented as states each having an m ⁇ n array.
  • the input data A is an element of the extension field GF (2 s ) mn
  • Input data A (a 0 a 1 a 2 ... A mn ⁇ 2 a mn ⁇ 1 ).
  • a 0 MSB
  • a mn-1 is the bit data of the LSB side.
  • the output data B is an element of the extension field GF (2 s ) mn
  • Output data B (b 0 b 1 b 2 ... B mn ⁇ 2 b mn ⁇ 1 ).
  • B 0 is MSB and b mn ⁇ 1 is bit data on the LSB side.
  • an m ⁇ n array state includes m ⁇ n elements.
  • state A shown in FIG. 11 includes mn elements a 0 to a nm ⁇ 1 .
  • the elements of state B are mn elements from b 0 to b nm ⁇ 1 .
  • each element is bit data such as 4-bit data and 8-bit (1 byte) data, for example.
  • bit data such as 4-bit data and 8-bit (1 byte) data
  • FIG. 12 shows an example of the 4 ⁇ 4 state when each of the 16 elements included in the 4 ⁇ 4 state is 4-bit data.
  • the input data is A
  • the output data after some data conversion is B
  • the input data A is an element of the extension field GF (2 4 ) 4 ⁇ 4
  • Input data A (a 0 a 1 a 2 ... A 14 a 15 ).
  • a 0 is MSB
  • a 15 is the bit data of the LSB side.
  • the output data B is an element of the expansion field GF (2 4 ) 4 ⁇ 4
  • Output data B (b 0 b 1 b 2 ... B 14 b 15 ).
  • B 0 is MSB and b 15 is bit data on the LSB side.
  • the example shown in FIG. 12 is an example in which input data A and output data B are expressed as a state having a 4 ⁇ 4 arrangement in which each element is composed of 4-bit data.
  • state A shown in FIG. 12 includes 16 elements a 0 to a 15 , each of which is 4-bit data. That is, when the 64-bit input data A is shown as a state, each element shown in FIG. 12 can be expressed as a state A having a 4 ⁇ 4 arrangement of 4-bit data.
  • state B shown in FIG. 12 includes 16 elements b 0 to b 15 , each of which is 4-bit data. That is, when the 64-bit output data B is shown as a state, each element shown in FIG. 12 can be expressed as a state B having a 4 ⁇ 4 array of 4-bit data.
  • the output data B is calculated by an exclusive OR operation between the round key K output from the key schedule unit and the input data A. All of the input data A, the round key K, and the output data B are 64-bit data expressed in a state composed of 16 4-bit elements.
  • (XOR) indicates an exclusive OR operation.
  • One round operation is set by a combination of operations that sequentially execute the above operations (1) to (3) in a predetermined sequence.
  • a round operation is repeatedly executed on the input data to generate and output output data, for example, encrypted data.
  • the basic round operation is set such that exclusive OR operation with a round key, linear conversion processing, and nonlinear conversion processing are executed once each.
  • an irregular round operation configuration can be set in the round operation executed in the cryptographic processing sequence.
  • many configurations are used in which only the operation with the round key is executed at the beginning or end of the cryptographic processing sequence. This process is called a key whitening process and is not generally counted as the number of rounds.
  • Each of X 0 , X 1 ,..., X n ⁇ 1 is an m ⁇ m matrix in which each element is composed of elements on GF (2 s ).
  • FIG. MC [X 0 , X 1 ,..., X n ⁇ 1 ]
  • the elements of the state columns (0 to n ⁇ 1) and the matrix X 0 , X 1, ..., X n ⁇ 1 corresponding to each column are applied to the elements of the state expression data.
  • Matrix operations are defined as column diffusion operations. Note that MC means diffusion (Mix) in units of columns (Column), that is, (MixColumn).
  • a matrix operation in which one matrix X k is applied to an element of one column of the state is performed.
  • the matrix X k applied to each of a plurality of columns constituting the state can be set to be the same matrix or set to be different.
  • an arithmetic expression for calculating the state B, which is output data, by executing a column diffusion operation on the state A, which is input data can be expressed as follows.
  • B MC [X 0 , X 1 ,..., X n ⁇ 1 ] (A)
  • t (b 1 b 2 ... B k ) represents a transposed matrix of (b 1 b 2 ... B k ).
  • FIG. Input data A is 64-bit data and state A is state A consisting of 16 4-bit data elements.
  • the output data B is also 64-bit data, and the state B is a state B composed of 16 4-bit data elements.
  • the elements of state B calculated by the above arithmetic expression are as follows.
  • t (b 0 b 1 b 2 b 3 ) X 0 ⁇ t (a 0 a 1 a 2 a 3 ),
  • t (b 4 b 5 b 6 b 7) X 1 ⁇ t (a 4 a 5 a 6 a 7),
  • t (b 8 b 9 b 10 b 11) X 2 ⁇ t (a 8 a 9 a 10 a 11),
  • t (b 12 b 13 b 14 b 15 ) X 3 ⁇ t (a 12 a 13 a 14 a 15 )
  • the above arithmetic expressions are shown in accordance with the actual element arrays of states A and B, the following arithmetic expressions are obtained as shown in the lower part of FIG.
  • MC [X] when performing a matrix operation applying the same matrix X to each column element of the state, MC [X] Sometimes expressed. That is, MC [X] and MC [X, X,.
  • Each of X 0 , X 1 ,..., X m ⁇ 1 is an n ⁇ n matrix in which each element is composed of elements on GF (2 s ).
  • MR [X 0 , X 1 ,..., X m ⁇ 1 ]
  • a matrix operation in which the above operation is applied to the elements of the state expression data by applying the elements of each row (0 to n ⁇ 1) of the state and the matrix X 0 , X 1, ..., X m ⁇ 1 corresponding to each row. Is defined as a row diffusion operation.
  • MR means diffusion (Mix) in units of rows, that is, (MixRow).
  • a matrix operation in which one matrix X k is applied to elements in one row of the state is performed.
  • the matrix X k applied to each of a plurality of rows constituting the state can be set to be the same matrix or different matrix settings.
  • an arithmetic expression for calculating the state B that is the output data by performing the row diffusion operation on the state A that is the input data can be expressed as follows.
  • B MR [X 0 , X 1 ,..., X m ⁇ 1 ] (A)
  • This row diffusion calculation process is the process shown in the lower part of FIG.
  • FIG. Input data A is 64-bit data and state A is state A consisting of 16 4-bit data elements.
  • the output data B is also 64-bit data, and the state B is a state B composed of 16 4-bit data elements, Row diffusion operation: MR [X 0 , X 1 , X 2 , X 3 ] It is the figure which showed the example of application processing.
  • the elements of state B calculated by the above arithmetic expression are as follows.
  • t (b 0 b 4 b 8 b 12) X 0 ⁇ t (a 0 a 4 a 8 a 12),
  • t (b 1 b 5 b 9 b 13 ) X 1 ⁇ t (a 1 a 5 a 9 a 13 ),
  • t (b 2 b 6 b 10 b 14 ) X 2 ⁇ t (a 2 a 6 a 10 a 14 ),
  • t (b 3 b 7 b 11 b 15 ) X 3 ⁇ t (a 3 a 7 a 11 a 15 )
  • the above arithmetic expression is shown according to the actual element arrangement of states A and B, the following arithmetic expression is obtained as shown in the lower part of FIG.
  • MR [X] when performing a matrix operation applying the same matrix X to each row element of the state, MR [X] Sometimes expressed. That is, MR [X] and MR [X, X,..., X] are the same calculation.
  • D (C, k1, k2,..., Kr) E (C, KR,..., K2, K1) That is, when the decryption function D is configured to use the same function only by reversing the order of application of the round keys in the encryption function E, This common key block cipher is said to have involution.
  • the common key block cipher that can form the decryption function D only by changing the input order of the round keys using the encryption function E has involution.
  • the Feistel type common key block cipher usually has an involution property because it is known that the encryption function and the decryption function can be performed by the same circuit only by reversing the use order of the round keys to be used.
  • An involution common key block cipher basically implements an encryption function and implements an encryption function and a decryption function only by implementing an encryption function, so it requires fewer circuits and can be reduced in weight (miniaturized). Yes, mounting efficiency is high.
  • the differential attack is an attack in which data having a specific difference is input to the cryptographic apparatus, data that reflects the input difference is detected from the output, and a key is estimated. Note that the propagation probability of the difference value is called the difference probability.
  • a linear attack is an attack that attempts to estimate a key by observing the correlation between the exclusive OR of specific bits at the input and the exclusive OR of specific bits at the output, and finding a strong correlation. is there. Note that the correlation coefficient of specific bits of input and output is called linear probability.
  • Highly secure ciphers are ciphers that are highly resistant to various attacks as described above, that is, ciphers that are difficult to decipher secret information applied to cryptographic processing, such as keys.
  • ciphers that are difficult to decipher secret information applied to cryptographic processing, such as keys.
  • cryptographic processing such as keys.
  • a plurality of data serving as the security index of the encryption algorithm will be described.
  • Branch n ( ⁇ ) min ⁇ ⁇ 0 ⁇ hw n ( ⁇ ) + hw n ( ⁇ ( ⁇ )) ⁇
  • min ⁇ ⁇ 0 ⁇ X ⁇ represents the minimum value of all X ⁇ satisfying ⁇ ⁇
  • hw n (Y) is a function that returns the number of elements in which all n-bit data is not 0 (non-zero) when the bit string Y is divided into n bits.
  • a mapping ⁇ such that the branch number Branch n ( ⁇ ) is b + 1 is called an optimal diffusion mapping (Optical Diffusion Mappings).
  • the MDS matrix is a matrix in which an arbitrary small matrix constituting the matrix is a regular matrix.
  • a regular matrix is a matrix having an inverse matrix, where the matrix is A and the inverse matrix is A ⁇ 1 .
  • an S box (S-box) that performs nonlinear transformation in units of s bits is used for the nonlinear transformation unit set in the common key block cipher.
  • S-box an S box that performs nonlinear transformation in units of s bits
  • a minimum number of differential active S-boxes included in a differential path expressing a differential connection relationship that is, a minimum differential active S-box number.
  • the difference path is a specific difference value specified for all data parts except key data in the encryption function.
  • the difference value is not freely determined, and the difference values before and after the conversion process are related to each other.
  • the relationship between the input difference and the output difference is determined one-to-one.
  • the relationship between the input difference and the output difference is not one-to-one, but the concept of probability is introduced.
  • the probability for a certain input difference and output difference can be calculated in advance. The sum of the probabilities for all outputs is 1.
  • the difference path having a probability other than 0 is a set of difference data starting from the difference value for the plaintext (input) and reaching the difference value for the ciphertext (output), and for all S-boxes.
  • Difference values given before and after have a probability other than zero.
  • a difference value input to an S-box of a certain differential path having a probability other than 0 is not 0, and is called a differential active S-box.
  • the smallest number among the differential active S-box numbers of all differential paths having a probability other than 0 is called the minimum differential active S-box number, and this value is well known as a safety index against differential attacks.
  • the linear path is often called a linear approximation, but the term “path” is used here in order to correspond to the difference.
  • the linear path is a path in which a specific linear mask value is designated for all data portions except key data in the encryption function.
  • the linear mask value is not freely determined, and the linear mask values before and after the conversion process are related to each other. Before and after the linear conversion process, the relationship between the input linear mask value and the output linear mask value is determined one-to-one.
  • the relationship between the input linear mask value and the output linear mask value is not determined one-to-one, but the concept of probability is introduced.
  • For an input linear mask value there is a set of one or more linear mask values that can be output, and the probability that each will be output can be calculated in advance. The sum of the probabilities for all outputs is 1.
  • a linear path having a probability other than 0 is a set of linear mask value data starting from a linear mask value for plaintext (input) to a linear mask value for ciphertext (output).
  • the linear mask values given before and after the box (S-box) have a probability other than zero.
  • a non-zero linear mask value input to an S box (S-box) of a certain linear path having a probability other than 0 is referred to as a linear active S box (S-box).
  • the smallest number of active S-boxes (S-boxes) of all linear paths with non-zero probabilities is called the minimum linear active S-box (S-box) number, and this number is a safety measure against linear attacks.
  • S-box The minimum linear active S-box
  • the cryptographic processing device of the present disclosure described below is a device that executes a common key block cipher (block cipher), and is a device that has a Substitution-Permutation Network (SPN) structure round function.
  • block cipher common key block cipher
  • SPN Substitution-Permutation Network
  • the cryptographic processing apparatus 100 includes a key schedule unit 110 and a cryptographic processing unit 120.
  • the key schedule unit 110 receives the secret key K and outputs a round key to be applied in each round of the encryption processing unit 120 according to a predetermined key generation algorithm.
  • the cryptographic processing unit 120 receives the round key from the key scheduling unit 110, converts the plaintext P data, and outputs the ciphertext C.
  • the encryption processing unit 120 can also execute a decryption process in which the ciphertext C is input and the plaintext P is output. When executing the decryption process, a process in which the round keys supplied from the key schedule unit 110 are applied in the reverse order of the encryption process is executed.
  • the encryption processing unit 120 An exclusive OR unit 121 that performs an exclusive OR operation between the input data and the round key, A non-linear transformation unit 122 that performs non-linear transformation processing on input data; A linear transformation unit 123 that performs linear transformation processing on input data; Have
  • the cryptographic processing unit 120 of the cryptographic processing device 100 of the present disclosure has a configuration in which an exclusive OR unit 121, a nonlinear conversion unit 122, a linear conversion unit 123, and these three different data conversion processes are repeatedly executed. Have.
  • the plaintext P as input data and the ciphertext C as output data are the state expression data described above, and each element is composed of 4 bits and 16 elements of 4 ⁇ 4. This is 64-bit data. Note that the round key input from the key schedule unit 110 is also 64-bit data expressed in a state consisting of 16 4-bit data elements.
  • the non-linear conversion process executed in the non-linear conversion unit of the cryptographic processing unit 120 is executed using a plurality of S boxes (S-boxes) as shown in FIG. 22 (1), for example.
  • the linear transformation process performed in the linear transformation part of the encryption processing part 120 is performed as a matrix calculation process as shown, for example in FIG. 22 (2).
  • the cryptographic processing unit 120 of the cryptographic processing device 100 has a configuration in which an exclusive OR operation, a non-linear conversion, and a linear conversion process with a round key are repeatedly executed for a plurality of rounds. .
  • One of the features of the cryptographic processing apparatus according to the present disclosure is that the linear conversion process executed in each round is executed as a different process for each round.
  • details of the linear conversion processing executed by the cryptographic processing device according to the present disclosure will be described.
  • FIG. 23 is a diagram illustrating a configuration example of a different linear conversion unit included in the cryptographic processing unit of the cryptographic processing device according to the present disclosure.
  • the configuration diagram of FIG. 23 is a configuration diagram in which the exclusive OR unit is omitted.
  • Linear converters P1, 201, Linear converters P2, 202, Linear converters P3, 203 These three different linear conversion units are configured to execute any one of these three different linear conversion processes in each round, and different linear conversion processes are performed without continuing the same linear change process in successive rounds. It is in setting.
  • the above four different matrices M 0 to M 3 are used in combination.
  • the above four matrices are non-MDS matrices that are not the above-described MDS (Maximum Distance Separable) matrix.
  • MDS Maximum Distance Separable
  • FIG. 24 (2) is a diagram illustrating a specific matrix calculation mode of the linear conversion processes P1 to P3.
  • a 4 ⁇ 4 rectangle shown in FIG. 24 (2) indicates a state composed of 16 elements each having 4 bits for a linear conversion process. That is, it is a 64-bit 4 ⁇ 4 state.
  • a matrix operation using a combination of the matrices M 0 to M 3 is executed on the 4 ⁇ 4 state input data.
  • the linear transformation process P1 is For each column element of 4 ⁇ 4 state input data, a matrix operation is performed by applying one matrix M 0 for each column. This is the column diffusion operation (MixColumn) described above with reference to FIGS.
  • the linear transformation process P1 is MC [M 0 ] It is a column diffusion calculation (MC) shown by the above formula.
  • MC [M 0 ] is an expression indicating a matrix operation in which the same matrix M 0 is applied to each column of the state, and an expression individually indicating a matrix to be applied to each column of the state, MC [M 0 , M 0 , M 0 , M 0 ] It has the same meaning as the above formula.
  • the linear transformation process P2 is MR [M 0 , M 1 , M 2 , M 3 ]
  • This is a row diffusion operation (MixRow) represented by the above equation.
  • the linear conversion process P3 will be described. Similarly to the linear conversion process P2, the linear conversion process P3 performs a matrix operation in which a different matrix is applied to each row element of 4 ⁇ 4 state input data as shown in FIG. 24 (2). . Unlike the linear transformation process P2, the linear transformation process P3 executes a matrix operation that applies the following matrix to the first to fourth rows. 1st row: application matrix M 2 , Second row: application matrix M 0 , 3rd row: application matrix M 1 , 4th row: application matrix M 3 , This is the row diffusion operation (MixRow) described above with reference to FIGS.
  • the linear transformation process P2 is performed as row diffusion calculation type 1 (MixRow1)
  • the linear transformation process P3 is performed by row diffusion calculation type 2 (MixRow2), Call it.
  • the linear transformation process P1 is a column diffusion calculation (MixColumn).
  • FIG. 25 is a diagram for explaining a specific calculation process example of the linear conversion process P1, that is, the column diffusion calculation (MixColumn).
  • Input A is a state composed of 16 elements a 0 to a 15 of n-bit data.
  • the output B is also a state composed of 16 elements b 0 to b 15 of n-bit data.
  • n 4
  • each element has 4-bit data
  • both input A and output B are 64 bits.
  • FIG. 25 (2) shows a specific calculation process example of the linear conversion process P1, that is, the column diffusion calculation (MixColumn).
  • the column diffusion operation (MixColumn) performed as the linear transformation process P1 is a matrix operation according to the following equation.
  • the 16 elements b 0 to b 15 of the output B are calculated by the following calculation based on the matrix M 0 and the 16 elements a 0 to a 15 of the input A.
  • b 0 a 1 (+) a 2 (+) a 3
  • b 1 a 0 (+) a 2 (+) a 3
  • b 2 a 0 (+) a 1 (+) a 3
  • b 3 a 0 (+) a 1 (+) a 2
  • b 4 a 5 (+) a 6 (+) a 7
  • b 5 a 4 (+) a 6 (+) a 7
  • b 6 a 4 (+) a 5 (+) a 7
  • b 7 a 4 (+) a 5 (+) a 6
  • b 8 a 9 (+) a 10 (+) a 11
  • b 9 a 8 (+) a 10 (+) a 11
  • b 10 a 8 (+) a 9 (+) a 9 (+) a 10 (+
  • the column diffusion calculation (MixColumn) performed as the linear conversion process P1 is performed according to the calculation process described above, based on the matrix M 0 and the 16 elements a 0 to a 15 of the input A to the 16 elements b 0 to b of the output B. to calculate the b 15.
  • FIG. 26 is a diagram for explaining a specific calculation process example of the linear conversion process P2, that is, the row diffusion calculation type 1 (MixRow1).
  • Input A is a state composed of 16 elements a 0 to a 15 of n-bit data.
  • the output B is also a state composed of 16 elements b 0 to b 15 of n-bit data.
  • n 4
  • each element has 4-bit data
  • both input A and output B are 64 bits.
  • FIG. 26 (2) shows a specific calculation process example of the linear conversion process P2, that is, the row diffusion calculation type 1 (MixRow1).
  • the row diffusion calculation type 1 (MixRow1) performed as the linear transformation process P2 is a matrix calculation according to the following equation.
  • the 16 elements b 0 to b 15 of the output B are calculated by the following calculation based on the matrices M 0 , M 1 , M 2 , and M 3 and the 16 elements a 0 to a 15 of the input A. .
  • b 0 a 4 (+) a 8 (+) a 12
  • b 1 a 1 (+) a 5 (+) a 13
  • b 2 a 2 (+) a 6 (+) a 10
  • b 3 a 3 (+) a 11 (+) a 15
  • b 4 a 0 (+) a 8 (+) a 12
  • b 5 a 1 (+) a 5 (+) a 9
  • b 6 a 2 (+) a 6 (+) a 14
  • b 7 a 7 (+) a 11 (+) a 15
  • b 8 a 0 (+) a 4 (+) a 12
  • b 9 a 5 (+) a 9 (+) a 13
  • b 10 a 2 (+) a 10 (+) a 14
  • b 11 a 3 (+) a 7 (+) a 11
  • b 12 a 0 (+) a 4 (+) a 12
  • b 9 a 5 (+) a 9 (+) a 13
  • the row diffusion calculation type 1 (MixRow1) performed as the linear conversion process P2 is based on the matrix M 0 , M 1 , M 2 , M 3 and the 16 elements a 0 to a 15 of the input A according to the above calculation process.
  • 16 elements b 0 to b 15 of the output B are calculated.
  • FIG. 27 is a diagram for explaining a specific calculation example of the linear conversion process P3, that is, the row diffusion calculation type 2 (MixRow2).
  • Input A is a state composed of 16 elements a 0 to a 15 of n-bit data.
  • the output B is also a state composed of 16 elements b 0 to b 15 of n-bit data.
  • n 4
  • each element has 4-bit data
  • both input A and output B are 64 bits.
  • FIG. 27 (2) shows a specific calculation process example of the linear conversion process P2, that is, the row diffusion calculation type 2 (MixRow2).
  • the row diffusion calculation type 2 (MixRow2) performed as the linear conversion process P3 is a matrix calculation according to the following equation.
  • the 16 elements b 0 to b 15 of the output B are calculated by the following calculation based on the matrices M 0 , M 1 , M 2 , and M 3 and the 16 elements a 0 to a 15 of the input A. .
  • b 0 a 0 (+) a 4 (+) a 8
  • b 1 a 5 (+) a 9 (+) a 13
  • b 2 a 2 (+) a 6 (+) a 14
  • b 3 a 3 (+) a 11 (+) a 15
  • b 4 a 0 (+) a 4 (+) a 12
  • b 5 a 1 (+) a 9 (+) a 13
  • b 6 a 2 (+) a 6 (+) a 10
  • b 7 a 7 (+) a 11 (+) a 15
  • b 8 a 0 (+) a 8 (+) a 12
  • b 9 a 1 (+) a 5 (+) a 13
  • b 10 a 6 (+) a 10 (+) a 14
  • b 11 a 3 (+) a 7 (+) a 11
  • the row diffusion calculation type 2 (MixRow2) performed as the linear conversion process P3 is based on the matrix M 0 , M 1 , M 2 , M 3 and the 16 elements a 0 to a 15 of the input A according to the calculation process.
  • 16 elements b 0 to b 15 of the output B are calculated.
  • the number of active S boxes in the cryptographic processing device of the present disclosure that is, the cryptographic processing device that executes three different types of linear transformation processing P1 to P3 and the cryptographic processing device that repeatedly executes a single type of linear transformation processing of the conventional type Verified.
  • the cryptographic processing device of the present disclosure has a configuration in which three types of linear conversion processing are used in the cryptographic processing sequence, and these are switched and executed for each round.
  • the exclusive OR operation unit with the round key is omitted.
  • the number of non-linear conversion units is the number of rounds.
  • seven round keys of the round keys RK 1 to RK 7 are applied. However, since there are six layers of non-linear conversion units, it is assumed that the encryption processing apparatus is six rounds.
  • Linear transformation processing P1 is a sequence spreading operation of applying the matrix M 0 (MixColumn).
  • the linear transformation process P2 is a row diffusion calculation type 1 (MixRow1) to which the matrices M 0 , M 1 , M 2 , and M 3 are applied.
  • the linear transformation process P3 is a row diffusion calculation type 2 (MixRow2) to which the matrices M 0 , M 1 , M 2 , and M 3 are applied.
  • FIG. 29 shows an example of a cryptographic processing apparatus that executes a conventional single linear conversion process for the cryptographic processing apparatus shown in FIG.
  • the cryptographic processing apparatus shown in FIG. 29 also has a 6-round configuration, but the linear conversion processing in each round is configured to perform the same linear conversion processing.
  • Both the configurations of FIG. 28 and FIG. 29 are settings for executing the encryption process on the 64-bit input plaintext P and outputting the 64-bit ciphertext C.
  • the S box is set in each nonlinear conversion unit, and each S box is configured to execute a 4-bit input / output nonlinear conversion as described above with reference to FIG.
  • FIG. 30 shows the result of counting the number of minimum differential / linear differential active S boxes by configuring cryptographic processing apparatuses having different round numbers of 4 to 24 rounds.
  • the number of active S-boxes is 4 and the same value in both the conventional configuration in which the same linear conversion unit is repeatedly executed and the configuration in which the different linear conversion processing of the present disclosure is executed. In all cases (except 8), the number of active S boxes is larger in the configuration in which the different linear transformation processing of the present disclosure is performed in any case. This result is shown as a graph in FIG.
  • the input data is a state composed of 4 ⁇ 4 elements each having 4 bits
  • the linear conversion unit uses four types of matrices M 0 , M 1 , M 2 , and M 3 .
  • the configuration for executing the linear transformation process by the matrix operation has been described. However, when the above process is generalized, the following setting is made.
  • the linear conversion unit applies a column spreading operation for performing a linear conversion by applying a matrix for each column element of the state, and a state
  • the matrix operation is performed in a round operation in one of row diffusion operations in which a matrix is applied in units of each row element to perform linear transformation.
  • the linear conversion unit is configured to execute linear conversion processing by matrix operation using a plurality of types of matrices M0 to Mk (k is an integer of 1 or more), and the matrix M0 to Mk for each column element of the state.
  • a column diffusion operation that performs linear transformation by applying a selection matrix selected from the above to each column in a specific order, and a selection matrix selected from the matrices M0 to Mk for each row element of the state is applied to each row in a specific order
  • the row diffusion operation for performing linear transformation is switched and executed according to the round transition.
  • An example of a specific linear transformation processing configuration is, for example, the following configuration.
  • A a column diffusion operation that performs linear transformation by applying a selection matrix selected from the matrices M0 to Mk to each column in a specific order for each column element of the state;
  • B a row diffusion operation type 1 that performs linear transformation by applying a selection matrix selected from the matrices M0 to Mk to each row in a specific order A for each row element of the state;
  • C A row diffusion operation type 2 for performing linear transformation by applying a selection matrix selected from the matrices M0 to Mk in each row element unit of the state to each row in a different order B from a specific order A.
  • a cryptographic processing apparatus that executes by switching according to round transition.
  • a column diffusion operation for performing linear transformation by applying a selection matrix selected from the matrices M0 to Mk to each row in a specific order for each row element of the state
  • B a row diffusion operation type 1 that performs linear transformation by applying a selection matrix selected from the matrices M0 to Mk to each column in a specific order A for each column element of the state
  • C A row diffusion operation type 2 for performing linear transformation by applying a selection matrix selected from the matrices M0 to Mk to each column in a sequence B different from the specific sequence A in units of column elements of the state,
  • a cryptographic processing apparatus that executes by switching according to round transition.
  • the linear conversion unit is configured to execute linear conversion processing by matrix calculation using four types of matrices M0, M1, M2, and M3.
  • A a column diffusion operation for performing linear transformation by applying the matrix M0 in units of column elements of the state
  • B Row diffusion operation type 1 that performs linear transformation by applying each matrix in the order of the matrices M0, M1, M2, and M3 in units of each row element of the state
  • C a row diffusion operation type 2 that performs linear transformation by applying each matrix in a different order from the type 1 for each row element of the state
  • a cryptographic processing apparatus that switches and executes the three types of matrix operations in accordance with a round transition.
  • the combination of the matrix applied in units of each row element of the state in the row diffusion calculation type 1 and the matrix applied in units of each row element of the state in the row diffusion calculation type 2 is combined in any two rows of the state.
  • a total of four matrices that is, two matrices applied in type 1 and two matrices applied in type 2 are assumed to be combinations composed of at least three types of matrices.
  • a matrix to be applied to each row of 4 ⁇ 4 states first to fourth rows, M1, M3, M0, M2
  • each row of 4 ⁇ 4 states the matrix applied to the first to fourth rows, M0, M2, M3, M1
  • a total of four matrices including two matrices applied in type 1 and two matrices applied in type 2 for any two rows of 4 ⁇ 4 states are composed of at least three types of matrices. It becomes a combination.
  • the above setting is a combination of at least three types of matrixes including a total of four matrices including two matrices applied in type 1 and two matrices applied in type 2 in any other combination of two rows. .
  • the linear conversion unit is configured to execute linear conversion processing by matrix calculation using four types of matrices M0, M1, M2, and M3.
  • A a row diffusion operation for performing linear transformation by applying the matrix M0 for each row element of the state;
  • B Column diffusion operation type 1 that performs linear transformation by applying each matrix in the order of matrices M0, M1, M2, and M3 in units of column elements of the state;
  • C Column diffusion operation type 2 for performing linear transformation by applying each matrix in the order different from type 1 for each column element of the state;
  • a cryptographic processing apparatus that switches and executes the three types of matrix operations in accordance with a round transition.
  • the combination of the matrix applied in units of each column element of the state in the row diffusion calculation type 1 and the matrix applied in units of each column element of the state in the row diffusion calculation type 2 is an arbitrary state. Assume that a total of four matrices including two matrices applied in type 1 and two matrices applied in type 2 for two columns are composed of at least three types of matrices.
  • the cryptographic processing apparatus 100 includes the key schedule unit 110 and the cryptographic processing unit 120.
  • the key schedule unit 110 generates a round key to be applied in each round of the cryptographic processing unit 120 according to a predetermined key generation algorithm based on the secret key K, for example, and outputs the round key to the cryptographic processing unit 120.
  • the cryptographic processing unit 120 receives the round key from the key scheduling unit 110, converts the plaintext P data, and outputs the ciphertext C. Note that the same processing is performed in the decoding processing.
  • the configuration and processing of the key schedule unit 110 that executes the round key generation and supply processing will be described.
  • FIG. 32 is a diagram illustrating a configuration example of a key schedule unit in the cryptographic processing device according to the present disclosure.
  • the key scheduling part 300 includes a key supply unit (key register) 301 as a storage unit for storing a secret key K 1.
  • the key schedule unit 300 outputs the key K 1 to the exclusive OR unit (round key calculation unit) 321 of the first round of the cryptographic processing unit 320. That key K 1 is used as a round key for the first round.
  • the key scheduling part 300 inputs the key K 1 in the key conversion unit 302a.
  • the key conversion unit 302a generates a conversion key Kd 1 executes a predetermined operation on the key K 1. Further, the conversion key Kd 1 generated by the key conversion unit 302 a is output to the exclusive OR unit (round key calculation unit) 322 of the second round of the encryption processing unit 320. That is, the conversion key Kd 1 is used as a round key for the second round.
  • the key scheduling part 300 inputs the conversion key Kd 1 in the key conversion unit 302b.
  • the key conversion unit 302b generates the key K 1 by performing a predetermined operation on the conversion key Kd 1.
  • This key K 1 is the same key as the key K 1 that is the generation source of the conversion key Kd 1 .
  • the key schedule unit 300 outputs the key K 1 generated by the key conversion unit 302 b to the third round exclusive OR unit (round key calculation unit) 323 of the encryption processing unit 320. That key K 1 is used as a round key for the third round.
  • the key conversion unit 302c ⁇ f, the key K 1 and the key K 1d are alternately generated, and outputs the generated key to the exclusive OR unit 324 to 327 of the encryption processing unit.
  • All of the key conversion units 302a to 302f execute the same calculation. That is, by the same arithmetic processing, A conversion key Kd 1 is generated from the key K 1 , A key K 1 is generated from the conversion key Kd 1 .
  • FIG. 33 shows the key K 1 described in FIG. 32 as the base key K and the conversion key Kd 1 as the conversion key Kd.
  • Each key shown in FIG. 33 is expressed as 4 ⁇ 4 states of 16 4-bit elements. That is, both are 64-bit key data.
  • FIG. 34 is a diagram for explaining processing for generating the conversion key Kd from the base key K.
  • the process of generating the conversion key Kd from the base key K is configured by the following two steps.
  • S1 An intermediate key S is generated by executing an operation to which the intermediate key generation sequence spreading operation (MixColumn_KSF ()) is applied to the base key K.
  • S2 The conversion key Kd is generated by executing an operation to which the conversion key generation sequence spreading operation (MixRow_KSF ()) is applied to the intermediate key S.
  • the column diffusion operation (MixColumn) executed in step S1 and the row diffusion operation (MixRow) executed in step S2 are matrix application operations similar to those described above with reference to FIGS. However, the matrix M D to be applied in this key conversion processing is a matrix shown below.
  • Matrix M D shown above is a matrix called Hadamard (Hadamard) MDS matrix.
  • the MDS matrix is a matrix in which an arbitrary small matrix constituting the matrix is a regular matrix.
  • a regular matrix is a matrix having an inverse matrix, where the matrix is A and the inverse matrix is A ⁇ 1 .
  • a matrix A having an inverse matrix A ⁇ 1 in which the above equation holds is a regular matrix.
  • the mapping ⁇ in which the branch number Branch ( ⁇ ) is b + 1 is called an optimal diffusion transformation
  • the MDS matrix is a matrix that performs the optimum diffusion transformation.
  • the Hadamard (Hadamard) MDS matrix M D is applied, to perform a column spreading operation in step S1 shown in FIG. 34, the row spreading operation in step S2.
  • the column diffusion calculation in step S1 is represented by the following calculation expression.
  • MC [M D ] MC [M D , M D , M D , M D ]
  • the row diffusion calculation in step S2 is expressed by the following calculation expression.
  • MR [M D ] MR [M D , M D , M D , M D ]
  • the column spreading operation in step S1 is run against all four columns of the state representation data of 4 ⁇ 4 consisting of 4-bit elements, the applied matrix operation the same Hadamard (Hadamard) MDS matrix M D .
  • the row spreading operation in Step S2 is for all four rows of four states represent data ⁇ 4 consisting of 4-bit elements to perform the applied matrix operation the same Hadamard (Hadamard) MDS matrix M D .
  • the column diffusion operation MC [M D ] in step S1 shown in FIG. 34 is a matrix operation according to the following equation.
  • the row diffusion operation MR [M D ] in step S2 shown in FIG. 34 is a matrix operation according to the following equation.
  • the key conversion unit 302 of the key scheduling part 300 shown in FIG. 32 in step S1 shown in FIG. 34, and executes the sequence spreading operation MC of applying the matrix M D [M D], the matrix M in step S2 A row diffusion operation MR [M D ] to which D is applied is executed.
  • the conversion key Kd is generated from the base key K by continuously executing these two matrix operations.
  • the function G composed of continuous processing of the column diffusion operation MC [M D ] and the row diffusion operation MR [M D ] has involution properties and is in the forward direction. Since the function G and the backward function G ⁇ 1 are the same, the original value is calculated by repeating twice.
  • the key conversion unit 302 constitutes a column spreading operation MC of applying the matrix M D [M D], by executing the matrix M D applied row diffusion operation MR [M D], the input data 4
  • All of the x4 state components i.e. all 16 components, can affect all 16 components of the output data. That is, data diffusion is performed between all elements in the input / output state.
  • Such a data conversion mode is defined as “full diffusion conversion” or diffusion having full diffusion properties.
  • the input and output are states each consisting of 16 n-bit elements, and a conversion function f to be applied to the input is assumed.
  • B f (A)
  • the output state B is set to be calculated according to the above formula.
  • Input state A (a 0 , a 1 , a 2 ,... A 15 )
  • Output state B (b 0 , b 1 , b 2 ,... B 15 ) It is.
  • a i and b i are elements of states A and B.
  • the execution function G of the key conversion unit 302 is a function having the following two properties. (1) Full diffusion property that realizes full diffusion conversion, (2) Involution property in which the forward function G and the backward function G ⁇ 1 are the same, It has these two properties.
  • the base key K is input to the exclusive OR unit 331 of the encryption processing unit, and an exclusive OR operation with the input state A is performed. Thereafter, the nonlinear / linear conversion unit (S & P) 332 performs nonlinear conversion processing and linear conversion processing. Further, an exclusive OR operation with the conversion key Kd is executed in the exclusive OR operation unit 333 for the output. The output of the exclusive OR operation unit 333 is set to state B.
  • This property can be said to be a property that contributes to the safety and implementation performance of the cryptographic processing device. Specifically, improvement of data diffusibility by a key is realized, and high diffusion performance can be exhibited even if the number of rounds is reduced. As a result, it is possible to increase resistance to various attacks. For example, it is possible to further improve resistance to key analysis processing based on an intermediate value matching attack using key dependency.
  • the diffusion performance of the data to be converted in the encryption processing unit is improved, and the resistance to various attacks such as encryption processing that is safe with a smaller number of rounds, such as key analysis, is high.
  • Cryptographic processing is realized.
  • FIG. (1) Cryptographic processing configuration in which the same round key is applied without performing key conversion in each round
  • 2 3 shows an example of one encryption processing configuration.
  • the box G shown in FIG. 36 (2) corresponds to the key conversion unit 302 shown in FIG.
  • the number of rounds necessary for spreading the configuration information (bit string) of the applied key to all the bits of the input plaintext P that is the conversion target data is (Full diffusion).
  • R the round function
  • the configuration information (bit string) of the applied key is diffused (Full diffusion) to all the bits of the input plaintext P that is the conversion target data.
  • the number of rounds required for the number of rounds is the number of rounds in which two base keys K 1 and two conversion keys Kd 1 are used. In the example shown in the figure, there are one round.
  • the processing of the present disclosure is applied, the diffusion of the configuration information of the key data with respect to the conversion target data is realized in one round, and a larger diffusion performance is guaranteed without depending on the processing of the round function (R). That is, secure cryptographic processing with high resistance to attacks is realized with a small number of rounds. As a result, high-speed processing and weight reduction are realized.
  • the key conversion unit 302 of the key schedule unit 300 of the present disclosure realizes the forward function G and the backward function G- 1 with the same function. Has involution properties. Hereinafter, the effect based on this involution property will be described.
  • the cryptographic processing unit includes a number of round function execution units corresponding to the specified number of rounds as hardware.
  • the effect of the involution property of the key conversion unit of the present disclosure when the cryptographic processing unit is unrolled-mounted will be described.
  • FIG. 37 and FIG. 38 show implementation examples of the following cryptographic processing apparatuses.
  • FIG. 37 (1) Hardware implementation example when the key conversion unit (F) does not have the involution property
  • FIGS. 38 (2a) and (2b) The key conversion unit (G) has the involution property.
  • FIGS. 38 (2a) and (2b) are hardware implementation examples when the key conversion unit (G) has the involution property.
  • the example shown in FIG. 38 (2a) is for generating an input key (round key) for the exclusive OR part (round key operation part) of the encryption processing part, similarly to the hardware configuration shown in FIG. 37 (1).
  • the key conversion unit G is set in association with each round.
  • FIG. 38 (2b) as set a key transformation unit G of only one, the base key K 1 held in advance, exclusive of the cryptographic processing unit to convert the key Kd 1 generated by the key conversion unit G
  • This is a configuration in which input is alternately performed with respect to the sum part (round key calculation part).
  • keys generated by repetition of conversion processing by the key conversion unit are repetitions of K 1 , Kd 1 , K 1 , Kd 1 , K 1 .
  • a base key K 1 the conversion key Kd 1 produced by a single key conversion process performed by the key conversion unit G encryption It becomes possible to alternately input to the exclusive OR part (round key operation part) of the processing part.
  • the number of key conversion units G can be reduced to one, and the weight reduction (miniaturization) of hardware mounting is realized.
  • FIG. 39 shows a configuration example of a cryptographic processing apparatus corresponding to the configuration shown in FIG. 38 (2b).
  • the key conversion unit (G) 302 of the key schedule unit 300 has only one base key held in advance for each exclusive OR unit (round key operation unit) of the encryption processing unit 320. and K 1, it is possible to enter the conversion key Kd 1 generated by the key conversion unit G alternately.
  • FIG. 40 shows (a1) cryptographic processing configuration and (a2) round implementation example when the key conversion unit does not have involution property.
  • FIG. 41 shows (b1) encryption processing configuration and (b2) round implementation example when the key conversion unit has involution property.
  • the encryption processing configuration shown in FIG. 40 (a1) is the same as the configuration described above with reference to FIG. That is, since the key conversion unit F does not have the involution property, the keys obtained as conversion results by the key conversion unit F are sequentially different keys. As shown in FIG. 40 (a1), Kd1, Kd2, Kd3, Kd4, Kd5, and Kd6 are sequentially generated based on the key K1 by the conversion process of the key conversion unit F, and each of these keys is used as a round key. It becomes a structure which inputs sequentially to the exclusive OR part (round key calculating part) of a cryptographic processing part.
  • the cryptographic processing unit 350 can be configured with one exclusive OR unit (round key calculation unit) 351 and one nonlinear / linear conversion unit 352.
  • the key schedule unit 360 includes a key register 361 for storing and supplying the base key K 1 , a key register 362 for storing and supplying the conversion keys Kd 1 to Kd 6 , a key conversion unit (F) 363, a key
  • the switch 364 executes the output switching of the registers 361 and 362.
  • the cryptographic processing configuration shown in FIG. 41 (b1) is similar to the configuration described above with reference to FIG. 38 (2b), and the cryptographic processing configuration in which the key conversion unit G has the involution property. It is. That is, since the key conversion unit G has involution properties, the keys generated by repeating the conversion process by the key conversion unit are K 1 , Kd 1 , K 1 , Kd 1 , K 1 . Repeat. Based on this property, as one key conversion unit G as shown in FIG. 41 (b1), a base key K 1, the conversion key Kd 1 produced by a single key conversion process performed by the key conversion unit G encryption It becomes possible to alternately input to the exclusive OR part (round key operation part) of the processing part.
  • the cryptographic processing unit 350 can be configured with one exclusive OR unit (round key calculation unit) 351 and one nonlinear / linear conversion unit 352.
  • the key schedule unit 370 includes a key register 371 that stores and supplies the base key K 1 and the conversion key Kd 1 and a key conversion unit (G) 372.
  • the key schedule unit 360 requires two key registers, one key conversion unit, and one switch. It becomes.
  • the key schedule unit 370 having a round implementation configuration when the key conversion unit (G) illustrated in FIG. 41 (b2) has the involution property is configured by one key register and one key conversion unit. It is proved that the weight reduction (miniaturization) of the hardware configuration is realized.
  • a key register for sequentially generating, storing, and supplying a plurality of different conversion keys And a new hardware circuit corresponding to the number of gates for the key register is required.
  • the key conversion unit of the key schedule unit configured in the cryptographic processing device of the present disclosure has the following two characteristics. (1) Full diffusion property that realizes full diffusion conversion, (2) Involution property in which the forward function G and the backward function G ⁇ 1 are the same, It has these two characteristics.
  • FIG. 42 is a diagram illustrating a configuration example of an encryption processing apparatus including a key schedule unit 380 having a key conversion unit having the above-described two characteristics.
  • the cryptographic processing apparatus shown in FIG. 42 includes a key schedule unit 380 and a cryptographic processing unit 385.
  • the key register 381 of the key schedule unit 380 stores a secret key K generated in advance.
  • the secret key K is a consolidated data of the key K 1 and the key K 2.
  • the keys K 1 and K 2 are 64-bit keys, and the concatenated data, the secret key K, is 128-bit data.
  • G shown in the figure is a key conversion unit, and a function G having these two characteristics, full diffusion property and involution property, is applied, similar to the key conversion unit 302 described above with reference to FIG. A key conversion unit that performs key conversion processing.
  • the key schedule unit 380 shown in FIG. 42 includes keys K 1 and K 2 that are divided data of the secret key K stored in the key register 381, and a conversion key Kd obtained by converting these keys in the key conversion unit (G). 1 and Kd 2 are sequentially output to the exclusive OR unit (round key operation unit) of the encryption processing unit 385.
  • the keys K 1 and K 2 are 64-bit keys
  • the plaintext P to be converted by the encryption processing unit 385 is also 64-bit data.
  • the output order of the keys is as follows. Key K 1 , Key K 2 , Conversion key Kd 1 , Conversion key Kd 2 , Key K 1 , Key K 2 , Conversion key Kd 1 , In this order, four types of keys are input to the encryption processing unit 385. Various settings can be made for the key input order.
  • FIG. 42 shows a plurality of key conversion units (G).
  • this key conversion unit (G) has only one configuration. Is possible.
  • FIG. 43 shows the following figures.
  • A Configuration of key schedule unit
  • b Key output configuration by key schedule unit
  • a secret key K generated in advance is stored in the key register 391 of the key schedule unit.
  • the secret key K is a consolidated data of the key K 1 and the key K 2.
  • the keys K 1 and K 2 are 64-bit keys, and the concatenated data, the secret key K, is 128-bit data.
  • the key schedule unit shown in FIG. 43A includes a key conversion unit G393 and exclusive OR units 392 and 394. Similar to the key conversion unit 302 described above with reference to FIG. 32 and subsequent drawings, the key conversion unit G393 performs key conversion processing using a function G having the two characteristics of full diffusion and involution. It is a conversion unit.
  • the key schedule unit shown in FIG. 43 (a) generates the following six types of keys based on these components. Key K 1 , Key K 2 , Conversion key Kd 1 , Conversion key Kd 2 , Exclusive OR key K 1 (+) K 2 , Exclusive OR operation conversion key Kd 1 (+) Kd 2 , The key schedule unit shown in FIG. 43A generates these six types of keys and sequentially outputs them to the encryption processing unit.
  • the plaintext P to be converted by the encryption processing unit is also 64-bit data.
  • the key output order is as follows. Key K 1 , Key K 2 , Conversion key Kd 1 , Conversion key Kd 2 , Exclusive OR key K 1 (+) K 2 , Exclusive OR operation conversion key Kd 1 (+) Kd 2 , Exclusive OR key K 1 (+) K 2 , Exclusive OR operation conversion key Kd 1 (+) Kd 2 , Exclusive OR key K 1 (+) K 2 , Conversion key Kd 2 , Conversion key Kd 1 , Key K 2 , Key K 1 , In this order, six types of keys are input to the encryption processing unit.
  • the key input sequence is the same sequence in the reverse order. This means that the key input order in the encryption process for generating the ciphertext C from the plaintext P and the key input order in the decryption process for generating the plaintext P from the ciphertext C can be set to the same setting. This means that hardware and programs applied to encryption processing and decryption processing can be shared, and is a setting that contributes to weight reduction (downsizing) of the apparatus.
  • the specific configuration of the cryptographic processing apparatus having the key schedule unit shown in FIG. 43 will be further described later.
  • FIG. 44 is a diagram showing that the full diffusion property of the internal state S of the input data (P) is guaranteed when the key conversion function G has full diffusion property.
  • the base key K 1 is input to the exclusive OR of the encryption processing unit, is XORed with the input state is made. Thereafter, the round calculation unit R 1 further performs non-linear conversion processing and linear conversion processing. Further, an exclusive OR operation with the conversion key Kd 1 is performed on the output in the exclusive OR operation unit.
  • the output (S) of the exclusive OR operation unit Consider the output (S) of the exclusive OR operation unit.
  • Full diffusion property is guaranteed between the base key K 1 and the conversion key Kd 1.
  • This property can be said to be a property that contributes to the safety and implementation performance of the cryptographic processing device. Specifically, improvement of data diffusibility by a key is realized, and high diffusion performance can be exhibited even if the number of rounds is reduced. As a result, it is possible to increase resistance to various attacks. For example, it is possible to further improve resistance to key analysis processing based on an intermediate value matching attack using key dependency.
  • the round necessary for spreading the configuration information (bit string) of the applied key to all the bits of the input plaintext P that is the conversion target data (Full diffusion).
  • the number will depend on the round function (R) processing.
  • the number of rounds required for spreading the configuration information (bit string) of the applied key to all the bits of the input plaintext P that is the conversion target data is (Full diffusion).
  • the diffusion of the configuration information of the key data with respect to the conversion target data is realized in one round, and a larger diffusion performance is guaranteed without depending on the processing of the round function (R). That is, secure cryptographic processing with high resistance to attacks is realized with a small number of rounds. As a result, high-speed processing and weight reduction are realized.
  • G function having the full diffusion property
  • the G function described below is configured by a combination of the following two functions.
  • Df 4 Full diffusion 4-bit function
  • B 16-bit replacement function
  • the full diffusion 4-bit function is a conversion function with input / output 4 bits, and has a function of full diffusion in which the influence of the input 4 bits appears on all the bits of the output 4 bits. That is, Input: x 0, x 1, x 2, x 3 ( each 1bit) Output: y 0 , y 1 , y 2 , y 3 (1 bit each)
  • i 0, 1, 2, 3 It is a function with the above properties.
  • FIG. 46 shows an example of a 16-bit replacement function (Bp 16 ).
  • the input X is 16 bit data of x 0 , x 1 , x 2 ,... X 15 ,
  • After input X is input to conversion function G and converted,
  • X i and y i are 1-bit data of 0 or 1, respectively.
  • B) 16-bit replacement function (Bp 16 ) It is a figure which shows the key conversion process example (processing example 1) which applied G function with the full diffusion property comprised from these two functions.
  • the base key is A and the conversion key B. Both are 4 ⁇ 4 state data of 4 bits for each element.
  • the process of generating the conversion key B from the base key A includes the following four steps.
  • S11 Each of the 16 4-bit elements of the base key A is converted by applying a full diffusion 4-bit function (Df 4 ).
  • a 16-bit replacement function (Bp 16 ) is applied to each column of 16-bit data of the data (4 ⁇ 4 states) generated by the conversion process in step S11 and converted.
  • the full diffusion 4-bit function (Df 4 ) is applied to each of the 16 4-bit elements of the data (4 ⁇ 4 states) generated by the conversion process in step S12.
  • a 16-bit replacement function (Bp 16 ) is applied to each row of 16-bit data of the data (4 ⁇ 4 states) generated by the conversion process in step S13.
  • the conversion key B is generated from the base key A.
  • the elements b 0 to b 15 of the conversion key B are data affected by the elements a 0 to a 15 of the base key A, and the full diffusion property is guaranteed between the base key A and the conversion key B.
  • FIG. 48 also shows (A) Full diffusion 4-bit function (Df 4 ) (B) 16-bit replacement function (Bp 16 ) It is a figure which shows the key conversion process example (processing example 2) which applied G function with the full diffusion property comprised from these two functions.
  • the base key is A and the conversion key B. Both are 4 ⁇ 4 state data of 4 bits for each element.
  • the process of generating the conversion key B from the base key A is configured by the following five steps.
  • S21 Each of the 16 4-bit elements of the base key A is converted by applying the full diffusion 4-bit function (Df 4 ).
  • the 16-bit replacement function (Bp 16 ) is applied to each column of 16-bit data of the data (4 ⁇ 4 states) generated by the conversion process in step S21.
  • the full diffusion 4-bit function (Df 4 ) is applied to each of the 16 4-bit elements of the data (4 ⁇ 4 states) generated by the conversion process in step S22.
  • the 16-bit replacement function (Bp 16 ) is applied to each row of 16-bit data of the data (4 ⁇ 4 states) generated by the conversion process in step S23.
  • the full diffusion 4-bit function (Df 4 ) is applied to each of the 16 4-bit elements of the data (4 ⁇ 4 states) generated by the conversion process in step S24.
  • the conversion key B is generated from the base key A.
  • the elements b 0 to b 15 of the conversion key B are data affected by the elements a 0 to a 15 of the base key A, and the full diffusion property is guaranteed between the base key A and the conversion key B.
  • B) 16-bit replacement function (Bp 16 ) It is a figure which shows the key conversion process example (processing example 3) which applied G function with the full diffusion property comprised from these two functions.
  • the base key is A and the conversion key B. Both are 4 ⁇ 4 state data of 4 bits for each element.
  • Applied in Processing Example 3 (a) Full diffusion 4-bit function (Df 4 ) Is a function that also has involution properties.
  • the process of generating the conversion key B from the base key A is configured by the following five steps.
  • S31 Each of the 16 4-bit elements of the base key A is converted by applying a 4-bit function (Df 4 ) having involution characteristics and full diffusion characteristics.
  • S32 The 16-bit replacement function (Bp 16 ) is applied to each column of 16-bit data of the data (4 ⁇ 4 states) generated by the conversion process in step S31.
  • S33 A 4-bit function (Df 4 ) having involution property and full diffusion property for each of the 16 4-bit elements of the data (4 ⁇ 4 states) generated by the conversion process of step S32 Apply to convert.
  • (S34) The 16-bit replacement function (Bp 16 ) is applied to each row of 16-bit data of the data (4 ⁇ 4 states) generated by the conversion process in step S33.
  • (S35) A 4-bit function (Df 4 ) having involution property and full diffusion property for each of the 16 4-bit elements of the data (4 ⁇ 4 states) generated by the conversion process of step S34 Apply to convert.
  • the conversion key B is generated from the base key A.
  • the elements b 0 to b 15 of the conversion key B are data affected by the elements a 0 to a 15 of the base key A, and the full diffusion property is guaranteed between the base key A and the conversion key B.
  • the process of generating the conversion key B from the base key A is configured by the following five steps.
  • a 16-bit replacement function (Bp 16 ) is applied to each column of 16-bit data of the base key A (4 ⁇ 4 states) for conversion.
  • a 4-bit function (Df 4 ) having involution property and full diffusion property for each of the 16 4-bit elements of the data (4 ⁇ 4 states) generated by the conversion process of step S41 Apply to convert.
  • a 16-bit replacement function (Bp 16 ) is applied to each column of 16-bit data of the data (4 ⁇ 4 states) generated by the conversion process in step S42.
  • the conversion key B is generated from the base key A.
  • the elements b 0 to b 15 of the conversion key B are data affected by the elements a 0 to a 15 of the base key A, and the full diffusion property is guaranteed between the base key A and the conversion key B.
  • FIG. (A) Full diffusion 4-bit function (Df 4 ) (B) 16-bit replacement function (Bp 16 ) It is a figure which shows the key conversion process example (processing example 5) to which G function with the full diffusion property comprised from these two functions is applied.
  • the base key is A and the conversion key B. Both are 4 ⁇ 4 state data of 4 bits for each element.
  • (A) Full diffusion 4-bit function (Df 4 ) Is a function that also has involution properties.
  • the process of generating the conversion key B from the base key A includes the following five steps.
  • S51 Each of the 16 4-bit elements of the base key A is converted by applying a 4-bit function (Df 4 ) having involution property and full diffusion property.
  • Df 4 4-bit function
  • S52 A 16-bit replacement function (Bp 16 ) is applied to each row of 16-bit data of the data (4 ⁇ 4 states) generated by the conversion process in step S51.
  • S53 A 4-bit function (Df 4 ) having involution property and full diffusion property for each of the 16 4-bit elements of the data (4 ⁇ 4 states) generated by the conversion process of step S52 Apply to convert.
  • the conversion key B is generated from the base key A.
  • the elements b 0 to b 15 of the conversion key B are data affected by the elements a 0 to a 15 of the base key A, and the full diffusion property is guaranteed between the base key A and the conversion key B.
  • the configuration examples of the five key conversion functions G have been described with reference to FIGS. These key conversion functions are applicable when generating a conversion key from the base key K, and the conversion process for the split key generated by dividing the base key K described above with reference to FIG. It is also possible to apply to. Furthermore, the key conversion function applied to the two split keys may be set differently.
  • the cryptographic processing apparatus shown in FIG. 52 includes a key schedule unit 380 and a cryptographic processing unit 385.
  • the key register 381 of the key schedule unit 380 stores a secret key K generated in advance.
  • the secret key K is a consolidated data of the key K 1 and the key K 2.
  • the keys K 1 and K 2 are 64-bit keys, and the concatenated data, the secret key K, is 128-bit data.
  • G1 and G2 shown in the figure are key conversion units. These have at least full diffusion properties. Or it has these two characteristics, full diffusion property and involution property.
  • the combination of the key conversion functions G1 and G2 can be set as follows, for example.
  • (C) G1, G2 both having a full diffusion resistance, it sets G1 and G2 is the inverse function, i.e., a relationship of G2 G1 -1.
  • Various combinations as described above are possible as combinations of the key conversion functions G1 and G2.
  • a conventional constant input configuration there is a configuration as shown in FIG. 53 are round function execution units including an exclusive OR unit (round key calculation unit), a nonlinear conversion unit, and a linear conversion unit in the cryptographic processing unit.
  • Constants 1 (CON1) to 4 (CON4) are sequentially input to the round operation units 401a to 401d.
  • the input constant CON is subjected to an exclusive OR operation with conversion data or a round key in each round operation unit. In this way, by performing operations with various constants in each round, it is possible to eliminate the identity between the round operations and increase resistance to various attacks.
  • the encryption processing and the decryption processing can be executed by the same device.
  • the configuration of a plurality of conversion functions applied to the cryptographic processing unit of the cryptographic processing device is divided from the center to the left and right, the left half and the right half are inverse functions.
  • encryption processing and decryption processing can be executed by the same device. This is called a cryptographic processing device having involution properties.
  • the conversion functions E and 411 and the conversion functions E ⁇ 1 and 413 have an inverse function relationship.
  • the central linear conversion unit M outputs an output B to the input A and outputs an output A to the input B.
  • the conversion functions E and 411, the linear conversion unit 412, and the conversion functions E ⁇ 1 and 413 are applied to the plaintext P in this order.
  • each conversion unit is applied to the ciphertext C in the same order. That is, the original plaintext P is obtained by applying the conversion functions E and 411, the linear conversion unit 412, and the conversion functions E ⁇ 1 and 413 in this order.
  • Such a cryptographic processing device is called a cryptographic processing device having involution properties.
  • a cryptographic processing device having involution properties not only the execution sequence of the round function is the same sequence in both the forward and reverse directions, but the input order of the round keys applied in each round is also forward and reverse. Some of them have the same direction.
  • the key input sequence described above with reference to FIG. 43 is one key input sequence for realizing the involution property of the cryptographic processing device.
  • the linear conversion unit 412 performs linear conversion on the output values from the conversion functions E and 411, but the values of some of the constituent data (bits) may be output without change. Note that a point at which input / output values are the same in linear transformation is called a fixed point, and there are several fixed points in linear transformation processing applied in many cryptographic processing devices.
  • the input value X to the linear conversion unit 412 becomes the output X of the linear conversion unit 412 as it is due to the action of the fixed point of the linear conversion unit 412.
  • the value X is input to the conversion function E ⁇ 1 413. Since the conversion functions E ⁇ 1 and 413 are inverse functions of the conversion functions E and 411, the input value X is returned to the original value Y. That is, some output values Y constituting the ciphertext C become the same values as the configuration values Y of the input plaintext P. That is, a fixed point where the input / output value does not change occurs in the entire cryptographic processing apparatus.
  • Such a property is a property that brings vulnerability to various attacks, and is an undesirable property that impairs the security of the cryptographic processing device.
  • FIG. 55 (b) is a cryptographic processing device having the involution property similar to FIG. 55 (a).
  • the conversion function E, 411 performs an operation by inputting a constant 1 (CON1), and the conversion function E ⁇ . 1 and 413 are input to a constant 2 (CON2).
  • CON1 constant 1
  • CON2 constant 2
  • X the conversion result of the conversion functions E and 411 for the data Y.
  • the input value X to the linear conversion unit 412 is converted to X + ⁇ A by the linear conversion process by the linear conversion unit 412.
  • the value X + ⁇ A is input to the conversion function E ⁇ 1 413.
  • the conversion functions E ⁇ 1 and 413 are inverse functions of the conversion functions E and 411, and are configured to execute an operation that receives a constant 2 (CON 2), and a conversion that executes an operation that receives a constant 1 (CON 1). It is not a complete inverse function of functions E and 411. However, depending on how the constants are selected, as shown in the figure, the output value corresponding to the input X + ⁇ A for the conversion function E ⁇ 1 , 413 may be set to Y + ⁇ B.
  • the correspondence between the input and output values of the linear conversion unit is X, X + ⁇ A
  • the correspondence between the input / output values of the cryptographic processor is Y, Y + ⁇ B
  • Such a relationship between input and output data is also a property that causes vulnerability to various attacks, and is an undesirable property that impairs the security of the cryptographic processing device.
  • FIG. 56 is a diagram for explaining a constant input configuration example for the cryptographic processing unit according to the present embodiment.
  • FIG. 56A shows an encryption processing unit composed of a data conversion unit having involution properties, as described with reference to FIG. That is, the cryptographic processing unit Conversion functions E, 431, Linear conversion unit 432, Conversion functions E ⁇ 1 , 433, These data conversion units are provided, and the conversion functions E ⁇ 1 and 433 are inverse functions of the conversion function E 431.
  • the constant (CON) 435 is input to the conversion function E ⁇ 1 433.
  • the conversion functions E ⁇ 1 and 433 are configured by a plurality of round functions, and a constant (CON) is input to one or more round function units.
  • the constant (CON) input unit is set to be input to the conversion function E ⁇ 1 , 433, but may be set to be input to the conversion function E 431 side.
  • the encryption processing unit has involution property that sequentially executes the conversion function E 431 and the inverse function of the conversion function E 431, the conversion function E ⁇ 1 433, and the conversion function E or the inverse function E Only one of ⁇ 1 is configured to execute a round operation to which one or more constants are applied.
  • FIG. 56B shows a specific example of the input configuration of the constant (CON) 435.
  • the constant (CON) 435 is input to the exclusive OR unit 436 in the preceding stage of the linear conversion unit 437 of the encryption processing unit.
  • An exclusive OR operation is performed with the input data A to the exclusive OR unit 436.
  • the exclusive OR unit 436 is a round key operation unit that performs an exclusive OR operation with the round key Kr.
  • the exclusive OR unit 436 is an output from the previous round operation unit shown in the figure.
  • An exclusive OR operation of the data A, the round key Kr, and the constant CON is executed. That is, the exclusive OR unit 436 calculates B as a result of the following calculation execution and outputs it to the linear transformation processing unit 437 of the subsequent round calculation unit.
  • B A (+) Kr (+) CON In the above formula, (+) indicates an exclusive OR operation.
  • condition A linear conversion unit adjacent to the exclusive OR unit 437, and in the example shown in the figure, the input / output value difference in the linear conversion process in the linear conversion unit 437 is set to a value that does not decrease.
  • the above condition is that all elements obtained as a result of matrix operation between the constant CON and the linear transformation matrix applied in the linear transformation unit 437 are non-zero, that is, non-zero values.
  • FIG. 57 shows a 4 ⁇ 4 matrix constituting the constant CON435 input to the exclusive OR unit 436 and a linear transformation matrix M used in the linear transformation unit 437.
  • the constant CON435 is a 4 ⁇ 4 state in which each element (con 0 to con 15 ) is 4-bit data, and is 64-bit data.
  • the linear transformation matrix M is 4 ⁇ 4 matrix data. That is, the following linear transformation matrix.
  • the condition of the constant CON is that all elements obtained as a result of matrix operation between the constant CON and the linear transformation matrix applied in the linear transformation unit 437 are non-zero, that is, non-zero values. That is, all values obtained by the following matrix operation are non-zero.
  • the constant CON is set so that the 16 values calculated by the matrix arithmetic expression are not all zero, that is, non-zero. With such a setting, it is possible to prevent the difference between the input and output values of the linear conversion processing in the linear conversion unit adjacent to the exclusive OR unit that inputs the constant CON, in the example shown in FIG. As a result, the number of minimum differential active S boxes can be maintained at a predetermined number or more.
  • the linear conversion unit 437 adjacent to the exclusive OR unit 436 to which the constant CON435 is input is set as the linear conversion unit P1 described above with reference to FIGS.
  • this is an example in which column diffusion calculation (MixColumn) is applied to which the following matrix is applied.
  • the linear conversion unit 437 applies column diffusion calculation (MixColumn) to which the matrix M 0 is applied, that is, MC [M 0 ] Execute.
  • the condition of the constant CON is that all elements obtained as a result of matrix operation between the linear transformation matrix M 0 applied in the linear transformation unit 437 and the constant CON are non-zero, that is, non-zero values. is there.
  • An example of such a constant CON is the constant CON shown in FIG. 58, which is a 4 ⁇ 4 state having the following element configuration.
  • FIG. 59 is a diagram showing an example of the input configuration and calculation configuration of the round key and the constant CON for the cryptographic processing unit of the cryptographic processing device having the input configuration of the constant CON that satisfies the above-described constant conditions.
  • plaintext P is input from the lower left
  • ciphertext C is output from the lower right.
  • the cryptographic processing unit 451 (E) of the cryptographic processing device shown in FIG. 59 corresponds to the conversion functions E and 431 shown in FIG. 56 (a).
  • the linear conversion unit (P2) 452 corresponds to the linear conversion unit 432 illustrated in FIG.
  • the cryptographic processing unit 453 (E ⁇ 1 ) corresponds to the conversion functions E ⁇ 1 and 433 shown in FIG.
  • the cryptographic processing device configuration shown in FIG. 59 is a cryptographic processing device having involution properties.
  • the round key input example shown in FIG. 59 corresponds to the configuration example described above with reference to FIG. That is, the input order of round keys to the exclusive OR unit configured in the encryption processing unit is as follows. Key K 1 , Key K 2 , Conversion key Kd 1 , Conversion key Kd 2 , Exclusive OR key K 1 (+) K 2 , Exclusive OR operation conversion key Kd 1 (+) Kd 2 , Exclusive OR key K 1 (+) K 2 , Exclusive OR key K 1 (+) K 2 , Exclusive OR operation conversion key Kd 1 (+) Kd 2 , Exclusive OR key K 1 (+) K 2 , Conversion key Kd 2 , Conversion key Kd 1 , Key K 2 , Key K 1 ,
  • the exclusive OR key K 1 (+) K 2 is set to be input to the round calculation unit R 6.
  • the linear conversion unit 452 is set. Before and after, the exclusive OR key K 1 (+) K 2 is repeatedly input.
  • the round key supply unit of the key schedule unit outputs six types of keys in the above order.
  • This key input sequence is the same sequence in the reverse order.
  • the key input order in the encryption process for generating the ciphertext C from the plaintext P and the key input order in the decryption process for generating the plaintext P from the ciphertext C can be set to the same setting.
  • it is a key input sequence having involution properties, and can be used in common with hardware and programs applied to encryption processing and decryption processing, and is a setting that contributes to weight reduction (downsizing) of the apparatus.
  • the constant CON includes an exclusive OR unit 461, an exclusive OR unit 463, an exclusive OR unit 465, and each of these exclusive OR units of the encryption processing unit 453 (E ⁇ 1 ). To enter.
  • constants CON are, for example, the 4 ⁇ 4 state constants CON described with reference to FIG.
  • the linear transformation units 462, 464, and 466 adjacent to these three exclusive OR units 461, 463, and 465 are all column diffusion operations (MixColumns) to which the matrix M 0 is applied, that is, MC [M 0 ] Execute.
  • the cryptographic processing unit shown in FIG. 59 has an involution property that can generate plaintext P from ciphertext C by executing a sequence that generates ciphertext C from plaintext P and a reverse sequence.
  • the encryption process and the decryption process can be performed by applying the same hardware or the same program.
  • the key supply processing of the key schedule unit can be executed as processing using the same hardware or the same program.
  • an S box that performs nonlinear transformation in units of s bits is used for the nonlinear transformation unit set in the common key block cipher.
  • S-box an S box that performs nonlinear transformation in units of s bits is used for the nonlinear transformation unit set in the common key block cipher.
  • an index for improving resistance against a differential attack there is a minimum number of differential active S boxes included in a differential path expressing a differential connection relationship, that is, a minimum differential active S box number.
  • the non-linear transformation is only the processing part by the S box.
  • data P1 and P2 having a specific difference ⁇ X are individually input to a block cipher apparatus that executes block cipher to obtain cryptographic processing results C1 and C2. .
  • an S box into which a difference value is input is defined as an active S box.
  • the ease of analysis increases. In other words, resistance to attacks is weakened.
  • the number of S boxes into which difference values generated when two inputs P1 and P2 having a predetermined difference ⁇ X are set is defined as an active S box.
  • Safety evaluation is performed by counting the number.
  • FIG. 61 shows an encryption processing unit including the data conversion unit having the involution property shown in FIG. 56 (a). That is, the cryptographic processing unit Conversion functions E, 431, Linear conversion unit 432, Conversion functions E ⁇ 1 , 433, These data conversion units are provided, and the conversion functions E ⁇ 1 and 433 are inverse functions of the conversion function E 431.
  • the constant (CON) 435 is input to the conversion function E ⁇ 1 433.
  • the conversion functions E ⁇ 1 and 433 are configured by a plurality of round functions, and a constant (CON) is input to one or more round function units.
  • the cryptographic processing unit has an involution property of sequentially executing the conversion function E 431 and the inverse function of the conversion function E 431 and the conversion function E ⁇ 1 433, and the conversion function E or the inverse function E ⁇ 1. In only one of these, a round operation is applied to which one or more constants are applied.
  • the input S 1 is input from the linear conversion unit 432 side to the conversion function E 431 to obtain the output T.
  • the two functions i.e., the conversion function E431, transformation function E -1 is an inverse function of the conversion function E431, relative to 433, as shown in FIG. 61, the input value S1, which in the opposite direction has a difference [Delta] X, S2
  • S is input, among the S boxes at corresponding positions in each function, the S box into which the difference is input is set as the active S box.
  • FIG. 62 is a diagram for explaining the configuration for calculating the number of active S boxes in the cryptographic processing configuration shown in FIG. 59 described above.
  • the input value S1 is input from the linear conversion unit 452 side of the cryptographic processing unit 451 (E) of the cryptographic processing device shown in FIG. 62, and cryptographic processing to which the cryptographic processing unit 451 (E) is applied is executed.
  • the input value S2 in which the difference ⁇ X is set with respect to the input value S1 is input from the linear conversion unit 452 side of the encryption processing unit 453 (E ⁇ 1 ) which is an inverse function of the encryption processing unit 451 (E), and the encryption processing is performed.
  • the encryption process to which the unit 453 (E ⁇ 1 ) is applied is executed.
  • the S box into which the difference is input is set as the active S box among the S boxes at the corresponding positions in the cryptographic processing units (E) and (E ⁇ 1 ).
  • the function E or the inverse function E ⁇ 1 is applied to the encryption processing apparatus having the involution property that sequentially executes the data conversion function E and the inverse function E ⁇ 1 of the data conversion function E.
  • a configuration has been described in which the constant CON is input to only one of them and the round operation is performed by applying the constant. With such a setting, it is possible to prevent the difference between the input and output values of the linear conversion processing in the linear conversion unit adjacent to the exclusive OR unit that inputs the constant CON, in the example shown in FIG. As a result, the number of minimum differential active S boxes can be maintained at a predetermined number or more.
  • This constant input configuration is not limited to only one of the functions E or the inverse function E -1,, performing round operations to which the one or more constants in both function E, and the inverse function E -1 It is good also as a structure.
  • the constant application position is not a corresponding position of the function E and the inverse function E- 1 , but is a position shifted from the corresponding position (non-corresponding position).
  • FIG. 63 shows a configuration example of a cryptographic processing apparatus having this constant input configuration.
  • plaintext P is input from the lower left
  • ciphertext C is output from the lower right.
  • the encryption processing unit 451 (E) of the encryption processing apparatus shown in FIG. 63 corresponds to the conversion functions E and 431 shown in FIG. 56 (a).
  • the linear conversion unit (P2) 452 corresponds to the linear conversion unit 432 illustrated in FIG.
  • the cryptographic processing unit 453 (E ⁇ 1 ) corresponds to the conversion functions E ⁇ 1 and 433 shown in FIG.
  • the configuration of the cryptographic processing unit shown in FIG. 63 is a cryptographic processing unit having involution properties.
  • the round key input example shown in FIG. 63 corresponds to the configuration example described above with reference to FIG. That is, the input order of round keys to the exclusive OR unit configured in the encryption processing unit is as follows. Key K 1 , Key K 2 , Conversion key Kd 1 , Conversion key Kd 2 , Exclusive OR key K 1 (+) K 2 , Exclusive OR operation conversion key Kd 1 (+) Kd 2 , Exclusive OR key K 1 (+) K 2 , Exclusive OR key K 1 (+) K 2 , Exclusive OR operation conversion key Kd 1 (+) Kd 2 , Exclusive OR key K 1 (+) K 2 , Conversion key Kd 2 , Conversion key Kd 1 , Key K 2 , Key K 1 ,
  • the exclusive OR key K 1 (+) K 2 is set to be input to the round calculation unit R 6.
  • the linear conversion unit 452 is set. Before and after, the exclusive OR key K 1 (+) K 2 is repeatedly input.
  • the round key supply unit of the key schedule unit outputs six types of keys in the above order.
  • This key input sequence is the same sequence in the reverse order.
  • the key input order in the encryption process for generating the ciphertext C from the plaintext P and the key input order in the decryption process for generating the plaintext P from the ciphertext C can be set to the same setting.
  • it is a key input sequence having involution properties, and can be used in common with hardware and programs applied to encryption processing and decryption processing, and is a setting that contributes to weight reduction (downsizing) of the apparatus.
  • the constant CON is The data is input to the exclusive OR unit 471, the exclusive OR unit 472, and each of these exclusive OR units of the encryption processing unit 451 (E). Further, the data is also input to the exclusive OR unit 473 of the encryption processing unit 453 (E ⁇ 1 ).
  • the constant CON is, for example, the 4 ⁇ 4 state constant CON described with reference to FIG.
  • the linear transformation units 481, 482, 483 adjacent to these three exclusive OR units 471, 472, 473 are all column diffusion operations (MixColumn) to which the matrix M 0 is applied, that is, MC [M 0 ] Execute.
  • constant input structure function E or inverse not limited to only one of E -1, function E, and both the applied round operations once or more constants in the inverse function E -1, It is good also as a structure which performs.
  • the constant application position is not a corresponding position of the function E and the inverse function E ⁇ 1 but a shifted position (non-corresponding position).
  • the encryption processing unit shown in FIG. 63 has an involution property that can generate plaintext P from ciphertext C by executing a sequence that generates ciphertext C from plaintext P and a reverse sequence.
  • the encryption process and the decryption process can be performed by applying the same hardware or the same program.
  • the key supply processing of the key schedule unit can be executed as processing using the same hardware or the same program.
  • the involution of the cryptographic processing unit 120 that is, the hardware or program that generates and outputs the ciphertext C from the plaintext P and the plaintext P from the ciphertext C are generated.
  • the non-linear conversion unit 122 configured in the cryptographic processing unit 120 is also required to have involution.
  • the non-linear transformation unit 122 in the cryptographic processing unit 120 of the cryptographic processing apparatus 100 illustrated in FIG. 19 includes a plurality of S boxes as illustrated in FIG. (S-box).
  • This 4-bit input / output S box (S-box) needs to have a configuration with involution. That is, when a 4-bit output value is obtained for a 4-bit input value, the original 4-bit input value must be obtained when the 4-bit output value is input to the same S box. It is.
  • f (x) having the involution property is obtained for all input values x.
  • f (f (x)) x A function that satisfies the above.
  • the nonlinear conversion unit 122 configured in the cryptographic processing unit 120 is required to be the function f (x) having the involution property.
  • FIG. 64 (1) is a diagram illustrating a configuration example of the nonlinear conversion unit, similar to FIG. 22 (1) described above. That is, this is a configuration example of the non-linear conversion unit 122 configured in the cryptographic processing unit 120 of the cryptographic processing apparatus 100 illustrated in FIG.
  • the nonlinear conversion unit 122 has a configuration in which a plurality of S boxes (S-boxes) for executing nonlinear conversion processing are arranged. Each S box performs non-linear transformation of 4-bit data.
  • S-boxes S boxes
  • FIG. 64 (2) shows a configuration of one S box (S-box) configured in the nonlinear conversion unit.
  • S box (S-box) Nonlinear conversion layer 1,521, Linear transformation layer 522, Nonlinear conversion layer 2,523, It can be divided into these three layers.
  • the nonlinear conversion layers 2 and 523 are inverse functions of the nonlinear conversion layers 1 and 521.
  • FIG. 65 shows a specific circuit configuration example of the S box (S-box).
  • the nonlinear conversion layers 1 and 521 are configured by two exclusive OR operation units (XOR) and two basic operators.
  • XOR exclusive OR operation units
  • FIG. 65 an example in which a NOR circuit is set as a basic operator is shown.
  • the basic operator performs an arithmetic operation of any one of two inputs and one output of an AND circuit, an OR circuit, and a NAND circuit. It can be replaced with a basic operator.
  • the two basic operators may be a combination of the same basic operators or a combination of different basic operators.
  • the linear conversion layer 522 is a linear conversion layer that performs an input 4-bit replacement process, and basically has involution properties.
  • the nonlinear conversion layers 2 and 523 are configured by an inverse function of the nonlinear conversion layers 1 and 521.
  • the S box circuit constituted by these three layers is a non-linear conversion circuit having involution properties.
  • the lower part of FIG. 65 shows correspondence data between the input value (in) and the output value (out) for the S box shown in FIG.
  • the input / output values are all 4-bit data and are 0000 to 1111 data.
  • the table shown in FIG. 65 shows a correspondence table between input values and output values of 0 to 15 in which 0000 to 1111 are expressed in decimal notation. As can be understood from this table, an output value Y obtained from an arbitrary input value X and an output value obtained as the input value Y is the original input value X.
  • the 4-bit input / output S box shown in FIG. 65 is a non-linear conversion circuit having involution characteristics.
  • FIG. 66 shows a data conversion formula using this S box (S-box). 4-bit input to S box (S-box) a in , b in , c in , d in , 4-bit output from S box (S-box) a out , b out , c out , d out , And
  • the data conversion formula using the S box (S-box) is as follows.
  • y) indicates negation of the value in () (NOT). Specifically, the output value of the NOR circuit when the input values to the NOR circuit are x and y is shown.
  • the S box that performs data conversion represented by the above arithmetic expression has involution.
  • the S box circuit shown in FIG. 66 has a difference probability and a linear probability of 2-2 , and has sufficient safety.
  • the encryption processing unit configuration described with reference to FIG. 54 that is, Conversion function E411, Linear conversion unit 412, Conversion function E ⁇ 1 413,
  • the S function shown in FIGS. 64 to 66 for the conversion function E411 in the encryption processing unit having these configurations and the nonlinear conversion unit in the conversion function E ⁇ 1 413, the entire encryption processing unit is installed. The volume is realized.
  • FIG. 67 shows a setting example of the linear conversion layer in the 4-bit input / output S box. Similar to the S box described with reference to FIGS. 65 and 66, Nonlinear conversion layer 1, Linear transformation layer, Nonlinear conversion layer 2, In the 4-bit input / output S box having these three-layer configurations, the linear conversion layer has, for example, one of the settings shown in FIG.
  • the condition of the permutation function P4 of the linear conversion layer that performs 4-bit permutation can be expressed by the following equation.
  • the above (a) is a conditional expression indicating that the replacement function P4 has involution properties.
  • (B) is a conditional expression indicating that the input / output bits are not the same.
  • the linear conversion layer needs to be configured to perform replacement processing that satisfies the above conditions.
  • Nonlinear conversion layer 1,531 Linear transformation layer 532
  • Nonlinear conversion layer 2,533 This is a 4-bit input / output S box having these three layers.
  • the nonlinear conversion layers 1 and 531 include two exclusive OR operation units (XOR), a NAND circuit, and a NOR circuit.
  • the linear conversion layer 532 is a linear conversion layer that performs an input 4-bit replacement process, and has involution properties.
  • the nonlinear conversion layers 2 and 533 are configured by an inverse function of the nonlinear conversion layers 1 and 531.
  • the S box circuit constituted by these three layers is a non-linear conversion circuit having involution properties.
  • 68 shows correspondence data between the input value (in) and the output value (out) for the S box shown in FIG.
  • the input / output values are all 4-bit data and are 0000 to 1111 data.
  • the table shown in FIG. 68 is a correspondence table of input values and output values of 0 to 15 in which 0000 to 1111 are represented in decimal notation. As can be understood from this table, an output value Y obtained from an arbitrary input value X and an output value obtained as the input value Y is the original input value X.
  • the 4-bit input / output S box shown in FIG. 68 is a non-linear conversion circuit having involution characteristics.
  • FIG. 69 shows a data conversion formula using this S box (S-box). 4-bit input to S box (S-box) a in , b in , c in , d in , 4-bit output from S box (S-box) a out , b out , c out , d out , And
  • the data conversion formula using the S box (S-box) is as follows.
  • y) indicate the output values of the NOR circuit when the input values to the NOR circuit are x and y.
  • ⁇ (x & y) indicate output values of the NAND circuit when the input values to the NAND circuit are x and y.
  • the S box that performs data conversion represented by the above arithmetic expression has involution.
  • the S box circuit shown in FIG. 69 has a difference probability and a linear probability of 2-2 , and has sufficient safety.
  • the S box shown in FIG. 69 includes four exclusive OR operators (XOR), two NOR circuits, and two NAND circuits.
  • the encryption processing unit configuration described with reference to FIG. 54 that is, Conversion function E411, Linear conversion unit 412, Conversion function E ⁇ 1 413
  • the S function shown in FIG. 69 for the conversion function E411 in the encryption processing unit having these configurations and the nonlinear conversion unit in the conversion function E ⁇ 1 413, the involution of the entire encryption processing unit can be improved. Realized.
  • the nonlinear conversion layers 1 and 541 are configured by two exclusive OR operation units (XOR) and two OR circuits.
  • the linear conversion layer 542 is a linear conversion layer that performs an input 4-bit replacement process, and has involution properties.
  • the nonlinear conversion layer 2 543 is configured by an inverse function of the nonlinear conversion layer 1 541.
  • the S box circuit constituted by these three layers is a non-linear conversion circuit having involution properties.
  • the lower part of FIG. 70 shows correspondence data between the input value (in) and the output value (out) for the S box shown in FIG.
  • the input / output values are all 4-bit data and are 0000 to 1111 data.
  • the table shown in FIG. 70 is a correspondence table between input values and output values of 0 to 15 in which 0000 to 1111 are represented in decimal notation. As can be understood from this table, an output value Y obtained from an arbitrary input value X and an output value obtained as the input value Y is the original input value X.
  • the 4-bit input / output S box shown in FIG. 70 is a non-linear conversion circuit having involution characteristics.
  • FIG. 71 shows a data conversion formula using this S box (S-box). 4-bit input to S box (S-box) a in , b in , c in , d in , 4-bit output from S box (S-box) a out , b out , c out , d out , And
  • the data conversion formula using the S box (S-box) is as follows.
  • y) indicates the output value of the OR circuit when the input values to the OR circuit are x and y.
  • the S box that performs data conversion represented by the above arithmetic expression has involution.
  • the S box circuit shown in FIG. 71 has a difference probability and a linear probability of 2-2 , and has sufficient safety.
  • the S box shown in FIG. 71 is composed of four exclusive OR operators (XOR) and four OR circuits.
  • the encryption processing unit configuration described with reference to FIG. 54 that is, Conversion function E411, Linear conversion unit 412, Conversion function E ⁇ 1 413,
  • Conversion function E411 the encryption processing unit having these configurations
  • the non-linear conversion unit in the conversion function E ⁇ 1 413 the involution of the entire encryption processing unit is achieved. Realized.
  • a cryptographic processing apparatus 700 shown in FIG. 72 is a diagram illustrating an example of a cryptographic processing apparatus having all the above-described configurations.
  • the cryptographic processing apparatus 700 includes a key schedule unit 720 and a cryptographic processing unit 750.
  • the cryptographic processing unit 750 includes data conversion units such as an exclusive OR unit 751, a non-linear conversion unit 752, and a linear conversion unit 753, and has a configuration that repeatedly executes these processes.
  • the key schedule unit 720 outputs the round key RKn to each of the exclusive OR units configured in the encryption processing unit 750, and executes the exclusive OR operation with the conversion target data.
  • the key schedule unit 720 includes a round key supply unit 721 and a constant supply unit (constant register) 725.
  • the round key supply unit 721 includes a key register 722 that stores the secret key K and a key conversion unit 723.
  • each round key RKn is also 64 bits.
  • Each of these 64-bit data is a 4 ⁇ 4 state composed of 16 elements each having 4 bits.
  • the cipher processing unit 750 can output the ciphertext C as output data by repeating the round operation using the plaintext P as input data, and sets the execution sequence of the round operation in reverse order using the ciphertext C as input data. It is the structure which has the involution property which can produce
  • each conversion process is executed from the upper stage to the lower stage of the cryptographic processing unit 750 shown in the figure.
  • each conversion process is executed from the lower stage to the upper stage of the cryptographic processing unit 750 shown in the figure.
  • the round key supply unit 721 of the key schedule unit 720 has an involution property in which the key supply sequence when the ciphertext C is generated from the plaintext P and the key supply sequence when the plaintext P is generated from the ciphertext C match. It is the structure which performs the key supply process which has. Note that the key schedule unit 720 performs a calculation using a constant on a part of the supplied key during the key supply process to the encryption processing unit 750, and outputs key data as a calculation result to the encryption processing unit 750.
  • each conversion function is in the sequence of the conversion function E, the linear conversion function, and the conversion function E- 1.
  • the configuration is set and has involution properties.
  • the linear conversion processing unit 750 the item [4.
  • the linear conversion processing unit that executes three different types of linear conversion processing is set. That is, Linear converter P1, Linear converter P2, Linear converter P3, These three different linear conversion units are included, and the linear conversion process executed for each round is changed in the encryption process. That is, the same linear conversion processing is not performed in the continuous round.
  • Linear transformation unit P1 for each column of elements of the input data of 4 ⁇ 4 states, in units of columns, performs the applied matrix operation of one of the matrix M 0. This is the column diffusion operation (MixColumn) described above with reference to FIGS. That is, the linear transformation processing unit P1 MC [M 0 ] A column diffusion operation (MC) indicated by the above formula is executed.
  • MC [M 0 ] is an expression indicating a matrix operation in which the same matrix M 0 is applied to each column of the state, and an expression individually indicating a matrix to be applied to each column of the state, MC [M 0 , M 0 , M 0 , M 0 ] It has the same meaning as the above formula.
  • the linear conversion unit P2 performs a matrix operation that applies a different matrix for each row to the elements in each row of the input data in the 4 ⁇ 4 state. .
  • a matrix operation to which the following matrix is applied is executed for the upper first to fourth rows.
  • the row diffusion calculation (MixRow) indicated by the above formula is executed.
  • the linear transformation processing unit P3 also performs matrix calculation by applying a different matrix for each row element to each row element of 4 ⁇ 4 state input data, as shown in FIG. 24 (2). I do. Unlike the linear transformation process P2, the linear transformation process P3 executes a matrix operation that applies the following matrix to the first to fourth rows. 1st row: application matrix M 2 , Second row: application matrix M 0 , 3rd row: application matrix M 1 , 4th row: application matrix M 3 , This is the row diffusion operation (MixRow) described above with reference to FIG. That is, the linear transformation processing unit P3 MR [M 2 , M 0 , M 1 , M 3 ] The row diffusion calculation (MixRow) indicated by the above formula is executed.
  • the number of active S boxes can be increased as described above with reference to FIG. This enables encryption processing (encryption processing and decryption processing) with higher security.
  • the encryption processing unit 750 shown in FIG. 72 executes data conversion processing in which the following data conversion units are sequentially applied.
  • Non-linear converter S An exclusive OR part for performing an exclusive OR operation with the round key RK 7 ;
  • Linear converter P2 An exclusive OR part for performing an exclusive OR operation with the round key RK 7 ;
  • Non-linear converter S
  • An exclusive OR part for performing an exclusive OR operation with the round key RK 8 Linear converter P1, Non-linear converter S, An exclusive OR part for performing an exclusive OR operation with the round key RK 9 ; Linear converter P3, Non-linear converter S, An exclusive OR part for performing an exclusive OR operation with the round key RK 10 ; Linear converter P1, Non-linear converter S, An exclusive OR part for performing an exclusive OR operation with the round key RK 11 , Linear converter P2, Non-linear converter S, An exclusive OR part for performing an exclusive OR operation with the round key RK 12 ; Linear converter P1, Non-linear converter S, An exclusive OR part for performing an exclusive OR operation with the round key RK 13 ;
  • the round key supply unit 721 of the key schedule unit 720 includes a key register 722 and a key conversion unit 723.
  • the processing executed by the round key supply unit 721 is performed by the item [5.
  • the secret key K stored in the key register is 128-bit key data which is concatenated data of 64-bit base keys K 1 and K 2 .
  • the key conversion unit 723 generates a conversion key Kd 1 based on the base key K 1 and generates a conversion key Kd 2 by conversion processing based on the base key K 2 .
  • This conversion process is expressed as follows using the conversion function G and the inverse function G ⁇ 1 .
  • Kd 1 G (K 1 )
  • K 1 G ⁇ 1 (Kd 1 )
  • G G ⁇ 1 Is established. That is, the data conversion function G applied to the key conversion in the key conversion unit 723 is involution property, that is, the property that the forward function G and the backward function G ⁇ 1 are the same function as shown in FIG. have.
  • the column spreading operation in step S1 of FIG. 34 with respect to all four columns of four states represent data ⁇ 4 consisting of 4-bit elements, matrix operation of applying the same Hadamard (Hadamard) MDS matrix M D Execute.
  • the row spreading operation in Step S2 is for all four rows of four states represent data ⁇ 4 consisting of 4-bit elements to perform the applied matrix operation the same Hadamard (Hadamard) MDS matrix M D .
  • the function G consisting of continuous processing of the column diffusion operation MC [M D ] and the row diffusion operation MR [M D ] has involution properties, and the forward function G and the backward function G ⁇ 1 are the same. By repeating twice, the original value is calculated.
  • the data diffusion between all the elements in the input / output state is performed by the column diffusion operation MC [M D ] applying the matrix M D executed in the key conversion unit 723 and the row diffusion operation MR [M D ] applying the matrix M D.
  • Diffusion ie, “full diffusion conversion” is performed.
  • the round key supply configuration executed by the round key supply unit 721 is as follows. (1) Full diffusion property that realizes full diffusion conversion, (2) Involution property in which the forward function G and the backward function G ⁇ 1 are the same, It has these two properties. These two characteristics bring about the following effects as described above.
  • the diffusion of the configuration information of the key data with respect to the conversion target data is realized with a small number of rounds, and is larger without depending on the processing of the round function (R). Diffusion performance is guaranteed. That is, secure cryptographic processing with high resistance to attacks is realized with a small number of rounds. As a result, high-speed processing and weight reduction are realized.
  • the round key supply unit 721 outputs keys in the following order. Key K 1 , Key K 2 , Conversion key Kd 1 , Conversion key Kd 2 , Exclusive OR key K 1 (+) K 2 , Exclusive OR operation conversion key Kd 1 (+) Kd 2 , Exclusive OR key K 1 (+) Kd 2 , Exclusive OR operation conversion key Kd 1 (+) Kd 2 , Exclusive OR key K 1 (+) K 2 , Conversion key Kd 2 , Conversion key Kd 1 , Key K 2 , Key K 1 , In this order, 6 types of keys are output.
  • round keys K 1 to K 13 input to the cryptographic processing unit 750 are generated by using the above keys as they are or by applying a constant CON.
  • the exclusive OR key K 1 (+) K 2 is repeatedly used as the round key K 7 before and after the linear conversion unit P2 at the center position of the cryptographic processing unit 750.
  • the round keys RK 8 , RK 10 , and RK 12 are generated by exclusive ORing the constant CON supplied from the constant supply unit 725 with the key supplied from the round key supply unit 721.
  • the key input sequence is the same as the sequence described above with reference to FIG. 59, and the reverse order is the same sequence.
  • the round key supply unit 721 performs key generation and output in the same sequence in the key input order in the encryption process for generating the ciphertext C from the plaintext P and in the decryption process for generating the plaintext P from the ciphertext C.
  • the constant supply unit 725 set in the key schedule unit 720 first sets the item [6. In the configuration for realizing improvement in safety by inputting constants], constant supply processing according to the processing described with reference to FIGS. 53 to 59 is executed.
  • the constant (CON) is Round key RK 8 , Round key RK 10 Round key RK 12 , When these round keys are generated, an exclusive OR operation is performed on the key data generated by the round key supply unit.
  • RK 1 K 1
  • RK 2 K 2
  • RK 3 Kd 1
  • RK 4 Kd 2
  • RK 5 K 1 (+) K 2
  • RK 6 Kd 1 (+) Kd 2
  • RK 7 K 1 (+) K 2
  • RK 7 K 1 (+) K 2
  • RK 8 Kd 1 (+) Kd 2 (+) CON
  • RK 9 K 1 (+) K 2
  • RK 10 Kd 2 (+) CON
  • RK 11 Kd 1
  • RK 12 K 2 (+) CON
  • RK 13 K 1
  • (+) means exclusive OR operation.
  • RK 7 is set to input the same round key twice before and after the linear conversion unit (P2).
  • the constant (CON) is subjected to exclusive OR processing on the key generated by the round key supply unit when the round key is generated.
  • a constant may be input to the exclusive OR unit of the encryption processing unit separately from the round key to perform exclusive OR processing with the converted data. In this case, the result is the same.
  • the constant (CON) is the result of matrix operation between the constant CON and the linear transformation matrix applied in the linear transformation unit adjacent to the exclusive OR unit of the encryption processing unit that inputs the constant CON.
  • a constant (CON) is used in which all elements are non-zero, that is, a non-zero value.
  • the non-linear conversion unit set in the encryption processing unit 750 is the item [7. Specific example of configuration of S box (S-box) applied to non-linear conversion unit]], 4-bit input / output k and box (S-box) having the involution described with reference to FIGS.
  • This is a configuration in which a plurality of are set.
  • the cryptographic processing unit 750 includes a conversion function E, a linear conversion unit, and a conversion function E ⁇ 1 , and the conversion function E and the non-linear conversion unit of the conversion function E ⁇ are shown in FIG. With the configuration using the S box shown in FIG. 66, the involution property of the entire cryptographic processing unit is realized.
  • the cryptographic processing apparatus that performs cryptographic processing according to the above-described embodiments can be mounted on various information processing apparatuses that perform cryptographic processing. Specifically, PC, TV, recorder, player, communication device, RFID, smart card, sensor network device, dent / battery authentication module, health / medical device, self-supporting network device, etc., for example, data processing and communication processing It can be used in various devices that execute cryptographic processing associated with the above.
  • FIG. 73 shows a configuration example of the IC module 800 as an example of an apparatus that executes the cryptographic processing of the present disclosure.
  • the above-described processing can be executed in various information processing apparatuses such as a PC, an IC card, a reader / writer, a smartphone, and a wearable device, and the IC module 800 illustrated in FIG. 73 can be configured in these various devices. It is.
  • a CPU (Central processing Unit) 801 shown in FIG. 73 is a processor that executes start and end of cryptographic processing, control of data transmission / reception, data transfer control between each component, and other various programs.
  • a memory 802 is a ROM (Read-Only-Memory) that stores programs executed by the CPU 801 or fixed data such as calculation parameters, a program executed in the processing of the CPU 801, and a parameter storage area that changes as appropriate in the program processing, It consists of RAM (Random Access Memory) used as a work area.
  • the memory 802 can be used as a storage area for key data necessary for encryption processing, data to be applied to a conversion table (substitution table) or conversion matrix applied in the encryption processing, and the like.
  • the data storage area is preferably configured as a memory having a tamper resistant structure.
  • the cryptographic processing unit 803 has the cryptographic processing configuration described above, and executes cryptographic processing and decryption processing according to the common key block cryptographic processing algorithm.
  • the cryptographic processing means is an individual module, but such an independent cryptographic processing module is not provided, for example, a cryptographic processing program is stored in the ROM, and the CPU 801 reads and executes the ROM stored program. You may comprise.
  • the random number generator 804 executes random number generation processing necessary for generating a key necessary for encryption processing.
  • the transmission / reception unit 805 is a data communication processing unit that performs data communication with the outside.
  • the data transmission / reception unit 805 performs data communication with an IC module such as a reader / writer, and outputs a ciphertext generated in the IC module or an external reader. Data input from devices such as writers is executed.
  • the encryption processing apparatus described in the above-described embodiment is not only applicable to encryption processing for encrypting plaintext as input data, but also for decryption processing for restoring ciphertext as input data to plaintext. Applicable.
  • the configurations described in the above-described embodiments can be applied to both the encryption process and the decryption process.
  • FIG. 74 is a block diagram illustrating an example of a schematic configuration of the smartphone 900 that executes the cryptographic processing according to the present disclosure.
  • the smartphone 900 includes a processor 901, a memory 902, a storage 903, an external connection interface 904, a camera 906, a sensor 907, a microphone 908, an input device 909, a display device 910, a speaker 911, a wireless communication interface 913, an antenna switch 914, an antenna 915, A bus 917, a battery 918, and an auxiliary controller 919 are provided.
  • the processor 901 may be, for example, a CPU (Central Processing Unit) or an SoC (System on Chip), and controls the functions of the application layer and other layers of the smartphone 900 and also controls encryption processing.
  • the memory 902 includes a RAM (Random Access Memory) and a ROM (Read Only Memory), and stores programs and data executed by the processor 901.
  • the memory 902 can be used as a storage area for key data necessary for encryption processing, data to be applied to a conversion table (substitution table) or conversion matrix applied in the encryption processing, and the like.
  • the data storage area is preferably configured as a memory having a tamper resistant structure.
  • the storage 903 can include a storage medium such as a semiconductor memory or a hard disk.
  • the external connection interface 904 is an interface for connecting an external device such as a memory card or a USB (Universal Serial Bus) device to the smartphone 900.
  • the camera 906 includes, for example, an imaging element such as a charge coupled device (CCD) or a complementary metal oxide semiconductor (CMOS), and generates a captured image.
  • the sensor 907 may include a sensor group such as a positioning sensor, a gyro sensor, a geomagnetic sensor, and an acceleration sensor.
  • the microphone 908 converts sound input to the smartphone 900 into an audio signal.
  • An image generated by the camera 906, sensor data acquired by the sensor 907, an audio signal acquired by the microphone 908, and the like may be encrypted by the processor 901 and transmitted to another device via the wireless communication interface 913. .
  • the input device 909 includes, for example, a touch sensor that detects a touch on the screen of the display device 910, a keypad, a keyboard, a button, or a switch, and receives an operation or information input from a user.
  • the display device 910 has a screen such as a liquid crystal display (LCD) or an organic light emitting diode (OLED) display, and displays an output image of the smartphone 900.
  • the speaker 911 converts an audio signal output from the smartphone 900 into audio.
  • the wireless communication interface 913 performs wireless communication, and typically includes a baseband processor, an RF (Radio Frequency) circuit, a power amplifier, and the like.
  • the wireless communication interface 913 may be a one-chip module in which a memory that stores a communication control program, a processor that executes the program, and related circuits are integrated.
  • the wireless communication interface 913 may support other types of wireless communication methods such as a short-range wireless communication method, a proximity wireless communication method, or a cellular communication method in addition to the wireless LAN method.
  • the bus 917 connects the processor 901, memory 902, storage 903, external connection interface 904, camera 906, sensor 907, microphone 908, input device 909, display device 910, speaker 911, wireless communication interface 913, and auxiliary controller 919 to each other.
  • the battery 918 supplies power to each block of the smartphone 900 shown in FIG. 74 via a power supply line partially shown by a broken line in the drawing.
  • the auxiliary controller 919 operates the minimum necessary functions of the smartphone 900 in the sleep mode.
  • the encryption processing in the smartphone described in the above-described embodiment is not only applicable to encryption processing for encrypting plaintext as input data, but also for decryption processing for restoring ciphertext as input data to plaintext. Is also applicable.
  • the configurations described in the above-described embodiments can be applied to both the encryption process and the decryption process.
  • the IC module 800 shown in FIG. 73 may be mounted on the smartphone 900 shown in FIG. 74, and the encryption processing according to the above-described embodiment may be executed in the IC module 800.
  • the technology disclosed in this specification can take the following configurations.
  • the key schedule part A key register storing a secret key K;
  • the secret key K and the conversion key Kd are configured to be a round key that is output to the encryption processing unit, or round key generation data.
  • the conversion function G is a cryptographic processing device which is an involution function in which the inverse function G ⁇ 1 is the same function as the function G.
  • Each of the secret key K and the conversion key Kd is a state composed of m ⁇ n elements each having 1 or more bits, and the conversion function G is a state element of the secret key K.
  • the conversion function G applies a column spreading operation for performing a linear transformation by applying a matrix for each column element of the state of the secret key K, and a matrix for each row element of the state of the secret key K.
  • Each of the secret key K and the conversion key Kd is a state composed of 4 ⁇ 4 elements each having 4 bits, and the conversion function G includes all the state elements of the secret key K.
  • the cryptographic processing device according to any one of (1) to (3), wherein is a function having a full diffusion property that affects all the state elements of the conversion key Kd.
  • the conversion function G includes a column spreading operation that performs linear conversion by applying a Hadamard MDS matrix in units of each column element of the state of the secret key K, and each row element of the state of the secret key K
  • the cryptographic processing apparatus according to (4), wherein the conversion key Kd is generated by executing a row diffusion operation for performing linear conversion by applying a Hadamard MDS (Hadamard MDS) matrix in units.
  • the secret key K is concatenated data of split keys K1 and K2, and the key conversion unit converts the conversion function G applied to each of the split keys K1 and K2.
  • the key conversion unit converts the conversion function G applied to each of the split keys K1 and K2.
  • the cryptographic processing device according to any one of the above.
  • the key schedule part (A) the split keys K1, K2, (B) the conversion keys Kd1, Kd2, (C) a key generated by an exclusive OR operation between the split key K1 and the split key K2. (D) a key generated by an exclusive OR operation between the conversion key Kd1 and the conversion key Kd2.
  • the cryptographic processing device wherein the six types of keys (a) to (d) are used as round keys to be output to the cryptographic processing unit or round key generation data.
  • the cipher processing unit repeats the round operation using the plaintext P as input data, outputs ciphertext C as output data, and uses the ciphertext C as input data to reverse the execution sequence of the round operations.
  • the cryptographic processing apparatus according to any one of (1) to (7), wherein the cryptographic processing apparatus has an involution property that can generate the plaintext P as output data by the set data conversion processing.
  • the key schedule unit has an involution property in which the key supply sequence when the ciphertext C is generated from the plaintext P and the key supply sequence when the plaintext P is generated from the ciphertext C match.
  • the key schedule unit performs a calculation with a constant on a part of the supplied key during the key supply process to the cryptographic processing unit, and outputs key data as a calculation result to the cryptographic processing unit.
  • the cryptographic processing device according to any one of the above.
  • the round operation executed by the cryptographic processing unit is an operation including a linear conversion process by a linear conversion unit, and the linear conversion unit changes the linear conversion mode according to the round transition.
  • the cryptographic processing device according to any one of the above.
  • the round operation includes a non-linear transformation process, and the S box that executes the non-linear transformation process has an involution property in which the input value can be obtained by re-inputting an output value obtained from the input value.
  • the cryptographic processing device according to any one of (1) to (11), wherein
  • (13) a cryptographic processing unit that performs a round operation on input data to generate output data;
  • a key schedule unit that outputs a round key applied in a round operation in the cryptographic processing unit to the cryptographic processing unit;
  • the key schedule part A key register storing a secret key K;
  • a key conversion unit that generates a conversion key Kd by a conversion process in which a conversion function G is applied to the secret key K;
  • the secret key K and the conversion key Kd are configured to be a round key that is output to the encryption processing unit, or round key generation data.
  • Each of the secret key K and the conversion key Kd is a state composed of m ⁇ n elements each having 1 bit or more
  • the conversion function G is a cryptographic processing device in which all the state elements of the secret key K have a full diffusion property that affects all the state elements of the conversion key Kd.
  • Each of the secret key K and the conversion key Kd is a state composed of 4 ⁇ 4 elements each having 4 bits, and the conversion function G includes a full diffusion 4-bit conversion function and 16 bits.
  • the secret key K is concatenated data of the split keys K1 and K2, and the key conversion unit obtains the conversion key Kd1 by a conversion process using a conversion function G1 for the split key K1.
  • the cryptographic processing device according to any one of (13) to (15), which is a combination of any of (a) to (c) above.
  • a cryptographic processing method executed in the cryptographic processing device includes: An encryption processing unit that performs round operation on input data to generate output data; A key schedule unit that outputs a round key applied in a round operation in the cryptographic processing unit to the cryptographic processing unit;
  • the key schedule part A conversion key Kd is generated by a conversion process in which a conversion function G is applied to the secret key K stored in the key register, A process of setting the secret key K and the conversion key Kd as a round key to be output to the cryptographic processing unit or data for generating a round key;
  • the conversion function G is a cryptographic processing method in which the inverse function G ⁇ 1 is a function having an involution property in which the function G is the same as the function G.
  • a cryptographic processing method executed in the cryptographic processing device includes: An encryption processing unit that performs round operation on input data to generate output data; A key schedule unit that outputs a round key applied in a round operation in the cryptographic processing unit to the cryptographic processing unit;
  • the key schedule part A conversion key Kd is generated by a conversion process in which a conversion function G is applied to the secret key K stored in the key register, A process of setting the secret key K and the conversion key Kd as a round key to be output to the cryptographic processing unit or data for generating a round key;
  • Each of the secret key K and the conversion key Kd is a state composed of m ⁇ n elements each having 1 bit or more,
  • the conversion function G is a cryptographic processing method in which all the state elements of the secret key K have a full diffusion property that affects all the state elements of the conversion key Kd.
  • a program for executing cryptographic processing in the cryptographic processing device includes: An encryption processing unit that performs round operation on input data to generate output data; A key schedule unit that outputs a round key applied in a round operation in the cryptographic processing unit to the cryptographic processing unit;
  • the program is stored in the key schedule unit.
  • the conversion function G is a program having an involution property in which the inverse function G ⁇ 1 is the same function as the function G.
  • a program for executing cryptographic processing in the cryptographic processing device includes: An encryption processing unit that performs round operation on input data to generate output data; A key schedule unit that outputs a round key applied in a round operation in the cryptographic processing unit to the cryptographic processing unit;
  • the program is stored in the key schedule unit.
  • Each of the secret key K and the conversion key Kd is a state composed of m ⁇ n elements each having 1 bit or more,
  • the conversion function G is a program in which all the state elements of the secret key K have a full diffusion property that affects all the state elements of the conversion key Kd.
  • the series of processes described in the specification can be executed by hardware, software, or a combined configuration of both.
  • the program recording the processing sequence is installed in a memory in a computer incorporated in dedicated hardware and executed, or the program is executed on a general-purpose computer capable of executing various processing. It can be installed and run.
  • the program can be recorded in advance on a recording medium.
  • the program can be received via a network such as a LAN (Local Area Network) or the Internet and installed on a recording medium such as a built-in hard disk.
  • the various processes described in the specification are not only executed in time series according to the description, but may be executed in parallel or individually according to the processing capability of the apparatus that executes the processes or as necessary.
  • the system is a logical set configuration of a plurality of devices, and the devices of each configuration are not limited to being in the same casing.
  • a highly secure cryptographic processing configuration with improved resistance to various attacks has a cryptographic processing unit that repeats a round operation on input data to generate output data, and a key schedule unit that outputs a round key applied in the round operation in the cryptographic processing unit to the cryptographic processing unit.
  • the unit includes a key register that stores the secret key K, and a key conversion unit that generates a conversion key Kd by a conversion process in which the conversion function G is applied to the secret key K.
  • the secret key K and the conversion key Kd are The round key to be output to the encryption processing unit or round key generation data.

Landscapes

  • Engineering & Computer Science (AREA)
  • Computer Security & Cryptography (AREA)
  • Computer Networks & Wireless Communication (AREA)
  • Signal Processing (AREA)
  • Physics & Mathematics (AREA)
  • General Physics & Mathematics (AREA)
  • Theoretical Computer Science (AREA)
  • Storage Device Security (AREA)

Abstract

各種の攻撃に対する耐性を向上させた安全性の高い暗号処理構成を実現する。入力データに対するラウンド演算を繰り返して出力データを生成する暗号処理部と、暗号処理部におけるラウンド演算において適用するラウンド鍵を暗号処理部に出力する鍵スケジュール部を有し、鍵スケジュール部は、秘密鍵Ｋを格納した鍵レジスタと、秘密鍵Ｋに対して変換関数Ｇを適用した変換処理により変換鍵Ｋｄを生成する鍵変換部を有し、秘密鍵Ｋ、および変換鍵Ｋｄを暗号処理部に出力するラウンド鍵、またはラウンド鍵生成用データとする。変換関数Ｇとして、逆関数Ｇ－１が関数Ｇと同じ関数となるインボリューション性と、フルディフュージョン性を有する関数を適用する。

Description

暗号処理装置、および暗号処理方法、並びにプログラム
　本開示は、暗号処理装置、および暗号処理方法、並びにプログラムに関する。さらに詳細には、共通鍵系暗号を実行する暗号処理装置、および暗号処理方法、並びにプログラムに関する。
　情報化社会が発展すると共に、扱う情報を安全に守るための情報セキュリティ技術の重要性が増してきている。情報セキュリティ技術の構成要素の一つとして暗号技術があり、現在では様々な製品やシステムで暗号技術が利用されている。
　暗号処理アルゴリズムには様々なものがあるが、基本的な技術の一つとして、共通鍵ブロック暗号と呼ばれるものがある。共通鍵ブロック暗号では、暗号化用の鍵と復号用の鍵が共通のものとなっている。暗号化処理、復号処理共に、その共通鍵から複数の鍵を生成し、あるブロック単位、例えば６４ビット、１２８ビット、２５６ビット等のブロックデータ単位でデータ変換処理を繰り返し実行する。
　代表的な共通鍵ブロック暗号のアルゴリズムとしては、過去の米国標準であるＤＥＳ（Ｄａｔａ　Ｅｎｃｒｙｐｔｉｏｎ　Ｓｔａｎｄａｒｄ）や現在の米国標準であるＡＥＳ（Ａｄｖａｎｃｅｄ　Ｅｎｃｒｙｐｔｉｏｎ　Ｓｔａｎｄａｒｄ）が知られている。他にも様々な共通鍵ブロック暗号が現在も提案され続けており、２００７年にソニー株式会社が提案したＣＬＥＦＩＡも共通鍵ブロック暗号の一つである。
　なお、共通鍵ブロック暗号について開示した従来技術として、例えば特許文献１（特開２０１２－２１５８１３号公報）等がある。
　このような、共通鍵ブロック暗号のアルゴリズムは、主として、入力データの変換を繰り返し実行するラウンド関数実行部を有する暗号処理部と、ラウンド関数部の各ラウンドで適用するラウンド鍵を生成する鍵スケジュール部とによって構成される。鍵スケジュール部は、秘密鍵であるマスター鍵（主鍵）に基づいて、まずビット数を増加させた拡大鍵を生成し、生成した拡大鍵に基づいて、暗号処理部の各ラウンド関数部で適用するラウンド鍵（副鍵）を生成する。
　このようなアルゴリズムを実行する具体的な構造として、線形変換部および非線形変換部を有するラウンド関数を繰り返し実行する構造が知られている。例えば代表的な構造として、ＳＰＮ（Ｓｕｂｓｔｉｔｕｔｉｏｎ－Ｐｅｒｍｕｔａｔｉｏｎ　Ｎｅｔｗｏｒｋ）構造、Ｆｅｉｓｔｅｌ構造、拡張Ｆｅｉｓｔｅｌ構造等がある。
　これらは、いずれも線形変換部および非線形変換部を有するラウンド関数を繰り返し実行して平文を暗号文に変換する構造を持つ。
特開２０１２－２１５８１３号公報
　例えば暗号アルゴリズムや秘密鍵の解読を試みる攻撃として差分攻撃、線形攻撃等がある。暗号処理装置は、これらの様々な攻撃に対する耐性や、高速処理、あるいは小型化などが求められている。
　本開示は、例えば上述の状況に鑑みてなされたものであり、安全性、高速性、あるいは小型化等、暗号処理装置に要求される様々な要素の向上を実現する暗号処理装置、および暗号処理方法、並びにプログラムを提供することを目的とする。
　本開示の第１の側面は、
　入力データに対するラウンド演算を実行して出力データを生成する暗号処理部と、
　前記暗号処理部におけるラウンド演算において適用するラウンド鍵を前記暗号処理部に出力する鍵スケジュール部を有し、
　前記鍵スケジュール部は、
　秘密鍵Ｋを格納した鍵レジスタと、
　前記秘密鍵Ｋに対して変換関数Ｇを適用した変換処理により変換鍵Ｋｄを生成する鍵変換部を有し、
　前記秘密鍵Ｋ、および前記変換鍵Ｋｄを前記暗号処理部に出力するラウンド鍵、またはラウンド鍵生成用データとする構成であり、
　前記変換関数Ｇは、逆関数Ｇ－１が関数Ｇと同じ関数となるインボリューション性を有する関数である暗号処理装置にある。
　さらに、本開示の第２の側面は、
　入力データに対するラウンド演算を実行して出力データを生成する暗号処理部と、
　前記暗号処理部におけるラウンド演算において適用するラウンド鍵を前記暗号処理部に出力する鍵スケジュール部を有し、
　前記鍵スケジュール部は、
　秘密鍵Ｋを格納した鍵レジスタと、
　前記秘密鍵Ｋに対して変換関数Ｇを適用した変換処理により変換鍵Ｋｄを生成する鍵変換部を有し、
　前記秘密鍵Ｋ、および前記変換鍵Ｋｄを前記暗号処理部に出力するラウンド鍵、またはラウンド鍵生成用データとする構成であり、
　前記秘密鍵Ｋ、および前記変換鍵Ｋｄは、いずれも各要素が１ビット以上のｍ×ｎ個の要素からなるステートであり、
　前記変換関数Ｇは、前記秘密鍵Ｋのステート要素の全てが、前記変換鍵Ｋｄのステート要素全てに影響を及ぼすフルディフュージョン性を有する関数である暗号処理装置にある。
　さらに、本開示の第３の側面は、
　暗号処理装置において実行する暗号処理方法であり、
　前記暗号処理装置は、
　入力データに対するラウンド演算を実行して出力データを生成する暗号処理部と、
　前記暗号処理部におけるラウンド演算において適用するラウンド鍵を前記暗号処理部に出力する鍵スケジュール部を有し、
　前記鍵スケジュール部は、
　鍵レジスタに格納した秘密鍵Ｋに対して変換関数Ｇを適用した変換処理により変換鍵Ｋｄを生成し、
　前記秘密鍵Ｋ、および前記変換鍵Ｋｄを前記暗号処理部に出力するラウンド鍵、またはラウンド鍵生成用データとする処理を行ない、
　前記変換関数Ｇは、逆関数Ｇ－１が関数Ｇと同じ関数となるインボリューション性を有する関数である暗号処理方法にある。
　さらに、本開示の第４の側面は、
　暗号処理装置において実行する暗号処理方法であり、
　前記暗号処理装置は、
　入力データに対するラウンド演算を実行して出力データを生成する暗号処理部と、
　前記暗号処理部におけるラウンド演算において適用するラウンド鍵を前記暗号処理部に出力する鍵スケジュール部を有し、
　前記鍵スケジュール部は、
　鍵レジスタに格納した秘密鍵Ｋに対して変換関数Ｇを適用した変換処理により変換鍵Ｋｄを生成し、
　前記秘密鍵Ｋ、および前記変換鍵Ｋｄを前記暗号処理部に出力するラウンド鍵、またはラウンド鍵生成用データとする処理を行ない、
　前記秘密鍵Ｋ、および前記変換鍵Ｋｄは、いずれも各要素が１ビット以上のｍ×ｎ個の要素からなるステートであり、
　前記変換関数Ｇは、前記秘密鍵Ｋのステート要素の全てが、前記変換鍵Ｋｄのステート要素全てに影響を及ぼすフルディフュージョン性を有する関数である暗号処理方法にある。
　さらに、本開示の第５の側面は、
　暗号処理装置において暗号処理を実行させるプログラムであり、
　前記暗号処理装置は、
　入力データに対するラウンド演算を実行して出力データを生成する暗号処理部と、
　前記暗号処理部におけるラウンド演算において適用するラウンド鍵を前記暗号処理部に出力する鍵スケジュール部を有し、
　前記プログラムは、前記鍵スケジュール部に、
　鍵レジスタに格納した秘密鍵Ｋに対して変換関数Ｇを適用した変換処理により変換鍵Ｋｄを生成する処理と、
　前記秘密鍵Ｋ、および前記変換鍵Ｋｄを前記暗号処理部に出力するラウンド鍵、またはラウンド鍵生成用データとする処理を実行させ、
　前記変換関数Ｇは、逆関数Ｇ－１が関数Ｇと同じ関数となるインボリューション性を有する関数であるプログラムにある。
　さらに、本開示の第６の側面は、
　暗号処理装置において暗号処理を実行させるプログラムであり、
　前記暗号処理装置は、
　入力データに対するラウンド演算を実行して出力データを生成する暗号処理部と、
　前記暗号処理部におけるラウンド演算において適用するラウンド鍵を前記暗号処理部に出力する鍵スケジュール部を有し、
　前記プログラムは、前記鍵スケジュール部に、
　鍵レジスタに格納した秘密鍵Ｋに対して変換関数Ｇを適用した変換処理により変換鍵Ｋｄを生成する処理と、
　前記秘密鍵Ｋ、および前記変換鍵Ｋｄを前記暗号処理部に出力するラウンド鍵、またはラウンド鍵生成用データとする処理を実行させ、
　前記秘密鍵Ｋ、および前記変換鍵Ｋｄは、いずれも各要素が１ビット以上のｍ×ｎ個の要素からなるステートであり、
　前記変換関数Ｇは、前記秘密鍵Ｋのステート要素の全てが、前記変換鍵Ｋｄのステート要素全てに影響を及ぼすフルディフュージョン性を有する関数であるプログラムにある。
　なお、本開示のプログラムは、例えば、様々なプログラム・コードを実行可能な情報処理装置やコンピュータ・システムに対して例えば記憶媒体によって提供されるプログラムである。このようなプログラムを情報処理装置やコンピュータ・システム上のプログラム実行部で実行することでプログラムに応じた処理が実現される。
　本開示のさらに他の目的、特徴や利点は、後述する本発明の実施例や添付する図面に基づくより詳細な説明によって明らかになるであろう。なお、本明細書においてシステムとは、複数の装置の論理的集合構成であり、各構成の装置が同一筐体内にあるものには限らない。
　本開示の一実施例の構成によれば、各種の攻撃に対する耐性を向上させた安全性の高い暗号処理構成が実現される。
　具体的には、入力データに対するラウンド演算を繰り返して出力データを生成する暗号処理部と、暗号処理部におけるラウンド演算において適用するラウンド鍵を暗号処理部に出力する鍵スケジュール部を有し、鍵スケジュール部は、秘密鍵Ｋを格納した鍵レジスタと、秘密鍵Ｋに対して変換関数Ｇを適用した変換処理により変換鍵Ｋｄを生成する鍵変換部を有し、秘密鍵Ｋ、および変換鍵Ｋｄを暗号処理部に出力するラウンド鍵、またはラウンド鍵生成用データとする。変換関数Ｇとして、逆関数Ｇ－１が関数Ｇと同じ関数となるインボリューション性と、フルディフュージョン性を有する関数を適用する。
　本構成により拡散特性が向上し、各種の攻撃に対する耐性を向上させた安全性の高い暗号処理構成が実現される。
　なお、本明細書に記載された効果はあくまで例示であって限定されるものではなく、また付加的な効果があってもよい。
ｋビットの鍵長に対応したｎビット共通鍵ブロック暗号アルゴリズムを説明する図である。 図１に示すｋビットの鍵長に対応したｎビット共通鍵ブロック暗号アルゴリズムに対応する復号アルゴリズムを説明する図である。 鍵スケジュール部と暗号処理部の関係について説明する図である。 暗号処理部の構成例について説明する図である。 ＳＰＮ構造のラウンド関数の例について説明する図である。 Ｆｅｉｓｔｅｌ構造のラウンド関数の一例について説明する図である。 拡張Ｆｅｉｓｔｅｌ構造の一例について説明する図である。 拡張Ｆｅｉｓｔｅｌ構造の一例について説明する図である。 非線形変換部の構成例について説明する図である。 線形変換部の構成例について説明する図である。 ステート（ステート表現データ）に対するデータ変換処理例について説明する図である。 ステートに対するデータ変換処理例について説明する図である。 ステートに対するデータ変換処理例について説明する図である。 ステートに対するデータ変換処理例について説明する図である。 ステートに対する列拡散演算処理について説明する図である。 ステートに対する列拡散演算処理について説明する図である。 ステートに対する行拡散演算処理について説明する図である。 ステートに対する行拡散演算処理について説明する図である。 本開示の一実施例に係る暗号処理装置の構成例について説明する図である。 本開示の一実施例に係る暗号処理装置の構成例について説明する図である。 暗号処理部において実行するデータ変換処理例について説明する図である。 暗号処理部の非線形変換部と線形変換部の構成と処理について説明する図である。 暗号処理部の線形変換部の構成と処理について説明する図である。 線形変換処理に適用する行列について説明する図である。 線形変換部Ｐ１の実行する列拡散演算について説明する図である。 線形変換部Ｐ２の実行する行拡散演算について説明する図である。 線形変換部Ｐ３の実行する行拡散演算について説明する図である。 暗号処理部の線形変換部の構成と処理について説明する図である。 暗号処理部の線形変換部を同一の線形変換処理とした場合の構成について説明する図である。 暗号処理部の線形変換部を異なる線形変換処理実行構成とした場合しと、同一の線形変換処理を実行する構成とした場合のアクティブＳボックスの数の比較データについて説明する図である。 暗号処理部の線形変換部を異なる線形変換処理実行構成とした場合しと、同一の線形変換処理を実行する構成とした場合のアクティブＳボックスの数の比較データについて説明する図である。 鍵スケジュール部の構成と処理について説明する図である。 鍵スケジュール部の鍵変換部の構成と処理について説明する図である。 鍵スケジュール部の鍵変換部の構成と処理について説明する図である。 鍵スケジュール部の鍵変換部の変換処理にるデータ拡散処理について説明する図である。 鍵変換処理の実行構成と実行しない構成との対比について説明する図である。 鍵変換処理の実行構成と実行しない構成との対比について説明する図である。 鍵変換処理の実行構成と実行しない構成との対比について説明する図である。 鍵スケジュール部の構成と処理について説明する図である。 鍵変換関数がインボリューション性を有していない場合の鍵スケジュール部の構成と処理について説明する図である。 鍵変換関数がインボリューション性を有している場合の鍵スケジュール部の構成と処理について説明する図である。 鍵スケジュール部の構成と処理について説明する図である。 鍵スケジュール部の構成と処理について説明する図である。 鍵変換関数Ｇがフルディフュージョン性を有する場合の暗号処理構成について説明する図である。 鍵変換を実行しない場合の構成と処理について説明する図である。 １６ビット置換処理について説明する図である。 フルディフューション４ビット関数と１６ビット置換関数を適用した鍵変換処理例について説明する図である。 フルディフューション４ビット関数と１６ビット置換関数を適用した鍵変換処理例について説明する図である。 フルディフューション４ビット関数と１６ビット置換関数を適用した鍵変換処理例について説明する図である。 フルディフューション４ビット関数と１６ビット置換関数を適用した鍵変換処理例について説明する図である。 フルディフューション４ビット関数と１６ビット置換関数を適用した鍵変換処理例について説明する図である。 分割鍵に対する置換関数Ｇ１，Ｇ２の設定例について説明する図である。 暗号処理部に対する定数入力構成例について説明する図である。 インボリーション性を有する暗号処理部の構成例について説明する図である。 インボリーション性を有する暗号処理部の問題点について説明する図である。 暗号処理部に対する定数入力構成例について説明する図である。 暗号処理部に対する定数入力構成例について説明する図である。 暗号処理部に対する定数入力構成例について説明する図である。 暗号処理部に対する定数入力構成例について説明する図である。 アクティブＳボックスに基づく安全性評価処理について説明する図である。 アクティブＳボックスに基づく安全性評価処理について説明する図である。 アクティブＳボックスに基づく安全性評価処理について説明する図である。 暗号処理部に対する定数入力構成例について説明する図である。 暗号処理部の非線形変換部のＳボックス（Ｓ－ｂｏｘ）の構成例について説明する図である。 暗号処理部の非線形変換部のＳボックス（Ｓ－ｂｏｘ）の構成例について説明する図である。 暗号処理部の非線形変換部のＳボックス（Ｓ－ｂｏｘ）の構成例について説明する図である。 暗号処理部の非線形変換部のＳボックス（Ｓ－ｂｏｘ）の線形変換層の構成例について説明する図である。 暗号処理部の非線形変換部のＳボックス（Ｓ－ｂｏｘ）の構成例について説明する図である。 暗号処理部の非線形変換部のＳボックス（Ｓ－ｂｏｘ）の構成例について説明する図である。 暗号処理部の非線形変換部のＳボックス（Ｓ－ｂｏｘ）の構成例について説明する図である。 暗号処理部の非線形変換部のＳボックス（Ｓ－ｂｏｘ）の構成例について説明する図である。 暗号処理装置の一構成例について説明する図である。 暗号処理装置としてのＩＣモジュール７００の構成例を示す図である。 暗号処理実行機能を有するスマートフォンの構成例を示す図である。
　以下、図面を参照しながら本開示に係る暗号処理装置、および暗号処理方法、並びにプログラムの詳細について説明する。説明は、以下の項目に従って行う。
　１．共通鍵ブロック暗号の概要
　２．共通鍵ブロック暗号における安全性の指標について
　３．安全性を高めた共通鍵暗号処理の全体構成概要について
　４．暗号処理部の線形変換部の構成と処理について
　５．鍵スケジュール部の構成と処理について
　５－１．鍵スケジュール部の構成と処理の説明
　５－２．鍵スケジュール部のフルディフュージョン性に基づく効果について
　５－３．鍵変換部のインボリューション性に基づく効果について
　５－３－ａ．アンロールド（Ｕｎｒｏｌｌｅｄ）実装における効果について
　５－３－ｂ．ラウンド実装における効果について
　５－４．本開示の鍵スケジュール部の構成と効果のまとめ
　５－５．鍵スケジュール部のその他の構成例について
　５－６．フルディフュージョン性を持つ鍵変換部を有する構成例について
　６．定数入力による安全性向上を実現する構成について
　６－１．定数入力による安全性向上を実現した従来構成とその問題点について
　６－２．安全性の高い定数入力構成を持つ暗号処理装置の構成について
　６－３．定数挿入位置のバリエーションについて
　７．非線形変換部に適用するＳボックス（Ｓ－ｂｏｘ）の具体的構成例について
　８．暗号処理装置の具体例について
　９．暗号処理装置の実装例について
　１０．本開示の構成のまとめ
　　［１．共通鍵ブロック暗号の概要］
　まず、共通鍵ブロック暗号の概要について説明する。
　　（１－１．共通鍵ブロック暗号）
　ここでは共通鍵ブロック暗号（以下ではブロック暗号と呼ぶ場合がある）は以下に定義するものを指すものとする。
　ブロック暗号は入力として平文Ｐと鍵Ｋを取り、暗号文Ｃを出力する。平文と暗号文のビット長をブロックサイズと呼び、例えばブロックサイズ＝ｎとする。ｎは任意の整数値を取りうるが、通常、ブロック暗号アルゴリズムごとに、あらかじめひとつに決められている値である。ブロック長がｎのブロック暗号のことをｎビットブロック暗号と呼ぶこともある。
　鍵のビット長をｋで表す。鍵は任意の整数値を取りうる。共通鍵ブロック暗号アルゴリズムは１つまたは複数の鍵サイズに対応することになる。例えば、あるブロック暗号アルゴリズムＡはブロックサイズｎ＝１２８であり、ｋ＝１２８またはｋ＝１９２またはｋ＝２５６の鍵サイズに対応するという構成もありうるものとする。
　平文Ｐ：ｎビット
　暗号文Ｃ：ｎビット
　鍵Ｋ：ｋビット
　図１にｋビットの鍵長に対応したｎビット共通鍵ブロック暗号アルゴリズムＥの図を示す。
　暗号化アルゴリズムＥに対応する復号アルゴリズムＤは暗号化アルゴリズムＥの逆関数Ｅ－１と定義でき、入力として暗号文Ｃと鍵Ｋを受け取り，平文Ｐを出力する。図２に図１に示した暗号アルゴリズムＥに対応する復号アルゴリズムＤの図を示す。
　　（１－２．内部構成）
　ブロック暗号は２つの部分に分けて考えることができる。ひとつは秘密鍵Ｋを入力とし、ある定められたステップにより暗号処理部の各ラウンドで適用するラウンド鍵を出力する「鍵スケジュール部」と、もうひとつは平文Ｐと鍵スケジュール部からラウンド鍵を入力してデータ変換を行い暗号文Ｃを出力する「暗号処理部」である。
　２つの部分の関係は図３に示される。
　なお、暗号処理部は、暗号文Ｃを入力して平文Ｐを出力する復号処理も実行可能な構成である場合が多い。この場合も、鍵スケジュール部から供給されるラウンド鍵を適用した復号処理を実行する。
　２つの部分の関係は図３に示される。
　　（１－３．暗号処理部）
　以下の実施例において用いる暗号処理部はラウンド関数という処理単位に分割できるものとする。ラウンド関数は入力データに対して所定のデータ変換を施し、変換データを出力する。ラウンド関数に対する入力データは、例えば暗号化途中のｎビットデータである。あるラウンドにおけるラウンド関数の出力が次のラウンドの入力として供給される構成となる。また、ラウンド関数の一構成として、鍵スケジュール部から出力された鍵に基づいて生成されるラウンド鍵との演算構成が含まれる。具体的には暗号化途中のｎビットデータとラウンド鍵との排他的論理和演算が行われる。
　またラウンド関数の総数は総ラウンド数と呼ばれ、暗号アルゴリズムごとにあらかじめ定められている値である。
　暗号処理部の入力側から見て１ラウンド目の入力データをＸ１とし、ｉ番目のラウンド関数に入力されるデータをＸｉ、ラウンド鍵をＲＫｉとすると、暗号処理部全体は図４のように示される。
　　（１－４．ラウンド関数）
　ブロック暗号アルゴリズムによってラウンド関数はさまざまな形態をとりうる。ラウンド関数はその暗号アルゴリズムが採用する構造（ｓｔｒｕｃｔｕｒｅ）によって分類できる。代表的な構造としてここではＳＰＮ（Ｓｕｂｓｔｉｔｕｔｉｏｎ－Ｐｅｒｍｕｔａｔｉｏｎ　Ｎｅｔｗｏｒｋ）構造、Ｆｅｉｓｔｅｌ構造、拡張Ｆｅｉｓｔｅｌ構造を例示する。
　　（ア）ＳＰＮ（Ｓｕｂｓｔｉｔｕｔｉｏｎ－Ｐｅｒｍｕｔａｔｉｏｎ　Ｎｅｔｗｏｒｋ）構造ラウンド関数
　ｎビットの入力データすべてに対して、ラウンド鍵との排他的論理和演算、非線形変換、線形変換処理などが適用される構成。各演算の順番は特に決まっていない。図５にＳＰＮ構造のラウンド関数の例を示す。線形変換部をＰ層（Ｐｅｒｍｕｔａｔｉｏｎ－ｌａｙｅｒ）と呼ぶこともある。
　　（イ）Ｆｅｉｓｔｅｌ構造
　ｎビットの入力データはｎ／２ビットの２つのデータに分割される。うち片方のデータとラウンド鍵を入力として持つ関数（Ｆ関数）が適用され、出力がもう片方のデータに排他的論理和される。そののちデータの左右を入れ替えたものを出力データとする。Ｆ関数の内部構成にもさまざまなタイプのものがあるが、基本的にはＳＰＮ構造同様にラウンド鍵データとの排他的論理和演算、非線形演算、線形変換の組み合わせで実現される。図６にＦｅｉｓｔｅｌ構造のラウンド関数の一例を示す。
　　（ウ）拡張Ｆｅｉｓｔｅｌ構造
　拡張Ｆｅｉｓｔｅｌ構造はＦｅｉｓｔｅｌ構造ではデータ分割数が２であったものを，３以上に分割する形に拡張したものである。分割数をｄとすると、ｄによってさまざまな拡張Ｆｅｉｓｔｅｌ構造を定義することができる。Ｆ関数の入出力のサイズが相対的に小さくなるため、小型実装に向いているとされる。図７にｄ＝４でかつ、ひとつのラウンド内に２つのＦ関数が並列に適用される場合の拡張Ｆｅｉｓｔｅｌ構造の一例を示す。また，図８にｄ＝８でかつ，ひとつのラウンド内に１つのＦ関数が適用される場合の拡張Ｆｅｉｓｔｅｌ構造の一例を示す。
　　（１－５．非線形変換部）
　非線形変換部は、入力されるデータのサイズが大きくなると実装上のコストが高くなる傾向がある。それを回避するために対象データを複数の単位に分割し、それぞれに対して非線形変換を施す構成がとられることが多い。例えば入力サイズをｍｓビットとして、それらをｓビットずつのｍ個のデータに分割して、それぞれに対してｓビット入出力を持つ非線形変換を行う構成である。それらのｓビット単位の非線形変換実行部をＳボックス（Ｓ－ｂｏｘ）と呼ぶ。Ｓボックス（Ｓ－ｂｏｘ）の例を図９に示す。
　図９に示す例は、ｍｓビットからなる入力データを、ｍ個のｓビットデータに分割し、各分割データを、各々ｓビットの非線形変換処理を実行するｍ個のＳボックスに入力して、各Ｓボックスの出力を連結してｍｓビットの非線形変換結果を得る構成である。
　　（１－６．線形変換部）
　線形変換部はその性質上、行列として定義することが可能である。行列の要素は拡大体ＧＦ（２８）の体の要素やＧＦ（２）の要素など、一般的にはさまざまな表現ができる。図１０にｍｓビット入出力をもち、ＧＦ（２ｓ）の上で定義されるｍ×ｍの行列により定義される線形変換部の例を示す。
　　（１－７．ステートを用いたデータ表現）
　各データ（平文、暗号文、鍵など）を表現する際に、データをｍ行（ｒｏｗ）、ｎ列（ｃｏｌｕｍｎ）のマトリックス型としたｍ×ｎ配列データとして表現することがある。このｍ×ｎ配列によって表現されたデータをステート（ｓｔａｔｅ）、あるいはステート表現データと呼ぶ。
　図１１には、入力データをＡ、入力データＡに対するデータ変換後の出力データをＢとして、入力データＡ、出力データＢをそれぞれｍ×ｎ配列を持つステートとして表現した例を示している。
　入力データＡは、拡大体ＧＦ（２ｓ）ｍｎの要素であり、
　入力データＡ＝（ａ０ａ１ａ２・・・ａｍｎ－２ａｍｎ－１）である。
　なお、ａ０はＭＳＢ、ａｍｎ－１はＬＳＢ側のビットデータである。
　同様に、出力データＢも、拡大体ＧＦ（２ｓ）ｍｎの要素であり、
　出力データＢ＝（ｂ０ｂ１ｂ２・・・ｂｍｎ－２ｂｍｎ－１）である。
　なお、ｂ０はＭＳＢ、ｂｍｎ－１はＬＳＢ側のビットデータである。
　図に示すように、ｍ×ｎ配列のステートにはｍ×ｎ個の要素が含まれる。
　例えば図１１に示すステートＡにはａ０～ａｎｍ－１のｍｎ個の要素が含まれる。ステートＢの要素は、ｂ０～ｂｎｍ－１のｍｎ個の要素である。
　これらのｍｎ個の要素の各々は、それぞれｓ（ｓ＝１以上）ビットデータからなる。具体的には、各要素は、例えば各々４ビットデータ、８ビット（１バイト）データ等のビットデータである。
　なお、以下の実施例では、各要素を４ビットデータとした実施例について説明するが、本開示の処理は、４ビット要素データ以外の構成に対しても適用可能である。
　図１２に４×４ステートに含まれる１６個の要素の各要素を４ビットデータとした場合の４×４ステートの例を示す。
　図１２に示す例も図１１と同様、入力データをＡ、何らかのデータ変換後の出力データをＢとしている。
　入力データＡは、拡大体ＧＦ（２４）４×４の要素であり、
　入力データＡ＝（ａ０ａ１ａ２・・・ａ１４ａ１５）である。
　なお、ａ０はＭＳＢ、ａ１５はＬＳＢ側のビットデータである。
　同様に、出力データＢも、拡大体ＧＦ（２４）４×４の要素であり、
　出力データＢ＝（ｂ０ｂ１ｂ２・・・ｂ１４ｂ１５）である。
　なお、ｂ０はＭＳＢ、ｂ１５はＬＳＢ側のビットデータである。
　図１２に示す例は、入力データＡ、出力データＢが各要素が４ビットデータからなる４×４配列を持つステートとして表現した例である。
　例えば図１２に示すステートＡにはａ０～ａ１５の１６個の要素が含まれ、これらの各要素は各々が４ビットデータである。
　すなわち、６４ビットの入力データＡをステートとして示すと、図１２に示す各要素が４ビットデータからなる４×４配列を持つステートＡとして表現できる。
　同様に、図１２に示すステートＢにはｂ０～ｂ１５の１６個の要素が含まれ、これらの各要素も各々が４ビットデータである。
　すなわち、６４ビットの出力データＢをステートとして示すと、図１２に示す各要素が４ビットデータからなる４×４配列を持つステートＢとして表現できる。
　　（１－８．ステート表現データに対する基本的演算）
　次に、ステート（ステート表現データ）に対する演算処理について説明する。
　（１）非線形変換処理（Ｓ）
　例えば、ステートの各要素４ビット単位で非線形変換を行う複数のＳボックスを適用して非線形変換処理を実行する。
　図１３（１）に示すように、入力ステートＡに対する非線形変換処理によって、ステートＢが生成されるとする。
　この場合の各要素４ビット単位の出力ｂｉと入力ａｉの関係は、
　ｂｉ＝Ｓ（ａｉ）
　ｉ＝０，1，・・・，１５、
　である。
　（２）線形変換処理（Ｐ）
　図１３（２）に示すように、入力ステートＡに対する線形変換処理によって、ステートＢが生成されるとする。
　４×４ステートに対する線形変換処理は、例えば４×４ステートの行ごとの４つのデータをベクトルとみなし４×４の行列［Ｍ］による演算を施して値を更新する演算として実行する。これを行拡散演算と呼ぶ。
　変換処理後のステート各要素４ビット単位の出力ｂｉと入力ａｉの関係は、
　ｔ（ｂｉ，ｂｉ＋４，ｂｉ＋８，ｂｉ＋１２）＝Ｍ×ｔ（ａｉ，ａｉ＋４，ａｉ＋８，ａｉ＋１２）
　ｉ＝０，１，２，３、
　である。なお、ｔXは、Xの転置行列を示している。線形変換処理としては、このような行拡散演算の他、列拡散演算や、ビット置換など、様々な処理方法がある。
　（３）排他的論理和演算（鍵適用演算処理（Ｋ））
　図１４に示すように、入力ステートＡに対する排他的論理和演算処理によって、ステートＢが生成されるとする。
　例えば鍵スケジュール部から出力されたラウンド鍵Ｋと入力データＡとの排他的論理和演算により、出力データＢを算出する演算である。入力データＡ、ラウンド鍵Ｋ、出力データＢのいずれも、１６個の４ビット要素からなるステート表現された６４ビットデータである。
　変換処理後のステート各要素４ビット単位の出力ｂｉと入力ａｉ、ラウンド鍵ｋｉとの関係は、
　ｂｉ＝ａｉ（ＸＯＲ）ｋｉ
　ｉ＝０，1，・・・，１５、
　である。なお、上記式において（ＸＯＲ）は排他的論理和演算を示している。
　上記の各演算（１）～（３）を所定シーケンスで順次実行する演算の組み合わせによって、１つのラウンド演算が設定される。入力データに対して、ラウンド演算を繰り返し実行し出力データ、例えば暗号化データを生成して出力する。
　なお、基本的なラウンド演算は、ラウンド鍵との排他的論理和演算と、線形変換処理と、非線形変換処理を各々１回ずつ実行するものとして設定される。ただし、暗号処理シーケンスにおいて実行されるラウンド演算の中には、変則的なラウンド演算構成も設定可能である。例えばラウンド鍵との排他的論理和演算を複数回含むラウンド演算や、線形変化処理を省略した構成など、他のラウンド演算とは異なるラウンド演算を設定することも可能である。
　また、暗号処理シーケンスの最初や最後にラウンド鍵との演算のみを実行する構成も多く利用されている。この処理は鍵ホワイトニング処理と呼ばれ、一般的にはラウンド数としてはカウントしない。
　　（１－９．ステート表現データに対する列拡散演算）
　次にｍ×ｎのマトリクス配列として示されたステート表現データに対する列拡散演算処理について、図１５、図１６を参照して説明する。
　Ｘ０，Ｘ１，・・・，Ｘｎ－１の各々を、各要素がＧＦ（２ｓ）上の要素からなるｍ×ｍ行列とする。
　図１５に示すように、
　ＭＣ［Ｘ０，Ｘ１，・・・，Ｘｎ－１］
　上記演算を、ステート表現データの要素に対して、ステートの各列（０～ｎ－１）の要素と、各列対応の行列Ｘ０，Ｘ１，・・・，Ｘｎ－１を適用した行列演算を列拡散演算と定義する。
　なお、ＭＣは、列（Ｃｏｌｕｍｎ）単位の拡散（Ｍｉｘ）、すなわち（ＭｉｘＣｏｌｕｍｎ）を意味する。
　列拡散演算では、ステートの１つの列の要素に対して１つの行列Ｘｋを適用した行列演算を行う。
　なお、ステートを構成する複数の列各々に対して適用する行列Ｘｋは、同じ行列とする設定と、異なる行列とする設定とのいずれの設定も可能である。
　例えば、入力データであるステートＡに対して、列拡散演算を実行して出力データであるステートＢを算出する演算式は、以下のように表現できる。
　Ｂ＝ＭＣ［Ｘ０，Ｘ１，・・・，Ｘｎ－１］（Ａ）
　この列拡散演算処理は、図１５の下段に示すように、以下の式によって示される処理である。
　すなわち、上記演算式によって算出されるステートＢの要素は、以下の通りである。
　ｔ（ｂ０ｂ１・・・ｂｍ－１）＝Ｘ０×ｔ（ａ０ａ１・・・ａｍ－１）、
　ｔ（ｂｍｂｍ＋１・・・ｂ２ｍ－１）＝Ｘ１×ｔ（ａｍａｍ＋１・・・ａ２ｍ－１）、
　　　・・・
　ｔ（ｂ（ｎ－１）ｍｂ（ｎ－１）ｍ＋１・・・ｂｎｍ－１）＝Ｘｎ－１×ｔ（ａ（ｎ－１）ｍａ（ｎ－１）ｍ＋１・・・ａｎｍ－１）、
　なお、上記式においてｔ（ｂ１ｂ２・・・ｂｋ）は、（ｂ１ｂ２・・・ｂｋ）の転置行列を示す。
　実際のステートＡ，Ｂの要素配列に従って上記演算式を示すと、図１５の下段に示すように以下の演算式となる。
Figure JPOXMLDOC01-appb-M000001
　図１６は、
　入力データＡを６４ビットデータとしてステートＡを１６個の４ビットデータ要素からなるステートＡとし、
　出力データＢも６４ビットデータとして、ステートＢを１６個の４ビットデータ要素からなるステートＢとした場合の、
　列拡散演算：ＭＣ［Ｘ０，Ｘ１，Ｘ２，Ｘ３］
　の適用処理例を示した図である。
　すなわち、図１５を参照して説明したと同様、
　Ｂ＝ＭＣ［Ｘ０，Ｘ１，Ｘ２，Ｘ３］（Ａ）
　上記列拡散演算処理によりステートＢの各要素の算出処理例を示している。
　すなわち、上記演算式によって算出されるステートＢの要素は、以下の通りである。
　ｔ（ｂ０ｂ１ｂ２ｂ３）＝Ｘ０×ｔ（ａ０ａ１ａ２ａ３）、
　ｔ（ｂ４ｂ５ｂ６ｂ７）＝Ｘ１×ｔ（ａ４ａ５ａ６ａ７）、
　ｔ（ｂ８ｂ９ｂ１０ｂ１１）＝Ｘ２×ｔ（ａ８ａ９ａ１０ａ１１）、
　ｔ（ｂ１２ｂ１３ｂ１４ｂ１５）＝Ｘ３×ｔ（ａ１２ａ１３ａ１４ａ１５）、
　実際のステートＡ，Ｂの要素配列に従って上記演算式を示すと、図１６の下段に示すように、以下の演算式となる。
Figure JPOXMLDOC01-appb-M000002
　なお、ステートの各列要素に対して同じ行列Ｘを適用した行列演算行う場合、
　ＭＣ［Ｘ］
　と表現することもある。
　つまり、ＭＣ［Ｘ］とＭＣ［Ｘ，Ｘ，・・・，Ｘ］は同じ演算である。
　　（１－１０．ステート表現データに対する行拡散演算）
　次にｍ×ｎのマトリクス配列として示されたステート表現データに対する行拡散演算処理について、図１７、図１８を参照して説明する。
　Ｘ０，Ｘ１，・・・，Ｘｍ－１の各々を、各要素がＧＦ（２ｓ）上の要素からなるｎ×ｎ行列とする。
　図１７に示すように、
　ＭＲ［Ｘ０，Ｘ１，・・・，Ｘｍ－１］
　上記演算を、ステート表現データの要素に対して、ステートの各行（０～ｎ－１）の要素と、各行対応の行列Ｘ０，Ｘ１，・・・，Ｘｍ－１を適用した行列演算を行拡散演算と定義する。
　なお、ＭＲは、行（Ｒｏｗ）単位の拡散（Ｍｉｘ）、すなわち（ＭｉｘＲｏｗ）を意味する。
　行拡散演算では、ステートの１つの行の要素に対して１つの行列Ｘｋを適用した行列演算を行う。
　なお、ステートを構成する複数の行各々に対して適用する行列Ｘｋは、同じ行列とする設定と、異なる行列とする設定とのいずれの設定も可能である。
　例えば、入力データであるステートＡに対して、行拡散演算を実行して出力データであるステートＢを算出する演算式は、以下のように表現できる。
　Ｂ＝ＭＲ［Ｘ０，Ｘ１，・・・，Ｘｍ－１］（Ａ）
　この行拡散演算処理は、図１７の下段に示す処理である。
　すなわち、上記演算式によって算出されるステートＢの要素は、以下の通りである。
　ｔ（ｂ０ｂｍ・・・ｂ（ｎ－１）ｍ）＝Ｘ０×ｔ（ａ０ａｍ・・・ａ（ｎ－１）ｍ）、
　ｔ（ｂ１ｂｍ＋１・・・ｂ（ｎ－１）ｍ＋１）＝Ｘ１×ｔ（ａ１ａｍ＋１・・・ａ（ｎ－１）ｍ＋１）、
　　　・・・
　ｔ（ｂｍ－１ｂ２ｍ－１・・・ｂｎｍ－１）＝Ｘｍ－１×ｔ（ａｍ－１ａ２ｍ－１・・・ａｎｍ－１）、
　なお、上記式においてｔ（ｂ１ｂ２・・・ｂｋ）は、（ｂ１ｂ２・・・ｂｋ）の転置行列であることを示す。
　実際のステートＡ，Ｂの要素配列に従って上記演算式を示すと、図１７の下段に示すように、以下の演算式となる。
Figure JPOXMLDOC01-appb-M000003
　図１８は、
　入力データＡを６４ビットデータとしてステートＡを１６個の４ビットデータ要素からなるステートＡとし、
　出力データＢも６４ビットデータとして、ステートＢを１６個の４ビットデータ要素からなるステートＢとした場合の、
　行拡散演算：ＭＲ［Ｘ０，Ｘ１，Ｘ２，Ｘ３］
　の適用処理例を示した図である。
　すなわち、図１７を参照して説明したと同様、
　Ｂ＝ＭＲ［Ｘ０，Ｘ１，Ｘ２，Ｘ３］（Ａ）
　上記行拡散演算処理によりステートＢの各要素の算出処理例を示している。
　すなわち、上記演算式によって算出されるステートＢの要素は、以下の通りである。
　ｔ（ｂ０ｂ４ｂ８ｂ１２）＝Ｘ０×ｔ（ａ０ａ４ａ８ａ１２）、
　ｔ（ｂ１ｂ５ｂ９ｂ１３）＝Ｘ１×ｔ（ａ１ａ５ａ９ａ１３）、
　ｔ（ｂ２ｂ６ｂ１０ｂ１４）＝Ｘ２×ｔ（ａ２ａ６ａ１０ａ１４）、
　ｔ（ｂ３ｂ７ｂ１１ｂ１５）＝Ｘ３×ｔ（ａ３ａ７ａ１１ａ１５）、
　実際のステートＡ，Ｂの要素配列に従って上記演算式を示すと、図１８の下段に示すように、以下の演算式となる。
Figure JPOXMLDOC01-appb-M000004
　なお、ステートの各行要素に対して同じ行列Ｘを適用した行列演算行う場合、
　ＭＲ［Ｘ］
　と表現することもある。
　つまり、ＭＲ［Ｘ］とＭＲ［Ｘ，Ｘ，・・・，Ｘ］は同じ演算である。
　　（１－１１．インボリューション性について）
　平文Ｐから暗号文Ｃを生成する共通鍵ブロック暗号において、各ラウンドに適用するラウンド鍵をＫ１，Ｋ２，・・・，ＫＲとしたとき、
　平文Ｐから、暗号文Ｃを算出する暗号化関数Ｅは、以下のように示すことができる。
　Ｃ＝Ｅ（Ｐ，Ｋ１，Ｋ２，・・・，ＫＲ）
　このとき、暗号文Ｃから平文Ｐを算出する復号関数Ｄは、
　Ｐ＝Ｄ（Ｃ，ｋ１，ｋ２，・・・ｋｒ）
　となるが、
　上記の復号関数Ｄが、以下を満たすとき、
　Ｄ（Ｃ，ｋ１，ｋ２，・・・ｋｒ）＝Ｅ（Ｃ，ＫＲ，・・・，Ｋ２，Ｋ１）
　すなわち、復号関数Ｄが、暗号化関数Ｅにおけるラウンド鍵の適用順を逆順にするのみで、他は、同一関数を利用できる構成である場合、
　この共通鍵ブロック暗号はインボリューション性を持つという。
　このように、暗号化関数Ｅを用い，そのラウンド鍵の入力順を変更するのみで，復号関数Ｄが構成できるような共通鍵ブロック暗号はインボリューション性を持つといえる。例えば，Ｆｅｉｓｔｅｌ型共通鍵ブロック暗号は、通常、使用するラウンド鍵の使用順序を逆にするだけで暗号化関数と復号関数が同じ回路で行えることが知られており、インボリューション性を持つといえる。
　インボリューション性を持つ共通鍵ブロック暗号は、基本的には暗号化関数を実装するのみで、暗号化機能と復号機能を実現できるため、必要な回路が少なく、軽量化（小型化）が可能であり、実装効率が高くなる。
　　［２．共通鍵ブロック暗号における安全性の指標について］
　共通鍵ブロック暗号に対する攻撃、例えば秘密鍵の解読等を目的とした様々な攻撃が知られている。具体的には、差分攻撃、線形攻撃などがある。
　差分攻撃は、暗号装置に対して特定の差分を持つデータを入力し、出力から入力差分を反映するデータを検出して鍵の推定を行なおうとする攻撃である。なお、差分値の伝播確率を差分確率と呼ぶ。
　線形攻撃は、入力の特定ビットの排他的論理和と出力の特定ビットの排他的論理和の間の相関を観測して、強い相関関係が見つけることで、鍵の推定を行なおうとする攻撃である。なお、入出力の特定ビットの相関係数を線形確率と呼ぶ。
　安全性の高い暗号とは、上記のような各種の攻撃に対する耐性が高い暗号、すなわち暗号処理に適用される秘密情報、例えば鍵等の解読困難性の高い暗号である。
　以下、暗号アルゴリズムの安全性指標となる複数のデータについて説明する。
　　（２－１．分岐数について）
　共通鍵ブロック暗号においては、例えば、上述した線形変換、非線形変換、あるいは排他的論理和演算など、様々なデータ変換が実行される。
　このようなデータ変換の解読困難性に関する安全性指標として分岐数がある。
　例えば、ｎ×ａビットデータからｎ×ｂビットデータへの写像θを、
　θ：｛０，１｝ｎａ→｛０，１｝ｎｂ
　とする。
　上記の写像θに対して分岐数（Ｂｒａｎｃｈｎ（θ））を次のように定義する。
　Ｂｒａｎｃｈｎ（θ）＝ｍｉｎα≠０｛ｈｗｎ（α）＋ｈｗｎ（θ（α））｝
　ただし、
　ｍｉｎα≠０｛Ｘα｝は，α≠０を満たすすべてのＸαのうちの最小値を表し、
　ｈｗｎ（Ｙ）はビット列Ｙをｎビット毎に区切って表したときに、ｎビットのデータ全てが０ではない（非ゼロ）要素の数を返す関数とする。
　一般的に、分岐数が高いほど解読困難性が高くなり、差分攻撃や線形攻撃に対する耐性が向上すると言われる。
　なお、分岐数Ｂｒａｎｃｈｎ（θ）がｂ＋１であるような写像θは、最適拡散変換（Ｏｐｔｉｍａｌ　Ｄｉｆｆｕｓｉｏｎ　Ｍａｐｐｉｎｇｓ）と呼ばれる。
　分岐数の高い線形変換用の行列として、例えば、最適拡散変換を実行するＭＤＳ（Ｍａｘｉｍｕｍ　Ｄｉｓｔａｎｃｅ　Ｓｅｐａｒａｂｌｅ）行列がある。ＭＤＳ行列は、行列を構成する任意の小行列が正則行列となる行列である。なお、正則行列は、逆行列を持つ行列であり、行列をＡとし、逆行列をＡ－１とすると、
　ＡＡ－１＝Ａ－１Ａ＝Ｅ、
　ただしＥは単位行列、
　上記式が成立する逆行列Ａ－１を持つ行列Ａが正則行列である。
　　（２－２．最小差分アクティブＳ－ｂｏｘ数について）
　前述したように共通鍵ブロック暗号に設定される非線形変換部には、ｓビット単位の非線形変換を実行するＳボックス（Ｓ－ｂｏｘ）が用いられる。
　差分攻撃に対する耐性を図る指標として，差分の接続関係を表現した差分パスに含まれる差分アクティブＳ－ｂｏｘの最小数、すなわち、最小差分アクティブＳ－ｂｏｘ数がある。
　差分パスとは、暗号化関数中の鍵データを除くすべてのデータ部分に対して特定の差分値を指定したものである。差分値は自由に決められるものではなく変換処理の前後の差分値は互いに関連しあっている。線形変換処理の前後では、入力差分と出力差分の関係は一対一に決定される。非線形変換の前後では、入力差分と出力差分の関係は一対一にはきまらないが、確率という概念が導入される。ある入力差分と出力差分に対する確率は事前に計算することができるものとする。すべての出力に対する確率をすべて足し合わせると１となっている。
　一般的な暗号（ブロック暗号など）において、非線形変換はＳ－ｂｏｘによる処理の部分のみである。したがって、この場合、０以外の確率をもつ差分パスとは、平文（入力）に対する差分値から始まって暗号文（出力）の差分値までに至る差分データの集合であり、すべてのＳ－ｂｏｘの前後で与えられる差分値は０以外の確率をもつものである。０以外の確率をもつある差分パスのＳ－ｂｏｘに入力される差分値が０でないものを差分アクティブＳ－ｂｏｘと呼ぶものとする。０以外の確率を持つすべての差分パスの差分アクティブＳ－ｂｏｘ数のうちで最も少ない数を最小差分アクティブＳ－ｂｏｘ数とよび、この数値が差分攻撃に対する安全性指標としてよく知られている。
　一般的には、最小差分アクティブＳ－ｂｏｘ数が十分大きくなることを保証することで差分攻撃に対する安全性を示すことが可能であり、少ないラウンド関数の繰り返し回数でより多くの最小差分アクティブＳ－ｂｏｘ数を保証できるような暗号は、より性能の高い暗号と考えることができる。なお、すべての差分値が０であるような差分パスは、確率が１となり攻撃として意味をなさない。
　　（２－３．最小線形アクティブＳボックス（Ｓ－ｂｏｘ）数について）
　線形攻撃に対する耐性を示す指標の一つとして、線形マスクの接続関係を表現した線形パスに含まれる線形アクティブＳボックス（Ｓ－ｂｏｘ）の最小数が挙げられる。
　なお、線形パスは、線形近似と呼ばれることも多いが、差分と対応させるためここではパスという言葉を用いる。
　線形パスとは、暗号化関数中の鍵データを除くすべてのデータ部分に対して特定の線形マスク値を指定したものである。線形マスク値は自由に決められるものではなく変換処理の前後の線形マスク値は互いに関連しあっている。線形変換処理の前後では、入力線形マスク値と出力線形マスク値の関係は一対一に決定される。非線形変換の前後では、入力線形マスク値と出力線形マスク値の関係は一対一には決まらないが、確率という概念が導入される。入力線形マスク値に対して、出力されうる一つ以上の線形マスク値の集合が存在し、それぞれが出力される確率を事前に計算することができる。すべての出力に対する確率をすべて足し合わせると１となっている。
　一般的な暗号（ブロック暗号など）では、非線形変換はＳボックス（Ｓ－ｂｏｘ）による処理の部分のみである。したがって、この場合、０以外の確率を持つ線形パスとは平文（入力）に対する線形マスク値から始まって暗号文（出力）の線形マスク値までに至る線形マスク値データの集合であり、すべてのＳボックス（Ｓ－ｂｏｘ）の前後で与えられる線形マスク値は０以外の確率を持つものである。０以外の確率をもつある線形パスのＳボックス（Ｓ－ｂｏｘ）に入力される線形マスク値が０でないものを線形アクティブＳボックス（Ｓ－ｂｏｘ）と呼ぶものとする。０以外の確率を持つすべての線形パスのアクティブＳボックス（Ｓ－ｂｏｘ）数のうちで最も少ない数を最小線形アクティブＳボックス（Ｓ－ｂｏｘ）数とよび、この数値が線形攻撃に対する安全性指標としてよく知られている。
　一般的には、最小線形アクティブＳボックス（Ｓ－ｂｏｘ）数が十分大きくなることを保証することで線形攻撃に対する安全性を示すことが可能であり、少ないラウンド関数の繰り返し回数でより多くの最小線形アクティブＳボックス（Ｓ－ｂｏｘ）数を保証できるような暗号は、より性能の高い暗号と考えることができる。なお、すべての線形マスク値が０であるような線形パスは、確率が１となり攻撃として意味をなさない。
　　［３．安全性を高めた共通鍵暗号処理の全体構成概要について］
　次に、安全性を高めた本開示の共通鍵暗号処理装置の構成と処理について説明する。
　以下に説明する本開示の暗号処理装置は、共通鍵ブロック暗号（ブロック暗号）を実行する装置であり、ＳＰＮ（Ｓｕｂｓｔｉｔｕｔｉｏｎ－Ｐｅｒｍｕｔａｔｉｏｎ　Ｎｅｔｗｏｒｋ）構造ラウンド関数を有する装置である。
　ｎビットの入力データすべてに対して、ラウンド鍵との排他的論理和演算、非線形変換、線形変換処理を、複数ラウンド繰り返し実行する構成である。
　本開示の共通鍵暗号処理装置の１つの具体的構成例を、図１９に示す。
　図１９に示すように、暗号処理装置１００は、鍵スケジュール部１１０と、暗号処理部１２０を有する。
　鍵スケジュール部１１０は、秘密鍵Ｋを入力とし、所定の鍵生成アルゴリズムに従って、暗号処理部１２０の各ラウンドで適用するラウンド鍵を出力する。暗号処理部１２０は、鍵スケジュール部１１０からラウンド鍵を入力して平文Ｐのデータ変換を行い暗号文Ｃを出力する。
　なお、暗号処理部１２０は、暗号文Ｃを入力して平文Ｐを出力する復号処理も実行可能である。復号処理を実行する際は、鍵スケジュール部１１０から供給されるラウンド鍵を暗号化処理とは逆順に適用した処理を実行する。
　暗号処理部１２０は、
　入力データと、ラウンド鍵との排他的論理和演算を実行する排他的論理和部１２１、
　入力データに対して非線形変換処理を実行する非線形変換部１２２、
　入力データに対して線形変換処理を実行する線形変換部１２３、
　を有する。
　図に示すように、本開示の暗号処理装置１００の暗号処理部１２０は、排他的論理和部１２１、非線形変換部１２２、線形変換部１２３、これら３つの異なるデータ変換処理を繰り返し実行する構成を有する。
　なお、入力データとしての平文Ｐ、出力データとしての暗号文Ｃは、図２０に示すように、前述したステート表現データであり、各要素の各々を４ビットデータとして、４×４の１６要素によって構成される６４ビットデータである。
　なお、鍵スケジュール部１１０から入力するラウンド鍵も、１６個の４ビットデータ要素からなるステート表現された６４ビットデータである。
　暗号処理部１２０では、図２１に示すように、以下の３種類のデータ変換処理が繰り返し実行される。
　（ａ）排他的論理和演算処理
　（ｂ）非線形変換処理
　（ｃ）線形変換処理
　これらの各処理をステートに対する処理として実行する。ステートに対するこれらの処理については、図１３、図１４を参照して説明した通りである。
　暗号処理部１２０の非線形変換部において実行する非線形変換処理は、例えば図２２（１）に示すように、複数のＳボックス（Ｓ－ｂｏｘ）を利用して実行される。
　各Ｓボックスは例えば、４ビット入出力構成を持つ非線形変換部であり、１６個のＳボックスによる並列処理によって４×１６＝６４ビットの非線形変換処理を実行する。
　また、暗号処理部１２０の線形変換部において実行する線形変換処理は、例えば図２２（２）に示すように、行列演算処理として実行する。
　　［４．暗号処理部の線形変換部の構成と処理について］
　図１９を参照して説明したように、本開示の暗号処理装置１００の暗号処理部１２０は、ラウンド鍵との排他的論理和演算、非線形変換、線形変換処理を複数ラウンド繰り返し実行する構成を持つ。
　本開示の暗号処理装置の特徴の１つは、各ラウンドにおいて実行する線形変換処理をラウンド毎に異なる処理として実行する構成としたことにある。
　以下、本開示の暗号処理装置の実行する線形変換処理の詳細について説明する。
　図２３は、本開示の暗号処理装置の暗号処理部に構成する異なる線形変換部の構成例について説明する図である。
　なお、図２３の構成図は、排他的論理和部は省略して示した構成図である。
　図２３に示す例では、３つの異なる線形変換処理を実行する線形変換部を有する構成としている。すなわち、
　線形変換部Ｐ１，２０１、
　線形変換部Ｐ２，２０２、
　線形変換部Ｐ３，２０３、
　これらの３つの異なる線形変換部を有し、これら３種類の異なる線形変換処理のいずれかを各ラウンドにおいて実行する構成とし、連続ラウンドでは同じ線形変更処理を続けることなく、異なる線形変換処理を行なう設定としたことにある。
　図２３に示す例では、
　平文Ｐの入力側から順に、
　線形変換部Ｐ１，
　線形変換部Ｐ２，
　線形変換部Ｐ１，
　線形変換部Ｐ３，
　線形変換部Ｐ１，
　上記シーケンスで、５回の線形変換処理を行なう。
　この５回の線形変換処理において、連続ラウンドでは同じ線形変更処理を続けることなく、ラウンド切り替えに応じて、異なる線形変換処理を実行する。
　上記の例では、３種類の異なる線形変換Ｐ１，Ｐ２，Ｐ３を組み合わせて実行することで、連続するラウンドにおいては同じ線形変換を実行しない設定としている。
　このように、暗号処理において、ラウンド遷移に応じて線形変換態様を変更することで、最小差分アクティブＳボックス、および最小線形アクティブＳボックスの数を増加させることが可能となり、差分攻撃や線形攻撃に対する耐性を向上させることができる。
　３種類の線形変換処理の具体的な処理について、図２４以下を参照して説明する。
　線形変換処理Ｐ１～Ｐ３には、図２４（１）に示す４つの異なる行列Ｍ０～Ｍ３を組み合わせて利用する。すなわち、以下に示す４×４の行列（Ｍａｔｒｉｘ）Ｍ０～Ｍ３を組み合わせて構成する。
Figure JPOXMLDOC01-appb-M000005
　線形変換処理Ｐ１～Ｐ３には、上記の４つの異なる行列Ｍ０～Ｍ３を組み合わせて利用する。
　なお、上記の４つの行列は、前述したＭＤＳ（Ｍａｘｉｍｕｍ　Ｄｉｓｔａｎｃｅ　Ｓｅｐａｒａｂｌｅ）行列ではないｎｏｎ－ＭＤＳ行列である。
　以下に説明する実施例では、ｎｏｎ－ＭＤＳ行列を利用した線形変換処理例について説明するが、ＭＤＳ行列を適用した構成としてもよい。
　図２４（２）は、線形変換処理Ｐ１～Ｐ３の具体的な行列演算の態様を説明する図である。
　図２４（２）に示す４×４の矩形は、線形変換処理対象となる各要素４ビットの１６個の要素からなるステートを示している。すなわち６４ビットの４×４ステートである。
　この４×４ステートの入力データに対して、行列Ｍ０～Ｍ３を組み合わせて利用した行列演算を実行する。
　線形変換処理Ｐ１は、
　４×４ステートの入力データの各列の要素に対して、各列単位で、１つの行列Ｍ０を適用した行列演算を行う。
　これは、先に、図１５、図１６を参照して説明した列拡散演算（ＭｉｘＣｏｌｕｍ）である。
　すなわち、線形変換処理Ｐ１は、
　ＭＣ［Ｍ０］
　上記式によって示される列拡散演算（ＭＣ）である。
　なお、ＭＣ［Ｍ０］は、ステートの各列に対して、同一の行列Ｍ０を適用した行列演算を示す式であり、ステートの各列に対して適用する行列を個別に示した式、
　ＭＣ［Ｍ０，Ｍ０，Ｍ０，Ｍ０］
　上記式と同じ意味である。
　次に、線形変換処理Ｐ２について説明する。
　線形変換処理Ｐ２は、図２４（２）に示すように、４×４ステートの入力データの各行の要素に対して、各行単位で異なる行列を適用した行列演算を行う。上位の第１行から第４行に対して、以下の行列を適用した行列演算を実行する。
　第１行：適用行列Ｍ０、
　第２行：適用行列Ｍ１、
　第３行：適用行列Ｍ２、
　第４行：適用行列Ｍ３、
　これは、先に、図１７、図１８を参照して説明した行拡散演算（ＭｉｘＲｏｗ）である。
　すなわち、線形変換処理Ｐ２は、
　ＭＲ［Ｍ０，Ｍ１，Ｍ２，Ｍ３］
　上記式によって示される行拡散演算（ＭｉｘＲｏｗ）である。
　次に、線形変換処理Ｐ３について説明する。
　線形変換処理Ｐ３も、線形変換処理Ｐ２と同様、図２４（２）に示すように、４×４ステートの入力データの各行の要素に対して、各行単位で異なる行列を適用した行列演算を行う。線形変換処理Ｐ３は、線形変換処理Ｐ２とは異なり、上位の第１行から第４行に対して、以下の行列を適用した行列演算を実行する。
　第１行：適用行列Ｍ２、
　第２行：適用行列Ｍ０、
　第３行：適用行列Ｍ１、
　第４行：適用行列Ｍ３、
　これは、先に、図１７、図１８を参照して説明した行拡散演算（ＭｉｘＲｏｗ）である。
　すなわち、線形変換処理Ｐ３は、
　ＭＲ［Ｍ２，Ｍ０，Ｍ１，Ｍ３］
　上記式によって示される行拡散演算（ＭｉｘＲｏｗ）である。
　なお、以下では、線形変換処理Ｐ２と、Ｐ３を区別するため、
　線形変換処理Ｐ２を行拡散演算タイプ１（ＭｉｘＲｏｗ１）、
　線形変換処理Ｐ３を行拡散演算タイプ２（ＭｉｘＲｏｗ２）、
　と呼ぶ。
　線形変換処理Ｐ１は、列拡散演算（ＭｉｘＣｏｌｕｍｎ）である。
　これら３つの線形変換処理Ｐ１～Ｐ３の具体的な行列演算の計算処理例について、図２５以下を参照して説明する。
　図２５は、線形変換処理Ｐ１、すなわち列拡散演算（ＭｉｘＣｏｌｕｍｎ）の具体的な計算処理例を説明する図である。
　図２５（１）には。線形変換部Ｐ１に対する入出力データの例を示している。
　入力Ａはｎビットデータの１６個の要素ａ０～ａ１５からなるステートである。
　出力Ｂもｎビットデータの１６個の要素ｂ０～ｂ１５からなるステートである。
　なお、入出力データの各要素ａｉ，ｂｉ（ただしｉ＝０～１５）は、０，１のいずれかの値から構成されるｎビットデータである。
　なお、本実施例では、ｎ＝４であり、各要素は４ビットデータあり、入力Ａ、出力Ｂとも６４ビットである。
　図２５（２）には、線形変換処理Ｐ１、すなわち列拡散演算（ＭｉｘＣｏｌｕｍｎ）の具体的な計算処理例を示している。
　線形変換処理Ｐ１として行われる列拡散演算（ＭｉｘＣｏｌｕｍｎ）は、以下の式に従った行列演算である。
Figure JPOXMLDOC01-appb-M000006
　出力Ｂの１６個の要素ｂ０～ｂ１５は、行列Ｍ０と、入力Ａの１６個の要素ａ０～ａ１５に基づいて以下の演算によって算出される。
　ｂ０＝ａ１（＋）ａ２（＋）ａ３，
　ｂ１＝ａ０（＋）ａ２（＋）ａ３，
　ｂ２＝ａ０（＋）ａ１（＋）ａ３，
　ｂ３＝ａ０（＋）ａ１（＋）ａ２，
　ｂ４＝ａ５（＋）ａ６（＋）ａ７，
　ｂ５＝ａ４（＋）ａ６（＋）ａ７，
　ｂ６＝ａ４（＋）ａ５（＋）ａ７，
　ｂ７＝ａ４（＋）ａ５（＋）ａ６，
　ｂ８＝ａ９（＋）ａ１０（＋）ａ１１，
　ｂ９＝ａ８（＋）ａ１０（＋）ａ１１，
　ｂ１０＝ａ８（＋）ａ９（＋）ａ１１，
　ｂ１１＝ａ８（＋）ａ９（＋）ａ１０，
　ｂ１２＝ａ１３（＋）ａ１４（＋）ａ１５，
　ｂ１３＝ａ１２（＋）ａ１４（＋）ａ１５，
　ｂ１４＝ａ１２（＋）ａ１３（＋）ａ１５，
　ｂ１５＝ａ１２（＋）ａ１３（＋）ａ１４
　なお、上記式において、演算子（＋）は、排他的論理和演算を意味する。
　線形変換処理Ｐ１として行われる列拡散演算（ＭｉｘＣｏｌｕｍｎ）は、上記演算処理に従って、行列Ｍ０と、入力Ａの１６個の要素ａ０～ａ１５に基づいて出力Ｂの１６個の要素ｂ０～ｂ１５を算出する。
　図２６は、線形変換処理Ｐ２、すなわち行拡散演算タイプ１（ＭｉｘＲｏｗ１）の具体的な計算処理例を説明する図である。
　図２６（１）には。線形変換部Ｐ２に対する入出力データの例を示している。
　入力Ａはｎビットデータの１６個の要素ａ０～ａ１５からなるステートである。
　出力Ｂもｎビットデータの１６個の要素ｂ０～ｂ１５からなるステートである。
　なお、入出力データの各要素ａｉ，ｂｉ（ただしｉ＝０～１５）は、０，１のいずれかの値から構成されるｎビットデータである。
　なお、本実施例では、ｎ＝４であり、各要素は４ビットデータあり、入力Ａ、出力Ｂとも６４ビットである。
　図２６（２）には、線形変換処理Ｐ２、すなわち行拡散演算タイプ１（ＭｉｘＲｏｗ１）の具体的な計算処理例を示している。
　線形変換処理Ｐ２として行われる行拡散演算タイプ１（ＭｉｘＲｏｗ１）は、以下の式に従った行列演算である。
Figure JPOXMLDOC01-appb-M000007
　出力Ｂの１６個の要素ｂ０～ｂ１５は、行列Ｍ０，Ｍ１，Ｍ２，Ｍ３と、入力Ａの１６個の要素ａ０～ａ１５に基づいて以下の演算によって算出される。
　ｂ０＝ａ４（＋）ａ８（＋）ａ１２，
　ｂ１＝ａ１（＋）ａ５（＋）ａ１３，
　ｂ２＝ａ２（＋）ａ６（＋）ａ１０，
　ｂ３＝ａ３（＋）ａ１１（＋）ａ１５，
　ｂ４＝ａ０（＋）ａ８（＋）ａ１２，
　ｂ５＝ａ１（＋）ａ５（＋）ａ９，
　ｂ６＝ａ２（＋）ａ６（＋）ａ１４，
　ｂ７＝ａ７（＋）ａ１１（＋）ａ１５，
　ｂ８＝ａ０（＋）ａ４（＋）ａ１２，
　ｂ９＝ａ５（＋）ａ９（＋）ａ１３，
　ｂ１０＝ａ２（＋）ａ１０（＋）ａ１４，
　ｂ１１＝ａ３（＋）ａ７（＋）ａ１１，
　ｂ１２＝ａ０（＋）ａ４（＋）ａ８，
　ｂ１３＝ａ１（＋）ａ９（＋）ａ１３，
　ｂ１４＝ａ６（＋）ａ１０（＋）ａ１４，
　ｂ１５＝ａ３（＋）ａ７（＋）ａ１５
　なお、上記式において、演算子（＋）は、排他的論理和演算を意味する。
　線形変換処理Ｐ２として行われる行拡散演算タイプ１（ＭｉｘＲｏｗ１）は、上記演算処理に従って、行列Ｍ０，Ｍ１，Ｍ２，Ｍ３と、入力Ａの１６個の要素ａ０～ａ１５に基づいて出力Ｂの１６個の要素ｂ０～ｂ１５を算出する。
　図２７は、線形変換処理Ｐ３、すなわち行拡散演算タイプ２（ＭｉｘＲｏｗ２）の具体的な計算処理例を説明する図である。
　図２７（１）には。線形変換部Ｐ２に対する入出力データの例を示している。
　入力Ａはｎビットデータの１６個の要素ａ０～ａ１５からなるステートである。
　出力Ｂもｎビットデータの１６個の要素ｂ０～ｂ１５からなるステートである。
　なお、入出力データの各要素ａｉ，ｂｉ（ただしｉ＝０～１５）は、０，１のいずれかの値から構成されるｎビットデータである。
　なお、本実施例では、ｎ＝４であり、各要素は４ビットデータあり、入力Ａ、出力Ｂとも６４ビットである。
　図２７（２）には、線形変換処理Ｐ２、すなわち行拡散演算タイプ２（ＭｉｘＲｏｗ２）の具体的な計算処理例を示している。
　線形変換処理Ｐ３として行われる行拡散演算タイプ２（ＭｉｘＲｏｗ２）は、以下の式に従った行列演算である。
Figure JPOXMLDOC01-appb-M000008
　出力Ｂの１６個の要素ｂ０～ｂ１５は、行列Ｍ０，Ｍ１，Ｍ２，Ｍ３と、入力Ａの１６個の要素ａ０～ａ１５に基づいて以下の演算によって算出される。
　ｂ０＝ａ０（＋）ａ４（＋）ａ８，
　ｂ１＝ａ５（＋）ａ９（＋）ａ１３，
　ｂ２＝ａ２（＋）ａ６（＋）ａ１４，
　ｂ３＝ａ３（＋）ａ１１（＋）ａ１５，
　ｂ４＝ａ０（＋）ａ４（＋）ａ１２，
　ｂ５＝ａ１（＋）ａ９（＋）ａ１３，
　ｂ６＝ａ２（＋）ａ６（＋）ａ１０，
　ｂ７＝ａ７（＋）ａ１１（＋）ａ１５，
　ｂ８＝ａ０（＋）ａ８（＋）ａ１２，
　ｂ９＝ａ１（＋）ａ５（＋）ａ１３，
　ｂ１０＝ａ６（＋）ａ１０（＋）ａ１４，
　ｂ１１＝ａ３（＋）ａ７（＋）ａ１１，
　ｂ１２＝ａ４（＋）ａ８（＋）ａ１２，
　ｂ１３＝ａ１（＋）ａ５（＋）ａ９，
　ｂ１４＝ａ２（＋）ａ１０（＋）ａ１４，
　ｂ１５＝ａ３（＋）ａ７（＋）ａ１５
　なお、上記式において、演算子（＋）は、排他的論理和演算を意味する。
　線形変換処理Ｐ３として行われる行拡散演算タイプ２（ＭｉｘＲｏｗ２）は、上記演算処理に従って、行列Ｍ０，Ｍ１，Ｍ２，Ｍ３と、入力Ａの１６個の要素ａ０～ａ１５に基づいて出力Ｂの１６個の要素ｂ０～ｂ１５を算出する。
　このように、１回の暗号処理シーケンスにおいて実行する複数の線形変換処理をラウンド毎に変更することで、最小差分アクティブＳボックス、および最小線形アクティブＳボックスの数を増加させることが可能となり、差分攻撃や線形攻撃に対する耐性を向上させることができる。
　アクティブＳボックスの数についての検証結果について説明する。
　本開示の暗号処理装置、すなわち、３種類の異なる線形変換処理Ｐ１～Ｐ３を実行する暗号処理装置と、従来型の単一種類の線形変換処理を繰り返し実行する暗号処理装置におけるアクティブＳボックスの数を検証した。
　本開示の暗号処理装置は、図２８に示すように、暗号処理シーケンスにおいて、３種類の線形変換処理を用い、これらをラウンド毎に切り替えて実行する構成である。
　なお、図２８に示す図はラウンド鍵との排他的論理和演算部を省略して示している。
　図２８に示す暗号処理装置は、非線形変換部数＝６であるので６ラウンド構成とする。なお、ラウンド数の定義のしかたは、いくつかの方法があるが、ここでは、非線形変換部の数をラウンド数としている。
　図２８に示す例ではラウンド鍵ＲＫ１～ＲＫ7の7個のラウンド鍵を適用しているが非線形変換部は6層存在するので６ラウンドの暗号処理装置であるとする。
　図２８に示すように、暗号処理過程において、３つの異なる線形変換処理を少なくとも１回実行する。
　線形変換処理Ｐ１は、行列Ｍ０を適用した列拡散演算（ＭｉｘＣｏｌｕｍｎ）である。
　線形変換処理Ｐ２は、行列Ｍ０、Ｍ１、Ｍ２、Ｍ３を適用した行拡散演算タイプ１（ＭｉｘＲｏｗ１）である。
　線形変換処理Ｐ３は、行列Ｍ０、Ｍ１、Ｍ２、Ｍ３を適用した行拡散演算タイプ２（ＭｉｘＲｏｗ２）である。
　図２８に示す暗号処理装置に対して、従来型の単一の線形変換処理を実行する暗号処理装置の例を図２９に示す。
　図２９に示す暗号処理装置も６ラウンド構成であるが、各ラウンドの線形変換処理は同じ線形変換処理を行なう構成である。
　図２９の暗号処理装置の全ての線形変換処理部は、図２８の暗号処理装置でも用いた行列Ｍ０のみを利用した線形変換処理Ｐ１、すなわち、行列Ｍ０を用いた列拡散演算を行う設定とした。
　図２８に示す複数の異なる線形変換処理を実行する暗号処理装置と、図２９に示す単一の線形変換処理を実行する従来型の装置について、様々なラウンド数の装置を構成して、最小差分アクティブＳボックス、および最小線形アクティブＳボックスの数を検証した。
　図２８、図２９の構成とも、６４ビットの入力平文Ｐに対する暗号化処理を実行して６４ビット暗号文Ｃを出力する設定である。
　Ｓボックスは、各非線形変換部に設定されており、各Ｓボックスは、先に図２２を参照して説明したように４ビット入出力の非線形変換を実行する構成である。
　図２８、図２９の暗号処理装置の各非線形変換部には、４ビット入出力Ｓボックスが１６個設けられており、４×１６＝６４ビットデータの非線形変換を実行する。
　図２８、図２９に示す６ラウンド型の暗号処理装置には、６つの非線形変換部が設定されているのまで、Ｓボックスの総数は１６×６＝９６となる。
　この総数９６個のＳボックスのうち、全ての入力パターンにおけるアクティブＳボックスの数をカウントし、最小差分アクティブＳボックス、および最小線形アクティブＳボックスの数を検証した。
　この検証結果を図３０、図３１に示す。
　図３０に示すように、ラウンド数４～２４の異なるラウンド数の暗号処理装置を構成して最小差分／線形差分アクティブＳボックスの数をカウントした結果である。
　ラウンド数＝４では、
　従来型の同一線形変換部を繰り返し実行する構成でも、本開示の異なる線形変換処理を実行する構成でも、アクティブＳボックスの数は４であり、同じ値となるが、ラウンド数＝６～２４の場合(８を除く)は、いずれの場合も、本開示の異なる線形変換処理を実行する構成の方がアクティブＳボックスの数が多くなっている。
　この結果をグラフとして示したのが図３１に示すグラフである。
　なお、上述した実施例では、入力データを各要素が４ビットの４×４個の要素からなるステートとし、線形変換部が４種類の行列Ｍ０，Ｍ１，Ｍ２，Ｍ３を利用した行列演算による線形変換処理を実行する構成について説明したが、上記処理を一般化した構成として説明すると以下のような設定となる。
　入力データを各要素が１ビット以上のｍ×ｎ個の要素からなるステートとした場合、線形変換部は、ステートの各列要素単位で行列を適用して線形変換を行う列拡散演算と、ステートの各行要素単位で行列を適用して線形変換を行う行拡散演算のいずれかの行列演算をラウンド演算において実行する構成となる。
　ここで、線形変換部は、複数種類の行列Ｍ０～Ｍｋ（ｋは１以上の整数）を利用した行列演算による線形変換処理を実行する構成であり、ステートの各列要素単位で行列Ｍ０～Ｍｋから選択した選択行列を特定の順番で各列に適用して線形変換を行う列拡散演算と、ステートの各行要素単位で行列Ｍ０～Ｍｋから選択した選択行列を特定の順番で各行に適用して線形変換を行う行拡散演算をラウンド遷移に応じて切り替えて実行する。
　具体的な線形変換処理構成の一例は、例えば以下の構成となる。
　（ａ）ステートの各列要素単位で行列Ｍ０～Ｍｋから選択した選択行列を特定の順番で各列に適用して線形変換を行う列拡散演算と、
　（ｂ）ステートの各行要素単位で行列Ｍ０～Ｍｋから選択した選択行列を特定の順番Ａで各行に適用して線形変換を行う行拡散演算タイプ１と、
　（ｃ）ステートの各行要素単位で行列Ｍ０～Ｍｋから選択した選択行列を特定の順番Ａと異なる順番Ｂで各行に適用して線形変換を行う行拡散演算タイプ２を、
　ラウンド遷移に応じて切り替えて実行する暗号処理装置。
　さらに、上記の構成における列拡散演算と行拡散演算を入れ替えた以下の構成としてもよい。
　（ａ）ステートの各行要素単位で行列Ｍ０～Ｍｋから選択した選択行列を特定の順番で各行に適用して線形変換を行う列拡散演算と、
　（ｂ）ステートの各列要素単位で行列Ｍ０～Ｍｋから選択した選択行列を特定の順番Ａで各列に適用して線形変換を行う行拡散演算タイプ１と、
　（ｃ）ステートの各列要素単位で行列Ｍ０～Ｍｋから選択した選択行列を特定の順番Ａと異なる順番Ｂで各列に適用して線形変換を行う行拡散演算タイプ２を、
　ラウンド遷移に応じて切り替えて実行する暗号処理装置。
　また、入力データが各要素４ビットの４×４個の要素からなるステートの場合の線形変換処理の具体化構成としては以下の構成が可能である。
　線形変換部は、４種類の行列Ｍ０，Ｍ１，Ｍ２，Ｍ３を利用した行列演算による線形変換処理を実行する構成であり、
　（ａ）ステートの各列要素単位で行列Ｍ０を適用して線形変換を行う列拡散演算と、
　（ｂ）ステートの各行要素単位で行列Ｍ０，Ｍ１，Ｍ２，Ｍ３の順に各行列を適用して線形変換を行う行拡散演算タイプ１と、
　（ｃ）ステートの各行要素単位で前記タイプ１と異なる順に各行列を適用して線形変換を行う行拡散演算タイプ２、
　上記３種類の行列演算をラウンド遷移に応じて切り替えて実行する暗号処理装置。
　なお、ここで、行拡散演算タイプ１においてステートの各行要素単位で適用する行列と、行拡散演算タイプ２においてステートの各行要素単位で適用する行列との組み合わせは、ステートの任意の２つの行に対してタイプ１で適用する２つの行列とタイプ２で適用する２つの行列の計４つの行列が少なくとも３種類以上の行列によって構成される組み合わせとする。
　例えば、タイプ１において、４×４ステートの各行：第１～４行に適用する行列を、
　Ｍ１，Ｍ３，Ｍ０，Ｍ２
　としたとき、
　タイプ２において４×４ステートの各行：第１～４行に適用する行列を、
　Ｍ０，Ｍ２，Ｍ３，Ｍ１
　このような設定とする。
　上記設定では、４×４ステートの任意の２つの行に対してタイプ１で適用する２つの行列とタイプ２で適用する２つの行列の計４つの行列が少なくとも３種類以上の行列によって構成される組み合わせとなる。
　すなわち、上記設定において、４×４ステートの第１行に適用する行列は、
　タイプ１＝Ｍ１、
　タイプ２＝Ｍ０、
　４×４ステートの第２行に適用する行列は、
　タイプ１＝Ｍ３、
　タイプ２＝Ｍ２、
　このような組み合わせとなり、第１行と第２行に対してタイプ１，２の双方で適用される行列がＭ０～Ｍ３の４種類となる。
　上記設定は、その他の任意の２行の組み合わせにおいて、タイプ１で適用する２つの行列とタイプ２で適用する２つの行列の計４つの行列が少なくとも３種類以上の行列によって構成される組み合わせとなる。
　さらに、上記の構成における列拡散演算と行拡散演算を入れ替えた以下の構成としてもよい。
　線形変換部は、４種類の行列Ｍ０，Ｍ１，Ｍ２，Ｍ３を利用した行列演算による線形変換処理を実行する構成であり、
　（ａ）ステートの各行要素単位で行列Ｍ０を適用して線形変換を行う行拡散演算と、
　（ｂ）ステートの各列要素単位で行列Ｍ０，Ｍ１，Ｍ２，Ｍ３の順に各行列を適用して線形変換を行う列拡散演算タイプ１と、
　（ｃ）ステートの各列要素単位で前記タイプ１と異なる順に各行列を適用して線形変換を行う列拡散演算タイプ２、
　上記３種類の行列演算をラウンド遷移に応じて切り替えて実行する暗号処理装置。
　なお、この構成においても、行拡散演算タイプ１においてステートの各列要素単位で適用する行列と、行拡散演算タイプ２においてステートの各列要素単位で適用する行列との組み合わせは、ステートの任意の２つの列に対してタイプ１で適用する２つの行列とタイプ２で適用する２つの行列の計４つの行列が少なくとも３種類以上の行列によって構成される組み合わせとする。
　このように１回の暗号処理シーケンスにおいて実行する線形変換処理をラウンド毎に変更することで、最小差分アクティブＳボックス、および最小線形アクティブＳボックスの数を増加させることが可能となり、差分攻撃や線形攻撃に対する耐性を向上させることができる。
　　［５．鍵スケジュール部の構成と処理について］
　次に、本開示の暗号処理装置における鍵スケジュール部の構成と処理について説明する。
　　［５－１．鍵スケジュール部の構成と処理の説明］
　先に図１９を参照して説明したように、本開示の暗号処理装置１００は、鍵スケジュール部１１０と、暗号処理部１２０を有する。
　鍵スケジュール部１１０は、例えば秘密鍵Ｋに基づいて所定の鍵生成アルゴリズムに従って、暗号処理部１２０の各ラウンドで適用するラウンド鍵を生成して暗号処理部１２０に出力する。暗号処理部１２０は、鍵スケジュール部１１０からラウンド鍵を入力して平文Ｐのデータ変換を行い暗号文Ｃを出力する。
　なお、復号処理に際しても同様の処理が行われる。
　以下、このラウンド鍵生成、供給処理を実行する鍵スケジュール部１１０の構成と処理について説明する。
　図３２は、本開示の暗号処理装置における鍵スケジュール部の一構成例を示す図である。
　鍵スケジュール部３００は、秘密鍵Ｋ１を格納した記憶部としての鍵供給部（鍵レジスタ）３０１を有する。
　鍵スケジュール部３００は、この鍵Ｋ１を、暗号処理部３２０の第１ラウンドの排他的論理和部（ラウンド鍵演算部）３２１に出力する。すなわち鍵Ｋ１が、第１ラウンドのラウンド鍵として利用される。
　さらに、鍵スケジュール部３００は、鍵Ｋ１を鍵変換部３０２ａに入力する。鍵変換部３０２ａは、鍵Ｋ１に対する所定の演算を実行して変換鍵Ｋｄ１を生成する。
　さらに、鍵変換部３０２ａの生成した変換鍵Ｋｄ１を暗号処理部３２０の第２ラウンドの排他的論理和部（ラウンド鍵演算部）３２２に出力する。すなわち変換鍵Ｋｄ１が、第２ラウンドのラウンド鍵として利用される。
　さらに、鍵スケジュール部３００は、変換鍵Ｋｄ１を鍵変換部３０２ｂに入力する。鍵変換部３０２ｂは、変換鍵Ｋｄ１に対する所定の演算を実行して鍵Ｋ１を生成する。
　この鍵Ｋ１は、変換鍵Ｋｄ１の生成元となった鍵Ｋ１と同じ鍵である。
　鍵スケジュール部３００は、鍵変換部３０２ｂの生成した鍵Ｋ１を暗号処理部３２０の第３ラウンドの排他的論理和部（ラウンド鍵演算部）３２３に出力する。すなわち鍵Ｋ１が、第３ラウンドのラウンド鍵として利用される。
　以下、同様の処理を繰り返し、鍵変換部３０２ｃ～ｆにおいて、鍵Ｋ１と鍵Ｋ１ｄが交互に生成し、生成した鍵を暗号処理部の排他的論理和部３２４～３２７に出力する。
　鍵変換部３０２ａ～３０２ｆはいずれも同じ演算を実行する。すなわち同一の演算処理により、
　鍵Ｋ１から変換鍵Ｋｄ１を生成し、
　変換鍵Ｋｄ１から鍵Ｋ１を生成する。
　変換関数Ｇ、および逆関数Ｇ－１を用いて式で示すと以下の通りとなる。
　Ｋｄ１＝Ｇ（Ｋ１）
　Ｋ１＝Ｇ－１（Ｋｄ１）
　である。
　なお、
　Ｇ＝Ｇ－１が成立する。
　すなわち、鍵変換部３０２ａ～３０２ｆにおいて鍵変換に適用するデータ変換関数Ｇは、インボリューション性、すなわち、図３３に示すように、順方向関数Ｇと逆方向関数Ｇ－１とが同じ関数であるという性質を持つ。
　図３３には、図３２で説明した鍵Ｋ１をベース鍵Ｋ、変換鍵Ｋｄ１を変換鍵Ｋｄとして示している。図３３に示す各鍵は１６個の４ビット要素の４×４ステートとして表現している。すなわち、いずれも６４ビット鍵データである。
　鍵変換部３０２の実行する鍵変換処理例について、図３４を参照して説明する。
　図３４は、ベース鍵Ｋから変換鍵Ｋｄを生成する処理を説明する図である。
　ベース鍵Ｋから変換鍵Ｋｄを生成する処理は、以下の２つのステップによって構成される。
　（Ｓ１）ベース鍵Ｋに対して、中間鍵生成列拡散演算（ＭｉｘＣｏｌｕｍｎ＿ＫＳＦ（））を適用した演算を実行して中間鍵Ｓを生成する。
　（Ｓ２）中間鍵Ｓに対して、変換鍵生成列拡散演算（ＭｉｘＲｏｗ＿ＫＳＦ（））を適用した演算を実行して変換鍵Ｋｄを生成する。
　ステップＳ１で実行する列拡散演算（ＭｉｘＣｏｌｕｍｎ）、およびステップＳ２で実行する行拡散演算（ＭｉｘＲｏｗ）は、先に図２４～図２７を参照して説明したと同様の行列適用演算である。
　ただし、この鍵変換処理において適用する行列ＭＤは、以下に示す行列である。
Figure JPOXMLDOC01-appb-M000009
　上記に示す行列ＭＤは、アダマール（Ｈａｄａｍａｒｄ）ＭＤＳ行列とよばれる行列である。
　ＭＤＳ行列は、行列を構成する任意の小行列が正則行列となる行列である。なお、正則行列は、逆行列を持つ行列であり、行列をＡとし、逆行列をＡ－１とすると、
　ＡＡ－１＝Ａ－１Ａ＝Ｅ、
　ただしＥは単位行列、
　上記式が成立する逆行列Ａ－１を持つ行列Ａが正則行列である。
　前述したように、分岐数Ｂｒａｎｃｈ（θ）がｂ＋１であるような写像θは、最適拡散変換（Ｏｐｔｉｍａｌ　Ｄｉｆｆｕｓｉｏｎ　Ｍａｐｐｉｎｇｓ）と呼ばれ、ＭＤＳ行列は、最適拡散変換を実行する行列である。
　このアダマール（Ｈａｄａｍａｒｄ）ＭＤＳ行列ＭＤを適用して、図３４に示すステップＳ１の列拡散演算と、ステップＳ２の行拡散演算を実行する。
　ステップＳ１の列拡散演算は、以下の演算式によって示される。
　ＭＣ［ＭＤ］＝ＭＣ［ＭＤ，ＭＤ，ＭＤ，ＭＤ］
　また、ステップＳ２の行拡散演算は、以下の演算式によって示される。
　ＭＲ［ＭＤ］＝ＭＲ［ＭＤ，ＭＤ，ＭＤ，ＭＤ］
　すなわち、ステップＳ１の列拡散演算は、４ビット要素からなる４×４のステート表現データの４つの全ての列に対して、同一のアダマール（Ｈａｄａｍａｒｄ）ＭＤＳ行列ＭＤを適用した行列演算を実行する。
　また、ステップＳ２の行拡散演算は、４ビット要素からなる４×４のステート表現データの４つの全ての行に対して、同一のアダマール（Ｈａｄａｍａｒｄ）ＭＤＳ行列ＭＤを適用した行列演算を実行する。
　アダマール（Ｈａｄａｍａｒｄ）ＭＤＳ行列ＭＤを適用した行列演算のアルゴリズムは以下のように示すことができる。
　ＭＤ（）：｛０，１｝１６→｛０，１｝１６
　　Ｉｎｐｕｔ：｛ｘ０，ｘ１，ｘ２，ｘ３｝，ｘｉ∈｛０，１｝４
　　Ｏｕｔｐｕｔ：｛ｙ０，ｙ１，ｙ２，ｙ３｝，ｙｉ∈｛０，１｝４
　　Ｏｐｅｒａｔｉｏｎ
　　　　・ｙ０＝ｘ０（＋）２（×）ｘ１（＋）４（×）ｘ３（＋）６（×）ｘ４
　　　　・ｙ１＝２（×）ｘ０（＋）ｘ２（＋）６（×）ｘ３（＋）４（×）ｘ４
　　　　・ｙ２＝４（×）ｘ０（＋）６（×）ｘ２（＋）ｘ３（＋）２（×）ｘ４
　　　　・ｙ３＝６（×）ｘ０（＋）４（×）ｘ２（＋）２（×）ｘ３（＋）ｘ４
　ただし、
　（＋）は、排他的論理和演算、
　（×）は、既約多項式：x４＋ｘ＋１によって規定される拡大体ＧＦ（２４）上の乗算を示す。
　図３４に示すステップＳ１の列拡散演算ＭＣ［ＭＤ］は、以下の式に従った行列演算である。
Figure JPOXMLDOC01-appb-M000010
　上記の列拡散演算ＭＣ［ＭＤ］のアルゴリズムは以下のように示すことができる。
　ＭｉｘＣｏｌｕｍｎ＿ＫＳＦ（）：｛０，１｝６４→｛０，１｝６４
　　Ｉｎｐｕｔ：｛ｋ０，ｋ１，・・・，ｋ１５｝，ｋｉ∈｛０，１｝４
　　Ｏｕｔｐｕｔ：｛ｓ０，ｓ１，・・・，ｓ１５｝，ｓｉ∈｛０，１｝４
　　Ｏｐｅｒａｔｉｏｎ
　　　　・（ｓ０，ｓ１，ｓ２，ｓ３）＝ＭＤ（ｋ０，ｋ１，ｋ２，ｋ３）
　　　　・（ｓ４，ｓ５，ｓ６，ｓ７）＝ＭＤ（ｋ４，ｋ５，ｋ６，ｋ７）
　　　　・（ｓ８，ｓ９，ｓ１０，ｓ１１）＝ＭＤ（ｋ８，ｋ９，ｋ１０，ｋ１１）
　　　　・（ｓ１２，ｓ１３，ｓ１４，ｓ１５）＝ＭＤ（ｋ１２，ｋ１３，ｋ１４，ｋ１５）
　また、図３４に示すステップＳ２の行拡散演算ＭＲ［ＭＤ］は、以下の式に従った行列演算である。
Figure JPOXMLDOC01-appb-M000011
　上記の行拡散演算ＭＲ［ＭＤ］のアルゴリズムは以下のように示すことができる。
　ＭｉｘＲｏｗ＿ＫＳＦ（）：｛０，１｝６４→｛０，１｝６４
　　Ｉｎｐｕｔ：｛ｓ０，ｓ１，・・・，ｓ１５｝，ｓｉ∈｛０，１｝４
　　Ｏｕｔｐｕｔ：｛ｋｄ０，ｋｄ１，・・・，ｋｄ１５｝，ｋｄｉ∈｛０，１｝４
　　Ｏｐｅｒａｔｉｏｎ
　　　　・（ｋｄ０，ｋｄ４，ｋｄ８，ｋｄ１２）＝ＭＤ（ｓ０，ｓ４，ｓ８，ｓ１２）
　　　　・（ｋｄ１，ｋｄ５，ｋｄ９，ｋｄ１３）＝ＭＤ（ｓ１，ｓ５，ｓ９，ｓ１３）
　　　　・（ｋｄ２，ｋｄ６，ｋｄ１０，ｋｄ１４）＝ＭＤ（ｓ２，ｓ６，ｓ１０，ｓ１４）
　　　　・（ｋｄ３，ｋｄ７，ｋｄ１１，ｋｄ１５）＝ＭＤ（ｓ３，ｓ７，ｓ１１，ｓ１５）
　このように、図３２に示す鍵スケジュール部３００の鍵変換部３０２では、図３４に示すステップＳ１において、行列ＭＤを適用した列拡散演算ＭＣ［ＭＤ］を実行し、ステップＳ２において行列ＭＤを適用した行拡散演算ＭＲ［ＭＤ］を実行する。
　これらの２つの行列演算を連続して実行することで、ベース鍵Ｋから変換鍵Ｋｄを生成する。
　なお、変換鍵Ｋｄからベース鍵Ｋを生成する場合も、図３４に示す処理と同様の処理を行なう。
　すなわち、先に図３３を参照して説明したように、列拡散演算ＭＣ［ＭＤ］と、行拡散演算ＭＲ［ＭＤ］の連続処理からなる関数Ｇは、インボリューション性を持ち、順方向関数Ｇと、逆方向関数Ｇ－１が同一であるため、２回繰り返すことで、元の値が算出される。
　さらに、鍵変換部３０２は、行列ＭＤを適用した列拡散演算ＭＣ［ＭＤ］と、行列ＭＤを適用した行拡散演算ＭＲ［ＭＤ］を実行することで、入力データを構成する４×４のステートの構成要素のすべて、すなわち１６個の構成要素のすべてが、出力データの１６個の構成要素のすべてに影響を及ぼすことが可能となる。
　すなわち、入出力ステート全要素間でデータ拡散（ｄｉｆｆｕｓｉｏｎ）がなされている。このようなデータ変換態様を「全拡散（ｆｕｌｌ　ｄｉｆｆｕｓｉｏｎ）変換」、あるいはフルディフュージョン性を有する拡散であると定義する。
　例えば、入力、出力がそれぞれｎビット要素１６個からなるステートであり、入力に対して適用する変換関数ｆとし、
　Ｂ＝ｆ（Ａ）
　上記式に従って出力ステートＢを算出する設定とする。
　入力ステートＡ＝（ａ０，ａ１，ａ２，・・・ａ１５）
　出力ステートＢ＝（ｂ０，ｂ１，ｂ２，・・・ｂ１５）
　である。
　ただし、ａｉ，ｂｉはステートＡ，Ｂの要素である。
　このとき、
　出力ステートＢの任意の要素ｂｉが以下の式によって表現できる場合、関数ｆは、全拡散（ｆｕｌｌ　ｄｉｆｆｕｓｉｏｎ）変換であるという。
　ｂｉ＝ｆ（ａ０，ａ１，ａ２，・・・ａ１５）
　このように、鍵変換部３０２の実行関数Ｇは、以下の２つの性質を有する関数である。
　（１）全拡散（ｆｕｌｌ　ｄｉｆｆｕｓｉｏｎ）変換を実現するフルディフュージョン性、
　（２）順方向関数Ｇと、逆方向関数Ｇ－１が同一であるインボリューション性、
　これら２つの性質を持つ。
　　［５－２．鍵スケジュール部のフルディフュージョン性に基づく効果について］
　鍵変換部３０２の性質であるフルディフュージョン性は、結果として、図３２に示す暗号処理部３２０における変換対象データと鍵との間にもフルディフュージョン性を保証することになる。図３５を参照して説明する。
　図３５には、
　ベース鍵Ｋ＝（ｋ０，ｋ１，ｋ２，・・・ｋ１５）
　変換鍵Ｋｄ＝（ｋｄ０，ｋｄ１，ｋｄ２，・・・ｋｄ１５）
　を示している。
　ベース鍵Ｋは、暗号処理部の排他的論理和部３３１に入力されて、入力ステートＡとの排他的論理和演算がなされる。その後、さらに、非線形／線形変換部（Ｓ＆Ｐ）３３２において非線形変換処理と、線形変換処理がなされる。
　さらにその出力に対して、排他的論理和演算部３３３において、変換鍵Ｋｄとの排他的論理和演算が実行される。
　排他的論理和演算部３３３の出力をステートＢとする。
　この時、ベース鍵Ｋと変換鍵Ｋｄとの間の関係は、
　Ｋｄｉ＝ｆ（ｋ０，ｋ１，ｋ２，・・・ｋ１５）
　ただし、ｉ＝０～１５
　上記関係式が成立する。
　すなわち、フルディフュージョン性が保証されている。
　上記関係式から、
　ステートＢと、ベース鍵Ｋとの間にも、以下の関係式が成立する。
　ｂｉ＝ｆ（ｋ０，ｋ１，ｋ２，・・・ｋ１５）
　ただし、ｉ＝０～１５
　上記関係式が成立する。
　すなわち、ベース鍵Ｋと変換データＢとの間でもフルディフュージョン性が保証される。
　この性質は、暗号処理装置の安全性や、実装性能に貢献をもたらす性質であると言える。
　具体的には、鍵によるデータ拡散性の向上が実現され、ラウンド数を削減しても高い拡散性能を発揮させることが可能になる。この結果、各種の攻撃に対する耐性を高めることが可能となる。たとえば、鍵依存度を利用した中間値一致攻撃等に基づく鍵解析処理に対する耐性をより向上させることができる。
　上述したように、本開示の構成を適用することで、暗号処理部における変換対象データの拡散性能が向上し、より少ないラウンド数で安全な暗号処理、例えば鍵解析等の各種攻撃に対する耐性の高い暗号処理が実現されることになる。
　図３６には、
　（１）各ラウンドにおいて鍵変換を実行せず、同じラウンド鍵を適用する暗号処理構成
　（２）本開示の鍵変換を実行して、交互に２種類のラウンド鍵を適用する暗号処理構成
　これら２つの暗号処理構成例を示している。
　なお、図３６（２）に示すＧのボックスは、図３２に示す鍵変換部３０２に相当する。
　図３６（１）の鍵変換を実行しない暗号処理構成では、適用鍵の構成情報（ビット列）が変換対象データである入力平文Ｐの全ビットに拡散（Ｆｕｌｌ　ｄｉｆｆｕｓｉｏｎ）するのに必要なラウンド数は、ラウンド関数（Ｒ）の処理に依存することになる。
　従って、ラウンド関数の拡散性能が低い場合、拡散レベルを高くするためには、多くのラウンド数が必要となり、結果として、高速処理や軽量化を実現することが困難となる。
　一方、図３６（２）に示す本開示の鍵変換を実行する暗号処理構成では、適用鍵の構成情報（ビット列）が変換対象データである入力平文Ｐの全ビットに拡散（Ｆｕｌｌ　ｄｉｆｆｕｓｉｏｎ）するのに必要なラウンド数は、ベース鍵Ｋ１と、変換鍵Ｋｄ１が２つ利用されるラウンド数となる。
　図の例では１ラウンドになる。
　すなわち、本開示の処理を適用すれば、変換対象データに対する鍵データの構成情報の拡散が１ラウンドで実現され、ラウンド関数（Ｒ）の処理に依存することなくより大きな拡散性能が保証される。
　すなわち、少ないラウンド数で攻撃に対する耐性の高い安全な暗号処理が実現される。結果として、高速処理や軽量化が実現される。
　　［５－３．鍵変換部のインボリューション性に基づく効果について］
　先に図３２、図３３等を参照して説明したように、本開示の鍵スケジュール部３００の鍵変換部３０２は、順方向関数Ｇと逆方向関数Ｇ－１が同一の関数で実現されるインボリューション性を有する。
　以下、このインボリューション性に基づく効果について説明する。
　なお、同一のデータ変換処理であるラウンド関数を繰り返し実行する暗号処理装置のハードウェア実装構成としては、以下の２つのタイプがある。
　（ａ）規定ラウンド数に相当する数のラウンド関数実行部をハードウェアとして構成する「アンロールド（Ｕｎｒｏｌｌｅｄ）実装」、
　（ｂ）ハードウェアとしてのラウンド関数実行部を１つ構成し、そのラウンド関数実行部の出力を同じラウンド関数実行部にフィードバック入力して、規定ラウンド数のラウンド関数を繰り返し実行する「ラウンド実装」、
　以下、これら２つのタイプにおけるインボリューション性に基づく効果について、順次、説明する。
　　［５－３－ａ．アンロールド（Ｕｎｒｏｌｌｅｄ）実装における効果について］
　まず、暗号処理部をアンロールド実装した場合に、本開示の鍵変換部のインボリューション性がもたらす効果について説明する。
　アンロールド（Ｕｎｒｏｌｌｅｄ）実装では、暗号処理部には、規定ラウンド数に相当する数のラウンド関数実行部がハードウェアとして構成される。
　図３７、図３８を参照して、暗号処理部をアンロールド実装した場合に、本開示の鍵変換部のインボリューション性がもたらす効果について説明する。
　図３７、図３８に、以下の暗号処理装置の実装例を示す。
　図３７（１）鍵変換部（Ｆ）がインボリューション性を有していない場合のハードウェア実装例
　図３８（２ａ）、（２ｂ）鍵変換部（Ｇ）がインボリューション性を有している場合のハードウェア実装例
　図３８（２ａ），（２ｂ）は、本開示の鍵変換部、すなわちインボリューション性を有する場合の実装例に相当する。
　図３７は、鍵変換部Ｆがインボリューション性を有していないため、鍵変換部Ｆによる変換結果として得られる鍵は、逐次、異なる鍵となる。図３７に示すように、鍵変換部Ｆの変換処理によって、鍵Ｋ１に基づいて、Ｋｄ１、Ｋｄ２、Ｋｄ３、Ｋｄ４、Ｋｄ５、Ｋｄ６が順次、生成され、これらの各鍵がラウンド鍵として暗号処理部の排他的論理和部（ラウンド鍵演算部）に順次入力する構成となる。
　これに対して、図３８（２ａ），（２ｂ）に示す例は、鍵変換部（Ｇ）がインボリューション性を有している場合のハードウェア実装例である。
　図３８（２ａ）に示す例は、図３７（１）に示すハードウェア構成と同様、暗号処理部の排他的論理和部（ラウンド鍵演算部）に対する入力鍵（ラウンド鍵）を生成するための鍵変換部Ｇを各ラウンドに対応付けて設定した構成である。
　一方、図３８（２ｂ）は、鍵変換部Ｇを１つのみの設定として、予め保持するベース鍵Ｋ１と、鍵変換部Ｇによって生成される変換鍵Ｋｄ１を暗号処理部の排他的論理和部（ラウンド鍵演算部）に対して交互に入力する設定とした構成である。
　鍵変換部Ｇは、インボリューション性を有するため、鍵変換部による変換処理の繰り返しによって生成される鍵は、Ｋ１，Ｋｄ１，Ｋ１，Ｋｄ１，Ｋ１・・・の繰り返しとなる。この性質に基づいて、図３８（２ｂ）に示すように鍵変換部Ｇを１つとして、ベース鍵Ｋ１と、鍵変換部Ｇによる１回の鍵変換処理によって生成した変換鍵Ｋｄ１を暗号処理部の排他的論理和部（ラウンド鍵演算部）に交互に入力することが可能となる。
　この結果、鍵変換部Ｇの数を１つとすることが可能となり、ハードウェア実装の軽量化（小型化）が実現される。
　図３８（２ｂ）に示す構成に対応する暗号処理装置の構成例を図３９に示す。
　図３９に示すように、鍵スケジュール部３００の鍵変換部（Ｇ）３０２は、１つのみとして暗号処理部３２０の各排他的論理和部（ラウンド鍵演算部）に対して予め保持するベース鍵Ｋ１と、鍵変換部Ｇによって生成される変換鍵Ｋｄ１を交互に入力することが可能となる。
　　［５－３－ｂ．ラウンド実装における効果について］
　次に、暗号処理装置をラウンド実装した場合に、本開示の鍵変換部のインボリューション性がもたらす効果について説明する。
　ラウンド実装では、暗号処理部に設定された１つのラウンド関数を繰り返し利用する構成となる。
　図４０に、鍵変換部がインボリューション性を有していない場合の（ａ１）暗号処理構成と、（ａ２）ラウンド実装例を示す。
　図４１に、鍵変換部がインボリューション性を有している場合の（ｂ１）暗号処理構成と、（ｂ２）ラウンド実装例を示す。
　図４０（ａ１）に示す暗号処理構成は、先に図３７を参照して説明した構成と同様の構成である。
　すなわち、鍵変換部Ｆがインボリューション性を有していないため、鍵変換部Ｆによる変換結果として得られる鍵は、逐次、異なる鍵となる。図４０（ａ１）に示すように、鍵変換部Ｆの変換処理によって、鍵Ｋ１に基づいて、Ｋｄ１、Ｋｄ２、Ｋｄ３、Ｋｄ４、Ｋｄ５、Ｋｄ６が順次、生成され、これらの各鍵がラウンド鍵として暗号処理部の排他的論理和部（ラウンド鍵演算部）に順次入力する構成となる。
　この構成をラウンド型のハードウェア実装とした場合、図４０（ａ２）に示す構成となる。暗号処理部３５０は、１つの排他的論理和部（ラウンド鍵演算部）３５１と、１つの非線形／線形変換部３５２の構成とすることが可能となる。
　一方、鍵スケジュール部３６０は、ベース鍵Ｋ１を格納し供給する鍵レジスタ３６１と、変換鍵Ｋｄ１～Ｋｄ６を格納し供給するための鍵レジスタ３６２と、鍵変換部（Ｆ）３６３、鍵レジスタ３６１，３６２の出力切り換えを実行するスイッチ３６４を有する構成となる。
　これに対して、図４１（ｂ１）に示す暗号処理構成は、先に図３８（２ｂ）を参照して説明した構成と同様、鍵変換部Ｇがインボリューション性を有する構成とした暗号処理構成である。
　すなわち、鍵変換部Ｇがインボリューション性を有しているため、鍵変換部による変換処理の繰り返しによって生成される鍵は、Ｋ１，Ｋｄ１，Ｋ１，Ｋｄ１，Ｋ１・・・の繰り返しとなる。この性質に基づいて、図４１（ｂ１）に示すように鍵変換部Ｇを１つとして、ベース鍵Ｋ１と、鍵変換部Ｇによる１回の鍵変換処理によって生成した変換鍵Ｋｄ１を暗号処理部の排他的論理和部（ラウンド鍵演算部）に交互に入力することが可能となる。
　この構成をラウンド型のハードウェア実装とした場合、図４１（ｂ２）に示す構成となる。暗号処理部３５０は、１つの排他的論理和部（ラウンド鍵演算部）３５１と、１つの非線形／線形変換部３５２の構成とすることが可能となる。
　一方、鍵スケジュール部３７０は、ベース鍵Ｋ１、および変換鍵Ｋｄ１を格納し供給する鍵レジスタ３７１と、鍵変換部（Ｇ）３７２を有する構成となる。
　図４０（ａ２）に示す鍵変換部（Ｆ）がインボリューション性を持たない場合のラウンド実装構成では、鍵スケジュール部３６０には、２つの鍵レジスタ、１つの鍵変換部、１つのスイッチが必要となる。これに対して、図４１（ｂ２）に示す鍵変換部（Ｇ）がインボリューション性を有する場合のラウンド実装構成の鍵スケジュール部３７０は、１つの鍵レジスタと１つの鍵変換部によって構成され、ハードウェア構成の軽量化（小型化）が実現されることが証明される。
　例えば、図４０（ａ２）に示すインボリューション性を持たない鍵変換部（Ｆ）を持つ場合のラウンド実装構成では、複数の異なる変換鍵を、順次、生成して格納、供給するための鍵レジスタが必要となり、この鍵レジスタ用のゲート数分の新たなハードウェア回路が必要となる。
　　［５－４．本開示の鍵スケジュール部の構成と効果のまとめ］
　上述したように、本開示の暗号処理装置に構成される鍵スケジュール部の鍵変換部は、以下の２つの特性を持つ。
　（１）全拡散（ｆｕｌｌ　ｄｉｆｆｕｓｉｏｎ）変換を実現するフルディフュージョン性、
　（２）順方向関数Ｇと、逆方向関数Ｇ－１が同一であるインボリューション性、
　これら２つの特性を持つ。
　これらの２つの特性に基づいて、以下の効果が発揮される。
　（効果１）フルディフュージョン性に基づいて、変換対象とするデータについてのフルディフュージョン性を少ないラウンドで実現できる。
　この結果、少ないラウンドで安全性の高い暗号処理を行なうことができ、処理の高速化（低遅延化）、および装置の軽量化（小型化）が実現される。
　（効果２）ハードウェア構成をアンロール実装とした場合、インボリューション性に基づいて、鍵変換部を１つのみの構成とすることが可能となり、装置の軽量化（小型化）が実現される。
　（効果３）ハードウェア構成をラウンド実装とした場合、インボリューション性に基づいて、鍵レジスタと、鍵変換部を各々１つのみとした鍵スケジュール部の実装が可能となり、装置の軽量化（小型化）が実現される。
　　［５－５．鍵スケジュール部のその他の構成例について］
　次に、上述した以下の２つの特性、すなわち、
　（１）全拡散（ｆｕｌｌ　ｄｉｆｆｕｓｉｏｎ）変換を実現するフルディフュージョン性、
　（２）順方向関数Ｇと、逆方向関数Ｇ－１が同一であるインボリューション性、
　これら２つの特性を持つ関数Ｇを適用した鍵変換処理を実行する鍵変換部を有する鍵スケジュール部のその他の構成例について、図４２以下を参照して説明する。
　図４２は、上述の２つの特性を有する鍵変換部を持つ鍵スケジュール部３８０を有する暗号処理装置の一構成例を示す図である。
　図４２に示す暗号処理装置は、鍵スケジュール部３８０と、暗号処理部３８５を有する。
　鍵スケジュール部３８０の鍵レジスタ３８１には、予め生成された秘密鍵Ｋが格納される。
　秘密鍵Ｋは、鍵Ｋ１と鍵Ｋ２の連結データである。
　例えば鍵Ｋ１、Ｋ２は６４ビット鍵であり、その連結データである秘密鍵Ｋは１２８ビットデータである。
　図に示すＧは、鍵変換部であり、先に図３２以下を参照して説明した鍵変換部３０２と同様、フルディフュージョン性と、インボリューション性、これら２つの特性を持つ関数Ｇを適用した鍵変換処理を行なう鍵変換部である。
　図４２に示す鍵スケジュール部３８０は、鍵レジスタ３８１に格納された秘密鍵Ｋの分割データである鍵Ｋ１、Ｋ２、さらに、これらの鍵を鍵変換部（Ｇ）において変換した変換鍵Ｋｄ１、Ｋｄ２を暗号処理部３８５の排他的論理和部（ラウンド鍵演算部）に順次出力する。
　なお、図に示す例において、鍵Ｋ１、Ｋ２が６４ビット鍵である場合、暗号処理部３８５の変換対象となる平文Ｐも６４ビットデータとなる。
　図４２に示す例では、鍵の出力順は、以下の通りである。
　鍵Ｋ１、
　鍵Ｋ２、
　変換鍵Ｋｄ１、
　変換鍵Ｋｄ２、
　鍵Ｋ１、
　鍵Ｋ２、
　変換鍵Ｋｄ１、
　この順番で、４種類の鍵を暗号処理部３８５に入力する。
　なお、鍵入力順は様々な設定が可能である。
　なお、図４２には、鍵変換部（Ｇ）を複数、示しているが、先に図４１を参照して説明したラウンド実装を行う場合、この鍵変換部（Ｇ）は１つのみの構成とすることが可能である。
　図４３を参照して鍵スケジュール部のもう１つの構成例について説明する。
　図４３には、以下の各図を示している。
　（ａ）鍵スケジュール部の構成
　（ｂ）鍵スケジュール部による鍵出力構成
　図４３（ａ）に示すように、鍵スケジュール部の鍵レジスタ３９１には、予め生成された秘密鍵Ｋが格納される。
　秘密鍵Ｋは、鍵Ｋ１と鍵Ｋ２の連結データである。
　例えば鍵Ｋ１、Ｋ２は６４ビット鍵であり、その連結データである秘密鍵Ｋは１２８ビットデータである。
　図４３（ａ）に示す鍵スケジュール部は、鍵変換部Ｇ３９３と、排他的論理和部３９２，３９４を有する。
　鍵変換部Ｇ３９３は、先に図３２以下を参照して説明した鍵変換部３０２と同様、フルディフュージョン性と、インボリューション性、これら２つの特性を持つ関数Ｇを適用した鍵変換処理を行なう鍵変換部である。
　図４３（ａ）に示す鍵スケジュール部は、これらの各構成に基づいて、以下の６種類の鍵を生成する。
　鍵Ｋ１、
　鍵Ｋ２、
　変換鍵Ｋｄ１、
　変換鍵Ｋｄ２、
　排他的論理和演算鍵Ｋ１（＋）Ｋ２、
　排他的論理和演算変換鍵Ｋｄ１（＋）Ｋｄ２、
　図４３（ａ）に示す鍵スケジュール部は、これら６種類の鍵を生成して、暗号処理部に順次、出力する。
　なお、上記６種類の鍵は、鍵Ｋ＝１２８ビットである場合、すべて６４ビット鍵となる。この場合、暗号処理部の変換対象となる平文Ｐも６４ビットデータとなる。
　図４３（ｂ）に示す例では、鍵の出力順は、以下の通りである。
　鍵Ｋ１、
　鍵Ｋ２、
　変換鍵Ｋｄ１、
　変換鍵Ｋｄ２、
　排他的論理和演算鍵Ｋ１（＋）Ｋ２、
　排他的論理和演算変換鍵Ｋｄ１（＋）Ｋｄ２、
　排他的論理和演算鍵Ｋ１（＋）Ｋ２、
　排他的論理和演算変換鍵Ｋｄ１（＋）Ｋｄ２、
　排他的論理和演算鍵Ｋ１（＋）Ｋ２、
　変換鍵Ｋｄ２、
　変換鍵Ｋｄ１、
　鍵Ｋ２、
　鍵Ｋ１、
　この順番で、６種類の鍵を暗号処理部に入力する。
　上記鍵の入力シーケンスは、逆の順番も同一シーケンスとなる。
　これは、平文Ｐから暗号文Ｃを生成する暗号処理における鍵入力順と、暗号文Ｃから平文Ｐを生成する復号処理における鍵入力順を同じ設定とすることが可能であることを意味する。これは、暗号処理および復号処理に適用するハードウェアやプログラムを共通化可能であることを意味し、装置の軽量化（小型化）に寄与する設定である。
　なお、図４３に示す鍵スケジュール部を有する暗号処理装置の具体的構成については、さらに、後段で説明する。
　　［５－６．フルディフュージョン性を持つ鍵変換部を有する構成例について］
　上述した実施例では、秘密鍵Ｋに対して変換関数Ｇを適用した変換処理により変換鍵Ｋｄを生成する鍵変換部がインボリューション性と、フルディフュージョン性の２つの性質を持つものとして説明したが、インボリューション性を持たずフルディフュージョン性のみを有する鍵変換部を適用した場合においても、入力データに対する拡散性能が向上し、各種攻撃に対する耐性の高い安全な暗号処理構成が実現される。
　以下、フルディフュージョン性を有する暗号処理構成についての実施例について説明する。
　図４４は、鍵変換関数Ｇがフルディフュージョン性を有する場合、入力データ（Ｐ）の内部状態Ｓのフルディフュージョン性が保証されることを示す図である。先の項目［５－２．鍵スケジュール部のフルディフュージョン性に基づく効果について］において図３５等を参照して説明したように、鍵変換部の鍵変換関数Ｇがフルディフュージョン性を有する場合、変換対象データと鍵との間にもフルディフュージョン性を保証することになる。
　図４４に示す構成において、ベース鍵Ｋ１は、暗号処理部の排他的論理和部に入力されて、入力ステートとの排他的論理和演算がなされる。その後、さらに、ラウンド演算部Ｒ１において非線形変換処理と、線形変換処理がなされる。
　さらにその出力に対して、排他的論理和演算部において、変換鍵Ｋｄ１との排他的論理和演算が実行される。
　排他的論理和演算部の出力（Ｓ）について考察する。
　ベース鍵Ｋ１と変換鍵Ｋｄ１との間にはフルディフュージョン性が保証されている。
　変換対象データは、ラウンド演算部Ｒ１において非線形変換処理と、線形変換処理がなされた後、変換鍵Ｋｄ１との排他的論理和演算が実行される。
　この結果、ベース鍵Ｋ１と変換データとの間でもフルディフュージョン性が保証される。
　この性質は、暗号処理装置の安全性や、実装性能に貢献をもたらす性質であると言える。
　具体的には、鍵によるデータ拡散性の向上が実現され、ラウンド数を削減しても高い拡散性能を発揮させることが可能になる。この結果、各種の攻撃に対する耐性を高めることが可能となる。たとえば、鍵依存度を利用した中間値一致攻撃等に基づく鍵解析処理に対する耐性をより向上させることができる。
　なお、図４５に示すような鍵変換を実行しない暗号処理構成では、適用鍵の構成情報（ビット列）が変換対象データである入力平文Ｐの全ビットに拡散（Ｆｕｌｌ　ｄｉｆｆｕｓｉｏｎ）するのに必要なラウンド数は、ラウンド関数（Ｒ）の処理に依存することになる。
　これに対して、図４４に示す鍵変換を行う構成では、適用鍵の構成情報（ビット列）が変換対象データである入力平文Ｐの全ビットに拡散（Ｆｕｌｌ　ｄｉｆｆｕｓｉｏｎ）するのに必要なラウンド数は、ベース鍵Ｋ１と、変換鍵Ｋｄ１が２つ利用されるラウンド数となる。
　図の例では１ラウンドになる。
　すなわち、本開示の処理を適用すれば、変換対象データに対する鍵データの構成情報の拡散が１ラウンドで実現され、ラウンド関数（Ｒ）の処理に依存することなくより大きな拡散性能が保証される。
　すなわち、少ないラウンド数で攻撃に対する耐性の高い安全な暗号処理が実現される。結果として、高速処理や軽量化が実現される。
　フルディフュージョン性を持つＧ関数の具体例について説明する。
　以下で説明するＧ関数は、以下の２つの関数の組み合わせによって構成される。
　（ａ）フルディフュージョン４ビット関数（Ｄｆ４）
　（ｂ）１６ビット置換関数（Ｂｐ１６）
　（ａ）フルディフュージョン４ビット関数は、入出力４ビットとする変換関数であり、出力４ビットのすべてのビットに入力４ビットの影響が表れるフルディフュージョン性を持つ関数である。
　すなわち、
　入力：ｘ０，ｘ１，ｘ２，ｘ３（各１ｂｉｔ）
　出力：ｙ０，ｙ１，ｙ２，ｙ３（各１ｂｉｔ）
　このとき、関数ｆは、
　ｙｉ＝ｆ（ｘ０，ｘ１，ｘ２，ｘ３）
　ただしｉ＝０，１，２，３
　上記性質を持つ関数である。
　次に、（ｂ）１６ビット置換関数（Ｂｐ１６）について図４６を参照して説明する。
　図４６には、１６ビット置換関数（Ｂｐ１６）の一例を示している。
　入力Ｘをｘ０，ｘ１，ｘ２，・・・ｘ１５の１６ビットデータとし、
　入力Ｘを変換関数Ｇに入力して変換された後の、
　出力Ｙをｙ０，ｙ１，ｙ２，・・・ｙ１５の１６ビットデータとする。
　なお、ｘｉ，ｙｉはそれぞれ０または１の１ビットデータである
　１６ビット置換関数（Ｂｐ１６）による入出力ビットの関係は以下の対応関係となる。
　入力：ｘ０，ｘ１，・・・，ｘ１５（各１ｂｉｔ）
　出力：ｙ０，ｙ１，・・・，ｙ１５（各１ｂｉｔ）
　関数：ｙ０＝ｘ０，ｙ１＝ｘ４，ｙ２＝ｘ８，ｙ３＝ｘ１２
　　　　ｙ４＝ｘ１，ｙ５＝ｘ５，ｙ６＝ｘ９，ｙ７＝ｘ１３
　　　　ｙ８＝ｘ２，ｙ９＝ｘ６，ｙ１０＝ｘ１０，ｙ１１＝ｘ１４
　　　　ｙ１２＝ｘ３，ｙ１３＝ｘ７，ｙ１４＝ｘ１１，ｙ１５＝ｘ１５
　図４７は、
　（ａ）フルディフュージョン４ビット関数（Ｄｆ４）
　（ｂ）１６ビット置換関数（Ｂｐ１６）
　これらの２つの関数から構成されるフルディフュージョン性を持つＧ関数を適用した鍵変換処理例（処理例１）を示す図である。
　ベース鍵をＡとし、変換鍵Ｂとする。いずれも各要素４ビットの４×４ステートデータである。
　図４７に示す例において、ベース鍵Ａから変換鍵Ｂを生成する処理は、以下の４つのステップによって構成される。
　（Ｓ１１）ベース鍵Ａの１６個の４ビット要素各々に対してフルディフュージョン４ビット関数（Ｄｆ４）を適用して変換する。
　（Ｓ１２）ステップＳ１１の変換処理によって生成されたデータ（４×４ステート）の各列１６ビットデータ各々に対して、１６ビット置換関数（Ｂｐ１６）を適用して変換する。
　（Ｓ１３）ステップＳ１２の変換処理によって生成されたデータ（４×４ステート）の１６個の４ビット要素各々に対してフルディフュージョン４ビット関数（Ｄｆ４）を適用して変換する。
　（Ｓ１４）ステップＳ１３の変換処理によって生成されたデータ（４×４ステート）の各行１６ビットデータ各々に対して、１６ビット置換関数（Ｂｐ１６）を適用して変換する。
　これらの処理によって、ベース鍵Ａから変換鍵Ｂを生成する。
　変換鍵のＢの各要素ｂ０～ｂ１５は、ベース鍵Ａの各要素ａ０～ａ１５の影響を受けたデータとなりベース鍵Ａと変換鍵Ｂとの間にはフルディフュージョン性が保証される。
　図４８も、
　（ａ）フルディフュージョン４ビット関数（Ｄｆ４）
　（ｂ）１６ビット置換関数（Ｂｐ１６）
　これらの２つの関数から構成されるフルディフュージョン性を持つＧ関数を適用した鍵変換処理例（処理例２）を示す図である。
　ベース鍵をＡとし、変換鍵Ｂとする。いずれも各要素４ビットの４×４ステートデータである。
　図４８に示す例において、ベース鍵Ａから変換鍵Ｂを生成する処理は、以下の５つのステップによって構成される。
　（Ｓ２１）ベース鍵Ａの１６個の４ビット要素各々に対してフルディフュージョン４ビット関数（Ｄｆ４）を適用して変換する。
　（Ｓ２２）ステップＳ２１の変換処理によって生成されたデータ（４×４ステート）の各列１６ビットデータ各々に対して、１６ビット置換関数（Ｂｐ１６）を適用して変換する。
　（Ｓ２３）ステップＳ２２の変換処理によって生成されたデータ（４×４ステート）の１６個の４ビット要素各々に対してフルディフュージョン４ビット関数（Ｄｆ４）を適用して変換する。
　（Ｓ２４）ステップＳ２３の変換処理によって生成されたデータ（４×４ステート）の各行１６ビットデータ各々に対して、１６ビット置換関数（Ｂｐ１６）を適用して変換する。
　（Ｓ２５）ステップＳ２４の変換処理によって生成されたデータ（４×４ステート）の１６個の４ビット要素各々に対してフルディフュージョン４ビット関数（Ｄｆ４）を適用して変換する。
　これらの処理によって、ベース鍵Ａから変換鍵Ｂを生成する。
　変換鍵のＢの各要素ｂ０～ｂ１５は、ベース鍵Ａの各要素ａ０～ａ１５の影響を受けたデータとなりベース鍵Ａと変換鍵Ｂとの間にはフルディフュージョン性が保証される。
　図４９も、
　（ａ）フルディフュージョン４ビット関数（Ｄｆ４）
　（ｂ）１６ビット置換関数（Ｂｐ１６）
　これらの２つの関数から構成されるフルディフュージョン性を持つＧ関数を適用した鍵変換処理例（処理例３）を示す図である。
　ベース鍵をＡとし、変換鍵Ｂとする。いずれも各要素４ビットの４×４ステートデータである。
　この処理例３において適用する
　（ａ）フルディフュージョン４ビット関数（Ｄｆ４）
　は、インボリューション性も有する関数である。
　図４９に示す例において、ベース鍵Ａから変換鍵Ｂを生成する処理は、以下の５つのステップによって構成される。
　（Ｓ３１）ベース鍵Ａの１６個の４ビット要素各々に対してインボリューション性を有し、かつフルディフュージョン性を有する４ビット関数（Ｄｆ４）を適用して変換する。
　（Ｓ３２）ステップＳ３１の変換処理によって生成されたデータ（４×４ステート）の各列１６ビットデータ各々に対して、１６ビット置換関数（Ｂｐ１６）を適用して変換する。
　（Ｓ３３）ステップＳ３２の変換処理によって生成されたデータ（４×４ステート）の１６個の４ビット要素各々に対してインボリューション性を有し、かつフルディフュージョン性を有する４ビット関数（Ｄｆ４）を適用して変換する。
　（Ｓ３４）ステップＳ３３の変換処理によって生成されたデータ（４×４ステート）の各行１６ビットデータ各々に対して、１６ビット置換関数（Ｂｐ１６）を適用して変換する。
　（Ｓ３５）ステップＳ３４の変換処理によって生成されたデータ（４×４ステート）の１６個の４ビット要素各々に対してインボリューション性を有し、かつフルディフュージョン性を有する４ビット関数（Ｄｆ４）を適用して変換する。
　これらの処理によって、ベース鍵Ａから変換鍵Ｂを生成する。
　変換鍵のＢの各要素ｂ０～ｂ１５は、ベース鍵Ａの各要素ａ０～ａ１５の影響を受けたデータとなりベース鍵Ａと変換鍵Ｂとの間にはフルディフュージョン性が保証される。さらに、（ａ）フルディフュージョン４ビット関数（Ｄｆ４）、（ｂ）１６ビット置換関数（Ｂｐ１６）これらの関数が双方ともインボリューション性を有しているため、ベース鍵Ａと変換鍵Ｂとの間にはインボリューション性も保証される。
　図５０も、
　（ａ）フルディフュージョン４ビット関数（Ｄｆ４）
　（ｂ）１６ビット置換関数（Ｂｐ１６）
　これらの２つの関数から構成されるフルディフュージョン性を持つＧ関数を適用した鍵変換処理例（処理例４）を示す図である。
　ベース鍵をＡとし、変換鍵Ｂとする。いずれも各要素４ビットの４×４ステートデータである。
　この処理例４において適用する
　（ａ）フルディフュージョン４ビット関数（Ｄｆ４）
　は、インボリューション性も有する関数である。
　図５０に示す例において、ベース鍵Ａから変換鍵Ｂを生成する処理は、以下の５つのステップによって構成される。
　（Ｓ４１）ベース鍵Ａ（４×４ステート）の各列１６ビットデータ各々に対して、１６ビット置換関数（Ｂｐ１６）を適用して変換する。
　（Ｓ４２）ステップＳ４１の変換処理によって生成されたデータ（４×４ステート）の１６個の４ビット要素各々に対してインボリューション性を有し、かつフルディフュージョン性を有する４ビット関数（Ｄｆ４）を適用して変換する。
　（Ｓ４３）ステップＳ４２の変換処理によって生成されたデータ（４×４ステート）の各列１６ビットデータ各々に対して、１６ビット置換関数（Ｂｐ１６）を適用して変換する。
　（Ｓ４４）ステップＳ４３の変換処理によって生成されたデータ（４×４ステート）の１６個の４ビット要素各々に対してインボリューション性を有し、かつフルディフュージョン性を有する４ビット関数（Ｄｆ４）を適用して変換する。
　（Ｓ４５）ステップＳ４４の変換処理によって生成されたデータ（４×４ステート）の各行１６ビットデータ各々に対して、１６ビット置換関数（Ｂｐ１６）を適用して変換する。
　これらの処理によって、ベース鍵Ａから変換鍵Ｂを生成する。
　変換鍵のＢの各要素ｂ０～ｂ１５は、ベース鍵Ａの各要素ａ０～ａ１５の影響を受けたデータとなりベース鍵Ａと変換鍵Ｂとの間にはフルディフュージョン性が保証される。さらに、（ａ）フルディフュージョン４ビット関数（Ｄｆ４）、（ｂ）１６ビット置換関数（Ｂｐ１６）これらの関数が双方ともインボリューション性を有しているため、ベース鍵Ａと変換鍵Ｂとの間にはインボリューション性も保証される。
　図５１も、
　（ａ）フルディフュージョン４ビット関数（Ｄｆ４）
　（ｂ）１６ビット置換関数（Ｂｐ１６）
　これらの２つの関数から構成されるフルディフュージョン性を持つＧ関数を適用した鍵変換処理例（処理例５）を示す図である。
　ベース鍵をＡとし、変換鍵Ｂとする。いずれも各要素４ビットの４×４ステートデータである。
　この処理例５において適用する
　（ａ）フルディフュージョン４ビット関数（Ｄｆ４）
　は、インボリューション性も有する関数である。
　図５１に示す例において、ベース鍵Ａから変換鍵Ｂを生成する処理は、以下の５つのステップによって構成される。
　（Ｓ５１）ベース鍵Ａの１６個の４ビット要素各々に対してインボリューション性を有し、かつフルディフュージョン性を有する４ビット関数（Ｄｆ４）を適用して変換する。
　（Ｓ５２）ステップＳ５１の変換処理によって生成されたデータ（４×４ステート）の各行１６ビットデータ各々に対して、１６ビット置換関数（Ｂｐ１６）を適用して変換する。
　（Ｓ５３）ステップＳ５２の変換処理によって生成されたデータ（４×４ステート）の１６個の４ビット要素各々に対してインボリューション性を有し、かつフルディフュージョン性を有する４ビット関数（Ｄｆ４）を適用して変換する。
　（Ｓ５４）ステップＳ５３の変換処理によって生成されたデータ（４×４ステート）の各列１６ビットデータ各々に対して、１６ビット置換関数（Ｂｐ１６）を適用して変換する。
　（Ｓ５５）ステップＳ５４の変換処理によって生成されたデータ（４×４ステート）の１６個の４ビット要素各々に対してインボリューション性を有し、かつフルディフュージョン性を有する４ビット関数（Ｄｆ４）を適用して変換する。
　これらの処理によって、ベース鍵Ａから変換鍵Ｂを生成する。
　変換鍵のＢの各要素ｂ０～ｂ１５は、ベース鍵Ａの各要素ａ０～ａ１５の影響を受けたデータとなりベース鍵Ａと変換鍵Ｂとの間にはフルディフュージョン性が保証される。さらに、（ａ）フルディフュージョン４ビット関数（Ｄｆ４）、（ｂ）１６ビット置換関数（Ｂｐ１６）これらの関数が双方ともインボリューション性を有しているため、ベース鍵Ａと変換鍵Ｂとの間にはインボリューション性も保証される。
　図４７～図５１まで５つの鍵変換関数Ｇの構成例を説明した。
　これらの鍵変換関数は、ベース鍵Ｋから変換鍵を生成する場合に適用可能であり、また、先に図４２を参照して説明したベース鍵Ｋを分割して生成される分割鍵に対する変換処理に適用することも可能である。
　さらに、２つの分割鍵に対して適用する鍵変換関数を異なる設定としてもよい。
　図５２に示す暗号処理装置は、鍵スケジュール部３８０と、暗号処理部３８５を有する。鍵スケジュール部３８０の鍵レジスタ３８１には、予め生成された秘密鍵Ｋが格納される。
　秘密鍵Ｋは、鍵Ｋ１と鍵Ｋ２の連結データである。
　例えば鍵Ｋ１、Ｋ２は６４ビット鍵であり、その連結データである秘密鍵Ｋは１２８ビットデータである。
　図に示すＧ１、Ｇ２は、鍵変換部である。
　これらは、少なくともフルディフュージョン性を有する。
　あるいはフルディフュージョン性と、インボリューション性、これら２つの特性を有する。
　鍵変換関数Ｇ１，Ｇ２の組み合わせとしては、例えば以下のような設定すが可能である。
　（ａ）Ｇ１，Ｇ２ともフルディフュージョン性を有するがインボリューション性を有さない。
　（ｂ）Ｇ１，Ｇ２ともフルディフュージョン性と、インボリューション性を有する。
　（ｃ）Ｇ１，Ｇ２ともフルディフュージョン性を有し、Ｇ１とＧ２が逆関数の設定、すなわち、Ｇ２＝Ｇ１－１の関係にある。
　鍵変換関数Ｇ１，Ｇ２の組み合わせとしては上記のような様々な設定が可能である。
　　［６．定数入力による安全性向上を実現する構成について］
　次に、ラウンド演算を繰り返し実行する暗号処理部に対して定数（Ｃｏｎｓｔａｎｔ）を入力して、変換対象データあるいはラウンド鍵と、定数との演算を実行し、拡散性能を高めた暗号処理装置について説明する。
　　［６－１．定数入力による安全性向上を実現した従来構成とその問題点について］
　ラウンド関数によるラウンド演算を繰り返し実行する構成において、ラウンド毎の変換処理の同一性を排除するため、ラウンド毎に異なる定数を作用させる構成については、従来から提案されている。
　このような定数入力処理は、スライドアタック、リフレクションアタックと呼ばれる攻撃に対する耐性を高めるために有効な手法であると言われている。
　まず、従来型の定数入力構成の概略と問題点について説明する。
　従来型の定数入力構成例としては、例えば図５３に示すような構成がある。
　図５３に示すラウンド演算実行部４０１ａ～ｄは暗号処理部における排他的論理和部（ラウンド鍵演算部）、非線形変換部、線形変換部を含むラウンド関数実行部である。
　この各ラウンド演算部４０１ａ～ｄに、定数１（ＣＯＮ１）～定数４（ＣＯＮ４）を順次、入力する。
　なお、入力された定数ＣＯＮは、各ラウンド演算部における変換データ、あるいはラウンド鍵との排他的論理和演算が実行される。
　このように、各ラウンドに様々な定数による演算を実行することでラウンド演算間の同一性を排除して、様々な攻撃に対する耐性を高めることができる。
　次に、このような定数入力構成における問題点について説明する。
　暗号処理装置において、ラウンド関数の設定を工夫することで、暗号処理と復号処理を同じ装置で実行可能となる。
　具体的には、図５４に示すように、暗号処理装置の暗号処理部に適用する複数の変換関数の構成を中心から左右に分割したとき、左半分と右半分が逆関数となる関係とすることで、暗号処理と復号処理を同じ装置で実行可能となる。
　これは、インボリューション性を有する暗号処理装置と呼ばれる。
　なお、図５４に示す例では、変換関数Ｅ，４１１と、変換関数Ｅ－１，４１３は逆関数の関係にある。中心の線形変換部Ｍは、入力Ａに対して、出力Ｂを出力し、入力Ｂに対して出力Ａを出力する。
　平文Ｐに対して、変換関数Ｅ，４１１、線形変換部４１２、変換関数Ｅ－１，４１３をこの順番で適用して暗号文Ｃが得られる。
　また、暗号文Ｃに対して、同じ順番で各変換部を適用。すなわち、変換関数Ｅ，４１１、線形変換部４１２、変換関数Ｅ－１，４１３をこの順番で適用することで、元の平文Ｐが得られる。
　このような暗号処理装置を、インボリューション性を持つ暗号処理装置という。なお、インボリューション性を持つ暗号処理装置のなかには、ラウンド関数の実行シーケンスが順方向、逆方向でいずれも同一シーケレンスであるのみならず、各ラウンドにおいて適用するラウンド鍵の入力順も順方向、逆方向とも同一となるようなものも存在する。
　例えば、先に図４３を参照して説明した鍵入力シーケンスが暗号処理装置のインボリューション性を実現する１つの鍵入力シーケンスである。
　しかし、このようなインボリューション性を持つ暗号処理装置の一つの問題として安全性の問題がある。
　この問題点について、図５５を参照して説明する。
　図５５（ａ）は、インボリューション性を持つ暗号処理装置に、定数を入力しない場合の各変換部のデータ入出力値の関係を説明する図である。
　平文Ｐの一部の構成データ＝Ｙとする。
　データＹに対する変換関数Ｅ，４１１の変換結果をＸとする。
　線形変換部４１２は、変換関数Ｅ，４１１からの出力値に対する線形変換を実行するが、その一部の構成データ（ビット）の値は変化しないでそのまま出力される場合がある。なお、線形変換において入出力値が同じ値となる点を不動点とよび、多くの暗号処理装置で適用される線形変換処理には、いくつかの不動点が存在する。
　図５５（ａ）に示す例では、線形変換部４１２に対する入力値Ｘが、線形変換部４１２の不動点の作用によって、そのまま線形変換部４１２の出力Ｘとなったものとする。
　この場合、値Ｘは、変換関数Ｅ－１，４１３に入力される。変換関数Ｅ－１，４１３は、変換関数Ｅ，４１１の逆関数であるため、入力値Ｘは元の値Ｙに戻されることになる。
　すなわち、暗号文Ｃを構成する一部の出力値Ｙは、入力平文Ｐの構成値Ｙと同じ値になってしまう。すなわち暗号処理装置全体においても入出力値が変わらない不動点が発生することになる。
　このような性質は、様々な攻撃に対する脆弱性をもたらす性質であり、暗号処理装置としての安全性を損なう好ましくない性質である。
　図５５（ｂ）は、図５５（ａ）と同様インボリューション性を持つ暗号処理装置であるが、変換関数Ｅ，４１１において定数１（ＣＯＮ１）を入力した演算を行い、また、変換関数Ｅ－１，４１３に定数２（ＣＯＮ２）を入力した演算を行う構成としている。
　これらの定数を入力した場合の各変換部のデータ入出力値の関係を示している。
　平文Ｐの一部の構成データ＝Ｙとする。
　データＹに対する変換関数Ｅ，４１１の変換結果をＸとする。
　この例では、線形変換部４１２に対する入力値Ｘが、線形変換部４１２による線形変換処理によってＸ＋ΔＡに変換されたものとする。
　この場合、値Ｘ＋ΔＡが、変換関数Ｅ－１，４１３に入力される。変換関数Ｅ－１，４１３は、変換関数Ｅ，４１１の逆関数であるが、定数２（ＣＯＮ２）を入力した演算を実行する構成であり、定数１（ＣＯＮ１）を入力した演算を実行する変換関数Ｅ，４１１の完全な逆関数とはならない。
　しかし、定数の選択のしかたによっては、図に示すように、変換関数Ｅ－１，４１３に対する入力Ｘ＋ΔＡに対応する出力値がＹ＋ΔＢのような設定となる場合がある。
　すなわち、
　線形変換部の入出力値の対応が、Ｘと、Ｘ＋ΔＡ、
　暗号処理装置の入出力値の対応が、Ｙと、Ｙ＋ΔＢ、
　このように、入力データに対して特定の差分データを追加した関係性が発生する場合がある。
　このような入出力データの関係性も、やはり様々な攻撃に対する脆弱性をもたらす性質であり、暗号処理装置としての安全性を損なう好ましくない性質である。
　　［６－２．安全性の高い定数入力構成を持つ暗号処理装置の構成について］
　次に、上記のような従来構成の問題点を解決した安全性の高い定数入力構成を持つ暗号処理装置の構成について説明する。
　図５６以下を参照して本実施例にかかる暗号処理装置の構成例について説明する。
　図５６は、本実施例に係る暗号処理部に対する定数入力構成例を説明する図である。
　図５６（ａ）には、図５４を参照して説明したと同様、インボリューション性を有するデータ変換部からなる暗号処理部を示している。
　すなわち、暗号処理部は、
　変換関数Ｅ，４３１、
　線形変換部４３２、
　変換関数Ｅ－１，４３３、
　これらのデータ変換部を有し、変換関数Ｅ－１，４３３、は、変換関数Ｅ４３１の逆関数である。
　本実施例において、定数（ＣＯＮ）４３５は、変換関数Ｅ－１，４３３に入力する。
　なお、変換関数Ｅ－１，４３３は、複数のラウンド関数によって構成され、定数（ＣＯＮ）は、１つ以上のラウンド関数部に対して入力する構成とする。
　なお、ここに示す実施例では、定数（ＣＯＮ）の入力部は、変換関数Ｅ－１，４３３に入力する設定としているが、変換関数Ｅ，４３１側に入力する設定としてもよい。
　すなわち、暗号処理部は、変換関数Ｅ，４３１と、変換関数Ｅ，４３１の逆関数で変換関数Ｅ－１４３３をシーケンシャルに実行するインボリューション性を有し、変換関数Ｅ、または、逆関数Ｅ－１のいずれか一方のみにおいて、１回以上の定数を適用したラウンド演算を実行する構成とする。
　図５６（ｂ）は、定数（ＣＯＮ）４３５の入力構成の具体例を示している。定数（ＣＯＮ）４３５は、暗号処理部の線形変換部４３７の前段の排他的論理和部４３６に入力され。排他的論理和部４３６に対する入力データＡと、排他的論理和演算を実行する。
　なお、排他的論理和部４３６は、ラウンド鍵Ｋｒとの排他的論理和演算を行うラウンド鍵演算部であり、排他的論理和部４３６では、図に示す前段のラウンド演算部からの出力であるデータＡと、ラウンド鍵Ｋｒと、定数ＣＯＮとの排他的論理和演算が実行されることになる。
　すなわち、排他的論理和部４３６では、以下の演算実行結果としてのＢが算出され、後段のラウンド演算部の線形変換処理部４３７に出力される。
　Ｂ＝Ａ（＋）Ｋｒ（＋）ＣＯＮ
　なお、上記式において、（＋）は排他的論理和演算を示すものとする。
　この構成において、入力する定数（ＣＯＮ）４３５の条件として、以下の条件を設定する。
　条件：排他的論理和部４３７に隣接する線形変換部、図に示す例では線形変換部４３７における線形変換処理における入出力値の差分が減少しない値に設定する。
　上記条件は、具体的には、定数ＣＯＮと、線形変換部４３７において適用する線形変換行列との行列演算の結果として得られる全ての要素が非ゼロ、すなわちゼロでない値となることである。
　図５７を参照してこの条件について説明する。
　図５７には、排他的論理和部４３６に入力する定数ＣＯＮ４３５を構成する４×４マトリックスと、線形変換部４３７において起用する線形変換行列Ｍを示している。
　定数ＣＯＮ４３５は、各要素（ｃｏｎ０～ｃｏｎ１５）が４ビットデータである４×４ステートであり、６４ビットデータである。
　また、線形変換行列Ｍは、４×４の行列データである。
　すなわち、以下に示す線形変換行列である。
Figure JPOXMLDOC01-appb-M000012
　定数ＣＯＮの条件は、定数ＣＯＮと、線形変換部４３７において適用する線形変換行列との行列演算の結果として得られる全ての要素が非ゼロ、すなわちゼロでない値となることである。
　すなわち、以下の行列演算によって得られる値が、すべて非ゼロとなることである。
Figure JPOXMLDOC01-appb-M000013
　上記行列演算式によって算出される１６個の値がすべてゼロでない、すなわち非ゼロとなるように、定数ＣＯＮを設定する。
　このような設定により、定数ＣＯＮを入力する排他的論理和部に隣接する線形変換部、図５７に示す例では線形変換部４３７における線形変換処理の入出力値の差分の減少を防止でき、結果として、最小差分アクティブＳボックスの数を所定数以上に維持することが可能となる。
　具体的な定数ＣＯＮの設定例について、図５８を参照して説明する。
　図５８に示す例は、定数ＣＯＮ４３５を入力する排他的論理和部４３６に隣接する線形変換部４３７を、先に図２３～図３０を参照して説明した線形変換部Ｐ１とした設定である。すなわち、以下に示す行列を適用した列拡散演算（ＭｉｘＣｏｌｕｍｎ）を行う設定とした例である。
Figure JPOXMLDOC01-appb-M000014
　線形変換部４３７は、上記の行列Ｍ０を適用した列拡散演算（ＭｉｘＣｏｌｕｍｎ）、すなわち、
　ＭＣ［Ｍ０］
　を実行する。
　このとき、定数ＣＯＮの条件は、この線形変換部４３７において適用する線形変換行列Ｍ０と、定数ＣＯＮとの行列演算の結果として得られる全ての要素が非ゼロ、すなわちゼロでない値となることである。
　このような定数ＣＯＮの例が、図５８に示す定数ＣＯＮであり、以下の要素構成を持つ４×４ステートとなる。
Figure JPOXMLDOC01-appb-M000015
　上記設定を持つ４×４ステートの定数を行列Ｍ０を適用した列拡散演算（ＭｉｘＣｏｌｕｍｎ）：Ｍｃ［Ｍ０］を実行する線形変換部に隣接する排他的論理和部に入力して排他的論理和演算を実行する。この構成によって、線形変換部の線形変換による差分減少が防止される。この結果、最小差分アクティブＳボックスの数の減少を防止することが可能となり、各種の攻撃に対する耐性を高めた安全性の高い暗号処理構成が実現される。
　図５９は、上記の定数条件を満足する定数ＣＯＮの入力構成を持つ暗号処理装置の暗号処理部に対するラウンド鍵と定数ＣＯＮの入力構成と演算構成例を示す図である。
　図５９において、平文Ｐは、左下から入力され、暗号文Ｃは右下から出力される。
　図５９に示す暗号処理装置の暗号処理部４５１（Ｅ）は、図５６（ａ）に示す変換関数Ｅ，４３１に相当する。
　また、線形変換部（Ｐ２）４５２は、図５６（ａ）に示す線形変換部４３２に相当する。
　また、暗号処理部４５３（Ｅ－１）は、図５６（ａ）に示す変換関数Ｅ－１，４３３に相当する。
　図５９に示す暗号処理装置構成は、インボリューション性を持つ暗号処理装置である。
　図５９に示すラウンド鍵入力例は、先に図４３を参照して説明した構成例に対応する。すなわち、暗号処理部に構成された排他的論理和部に対するラウンド鍵の入力順は、以下の通りである。
　鍵Ｋ１、
　鍵Ｋ２、
　変換鍵Ｋｄ１、
　変換鍵Ｋｄ２、
　排他的論理和演算鍵Ｋ１（＋）Ｋ２、
　排他的論理和演算変換鍵Ｋｄ１（＋）Ｋｄ２、
　排他的論理和演算鍵Ｋ１（＋）Ｋ２、
　排他的論理和演算鍵Ｋ１（＋）Ｋ２、
　排他的論理和演算変換鍵Ｋｄ１（＋）Ｋｄ２、
　排他的論理和演算鍵Ｋ１（＋）Ｋ２、
　変換鍵Ｋｄ２、
　変換鍵Ｋｄ１、
　鍵Ｋ２、
　鍵Ｋ１、
　なお、図４３に示す設定では、ラウンド演算部Ｒ６に対して、排他的論理和演算鍵Ｋ１（＋）Ｋ２を入力する設定としているが、図５９に示す例では、線形変換部４５２の前後において、排他的論理和演算鍵Ｋ１（＋）Ｋ２、を繰り返し入力する設定である。
　図５９に示す構成は、図４３に示すラウンド演算部Ｒ６を、
　線形変換部４５２と、線形変換部４５２前後の２つの、
　排他的論理和演算鍵Ｋ１（＋）Ｋ２との排他的論理和部、
　非線形変換部、
　これらの変換部によって構成されるラウンド演算部とする設定した場合の構成に対応する。
　鍵スケジュール部のラウンド鍵供給部は、上記の順番で６種類の鍵を出力する。この鍵の入力シーケンスは、逆の順番も同一シーケンスとなる。
　これは、平文Ｐから暗号文Ｃを生成する暗号処理における鍵入力順と、暗号文Ｃから平文Ｐを生成する復号処理における鍵入力順を同じ設定とすることが可能であることを意味する。すなわち、インボリューション性を持つ鍵入力シーケンスであり、暗号処理および復号処理に適用するハードウェアやプログラムの共通化が可能であり、装置の軽量化（小型化）に寄与する設定である。
　図５９に示す構成において、定数ＣＯＮは、暗号処理部４５３（Ｅ－１）の排他的論理和部４６１、排他的論理和部４６３、排他的論理和部４６５、これらの各排他的論理和部に入力する。
　これらの定数ＣＯＮは、例えば、図５８を参照して説明した４×４ステートの定数ＣＯＮである。
　また、これら３つの排他的論理和部４６１，４６３，４６５に隣接する線形変換部４６２，４６４，４６６は、いずれも前述の行列Ｍ０を適用した列拡散演算（ＭｉｘＣｏｌｕｍｎ）、すなわち、
　ＭＣ［Ｍ０］
　を実行する。
　この図５９に示す暗号処理部は、平文Ｐから暗号文Ｃを生成するシーケンスと、逆のシーケンスを実行することで、暗号文Ｃから平文Ｐを生成することも可能なインボリューション性を持つ構成であり、同一のハードウェア、あるいは同一プログラムを適用して暗号化処理と復号処理を行なうことが可能となる。
　また、鍵入力シーケンスも暗号化と復号処理において同一のシーケンスとなるため、鍵スケジュール部の鍵供給処理も同一のハードウェア、あるいは同一プログラムを適用した処理として実行可能となる。
　上述した定数入力構成によって、最小差分アクティブＳボックスの数の減少を防止することが可能となり、各種の攻撃に対する耐性を高めた安全性の高い暗号処理構成が実現される。
　なお、一般的な暗号処理におけるアクティブＳボックスに基づく評価処理と、本開示の定数入力構成におけるアクティブＳボックスに基づく評価処理とはやや異なっており、この点について、図６０、図６１を参照して説明する。
　前述したように共通鍵ブロック暗号に設定される非線形変換部には、ｓビット単位の非線形変換を実行するＳボックス（Ｓ－ｂｏｘ）が用いられる。
　差分攻撃に対する耐性を図る指標として，差分の接続関係を表現した差分パスに含まれる差分アクティブＳボックスの最小数、すなわち、最小差分アクティブＳボックス数がある。
　一般的なブロック暗号において、非線形変換はＳボックスによる処理の部分のみである。図６０（Ａ），（Ｂ）に示すように、ブロック暗号を実行するブロック暗号装置に対して、特定の差分ΔＸを持つデータＰ１，Ｐ２を個別に入力して暗号処理結果Ｃ１，Ｃ２を得る。
　この２つの暗号処理（Ａ），（Ｂ）において、差分値が入力されるＳボックスをアクティブＳボックスと定義する。差分値が入力されるＳボックスを特定することで、解析容易性が高まる。すなわち攻撃に対する耐性が弱まることになる。
　一般的には、この図６０に示すように所定の差分ΔＸを有する２つの入力Ｐ１，Ｐ２を設定した場合に発生する差分値が入力されるＳボックスの数をアクティブＳボックスと定義し、この数をカウントすることで安全性評価を行う。
　図６１は、上述した図５６（ａ）に示すインボリューション性を有するデータ変換部からなる暗号処理部を示している。
　すなわち、暗号処理部は、
　変換関数Ｅ，４３１、
　線形変換部４３２、
　変換関数Ｅ－１，４３３、
　これらのデータ変換部を有し、変換関数Ｅ－１，４３３、は、変換関数Ｅ４３１の逆関数である。
　定数（ＣＯＮ）４３５は、変換関数Ｅ－１，４３３に入力する。
　なお、変換関数Ｅ－１，４３３は、複数のラウンド関数によって構成され、定数（ＣＯＮ）は、１つ以上のラウンド関数部に対して入力する。
　暗号処理部は、変換関数Ｅ，４３１と、変換関数Ｅ，４３１の逆関数で変換関数Ｅ－１４３３をシーケンシャルに実行するインボリューション性を有し、変換関数Ｅ、または、逆関数Ｅ－１のいずれか一方のみにおいて、１回以上の定数を適用したラウンド演算を実行する。
　この構成において、変換関数Ｅ４３１に対して、線形変換部４３２側から入力Ｓ１を入力して、出力Ｔを得る。
　一方、変換関数Ｅ－１，４３３に対して、同様に線形変換部４３２側から、上記の入力値Ｓ１に対して差分値ΔＸを付加した入力Ｓ２（＝Ｓ１（＋）ΔＸ）を入力して、出力Ｔ（＋）ΔＹを得る。
　この２つの関数、すなわち、変換関数Ｅ４３１と、変換関数Ｅ４３１の逆関数である変換関数Ｅ－１，４３３に対して、図６１に示すように、逆方向に差分ΔＸを有する入力値Ｓ１，Ｓ２を入力したときに、各関数において対応位置にあるＳボックス中、差分が入力されるＳボックスをアクティブＳボックスとする。
　図６２は、前述の図５９に示す暗号処理構成におけるアクティブＳボックスの数の算出構成を説明する図である。
　図６２に示す暗号処理装置の暗号処理部４５１（Ｅ）の線形変換部４５２側から入力値Ｓ１を入力し、暗号処理部４５１（Ｅ）を適用した暗号処理を実行する。
　一方、暗号処理部４５１（Ｅ）の逆関数である暗号処理部４５３（Ｅ－１）の線形変換部４５２側から入力値Ｓ１に対して差分ΔＸを設定した入力値Ｓ２を入力し、暗号処理部４５３（Ｅ－１）を適用した暗号処理を実行する。
　この２つの暗号処理において各暗号処理部（Ｅ），（Ｅ－１）において対応位置にあるＳボックス中、差分が入力されるＳボックスをアクティブＳボックスとする。
　なお、アクティブＳボックスの数が減少すると、例えばスライド攻撃やリフレクション攻撃と呼ばれる攻撃に対する耐性が弱くなり、アクティブＳボックスの数を一定以上に維持することで、これらの攻撃に対する耐性が高めることが可能となり、安全性を向上させることができる。上述した定数入力構成によって、アクティブＳボックスの数の減少を防止することが可能となり、各種の攻撃に対する耐性を高めた安全性の高い暗号処理構成が実現される。
　　［６－３．定数挿入位置のバリエーションについて］
　上述した実施例では、データ変換関数Ｅと、データ変換関数Ｅの逆関数Ｅ－１をシーケンシャルに実行するインボリューション性を有する暗号処理装置に対して、関数Ｅ、または逆関数Ｅ－１のいずれか一方のみに定数ＣＯＮを入力して定数を適用したラウンド演算を実行する構成について説明した。
　このような設定により、定数ＣＯＮを入力する排他的論理和部に隣接する線形変換部、図５７に示す例では線形変換部４３７における線形変換処理の入出力値の差分の減少を防止でき、結果として、最小差分アクティブＳボックスの数を所定数以上に維持することが可能となる。
　この定数入力構成は、関数Ｅ、または逆関数Ｅ－１のいずれか一方のみに限定されず、関数Ｅ、および逆関数Ｅ－１の双方において１回以上の定数を適用したラウンド演算を実行する構成としてもよい。ただし、定数適用位置は、関数Ｅ、および逆関数Ｅ－１の対応位置ではない、対応位置からずれた位置（非対応位置）とする。
　この定数入力構成を持つ暗号処理装置の構成例を図６３に示す。
　図６３において、平文Ｐは、左下から入力され、暗号文Ｃは右下から出力される。
　図６３に示す暗号処理装置の暗号処理部４５１（Ｅ）は、図５６（ａ）に示す変換関数Ｅ，４３１に相当する。
　また、線形変換部（Ｐ２）４５２は、図５６（ａ）に示す線形変換部４３２に相当する。
　また、暗号処理部４５３（Ｅ－１）は、図５６（ａ）に示す変換関数Ｅ－１，４３３に相当する。
　図６３に示す暗号処理部の構成は、インボリューション性を持つ暗号処理部である。
　図６３に示すラウンド鍵入力例は、先に図４３を参照して説明した構成例に対応する。すなわち、暗号処理部に構成された排他的論理和部に対するラウンド鍵の入力順は、以下の通りである。
　鍵Ｋ１、
　鍵Ｋ２、
　変換鍵Ｋｄ１、
　変換鍵Ｋｄ２、
　排他的論理和演算鍵Ｋ１（＋）Ｋ２、
　排他的論理和演算変換鍵Ｋｄ１（＋）Ｋｄ２、
　排他的論理和演算鍵Ｋ１（＋）Ｋ２、
　排他的論理和演算鍵Ｋ１（＋）Ｋ２、
　排他的論理和演算変換鍵Ｋｄ１（＋）Ｋｄ２、
　排他的論理和演算鍵Ｋ１（＋）Ｋ２、
　変換鍵Ｋｄ２、
　変換鍵Ｋｄ１、
　鍵Ｋ２、
　鍵Ｋ１、
　なお、図４３に示す設定では、ラウンド演算部Ｒ６に対して、排他的論理和演算鍵Ｋ１（＋）Ｋ２を入力する設定としているが、図６３に示す例では、線形変換部４５２の前後において、排他的論理和演算鍵Ｋ１（＋）Ｋ２、を繰り返し入力する設定である。
　図６３に示す構成は、図４３に示すラウンド演算部Ｒ６を、
　線形変換部４５２と、線形変換部４５２前後の２つの、
　排他的論理和演算鍵Ｋ１（＋）Ｋ２との排他的論理和部、
　非線形変換部、
　これらの変換部によって構成されるラウンド演算部とする設定した場合の構成に対応する。
　鍵スケジュール部のラウンド鍵供給部は、上記の順番で６種類の鍵を出力する。この鍵の入力シーケンスは、逆の順番も同一シーケンスとなる。
　これは、平文Ｐから暗号文Ｃを生成する暗号処理における鍵入力順と、暗号文Ｃから平文Ｐを生成する復号処理における鍵入力順を同じ設定とすることが可能であることを意味する。すなわち、インボリューション性を持つ鍵入力シーケンスであり、暗号処理および復号処理に適用するハードウェアやプログラムの共通化が可能であり、装置の軽量化（小型化）に寄与する設定である。
　図６３に示す構成において、定数ＣＯＮは、
　暗号処理部４５１（Ｅ）の排他的論理和部４７１、排他的論理和部４７２、これらの各排他的論理和部に入力する。
　さらに、暗号処理部４５３（Ｅ－１）の排他的論理和部４７３にも入力する。
　定数ＣＯＮは、例えば、図５８を参照して説明した４×４ステートの定数ＣＯＮである。
　また、これら３つの排他的論理和部４７１，４７２，４７３に隣接する線形変換部４８１，４８２，４８３は、いずれも前述の行列Ｍ０を適用した列拡散演算（ＭｉｘＣｏｌｕｍｎ）、すなわち、
　ＭＣ［Ｍ０］
　を実行する。
　このように、定数入力構成は、関数Ｅ、または逆関数Ｅ－１のいずれか一方のみに限定されず、関数Ｅ、および逆関数Ｅ－１の双方において１回以上の定数を適用したラウンド演算を実行する構成としてもよい。ただし、定数適用位置は、関数Ｅ、および逆関数Ｅ－１の対応位置ではない、ずれた位置（非対応位置）とする。
　この図６３に示す暗号処理部は、平文Ｐから暗号文Ｃを生成するシーケンスと、逆のシーケンスを実行することで、暗号文Ｃから平文Ｐを生成することも可能なインボリューション性を持つ構成であり、同一のハードウェア、あるいは同一プログラムを適用して暗号化処理と復号処理を行なうことが可能となる。
　また、鍵入力シーケンスも暗号化と復号処理において同一のシーケンスとなるため、鍵スケジュール部の鍵供給処理も同一のハードウェア、あるいは同一プログラムを適用した処理として実行可能となる。
　　［７．非線形変換部に適用するＳボックス（Ｓ－ｂｏｘ）の具体的構成例について］
　次に、非線形変換部に適用するＳボックス（Ｓ－ｂｏｘ）の具体的構成例について説明する。
　例えば図１９に示す暗号処理装置１００において、暗号処理部１２０のインボリューション性、すなわち、平文Ｐから暗号文Ｃを生成して出力するハードウェア、あるいはプログラムと、暗号文Ｃから平文Ｐを生成して出力するハードウェアあるいはプログラムを同一とするためには、暗号処理部１２０に構成される非線形変換部１２２についてもインボリューション性が要求される。
　以下、暗号処理部１２０に構成される非線形変換部１２２のインボリューション性を有する構成例について説明する。
　先に、図２２を参照して説明したように、図１９に示す暗号処理装置１００の暗号処理部１２０内の非線形変換部１２２は、例えば図２２（１）に示すように、複数のＳボックス（Ｓ－ｂｏｘ）を有する構成である。
　各Ｓボックスは例えば、４ビット入出力構成を持つ非線形変換部であり、１６個のＳボックスによる並列処理によって４×１６＝６４ビットの非線形変換処理を実行する。
　この４ビット入出力のＳボックス（Ｓ－ｂｏｘ）がインボリューション性を持つ構成であることが必要である。
　すなわち４ビット入力値に対して、ある４ビット出力値が得られた場合、その４ビット出力値を同一のＳボックスに入力した場合、元の４ビット入力値が得られる構成であることが必要である。
　なお、インボリューション性を有する関数ｆ（ｘ）は、すべての入力値ｘに対して、
　ｆ（ｆ（ｘ））＝ｘ
　上記を満たす関数である。
　暗号処理部１２０に構成される非線形変換部１２２は、このインボリューション性を有する関数ｆ（ｘ）であることが要求される。
　図６４以下を参照してインボリューション性を持つ４ビット入出力Ｓボックスの構成例について説明する。
　図６４（１）は、先に説明した図２２（１）と同様、非線形変換部の構成例を示す図である。
　すなわち、図１９に示す暗号処理装置１００の暗号処理部１２０に構成される非線形変換部１２２の構成例である。非線形変換部１２２は、非線形変換処理を実行するＳボックス（Ｓ－ｂｏｘ）を複数配置した構成を有する、
　各Ｓボックスは４ビットデータの非線形変換を実行する。
　図６４（２）は、非線形変換部内に構成される１つのＳボックス（Ｓ－ｂｏｘ）の構成を示している。Ｓボックス（Ｓ－ｂｏｘ）は、
　非線形変換層１，５２１、
　線形変換層５２２、
　非線形変換層２，５２３、
　これら３つの層に区分することができる。
　なお、非線形変換層２，５２３は、非線形変換層１，５２１の逆関数となっている。
　図６５に、具体的なＳボックス（Ｓ－ｂｏｘ）の回路構成例を示す。
　図６５に示すように、
　非線形変換層１，５２１は、２つの排他的論理和演算部（ＸＯＲ）と、２つの基本演算子によって構成される。
　なお、図６５に示す例では、基本演算子としてＮＯＲ回路を設定した例を示しているが、基本演算子は、ＡＮＤ回路、ＯＲ回路、ＮＡＮＤ回路、いずれかの２入力１出力の演算を行う基本演算子に置き換え可能である。
　また、２つの基本演算子は、同一の基本演算子の組み合わせとしても、異なる基本演算子の組み合わせとしてもよい。
　線形変換層５２２は、入力４ビットの入れ替え処理を行なう線形変換層であり、基本的にインボリューション性を有する。
　非線形変換層２，５２３は、非線形変換層１，５２１の逆関数によって構成される。
　これらの３つの層によって構成されるＳボックス回路は、インボリューション性を有する非線形変換回路となる。
　図６５の下部に、図６５に示すＳボックスに対する入力値（ｉｎ）と出力値（ｏｕｔ）との対応関係データを示す。
　なお、入出力値はいずれも４ビットデータであり、００００～１１１１のデータである。図６５に示す表は、００００～１１１１を１０進法で示す０～１５の入力値と出力値との対応表として示している。
　この表から理解されるように、任意の入力値Ｘから得られる出力値Ｙを、入力値Ｙとして得られる出力値は元の入力値Ｘとなる。
　すなわち、図６５に示す４ビット入出力Ｓボックスは、インボリューション性を有する持つ非線形変換回路である。
　図６６に、このＳボックス（Ｓ－ｂｏｘ）によるデータ変換式を示す。
　Ｓボックス（Ｓ－ｂｏｘ）に対する４ビット入力を、
　ａｉｎ，ｂｉｎ，ｃｉｎ，ｄｉｎとし、
　Ｓボックス（Ｓ－ｂｏｘ）からの４ビット出力を、
　ａｏｕｔ，ｂｏｕｔ，ｃｏｕｔ，ｄｏｕｔ、
　とする。
　Ｓボックス（Ｓ－ｂｏｘ）によるデータ変換式は、以下の通りである。
Figure JPOXMLDOC01-appb-M000016
　なお、上記式において、～（ｘ｜ｙ）は、（）内の値の否定（ＮＯＴ）を示す。具体的には、ＮＯＲ回路に対する入力値がｘとｙである場合のＮＯＲ回路の出力値を示す。
　上記演算式によって表現されるデータ変換を実行するＳボックスは、インボリューション性を有する。
　また、この図６６に示すＳボックス回路は、差分確率、線形確率がいずれも２－２であり、十分な安全性を有する。
　図６６に示すＳボックスは、４つの排他的論理和演算子（ＸＯＲ）と４つのＮＯＲ回路から構成され、ハードウェア回路上に必要なゲート数は１３ゲートとなる。
　なお、必要なゲート数は、排他的論理和演算子（ＸＯＲ）＝２．２５ゲート、ＮＯＲ回路＝１ゲートとして算出している。
　例えば図５４を参照して説明した暗号処理部構成、すなわち、
　変換関数Ｅ４１１、
　線形変換部４１２、
　変換関数Ｅ－１４１３、
　これらの構成を持つ暗号処理部内の変換関数Ｅ４１１と、変換関数Ｅ－１４１３内の非線形変換部に図６４～図６６に示すＳボックスを利用した構成とすることで、暗号処理部全体のインボリューション性が実現される。
　なお、図６５、図６６を参照して説明したＳボックスは、
　非線形変換層１、
　線形変換層、
　非線形変換層２、
　これらの３層構成となっているが、この３層構成を持つＳボックスの他の例について以下説明する。
　なお、上記３層構成中の線形変換層の必要条件として、インボリューション性を有し、かつ、入出力ビットが不変となる置換部を有していないビット置換を実行する構成であることが必要である。
　この線形変換層の条件について、図６７を参照して説明する。
　図６７には４ビット入出力Ｓボックスにおける線形変換層の設定例を示している。
　図６５、図６６を参照して説明したＳボックスと同様、
　非線形変換層１、
　線形変換層、
　非線形変換層２、
　これらの３層構成を持つ４ビット入出力Ｓボックスにおいて線形変換層は、例えば、図６７（１）に示す設定のいずれかとする。
　線形変換層に対する入力４ビットをＸ＝（ｘ０，ｘ１，ｘ２，ｘ３）、出力４ヒビットＹ＝（ｙ０，ｙ１，ｙ２，ｙ３）としたとき、
　インボリューション性を有し、かつ、入出力ビットが同一とならない設定、すなわち、
　ｙｉ≠ｘｉ
　ただしｉ＝０，１，２，３、
　上記式が成立することが線形変換層の条件となる。
　図６７（２）に示す線形変換構成は、上記条件を満たさず、不適合となる。
　４ビット置換を実行する線形変換層の置換関数Ｐ４の条件を、式で示すと以下のように示すことができる。
　（ａ）Ｐ４（Ｐ４（Ｘ））＝Ｘ
　（ｂ）　ｙｉ≠ｘｉ　　　ただしｉ＝０，１，２，３、
　上記（ａ）は置換関数Ｐ４がインボリューション性を有することを示す条件式である。
　（ｂ）は、入出力ビットが同一とならないことを示す条件式である。
　線形変換層は、上記条件を満たす置換処理を行なう構成であることが必要である。
　４ビット置換を行うＳボックスの例として、図６５、図６６を参照して構成と異なる構成を持つ例について、図６８以下を参照して説明する。
　図６８に示すＳボックスは、
　非線形変換層１，５３１、
　線形変換層５３２、
　非線形変換層２，５３３、
　これらの３層構成を持つ４ビット入出力Ｓボックスである。
　非線形変換層１，５３１は、２つの排他的論理和演算部（ＸＯＲ）と、ＮＡＮＤ回路とＮＯＲ回路によって構成されている。
　線形変換層５３２は、入力４ビットの入れ替え処理を行なう線形変換層であり、インボリューション性を有する。
　非線形変換層２，５３３は、非線形変換層１，５３１の逆関数によって構成される。
　これらの３つの層によって構成されるＳボックス回路は、インボリューション性を有する非線形変換回路となる。
　図６８の下部に、図６８に示すＳボックスに対する入力値（ｉｎ）と出力値（ｏｕｔ）との対応関係データを示す。
　なお、入出力値はいずれも４ビットデータであり、００００～１１１１のデータである。図６８に示す表は、００００～１１１１を１０進法で示す０～１５の入力値と出力値との対応表として示している。
　この表から理解されるように、任意の入力値Ｘから得られる出力値Ｙを、入力値Ｙとして得られる出力値は元の入力値Ｘとなる。
　すなわち、図６８に示す４ビット入出力Ｓボックスは、インボリューション性を有する持つ非線形変換回路である。
　図６９に、このＳボックス（Ｓ－ｂｏｘ）によるデータ変換式を示す。
　Ｓボックス（Ｓ－ｂｏｘ）に対する４ビット入力を、
　ａｉｎ，ｂｉｎ，ｃｉｎ，ｄｉｎとし、
　Ｓボックス（Ｓ－ｂｏｘ）からの４ビット出力を、
　ａｏｕｔ，ｂｏｕｔ，ｃｏｕｔ，ｄｏｕｔ、
　とする。
　Ｓボックス（Ｓ－ｂｏｘ）によるデータ変換式は、以下の通りである。
Figure JPOXMLDOC01-appb-M000017
　なお、上記式において、
　～（ｘ｜ｙ）は、ＮＯＲ回路に対する入力値がｘとｙである場合のＮＯＲ回路の出力値を示す。
　～（ｘ＆ｙ）は、ＮＡＮＤ回路に対する入力値がｘとｙである場合のＮＡＮＤ回路の出力値を示す。
　上記演算式によって表現されるデータ変換を実行するＳボックスは、インボリューション性を有する。
　また、この図６９に示すＳボックス回路も、差分確率、線形確率がいずれも２－２であり、十分な安全性を有する。
　図６９に示すＳボックスは、４つの排他的論理和演算子（ＸＯＲ）と２つのＮＯＲ回路と２つのＮＡＮＤ回路から構成される
　例えば図５４を参照して説明した暗号処理部構成、すなわち、
　変換関数Ｅ４１１、
　線形変換部４１２、
　変換関数Ｅ－１４１３、
　これらの構成を持つ暗号処理部内の変換関数Ｅ４１１と、変換関数Ｅ－１４１３内の非線形変換部に図６９に示すＳボックスを利用した構成とすることで、暗号処理部全体のインボリューション性が実現される。
　次に、図７０を参照してさらに異なる構成を持つ４ビット入出力Ｓボックスの例について説明する。
　図７０に示すＳボックスは、
　非線形変換層１，５４１、
　線形変換層５４２、
　非線形変換層２，５４３、
　これらの３層構成を持つ４ビット入出力Ｓボックスである。
　非線形変換層１，５４１は、２つの排他的論理和演算部（ＸＯＲ）と、２つのＯＲ回路によって構成されている。
　線形変換層５４２は、入力４ビットの入れ替え処理を行なう線形変換層であり、インボリューション性を有する。
　非線形変換層２，５４３は、非線形変換層１，５４１の逆関数によって構成される。
　これらの３つの層によって構成されるＳボックス回路は、インボリューション性を有する非線形変換回路となる。
　図７０の下部に、図６８に示すＳボックスに対する入力値（ｉｎ）と出力値（ｏｕｔ）との対応関係データを示す。
　なお、入出力値はいずれも４ビットデータであり、００００～１１１１のデータである。図７０に示す表は、００００～１１１１を１０進法で示す０～１５の入力値と出力値との対応表として示している。
　この表から理解されるように、任意の入力値Ｘから得られる出力値Ｙを、入力値Ｙとして得られる出力値は元の入力値Ｘとなる。
　すなわち、図７０に示す４ビット入出力Ｓボックスは、インボリューション性を有する持つ非線形変換回路である。
　図７１に、このＳボックス（Ｓ－ｂｏｘ）によるデータ変換式を示す。
　Ｓボックス（Ｓ－ｂｏｘ）に対する４ビット入力を、
　ａｉｎ，ｂｉｎ，ｃｉｎ，ｄｉｎとし、
　Ｓボックス（Ｓ－ｂｏｘ）からの４ビット出力を、
　ａｏｕｔ，ｂｏｕｔ，ｃｏｕｔ，ｄｏｕｔ、
　とする。
　Ｓボックス（Ｓ－ｂｏｘ）によるデータ変換式は、以下の通りである。
Figure JPOXMLDOC01-appb-M000018
　なお、上記式において、
　（ｘ｜ｙ）は、ＯＲ回路に対する入力値がｘとｙである場合のＯＲ回路の出力値を示す。
　上記演算式によって表現されるデータ変換を実行するＳボックスは、インボリューション性を有する。
　また、この図７１に示すＳボックス回路も、差分確率、線形確率がいずれも２－２であり、十分な安全性を有する。
　図７１に示すＳボックスは、４つの排他的論理和演算子（ＸＯＲ）と４つのＯＲ回路から構成される
　例えば図５４を参照して説明した暗号処理部構成、すなわち、
　変換関数Ｅ４１１、
　線形変換部４１２、
　変換関数Ｅ－１４１３、
　これらの構成を持つ暗号処理部内の変換関数Ｅ４１１と、変換関数Ｅ－１４１３内の非線形変換部に図７１に示すＳボックスを利用した構成とすることで、暗号処理部全体のインボリューション性が実現される。
　　［８．暗号処理装置の具体例について］
　次に、上述した説明に従った各構成、すなわち、以下の各構成を全て有する暗号処理装置の全体構成例について説明する。
　（１）安全性を高めた共通鍵暗号処理の全体構成（図１９～図２２）
　（２）複数の異なる線形変換行列を適用した線形変換を実行する構成（図２３～図３１）
　（３）ベース鍵と変換鍵を使用して生成したラウンド鍵を提供し、インボリューション性、フルディフュージョン性を実現する鍵スケジュール部の構成（図３２～図５２）
　（４）定数入力構成（図５３～図６３）
　（５）インボリューション性を持つＳボックスを適用した非線形変換部の構成（図６４～図７１）
　図７２に示す暗号処理装置７００は、上記の各構成を全て備えた暗号処理装置の一例を示す図である。
　暗号処理装置７００は、鍵スケジュール部７２０と、暗号処理部７５０を有する。
　暗号処理部７５０は、排他的論理和部７５１、非線形変換部７５２、線形変換部７５３の各データ変換部を有し、これらの処理を繰り返し実行する構成を有する。
　一方、鍵スケジュール部７２０は、暗号処理部７５０に構成された排他的論理和部の各々に対してラウンド鍵ＲＫｎを出力して、変換対象データとの排他的論理和演算を実行させる。
　鍵スケジュール部７２０は、ラウンド鍵供給部７２１と定数供給部（定数レジスタ）７２５を有する。
　また、ラウンド鍵供給部７２１は、秘密鍵Ｋを格納した鍵レジスタ７２２と、鍵変換部７２３を有する。
　図７２に示す暗号処理装置７００の暗号処理部７５０は、例えば６４ビットの平文Ｐを入力して、６４ビットの暗号文Ｃを出力する。また、この同じ暗号処理部７５０を適用して、暗号文Ｃを入力して平文Ｐを出力することが可能である。
　変換データが６４ビットである場合、各ラウンド鍵ＲＫｎも６４ビットである。
　なお、これらの各６４ビットデータは、いずれも各要素４ビットの１６要素からなる４×４ステートである。
　なお、暗号処理部７５０は、平文Ｐを入力データとしてラウンド演算を繰り返して出力データとしての暗号文Ｃを出力可能であるとともに、暗号文Ｃを入力データとして、ラウンド演算の実行シーケンスを逆順に設定したデータ変換処理により出力データとして前記平文Ｐを生成可能なインボリューション性を有する構成である。
　平文Ｐから暗号文Ｃを生成する場合は、図に示す暗号処理部７５０の上段から下段に向けて各変換処理を実行する。
　一方、暗号文Ｃから平文Ｐを生成する場合は、図に示す暗号処理部７５０の下段から上段に向けて各変換処理を実行する。
　また、鍵スケジュール部７２０のラウンド鍵供給部７２１は、平文Ｐから暗号文Ｃを生成する場合の鍵供給シーケンスと、暗号文Ｃから平文Ｐを生成する場合の鍵供給シーケンスが一致するインボリューション性を有する鍵供給処理を行なう構成である。なお、鍵スケジュール部７２０は、暗号処理部７５０に対する鍵供給処理に際して、供給鍵の一部に定数による演算を施し、演算結果である鍵データを暗号処理部７５０に出力する。
　このように、図７２に示す暗号処理部７５０の構成は、先に図５９を参照して説明した構成と同様、変換関数Ｅ、線形変換関数、変換関数Ｅ－１のシーケンスで各変換関数が設定されており、インボリューション性を有する構成である。
　暗号処理部７５０には、先に項目［４．暗号処理部の線形変換部の構成と処理について］において、図２３～図３１を参照して説明したように、３種類の異なる線形変換処理を実行する線形変換処理部が設定されている。
　すなわち、
　線形変換部Ｐ１、
　線形変換部Ｐ２、
　線形変換部Ｐ３、
　これらの３つの異なる線形変換部を有し、暗号処理において、ラウンド毎に実行する線形変換処理を変更する。すなわち、連続ラウンドでは同じ線形変換処理を行なわない設定としている。
　線形変換部Ｐ１は、４×４ステートの入力データの各列の要素に対して、各列単位で、１つの行列Ｍ０を適用した行列演算を行う。
　これは、先に、図２４、図２５を参照して説明した列拡散演算（ＭｉｘＣｏｌｕｍ）である。
　すなわち、線形変換処理部Ｐ１は、
　ＭＣ［Ｍ０］
　上記式によって示される列拡散演算（ＭＣ）を実行する。
　なお、ＭＣ［Ｍ０］は、ステートの各列に対して、同一の行列Ｍ０を適用した行列演算を示す式であり、ステートの各列に対して適用する行列を個別に示した式、
　ＭＣ［Ｍ０，Ｍ０，Ｍ０，Ｍ０］
　上記式と同じ意味である。
　線形変換部Ｐ２は、先に図２４、図２６等を参照して説明したように、４×４ステートの入力データの各行の要素に対して、各行単位で異なる行列を適用した行列演算を行う。上位の第１行から第４行に対して、以下の行列を適用した行列演算を実行する。
　第１行：適用行列Ｍ０、
　第２行：適用行列Ｍ１、
　第３行：適用行列Ｍ２、
　第４行：適用行列Ｍ３、
　すなわち、線形変換処理部Ｐ２は、
　ＭＲ［Ｍ０，Ｍ１，Ｍ２，Ｍ３］
　上記式によって示される行拡散演算（ＭｉｘＲｏｗ）を実行する。
　線形変換処理部Ｐ３も、線形変換処理部Ｐ２と同様、図２４（２）に示すように、４×４ステートの入力データの各行の要素に対して、各行単位で異なる行列を適用した行列演算を行う。線形変換処理Ｐ３は、線形変換処理Ｐ２とは異なり、上位の第１行から第４行に対して、以下の行列を適用した行列演算を実行する。
　第１行：適用行列Ｍ２、
　第２行：適用行列Ｍ０、
　第３行：適用行列Ｍ１、
　第４行：適用行列Ｍ３、
　これは、先に、図２７を参照して説明した行拡散演算（ＭｉｘＲｏｗ）である。
　すなわち、線形変換処理部Ｐ３は、
　ＭＲ［Ｍ２，Ｍ０，Ｍ１，Ｍ３］
　上記式によって示される行拡散演算（ＭｉｘＲｏｗ）を実行する。
　これらの複数の異なる線形変換処理を組み合わせて利用し、ラウンド毎に実行する線形変換処理を切り換えることで、先に図３０を参照して説明したように、アクティブＳボックスの数を増加させることが可能となり、より安全性の高い暗号処理（暗号化処理および復号処理）が実現される。
　なお、図７２に示す暗号処理部７５０は、以下の各データ変換部を順次適用したデータ変換処理を実行する。
　ラウンド鍵ＲＫ１との排他的論理和演算を行う排他的論理和部、
　非線形変換部Ｓ、
　線形変換部Ｐ１、
　ラウンド鍵ＲＫ２との排他的論理和演算を行う排他的論理和部、
　非線形変換部Ｓ、
　線形変換部Ｐ２、
　ラウンド鍵ＲＫ３との排他的論理和演算を行う排他的論理和部、
　非線形変換部Ｓ、
　線形変換部Ｐ１、
　ラウンド鍵ＲＫ４との排他的論理和演算を行う排他的論理和部、
　非線形変換部Ｓ、
　線形変換部Ｐ３、
　ラウンド鍵ＲＫ５との排他的論理和演算を行う排他的論理和部、
　非線形変換部Ｓ、
　線形変換部Ｐ１、
　ラウンド鍵ＲＫ６との排他的論理和演算を行う排他的論理和部、
　非線形変換部Ｓ、
　ラウンド鍵ＲＫ７との排他的論理和演算を行う排他的論理和部、
　線形変換部Ｐ２、
　ラウンド鍵ＲＫ７との排他的論理和演算を行う排他的論理和部、
　非線形変換部Ｓ、
　ラウンド鍵ＲＫ８との排他的論理和演算を行う排他的論理和部、
　線形変換部Ｐ１、
　非線形変換部Ｓ、
　ラウンド鍵ＲＫ９との排他的論理和演算を行う排他的論理和部、
　線形変換部Ｐ３、
　非線形変換部Ｓ、
　ラウンド鍵ＲＫ１０との排他的論理和演算を行う排他的論理和部、
　線形変換部Ｐ１、
　非線形変換部Ｓ、
　ラウンド鍵ＲＫ１１との排他的論理和演算を行う排他的論理和部、
　線形変換部Ｐ２、
　非線形変換部Ｓ、
　ラウンド鍵ＲＫ１２との排他的論理和演算を行う排他的論理和部、
　線形変換部Ｐ１、
　非線形変換部Ｓ、
　ラウンド鍵ＲＫ１３との排他的論理和演算を行う排他的論理和部、
　このラウンド演算実行構成は、先に図５９を参照して説明したと同様の構成であり、
　変換関数Ｅ、
　線形変換部、
　変換関数Ｅ－１、
　これらのシーケンスに設定され、インボリューション性を有する。
　なお、各非線形変換部は、先に図６４～図６６を参照して説明したインボリューション性を有するＳボックスによって構成されている。
　鍵スケジュール部７２０のラウンド鍵供給部７２１は、鍵レジスタ７２２と鍵変換部７２３を有する。このラウンド鍵供給部７２１の実行する処理は、先に項目［５．鍵スケジュール部の構成と処理について］において図３２～図４３を参照して説明した処理である。
　すなわち、ベース鍵と変換鍵を使用して生成したラウンド鍵を暗号処理部７５０に提供する。このラウンド鍵供給構成では、インボリューション性、フルディフュージョン性を実現している。
　鍵レジスタに格納された秘密鍵Ｋは６４ビットのベース鍵Ｋ１とＫ２との連結データである１２８ビット鍵データである。
　鍵変換部７２３は、ベース鍵Ｋ１に基づく変換鍵Ｋｄ１を生成し、ベース鍵Ｋ２に基づく変換処理によって変換鍵Ｋｄ２を生成する。
　この変換処理を、変換関数Ｇ、および逆関数Ｇ－１を用いて式で示すと以下の通りとなる。
　Ｋｄ１＝Ｇ（Ｋ１）
　Ｋ１＝Ｇ－１（Ｋｄ１）
　なお、
　ここで、Ｇ＝Ｇ－１
　が成立する。
　すなわち、鍵変換部７２３において鍵変換に適用するデータ変換関数Ｇは、インボリューション性、すなわち、図３３に示すように、順方向関数Ｇと逆方向関数Ｇ－１とが同じ関数であるという性質を持つ。
　なお、この鍵変換処理には、先に図３４等を参照して説明したように、アダマール（Ｈａｄａｍａｒｄ）ＭＤＳ行列ＭＤを適用して実行する。
　具体的には、図３４に示すステップＳ１の列拡散演算と、ステップＳ２の行拡散演算を実行する。
　ステップＳ１の列拡散演算は、以下の演算式によって示される。
　ＭＣ［ＭＤ］＝ＭＣ［ＭＤ，ＭＤ，ＭＤ，ＭＤ］
　また、ステップＳ２の行拡散演算は、以下の演算式によって示される。
　ＭＲ［ＭＤ］＝ＭＲ［ＭＤ，ＭＤ，ＭＤ，ＭＤ］
　すなわち、図３４のステップＳ１の列拡散演算は、４ビット要素からなる４×４のステート表現データの４つの全ての列に対して、同一のアダマール（Ｈａｄａｍａｒｄ）ＭＤＳ行列ＭＤを適用した行列演算を実行する。
　また、ステップＳ２の行拡散演算は、４ビット要素からなる４×４のステート表現データの４つの全ての行に対して、同一のアダマール（Ｈａｄａｍａｒｄ）ＭＤＳ行列ＭＤを適用した行列演算を実行する。
　列拡散演算ＭＣ［ＭＤ］と、行拡散演算ＭＲ［ＭＤ］の連続処理からなる関数Ｇは、インボリューション性を持ち、順方向関数Ｇと、逆方向関数Ｇ－１が同一であるため、２回繰り返すことで、元の値が算出される。
　さらに、鍵変換部７２３において実行する行列ＭＤを適用した列拡散演算ＭＣ［ＭＤ］と、行列ＭＤを適用した行拡散演算ＭＲ［ＭＤ］により、入出力ステート全要素間のデータ拡散（ｄｉｆｆｕｓｉｏｎ）、すなわち「全拡散（ｆｕｌｌ　ｄｉｆｆｕｓｉｏｎ）変換」が行われる。
　このフルディフュージョン性を持つラウンド鍵を暗号処理部に入力して変換対象データとの排他的論理和を実行することで、変換データの拡散性能も向上し、より安全性の高い暗号処理が実現される。
　なお、ラウンド鍵供給部７２１の実行するラウンド鍵供給構成は、
　（１）全拡散（ｆｕｌｌ　ｄｉｆｆｕｓｉｏｎ）変換を実現するフルディフュージョン性、
　（２）順方向関数Ｇと、逆方向関数Ｇ－１が同一であるインボリューション性、
　これら２つの性質を持つ。
　これらの２つの特性により、先に説明したように、以下の効果がもたらされる。
　全拡散（ｆｕｌｌ　ｄｉｆｆｕｓｉｏｎ）変換を実現するフルディフュージョン性に基づいて、変換対象データに対する鍵データの構成情報の拡散が少ないラウンド数で実現され、ラウンド関数（Ｒ）の処理に依存することなくより大きな拡散性能が保証される。
　すなわち、少ないラウンド数で攻撃に対する耐性の高い安全な暗号処理が実現される。結果として、高速処理や軽量化が実現される。
　また、インボリューション性に基づく効果としては、１つの鍵変換部を繰り返し利用する構成が可能であり、アンロールド実装、ラウンド実装のいずれにおいてもハードウェアの小型化が実現される。
　なお、図７２に示す例では、ラウンド鍵供給部７２１は、以下の順番で、鍵の出力を行う。
　鍵Ｋ１、
　鍵Ｋ２、
　変換鍵Ｋｄ１、
　変換鍵Ｋｄ２、
　排他的論理和演算鍵Ｋ１（＋）Ｋ２、
　排他的論理和演算変換鍵Ｋｄ１（＋）Ｋｄ２、
　排他的論理和演算鍵Ｋ１（＋）Ｋ２、
　排他的論理和演算変換鍵Ｋｄ１（＋）Ｋｄ２、
　排他的論理和演算鍵Ｋ１（＋）Ｋ２、
　変換鍵Ｋｄ２、
　変換鍵Ｋｄ１、
　鍵Ｋ２、
　鍵Ｋ１、
　この順番で、６種類の鍵を出力する。
　なお、暗号処理部７５０に対して入力されるラウンド鍵Ｋ１～Ｋ１３は、上記の各鍵をそのまま、あるいは、定数ＣＯＮを作用させて生成される。
　暗号処理部７５０の中心位置にある線形変換部Ｐ２の前後において、ラウンド鍵Ｋ７として、排他的論理和演算鍵Ｋ１（＋）Ｋ２、を繰り返し利用する。
　また、ラウンド鍵ＲＫ８，ＲＫ１０，ＲＫ１２は、定数供給部７２５から供給される定数ＣＯＮをラウンド鍵供給部７２１の供給する鍵に排他的論理和して生成される。
　上記鍵の入力シーケンスは、先に図５９を参照して説明したシーケンスと同様であり、逆の順番も同一シーケンスとなる。
　これは、平文Ｐから暗号文Ｃを生成する暗号処理における鍵入力順と、暗号文Ｃから平文Ｐを生成する復号処理において、ラウンド鍵供給部７２１は、同じシーケンスで鍵生成、出力を行うことが可能であることを意味する。これは、暗号処理および復号処理に適用するハードウェアやプログラムを共通化可能であることを意味し、装置の軽量化（小型化）に寄与する設定である。
　鍵スケジュール部７２０に設定された定数供給部７２５は、先に項目［６．定数入力による安全性向上を実現する構成について］において、図５３～図５９を参照して説明した処理に従った定数供給処理を実行する。
　図に示す例において、定数（ＣＯＮ）は、
　ラウンド鍵ＲＫ８、
　ラウンド鍵ＲＫ１０
　ラウンド鍵ＲＫ１２、
　これらのラウンド鍵生成時にラウンド鍵供給部の生成する鍵データに対して排他的論理和演算がなされる。
　すなわち、
　ラウンド鍵ＲＫ８＝Ｋｄ１（＋）Ｋｄ２（＋）ＣＯＮ
　ラウンド鍵ＲＫ１０＝Ｋｄ２（＋）ＣＯＮ
　ラウンド鍵ＲＫ１２＝Ｋ２（＋）ＣＯＮ
　なお、（＋）は排他的論理和演算を意味する。
　このような定数（ＣＯＮ）の入力処理の結果として、暗号処理部７５０に入力されるラウンド鍵ＲＫ１～ＲＫ１３の設定は以下の通りとなる。
　ＲＫ１＝Ｋ１、
　ＲＫ２＝Ｋ２、
　ＲＫ３＝Ｋｄ１、
　ＲＫ４＝Ｋｄ２、
　ＲＫ５＝Ｋ１（＋）Ｋ２、
　ＲＫ６＝Ｋｄ１（＋）Ｋｄ２、
　ＲＫ７＝Ｋ１（＋）Ｋ２、
　ＲＫ７＝Ｋ１（＋）Ｋ２、
　ＲＫ８＝Ｋｄ１（＋）Ｋｄ２（＋）ＣＯＮ、
　ＲＫ９＝Ｋ１（＋）Ｋ２、
　ＲＫ１０＝Ｋｄ２（＋）ＣＯＮ、
　ＲＫ１１＝Ｋｄ１、
　ＲＫ１２＝Ｋ２（＋）ＣＯＮ、
　ＲＫ１３＝Ｋ１、
　なお、（＋）は排他的論理和演算を意味する。
　ＲＫ７は、同じラウンド鍵を線形変換部（Ｐ２）の前後で２回入力する設定となっている。
　このように、定数（ＣＯＮ）はラウンド鍵の生成時にラウンド鍵供給部の生成する鍵に対して排他的論理和処理がなされる。
　なお、定数をラウンド鍵とは別に、暗号処理部の排他的論理和部に入力して、変換データとの排他的論理和処理を行なってもよい。この場合も結果は同じとなる。
　なお、定数（ＣＯＮ）は、前述したように、定数ＣＯＮと、定数ＣＯＮを入力する暗号処理部の排他的論理和部に隣接する線形変換部において適用する線形変換行列との行列演算の結果の全要素が非ゼロ、すなわちゼロでない値となる定数（ＣＯＮ）を利用する。
　この構成によって、線形変換部の線形変換による差分減少が防止される。この結果、最小差分アクティブＳボックスの数の減少を防止することが可能となり、各種の攻撃に対する耐性を高めた安全性の高い暗号処理構成が実現される。
　さらに、暗号処理部７５０に設定される非線形変換部は、先に項目［７．非線形変換部に適用するＳボックス（Ｓ－ｂｏｘ）の具体的構成例について］において、図６４～図６６を参照して説明したインボリューション性を有する４ビット入出力ｋとボックス（Ｓ－ｂｏｘ）を複数設定した構成である。
　先に説明たように、暗号処理部７５０は、変換関数Ｅと、線形変換部、変換関数Ｅ－１を有する構成であり、変換関数Ｅと、変換関数Ｅ－の非線形変換部に図６４～図６６に示すＳボックスを利用した構成とすることで、暗号処理部全体のインボリューション性が実現される。
　　［９．暗号処理装置の実装例について］
　最後に、上述した実施例に従った暗号処理を実行する暗号処理装置の実装例について説明する。
　上述した実施例に従った暗号処理を実行する暗号処理装置は、暗号処理を実行する様々な情報処理装置に搭載可能である。具体的には、ＰＣ、ＴＶ、レコーダ、プレーヤ、通信機器、さらに、ＲＦＩＤ、スマートカード、センサネットワーク機器、デンチ／バッテリー認証モジュール、健康・医療機器、自立型ネットワーク機器等、例えばデータ処理や通信処理に伴う暗号処理を実行する様々な機器において利用可能である。
　本開示の暗号処理を実行する装置の一例としてのＩＣモジュール８００の構成例を図７３に示す。上述の処理は、例えばＰＣ、ＩＣカード、リーダライタ、スマートフォンやウェアラブルデバイス等の様々な情報処理装置において実行可能であり、図７３に示すＩＣモジュール８００は、これら様々な機器に構成することが可能である。
　図７３に示すＣＰＵ（Ｃｅｎｔｒａｌ　ｐｒｏｃｅｓｓｉｎｇ　Ｕｎｉｔ）８０１は、暗号処理の開始や、終了、データの送受信の制御、各構成部間のデータ転送制御、その他の各種プログラムを実行するプロセッサである。メモリ８０２は、ＣＰＵ８０１が実行するプログラム、あるいは演算パラメータなどの固定データを格納するＲＯＭ（Ｒｅａｄ－Ｏｎｌｙ－Ｍｅｍｏｒｙ）、ＣＰＵ８０１の処理において実行されるプログラム、およびプログラム処理において適宜変化するパラメータの格納エリア、ワーク領域として使用されるＲＡＭ（Ｒａｎｄｏｍ　Ａｃｃｅｓｓ　Ｍｅｍｏｒｙ）等からなる。また、メモリ８０２は暗号処理に必要な鍵データや、暗号処理において適用する変換テーブル（置換表）や変換行列に適用するデータ等の格納領域として使用可能である。なおデータ格納領域は、耐タンパ構造を持つメモリとして構成されることが好ましい。
　暗号処理部８０３は、上記において説明した暗号処理構成を有しい、共通鍵ブロック暗号処理アルゴリズムに従った暗号処理、復号処理を実行する。
　なお、ここでは、暗号処理手段を個別モジュールとした例を示したが、このような独立した暗号処理モジュールを設けず、例えば暗号処理プログラムをＲＯＭに格納し、ＣＰＵ８０１がＲＯＭ格納プログラムを読み出して実行するように構成してもよい。
　乱数発生器８０４は、暗号処理に必要となる鍵の生成などにおいて必要となる乱数の発生処理を実行する。
　送受信部８０５は、外部とのデータ通信を実行するデータ通信処理部であり、例えばリーダライタ等、ＩＣモジュールとのデータ通信を実行し、ＩＣモジュール内で生成した暗号文の出力、あるいは外部のリーダライタ等の機器からのデータ入力などを実行する。
　なお、上述した実施例において説明した暗号処理装置は、入力データとしての平文を暗号化する暗号化処理に適用可能であるのみならず、入力データとしての暗号文を平文に復元する復号処理にも適用可能である。
　暗号化処理、復号処理、双方の処理において、上述した実施例において説明した構成を適用することが可能である。
　図７４は、本開示に係る暗号処理を実行するスマートフォン９００の概略的な構成の一例を示すブロック図である。スマートフォン９００は、プロセッサ９０１、メモリ９０２、ストレージ９０３、外部接続インタフェース９０４、カメラ９０６、センサ９０７、マイクロフォン９０８、入力デバイス９０９、表示デバイス９１０、スピーカ９１１、無線通信インタフェース９１３、アンテナスイッチ９１４、アンテナ９１５、バス９１７、バッテリー９１８及び補助コントローラ９１９を備える。
　プロセッサ９０１は、例えばＣＰＵ（Ｃｅｎｔｒａｌ　Ｐｒｏｃｅｓｓｉｎｇ　Ｕｎｉｔ）又はＳｏＣ（Ｓｙｓｔｅｍ　ｏｎ　Ｃｈｉｐ）であってよく、スマートフォン９００のアプリケーションレイヤ及びその他のレイヤの機能を制御し、また、暗号処理を制御する。メモリ９０２は、ＲＡＭ（Ｒａｎｄｏｍ　Ａｃｃｅｓｓ　Ｍｅｍｏｒｙ）及びＲＯＭ（Ｒｅａｄ　Ｏｎｌｙ　Ｍｅｍｏｒｙ）を含み、プロセッサ９０１により実行されるプログラム及びデータを記憶する。また、メモリ９０２は、暗号処理に必要な鍵データや、暗号処理において適用する変換テーブル（置換表）や変換行列に適用するデータ等の格納領域として使用可能である。なおデータ格納領域は、耐タンパ構造を持つメモリとして構成されることが好ましい。ストレージ９０３は、半導体メモリ又はハードディスクなどの記憶媒体を含み得る。外部接続インタフェース９０４は、メモリーカード又はＵＳＢ（Ｕｎｉｖｅｒｓａｌ　Ｓｅｒｉａｌ　Ｂｕｓ）デバイスなどの外付けデバイスをスマートフォン９００へ接続するためのインタフェースである。
　カメラ９０６は、例えば、ＣＣＤ（Ｃｈａｒｇｅ　Ｃｏｕｐｌｅｄ　Ｄｅｖｉｃｅ）又はＣＭＯＳ（Ｃｏｍｐｌｅｍｅｎｔａｒｙ　Ｍｅｔａｌ　Ｏｘｉｄｅ　Ｓｅｍｉｃｏｎｄｕｃｔｏｒ）などの撮像素子を有し、撮像画像を生成する。センサ９０７は、例えば、測位センサ、ジャイロセンサ、地磁気センサ及び加速度センサなどのセンサ群を含み得る。マイクロフォン９０８は、スマートフォン９００へ入力される音声を音声信号へ変換する。カメラ９０６で生成された画像や、センサ９０７で取得されたセンサデータ、マイクロフォン９０８で取得した音声信号などは、プロセッサ９０１により暗号化され無線通信インタフェース９１３を介して他の装置に送信されてもよい。入力デバイス９０９は、例えば、表示デバイス９１０の画面上へのタッチを検出するタッチセンサ、キーパッド、キーボード、ボタン又はスイッチなどを含み、ユーザからの操作又は情報入力を受け付ける。表示デバイス９１０は、液晶ディスプレイ（ＬＣＤ）又は有機発光ダイオード（ＯＬＥＤ）ディスプレイなどの画面を有し、スマートフォン９００の出力画像を表示する。スピーカ９１１は、スマートフォン９００から出力される音声信号を音声に変換する。
　無線通信インタフェース９１３は、無線通信を実行し、典型的には、ベースバンドプロセッサ、ＲＦ（Ｒａｄｉｏ　Ｆｒｅｑｕｅｎｃｙ）回路及びパワーアンプなどを含み得る。無線通信インタフェース９１３は、通信制御プログラムを記憶するメモリ、当該プログラムを実行するプロセッサ及び関連する回路を集積したワンチップのモジュールであってもよい。無線通信インタフェース９１３は、無線ＬＡＮ方式に加えて、近距離無線通信方式、近接無線通信方式又はセルラ通信方式などの他の種類の無線通信方式をサポートしてもよい。
　バス９１７は、プロセッサ９０１、メモリ９０２、ストレージ９０３、外部接続インタフェース９０４、カメラ９０６、センサ９０７、マイクロフォン９０８、入力デバイス９０９、表示デバイス９１０、スピーカ９１１、無線通信インタフェース９１３及び補助コントローラ９１９を互いに接続する。バッテリー９１８は、図中に破線で部分的に示した給電ラインを介して、図７４に示したスマートフォン９００の各ブロックへ電力を供給する。補助コントローラ９１９は、例えば、スリープモードにおいて、スマートフォン９００の必要最低限の機能を動作させる。
　なお、上述した実施例において説明したスマートフォンにおける暗号処理は、入力データとしての平文を暗号化する暗号化処理に適用可能であるのみならず、入力データとしての暗号文を平文に復元する復号処理にも適用可能である。
　暗号化処理、復号処理、双方の処理において、上述した実施例において説明した構成を適用することが可能である。
　また、図７４に示すスマートフォン９００に図７３に示すＩＣモジュール８００を搭載し、上述した実施例に従った暗号処理をＩＣモジュール８００において実行する構成としてもよい。
　　［１０．本開示の構成のまとめ］
　以上、特定の実施例を参照しながら、本開示の実施例について詳解してきた。しかしながら、本開示の要旨を逸脱しない範囲で当業者が実施例の修正や代用を成し得ることは自明である。すなわち、例示という形態で本発明を開示してきたのであり、限定的に解釈されるべきではない。本開示の要旨を判断するためには、特許請求の範囲の欄を参酌すべきである。
　なお、本明細書において開示した技術は、以下のような構成をとることができる。
　（１）　入力データに対するラウンド演算を実行して出力データを生成する暗号処理部と、
　前記暗号処理部におけるラウンド演算において適用するラウンド鍵を前記暗号処理部に出力する鍵スケジュール部を有し、
　前記鍵スケジュール部は、
　秘密鍵Ｋを格納した鍵レジスタと、
　前記秘密鍵Ｋに対して変換関数Ｇを適用した変換処理により変換鍵Ｋｄを生成する鍵変換部を有し、
　前記秘密鍵Ｋ、および前記変換鍵Ｋｄを前記暗号処理部に出力するラウンド鍵、またはラウンド鍵生成用データとする構成であり、
　前記変換関数Ｇは、逆関数Ｇ－１が関数Ｇと同じ関数となるインボリューション性を有する関数である暗号処理装置。
　（２）前記秘密鍵Ｋ、および前記変換鍵Ｋｄは、いずれも各要素が１ビット以上のｍ×ｎ個の要素からなるステートであり、前記変換関数Ｇは、前記秘密鍵Ｋのステート要素の全てが、前記変換鍵Ｋｄのステート要素全てに影響を及ぼすフルディフュージョン性を有する関数である前記（１）に記載の暗号処理装置。
　（３）前記変換関数Ｇは、前記秘密鍵Ｋのステートの各列要素単位で行列を適用して線形変換を行う列拡散演算と、前記秘密鍵Ｋのステートの各行要素単位で行列を適用して線形変換を行う行拡散演算を実行して前記変換鍵Ｋｄを生成する前記（２）に記載の暗号処理装置。
　（４）前記秘密鍵Ｋ、および前記変換鍵Ｋｄは、いずれも各要素が４ビットの４×４個の要素からなるステートであり、前記変換関数Ｇは、前記秘密鍵Ｋのステート要素の全てが、前記変換鍵Ｋｄのステート要素全てに影響を及ぼすフルディフュージョン性を有する関数である前記（１）～（３）いずれかに記載の暗号処理装置。
　（５）前記変換関数Ｇは、前記秘密鍵Ｋのステートの各列要素単位でアダマールＭＤＳ（Ｈａｄａｍａｒｄ　ＭＤＳ）行列を適用して線形変換を行う列拡散演算と、前記秘密鍵Ｋのステートの各行要素単位でアダマールＭＤＳ（Ｈａｄａｍａｒｄ　ＭＤＳ）行列を適用して線形変換を行う行拡散演算を実行して前記変換鍵Ｋｄを生成する前記（４）に記載の暗号処理装置。
　（６）前記鍵スケジュール部は、前記秘密鍵Ｋは、分割鍵Ｋ１、Ｋ２の連結データであり、前記鍵変換部は、前記分割鍵Ｋ１、Ｋ２の各々に対する前記変換関数Ｇを適用した変換処理により変換鍵Ｋｄ１、Ｋｄ２を生成し、前記分割鍵Ｋ１、Ｋ２、および前記変換鍵Ｋｄ１、Ｋｄ２を前記暗号処理部に出力するラウンド鍵、またはラウンド鍵生成用データとする前記（１）～（５）いずれかに記載の暗号処理装置。
　（７）前記鍵スケジュール部は、
　（ａ）前記分割鍵Ｋ１、Ｋ２、
　（ｂ）前記変換鍵Ｋｄ１、Ｋｄ２、
　（ｃ）前記分割鍵Ｋ１と前記分割鍵Ｋ２との排他的論理和演算によって生成した鍵、
　（ｄ）前記変換鍵Ｋｄ１と前記変換鍵Ｋｄ２との排他的論理和演算によって生成した鍵、
　上記（ａ）～（ｄ）の６種類の鍵を前記暗号処理部に出力するラウンド鍵、またはラウンド鍵生成用データとする前記（６）に記載の暗号処理装置。
　（８）前記暗号処理部は、平文Ｐを入力データとして前記ラウンド演算を繰り返して出力データとしての暗号文Ｃを出力し、前記暗号文Ｃを入力データとして、前記ラウンド演算の実行シーケンスを逆順に設定したデータ変換処理により出力データとして前記平文Ｐを生成可能なインボリューション性を有する構成である前記（１）～（７）いずれかに記載の暗号処理装置。
　（９）前記鍵スケジュール部は、平文Ｐから暗号文Ｃを生成する場合の鍵供給シーケンスと、暗号文Ｃから平文Ｐを生成する場合の鍵供給シーケンスが一致するインボリューション性を有する鍵供給処理を行なう構成である前記（１）～（８）いずれかに記載の暗号処理装置。
　（１０）前記鍵スケジュール部は、前記暗号処理部に対する鍵供給処理に際して、供給鍵の一部に定数による演算を施し、演算結果である鍵データを前記暗号処理部に出力する前記（１）～（９）いずれかに記載の暗号処理装置。
　（１１）前記暗号処理部が実行するラウンド演算は、線形変換部による線形変換処理を含む演算であり、前記線形変換部は、ラウンド遷移に応じて線形変換態様を変更する前記（１）～（１０）いずれかに記載の暗号処理装置。
　（１２）前記ラウンド演算は非線形変換処理を含み、前記非線形変換処理を実行するＳボックスは、入力値から得られる出力値を、再入力することで前記入力値が得られるインボリューション性を有する構成である前記（１）～（１１）いずれかに記載の暗号処理装置。
　（１３）　入力データに対するラウンド演算を実行して出力データを生成する暗号処理部と、
　前記暗号処理部におけるラウンド演算において適用するラウンド鍵を前記暗号処理部に出力する鍵スケジュール部を有し、
　前記鍵スケジュール部は、
　秘密鍵Ｋを格納した鍵レジスタと、
　前記秘密鍵Ｋに対して変換関数Ｇを適用した変換処理により変換鍵Ｋｄを生成する鍵変換部を有し、
　前記秘密鍵Ｋ、および前記変換鍵Ｋｄを前記暗号処理部に出力するラウンド鍵、またはラウンド鍵生成用データとする構成であり、
　前記秘密鍵Ｋ、および前記変換鍵Ｋｄは、いずれも各要素が１ビット以上のｍ×ｎ個の要素からなるステートであり、
　前記変換関数Ｇは、前記秘密鍵Ｋのステート要素の全てが、前記変換鍵Ｋｄのステート要素全てに影響を及ぼすフルディフュージョン性を有する関数である暗号処理装置。
　（１４）前記変換関数Ｇは、フルディフュージョン変換関数とビット置換関数の組み合わせである前記（１３）に記載の暗号処理装置。
　（１５）前記秘密鍵Ｋ、および前記変換鍵Ｋｄは、いずれも各要素が４ビットの４×４個の要素からなるステートであり、前記変換関数Ｇは、フルディフュージョン４ビット変換関数と１６ビット置換関数の組み合わせである前記（１３）または（１４）に記載の暗号処理装置。
　（１６）前記鍵スケジュール部は、前記秘密鍵Ｋは、分割鍵Ｋ１、Ｋ２の連結データであり、前記鍵変換部は、前記分割鍵Ｋ１に対する変換関数Ｇ１を適用した変換処理により変換鍵Ｋｄ１を生成し、前記分割鍵Ｋ２に対する変換関数Ｇ２を適用した変換処理により変換鍵Ｋｄ２を生成する構成であり、前記変換関数Ｇ１，Ｇ２は、
　（ａ）Ｇ１，Ｇ２ともフルディフュージョン性を有するがインボリューション性を有さない変換関数、
　（ｂ）Ｇ１，Ｇ２ともフルディフュージョン性と、インボリューション性を有する変換関数、
　（ｃ）Ｇ１，Ｇ２ともフルディフュージョン性を有し、Ｇ１とＧ２が逆関数の設定、すなわち、Ｇ２＝Ｇ１－１の関係にある変換関数、
　上記（ａ）～（ｃ）のいずれかの組み合わせである前記（１３）～（１５）いずれかに記載の暗号処理装置。
　（１７）　暗号処理装置において実行する暗号処理方法であり、
　前記暗号処理装置は、
　入力データに対するラウンド演算を実行して出力データを生成する暗号処理部と、
　前記暗号処理部におけるラウンド演算において適用するラウンド鍵を前記暗号処理部に出力する鍵スケジュール部を有し、
　前記鍵スケジュール部は、
　鍵レジスタに格納した秘密鍵Ｋに対して変換関数Ｇを適用した変換処理により変換鍵Ｋｄを生成し、
　前記秘密鍵Ｋ、および前記変換鍵Ｋｄを前記暗号処理部に出力するラウンド鍵、またはラウンド鍵生成用データとする処理を行ない、
　前記変換関数Ｇは、逆関数Ｇ－１が関数Ｇと同じ関数となるインボリューション性を有する関数である暗号処理方法。
　（１８）　暗号処理装置において実行する暗号処理方法であり、
　前記暗号処理装置は、
　入力データに対するラウンド演算を実行して出力データを生成する暗号処理部と、
　前記暗号処理部におけるラウンド演算において適用するラウンド鍵を前記暗号処理部に出力する鍵スケジュール部を有し、
　前記鍵スケジュール部は、
　鍵レジスタに格納した秘密鍵Ｋに対して変換関数Ｇを適用した変換処理により変換鍵Ｋｄを生成し、
　前記秘密鍵Ｋ、および前記変換鍵Ｋｄを前記暗号処理部に出力するラウンド鍵、またはラウンド鍵生成用データとする処理を行ない、
　前記秘密鍵Ｋ、および前記変換鍵Ｋｄは、いずれも各要素が１ビット以上のｍ×ｎ個の要素からなるステートであり、
　前記変換関数Ｇは、前記秘密鍵Ｋのステート要素の全てが、前記変換鍵Ｋｄのステート要素全てに影響を及ぼすフルディフュージョン性を有する関数である暗号処理方法。
　（１９）　暗号処理装置において暗号処理を実行させるプログラムであり、
　前記暗号処理装置は、
　入力データに対するラウンド演算を実行して出力データを生成する暗号処理部と、
　前記暗号処理部におけるラウンド演算において適用するラウンド鍵を前記暗号処理部に出力する鍵スケジュール部を有し、
　前記プログラムは、前記鍵スケジュール部に、
　鍵レジスタに格納した秘密鍵Ｋに対して変換関数Ｇを適用した変換処理により変換鍵Ｋｄを生成する処理と、
　前記秘密鍵Ｋ、および前記変換鍵Ｋｄを前記暗号処理部に出力するラウンド鍵、またはラウンド鍵生成用データとする処理を実行させ、
　前記変換関数Ｇは、逆関数Ｇ－１が関数Ｇと同じ関数となるインボリューション性を有する関数であるプログラム。
　（２０）　暗号処理装置において暗号処理を実行させるプログラムであり、
　前記暗号処理装置は、
　入力データに対するラウンド演算を実行して出力データを生成する暗号処理部と、
　前記暗号処理部におけるラウンド演算において適用するラウンド鍵を前記暗号処理部に出力する鍵スケジュール部を有し、
　前記プログラムは、前記鍵スケジュール部に、
　鍵レジスタに格納した秘密鍵Ｋに対して変換関数Ｇを適用した変換処理により変換鍵Ｋｄを生成する処理と、
　前記秘密鍵Ｋ、および前記変換鍵Ｋｄを前記暗号処理部に出力するラウンド鍵、またはラウンド鍵生成用データとする処理を実行させ、
　前記秘密鍵Ｋ、および前記変換鍵Ｋｄは、いずれも各要素が１ビット以上のｍ×ｎ個の要素からなるステートであり、
　前記変換関数Ｇは、前記秘密鍵Ｋのステート要素の全てが、前記変換鍵Ｋｄのステート要素全てに影響を及ぼすフルディフュージョン性を有する関数であるプログラム。
　また、明細書中において説明した一連の処理はハードウェア、またはソフトウェア、あるいは両者の複合構成によって実行することが可能である。ソフトウェアによる処理を実行する場合は、処理シーケンスを記録したプログラムを、専用のハードウェアに組み込まれたコンピュータ内のメモリにインストールして実行させるか、あるいは、各種処理が実行可能な汎用コンピュータにプログラムをインストールして実行させることが可能である。例えば、プログラムは記録媒体に予め記録しておくことができる。記録媒体からコンピュータにインストールする他、ＬＡＮ（Ｌｏｃａｌ　Ａｒｅａ　Ｎｅｔｗｏｒｋ）、インターネットといったネットワークを介してプログラムを受信し、内蔵するハードディスク等の記録媒体にインストールすることができる。
　なお、明細書に記載された各種の処理は、記載に従って時系列に実行されるのみならず、処理を実行する装置の処理能力あるいは必要に応じて並列的にあるいは個別に実行されてもよい。また、本明細書においてシステムとは、複数の装置の論理的集合構成であり、各構成の装置が同一筐体内にあるものには限らない。
　上述したように、本開示の一実施例の構成によれば、各種の攻撃に対する耐性を向上させた安全性の高い暗号処理構成が実現される。
　具体的には、入力データに対するラウンド演算を繰り返して出力データを生成する暗号処理部と、暗号処理部におけるラウンド演算において適用するラウンド鍵を暗号処理部に出力する鍵スケジュール部を有し、鍵スケジュール部は、秘密鍵Ｋを格納した鍵レジスタと、秘密鍵Ｋに対して変換関数Ｇを適用した変換処理により変換鍵Ｋｄを生成する鍵変換部を有し、秘密鍵Ｋ、および変換鍵Ｋｄを暗号処理部に出力するラウンド鍵、またはラウンド鍵生成用データとする。変換関数Ｇとして、逆関数Ｇ－１が関数Ｇと同じ関数となるインボリューション性と、フルディフュージョン性を有する関数を適用する。
　本構成により拡散特性が向上し、各種の攻撃に対する耐性を向上させた安全性の高い暗号処理構成が実現される。
　１００　暗号処理装置
　１１０　鍵スケジュール部
　１２０　暗号処理部
　１２１　排他的論理和部
　１２２　非線形変換部
　１２３　線形変換部
　２０１　線形変換部Ｐ１
　２０２　線形変換部Ｐ２
　２０３　線形変換部Ｐ３
　３００　鍵スケジュール部
　３０１　鍵供給部（鍵レジスタ）
　３０２　鍵変換部
　３２０　暗号処理部
　３２１～３２７　排他的論理和部
　３３１，３３３　排他的論理和部
　３３２　非線形／線形変換部（Ｓ＆Ｐ）
　３５０　暗号処理部
　３５１　排他的論理和部
　３５２　非線形／線形変換部（Ｓ＆Ｐ）
　３６０　鍵スケジュール部
　３６１，３６２　鍵レジスタ
　３６３　鍵変換部
　３７１　鍵レジスタ
　３７２　鍵変換部
　３８１　鍵レジスタ
　３９１　鍵レジスタ
　３９２，３９４　排他的論理和部
　３９３　鍵変換部
　４０１　ラウンド演算実行部
　４０２　定数入力部
　４１１　変換関数Ｅ
　４１２　線形変換部
　４１３　変換関数Ｅ－１
　４３１　変換関数Ｅ
　４３２　線形変換部
　４３３　変換関数Ｅ－１
　４３５　定数入力部
　４３６　排他的論理和部
　４３７　線形変換部
　４５１　変換関数Ｅ
　４５２　線形変換部
　４５３　変換関数Ｅ－１
　５２１　非線形変換層１
　５２２　線形変換層
　５２３　非線形変換層
　７００　暗号処理装置
　７２０　鍵スケジュール部
　７２１　ラウンド鍵供給部
　７２２　鍵レジスタ
　７２３　鍵変換部
　７２５　定数供給部
　７５０　暗号処理部
　７５１　排他的論理和部
　７５２　非線形変換部
　７５３　線形変換部
　８００　ＩＣモジュール
　８０１　ＣＰＵ（Ｃｅｎｔｒａｌ　ｐｒｏｃｅｓｓｉｎｇ　Ｕｎｉｔ）
　８０２　メモリ
　８０３　暗号処理部
　８０４　乱数生成部
　８０５　送受信部
　９００　スマートフォン
　９０１　プロセッサ
　９０２　メモリ
　９０３　ストレージ
　９０４　外部接続インタフェース
　９０６　カメラ
　９０７　センサ
　９０８　マイクロフォン
　９０９　入力デバイス
　９１０　表示デバイス
　９１１　スピーカ
　９１３　無線通信インタフェース
　９１４　アンテナスイッチ
　９１５　アンテナ
　９１７　バス
　９１８　バッテリー
　９１９　補助コントローラ

Claims (18)

  1. 　入力データに対するラウンド演算を実行して出力データを生成する暗号処理部と、
    　前記暗号処理部におけるラウンド演算において適用するラウンド鍵を前記暗号処理部に出力する鍵スケジュール部を有し、
    　前記鍵スケジュール部は、
    　秘密鍵Ｋを格納した鍵レジスタと、
    　前記秘密鍵Ｋに対して変換関数Ｇを適用した変換処理により変換鍵Ｋｄを生成する鍵変換部を有し、
    　前記秘密鍵Ｋ、および前記変換鍵Ｋｄを前記暗号処理部に出力するラウンド鍵、またはラウンド鍵生成用データとする構成であり、
    　前記変換関数Ｇは、逆関数Ｇ－１が関数Ｇと同じ関数となるインボリューション性を有する関数である暗号処理装置。
  2. 　前記秘密鍵Ｋ、および前記変換鍵Ｋｄは、いずれも各要素が１ビット以上のｍ×ｎ個の要素からなるステートであり、
    　前記変換関数Ｇは、前記秘密鍵Ｋのステート要素の全てが、前記変換鍵Ｋｄのステート要素全てに影響を及ぼすフルディフュージョン性を有する関数である請求項１に記載の暗号処理装置。
  3. 　前記変換関数Ｇは、
    　前記秘密鍵Ｋのステートの各列要素単位で行列を適用して線形変換を行う列拡散演算と、
    　前記秘密鍵Ｋのステートの各行要素単位で行列を適用して線形変換を行う行拡散演算を実行して前記変換鍵Ｋｄを生成する請求項２に記載の暗号処理装置。
  4. 　前記秘密鍵Ｋ、および前記変換鍵Ｋｄは、いずれも各要素が４ビットの４×４個の要素からなるステートであり、
    　前記変換関数Ｇは、前記秘密鍵Ｋのステート要素の全てが、前記変換鍵Ｋｄのステート要素全てに影響を及ぼすフルディフュージョン性を有する関数である請求項１に記載の暗号処理装置。
  5. 　前記変換関数Ｇは、
    　前記秘密鍵Ｋのステートの各列要素単位でアダマールＭＤＳ（Ｈａｄａｍａｒｄ　ＭＤＳ）行列を適用して線形変換を行う列拡散演算と、
    　前記秘密鍵Ｋのステートの各行要素単位でアダマールＭＤＳ（Ｈａｄａｍａｒｄ　ＭＤＳ）行列を適用して線形変換を行う行拡散演算を実行して前記変換鍵Ｋｄを生成する請求項４に記載の暗号処理装置。
  6. 　前記鍵スケジュール部は、
    　前記秘密鍵Ｋは、分割鍵Ｋ１、Ｋ２の連結データであり、
    　前記鍵変換部は、前記分割鍵Ｋ１、Ｋ２の各々に対する前記変換関数Ｇを適用した変換処理により変換鍵Ｋｄ１、Ｋｄ２を生成し、
    　前記分割鍵Ｋ１、Ｋ２、および前記変換鍵Ｋｄ１、Ｋｄ２を前記暗号処理部に出力するラウンド鍵、またはラウンド鍵生成用データとする請求項１に記載の暗号処理装置。
  7. 　前記鍵スケジュール部は、
    　（ａ）前記分割鍵Ｋ１、Ｋ２、
    　（ｂ）前記変換鍵Ｋｄ１、Ｋｄ２、
    　（ｃ）前記分割鍵Ｋ１と前記分割鍵Ｋ２との排他的論理和演算によって生成した鍵、
    　（ｄ）前記変換鍵Ｋｄ１と前記変換鍵Ｋｄ２との排他的論理和演算によって生成した鍵、
    　上記（ａ）～（ｄ）の６種類の鍵を前記暗号処理部に出力するラウンド鍵、またはラウンド鍵生成用データとする請求項６に記載の暗号処理装置。
  8. 　前記暗号処理部は、
    　平文Ｐを入力データとして前記ラウンド演算を繰り返して出力データとしての暗号文Ｃを出力し、
    　前記暗号文Ｃを入力データとして、前記ラウンド演算の実行シーケンスを逆順に設定したデータ変換処理により出力データとして前記平文Ｐを生成可能なインボリューション性を有する構成である請求項１に記載の暗号処理装置。
  9. 　前記鍵スケジュール部は、
    　平文Ｐから暗号文Ｃを生成する場合の鍵供給シーケンスと、
    　暗号文Ｃから平文Ｐを生成する場合の鍵供給シーケンスが一致するインボリューション性を有する鍵供給処理を行なう構成である請求項１に記載の暗号処理装置。
  10. 　前記鍵スケジュール部は、
    　前記暗号処理部に対する鍵供給処理に際して、供給鍵の一部に定数による演算を施し、演算結果である鍵データを前記暗号処理部に出力する請求項１に記載の暗号処理装置。
  11. 　前記暗号処理部が実行するラウンド演算は、線形変換部による線形変換処理を含む演算であり、
    　前記線形変換部は、ラウンド遷移に応じて線形変換態様を変更する請求項１に記載の暗号処理装置。
  12. 　前記ラウンド演算は非線形変換処理を含み、
    　前記非線形変換処理を実行するＳボックスは、入力値から得られる出力値を、再入力することで前記入力値が得られるインボリューション性を有する構成である請求項１に記載の暗号処理装置。
  13. 　入力データに対するラウンド演算を実行して出力データを生成する暗号処理部と、
    　前記暗号処理部におけるラウンド演算において適用するラウンド鍵を前記暗号処理部に出力する鍵スケジュール部を有し、
    　前記鍵スケジュール部は、
    　秘密鍵Ｋを格納した鍵レジスタと、
    　前記秘密鍵Ｋに対して変換関数Ｇを適用した変換処理により変換鍵Ｋｄを生成する鍵変換部を有し、
    　前記秘密鍵Ｋ、および前記変換鍵Ｋｄを前記暗号処理部に出力するラウンド鍵、またはラウンド鍵生成用データとする構成であり、
    　前記秘密鍵Ｋ、および前記変換鍵Ｋｄは、いずれも各要素が１ビット以上のｍ×ｎ個の要素からなるステートであり、
    　前記変換関数Ｇは、前記秘密鍵Ｋのステート要素の全てが、前記変換鍵Ｋｄのステート要素全てに影響を及ぼすフルディフュージョン性を有する関数である暗号処理装置。
  14. 　前記変換関数Ｇは、
    　フルディフュージョン変換関数とビット置換関数の組み合わせである請求項１３に記載の暗号処理装置。
  15. 　前記秘密鍵Ｋ、および前記変換鍵Ｋｄは、いずれも各要素が４ビットの４×４個の要素からなるステートであり、
    　前記変換関数Ｇは、
    　フルディフュージョン４ビット変換関数と１６ビット置換関数の組み合わせである請求項１３に記載の暗号処理装置。
  16. 　前記鍵スケジュール部は、
    　前記秘密鍵Ｋは、分割鍵Ｋ１、Ｋ２の連結データであり、
    　前記鍵変換部は、前記分割鍵Ｋ１に対する変換関数Ｇ１を適用した変換処理により変換鍵Ｋｄ１を生成し、前記分割鍵Ｋ２に対する変換関数Ｇ２を適用した変換処理により変換鍵Ｋｄ２を生成する構成であり、
    　前記変換関数Ｇ１，Ｇ２は、
    　（ａ）Ｇ１，Ｇ２ともフルディフュージョン性を有するがインボリューション性を有さない変換関数、
    　（ｂ）Ｇ１，Ｇ２ともフルディフュージョン性と、インボリューション性を有する変換関数、
    　（ｃ）Ｇ１，Ｇ２ともフルディフュージョン性を有し、Ｇ１とＧ２が逆関数の設定、すなわち、Ｇ２＝Ｇ１－１の関係にある変換関数、
    　上記（ａ）～（ｃ）のいずれかの組み合わせである請求項１３に記載の暗号処理装置。
  17. 　暗号処理装置において実行する暗号処理方法であり、
    　前記暗号処理装置は、
    　入力データに対するラウンド演算を実行して出力データを生成する暗号処理部と、
    　前記暗号処理部におけるラウンド演算において適用するラウンド鍵を前記暗号処理部に出力する鍵スケジュール部を有し、
    　前記鍵スケジュール部は、
    　鍵レジスタに格納した秘密鍵Ｋに対して変換関数Ｇを適用した変換処理により変換鍵Ｋｄを生成し、
    　前記秘密鍵Ｋ、および前記変換鍵Ｋｄを前記暗号処理部に出力するラウンド鍵、またはラウンド鍵生成用データとする処理を行ない、
    　前記変換関数Ｇは、逆関数Ｇ－１が関数Ｇと同じ関数となるインボリューション性を有する関数である暗号処理方法。
  18. 　暗号処理装置において実行する暗号処理方法であり、
    　前記暗号処理装置は、
    　入力データに対するラウンド演算を実行して出力データを生成する暗号処理部と、
    　前記暗号処理部におけるラウンド演算において適用するラウンド鍵を前記暗号処理部に出力する鍵スケジュール部を有し、
    　前記鍵スケジュール部は、
    　鍵レジスタに格納した秘密鍵Ｋに対して変換関数Ｇを適用した変換処理により変換鍵Ｋｄを生成し、
    　前記秘密鍵Ｋ、および前記変換鍵Ｋｄを前記暗号処理部に出力するラウンド鍵、またはラウンド鍵生成用データとする処理を行ない、
    　前記秘密鍵Ｋ、および前記変換鍵Ｋｄは、いずれも各要素が１ビット以上のｍ×ｎ個の要素からなるステートであり、
    　前記変換関数Ｇは、前記秘密鍵Ｋのステート要素の全てが、前記変換鍵Ｋｄのステート要素全てに影響を及ぼすフルディフュージョン性を有する関数である暗号処理方法。
PCT/JP2015/055280 2014-03-28 2015-02-24 暗号処理装置、および暗号処理方法、並びにプログラム WO2015146430A1 (ja)

Applications Claiming Priority (2)

Application Number Priority Date Filing Date Title
JP2014068291A JP2015191107A (ja) 2014-03-28 2014-03-28 暗号処理装置、および暗号処理方法、並びにプログラム
JP2014-068291 2014-03-28

Publications (1)

Publication Number Publication Date
WO2015146430A1 true WO2015146430A1 (ja) 2015-10-01

Family

ID=54194964

Family Applications (1)

Application Number Title Priority Date Filing Date
PCT/JP2015/055280 WO2015146430A1 (ja) 2014-03-28 2015-02-24 暗号処理装置、および暗号処理方法、並びにプログラム

Country Status (2)

Country Link
JP (1) JP2015191107A (ja)
WO (1) WO2015146430A1 (ja)

Cited By (3)

* Cited by examiner, † Cited by third party
Publication number Priority date Publication date Assignee Title
CN110785960A (zh) * 2017-06-27 2020-02-11 三菱电机株式会社 码生成装置、码生成方法和码生成程序
CN111373464A (zh) * 2017-08-10 2020-07-03 索尼公司 加密装置、加密方法、解密装置以及解密方法
US11838402B2 (en) 2019-03-13 2023-12-05 The Research Foundation For The State University Of New York Ultra low power core for lightweight encryption

Families Citing this family (2)

* Cited by examiner, † Cited by third party
Publication number Priority date Publication date Assignee Title
CN109375019A (zh) * 2018-11-06 2019-02-22 格力电器（武汉）有限公司 电器设备的检测方法、装置和系统
JP7244060B2 (ja) * 2019-02-20 2023-03-22 Ｎｅｃソリューションイノベータ株式会社 ブロック暗号装置、ブロック暗号方法およびプログラム

Citations (6)

* Cited by examiner, † Cited by third party
Publication number Priority date Publication date Assignee Title
JP2000066586A (ja) * 1998-08-24 2000-03-03 Toshiba Corp データ処理装置及び通信システム並びに記録媒体
JP2002023622A (ja) * 2000-07-12 2002-01-23 Toshiba Corp 暗号化装置、復号装置及び拡大鍵生成装置、拡大鍵生成方法並びに記録媒体
JP2005107078A (ja) * 2003-09-30 2005-04-21 Sony Corp 暗号処理装置、および暗号処理方法、並びにコンピュータ・プログラム
WO2008026625A1 (fr) * 2006-09-01 2008-03-06 Sony Corporation Dispositif de codage, procédé de codage et programme informatique
WO2009087972A1 (ja) * 2008-01-09 2009-07-16 Nec Corporation データ送信装置、データ受信装置、これらの方法、記録媒体、そのデータ通信システム
JP2012070048A (ja) * 2010-09-21 2012-04-05 Toshiba Corp 暗号化装置および復号装置

Patent Citations (6)

* Cited by examiner, † Cited by third party
Publication number Priority date Publication date Assignee Title
JP2000066586A (ja) * 1998-08-24 2000-03-03 Toshiba Corp データ処理装置及び通信システム並びに記録媒体
JP2002023622A (ja) * 2000-07-12 2002-01-23 Toshiba Corp 暗号化装置、復号装置及び拡大鍵生成装置、拡大鍵生成方法並びに記録媒体
JP2005107078A (ja) * 2003-09-30 2005-04-21 Sony Corp 暗号処理装置、および暗号処理方法、並びにコンピュータ・プログラム
WO2008026625A1 (fr) * 2006-09-01 2008-03-06 Sony Corporation Dispositif de codage, procédé de codage et programme informatique
WO2009087972A1 (ja) * 2008-01-09 2009-07-16 Nec Corporation データ送信装置、データ受信装置、これらの方法、記録媒体、そのデータ通信システム
JP2012070048A (ja) * 2010-09-21 2012-04-05 Toshiba Corp 暗号化装置および復号装置

Non-Patent Citations (3)

* Cited by examiner, † Cited by third party
Title
BARRETO, P. S.L.M. ET AL., THE ANUBIS BLOCK CIPHER, FIRST OPEN NESSIE WORKSHOP, November 2000 (2000-11-01), Retrieved from the Internet <URL:https://www.cosic.esat.kuleuven.be/nessie/workshop/submissions/anubis.zip,anubis/B/Anubis.pdf> [retrieved on 20150521] *
BORGHOFF, J. ET AL.: "PRINCE - A Low-latency Block Cipher for Pervasive Computing Applications", CRYPTOLOGY EPRINT ARCHIVE, 13 September 2012 (2012-09-13), Retrieved from the Internet <URL:https://eprint.iacr.org/2012/529/20120913:093817> [retrieved on 20150521] *
WANG, C. ET AL.: "AN ULTRA COMPACT BLOCK CIPHER FOR SERIALIZED ARCHITECTURE IMPLEMENTATIONS", 2009 CANADIAN CONFERENCE ON ELECTRICAL AND COMPUTER ENGINEERING, 2009, pages 1085 - 1090, XP031477492 *

Cited By (3)

* Cited by examiner, † Cited by third party
Publication number Priority date Publication date Assignee Title
CN110785960A (zh) * 2017-06-27 2020-02-11 三菱电机株式会社 码生成装置、码生成方法和码生成程序
CN111373464A (zh) * 2017-08-10 2020-07-03 索尼公司 加密装置、加密方法、解密装置以及解密方法
US11838402B2 (en) 2019-03-13 2023-12-05 The Research Foundation For The State University Of New York Ultra low power core for lightweight encryption

Also Published As

Publication number Publication date
JP2015191107A (ja) 2015-11-02

Similar Documents

Publication Publication Date Title
JP6406350B2 (ja) 暗号処理装置、および暗号処理方法、並びにプログラム
CN106233660B (zh) 加密处理设备、加密处理方法和程序
US9363074B2 (en) Encryption processing apparatus, encryption processing method, and computer program
WO2016059870A1 (ja) 暗号処理装置、および暗号処理方法、並びにプログラム
DK1686722T3 (en) Block encryption device and block encryption method comprising rotation key programming
CN103503362B (zh) 数据处理装置、数据处理方法以及程序
JP2007041620A5 (ja)
JP2008058830A (ja) データ変換装置、およびデータ変換方法、並びにコンピュータ・プログラム
US20120314857A1 (en) Block encryption device, block decryption device, block encryption method, block decryption method and program
WO2015146430A1 (ja) 暗号処理装置、および暗号処理方法、並びにプログラム
JP5680016B2 (ja) 復号処理装置、情報処理装置、および復号処理方法、並びにコンピュータ・プログラム
US20050147244A1 (en) Method for cryptographic transformation of binary data blocks
WO2015146432A1 (ja) 暗号処理装置、および暗号処理方法、並びにプログラム
JP2002510058A (ja) ２進データ・ブロックの暗号変換のための方法
JP6292107B2 (ja) 暗号処理装置、および暗号処理方法、並びにプログラム
Hassan New Approach for Modifying DES Algorithm Using 4-States Multi-keys

Legal Events

Date Code Title Description
121 Ep: the epo has been informed by wipo that ep was designated in this application

Ref document number: 15768977

Country of ref document: EP

Kind code of ref document: A1

NENP Non-entry into the national phase
122 Ep: pct application non-entry in european phase

Ref document number: 15768977

Country of ref document: EP

Kind code of ref document: A1