KR100755450B1 - 3d reconstruction apparatus and method using the planar homography - Google Patents
3d reconstruction apparatus and method using the planar homography Download PDFInfo
- Publication number
- KR100755450B1 KR100755450B1 KR1020060062238A KR20060062238A KR100755450B1 KR 100755450 B1 KR100755450 B1 KR 100755450B1 KR 1020060062238 A KR1020060062238 A KR 1020060062238A KR 20060062238 A KR20060062238 A KR 20060062238A KR 100755450 B1 KR100755450 B1 KR 100755450B1
- Authority
- KR
- South Korea
- Prior art keywords
- image
- homography
- planar
- calculating
- camera
- Prior art date
Links
Images
Classifications
-
- G—PHYSICS
- G06—COMPUTING; CALCULATING OR COUNTING
- G06T—IMAGE DATA PROCESSING OR GENERATION, IN GENERAL
- G06T7/00—Image analysis
- G06T7/30—Determination of transform parameters for the alignment of images, i.e. image registration
- G06T7/32—Determination of transform parameters for the alignment of images, i.e. image registration using correlation-based methods
-
- G—PHYSICS
- G06—COMPUTING; CALCULATING OR COUNTING
- G06T—IMAGE DATA PROCESSING OR GENERATION, IN GENERAL
- G06T15/00—3D [Three Dimensional] image rendering
- G06T15/04—Texture mapping
-
- G—PHYSICS
- G06—COMPUTING; CALCULATING OR COUNTING
- G06T—IMAGE DATA PROCESSING OR GENERATION, IN GENERAL
- G06T15/00—3D [Three Dimensional] image rendering
- G06T15/10—Geometric effects
- G06T15/20—Perspective computation
- G06T15/205—Image-based rendering
-
- G—PHYSICS
- G06—COMPUTING; CALCULATING OR COUNTING
- G06T—IMAGE DATA PROCESSING OR GENERATION, IN GENERAL
- G06T7/00—Image analysis
- G06T7/50—Depth or shape recovery
- G06T7/55—Depth or shape recovery from multiple images
-
- G—PHYSICS
- G06—COMPUTING; CALCULATING OR COUNTING
- G06T—IMAGE DATA PROCESSING OR GENERATION, IN GENERAL
- G06T2207/00—Indexing scheme for image analysis or image enhancement
- G06T2207/10—Image acquisition modality
- G06T2207/10004—Still image; Photographic image
- G06T2207/10012—Stereo images
Landscapes
- Engineering & Computer Science (AREA)
- Physics & Mathematics (AREA)
- Theoretical Computer Science (AREA)
- General Physics & Mathematics (AREA)
- Computer Vision & Pattern Recognition (AREA)
- Computer Graphics (AREA)
- Computing Systems (AREA)
- Geometry (AREA)
- Image Processing (AREA)
Abstract
Description
도 1은 본 발명의 3차원 재구성 장치에 대한 구성도,1 is a block diagram of a three-dimensional reconstruction device of the present invention,
도 2는 본 발명의 평면 패턴의 좌표계에 대한 예시도,2 is an exemplary diagram of a coordinate system of a planar pattern of the present invention;
도 3은 에피폴라에 대한 개념을 나타낸 예시도,3 is an exemplary view showing a concept for epipolar,
도 4a 및 도 4b는 카메라 교정의 실험예를 위한 입력 영상,4A and 4B show an input image for an experimental example of camera calibration;
도 4c는 카메라 교정의 실험예에 따른 결과표,4c is a result table according to an experimental example of a camera calibration;
도 5a 내지 도 5c는 본 발명에 따른 영상교정과 시차맵의 구성에 관한 실험예를 보인 예시도,5a to 5c are exemplary views showing an example of the configuration of the image correction and the parallax map according to the present invention,
도 6a 내지 도 6c는 본 발명에 3차원 재구성 실험예를 보인 예시도.6a to 6c is an exemplary view showing a three-dimensional reconstruction experiment example in the present invention.
** 도면의 주요 부분에 대한 부호의 설명 **** Description of symbols for the main parts of the drawing **
101 : 영상 로딩수단 103 : 특징점 추출수단101: image loading means 103: feature point extraction means
105 : XY 정렬수단 107 : 호모그래피 산출수단105: XY alignment means 107: homography calculation means
109 : 카메라 교정수단 111 : 기본행렬 계산수단109: camera calibration means 111: basic matrix calculation means
113 : 영상교정 수단 115 : 시차맵 구성수단113: image correction means 115: parallax map construction means
117 : 3차원 좌표 계산수단 119 : 다면체 구성수단117: three-dimensional coordinate calculation means 119: polyhedron construction means
121 : 텍스쳐 매핑수단121: texture mapping means
본 발명은 평면 호모그래피를 이용한 3차원 재구성 기술에 속하는 것으로서, 특히 단일의 영상 내에 존재하는 3장의 패턴 영상 간에 호모그래피를 계산함으로써 3차원 재구성을 보다 쉽고, 간단하게 구현할 수 있는 장치 및 방법에 관한 것이다.The present invention belongs to a three-dimensional reconstruction technique using planar homography, and more particularly, an apparatus and method for easily and simply implementing three-dimensional reconstruction by calculating homography between three pattern images existing in a single image. will be.
컴퓨터 그래픽스(CG), 애니메이션, 가상현실, 게임 등과 같은 디지털 영상 콘텐츠 제작 시, 3차원 영상으로 재구성하여 표현하면 입체적인 가상세계의 구현이 용이해 진다. 따라서 3차원 영상 재구성 기술은 증강현실 등 엔터테인먼트 관련 분야에서 널리 응용되고 있다[1][2][3].When producing digital image contents such as computer graphics (CG), animation, virtual reality, and games, reconstructing and representing three-dimensional images facilitates the implementation of a three-dimensional virtual world. Therefore, 3D image reconstruction technology is widely applied in entertainment related fields such as augmented reality [1] [2] [3].
3차원 영상 표현을 위한 기법으로는 CG에서 주로 이용되는 렌더링 기법이 있는데, 이 기법은 물체 표면 정보를 일일이 계산해야 하기 때문에 물체를 모델링하고 렌더링 하는데 비교적 많은 시간이 소요된다. The technique for 3D image representation is a rendering technique mainly used in CG, which requires relatively long time to model and render an object because it needs to calculate object surface information.
이러한 일반적 렌더링 기법과 달리, 교정된 카메라에 찍힌 다수의 영상(2D)을 토대로 3D의 물체를 복원하는 영상 기반 렌더링(Image Based Rendering)이 있다[3]. 이 기법은 건축물과 같은 정형화된 3D 실세계의 모델링 및 렌더링에 유효하며, 비교적 정형화되어 있는바 다양한 기본 모형(primitive model)을 이용할 수 있는 장점이 있으나, 반면 정교한 조작을 위해서는 사용자의 노력 및 숙련이 요구되고, 대상 영상이 자연 정경일 경우 표현이 용이치 않다는 단점이 있다.Unlike this general rendering technique, there is Image Based Rendering which restores a 3D object based on a plurality of images (2D) captured by a calibrated camera [3]. This technique is effective for modeling and rendering a 3D real world, such as a building, and has the advantage of being able to use a variety of primitive models. If the target image is a natural scene, it is not easy to express.
한편, 카메라로 찍은 연속된 영상을 이용하여 3차원 영상을 재구성하는 기법이 있다. 아래의 선행 문헌 [4], [5], [6]에 개시된 바에 따르면, 카메라 교정이 선행되어야 하는데, 이들의 카메라 교정에 필요한 계산이 어렵고, 따라서 재구성 자체가 복잡해지는 문제점을 안고 있다.On the other hand, there is a technique for reconstructing a three-dimensional image using a continuous image taken by the camera. As disclosed in the following documents [4], [5], and [6] below, camera calibration should be preceded, which has a problem that the calculation necessary for camera calibration thereof is difficult, and thus the reconstruction itself is complicated.
최근에 소개된 방법에 의하면, 한 장의 영상으로부터 3차원 재구성이 가능함을 보이고 있는데, 대상 영상 내의 소실점을 근간으로 카메라 교정을 수행한다. 그러나 이러한 방법의 적용은 소실점 계산 또는 추정이 가능한 건축물 등에 제한된다[7][8][9].According to the recently introduced method, three-dimensional reconstruction is possible from a single image, and a camera calibration is performed based on the vanishing point in the target image. However, the application of these methods is limited to buildings that can calculate or estimate vanishing points [7] [8] [9].
선행 문헌 정보Prior literature information
[1] R. T. Azuma,"A Survey of Augmented Reality", Presence: Teleoperators and Virtual Environments, vol. 6, no.4, pp. 355-385, 1997.[1] RT Azuma, "A Survey of Augmented Reality", Presence: Teleoperators and Virtual Environments , vol. 6, no. 4, pp. 355-385, 1997.
[2] Y. Ohta and H. Tamura, "Mixed Reality-Merging Real and Virtual Worlds", Ohmsha Ltd. & Springer-Verlag, 1999.[2] Y. Ohta and H. Tamura, "Mixed Reality-Merging Real and Virtual Worlds", Ohmsha Ltd. & Springer-Verlag , 1999.
[3] R P.E Debevec, C.J Taylor, and J. Malik, "Modeling and Rendering Architecture from Photographs: A Hybrid Geometry and Image-Based Approach", In Proceedings of ACM SIGGRAPH 1996, ACM Press / ACM SIGGRAPH, pp.11-21,Aug. 1996.[3] R PE Debevec, CJ Taylor, and J. Malik, "Modeling and Rendering Architecture from Photographs: A Hybrid Geometry and Image-Based Approach", In Proceedings of ACM SIGGRAPH 1996, ACM Press / ACM SIGGRAPH , pp. 11- 21, Aug. 1996.
[4] P.Beardsley,P.Torr and A.Zisserman, "3D Model Acquisition from Extended Image Sequences", In Proceeding 4th European Coference on Computer Vision, Cambridge, LNCS 1065, Volume II, page 683-695, Springer-Verlag, 1996.[4] P. Beardsley, P. Torr and A. Zisserman, "3D Model Acquisition from Extended Image Sequences", In Proceeding 4th European Coference on Computer Vision, Cambridge, LNCS 1065, Volume II , page 683-695, Springer-Verlag , 1996.
[5] M. Pollefeys, R. Koch and L. Van Gool,"Self-Calibration and Metric Reconstruction in spite of Varying and Unknown Internal Camera Parameters", International Journal of Computer Vision, 32(1), 7-25, 1999.[5] M. Pollefeys, R. Koch and L. Van Gool, "Self-Calibration and Metric Reconstruction in spite of Varying and Unknown Internal Camera Parameters", International Journal of Computer Vision , 32 (1), 7-25, 1999 .
[6] C.Tomasi and T. Kanade, "Shape and motion from image streams under orthography: a factorization method", International Journal of Computer Vision, 9(2), 137-154, 1990.[6] C. Tomasi and T. Kanade, "Shape and motion from image streams under orthography: a factorization method", International Journal of Computer Vision , 9 (2), 137-154, 1990.
[7] D. Liebowitz, A. Criminisi, and A. Zisserman, "Creating Architectural Models from Images", pp. 39-50, EUROGRAPHICS, 1999.[7] D. Liebowitz, A. Criminisi, and A. Zisserman, "Creating Architectural Models from Images", pp. 39-50, EUROGRAPHICS , 1999.
[8] Beardsley, P.A., Torr, P.H.S and Zisserman, A.P., "3D model acquisition from extended image sequence" OUEL Report 2089/96, Department of Engineering Science, University of Oxford. 1996.[8] Beardsley, PA, Torr, PHS and Zisserman, AP, "3D model acquisition from extended image sequence" OUEL Report 2089/96, Department of Engineering Science, University of Oxford . 1996.
본 발명은 전술한 문제점들을 해결하기 위해 창안된 것으로서, 앞서 언급한 종래의 기술에 비해 3차원 재구성 보다 쉽고, 간단하게 구현할 수 있는 장치 및 방법을 제공함에 기술적 과제를 둔다.SUMMARY OF THE INVENTION The present invention has been made to solve the above-described problems, and provides a technical problem to provide an apparatus and method that can be easily and simply implemented in three-dimensional reconstruction compared to the above-mentioned conventional technology.
본 발명에서 개시하고자 하는 기술적 요지는 비교정 영상에서 3장의 평면 패턴 영상을 한 장으로 찍어, 이들 평면 패턴 영상 간에 호모그래피(homography)를 산출하고, 카메라 교정을 수행함에 있다.The technical gist of the present invention is to take three plane pattern images from a non-correction image as one sheet, calculate homography between these plane pattern images, and perform camera calibration.
일반적으로 비교정 영상에서의 카메라 교정은 두 영상 간의 대응점을 찾아야 하는 어려움에 기인해 부가적 문제점이 속출한다. 특히 찾아진 대응점에 정확도 또는 오류가 최소화되어야 올바른 결과를 기대할 수 있다. In general, camera calibration in non-corrected images introduces additional problems due to the difficulty of finding a corresponding point between the two images. In particular, accuracy or errors should be minimized at the matched points so that correct results can be expected.
이와 같은 카메라 교정시의 오류 최소화를 위한 일환으로 Z. Zhang의 선행 문헌에는 연속된 3장의 평면 패턴 영상으로 교정하는 일련의 방법이 제안되어 있다[Z. Zhang,"A Flexible New Techinque for Camera Calibration", IEEE Transaction on Pattern Analysis and Machine Intelligence, vol.22, no.11, pp.1-20, 1998]. As a part of minimizing errors in camera calibration, Z. Zhang's prior literature proposes a series of methods for correcting three consecutive planar pattern images [Z. Zhang, "A Flexible New Techinque for Camera Calibration", IEEE Transaction on Pattern Analysis and Machine Intelligence , vol. 22, no. 11, pp. 1-20, 1998].
본 발명에서는 Z. Zhang이 제안한 교정 방법을 기반으로 하겠으나, 연속된 3장의 평면 패턴 영상이 아닌 3장의 평면 패턴을 포함하도록 촬영한 단일의 영상을 이용함으로써 단순화시킨다. 이러한 경우 사용자가 평면 패턴 영상에서 좌표계를 용이하게 설정할 수 있고, 3차원 좌표의 오류 제거가 제한조건으로 사용되기 때문에 종래에 비해 오차를 현저히 줄일 수 있게 된다.In the present invention, based on the correction method proposed by Z. Zhang, it is simplified by using a single image photographed to include three planar patterns instead of three consecutive planar pattern images. In this case, the user can easily set the coordinate system in the planar pattern image, and since the error elimination of the three-dimensional coordinates is used as a constraint, the error can be significantly reduced as compared with the conventional art.
상술한 기술적 과제에 대한 구체적인 특징 및 이점들은 첨부도면에 의거한 다음의 상세한 설명으로 더욱 명백해질 것이다.Specific features and advantages of the above technical problem will become more apparent from the following detailed description based on the accompanying drawings.
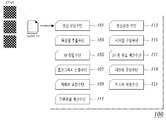
첨부된 도 1은 본 발명의 3차원 재구성 장치(100)의 구성을 나타낸 도면으로서, 영상 로딩수단(101), 특징점 추출수단(103), XY 정렬수단(105), 호모그래피 산출수단(107), 카메라 교정수단(109), 기본행렬 계산수단(111), 영상교정 수단(113), 시차맵 구성수단(115), 3차원 좌표 계산수단(117), 다면체 구성수단(119) 및 텍스쳐 매핑수단(121)을 포함하여 이루어지며, 이들은 컴퓨터 기반의 3차원 그래픽 소프트웨어 혹은 툴의 일부 기능으로서 구현되는 것으로 이해함이 바람직하다.1 is a view showing the configuration of the three-
구체적으로 영상 로딩수단(101)은 카메라(스테레오 영상을 위해 2대가 설정됨)가 3장의 평면 패턴을 포함하도록 촬영한 비교정된 영상(uncalibrated image)을 입력받는다. 이때 평면 패턴은 도 1에 보인바와 같이 반복된 체크 문양의 패턴이다. 체크 문양의 패턴에 대해서는 Z. Zhang의 선행 문헌[Z. Zhang, "A Flexible New Techinque for Camera Calibration", IEEE Transaction on Pattern Analysis and Machine Intelligence, vol.22, no.11, pp.1-20, 1998.]에 상세히 소개되어 있으며, 카메라 교정을 위해 이용된다. In detail, the image loading means 101 receives an uncalibrated image photographed by the camera (two sets for the stereo image) including three plane patterns. At this time, the planar pattern is a pattern of repeated check patterns as shown in FIG. 1. For the pattern of check patterns, see Z. Zhang's preceding literature. Zhang, "A Flexible New Techinque for Camera Calibration", IEEE Transaction on Pattern Analysis and Machine Intelligence , vol. 22, no.11, pp.1-20, 1998. .
일반적인 카메라 모델에 대해 살피면, 일반적인 세공(細孔, pin-hole) 카메라로 3차원 공간상의 한 점 와, 이에 대응되는 2차원 카메라 평면 영상 좌표계의 한 점 가 주어졌을 때, 아래의 카메라 사영 행렬에 의해 모든 점 i에 대하여 를 만족한다.If we look at the general camera model, a point in three-dimensional space with a general pin-hole camera And a point of the corresponding 2D camera plane image coordinate system. Is given, for all points i by the camera projection matrix below Satisfies.
....................... [수학식 1] ....................... Equation 1
위 식에서 사영 행렬은 11 자유도(degrees of freedom)가 있다. 다음의 [수학식 2]는 실세계 좌표계와 카메라 원점간의 관계를 표현하고 있다.In the above equation, the projection matrix has 11 degrees of freedom.
...................................... [수학식 2] ............ Equation (2)
단, 내부 변수 이며, , 는 카메라 영상의 x, y축에 대한 초점거리이고, 는 x, y 두 축의 기울기(또는 비틀림 정도)이며, , 는 카메라 중심과 카메라 투영 평면이 직교하는 주점(principle point)을 나타낸다. 그리고 과 는 외부 변수로서 카메라의 회전과 이동을 의미한다.Internal variables Is, , Is the focal length for the x and y axes of the camera image, Is the slope (or twist) of the two axes x, y, , Denotes a principal point at which the camera center and the camera projection plane are orthogonal to each other. And and Is an external variable that means the rotation and movement of the camera.
특징점 추출수단(103)은 해리스 특징점 검색 방법을 기반으로 상기 평면 패턴의 특징점을 추출한다. 해리스 특징점 검색 방법은 선행 문헌 "[C. Harris and M.Stephens, "A combined corner and edge detector", 4th Alvey Vision Conference, pp.147-151, 1988]"에 개시된 바와 같이, 아래의 [수학식 3]을 통해 이루어진다.The feature
...................... [수학식 3] .......... [Equation 3]
여기서, 이며, 밝기 영상 에서 와 는 와 방향으로의 미분을 나타낸다.here, Brightness image in Wow Is Wow The derivative in the direction is shown.
이와 같이 추출된 특징점들은 , 방향으로 정렬되어야 하는데, 이는 XY 정렬수단(105)에 의해 수행된다.The feature points extracted in this way are , Direction, which is performed by the XY alignment means 105.
호모그래피 산출수단(107)은 정렬된 특징점들을 이용하여 각각의 카메라에서 촬영한 영상 내에 포함된 3장의 평면 패턴 간의 호모그래피(homography)를 산출한다. 호모그래피는 두 평면 사이의 사영 변환(projective transformation) 관계를 나타내며, 도 2와 같이 평면 패턴의 가로, 세로를 3차원 좌표계의 x, y축, 평면 패턴과 법선 방향을 z방향으로 가정하면, 평면 패턴에서의 z좌표는 0이 된다. 회전행렬의 각 열을 , , , 이동 벡터를 라 하면, 아래의 관계가 성립한다.The
..................... [수학식 4] ........... [ Equation 4 ]
따라서 영상 내의 좌표 과 설정된 3차원 좌표 사이에는 의 호모그래피 관계가 성립한다.Thus coordinates in the image And set three-dimensional coordinates In between The homography relationship is established.
..................................... [수학식 5] ........... [ Equation 5 ]
여기서, 이다.here, to be.
카메라 교정수단(109)은 3차원 재구성시 요구되는 카메라의 내외부 변수를 산출하고 교정하는데, 이는 위에서 산출된 호모그래피와 카메라 모델을 기반으로 구현된다. 본 발명의 특징적인 양상에 따르면, 카메라 행렬 , [수학식 1], [수학식 2]로부터 회전행렬의 , , 의 성질을 이용하면, 내부 변수는 아래의 [수학식 6]과 같다.The camera calibration means 109 calculates and corrects the internal and external variables of the camera required for three-dimensional reconstruction, which are implemented based on the homography and camera model calculated above. According to a characteristic aspect of the invention, a camera matrix , From [Equation 1], [Equation 2] , , Using the property of, the internal variable is shown in [Equation 6] below.
..................................... [수학식 6] [ Equation 6 ]
여기서, , 이며, 위 [수학식 6]은 다음과 같이 정리될 수 있다. here, , [Equation 6] can be summarized as follows.
..................... [수학식 7] ..... [ Equation 7 ]
[수학식 7]의 좌측 행렬은 다음의 [수학식 8]로 표현된다.The left matrix of Equation 7 is expressed by Equation 8 below.
.......... [수학식 8] .......... [ Equation 8 ]
위 [수학식 7]과 [수학식 8]로부터 다음의 관계식이 성립한다.From the above [Equation 7] and [Equation 8], the following relation holds.
. ..... [수학식 9] . ..... [ Equation 9 ]
상기한 [수학식 9]에서 의 선형 방정식은 다음과 같다.In Equation 9 above The linear equation of is
.................. [수학식 10] .................. [Equation 10]
.................. [수학식 11] [ Equation 11 ]
행렬 은 5 자유도의 코닉(conic)의 계수이다. 코닉은 일반적인 위치에서 다섯 점들로 결정된다. 위 선형 방정식에서 을 라 정의하면, 가 된다. 따라서 로 표현될 수 있다. 여기서 은 대칭이므로 로 표현된다.procession Is the coefficient of conic of 5 degrees of freedom. Conic is determined by five points in the general position. In the linear equation above of If you define Becomes therefore It can be expressed as. here Is symmetric It is expressed as
상기 의 관계에서 [수학식 2]에서 정의한 를 대입하면 다음의 [수학식 13]이 유도된다.remind Defined in
................. [수학식 13] [ Equation 13 ]
상기 [수학식 13]에 의해 카메라의 내부 변수(intrinsic parameter)가 다음 과 같이 계산된다.The intrinsic parameter of the camera is calculated by Equation 13 as follows.
, , , ,
, , , ,
따라서 앞서 언급한 회전행렬과 이동행렬의 수식은 상기한 [수학식 6]을 기반으로 도출되는 것이며, 각각은 아래와 같다.Therefore, the above-mentioned equations of the rotation matrix and the movement matrix are derived based on Equation 6, each of which is described below.
............................... [수학식 14] ......................... [ Equation 14 ]
................................ [수학식 15] ......................... [Equation 15]
단, [수학식 15]의 는 상기 의 네 번째 열벡터이다.However, in [Equation 15] Above Is the fourth column vector of.
한편, 기본행렬 계산수단(111)은 상기 평면 패턴의 특징점들 간의 매칭 정보를 바탕으로 에피폴라 기하를 통해 기본행렬(fundamental matrix)을 계산한다.On the other hand, the basic matrix calculation means 111 calculates a fundamental matrix through the epipolar geometry based on the matching information between the feature points of the planar pattern.
주지된 바와 같이 에피폴라 기하(epipolar geometry)란 첨부된 도 3에 예시한 바와 같이, 두 대의 카메라에서 획득된 영상 사이의 관계는 점과 점의 대응이 아닌, 점과 선의 대응으로 정의될 수 있다는 것이 요지라 할 수 있다. As is well known, epipolar geometry is illustrated in the accompanying FIG. 3, the relationship between images obtained from two cameras may be defined as a point-to-line correspondence, not a point-to-point correspondence. That is the point.
공간의 임의의 점 을 서로 다른 위치의 카메라( ,)에 의한 이미지 평면(, )에 투영하면, 각각의 영상에 점 과 로 맺히며, 이러한 두 점을 대응점이라고 한다. 공간상의 점 과 두 카메라가 이루는 평면은 에피폴라 평면이며, 에피폴라 평면과 영상 평면이 교차하는 선을 에피폴라 선(, )이라고 하고, 두 카 메라를 연결하는 선분과 각 영상 평면의 교점을 에피폴(, )이라고 한다. 여기서 공간상의 점 M은 투영된 점 , 는 에피폴라 선상에 존재하며, 이를 에피폴라 구속 조건이라고 한다. 이에 대한 대수적 표현이 앞서 언급한 기본행렬(F)이며, 아래의 [수학식 16]과 같은 조건을 만족한다.Random point in space At different locations , Image plane by , ), A dot on each image and These two points are called correspondence points. Point in space The plane formed by the two cameras is the epipolar plane, and the epipolar line (the line where the epipolar plane and the image plane intersect) , ) And the intersection of the two cameras and the intersection of each image plane is called epipole ( , It is called). Where point M in space is the projected point , Is on the epipolar line and is called epipolar constraint. Thus for the default matrix (F) an algebraic expression is mentioned above, and satisfies the condition shown in [Equation 16] below.
................................. [수학식 16] [ Equation 16 ]
다음으로 영상교정 수단(113)은 두 영상의 에피폴라 선을 서로 평행하게 함으로써 영상을 교정한다. 종래의 영상교정에 대해서는 다음의 선행 문헌에 개시되어 있다[O. Faugeras,"Three-Dimensional Computer Vision: a Geometric Viewpoint", MIT press, 1993], [N. Ayache and C. Hansen,"Rectification of images for binocular and trinocular stereovision", Proc. International Conference on Pattern Recognition, pp. 11-16, 1988], [D. Papadimitriou and T. Dennis,"Epipolar line estimation and rectification for stereo image pairs", IEEE Trans. Image Processing, 5(4):672-676, 1996]. Next, the image correcting means 113 corrects the image by making the epipolar lines of the two images parallel to each other. Conventional image correction is disclosed in the following precedent documents [O. Faugeras, "Three-Dimensional Computer Vision: a Geometric Viewpoint", MIT press , 1993], [N. Ayache and C. Hansen, "Rectification of images for binocular and trinocular stereovision", Proc. International Conference on Pattern Recognition , pp. 11-16, 1988, [D. Papadimitriou and T. Dennis, "Epipolar line estimation and rectification for stereo image pairs", IEEE Trans. Image Processing , 5 (4): 672-676, 1996].
상기한 선행 문헌들의 요지는 두 영상의 3차원 공간을 한 평면의 영상으로 변형하는 것이라 할 수 있다. 그러나 본 발명에서는 영상의 x, y 기준 좌표계에서 에피폴, 좌표 거리와 각도를 사용한 변형 방법을 이용한다. 이 변형 방법은 불필요한 화소가 발생하지 않고, 직관적으로 좌표계가 변환되는 장점이 있다. 이에 대해서는 Pollefeys의 선행 문헌, "A simple and efficient rectification method for general motion", Computer Vision, 1999"에 상세히 소개되어 있으므로, 본 발명에 서는 그에 따른 효과만을 언급한다.The gist of the above-mentioned prior documents can be said to transform the three-dimensional space of two images into one plane image. However, the present invention uses a transformation method using epipole, coordinate distance and angle in the x, y reference coordinate system of the image. This deformation method has the advantage that the coordinate system is intuitively transformed without unnecessary pixels. As it is introduced in detail in Pollefeys' prior literature, "A simple and efficient rectification method for general motion", Computer Vision , 1999, the present invention refers only to the effects accordingly.
다음으로 시차맵 구성수단(115)은 교정된 두 영상에서 모든 정합된 대응점을 찾아 조밀한 시차맵(disparity map)을 구성한다. 본 발명에서는 오차의 발생률을 최소화해서 모델 구성으로 영상의 화소에 대해 일정 크기의 윈도우(window)를 설정한다. 영상에서 윈도우 내의 분산(variance)을 계산하고, 분산 문턱치(threshold)보다 큰 영상의 화소들은 1차 대응 후보점으로 추출한 후, 시차맵을 구성한다.Next, the disparity
보다 구체적으로 영상1(좌측 영상)에서 문턱치(threshold) 이상의 분산(variance)(수학식 17 참조)을 갖는 화소들을 검색한 후, 이 검색된 화소들과 부합하는 화소들을 영상2(우측 영상)에서 검색해서 정합한다.More specifically, after searching for pixels having a variance (see Equation 17) that is greater than or equal to a threshold in image 1 (left image), pixels corresponding to the searched pixels are searched in image 2 (right image). To match.
................ [수학식 17] [ Equation 17 ]
여기서, 이다.here, to be.
상기한 정합 방법은 다음과 같다.The matching method described above is as follows.
영상1에서 점 을 중심점으로 상관 윈도우 크기를 로 정의한다. 따라서 영상2에서 에 대응되는 점은 영상2의 에피폴라 선을 검색해서 영상1에서 에 대응되는 를 찾는다. 이를 위한 상관함수는 [수학식 18]로 표현된다.Point in Image 1 The correlation window size Defined as So in
[수학식 18] [ Equation 18 ]
여기서, 로서, 는 점 (, )에서의 평균을 나타내며, 는 (, )의 이웃하는 에서 영상 의 표준 편차를 나타내고, 상기 는 아래와 같이 정의된다.here, as, Points ( , ) Mean, Is ( , Neighbors Video from Represents the standard deviation of Is defined as
상관도(score)의 범위는 정규화를 거쳤기 때문에 -1에서 1 사이의 값을 가지며, 상관 윈도우가 완전히 부정확할 경우에는 -1이 되고, 정확할 경우에는 1이 된다. Since the range of the correlation has been normalized, it has a value between -1 and 1, and is -1 if the correlation window is completely inaccurate, and 1 if it is correct.
상기한 [수학식 17]을 고찰해 보기 위해 영상1의 점 (, )에 대응되는 영상2의 점 (, )가 검색되었다고 가정하면, 영상1의 (, )에서 영상2의 최대 상관도의 점이 (, )라 할지라도, 영상2의 (, )를 기준으로 영상1에서 검색 시, 정합점은 (, )가 아닐 가능성이 있다. 따라서 본 발명에서는 영상1의 한 점을 기준으로 영상2에서 검색한 후, 정합된 점을 기준으로 다시 영상1에서 검색하여 영상1에서 정합이 되었을 경우에만 최종 정합된 것으로 한다.In order to consider [Equation 17] above, , Of the image2 corresponding to) , ) Is found, the , ), The point of maximum correlation of
3차원 좌표 계산수단(117)은 상기 구성된 시차맵을 기반으로 역 투영법(back projection)에 의해 3차원 좌표를 계산한다. The three-dimensional coordinate
다면체 구성수단(119)은 계산된 3차원 좌표들을 들로니 삼각화법(Delauny triangulation)의 방법에 따라 다면체로 구성한다. 그리고 텍스쳐 매핑수단(121)은 상기 구성된 다면체에 텍스쳐를 매핑(mapping)한다. The polyhedron construction means 119 configures the calculated three-dimensional coordinates into a polyhedron according to the Delauny triangulation method. The
상술한 일련의 수단을 통해 앞서 로딩된 영상으로부터 3차원 재구성이 이루어진다.Three-dimensional reconstruction is performed from the previously loaded image through the series of means described above.
실 험 예Experimental example
1.One. 패턴 영상의 카메라 교정에 관한 실험. Experiment on Camera Calibration of Pattern Image.
상술한 카메라 교정에 대한 실험예로서, 카메라 두 대를 이용하여 좌우 영상에서 3개의 패턴 평면을 촬영한 후, 이를 입력 영상으로 실험하였다. 입력 영상은 첨부된 도 4a 및 도 4b이다. 도 4c는 본 발명에 따른 카메라 내외부 변수의 결과이다.As an experimental example of the above-described camera calibration, three pattern planes were taken from the left and right images using two cameras, and then experimented with the input images. The input image is shown in FIGS. 4A and 4B. 4C is the result of internal and external variables of the camera according to the present invention.
2.2. 영상교정과 시차맵의 구성에 관한 실험. Experiments on Image Correction and Parallax Map Construction.
샘플 좌우 영상에 대해, 기본행렬과 에피폴을 계산했다. 도 5a와 같이 좌우측의 에피폴라 선을 평행하게 맞춘 후, 이를 교정한 것이 도 5b의 영상이다. 교정된 영상에서 정확한 정합이 수행되어야 하기 때문에, 앞서 언급한 바와 같이 정합 후보점을 산출한다. 산출된 정합 후보점은 도 5c와 같다.For the sample left and right images, the base matrix and epipole were calculated. As shown in FIG. 5A, the epipolar lines on the left and right sides are aligned in parallel, and the images of FIG. 5B are corrected. Since accurate matching must be performed on the corrected image, a matching candidate point is calculated as mentioned above. The calculated matching candidate point is shown in FIG. 5C.
산출된 정합 후보점은 좌우 영상의 시차이며, 교정된 좌우 영상에서 에지(edge)로 시차맵이 구성된 후, 계산된 시차 분포는 도 5d의 표와 같다. 본 실험예에서는 문턱치 이하의 시차맵들이 오차로서 제거되었으며, 도 5d에 보이는 바와 같이 대략 108에서 156사이에 분포되어 있음을 알 수 있다.The calculated matching candidate point is the parallax of the left and right images, and after the parallax map is configured with an edge in the corrected left and right images, the calculated parallax distribution is shown in the table of FIG. 5D. In the present experimental example, parallax maps below the threshold were removed as an error, and as shown in FIG. 5D, it can be seen that they are distributed between approximately 108 and 156.
3.3. 3차원 재구성 실험. 3D reconstruction experiment.
계산된 3차원 좌표는 역 투영법에 의해 투영된다. 역 투영된 3차원 좌표들은 들로니 삼각화법(Delaunay Triangulation)에 의해 폴리곤을 형성한다. The calculated three-dimensional coordinates are projected by the reverse projection method. The back projected three-dimensional coordinates form a polygon by Delaunay triangulation.
첨부된 도 6a는 3차원 좌표들을 근간으로 재구성한 영상이며, 도 6b는 3차원 좌표들에 의한 폴리곤을 구성을 보이고 있다. 도 6c는 도 6b에서 구성된 폴리곤을 OpenGL로 구현한 것이다.6A is an image reconstructed based on 3D coordinates, and FIG. 6B shows a polygon formed by 3D coordinates. FIG. 6C is an implementation of the polygon constructed in FIG. 6B in OpenGL.
이상으로 본 발명의 기술적 사상을 예시하기 위한 바람직한 실시예와 관련하여 설명하고 도시하였지만, 본 발명은 이와 같이 도시되고 설명된 그대로의 구성 및 작용에만 국한되는 것이 아니며, 기술적 사상의 범주를 일탈함이 없이 본 발명에 대해 다수의 변경 및 수정이 가능함을 당업자들은 잘 이해할 수 있을 것이다. 따라서, 그러한 모든 적절한 변경 및 수정과 균등물들도 본 발명의 범위에 속하는 것으로 간주되어야 할 것이다. As described above and described with reference to a preferred embodiment for illustrating the technical idea of the present invention, the present invention is not limited to the configuration and operation as shown and described as described above, it is a deviation from the scope of the technical idea It will be understood by those skilled in the art that many modifications and variations can be made to the invention without departing from the scope of the invention. Accordingly, all such suitable changes and modifications and equivalents should be considered to be within the scope of the present invention.
영상 기반 모델링의 경우, 카메라 교정, 기본행렬 계산, 시차맵 구성, 역 투영법 등은 수행 시에 많은 오차를 포함한다. 본 발명에서는 이러한 점을 감안하여, 단일의 영상에 촬영된 3장의 평면 패턴에 대한 호모그래피를 이용함으로써 카메라 교정을 Z. Zhang의 방법에 비해 단순화시킬 수 있고, 대응점 후보의 분산을 기반으로 시차맵을 구성하되, 문턱치 이하의 시차를 제거함으로써 오차를 최소화시킬 수 있다.In the case of image-based modeling, camera calibration, basic matrix calculation, parallax map construction, and inverse projection method include a lot of errors in performance. In view of this point, the present invention can simplify camera calibration compared to Z. Zhang's method by using homography for three plane patterns captured on a single image, and disparity map based on the dispersion of corresponding candidate candidates. To configure the, it is possible to minimize the error by removing the parallax below the threshold.
Claims (4)
Priority Applications (1)
| Application Number | Priority Date | Filing Date | Title |
|---|---|---|---|
| KR1020060062238A KR100755450B1 (en) | 2006-07-04 | 2006-07-04 | 3d reconstruction apparatus and method using the planar homography |
Applications Claiming Priority (1)
| Application Number | Priority Date | Filing Date | Title |
|---|---|---|---|
| KR1020060062238A KR100755450B1 (en) | 2006-07-04 | 2006-07-04 | 3d reconstruction apparatus and method using the planar homography |
Publications (1)
| Publication Number | Publication Date |
|---|---|
| KR100755450B1 true KR100755450B1 (en) | 2007-09-04 |
Family
ID=38736496
Family Applications (1)
| Application Number | Title | Priority Date | Filing Date |
|---|---|---|---|
| KR1020060062238A KR100755450B1 (en) | 2006-07-04 | 2006-07-04 | 3d reconstruction apparatus and method using the planar homography |
Country Status (1)
| Country | Link |
|---|---|
| KR (1) | KR100755450B1 (en) |
Cited By (21)
| Publication number | Priority date | Publication date | Assignee | Title |
|---|---|---|---|---|
| KR100922273B1 (en) | 2008-01-04 | 2009-10-15 | 중앙대학교 산학협력단 | Mechanism for reconstructing a 3D model using key-frames selected from image sequences |
| WO2011112028A2 (en) * | 2010-03-12 | 2011-09-15 | Seok Bo Ra | Stereoscopic image generation method and a device therefor |
| CN102509304A (en) * | 2011-11-24 | 2012-06-20 | 江南大学 | Intelligent optimization-based camera calibration method |
| CN103150721A (en) * | 2013-01-10 | 2013-06-12 | 杭州先临三维科技股份有限公司 | Mistaking identification point removal method of scanner calibration plate image and calibration plate |
| CN103247053A (en) * | 2013-05-16 | 2013-08-14 | 大连理工大学 | Accurate part positioning method based on binocular microscopy stereo vision |
| KR101310589B1 (en) * | 2009-05-21 | 2013-09-23 | 인텔 코오퍼레이션 | Techniques for rapid stereo reconstruction from images |
| KR101431378B1 (en) * | 2013-04-08 | 2014-08-19 | 포항공과대학교 산학협력단 | Method for generating omni-directional image and apparatus therefor |
| CN104091324A (en) * | 2014-06-16 | 2014-10-08 | 华南理工大学 | Quick checkerboard image feature matching algorithm based on connected domain segmentation |
| KR101597163B1 (en) * | 2014-08-14 | 2016-02-24 | 아진산업(주) | Method and camera apparatus for calibration of stereo camera |
| KR101748674B1 (en) * | 2016-05-18 | 2017-06-19 | 연세대학교 산학협력단 | Method and apparatus for producing three-dimensional image |
| WO2017175888A1 (en) * | 2016-04-05 | 2017-10-12 | 삼성전자 주식회사 | Image processing method and apparatus |
| CN109285195A (en) * | 2018-10-18 | 2019-01-29 | 易思维(杭州)科技有限公司 | Distortion correction method and its application pixel-by-pixel of monocular optical projection system based on large scale target |
| WO2019144289A1 (en) * | 2018-01-23 | 2019-08-01 | SZ DJI Technology Co., Ltd. | Systems and methods for calibrating an optical system of a movable object |
| CN110910456A (en) * | 2019-11-22 | 2020-03-24 | 大连理工大学 | Stereo camera dynamic calibration algorithm based on Harris angular point mutual information matching |
| KR20200129657A (en) * | 2019-05-09 | 2020-11-18 | 스크린커플스(주) | Method for gaining 3D model video sequence |
| KR20210081983A (en) * | 2019-12-24 | 2021-07-02 | 한국도로공사 | System and method of Automatically Generating High Definition Map Based on Camera Images |
| CN116704046A (en) * | 2023-08-01 | 2023-09-05 | 北京积加科技有限公司 | Cross-mirror image matching method and device |
| CN116863086A (en) * | 2023-09-04 | 2023-10-10 | 武汉国遥新天地信息技术有限公司 | Rigid body stable reconstruction method for optical motion capture system |
| WO2023239717A1 (en) * | 2022-06-07 | 2023-12-14 | Canon U.S.A., Inc. | Apparatus and method for whiteboard rectification |
| CN117450955A (en) * | 2023-12-21 | 2024-01-26 | 成都信息工程大学 | Three-dimensional measurement method for thin object based on space annular feature |
| US12022052B2 (en) | 2020-08-25 | 2024-06-25 | Samsung Electronics Co., Ltd. | Method and apparatus for 3D reconstruction of planes perpendicular to ground |
Citations (2)
| Publication number | Priority date | Publication date | Assignee | Title |
|---|---|---|---|---|
| US5598515A (en) * | 1994-01-10 | 1997-01-28 | Gen Tech Corp. | System and method for reconstructing surface elements of solid objects in a three-dimensional scene from a plurality of two dimensional images of the scene |
| US20020024516A1 (en) * | 2000-05-03 | 2002-02-28 | Qian Chen | Three-dimensional modeling and based on photographic images |
-
2006
- 2006-07-04 KR KR1020060062238A patent/KR100755450B1/en active IP Right Grant
Patent Citations (2)
| Publication number | Priority date | Publication date | Assignee | Title |
|---|---|---|---|---|
| US5598515A (en) * | 1994-01-10 | 1997-01-28 | Gen Tech Corp. | System and method for reconstructing surface elements of solid objects in a three-dimensional scene from a plurality of two dimensional images of the scene |
| US20020024516A1 (en) * | 2000-05-03 | 2002-02-28 | Qian Chen | Three-dimensional modeling and based on photographic images |
Cited By (33)
| Publication number | Priority date | Publication date | Assignee | Title |
|---|---|---|---|---|
| KR100922273B1 (en) | 2008-01-04 | 2009-10-15 | 중앙대학교 산학협력단 | Mechanism for reconstructing a 3D model using key-frames selected from image sequences |
| US9053550B2 (en) | 2009-05-21 | 2015-06-09 | Intel Corporation | Techniques for rapid stereo reconstruction from images |
| KR101310589B1 (en) * | 2009-05-21 | 2013-09-23 | 인텔 코오퍼레이션 | Techniques for rapid stereo reconstruction from images |
| US9652849B2 (en) | 2009-05-21 | 2017-05-16 | Intel Corporation | Techniques for rapid stereo reconstruction from images |
| WO2011112028A2 (en) * | 2010-03-12 | 2011-09-15 | Seok Bo Ra | Stereoscopic image generation method and a device therefor |
| WO2011112028A3 (en) * | 2010-03-12 | 2012-01-12 | Seok Bo Ra | Stereoscopic image generation method and a device therefor |
| CN102714748A (en) * | 2010-03-12 | 2012-10-03 | 石保罗 | Stereoscopic image generation method and a device therefor |
| CN102509304A (en) * | 2011-11-24 | 2012-06-20 | 江南大学 | Intelligent optimization-based camera calibration method |
| CN103150721A (en) * | 2013-01-10 | 2013-06-12 | 杭州先临三维科技股份有限公司 | Mistaking identification point removal method of scanner calibration plate image and calibration plate |
| CN103150721B (en) * | 2013-01-10 | 2015-07-29 | 杭州先临三维科技股份有限公司 | The mistake identification point minimizing technology of scanner calibration plate image and scaling board |
| KR101431378B1 (en) * | 2013-04-08 | 2014-08-19 | 포항공과대학교 산학협력단 | Method for generating omni-directional image and apparatus therefor |
| CN103247053A (en) * | 2013-05-16 | 2013-08-14 | 大连理工大学 | Accurate part positioning method based on binocular microscopy stereo vision |
| CN104091324A (en) * | 2014-06-16 | 2014-10-08 | 华南理工大学 | Quick checkerboard image feature matching algorithm based on connected domain segmentation |
| KR101597163B1 (en) * | 2014-08-14 | 2016-02-24 | 아진산업(주) | Method and camera apparatus for calibration of stereo camera |
| WO2017175888A1 (en) * | 2016-04-05 | 2017-10-12 | 삼성전자 주식회사 | Image processing method and apparatus |
| KR101748674B1 (en) * | 2016-05-18 | 2017-06-19 | 연세대학교 산학협력단 | Method and apparatus for producing three-dimensional image |
| CN110998241A (en) * | 2018-01-23 | 2020-04-10 | 深圳市大疆创新科技有限公司 | System and method for calibrating an optical system of a movable object |
| WO2019144289A1 (en) * | 2018-01-23 | 2019-08-01 | SZ DJI Technology Co., Ltd. | Systems and methods for calibrating an optical system of a movable object |
| CN109285195A (en) * | 2018-10-18 | 2019-01-29 | 易思维(杭州)科技有限公司 | Distortion correction method and its application pixel-by-pixel of monocular optical projection system based on large scale target |
| CN109285195B (en) * | 2018-10-18 | 2020-09-04 | 易思维(杭州)科技有限公司 | Monocular projection system pixel-by-pixel distortion correction method based on large-size target and application thereof |
| KR20200129657A (en) * | 2019-05-09 | 2020-11-18 | 스크린커플스(주) | Method for gaining 3D model video sequence |
| KR102222290B1 (en) * | 2019-05-09 | 2021-03-03 | 스크린커플스(주) | Method for gaining 3D model video sequence |
| CN110910456A (en) * | 2019-11-22 | 2020-03-24 | 大连理工大学 | Stereo camera dynamic calibration algorithm based on Harris angular point mutual information matching |
| KR20210081983A (en) * | 2019-12-24 | 2021-07-02 | 한국도로공사 | System and method of Automatically Generating High Definition Map Based on Camera Images |
| KR102305328B1 (en) | 2019-12-24 | 2021-09-28 | 한국도로공사 | System and method of Automatically Generating High Definition Map Based on Camera Images |
| US12022052B2 (en) | 2020-08-25 | 2024-06-25 | Samsung Electronics Co., Ltd. | Method and apparatus for 3D reconstruction of planes perpendicular to ground |
| WO2023239717A1 (en) * | 2022-06-07 | 2023-12-14 | Canon U.S.A., Inc. | Apparatus and method for whiteboard rectification |
| CN116704046A (en) * | 2023-08-01 | 2023-09-05 | 北京积加科技有限公司 | Cross-mirror image matching method and device |
| CN116704046B (en) * | 2023-08-01 | 2023-11-10 | 北京积加科技有限公司 | Cross-mirror image matching method and device |
| CN116863086B (en) * | 2023-09-04 | 2023-11-24 | 武汉国遥新天地信息技术有限公司 | Rigid body stable reconstruction method for optical motion capture system |
| CN116863086A (en) * | 2023-09-04 | 2023-10-10 | 武汉国遥新天地信息技术有限公司 | Rigid body stable reconstruction method for optical motion capture system |
| CN117450955A (en) * | 2023-12-21 | 2024-01-26 | 成都信息工程大学 | Three-dimensional measurement method for thin object based on space annular feature |
| CN117450955B (en) * | 2023-12-21 | 2024-03-19 | 成都信息工程大学 | Three-dimensional measurement method for thin object based on space annular feature |
Similar Documents
| Publication | Publication Date | Title |
|---|---|---|
| KR100755450B1 (en) | 3d reconstruction apparatus and method using the planar homography | |
| US10388025B2 (en) | Interactive image based 3D panogragh | |
| Pollefeys et al. | From images to 3D models | |
| KR101310589B1 (en) | Techniques for rapid stereo reconstruction from images | |
| Pollefeys et al. | Visual modeling with a hand-held camera | |
| KR101410273B1 (en) | Method and apparatus for environment modeling for ar | |
| CN111127524A (en) | Method, system and device for tracking trajectory and reconstructing three-dimensional image | |
| CN109613974B (en) | AR home experience method in large scene | |
| CN107707899B (en) | Multi-view image processing method, device and electronic equipment comprising moving target | |
| Banno et al. | Omnidirectional texturing based on robust 3D registration through Euclidean reconstruction from two spherical images | |
| Siu et al. | Image registration for image-based rendering | |
| CN115035235A (en) | Three-dimensional reconstruction method and device | |
| Yuan et al. | 3D reconstruction of background and objects moving on ground plane viewed from a moving camera | |
| Mulligan et al. | Stereo-based environment scanning for immersive telepresence | |
| Knorr et al. | An image-based rendering (ibr) approach for realistic stereo view synthesis of tv broadcast based on structure from motion | |
| Yu et al. | Recursive three-dimensional model reconstruction based on Kalman filtering | |
| Lui et al. | An Iterative 5-pt Algorithm for Fast and Robust Essential Matrix Estimation. | |
| Wang et al. | What can we learn about the scene structure from three orthogonal vanishing points in images | |
| KR102375135B1 (en) | Apparatus and Method for Cailbrating Carmeras Loaction of Muti View Using Spherical Object | |
| Kimura et al. | 3D reconstruction based on epipolar geometry | |
| Ivekovic et al. | Fundamentals of Multiple‐View Geometry | |
| Wu et al. | Projective rectification based on relative modification and size extension for stereo image pairs | |
| Meerits | Real-time 3D reconstruction of dynamic scenes using moving least squares | |
| Schindler et al. | Fast on-site reconstruction and visualization of archaeological finds | |
| Sharma et al. | Parameterized variety based view synthesis scheme for multi-view 3DTV |
Legal Events
| Date | Code | Title | Description |
|---|---|---|---|
| A201 | Request for examination | ||
| E902 | Notification of reason for refusal | ||
| E701 | Decision to grant or registration of patent right | ||
| GRNT | Written decision to grant | ||
| FPAY | Annual fee payment |
Payment date: 20130805 Year of fee payment: 7 |
|
| FPAY | Annual fee payment |
Payment date: 20140703 Year of fee payment: 8 |
|
| FPAY | Annual fee payment |
Payment date: 20151028 Year of fee payment: 9 |
|
| FPAY | Annual fee payment |
Payment date: 20160629 Year of fee payment: 10 |
|
| FPAY | Annual fee payment |
Payment date: 20180525 Year of fee payment: 11 |
|
| R401 | Registration of restoration | ||
| FPAY | Annual fee payment |
Payment date: 20180827 Year of fee payment: 12 |
|
| FPAY | Annual fee payment |
Payment date: 20190828 Year of fee payment: 13 |