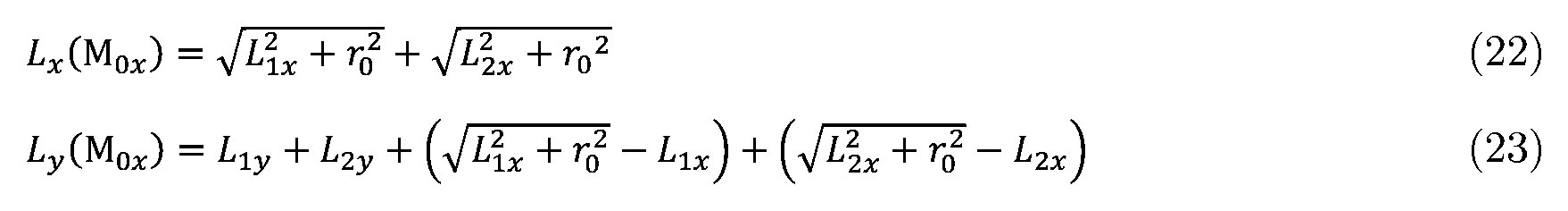JP7564522B2 - METHOD FOR DESIGNING MIRROR AND ASTAGITABER CONTROL MIRROR HAVING REFLECTING SURFACE WHEREIN THE DESIGN EQUATION IN THE METHOD APPLY - Google Patents
METHOD FOR DESIGNING MIRROR AND ASTAGITABER CONTROL MIRROR HAVING REFLECTING SURFACE WHEREIN THE DESIGN EQUATION IN THE METHOD APPLY Download PDFInfo
- Publication number
- JP7564522B2 JP7564522B2 JP2021003117A JP2021003117A JP7564522B2 JP 7564522 B2 JP7564522 B2 JP 7564522B2 JP 2021003117 A JP2021003117 A JP 2021003117A JP 2021003117 A JP2021003117 A JP 2021003117A JP 7564522 B2 JP7564522 B2 JP 7564522B2
- Authority
- JP
- Japan
- Prior art keywords
- point
- axis direction
- light source
- axis
- mirror
- Prior art date
- Legal status (The legal status is an assumption and is not a legal conclusion. Google has not performed a legal analysis and makes no representation as to the accuracy of the status listed.)
- Active
Links
- 238000000034 method Methods 0.000 title claims description 33
- 230000003287 optical effect Effects 0.000 claims description 33
- 201000009310 astigmatism Diseases 0.000 claims description 25
- 230000002093 peripheral effect Effects 0.000 claims description 9
- 239000000758 substrate Substances 0.000 claims description 9
- 239000000463 material Substances 0.000 claims 1
- 238000010586 diagram Methods 0.000 description 13
- 238000004088 simulation Methods 0.000 description 9
- 238000004364 calculation method Methods 0.000 description 5
- 230000008859 change Effects 0.000 description 2
- 238000006243 chemical reaction Methods 0.000 description 2
- 239000006185 dispersion Substances 0.000 description 2
- 238000006073 displacement reaction Methods 0.000 description 2
- 230000009466 transformation Effects 0.000 description 2
- 238000011144 upstream manufacturing Methods 0.000 description 2
- 230000009471 action Effects 0.000 description 1
- 230000001427 coherent effect Effects 0.000 description 1
- 230000007423 decrease Effects 0.000 description 1
- 238000009795 derivation Methods 0.000 description 1
- 238000005516 engineering process Methods 0.000 description 1
- 238000005286 illumination Methods 0.000 description 1
- 238000009434 installation Methods 0.000 description 1
- 230000007246 mechanism Effects 0.000 description 1
- 230000000644 propagated effect Effects 0.000 description 1
- 230000009467 reduction Effects 0.000 description 1
- 230000005469 synchrotron radiation Effects 0.000 description 1
- 238000000844 transformation Methods 0.000 description 1
Images
Landscapes
- Optical Elements Other Than Lenses (AREA)
Description
本発明は、基材の中空内周面または外周面に反射面を形成して作製されるミラーの設計方法、および該設計方法における設計式が成り立つ反射面を備えた非点収差制御ミラーに関する。 The present invention relates to a method for designing a mirror that is manufactured by forming a reflecting surface on the hollow inner or outer peripheral surface of a substrate, and to an astigmatism-controlled mirror that has a reflecting surface for which the design formula in the design method holds true.
放射光軟X線ビームは、鉛直方向と水平方向とで特性が異なるという特徴がある。ビームサイズは、水平方向に比べて鉛直方向が小さくなる傾向にある。コヒーレント幅は、水平方向に比べて鉛直方向が大きくなる。さらに、軟X線ビームラインに広く普及している回折格子を用いた分光システムでは、ビームの鉛直方向の発散角が増大してしまう。また、使用される回折格子を含む分光器は、分光方向にのみ軟X線を集光させるため、光源位置が分光方向と集光させない方向とで異なる「非点収差」が生じる。 A synchrotron radiation soft X-ray beam has the characteristic that its characteristics differ in the vertical and horizontal directions. The beam size tends to be smaller in the vertical direction than in the horizontal direction. The coherent width is larger in the vertical direction than in the horizontal direction. Furthermore, in spectroscopic systems using diffraction gratings, which are widely used in soft X-ray beamlines, the divergence angle of the beam in the vertical direction increases. In addition, the spectrometers containing the diffraction gratings used focus the soft X-rays only in the spectroscopic direction, resulting in "astigmatism," where the light source position is different in the spectroscopic direction and in directions where the light is not focused.
従来、このような鉛直方向と水平方向とで特性の異なるビームを取り扱う光学系の手法としては、たとえば鉛直方向・水平方向の各方向を扱う2枚のミラーを配置した二段階集光光学系とし、鉛直方向と水平方向とで光源点を独立に設定して集光点を一致させる手法が用いられている。具体的には、2枚の楕円筒ミラーを鉛直・水平に配置する手法や、2枚のベントミラー(機械曲げ円筒ミラー)を配置することで近似形状を成立させる手法、ベントミラーとサジタルシリンダーミラーの2枚をいずれも水平方向に対向して配置する手法などが知られている。しかしながら、このような2枚のミラーを組み合わせる手法の場合、機構が複雑になるうえ、チャンバーが増えるのでコストアップとなり、調整も難しくなる。 Conventionally, optical systems that handle beams with different characteristics in the vertical and horizontal directions have used a two-stage focusing optical system that arranges two mirrors to handle each of the vertical and horizontal directions, and sets the light source points independently in the vertical and horizontal directions to make the focusing points coincident. Specifically, known methods include arranging two elliptical mirrors vertically and horizontally, arranging two bent mirrors (mechanically bent cylindrical mirrors) to create an approximate shape, and arranging a bent mirror and a sagittal cylinder mirror facing each other in the horizontal direction. However, such a method of combining two mirrors results in a complex mechanism and an additional chamber, which increases costs and makes adjustments more difficult.
単一のミラーによって非点収差を除去できる可能性のあるものとしては、トロイダルミラーがある(非特許文献1)。しかしながら、トロイダルミラーは、既存の回転楕円ミラーを近似し、反射面の長手方向、短手方向それぞれに一様な曲率半径を設定することで作製を容易にしたミラーであり、非点収差を除去できたとしても、原理的に集光サイズが増大してしまうという欠点がある。 One possible single mirror that can eliminate astigmatism is the toroidal mirror (Non-Patent Document 1). However, a toroidal mirror is an approximation of an existing ellipsoidal mirror, and is easily manufactured by setting a uniform radius of curvature in both the long and short directions of the reflecting surface. Even if it can eliminate astigmatism, it has the drawback that, in principle, the focused light size increases.
トロイダルミラーよりも集光サイズを小さくでき、かつ鉛直・水平で独立した光源・集光点を設定可能なミラーとして、Astigmatic off-axis mirror(AOミラー)も提案されている(非特許文献2)。このミラーは、一点から発散するビームを別の点に集光させるためには楕円曲線を、一点から発散するビームを平行化するためには放物線を、一点に向かって集光するビームを別の点に向かって集光するビームに変換するためには双曲線を、それぞれ反射面の稜線として適用するとの原則のもと、長手方向と短手方向で異なる円錐曲線を設定し,それらを滑らかにつなぐ曲面を求める形状としたものである。 Astigmatic off-axis mirrors (AO mirrors) have also been proposed as mirrors that can reduce the focused size compared to toroidal mirrors and can set independent light sources and focusing points vertically and horizontally (Non-Patent Document 2). This mirror is shaped to obtain a curved surface that smoothly connects different conic sections in the long and short directions, based on the principle that an elliptical curve is used as the ridgeline of the reflecting surface to focus a beam diverging from one point to another, a parabola is used to parallelize a beam diverging from one point, and a hyperbola is used to convert a beam focused toward one point into a beam focused toward another point.
しかし、このAOミラーは、曲面を得るために長手方向の円錐曲線プロファイルを短手方向の円錐曲線の焦点を結ぶ直線(長軸)を中心に回転させることで定義されるミラーであり、反射面を軸対称形状に近似していることから、当該近似に起因して集光サイズの抑制に限界が生じる。波長の長いテラヘルツ領域のビームであれば問題ないが、X線領域のビームには対応できない。また、設計式が座標変換を数回含むなど、非常に複雑であり、パラメータも複雑で理解しにくく使いにくい。 However, this AO mirror is a mirror that is defined by rotating the longitudinal conic section profile around the straight line (major axis) connecting the foci of the transverse conic section to obtain a curved surface, and because the reflecting surface is approximated to an axially symmetric shape, this approximation creates a limit to the reduction in the focused size. This is not a problem for beams in the terahertz range with long wavelengths, but it cannot be used for beams in the X-ray range. In addition, the design formula is very complicated, including multiple coordinate transformations, and the parameters are also complicated, making it difficult to understand and use.
そこで、本発明が前述の状況に鑑み、解決しようとするところは、単一のミラーであって、鉛直方向と水平方向とで独立して光源位置及び集光位置を設定でき、これにより非点収差の自由な変換が可能であり、また、集光サイズをより小さく抑えてX線領域のビームにも対応することができ、設計式も単純で、応用の幅も広く、鉛直方向と水平方向とで特性が異なるビームを取り扱う光学系として好適に用いることができるミラーを作製できる、ミラーの設計方法を提供する点にある。 In view of the above situation, the present invention aims to provide a method for designing a mirror that can be used to create a single mirror that allows the light source position and focusing position to be set independently in the vertical and horizontal directions, thereby allowing free conversion of astigmatism, and that can also accommodate beams in the X-ray range by reducing the focusing size, has a simple design formula, is applicable in a wide range of applications, and can be used suitably as an optical system that handles beams with different characteristics in the vertical and horizontal directions.
本発明者は、かかる現況に鑑み、鋭意検討した結果、非点収差をもつビームの性質を幾何光学的に表現する方法として、鉛直方向と水平方向とでそれぞれ「光源線」および「集光線」を新たに定義し、ミラーの反射面を経由するすべての入射光線は鉛直方向および水平方向の各「光源線」を通り、ミラーの反射面から放たれるすべての出射光線が鉛直方向および水平方向の「集光線」を通るとし、これに光源位置から集光位置までの「光路長」が一定であるFermatの原理を適用することで、上記課題を解決できるミラーの設計方法を提供できることを見出し、本発明を完成するに至った。 In light of this current situation, the inventors conducted extensive research and discovered that a method for expressing the properties of a beam with astigmatism in geometrical optics can be provided by newly defining a "source ray" and a "focus ray" in the vertical and horizontal directions, respectively, and by assuming that all incident light rays passing through the reflective surface of the mirror pass through the "source rays" in the vertical and horizontal directions, and that all outgoing light rays emitted from the reflective surface of the mirror pass through the "focus rays" in the vertical and horizontal directions, and by applying Fermat's principle, which states that the "optical path length" from the light source position to the focus position is constant, it is possible to provide a design method for a mirror that can solve the above problems, which led to the completion of the present invention.
すなわち本発明は、以下の発明を包含する。
(1) 基材の中空内周面または外周面に反射面を形成して作製されるミラーの設計方法であって、前記基材の前記内周面または外周面の中心軸をz軸、これに直交する断面をxy平面とし、入射ビームが、z軸上所定位置からz軸方向に沿ってL1x変位した位置に、x軸方向の光源をもち、かつ前記z軸上所定位置からz軸方向に沿ってL1y変位した位置に、y軸方向の光源をもち、出射ビームが、x軸方向について前記z軸上所定位置からz軸方向に沿ってL2x変位した位置に集光し、かつy軸方向について前記z軸上所定位置からz軸方向に沿ってL2y変位した位置に集光し、ミラーを経由するすべての入射光線が、x軸方向における前記光源の位置を通り該x軸方向とz軸方向の双方に直交する方向に延びる第1の光源線、及びy軸方向における前記光源の位置を通り該y軸方向とz軸方向の双方に直交する方向に延びる第2の光源線を通過し、ミラーから放たれるすべての出射光線が、x軸方向における前記集光する位置を通り該x軸方向とz軸方向の双方に直交する方向に延びる第1の集光線、及びy軸方向における前記集光する位置を通り該y軸方向とz軸方向の双方に直交する方向に延びる第2の集光線を通過するとし、ミラーの反射面上の任意の点をMとして、第1の光源線とM点への入射光線との交点、及び第2の光源線とM点への入射光線との交点の各座標を、前記L1x、L1yを用いて表わし、且つ、前記M点からの出射光線と第1の集光線との交点、及びM点からの出射光線と第2の集光線との交点の各座標を、前記L2x、L2yを用いて表わし、これら座標、及び前記x軸方向及び前記y軸方向についてそれぞれ反射面上の任意の点に関して光源位置から集光位置までの光路長が一定であること、に基づき導かれる反射面の設計式を用いてミラーを設計することを特徴とする、ミラーの設計方法。
That is, the present invention includes the following inventions.
(1) A method for designing a mirror produced by forming a reflective surface on a hollow inner or outer peripheral surface of a substrate, the method including: setting a central axis of the inner or outer peripheral surface of the substrate as a z-axis, and a cross section perpendicular to the z-axis as an xy plane; an incident beam has a light source in the x-axis direction at a position displaced by L 1x along the z-axis from a predetermined position on the z-axis, and a light source in the y-axis direction at a position displaced by L 1y along the z-axis from the predetermined position on the z-axis; an outgoing beam is focused at a position displaced by L 2x along the z-axis from the predetermined position on the z-axis in the x-axis direction, and a light source in the y-axis direction at a position displaced by L 2x along the z-axis from the predetermined position on the z-axis in the y-axis direction; It is assumed that the light is focused at a position displaced by 2y from the mirror, all incident light rays passing through the mirror pass through a first light source line passing through the position of the light source in the x-axis direction and extending in a direction perpendicular to both the x-axis direction and the z-axis direction, and a second light source line passing through the position of the light source in the y-axis direction and extending in a direction perpendicular to both the y-axis direction and the z-axis direction, and all outgoing light rays emitted from the mirror pass through a first focused light line passing through the focusing position in the x-axis direction and extending in a direction perpendicular to both the x-axis direction and the z-axis direction, and a second focused light line passing through the focusing position in the y-axis direction and extending in a direction perpendicular to both the y-axis direction and the z-axis direction, and an arbitrary point on the reflecting surface of the mirror is denoted as M, and the coordinates of the intersection of the first light source line and the incident light ray at point M and the intersection of the second light source line and the incident light ray at point M are defined as L1x, L2x, L3x, L4x, L5x, L6x, L7x, L8x, L9x, L1x, L1x, L2x, L3x, L4x, L5x, L6x, L7x, L8x, L9x, L1x, L1x, L1x, L2x, L3x, L4x, L5x, L6x, L7x, L8x, L9x, L1x, L1x, L1x, L1x, L2x, L2x, L3x, L4x, L4x, L5x, L6x, L7x, L8x , L1 ... and expressing the coordinates of an intersection point between the outgoing light from point M and the first condensed light and an intersection point between the outgoing light from point M and the second condensed light using L2x , L2y , and designing the mirror using a design equation for the reflecting surface derived based on these coordinates and that the optical path length from the light source position to the condensed light position is constant for any point on the reflecting surface in each of the x-axis direction and the y-axis direction.
(2) 前記第1の光源線、前記第2の光源線を、それぞれy軸方向に延びる直線Sx、x軸方向に延びる直線Syとし、前記第1の集光線、前記第2の集光線を、それぞれy軸方向に延びる直線Fx、x軸方向に延びる直線Fyとし、前記x軸方向の光源位置からM点までの入射長は、前記第2の光源線Syとz軸との交点Py0を中心とし且つ第1の光源線Sxとz軸との交点Px0を通ってx軸に直交する方向に延びる円弧を、第1の光源線Sxを軸に回転させた回転円弧面を等位相面A1xとして、前記入射光線と該等位相面A1xとの2つの交点のうち第2の光源線Syに近い側の交点からM点までの距離として求め、M点から前記x軸方向の集光位置までの出射長は、前記第2の集光線Fyとz軸との交点Qy0を中心とし且つ第1の集光線Fxとz軸との交点Qx0を通ってx軸に直交する方向に延びる円弧を、第1の集光線Fxを軸に回転させた回転円弧面を等位相面A2xとして、前記出射光線と該等位相面A2xとの2つの交点のうち第2の集光線Fyに近い側の交点からM点までの距離として求め、前記y軸方向の光源位置からM点までの入射長は、前記第1の光源線Sxとz軸との交点Px0を中心とし且つ第2の光源線Syとz軸との交点Py0を通ってy軸に直交する方向に延びる円弧を、第2の光源線Syを軸に回転させた回転円弧面を等位相面A1yとして、前記入射光線と該等位相面A1yとの2つの交点のうち第1の光源線Sxに近い側の交点からM点までの距離として求め、M点から前記y軸方向の集光位置までの出射長は、前記第1の集光線Fxとz軸との交点Qx0を中心とし且つ第2の光源線Fyとz軸との交点Qy0を通ってy軸に直交する方向に延びる円弧を、第2の集光線Fyを軸に回転させた回転円弧面を等位相面A2yとして、前記出射光線と該等位相面A2yとの2つの交点のうち第1の集光線Fxに近い側の交点からM点までの距離として求め、これにより前記x軸方向及びy軸方向のそれぞれの集光に関して入射長と出射長の和である光路長を算出してなる、(1)記載のミラーの設計方法。 (2) The first light source line and the second light source line are respectively a straight line S x extending in the y-axis direction and a straight line S y extending in the x-axis direction, the first condensed light line and the second condensed light line are respectively a straight line F x extending in the y-axis direction and a straight line F y extending in the x-axis direction, the incident length from the light source position in the x-axis direction to point M is calculated as the distance from one of two intersection points between the incident light and the equiphase surface A 1x that is closer to the second light source line S y to point M, with an arc having an intersection point P y0 between the second light source line S y and the z-axis as its center and passing through the intersection point P x0 between the first light source line S x and the z-axis as its center, being rotated around the first light source line S x as an equiphase surface A 1x , and the exit length from point M to the condensed light position in the x-axis direction is calculated as the distance from the one of two intersection points between the incident light and the equiphase surface A 1x that is closer to the second light source line S y to point M, and the exit length from point M to the condensed light position in the x-axis direction to point M ... The incident length from the light source position in the y -axis direction to point M is calculated by rotating an arc having a center at an intersection point P x0 of the first light source line S x and the z-axis, passing through an intersection point Q x0 of the first light source line F x and the z-axis, and rotating the arc around the first light source line F x to obtain an equiphase surface A 2x , and calculating the distance from one of the two intersection points between the output light beam and the equiphase surface A 2x that is closer to the second light source line F y to point M. The incident length from the light source position in the y-axis direction to point M is calculated by rotating an arc having a center at an intersection point P x0 of the first light source line S x and the z-axis, passing through an intersection point P y0 of the second light source line S y and the z-axis to obtain an equiphase surface A 1y , and calculating the distance from one of the two intersection points between the input light beam and the equiphase surface A 1y that is closer to the first light source line S a distance from the intersection point closer to x to point M, and an emission length from point M to the focusing position in the y-axis direction is calculated by rotating an arc having an intersection point Qx0 of the first focusing line Fx and the z-axis as its center, passing through an intersection point Qy0 of the second light source line Fy and the z- axis and extending in a direction perpendicular to the y- axis , around the second focusing line Fy as an axis to obtain an equiphase surface A2y , and calculating an optical path length that is a sum of an incident length and an exit length for focusing in each of the x-axis and y-axis directions.
(3) 前記入射光線と等位相面A1xとの2つの交点のうち第2の光源線Syに近い側の交点からM点までの距離は、前記入射光線と前記第1の光源線Sxとの交点Pxから前記M点までの距離を求めるとともに、該距離に、前記交点Pxから前記等位相面A1xを定義している前記円弧までの距離を加算又は減算して求め、前記出射光線と等位相面A2xとの2つの交点のうち第2の集光線Fyに近い側の交点からM点までの距離は、前記出射光線と前記第1の集光線Fxとの交点Qxから前記M点までの距離を求めるとともに、該距離に、前記交点Qxから前記等位相面A2xを定義している前記円弧までの距離を加算又は減算して求め、前記入射光線と等位相面A1yとの2つの交点のうち第1の光源線Sxに近い側の交点からM点までの距離は、前記入射光線と前記第2の光源線Syとの交点Pyから前記M点までの距離を求めるとともに、該距離に、前記交点Pyから前記等位相面A1yを定義している前記円弧までの距離を加算又は減算して求め、前記出射光線と等位相面A2yとの2つの交点のうち第1の集光線Fxに近い側の交点からM点までの距離は、前記出射光線と前記第2の集光線Fyとの交点Qyから前記M点までの距離を求めるとともに、該距離に、前記交点Qyから前記等位相面A2yを定義している前記円弧までの距離を加算又は減算して求める、(2)記載のミラーの設計方法。 (3) The distance from one of the two intersection points between the incident light ray and the equiphase surface A1x that is closer to the second light source line S y to point M is obtained by calculating the distance from an intersection point P x between the incident light ray and the first light source line S x to point M, and adding or subtracting the distance from the intersection point P x to the arc that defines the equiphase surface A 1x to the distance. The distance from one of the two intersection points between the exit light ray and the equiphase surface A 2x that is closer to the second condenser line F y to point M is obtained by calculating the distance from an intersection point Q x between the exit light ray and the first condenser line F x to point M, and adding or subtracting the distance from the intersection point Q x to the arc that defines the equiphase surface A 2x to the distance. a distance from a point of intersection closer to x to point M is obtained by determining a distance from a point of intersection Py between the incident light beam and the second light source line S y to point M, and adding or subtracting a distance from the point of intersection Py to the arc defining the equiphase surface A 1y to that distance; and a distance from a point of intersection closer to a first focusing line Fx of two points of intersection between the exit light beam and the equiphase surface A 2y to point M is obtained by determining a distance from a point of intersection Qy between the exit light beam and the second focusing line Fy to point M, and adding or subtracting a distance from the point of intersection Qy to the arc defining the equiphase surface A 2y to that distance.
(4) 前記設計式が、前記x軸方向について光源点から集光点までの光路長が一定であることから導かれる第1の式fx(x,y,z)=0と、前記y軸方向について光源点から集光点までの光路長が一定であることから導かれる第2の式fy(x,y,z)=0とを重みづけした、下記式からなる、(1)~(3)の何れかに記載のミラーの設計方法。 (4) The method for designing a mirror according to any one of (1) to (3), wherein the design formula is the following formula obtained by weighting a first formula f x (x, y, z) = 0 derived from the fact that the optical path length from the light source point to the focusing point is constant in the x-axis direction, and a second formula f y (x, y, z) = 0 derived from the fact that the optical path length from the light source point to the focusing point is constant in the y-axis direction:
(5) (1)~(4)の何れかに記載のミラーの設計方法における前記設計式が成り立つ反射面を有するミラーであって、前記L1xとL1yの値が異なり、且つ前記L2xとL2yの値が一致しており、非点収差をもつ入射ビームから一点に集光する出射ビームが得られる、非点収差制御ミラー。 (5) An astigmatism controlled mirror having a reflecting surface for which the design formula in the mirror design method according to any one of (1) to (4) holds, wherein the values of L 1x and L 1y are different and the values of L 2x and L 2y are the same, and an outgoing beam that is focused to one point can be obtained from an incoming beam having astigmatism.
(6) (1)~(4)の何れかに記載のミラーの設計方法における前記設計式が成り立つ反射面を有するミラーであって、前記L1xとL1yの値が一致し、且つ前記L2xとL2yの値が異なっており、一点から発散する入射ビームから非点収差をもつ出射ビームが得られる、非点収差制御ミラー。 (6) An astigmatism controlled mirror having a reflecting surface for which the design formula in the mirror design method according to any one of (1) to (4) holds, the values of L 1x and L 1y are the same, and the values of L 2x and L 2y are different, and an outgoing beam having astigmatism is obtained from an incident beam diverging from a single point.
本発明に係るミラーの設計方法によれば、単一のミラーであって、鉛直方向と水平方向とで独立して光源位置及び集光位置を設定でき、これにより非点収差の自由な変換が可能なミラーを作製できる。また、集光サイズをより小さく抑えてX線領域のビームにも対応することができる。さらに、設計式も単純で、応用の幅も広く、鉛直方向と水平方向とで特性が異なるビームを取り扱う光学系として好適に用いることができるミラーを作製できる。 The mirror design method of the present invention allows the light source position and focusing position to be set independently in the vertical and horizontal directions on a single mirror, making it possible to fabricate a mirror that allows free conversion of astigmatism. It also makes it possible to reduce the focusing size and accommodate beams in the X-ray range. Furthermore, the design formula is simple, the range of applications is wide, and it is possible to fabricate a mirror that can be suitably used as an optical system that handles beams with different characteristics in the vertical and horizontal directions.
本発明のミラーの設計方法は、基材の中空内周面または外周面に反射面を形成して作製されるミラーの設計方法である。以下、本発明にかかるミラーの設計方法を、代表的な実施形態を挙げながら説明する。 The mirror design method of the present invention is a method for designing a mirror that is manufactured by forming a reflective surface on the hollow inner or outer peripheral surface of a substrate. Below, the mirror design method of the present invention will be explained with reference to a representative embodiment.
本発明は、非点収差の自由な変換を目的とし,『光は光学的距離が最短となる経路を通る』というFermatの原理に基づいて,より精度の高いミラーの設計を行う。Fermatの原理は、集光(あるいは拡散)ミラーに限定した場合、『ミラー表面(反射面)の任意の点に関して,光源点からの距離と集光点までの距離の和は一定である』という表現に変換することが可能である。入射ビーム又は出射ビームが非点収差を持つ場合、光路長一定の法則を直ちに適用することはできなくなる。なぜならば,非点収差を持つビームはその名の通り単一の光源点あるいは集光点を持たないためである。本発明では、「光源線」と「集光線」を新たに定義することを着想し、非点収差を持つビームの性質を幾何光学的に表現することを可能にすることで実現した設計手法である。 The present invention aims to freely convert astigmatism, and designs mirrors with higher accuracy based on Fermat's principle, which states that "light follows the path with the shortest optical distance." When limited to focusing (or diffusing) mirrors, Fermat's principle can be translated into the expression that "for any point on the mirror surface (reflecting surface), the sum of the distance from the light source point and the distance to the focusing point is constant." When the incident beam or outgoing beam has astigmatism, the law of constant optical path length cannot be immediately applied. This is because, as the name suggests, an astigmatized beam does not have a single light source point or focusing point. In this invention, the idea of newly defining "light source line" and "focusing line" has been conceived, and a design method has been realized by making it possible to express the properties of an astigmatized beam in terms of geometrical optics.
図1は、「光源線」、「集光線」を示す概念図である。基材の内周面または外周面の中心軸をz軸、これに直交する断面をxy平面とし、入射ビームが、z軸上所定位置からz軸方向に沿ってL1x変位した位置に、x軸方向(本例では水平方向)の光源をもち、かつ前記z軸上所定位置からz軸方向に沿ってL1y変位した位置に、y軸方向(本例では鉛直方向)の光源をもつとする。また、出射ビームは、x軸方向(水平方向)について前記z軸上所定位置からz軸方向に沿ってL2x変位した位置に集光し、かつy軸方向(鉛直方向)について前記z軸上所定位置からz軸方向に沿ってL2y変位した位置に集光するとする。 FIG. 1 is a conceptual diagram showing "light source line" and "light collecting line". The central axis of the inner or outer peripheral surface of the substrate is the z axis, and the cross section perpendicular to the z axis is the xy plane. The incident beam has a light source in the x axis direction (horizontal direction in this example) at a position displaced by L 1x along the z axis from a predetermined position on the z axis, and a light source in the y axis direction (vertical direction in this example) at a position displaced by L 1y along the z axis from the predetermined position on the z axis. In addition, the outgoing beam is collected at a position displaced by L 2x along the z axis from the predetermined position on the z axis in the x axis direction (horizontal direction), and is collected at a position displaced by L 2y along the z axis from the predetermined position on the z axis in the y axis direction (vertical direction).
そして、ミラーを経由するすべての入射光線は、x軸方向(水平方向)における前記光源の位置を通り該x軸方向(水平方向)とz軸方向の双方に直交する方向に延びる第1の光源線(Sx)、及びy軸方向(鉛直方向)における前記光源の位置を通り該y軸方向(鉛直方向)とz軸方向の双方に直交する方向に延びる第2の光源線(Sy)を通過すると考える。このように第1の光源線(Sx)、第2の光源線(Sy)を定義する。 All incident light rays passing through the mirror are considered to pass through a first light source line (S x ) that passes through the position of the light source in the x-axis direction (horizontal direction) and extends in a direction perpendicular to both the x-axis direction (horizontal direction) and the z-axis direction, and a second light source line (S y ) that passes through the position of the light source in the y-axis direction (vertical direction) and extends in a direction perpendicular to both the y-axis direction (vertical direction) and the z-axis direction. The first light source line (S x ) and the second light source line (S y ) are defined in this manner.
さらに、ミラーから放たれるすべての出射光線は、x軸方向(水平方向)における前記集光する位置を通り該x軸方向(水平方向)とz軸方向の双方に直交する方向に延びる第1の集光線(Fx)、及びy軸方向(鉛直方向)における前記集光する位置を通り該y軸方向(鉛直方向)とz軸方向の双方に直交する方向に延びる第2の集光線(Fy)を通過すると考える。このように第1の集光線(Fx)、第2の集光線(Fy)を定義する。 Furthermore, all of the emitted light rays emitted from the mirror are considered to pass through a first focusing line (F x ) that passes through the focusing position in the x-axis direction (horizontal direction) and extends in a direction perpendicular to both the x-axis direction (horizontal direction) and the z-axis direction, and a second focusing line (F y ) that passes through the focusing position in the y-axis direction (vertical direction) and extends in a direction perpendicular to both the y-axis direction (vertical direction) and the z-axis direction. The first focusing line (F x ) and the second focusing line (F y ) are defined in this manner.
なお、本例では、第1の光源線(Sx)、第2の光源線(Sy)、第1の集光線(Fx)、第2の集光線(Fy)をそれぞれ直線としているが、曲線であってもよい。また、図1では、L1x>L1y>0、かつL2x>L2y>0の場合を示しているが、L1xとL1yの大小関係が反転することや、L2xとL2yの大小関係が反転することも含まれ、これら定数が負の値をとることも可能である。L1xまたはL1yが負の値をとる場合、入射ビームは下流に向かって集光する途中でミラーの反射面によって反射される。L2xまたはL2yが負の値をとる場合、出射ビームはミラーよりも上流の位置から発散してきたような波面を持つ。 In this example, the first light source line (S x ), the second light source line (S y ), the first condensed light line (F x ), and the second condensed light line (F y ) are each straight lines, but they may be curved lines. FIG. 1 shows the case where L 1x > L 1y > 0 and L 2x > L 2y > 0, but the magnitude relationship between L 1x and L 1y may be reversed, or the magnitude relationship between L 2x and L 2y may be reversed, and these constants may be negative. When L 1x or L 1y has a negative value, the incident beam is reflected by the reflecting surface of the mirror while being condensed toward the downstream. When L 2x or L 2y has a negative value, the outgoing beam has a wavefront that diverges from a position upstream of the mirror.
上記のように「光源線」及び「集光線」を定義することで、ミラーの反射面の任意の点について、その点を通る入射光線及び出射光線を定義することができる。すなわち、ミラーの反射面上の任意の点をM(x,y,z)とし、第1の光源線(Sx)とM点への入射光線との交点(Px)、及び第2の光源線(Sy)とM点への入射光線との交点(Py)の各座標を、前記した変位L1x、L1yを用いて下記式(1)、式(2)で表わすことができる。同様に、前記M点からの出射光線と第1の集光線(Fx)との交点(Qx)、及びM点からの出射光線と第2の集光線(Fy)との交点(Qy)の各座標を、前記した変位L2x、L2yを用いて下記式(3)、式(4)で表わすことができる。 By defining the "light source line" and the "focus line" as described above, it is possible to define the incident light ray and the outgoing light ray passing through any point on the reflecting surface of the mirror. That is, assuming that any point on the reflecting surface of the mirror is M(x, y, z), the coordinates of the intersection (P x ) between the first light source line (S x ) and the incident light ray to the point M, and the intersection (P y ) between the second light source line (S y ) and the incident light ray to the point M can be expressed by the following formulas (1) and (2) using the above-mentioned displacements L 1x and L 1y . Similarly, the coordinates of the intersection (Q x ) between the outgoing light ray from the point M and the first focus line (F x ) , and the intersection (Q y ) between the outgoing light ray from the point M and the second focus line (F y ) can be expressed by the following formulas (3) and (4) using the above-mentioned displacements L 2x and L 2y .
そして、これらPx、Py、Qx、Qyの各座標、及び前記x軸方向及び前記y軸方向についてそれぞれ反射面上の任意の点に関して光源位置から集光位置までの光路長(入射長と出射長の和)が一定であることに基づき、反射面の設計式を導くことができる。 Then, based on the fact that the optical path length (the sum of the incident length and the exit length ) from the light source position to the focusing position is constant for any point on the reflecting surface in each of the coordinates Px , Py , Qx, and Qy, and in the x-axis direction and the y-axis direction, respectively, a design equation for the reflecting surface can be derived.
本実施形態では、上記した光源線、集光線上の各交点Px、Py、Qx、Qyと反射面上の任意の点M(x,y,z)との距離をそのまま入射長または出射長とするのではなく、直線で定義した光源線、集光線の上記交点の座標を用いつつ、より正確な設計式が得られるように次のような光路長の補償を行っている。 In this embodiment, the distance between each of the intersection points Px , Py, Qx , and Qy on the light source line and the condenser line and an arbitrary point M(x, y, z) on the reflecting surface is not directly determined as the incident length or the exit length, but the coordinates of the intersection points of the light source line and the condenser line defined by straight lines are used, and the optical path length is compensated as follows to obtain a more accurate design formula.
(光路長の補償)
通常の光源点と集光点が定義できる場合のFermatの原理を考える。光源点近傍の等位相面は光源点を中心とした球面であり、集光点近傍の等位相面は集光点を中心とした球面である。光線は常に等位相面に対して直交することを念頭に置くと、光路長一定の法則とは、光源点近傍の特定の等位相面上の任意の点と、それに対応する集光点近傍の特定の等位相面上の点を結ぶ光線の光学距離が一定であることと言い換えられる。本発明のような入射ビームに非点収差が含まれる場合にも、等位相面を考慮した補償を行うことで、より正確な設計式を導くことができる。
(Optical path length compensation)
Consider Fermat's principle when a normal light source point and a focal point can be defined. The equiphase surface near the light source point is a sphere centered on the light source point, and the equiphase surface near the focal point is a sphere centered on the focal point. Keeping in mind that light rays are always perpendicular to the equiphase surface, the law of constant optical path length can be rephrased as the optical distance of a light ray connecting an arbitrary point on a specific equiphase surface near the light source point and a corresponding point on a specific equiphase surface near the focal point is constant. Even when the incident beam contains astigmatism as in the present invention, a more accurate design formula can be derived by performing compensation taking into account the equiphase surface.
まず、入射側について、光源線Sx上の上記した交点Pxに対応する近傍の等位相面を考える。光源線Sxでは、光源線Syに向けて収束する波面が観察されるはずである。このような仮定のもとSx上の位相を定義することは厳密にはできないが、ここではSyとz軸との交点をPy0とおき、Sx上にはPy0からの距離に応じた位相分布が存在するもの、すなわち、ミラー(反射面)に入射する前のビームは、y軸方向(鉛直方向)には光源線Syに集約する波面を持つとする。この考えに基づき、図2に示すように、第2の光源線Syとz軸との交点Py0を中心とし且つ第1の光源線Sxとz軸との交点Px0を通ってx軸に直交する方向に延びる円弧B1xを、第1の光源線Sxを軸に回転させることで構成される回転円弧面を等位相面A1xとする。x軸方向の光源位置からM点までの入射長は、入射光線と該等位相面A1xとの2つの交点のうち第2の光源線Syに近い側の交点からM点までの距離として求めることがより正確である。 First, on the incident side, consider the equiphase surface in the vicinity of the intersection point P x on the light source line S x described above. On the light source line S x , a wavefront converging toward the light source line S y should be observed. Although it is not possible to strictly define the phase on S x under such assumptions, here, the intersection point between S y and the z axis is set as P y0 , and a phase distribution according to the distance from P y0 exists on S x , that is, the beam before entering the mirror (reflection surface) has a wavefront that converges to the light source line S y in the y-axis direction (vertical direction). Based on this idea, as shown in FIG. 2, an arc B 1x that is centered on the intersection point P y0 between the second light source line S y and the z axis and extends in a direction perpendicular to the x axis through the intersection point P x0 between the first light source line S x and the z axis is rotated around the first light source line S x to form an equiphase surface A 1x . It is more accurate to determine the incident length from the light source position in the x-axis direction to point M as the distance from one of two intersection points between the incident light ray and the equiphase surface A1x that is closer to the second light source line Sy to point M.
ここでは、この入射光線と等位相面A1xとの2つの交点のうち第2の光源線Syに近い側の交点からミラーの反射面上のM点までの距離は、まず入射光線と前記第1の光源線Sxとの交点PxからM点までの距離を求めるとともに、該距離に、交点Pxから前記等位相面A1xを定義している前記円弧B1xまでの距離、つまりPxから円弧B1xに下した垂線の足をH1xとしてPxH1x間の距離を加算又は減算(本図の例では減算)して求めている。すなわち、下記式(5)のH1xM間の距離をx軸方向の入射長とする。この式が近似である理由は,点H1xが直線PxM上に存在する保証がないためである。ただし、このような近似式以外の計算で求めるようにしても勿論よい。本例では、上記のようにPxから円弧B1xに下した垂線の足をH1xとしてPxH1x間の距離を加算/減算して近似的に求めているが、円弧B1xに下した垂線ではなく、Pxから、入射光線と該等位相面A1xとの2つの交点のうち第2の光源線Syに近い側の交点までの距離を用いて、より正確に算出するようにしてもよい。 Here, the distance from the intersection point closer to the second light source line S y of the two intersection points between the incident light ray and the equiphase surface A 1x to point M on the reflecting surface of the mirror is calculated by first calculating the distance from the intersection point P x between the incident light ray and the first light source line S x to point M, and then adding or subtracting (in the example shown in the figure, subtracting) the distance from the intersection point P x to the arc B 1x that defines the equiphase surface A 1x , that is, the distance between P x and H 1x , with H 1x being the foot of the perpendicular line from P x to the arc B 1x . That is, the distance between H 1x and M in the following formula (5) is set as the incidence length in the x-axis direction. The reason why this formula is an approximation is that there is no guarantee that the point H 1x exists on the straight line P x M. However, it is of course possible to calculate the distance using a formula other than this approximation. In this example, as described above, the foot of the perpendicular line from Px to the arc B1x is defined as H1x , and the distance between Px and H1x is added/subtracted to obtain an approximation. However, instead of the perpendicular line to the arc B1x , the distance may be calculated more accurately by using the distance from Px to one of the two intersection points between the incident ray and the equiphase surface A1x that is closer to the second light source line S y .
続いて、同じく入射側について、光源線Sy上の上記した交点Pyに対応する近傍の等位相面を考える。光源線Syでは、光源線Sxから発散してきた波面が観察されるはずである。このような仮定のもとSy上の位相を定義することは厳密にはできないが、ここではSxとz軸との交点をPx0とおき、Sy上にはPx0からの距離に応じた位相分布が存在するもの、すなわち、ミラー(反射面)に入射する前のビームは,x軸方向には光源線Sxから発散する波面を持つとする。この考え方に基づき、図3に示すように、第1の光源線Sxとz軸との交点Px0を中心とし且つ第2の光源線Syとz軸との交点Py0を通ってy軸に直交する方向に延びる円弧B1yを、第2の光源線Syを軸に回転させることにより構成される回転円弧面を、等位相面A1yとする。y軸方向の光源位置からM点までの入射長は、入射光線と該等位相面A1yとの2つの交点のうち第1の光源線Sxに近い側の交点からミラーの反射面上のM点までの距離として求まる。 Next, also on the incident side, consider an equiphase surface in the vicinity of the intersection point P y on the light source line S y . On the light source line S y , a wavefront diverging from the light source line S x should be observed. Although it is not possible to strictly define the phase on S y under such assumption, here, the intersection point of S x and the z axis is set as P x0 , and a phase distribution according to the distance from P x0 exists on S y , that is, the beam before entering the mirror (reflection surface) has a wavefront diverging from the light source line S x in the x-axis direction. Based on this idea, as shown in FIG. 3, an arc B 1y having a center at the intersection point P x0 of the first light source line S x and the z axis and passing through the intersection point P y0 of the second light source line S y and the z axis and extending in a direction perpendicular to the y axis is rotated around the second light source line S y as an equiphase surface A 1y . The incident length from the light source position in the y-axis direction to point M is determined as the distance from one of two intersection points between the incident light ray and the equiphase surface A1y that is closer to the first light source line Sx to point M on the reflecting surface of the mirror.
入射光線と等位相面A1yとの2つの交点のうち第1の光源線Sxに近い側の交点からM点までの距離は、まず入射光線と前記第2の光源線Syとの交点PyからM点までの距離を求めるとともに、該距離に、交点Pyから前記等位相面A1yを定義している前記円弧B1yまでの距離、つまりPyから円弧B1yに下した垂線の足をH1yとしてPyH1y間の距離を加算又は減算(本例では加算)して求める。すなわち、下記式(6)のH1yM間の距離をy軸方向の入射長とする。 The distance from the intersection point closer to the first light source line Sx of the two intersection points between the incident light ray and the equiphase surface A1y to point M is calculated by first calculating the distance from the intersection point Py between the incident light ray and the second light source line Sy to point M, and then adding or subtracting (adding in this example) to the distance, the distance from the intersection point Py to the arc B1y that defines the equiphase surface A1y , that is, the distance between Py and H1y , where H1y is the foot of the perpendicular line from Py to the arc B1y . That is, the distance between H1y and M in the following formula (6) is determined as the incident length in the y-axis direction.
出射側についても、入射側と同様、第1の集光線Fx上の上記交点Qxに対応する近傍の等位相面、第2の集光線Fy上の上記交点Qyに対応する近傍の等位相面、をそれぞれ考える。第1の集光線Fxでは、第2の集光線Fyから発散する波面が観察されるはずである。このような仮定のもとFx上の位相を定義することは厳密にはできないが、ここではFyと光軸zの交点をQy0とおき,Fx上にはQy0からの距離に応じた位相分布が存在するものとみなす。また、第2の集光線Fyでは、第1の集光線Fxに向けて収束する波面が観察されるはずである。このような仮定のもとFy上の位相を定義することは厳密にはできないが,ここではFxと出射光軸zの交点をQx0とおき、Fy上にはQx0からの距離に応じた位相分布が存在するものとみなす。 As for the exit side, similar to the entrance side, consider the equiphase surface near the intersection point Qx on the first focusing line Fx , and the equiphase surface near the intersection point Qy on the second focusing line Fy . In the first focusing line Fx , a wavefront diverging from the second focusing line Fy should be observed. Although it is not possible to strictly define the phase on Fx under such assumptions, here, the intersection point of Fy and the optical axis z is set as Qy0 , and it is assumed that there is a phase distribution on Fx according to the distance from Qy0 . In addition, in the second focusing line Fy , a wavefront converging toward the first focusing line Fx should be observed. Although it is not possible to strictly define the phase on Fy under such assumptions, here, the intersection point of Fx and the exit optical axis z is set as Qx0 , and it is assumed that there is a phase distribution on Fy according to the distance from Qx0 .
これらの考えに基づき、入射側と同様、より正確な出射長を求める。具体的には、図示は省略するが、上記と同様に交点Qxから等位相面を定義する円弧B2xまでの距離、つまりQxから円弧B2xに下した垂線の足をH2xとしたH2xQx間の距離や、交点Qyから等位相面を定義する円弧B2yまでの距離、つまりQyから円弧B2yに下した垂線の足をH2yとしたQyH2y間の距離を用いて加算または減算して補償を行い、下記式(7)、式(8)のようにx軸方向、y軸方向についてより正確な出射長を求めることができる。 Based on these considerations, a more accurate exit length is obtained, as in the case of the incident side. Specifically, although not shown in the figures, compensation is performed by adding or subtracting the distance from the intersection Qx to the arc B2x that defines the equiphase surface, that is, the distance between H2x and Qx, where H2x is the foot of the perpendicular line from Qx to the arc B2x , and the distance from the intersection Qy to the arc B2y that defines the equiphase surface, that is, the distance between Qy and H2y, where H2y is the foot of the perpendicular line from Qy to the arc B2y , to obtain a more accurate exit length in the x-axis direction and the y-axis direction as shown in the following formulas (7) and (8).
(光路長の計算)
このようにして求めた入射長、出射長を用いて、x軸方向、y軸方向の各方向の集光についての光路長の計算を行う。まず、x軸方向の集光に着目した場合の入射長f1x(x,y,z)は,式(5)より下記式(9)~(11)のように計算される。
(Calculation of optical path length)
Using the incident length and exit length thus obtained, the optical path length for focusing in each of the x-axis and y-axis directions is calculated. First, the incident length f 1x (x, y, z) when focusing on focusing in the x-axis direction is calculated from equation (5) using the following equations (9) to (11).
同様に、同じくx軸方向の集光に着目した出射長f2x(x,y,z)は、式(7.9)より下記式(12)~(14)で表される。 Similarly, the exit length f 2x (x, y, z) focusing on the light collection in the x-axis direction is expressed by the following equations (12) to (14) from equation (7.9).
そして、x軸方向集光における光源点から集光点までの基準光路長をLxと設定すると、x軸方向の集光に必要な条件式が、次の式(15)のように導かれる。 Then, when the reference optical path length from the light source point to the focusing point in the x-axis direction is set to Lx , the conditional equation required for focusing in the x-axis direction is derived as the following equation (15).
次に、y軸方向の集光に必要な条件式についても、同様の手順で導かれる。すなわち、y軸方向の集光に着目した入射長f1y(x,y,z)は、式(6)より下記式(16)のように求まる。 Next, the condition equation required for focusing in the y-axis direction is derived in a similar manner. That is, the incident length f 1y (x, y, z) for focusing in the y-axis direction is obtained from equation (6) as shown in the following equation (16).
同様に、y軸方向の集光に着目した出射長f2y(x,y,z)は、式(8)より以下の式(17)で表される。 Similarly, the exit length f 2y (x, y, z) in terms of light collection in the y-axis direction is expressed by the following equation (17) from equation (8).
そして、y軸方向集光における光源点から集光点までの基準光路長をLyと設定すると、y軸方向の集光に必要な条件式が、次の式(18)のように導かれる。 Then, when the reference optical path length from the light source point to the focusing point in the y-axis direction is set to Ly , the conditional expression required for focusing in the y-axis direction is derived as the following expression (18).
理想的には、式(15)のx軸方向の集光条件と、式(18)のy軸方向の集光条件とを同時に満たす点(x,y,z)の集合が、求めるミラーの反射面の形状となるが、このような連立方程式の解を設計式とすると、「L1x=L1yかつL2x=L2y」のような特殊な条件下でしか解が存在できなくなる。他の条件下でも成り立ち得る、より一般化した反射面の形状を表わす設計式を得るために、本発明者は、式(15)と式(18)を重みづけし、式(19)に示す新たな式f(x,y,z)を設計式とした。 Ideally, a set of points (x, y, z) that simultaneously satisfies the focusing condition in the x-axis direction of equation (15) and the focusing condition in the y-axis direction of equation (18) represents the desired shape of the reflecting surface of the mirror, but if the solution of such simultaneous equations is used as a design formula, the solution can only exist under special conditions such as " L1x = L1y and L2x = L2y . " In order to obtain a design formula that represents a more generalized shape of the reflecting surface that can be established under other conditions, the inventors weighted equations (15) and (18) and used a new formula f(x, y, z) shown in equation (19) as the design formula.
(設計式)
すなわち、設計式は、x軸方向について光源点から集光点までの光路長が一定であることから導かれる第1の式(x軸方向集光条件の式)であるfx(x,y,z)=0(式(15))と、y軸方向について光源点から集光点までの光路長が一定であることから導かれる第2の式(y軸方向集光条件の式)であるfy(x,y,z)=0(式(18))とを、α、βを用いて、下記(19)のように重みづけした式f(x,y,z)=0である。αは、x軸方向の集光に対する重みづけ係数、βは、y軸方向の集光に対する重みづけ係数である。
(Design formula)
That is, the design formula is f(x,y,z)=0 (formula (15)), which is the first formula (formula for the x-axis direction focusing condition) derived from the fact that the optical path length from the light source point to the focusing point is constant in the x-axis direction, and fy (x,y,z)=0 (formula (18)), which is the second formula (formula for the y-axis direction focusing condition) derived from the fact that the optical path length from the light source point to the focusing point is constant in the y-axis direction, weighted by α and β as shown in the following (19): f(x,y,z)=0. α is a weighting coefficient for focusing in the x-axis direction, and β is a weighting coefficient for focusing in the y-axis direction.
ここで、式(19)に式(9)から式(18)までを代入することで、反射面の設計式は式(20)に示す方程式として導出される。 By substituting equations (9) through (18) into equation (19), the design equation for the reflecting surface is derived as shown in equation (20).
式(20)から分かるように、x軸方向、y軸方向に対して対称性の良い方程式が得られたことを確認できる。これまでの導出で『L1x>L1y>0かつL2x>L2y>0』を仮定してきたが,この仮定がなくとも、すなわち大小関係の逆転やそれぞれの設定値が負の値をとったとしても式(20)に示す同じ方程式(設計式)が導かれる。ただし、L1x、L1y、L2x、L2yの4定数はいずれも、正か負の値であって、0にすることはできない。 As can be seen from equation (20), it can be confirmed that an equation with good symmetry in the x-axis and y-axis directions has been obtained. In the derivation so far, we have assumed that " L1x > L1y > 0 and L2x > L2y >0", but even if this assumption is not made, that is, even if the magnitude relationship is reversed or each setting value takes a negative value, the same equation (design equation) shown in equation (20) can be derived. However, all of the four constants L1x , L1y , L2x , and L2y are positive or negative values and cannot be 0.
さらに、具体的な設計式は、基材の中空内周面または外周面から作製される反射面であることから基準点を設定し、その座標を代入することで、上記式(20)中の定数項「αLx+βLy」の設定を行うことで得られる。 Furthermore, since the reflecting surface is made from the hollow inner or outer peripheral surface of the substrate, a specific design formula can be obtained by setting a reference point and substituting the coordinates thereof to set the constant term “αL x + βL y ” in the above formula (20).
基材の中空内周面または外周面に反射面が形成されたミラーの模式図を図4に示す。座標系の定義は図1と同じである。基準点M0x(r0,0,0)、M0y(0,r0,0)を設定する。ここでr0は基準半径を表す定数である。まずM0x(r0,0,0)が集光ミラー形状の陰関数表現である式(20)を満足させると仮定して、式(20)に基準点M0x(r0,0,0)の座標を代入することにより、下記式(21)を得る。 A schematic diagram of a mirror in which a reflective surface is formed on the hollow inner or outer peripheral surface of a substrate is shown in Figure 4. The definition of the coordinate system is the same as in Figure 1. Reference points M 0x (r 0 , 0, 0) and M 0y (0, r 0 , 0) are set, where r 0 is a constant representing the reference radius. First, assuming that M 0x (r 0 , 0, 0) satisfies equation (20), which is an implicit function expression of the collecting mirror shape, the following equation (21) is obtained by substituting the coordinates of the reference point M 0x (r 0 , 0, 0) into equation (20).
この式(21)が重みづけ係数αの設定にかかわらず成立するためには、Lx、Lyはそれぞれ式(22)、式(23)を満たす必要がある。 In order for this equation (21) to hold regardless of the setting of the weighting coefficient α, L x and Ly must satisfy equations (22) and (23), respectively.
同様に、基準点M0yの座標を式(20)に代入することにより、式(24)を得る。この式(24)から、同じくLx、Lyに対する制限が式(25)、式(26)のように導かれる。 Similarly, by substituting the coordinates of the reference point M 0y into equation (20), equation (24) is obtained. From equation (24), the constraints on L x and L y are similarly derived as equations (25) and (26).
求めるLx及びLyは、上記したx軸方向の集光に対する重みづけ係数α、y軸方向の集光に対する重みづけ係数βを用いて、基準点M0xとM0yから導かれる値を重みづけ相加平均する。すなわち、Lx、Lyは次の式(27)、(28)ように表される。 The values of Lx and Ly to be obtained are obtained by taking a weighted arithmetic average of the values derived from the reference points M0x and M0y using the weighting coefficient α for the light concentration in the x-axis direction and the weighting coefficient β for the light concentration in the y-axis direction. That is, Lx and Ly are expressed by the following equations (27) and (28).
式(27)及び式(28)を式(20)に代入することで、ミラー反射面の設計式が下記式(29)に示す方程式として導出される。 By substituting equations (27) and (28) into equation (20), the design equation for the mirror reflecting surface is derived as the equation shown below in equation (29).
(設計できるミラーの例)
式(29)の条件設定において、L1xとL1yの値を異なる値に設定し、且つL2xとL2yの値を一致する値(同じ値)に設定することで、非点収差をもつ入射ビームから一点に集光する出射ビームが得られる反射面を備える非点収差制御ミラーを設計することができる。逆に、L1xとL1yの値を一致する値に設定し、且つL2xとL2yの値を異なる値に設定することで、一点から発散する入射ビームから非点収差をもつ出射ビームが得られる反射面を備える非点収差制御ミラーを設計することができる。
(Examples of mirrors that can be designed)
In setting the condition of formula (29), by setting the values of L 1x and L 1y to different values and the values of L 2x and L 2y to the same value (the same value), it is possible to design an astigmatism control mirror having a reflecting surface that can obtain an outgoing beam that is focused to one point from an incident beam having astigmatism. Conversely, by setting the values of L 1x and L 1y to the same value and the values of L 2x and L 2y to different values, it is possible to design an astigmatism control mirror having a reflecting surface that can obtain an outgoing beam having astigmatism from an incident beam that diverges from one point.
また、設計式(式(29))を用いることで、x軸方向、y方向の両方向の光源・集光位置が一致する反射面を備えるミラーも設計できる。たとえば設計式(式(29))にL1x=L1y=L1>0、且つL2x=L2y=L2>0を代入することで、次の式(30)に示すように回転楕円面ミラーの式を得ることができる。 In addition, by using the design formula (formula (29)), it is possible to design a mirror with a reflecting surface where the light source and light collection positions coincide in both the x-axis direction and the y-axis direction. For example, by substituting L1x = L1y = L1 > 0 and L2x = L2y = L2 > 0 into the design formula (formula (29)), the formula for a rotational ellipsoidal mirror can be obtained as shown in the following formula (30).
また、設計式(式(29))にL1x=L1y=L1<0、且つL2x=L2y=L2>0を代入すれば、次の式(31)に示すように回転双曲面ミラーの式を得ることができる。 Furthermore, by substituting L 1x =L 1y =L 1 <0 and L 2x =L 2y =L 2 >0 into the design equation (equation (29)), the equation for the rotating hyperbolic mirror can be obtained as shown in the following equation (31).
さらに上記式(30)または式(31)において、L1を正または負の無限大に設定することで、次の式(32)に示すように回転放物面ミラーの式を得ることができる。 Furthermore, by setting L1 to positive or negative infinity in the above equation (30) or equation (31), the equation for the parabolic mirror of revolution can be obtained as shown in the following equation (32).
(設計限界)
まず、上述のとおり、L1x、L1y、L2xおよびL2yはいずれも0をとらない。また、例えばミラーの集光作用を鉛直方向のみに限定したとき、すなわち、L1x=+∞かつL2x=+∞のとき、L1y>0かつL1y>0かつα=0を与えた場合は、式(29)は次の式(33)の形になる。
(Design limit)
First, as described above, none of L 1x , L 1y , L 2x and L 2y is 0. Furthermore, for example, when the light-collecting action of the mirror is limited to only the vertical direction, that is, when L 1x = +∞ and L 2x = +∞, L 1y > 0, L 1y > 0 and α = 0 are given, equation (29) takes the form of the following equation (33).
式(33)は明確に楕円柱面の式である。2枚の楕円柱面ミラーが鉛直方向から光軸を挟み込むように配置されていることが読み取れ、設計の破綻を示す。破綻の理由は、鉛直方向と水平方向の双方に正の集光性能を持たせなかったことに起因する。ここで述べる正の集光性能とは、「ビームをより収束する方向に変化させる」能力である。この条件は、入射長をL1、出射長をL2として次の式(34)で表現される。 Equation (33) is clearly the equation for an elliptical cylindrical surface. It can be seen that two elliptical cylindrical mirrors are arranged to sandwich the optical axis from the vertical direction, indicating a design failure. The reason for the failure is that the design did not have positive focusing performance in both the vertical and horizontal directions. The positive focusing performance mentioned here is the ability to "change the beam in a more convergent direction." This condition is expressed by the following equation (34), where the entrance length is L1 and the exit length is L2 .
式(34)は、上流から発散する波面の曲率を正として定義した場合にミラーによる反射を経て曲率が減少することを示している。このときミラーの形状は凹となる。図5に,円錐曲線を稜線として持つ回転体ミラーを用いてビームを集光する例を挙げる。これらはいずれも式(34)を満たしている。中空型内面を利用するミラーを設計するためには、鉛直方向・水平方向ともに式(34)を満たすことが必要十分条件である。 Equation (34) indicates that if the curvature of the wavefront diverging from upstream is defined as positive, then the curvature decreases after reflection by a mirror. In this case, the shape of the mirror becomes concave. Figure 5 shows an example of focusing a beam using a rotating mirror with a conic section as its ridge. All of these satisfy equation (34). In order to design a mirror that uses a hollow inner surface, it is a necessary and sufficient condition that equation (34) be satisfied in both the vertical and horizontal directions.
円錐曲線は、同様に、その凸プロファイルを利用して波面の曲率を増大させることもまた可能である。図6に円錐曲線の回転体を用いて波面の曲率を増大させる例の一覧を示す。これらの例ではいずれも以下の式(35)を満たしている。鉛直・水平両方向について波面の曲率を増大させるミラーを本方式で設計すると、それは『柱状形状の外面を使用するミラー』となる。 It is also possible for a conic section to increase the curvature of a wavefront by utilizing its convex profile. Figure 6 shows a list of examples of increasing the curvature of a wavefront using a rotating conic section. All of these examples satisfy the following equation (35). When a mirror that increases the curvature of the wavefront in both the vertical and horizontal directions is designed using this method, it becomes a "mirror that uses a cylindrical outer surface."
波面の曲率が変化しないとき、すなわち1/L1=-1/L2が成立するとき、ミラーの稜線は曲率を持たない直線的なプロファイルとなり、設計が破綻する。まとめると、1/L1x>-1/L2x、かつ1/L1y>-1/L2yを満たすことが、中空内周面ミラーの設計式が成り立つ条件となり、1/L1x<-1/L2x、かつ1/L1y<-1/L2yを満たすことが、外周面ミラーの設計式が成り立つ条件となる。 When the curvature of the wavefront does not change, that is, when 1/ L1 = -1/ L2 holds, the ridgeline of the mirror will have a linear profile with no curvature, and the design will fail. In summary, the conditions for the design equation for the hollow inner surface mirror to hold are 1/ L1x > -1/ L2x and 1/ L1y > -1/ L2y , and the conditions for the design equation for the outer surface mirror to hold are 1/ L1x < -1/ L2x and 1/ L1y < -1/ L2y .
(断面プロファイル)
設計式(式(29))に、x=0またはy=0を代入することにより、反射面の断面プロファイルを確認することができる。たとえば、x=0、L1x>0、L1y>0、L2x>0、L2y>0のとき、yz平面とミラー反射面との交線(断面プロファイル)は次の式(36)、式(37)で表現される。式(36)は、y方向集光の光源点とy方向集光の集光点を焦点に持つ楕円関数を表している。式中のCは基準光路長を表す定数項である。
(Cross-Section Profile)
The cross-sectional profile of the reflecting surface can be confirmed by substituting x = 0 or y = 0 into the design equation (equation (29)). For example, when x = 0, L 1x > 0, L 1y > 0, L 2x > 0, and L 2y > 0, the intersection line (cross-sectional profile) between the yz plane and the mirror reflecting surface is expressed by the following equations (36) and (37). Equation (36) represents an elliptical function with the light source point of the y-direction focused light and the focusing point of the y-direction focused light as its foci. C in the equation is a constant term that represents the reference optical path length.
以上、本発明の実施形態について説明したが、本発明はこうした実施例に何ら限定されるものではなく、本発明の要旨を逸脱しない範囲において種々なる形態で実施し得ることは勿論である。本実施形態では、光源線、集光線を直線として、直線とその近傍の等位相面間の距離を補償したが、このような補償は必ずしも必要ではない。また、円弧線やその他の曲線を光源線、集光線として、補償なしまたは上記補償以外の補償方法または近似方法で求めることも好ましい。反射面の設計式の原点の位置は異なる位置でもよい。座標変換しても勿論よい。 Although the embodiment of the present invention has been described above, the present invention is not limited to these examples, and can of course be embodied in various forms within the scope of the present invention. In this embodiment, the light source line and the condenser line are straight lines, and the distance between the straight line and the equiphase surface in its vicinity is compensated for, but such compensation is not necessarily required. It is also preferable to use arc lines or other curves as the light source line and the condenser line, and to obtain the result without compensation or using a compensation method or approximation method other than the above compensation. The position of the origin of the design equation for the reflecting surface may be at a different position. Coordinate transformation may of course be performed.
次に、上記した本発明にかかる非点収差制御ミラーの設計例として、非点収差の解消を目的としたミラー(実施例1)と、非点収差の付加を目的としたミラー(実施例2)の2種類のミラーの設計を行い、各ミラーについて幾何光学、波動光学の双方を用いてシミュレーションにより性能を確認した結果について説明する。 Next, as design examples of the astigmatism control mirror according to the present invention described above, two types of mirrors were designed: a mirror intended to eliminate astigmatism (Example 1) and a mirror intended to add astigmatism (Example 2). The performance of each mirror was confirmed by simulation using both geometric optics and wave optics. The results are described below.
(シミュレーション手法)
実際の中空形状ミラーの使用例を鑑みて、図7に示すように、ミラー(反射面)の全周(360°)のうち一部のみを軟X線ビームが照明する部分照明条件下での集光性能を計算した。設置条件は水平(x軸方向)偏向とした。幾何光学に基づく光線追跡計算では,図1で示したx軸方向、y軸方向の光源線を通る光線群を定義し、ミラーの反射面に入射させる。光源線の太さ、すなわち光源の大きさは0とする。反射面の有効範囲全体に均一に光線を出射する。
(Simulation method)
Considering an actual use example of a hollow mirror, we calculated the focusing performance under partial illumination conditions where the soft X-ray beam illuminates only a part of the entire circumference (360°) of the mirror (reflecting surface) as shown in Figure 7. The installation condition was horizontal (x-axis direction) deflection. In the ray tracing calculation based on geometric optics, a group of rays passing through the light source line in the x-axis and y-axis directions shown in Figure 1 is defined and made to enter the reflecting surface of the mirror. The thickness of the light source line, i.e., the size of the light source, is set to 0. The light rays are emitted uniformly over the entire effective range of the reflecting surface.
ミラーの反射面上の各位置における法線ベクトルn(x,y,z)は、式(29)で定義された関数f(x,y,z)の勾配ベクトルに対して平行な単位ベクトルである(式(38))。図7に示すように、入射光線はミラーの反射面の法線ベクトルに対称に反射し、集光面にまで伝搬する。このようにして集光面における光線のばらつきが評価される。 The normal vector n(x, y, z) at each position on the mirror's reflecting surface is a unit vector parallel to the gradient vector of the function f(x, y, z) defined in equation (29) (equation (38)). As shown in Figure 7, the incident light ray is reflected symmetrically with respect to the normal vector of the mirror's reflecting surface and propagates to the focusing surface. In this way, the variation of the light ray at the focusing surface is evaluated.
波動光学に基づく回折積分計算では、ミラーの反射面に入射するビームの波面のx軸方向、y軸方向の曲率中心を,それぞれx軸方向集光の光源Sx、y軸方向集光の光源Syに一致させる。図8はその模式図である。太さの存在しない線光源を仮定し、反射面の有効領域全体に一様な強度をもってビームが入射するものとする。反射面上の点M(xM,yM,zM)におけるビームの波動場UM(xM,yM,zM)は次の式(39)、式(40)になる。 In diffraction integral calculations based on wave optics, the centers of curvature in the x-axis and y-axis directions of the wavefront of the beam incident on the reflecting surface of the mirror are made to coincide with the light source Sx that focuses the light in the x-axis direction and the light source Sy that focuses the light in the y-axis direction, respectively. Figure 8 is a schematic diagram. It is assumed that a line light source with no thickness exists, and that the beam is incident with uniform intensity over the entire effective area of the reflecting surface. The wave field U M (x M , y M , z M ) of the beam at point M (x M , y M , z M ) on the reflecting surface is expressed by the following equations (39) and (40).
式(39)においてλはビームの波長を表す任意の定数、I0は入射強度を表す任意の定数である。ミラーの反射面上の複素波動場UM(xM,yM,zM)を、以下の式(41)、式(42)に従って集光面上の座標Q(xQ,yQ,zQ)まで伝搬させる。 In equation (39), λ is an arbitrary constant representing the wavelength of the beam, and I0 is an arbitrary constant representing the incident intensity. The complex wave field U M (x M , y M , z M ) on the reflecting surface of the mirror is propagated to coordinate Q (x Q , y Q , z Q ) on the focusing surface according to the following equations (41) and (42).
式(41)において、dSは反射面上の微小面積を表し、θ(xM,yM,zM)は反射面上の各位置における斜入射角を表す。出力するのは、Q上の複素波動場UQ(xQ,yQ,zQ)の絶対値の二乗である強度分布である(式(43))。以上の手順により、波動光学に基づいて集光面における強度分布が計算される。 In equation (41), dS represents a small area on the reflecting surface, and θ( xM , yM , zM ) represents the oblique incidence angle at each position on the reflecting surface. The output is the intensity distribution, which is the square of the absolute value of the complex wave field UQ ( xQ , yQ , zQ ) on Q (equation (43)). By the above procedure, the intensity distribution on the focusing surface is calculated based on wave optics.
(実施例1のミラー設計)
表1に実施例1のミラー設計に用いた定数の一覧を示す。入射長がx軸方向(水平方向)とy軸方向(鉛直方向)とで異なり、出射長はx軸方向とy軸方向とで同一である。斜入射角が10mrad程度となるように、基準半径を5mmに設定した。光源線及び集光線とミラー(反射面)の配置を図9に示す。
(Mirror Design of Example 1)
Table 1 shows a list of constants used in the mirror design of Example 1. The incident length is different in the x-axis direction (horizontal direction) and the y-axis direction (vertical direction), and the exit length is the same in the x-axis direction and the y-axis direction. The reference radius was set to 5 mm so that the oblique incidence angle was about 10 mrad. The arrangement of the light source line, the condensed light line, and the mirror (reflecting surface) is shown in Figure 9.
ミラーの反射面形状を得るためには、式(29)の設計式で示した陰関数を解く。円筒座標系を用いて式(29)の解集合を得る。ここで、円柱座標系(z,φ,r)とデカルト座標系(x,y,z)は、次の式(44)の対応関係を持つものとする。 To obtain the shape of the mirror's reflecting surface, the implicit function shown in the design equation (29) is solved. A solution set for equation (29) is obtained using a cylindrical coordinate system. Here, the cylindrical coordinate system (z, φ, r) and the Cartesian coordinate system (x, y, z) are assumed to have the corresponding relationship shown in the following equation (44).
(実施例1の反射面の半径分布)
計算されたミラーの反射面の半径分布を図10に示す。図10(a)は,縦軸をz座標、横軸をφ座標に設定したときの半径r(z,φ)の二次元分布を示している。実施例1のミラーの反射面は、y軸方向(鉛直方向)とx軸方向(水平方向)とで直径が異なる潰れた中空型形状となる。
(Radius distribution of the reflecting surface in Example 1)
The calculated radius distribution of the reflecting surface of the mirror is shown in Fig. 10. Fig. 10(a) shows a two-dimensional distribution of radius r(z, φ) when the vertical axis is set to the z coordinate and the horizontal axis is set to the φ coordinate. The reflecting surface of the mirror in Example 1 has a hollow shape with different diameters in the y-axis direction (vertical direction) and the x-axis direction (horizontal direction).
また、図10(a)中において一点鎖線で示したφ=0°(z軸方向(長手方向))の反射面の半径プロファイルを図10(b)に示す。これはx軸方向(水平方向)集光に対応した楕円関数である。また、図10(a)中の破線で表したz=0(周方向)における反射面の半径プロファイルを図10(c)に示す。ミラーの潰れに起因して周方向に二山の分布がついていることが読み取れる。 Figure 10(b) shows the radial profile of the reflecting surface at φ=0° (z-axis direction (longitudinal direction)) indicated by the dashed line in Figure 10(a). This is an elliptical function corresponding to the focusing in the x-axis direction (horizontal direction). Figure 10(c) shows the radial profile of the reflecting surface at z=0 (circumferential direction) indicated by the dashed line in Figure 10(a). It can be seen that there are two peaks in the circumferential direction due to the crushing of the mirror.
(実施例1の集光性能のシミュレーション結果)
次に、集光性能のシミュレーション結果を図11に示す。図11(a)は、幾何光学に基づいて集光面における光線のばらつきを計算した結果を示している。全光線が鉛直・水平ともに1nm以下の領域に集約されていることが確認できる。
(Simulation results of light collection performance in Example 1)
Next, the results of a simulation of the focusing performance are shown in Fig. 11. Fig. 11(a) shows the results of calculating the dispersion of light rays on the focusing surface based on geometric optics. It can be seen that all light rays are concentrated in an area of 1 nm or less both vertically and horizontally.
また、図11(b)は、波動光学に基づいて計算された集光面における二次元強度分布を示している。光子エネルギーは300eVに設定した。ビームは430nm(x軸方向(水平方向))×170nm(y軸方向(鉛直方向))(FWHM)の領域に集光されている。 Figure 11(b) shows the two-dimensional intensity distribution at the focal plane calculated based on wave optics. The photon energy was set to 300 eV. The beam was focused to an area of 430 nm (x-axis direction (horizontal direction)) x 170 nm (y-axis direction (vertical direction)) (FWHM).
(実施例2のミラー設計)
表2に実施例2のミラー設計に用いた定数の一覧を示す。入射長がx軸方向(水平方向)とy軸方向(鉛直方向)とで同じであるのに対し、出射長はx軸方向とy軸方向とで異なる値をもつ。基準半径r0は、反射面への斜入射角が10mrad程度となるように設定した。光源線及び集光線とミラー(反射面)の配置を図12に示す。実施例1と同様、円筒座標系を用いて式(29)の解集合を得る。
(Mirror Design of Example 2)
Table 2 shows a list of constants used in the mirror design of Example 2. The incident length is the same in the x-axis direction (horizontal direction) and the y-axis direction (vertical direction), while the exit length has different values in the x-axis direction and the y-axis direction. The reference radius r0 was set so that the oblique incidence angle on the reflecting surface was about 10 mrad. The arrangement of the light source line, the focusing line, and the mirror (reflecting surface) is shown in Figure 12. As in Example 1, a solution set of equation (29) is obtained using a cylindrical coordinate system.
(実施例2の反射面の半径分布)
計算されたミラーの反射面の半径分布を図13に示す。実施例1のミラーと同様、y軸方向(鉛直方向)とx軸方向(水平方向)とで直径が異なる潰れた中空型形状となり、ミラーの潰れに起因して周方向に二山の分布がついていることが読み取れる。
(Radius distribution of the reflecting surface in Example 2)
The calculated radius distribution of the reflecting surface of the mirror is shown in Figure 13. As with the mirror in Example 1, it can be seen that the mirror has a hollow shape with different diameters in the y-axis direction (vertical direction) and the x-axis direction (horizontal direction), and that a two-peak distribution is formed in the circumferential direction due to the crushing of the mirror.
(実施例2の集光性能のシミュレーション結果)
集光性能のシミュレーション結果を図14に示す。図14(a)は、幾何光学に基づいてx軸方向(水平方向)集光面(z=L2x)における光線のばらつきを計算した結果を示している。全光線がx軸方向(水平方向)幅1nm以下の領域に集約されていることが確認できる。
(Simulation results of light collection performance in Example 2)
The results of a simulation of the focusing performance are shown in Fig. 14. Fig. 14(a) shows the results of calculating the dispersion of light rays on the focusing surface (z = L2x ) in the x-axis direction (horizontal direction) based on geometric optics. It can be seen that all light rays are concentrated in an area with a width of 1 nm or less in the x-axis direction (horizontal direction).
また、図14(b)は、波動光学に基づいて計算されたx軸方向(水平方向)集光面における二次元強度分布を示している。光子エネルギーは300eVに設定した。ビームはx軸方向(水平方向)幅52μm(FWHM)の領域に集光されている。 Figure 14(b) shows the two-dimensional intensity distribution at the focusing surface in the x-axis direction (horizontal direction) calculated based on wave optics. The photon energy was set to 300 eV. The beam is focused to an area 52 μm (FWHM) wide in the x-axis direction (horizontal direction).
同様に、y軸方向(鉛直方向)集光面(z=L2y)における集光性能のシミュレーション結果を図14(c),(d)に示す。y軸方向(鉛直方向)の集光幅は,幾何光学で130nm,波動光学で7.4μm(FWHM)であった。 14(c) and (d) show the simulation results of the focusing performance on the focusing surface (z = L2y ) in the y-axis direction (vertical direction). The focusing width in the y-axis direction (vertical direction) was 130 nm in geometric optics and 7.4 μm (FWHM) in wave optics.
Claims (6)
前記基材の前記内周面または外周面の中心軸をz軸、これに直交する断面をxy平面とし、
入射ビームが、z軸上所定位置からz軸方向に沿ってL1x変位した位置に、x軸方向の光源をもち、かつ前記z軸上所定位置からz軸方向に沿ってL1y変位した位置に、y軸方向の光源をもち、
出射ビームが、x軸方向について前記z軸上所定位置からz軸方向に沿ってL2x変位した位置に集光し、かつy軸方向について前記z軸上所定位置からz軸方向に沿ってL2y変位した位置に集光し、
ミラーを経由するすべての入射光線が、x軸方向における前記光源の位置を通り該x軸方向とz軸方向の双方に直交する方向に延びる第1の光源線、及びy軸方向における前記光源の位置を通り該y軸方向とz軸方向の双方に直交する方向に延びる第2の光源線を通過し、
ミラーから放たれるすべての出射光線が、x軸方向における前記集光する位置を通り該x軸方向とz軸方向の双方に直交する方向に延びる第1の集光線、及びy軸方向における前記集光する位置を通り該y軸方向とz軸方向の双方に直交する方向に延びる第2の集光線を通過するとし、
ミラーの反射面上の任意の点をMとして、第1の光源線とM点への入射光線との交点、及び第2の光源線とM点への入射光線との交点の各座標を、前記L1x、L1yを用いて表わし、且つ、前記M点からの出射光線と第1の集光線との交点、及びM点からの出射光線と第2の集光線との交点の各座標を、前記L2x、L2yを用いて表わし、
これら座標、及び前記x軸方向及び前記y軸方向についてそれぞれ反射面上の任意の点に関して光源位置から集光位置までの光路長が一定であること、に基づき導かれる反射面の設計式を用いてミラーを設計することを特徴とする、ミラーの設計方法。 A method for designing a mirror produced by forming a reflective surface on a hollow inner or outer peripheral surface of a substrate, comprising the steps of:
A central axis of the inner circumferential surface or the outer circumferential surface of the base material is defined as a z-axis, and a cross section perpendicular to the z-axis is defined as an xy-plane;
The incident beam has an x-axis direction light source at a position displaced by L 1x along the z-axis direction from a predetermined position on the z-axis, and has a y-axis direction light source at a position displaced by L 1y along the z-axis direction from the predetermined position on the z-axis;
the emitted beam is focused in the x-axis direction at a position displaced by L 2x along the z-axis from the predetermined position on the z-axis, and in the y-axis direction at a position displaced by L 2y along the z-axis from the predetermined position on the z-axis;
All incident light rays passing through the mirror pass through a first light source line passing through a position of the light source in an x-axis direction and extending in a direction perpendicular to both the x-axis direction and the z-axis direction, and a second light source line passing through a position of the light source in a y-axis direction and extending in a direction perpendicular to both the y-axis direction and the z-axis direction;
All of the emitted light rays emitted from the mirror pass through a first focusing line that passes through the focusing position in the x-axis direction and extends in a direction perpendicular to both the x-axis direction and the z-axis direction, and a second focusing line that passes through the focusing position in the y-axis direction and extends in a direction perpendicular to both the y-axis direction and the z-axis direction;
An arbitrary point on the reflecting surface of the mirror is denoted as M, and the coordinates of the intersection of the first light source line and the incident light to point M and the intersection of the second light source line and the incident light to point M are expressed using the L 1x and L 1y . In addition, the coordinates of the intersection of the outgoing light from point M and the first condensed light and the intersection of the outgoing light from point M and the second condensed light are expressed using the L 2x and L 2y .
A method for designing a mirror, comprising the steps of: designing a mirror using a design equation for the reflecting surface derived based on these coordinates and the fact that the optical path length from the light source position to the focusing position is constant for any point on the reflecting surface in both the x-axis direction and the y-axis direction.
前記第1の集光線、前記第2の集光線を、それぞれy軸方向に延びる直線Fx、x軸方向に延びる直線Fyとし、
前記x軸方向の光源位置からM点までの入射長は、前記第2の光源線Syとz軸との交点Py0を中心とし且つ第1の光源線Sxとz軸との交点Px0を通ってx軸に直交する方向に延びる円弧を、第1の光源線Sxを軸に回転させた回転円弧面を等位相面A1xとして、前記入射光線と該等位相面A1xとの2つの交点のうち第2の光源線Syに近い側の交点からM点までの距離として求め、
M点から前記x軸方向の集光位置までの出射長は、前記第2の集光線Fyとz軸との交点Qy0を中心とし且つ第1の集光線Fxとz軸との交点Qx0を通ってx軸に直交する方向に延びる円弧を、第1の集光線Fxを軸に回転させた回転円弧面を等位相面A2xとして、前記出射光線と該等位相面A2xとの2つの交点のうち第2の集光線Fyに近い側の交点からM点までの距離として求め、
前記y軸方向の光源位置からM点までの入射長は、前記第1の光源線Sxとz軸との交点Px0を中心とし且つ第2の光源線Syとz軸との交点Py0を通ってy軸に直交する方向に延びる円弧を、第2の光源線Syを軸に回転させた回転円弧面を等位相面A1yとして、前記入射光線と該等位相面A1yとの2つの交点のうち第1の光源線Sxに近い側の交点からM点までの距離として求め、
M点から前記y軸方向の集光位置までの出射長は、前記第1の集光線Fxとz軸との交点Qx0を中心とし且つ第2の光源線Fyとz軸との交点Qy0を通ってy軸に直交する方向に延びる円弧を、第2の集光線Fyを軸に回転させた回転円弧面を等位相面A2yとして、前記出射光線と該等位相面A2yとの2つの交点のうち第1の集光線Fxに近い側の交点からM点までの距離として求め、
これにより前記x軸方向及びy軸方向のそれぞれの集光に関して入射長と出射長の和である光路長を算出してなる、
請求項1記載のミラーの設計方法。 The first light source line and the second light source line are respectively defined as a straight line S x extending in the y-axis direction and a straight line S y extending in the x-axis direction,
The first collecting line and the second collecting line are respectively a straight line F x extending in the y-axis direction and a straight line F y extending in the x-axis direction,
The incident length from the light source position in the x-axis direction to point M is determined as the distance from one of two intersections between the incident light ray and the equiphase surface A1x that is closer to the second light source line S y out of two intersections between the incident light ray and the equiphase surface A1x , the incident length being determined as the distance from the ...
The emission length from point M to the focusing position in the x-axis direction is determined as the distance from one of two intersections between the emission light and the equiphase surface A2x , which is closer to the second focusing line Fy , to point M , when an arc extending in a direction perpendicular to the x-axis and centered at an intersection Qy0 between the second focusing line Fy and the z-axis and passing through an intersection Qx0 between the first focusing line Fx and the z-axis is rotated about the first focusing line Fx as an axis to obtain an equiphase surface A2x .
The incident length from the light source position in the y-axis direction to point M is determined as the distance from one of two intersections between the incident light ray and the equiphase surface A1y that is closer to the first light source line Sx , to point M, where an arc extending in a direction perpendicular to the y-axis is centered at an intersection Px0 between the first light source line Sx and the z-axis, passes through an intersection Py0 between the second light source line Sy and the z- axis , and is rotated about the second light source line Sy as an axis to form an equiphase surface A1y;
The emission length from point M to the focusing position in the y-axis direction is determined as the distance from one of two intersections between the emission light ray and the equiphase surface A2y that is closer to the first focusing line Fx , to point M , where an arc that is centered at an intersection Qx0 between the first focusing line Fx and the z-axis, passes through an intersection Qy0 between the second light source line Fy and the z-axis, and extends in a direction perpendicular to the y - axis, is rotated about the second focusing line Fy as an axis to obtain an equiphase surface A2y.
As a result, the optical path length, which is the sum of the incident length and the exit length, is calculated for each of the light collection in the x-axis direction and the y-axis direction.
The method for designing a mirror according to claim 1.
前記出射光線と等位相面A2xとの2つの交点のうち第2の集光線Fyに近い側の交点からM点までの距離は、前記出射光線と前記第1の集光線Fxとの交点Qxから前記M点までの距離を求めるとともに、該距離に、前記交点Qxから前記等位相面A2xを定義している前記円弧までの距離を加算又は減算して求め、
前記入射光線と等位相面A1yとの2つの交点のうち第1の光源線Sxに近い側の交点からM点までの距離は、前記入射光線と前記第2の光源線Syとの交点Pyから前記M点までの距離を求めるとともに、該距離に、前記交点Pyから前記等位相面A1yを定義している前記円弧までの距離を加算又は減算して求め、
前記出射光線と等位相面A2yとの2つの交点のうち第1の集光線Fxに近い側の交点からM点までの距離は、前記出射光線と前記第2の集光線Fyとの交点Qyから前記M点までの距離を求めるとともに、該距離に、前記交点Qyから前記等位相面A2yを定義している前記円弧までの距離を加算又は減算して求める、
請求項2記載のミラーの設計方法。 the distance from one of the two intersection points between the incident light ray and the equiphase surface A1x closer to the second light source line S y to point M is obtained by calculating the distance from an intersection point P x between the incident light ray and the first light source line S x to point M, and adding or subtracting the distance from the intersection point P x to the arc defining the equiphase surface A1x to the distance;
the distance from one of the two intersection points between the output light beam and the equiphase surface A2x closer to the second condenser line Fy to point M is obtained by calculating the distance from an intersection point Qx between the output light beam and the first condenser line Fx to point M, and adding or subtracting the distance from the intersection point Qx to the arc defining the equiphase surface A2x to the distance;
the distance from one of the two intersection points between the incident light ray and the equiphase surface A1y closer to the first light source line Sx to point M is obtained by calculating the distance from an intersection point Py between the incident light ray and the second light source line Sy to point M, and adding or subtracting the distance from the intersection point Py to the arc defining the equiphase surface A1y to the distance;
The distance from one of the two intersection points between the output light beam and the equiphase surface A2y closer to the first condensing line Fx to point M is obtained by calculating the distance from an intersection point Qy between the output light beam and the second condensing line Fy to point M, and adding or subtracting the distance from the intersection point Qy to the arc that defines the equiphase surface A2y to the calculated distance.
3. The method for designing a mirror according to claim 2.
前記x軸方向について光源点から集光点までの光路長が一定であることから導かれる第1の式fx(x,y,z)=0と、前記y軸方向について光源点から集光点までの光路長が一定であることから導かれる第2の式fy(x,y,z)=0とを重みづけした、下記式からなる、請求項1~3の何れか1項に記載のミラーの設計方法。
The method for designing a mirror according to any one of claims 1 to 3, comprising the following formula, which is a weighted version of a first formula f x (x, y, z) = 0 derived from the optical path length from the light source point to the focusing point being constant in the x-axis direction, and a second formula f y (x, y, z) = 0 derived from the optical path length from the light source point to the focusing point being constant in the y-axis direction:
前記L1xとL1yの値が異なり、且つ前記L2xとL2yの値が一致しており、
非点収差をもつ入射ビームから一点に集光する出射ビームが得られる、非点収差制御ミラー。 A mirror having a reflecting surface for which the design formula in the mirror design method according to any one of claims 1 to 4 is satisfied,
The values of L 1x and L 1y are different, and the values of L 2x and L 2y are the same;
An astigmatism control mirror that can obtain an output beam that is focused to a single point from an input beam that has astigmatism.
前記L1xとL1yの値が一致し、且つ前記L2xとL2yの値が異なっており、
一点から発散する入射ビームから非点収差をもつ出射ビームが得られる、非点収差制御ミラー。 A mirror having a reflecting surface for which the design formula in the mirror design method according to any one of claims 1 to 4 is satisfied,
The values of L 1x and L 1y are the same, and the values of L 2x and L 2y are different;
An astigmatism control mirror that produces an astigmatism-bearing output beam from an input beam diverging from a single point.
Priority Applications (1)
| Application Number | Priority Date | Filing Date | Title |
|---|---|---|---|
| JP2021003117A JP7564522B2 (en) | 2021-01-12 | 2021-01-12 | METHOD FOR DESIGNING MIRROR AND ASTAGITABER CONTROL MIRROR HAVING REFLECTING SURFACE WHEREIN THE DESIGN EQUATION IN THE METHOD APPLY |
Applications Claiming Priority (1)
| Application Number | Priority Date | Filing Date | Title |
|---|---|---|---|
| JP2021003117A JP7564522B2 (en) | 2021-01-12 | 2021-01-12 | METHOD FOR DESIGNING MIRROR AND ASTAGITABER CONTROL MIRROR HAVING REFLECTING SURFACE WHEREIN THE DESIGN EQUATION IN THE METHOD APPLY |
Publications (2)
| Publication Number | Publication Date |
|---|---|
| JP2022108208A JP2022108208A (en) | 2022-07-25 |
| JP7564522B2 true JP7564522B2 (en) | 2024-10-09 |
Family
ID=82556150
Family Applications (1)
| Application Number | Title | Priority Date | Filing Date |
|---|---|---|---|
| JP2021003117A Active JP7564522B2 (en) | 2021-01-12 | 2021-01-12 | METHOD FOR DESIGNING MIRROR AND ASTAGITABER CONTROL MIRROR HAVING REFLECTING SURFACE WHEREIN THE DESIGN EQUATION IN THE METHOD APPLY |
Country Status (1)
| Country | Link |
|---|---|
| JP (1) | JP7564522B2 (en) |
Families Citing this family (1)
| Publication number | Priority date | Publication date | Assignee | Title |
|---|---|---|---|---|
| JP7328589B2 (en) * | 2017-12-18 | 2023-08-17 | ミツミ電機株式会社 | ranging camera |
Citations (4)
| Publication number | Priority date | Publication date | Assignee | Title |
|---|---|---|---|---|
| JP2002221596A (en) | 2001-10-01 | 2002-08-09 | Nikon Corp | Aspherical mirror |
| JP2005530168A (en) | 2002-06-19 | 2005-10-06 | グズノク | X-ray optical device |
| JP2014163667A (en) | 2013-02-21 | 2014-09-08 | Fujitsu Ltd | Light condensing device, light condensing method, and method of manufacturing aspherical mirror |
| WO2015004934A1 (en) | 2013-07-12 | 2015-01-15 | 国立大学法人東京大学 | Optical design method for x-ray focusing system using rotating mirror, and x-ray focusing system |
-
2021
- 2021-01-12 JP JP2021003117A patent/JP7564522B2/en active Active
Patent Citations (5)
| Publication number | Priority date | Publication date | Assignee | Title |
|---|---|---|---|---|
| JP2002221596A (en) | 2001-10-01 | 2002-08-09 | Nikon Corp | Aspherical mirror |
| JP2005530168A (en) | 2002-06-19 | 2005-10-06 | グズノク | X-ray optical device |
| JP2005530170A (en) | 2002-06-19 | 2005-10-06 | グズノク | Optical assembly and manufacturing method thereof |
| JP2014163667A (en) | 2013-02-21 | 2014-09-08 | Fujitsu Ltd | Light condensing device, light condensing method, and method of manufacturing aspherical mirror |
| WO2015004934A1 (en) | 2013-07-12 | 2015-01-15 | 国立大学法人東京大学 | Optical design method for x-ray focusing system using rotating mirror, and x-ray focusing system |
Also Published As
| Publication number | Publication date |
|---|---|
| JP2022108208A (en) | 2022-07-25 |
Similar Documents
| Publication | Publication Date | Title |
|---|---|---|
| US7933383B2 (en) | X-ray generator with polycapillary optic | |
| KR102133912B1 (en) | Optical design method for x-ray focusing system using rotating mirror, and x-ray focusing system | |
| Sanchez del Rio et al. | Aspherical lens shapes for focusing synchrotron beams | |
| Rabl et al. | Reflector design for illumination with extended sources: the basic solutions | |
| JP7564522B2 (en) | METHOD FOR DESIGNING MIRROR AND ASTAGITABER CONTROL MIRROR HAVING REFLECTING SURFACE WHEREIN THE DESIGN EQUATION IN THE METHOD APPLY | |
| Balaic et al. | X-ray optics of tapered capillaries | |
| Baumgärtel et al. | RAY-UI: new features and extensions | |
| US11217357B2 (en) | X-ray mirror optics with multiple hyperboloidal/hyperbolic surface profiles | |
| CN103559927B (en) | A kind of aplanasia hard x rays focusing optic and method for designing thereof | |
| Goldberg | Analytic descriptions of parabolic X-ray mirrors | |
| US6746128B2 (en) | Ultra-high resolution imaging devices | |
| WO2022153978A1 (en) | Mirror design method, and astigmatism control mirror having reflection surface on which design equation in said method is established | |
| WO2022153979A1 (en) | Design method for mirror and astigmatism-control mirror having reflective surface that satisfies design formula in design method | |
| Poletto et al. | Design of a high-throughput grazing-incidence flat-field spectrometer | |
| Sutter et al. | Ideal Cartesian oval lens shape for refocusing an already convergent beam | |
| US7720197B2 (en) | High intensity x-ray beam system | |
| Kohn et al. | On the Possibility of the Nanoscale Focusing of Synchrotron Radiation Using an Adiabatic Refractive Lens | |
| Bennett | Advanced laser-backlit grazing-incidence x-ray imaging systems for inertial confinement fusion research. I. Design | |
| Lu et al. | Geometric characteristics of aberrations of plane-symmetric optical systems | |
| Moreno | Optimized IR synchrotron beamline design | |
| García et al. | A mathematical model to generate a light reflector that produces a uniform irradiance distribution from a point light source | |
| Lu | Prefocusing optics for soft-x-ray synchrotron-radiation monochromators | |
| Khaykovich et al. | On the challenge of flux concentration at grazing incidence for neutrons and x-rays | |
| Ding et al. | Tailoring high-performance illumination lenses for extended non-Lambertian sources | |
| Vishnyakov et al. | Normal-incidence imaging spectrograph based on an aperiodic spherical grating for the vacuum spectral region |
Legal Events
| Date | Code | Title | Description |
|---|---|---|---|
| A621 | Written request for application examination |
Free format text: JAPANESE INTERMEDIATE CODE: A621 Effective date: 20231212 |
|
| A977 | Report on retrieval |
Free format text: JAPANESE INTERMEDIATE CODE: A971007 Effective date: 20240627 |
|
| A131 | Notification of reasons for refusal |
Free format text: JAPANESE INTERMEDIATE CODE: A131 Effective date: 20240702 |
|
| A521 | Request for written amendment filed |
Free format text: JAPANESE INTERMEDIATE CODE: A523 Effective date: 20240807 |
|
| TRDD | Decision of grant or rejection written | ||
| A01 | Written decision to grant a patent or to grant a registration (utility model) |
Free format text: JAPANESE INTERMEDIATE CODE: A01 Effective date: 20240820 |
|
| A61 | First payment of annual fees (during grant procedure) |
Free format text: JAPANESE INTERMEDIATE CODE: A61 Effective date: 20240917 |
|
| R150 | Certificate of patent or registration of utility model |
Ref document number: 7564522 Country of ref document: JP Free format text: JAPANESE INTERMEDIATE CODE: R150 |