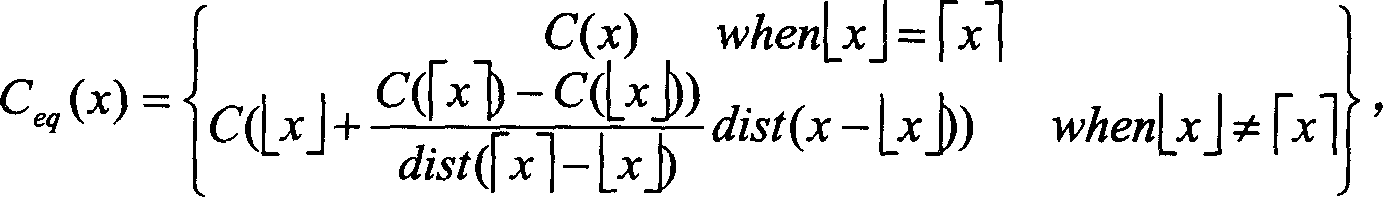CN1668996A - 解大型连续性或离散性最佳化问题的动态方法 - Google Patents
解大型连续性或离散性最佳化问题的动态方法 Download PDFInfo
- Publication number
- CN1668996A CN1668996A CNA038170116A CN03817011A CN1668996A CN 1668996 A CN1668996 A CN 1668996A CN A038170116 A CNA038170116 A CN A038170116A CN 03817011 A CN03817011 A CN 03817011A CN 1668996 A CN1668996 A CN 1668996A
- Authority
- CN
- China
- Prior art keywords
- point
- local optimum
- local
- search
- separate
- Prior art date
- Legal status (The legal status is an assumption and is not a legal conclusion. Google has not performed a legal analysis and makes no representation as to the accuracy of the status listed.)
- Pending
Links
Classifications
-
- G—PHYSICS
- G06—COMPUTING; CALCULATING OR COUNTING
- G06F—ELECTRIC DIGITAL DATA PROCESSING
- G06F17/00—Digital computing or data processing equipment or methods, specially adapted for specific functions
- G06F17/10—Complex mathematical operations
- G06F17/11—Complex mathematical operations for solving equations, e.g. nonlinear equations, general mathematical optimization problems
- G06F17/12—Simultaneous equations, e.g. systems of linear equations
-
- G—PHYSICS
- G06—COMPUTING; CALCULATING OR COUNTING
- G06F—ELECTRIC DIGITAL DATA PROCESSING
- G06F17/00—Digital computing or data processing equipment or methods, specially adapted for specific functions
- G06F17/10—Complex mathematical operations
- G06F17/11—Complex mathematical operations for solving equations, e.g. nonlinear equations, general mathematical optimization problems
-
- G—PHYSICS
- G06—COMPUTING; CALCULATING OR COUNTING
- G06N—COMPUTING ARRANGEMENTS BASED ON SPECIFIC COMPUTATIONAL MODELS
- G06N5/00—Computing arrangements using knowledge-based models
- G06N5/01—Dynamic search techniques; Heuristics; Dynamic trees; Branch-and-bound
Landscapes
- Engineering & Computer Science (AREA)
- Physics & Mathematics (AREA)
- General Physics & Mathematics (AREA)
- Mathematical Physics (AREA)
- Theoretical Computer Science (AREA)
- Pure & Applied Mathematics (AREA)
- Mathematical Optimization (AREA)
- Data Mining & Analysis (AREA)
- Mathematical Analysis (AREA)
- Computational Mathematics (AREA)
- Software Systems (AREA)
- General Engineering & Computer Science (AREA)
- Operations Research (AREA)
- Algebra (AREA)
- Databases & Information Systems (AREA)
- Computing Systems (AREA)
- Evolutionary Computation (AREA)
- Computational Linguistics (AREA)
- Artificial Intelligence (AREA)
- Management, Administration, Business Operations System, And Electronic Commerce (AREA)
- Complex Calculations (AREA)
Abstract
在目标函数可为封闭模式或黑盒模式的一般最佳化问题中,找到全局最佳解的动态方法系包括有以下步骤:首先从一个起始点开始而以确定性方法来寻找一局部最佳解,然后再从此局部最佳解来寻找到另一组局部最佳解,直到从任一点开始的所有局部最佳解被找到为止,并接着从所有局部最佳解集合中求得全局最佳解。
Description
发明背景
发明领域
本发明系相关于数值分析领域和非线性规划问题的最佳化技术。本发明尤其相关于用于有系统地求得连续性或离散性最佳化问题的所有的局部最佳解以及唯一全局最佳解的动态方法。
相关技术之描述
许多定量性(quantitative)的决策、设计、生产、规划和排程的问题,在科学、工程学和经济学领域中,可视为连续性或离散性最佳化问题。一般情形,系统的总表现往往可以多变量函数来做定量性表示,此函数可称此系统的目标函数。从这个观点而言,最佳化问题的最佳解时常以实数向量来表达,此实数向量所表达的可以是一个决策,或设计,或规划。在最佳化问题中的整个搜寻空间(search space)中,最佳解是满足约束条件并使得目标函数值为最小(或最大)。如果这个向量存在的话,此向量系被称为”全局最佳解”。在实际应用中的各种最佳化问题是非常复杂的,它的目标函数通常是非线性并包含大量的变量;因此在搜寻空间中搜寻全局最佳解的任务是非常困难的。主要的挑战在于(高维度空间中)有许多局部最佳解;全局最佳解只是许多局部最佳解中的一个,而且全局最佳解与局部最佳解两者皆具有同样的局部特性,这使得分辨所有搜寻到的局部最佳解是否为全局最佳解的工作较为困难。
一般而言,最佳化问题的解空间拥有有限个(通常非常大)或无限个可行解。在全部的可行解中,只有一个且为唯一的全局最佳解。一般而言,局部最佳解的正确数目是不可知的,而且可能是非常多的。此外,局部最佳解和全局最佳解的目标函数值可能差别非常大。因此这些强烈的动机促使我们发展出多种有效方法,来搜寻全局最佳解。
本发明接下来将主要讨论离散性最佳化问题。解决离散性最佳化问题的任务是非常具有挑战性的。它们具有NP-hard特性,这意谓计算时间跟问题的规模大小成指数关系增加。除此之外,许多离散性问题属于NP-complete,没有现存任何的算法可以有效的解决问题。NP-complete明确的定义可以在文献中找到。大概地说,NP-complete问题是很难计算;任何数值算法在最糟的情况下需要指数关系时间增加才能正确性地搜寻到全局最佳解。
一个普遍被应用到解决离散性最佳化问题的方法,是根据一个反复改进的搜寻算法[1]。它特征如下:从一个初始的可行解开始并在它的邻域搜寻到更好的解。如果较佳解存在的话,则把新解当作初始解,重复上述搜寻过程;否则停止局部搜寻过程。此种最佳解搜寻算法通常会搜寻某一个局部最佳解而停止,它通常无法找到全部解。事实上,现存绝大部分的离散性最佳解搜寻技术,通常在于提供局部最佳解,而非全局最佳解。
针对反复改进的局部搜寻算法(iterative improvement local searchalgorithms)的缺点,近年来几个较复杂的局部最佳解搜寻方法已经发展出来。这些算法不但可以脱离局部最佳解而且能够搜寻到更好解。某些绝大部分的搜寻方法”脱离”的机制是运用cost-deteriorating来脱离局部最佳解。上述这些局部搜寻算法(local search algorithms)包含:仿真退火法(simulated annealingalgorithm)、基因算法(genetic algorithm)、塔布搜寻法(Tabu search algorithm)和类神经网络法(neural network)。
在许多研究报告中,我们可以发现这些复杂的局部最佳解方法,在实际相关应用问题上,是需要大量的运算而且通常不能找到全局最佳解。
在搜寻全局最佳解的问题领域中,我们发展出几个有效方法来解决下列两个挑战性难题:
(i)该如何有效地脱离一个局部最佳解,并有效地移向另外一个局部最佳解;以及
(ii)该如何避免再次重复搜寻已知(已找过)的最佳解。
在过去,许多努力曾尝试解决这个问题,但只获得很小的进展。上述难题(i)是困难解决的,现存许多方法全都曾遇到这种困难。问题(ii)与搜寻效率有关,如何解决也是常遭遇到的困难,现存方法也全都曾遇到这种困难。这个问题(ii)通常会降低现存方法的求解效率:重复搜寻同样的局部最佳解;这个动作浪费计算资源。从计算的观点来说,避免重复搜寻同样的局部最佳解对于维持高效率的求解速度是重要的。
发明内容
搜寻全局最佳解(Global optimization)的任务,对于广大工程界及科学界是非常重要的。本发明提出唯一可靠的方法来搜寻全局最佳解,此方法采用独创的非线性技术来搜寻所有的局部最佳解,然后从它们找出全局最佳解。
本发明提出的方法也可用来解决一般性最佳化问题,首先找出多个局部最佳解(可为非全部的局部最佳解),然后从中找出最佳解(Best solution)。
本发明系发展出一个新的动态方法,它能够以确定性(Deterministic)的方法找出离散性或者是连续性的最佳化问题所有的局部最佳解。在本发明中,将详述解决下述各种最佳化问题的动态方法:
●一个解决在无限制条件下连续性最佳化问题(UnconstrainedContinous Optimization Problems)的动态方法。最佳化问题的目标函数可为封闭模式(closed-form)或黑盒模式(black-box)。(所谓黑盒模式(black-box)的目标函数是指在搜寻空间中,每一点的目标函数值是可以计算的,但却无法以一个封闭模式的表示式来表示目标函数)。
●一个解决在无限制条件下离散性最佳化问题(Unconstrained DiscreteOptimization Problems)的动态方法。最佳化问题的目标函数可为封闭模式或黑盒模式。
●一个解决在有限制条件下离散性最佳化问题(Constrained DiscreteOptimization Problems)的动态方法。最佳化问题的目标函数系为封闭模式。
●一个解决在有限制条件下离散性最佳化问题(Constrained DiscreteOptimization Problems)的动态方法。最佳化问题的目标函数系为黑盒模式。
为了解决上述问题(i),本发明发展一种基于动态分解点的数值方法,其组合了动态分解点搜寻方法,来执行一有系统的搜寻过程,从一个局部最佳解搜寻到另一个局部最佳解。为了解决上述问题(ii),本发明发展一套反重复(Anti-revisiting)搜寻方法来避免重复搜寻已知的局部最佳解。本发明所发展的反重复搜寻方法之理论基础是依据本发明所提出的动态分解点(Dynamicaldecomposition point DDP)。
本发明中这些有效的方法可用来克服问题(i)及(ii),并并入两个动态方法来找寻所有局部最佳解,此两个动态方法包括基于连续性(continous-based)的动态方法及基于离散性(discrete-based)的动态方法。这两个动态方法的一个显著特性是可与任何已存在的局部最佳求解方法(找寻局部最佳解)合并,以达成在求局部最佳解的计算高效率(并保有搜寻所有局部最佳解的能力)。
本发明的动态方法是可以和一个现成有效率的计算机软件(找寻局部最佳解)相结合,来彼此合作共同找出所有局部最佳解集合。本发明可设计一个接口环境方便与现成的计算机软件相连,不需要重新界定计算机软件的环境(包含使用者图形接口及数据库),便可搜寻到完整的局部最佳解集合和全局最佳解。本发明对于使用者来说,不需要重新学习一套新的软件。这个利用现有计算机软件的智能财产特性,使得本发明非常具有吸引力。
图示简单说明
图1系显示出以基于动态分解点的方法来从连续空间中之一已知局部最佳解中找出一个局部最佳解的图表。
图2系显示出以基于出口点的方法来从连续空间中之一已知局部最佳解中找出一个局部最佳解的图表。
图3系显示出以基于动态分解点的方法来从离散空间中之一已知局部最佳解中找出一个局部最佳解的图表。
图4系显示出以基于出口点的方法来从离散空间中之一已知局部最佳解中找出一个局部最佳解的图表。
图5系显示出找出所有局部最佳解的说明。
本发明的详细说明
一般的最佳化问题(General Optimization Problems)
本发明将一般的最佳化问题分类为非线性连续最佳化问题(Nonlinearcontinuous optimization problems)及非线性离散最佳化问题(Nonlinear discreteoptimization problems)。他们进而分成下列四种(依有无限制条件再细分):
●无限制条件连续性最佳化问题。最佳化问题的目标函数可为封闭模式或黑盒模式。
●有限制条件连续性最佳化问题。最佳化问题的目标函数可为封闭模式或黑盒模式。
●无限制条件离散性最佳化问题。最佳化问题的目标函数可为封闭模式或黑盒模式。
●有限制条件离散性最佳化问题。最佳化问题的目标函数可为封闭模式或黑盒模式。
无限制条件连续性最佳化问题
一般的无限制条件连续性最佳化问题,形式如下:
最小化 UC(x) (4-1)
此处目标函数UC∶Rn→R可为封闭模式或黑盒模式。标函数是有下限的函数,因此它的全局最小(佳)解是存在的且局部最小(佳)解的数量是有限的。对一个无法以表示式表达的黑盒模式目标函数,其目标函数值只能被计算。此类目标函数可视为一个外部子程序:读取其解向量x(solutione vector)值,然后计算出相对应的目标函数值UC(x)。
有限制条件连续性最佳化问题
一般的有限制条件连续性最佳化问题,形式如下:
最小化 C(x)
(4-2)
受限于 G(x)≤0
此处目标函数C∶Rn→R可为封闭模式或黑盒模式。满足不等式G(x)状态向量的集合被称为可行区域(feasible region)。目标函数C(x)是一个有下限的函数,因此它的全局最小(佳)解是存在的且局部最小(佳)解的数量是有限的。
无限制条件离散性最佳化问题
一般的无限制条件离散性最佳化问题,形式如下:
最小化UC(x) (4-3)
此处目标函数UC∶S→R可为封闭模式或黑盒模式。UC(x)是一个有下限的函数,因此全局最小(佳)解是存在的且局部最小(佳)解的数量为有限的。
有限制条件离散性最佳化问题
一般的有限制条件离散性最佳化问题,形式如下:
最小化 C(x) (4-4)
受限于x∈FS
此处目标函数C∶S→R可为封闭模式或黑盒模式。目标函数C(x)是一个有下限的函数,因此它的全局最小(佳)解是存在的且局部最小(佳)解的数量为有限的。限制集合FS包含所有的可行解(feasible solution)。限制集合FS可表示为一组限制方程式或由一个黑盒模式来表示,它也可视成一个外部子程序:只要读取其解向量x值,然后计算出相对应的限制满意度(satisfiability ofconstraints)。
显然的,上述的离散性最佳化问题系可以下述通式表达:
最小化 C(x)
受到限制G(x)≤0 (4-5)
此处目标函数C∶S→R可为封闭模式或黑盒模式。目标函数C(x)是一个有下限的函数,因此它的全局最小解是存在的且局部最小解的数量是为有限的。限制函数向量(constraint function vector)G∶S→Rm是以封闭模式表示。搜寻空间S为有限或无穷可数集合(countably infinite set)。
下文中将针对(4-1)(4-3)(4-5)各类最佳化问题,分别描述说明本发明的动态方法。
5.解决无限制条件连续性最佳化问题的动态方法
在此说明解决无限制条件连续性最佳化问题(4-1)的动态方法。
为解决无限制条件连续性最佳化问题(4-1),本发明发展出一个(利用下列非线性动态系统相关之轨迹特性)动态方法,来搜寻所有的局部最佳解。
其中x∈Rn,向量场(vector field)空间f(x)满足解的唯一性及存在性。
本发明针对运用非线性动态系统(5-1)的轨迹来找出最佳化问题(4-1)所有的局部最佳解的方法,提出下述充分条件。
(LC1)-非线性动态系统(5-1)的轨迹必须是收敛的,而且收敛至其中一个平衡点;及
(LC2)-最佳化问题(4-1)的每一个局部最佳解是系统(5-1)的一个稳定平衡点(stable equilibrium point),反之亦然。
(LC3)-最佳化问题(4-1)的目标函数值,沿着非线性动态系统(5-1)的轨迹是递减。
我们接下来说明,给予一个具有解析式的封闭模式或黑盒模式目标函数的无限制条件的连续性最佳化问题(4-1),我们可建构一个满足(LC1)~(LC3)充分条件的非线性动态系统(5-1)。
我们首先发展下面两个定理,为寻找非线性动力系统提供依据。
一个函数E(x)如果满足如下两个条件,我们称之为(5-1)的能量函数:(i)沿非线性动力系统(5-1)的任意系统轨线,函数E(x)的导数非正,即
(ii)如果x(t)不是非线性动力系统(5-1)的一个平衡点,则集合
沿x(t)在R中具有零测度。
定理5-1:如果动力系统(5-1)具有能量函数,则条件(LC1)满足;
定理5-2:如果无限制条件的连续最佳化问题(4-1)的目标函数是非线性动力系统(5-1)的一个能量函数,则条件(LC2)和(LC3)满足。
对一个最佳化问题(4-1)及具有可分析式的封闭模式目标函数UC,我们可以严格证明一例满足(LC1)~(LC3)充分条件的非线性动态系统是如下:
此处(UC)∶Rn→Rn是目标函数UC的梯度向量(gradient vector)。一般说来,除了此非线性动态系统(5-2)外,应该存在其它的非线性动态系统满足(LC1)~(LC3)的充分条件。我们将此类非线性动态系统以下述一般通式表达:
对一个最佳化问题(4-1),其有黑盒模式的目标函数UC,如何建构一个满足(LC1)~(LC3)充分条件的非线性动态系统是困难的。我们发展了许多方法来解决它;其中一个是依据黑盒模式的目标函数UC,将其利用分割差分(divided-difference)为基础来计算:
此处对x第i个组件的导数,可以用目标函数UC(x)的单向差分(one-sideddifferences)近似值表示,ei是Cartesian第i个基底向量,h是一个非常小的数。另外吾人对具有黑盒模式的目标函数,也可用中央差分(central differences)方法来建构另一个非线性动态系统,描述如下:
此处对x第i个组件的导数,可以用目标函数UC(x)的中央差分近似值表示,ei是Cartesian第i个基底向量,h是一个非常小的数。
对一个最佳化问题(4-1),其有黑盒模式的目标函数,除了上述(5-4)及(5-5),应该存在其它的非线性动态系统满足(LC1)~(LC3)的充分条件。我们将此类非线性动态系统以下列一般通式表达:
为了清楚及方便说明,我们将非线性动态系统(5-3)其具有可分析式封闭模式目标函数,及非线性动态系统(5-6)其具有黑盒模式的目标函数,用以下列一般非线性通式来表达:
我们以下说明相关于非线性动态系统(5-7)的一些基本定义及理论。对x∈Rn,系统(5-7)的解由t=0起称为轨迹,以φt(x)∶R→Rn表示。
如果FU(x)=0,状态向量x*∈Rn称为系统(5-7)的一个平衡点。如果F(·)在x*的Jacobian矩阵,其所有的特征值(eigenvalues)没有实数部分(with a zeroreal part)为零,我们则称平衡点x*∈Rn是双曲线型(hyperbolic)。如果双曲线型(hyperbolic)平衡点的Jacobian矩阵,有k个正实数之特征值,我们称此点为类型-k的平衡点。对一个平衡点,如果它所对应的Jacobian矩阵的所有特征值的实数部分皆为负值,则该点是稳定平衡点(stable equilibrium point),反之如果它所对应的Jacobian矩阵的所有特征值的实数部分皆为正值,则该点是不稳定平衡点(unstable equilibrium point)。一个类型-k的双曲线型(hyperbolic)平衡点,它的稳定流形Ws(x*)和不稳定流形Wu(x*)定义如下:
稳定流形Ws(x*)和不稳定流形Wu(x*)的面积维数分别是k及n-k。
如果系统(5-7)的每一个轨迹从此集合K内的某一点出发且都停留在此集合里(for all t∈R),则我们称集合K∈Rn,是此非线性系统(5-7)的不变量集合(invariant set)。如果系统的每个轨迹都收敛到其中一个的平衡点,则此动态系统被称为完全稳定的(completely stable)。
我们称稳定平衡点xs的稳定区域(stability region)(在数学上也称吸引域(region of attraction))是所有点其轨迹收敛到xs的集合。数学上以 表示,此处φt(x)表示系统(5-7)的一个轨迹且此轨迹是在时间t=0从x点出发的。稳定平衡点xs的准稳定区域(quasi-stabilityregion)Ap(xs),以
表示,其中
为稳定区域A(xs)的闭包(closure),并且
是
的内部(interior)。从拓扑的观点出发,A(xs)和Ap(xs)是路径连续的不变开集合;并且,它们是Rn的微分同胚。
如下定理[3],连同上述两个定理,给出了本发明发展的动态方法的理论基础,该方法利用满足条件(LC1)至(LC3)的非线性动力系统(5-7)解决无限制条件的连续性最佳化问题(4-1)。
定理5-3:考虑由(5-7)描述并且满足条件(LC1)的非线性动力系统。设Ap(xs)是xs的准稳定区域,xd∈Ap(xs)是一个动态分解点。如果Ap(xs)上的平衡点的稳定和不稳定流形的交叉满足横断性条件,则存在并且只存在(5-1)的另一个稳定平衡点
xs满足:
(1)
是对应于
xs的一个动态分解点;以及
(2)Wu(xd)∩Ap(xs)≠以及Wu(xd)∩Ap(
xs)≠
其中,动态分解点指位于非线性动力系统(5-7)的准稳定边界上的一个类型-1平衡点;Wu(xd)代表动态分解点xd的不稳定流形。
5.1混合式局部搜寻方法(Hybrid Local Search Method)
我们发展一个混合式局部搜寻方法,其结合一个以轨迹为基础的方法及一个有效的局部方法,来可靠的找寻局部最佳解。我们将此混合式局部搜寻方法配入我们所发明的动态方法内。
一个混合式的局部搜寻法,从一个起始点开始(在一个连续的空间中)来找寻无限制条件连续性最佳化问题(4-1)的局部最佳解,如下表示:
给予:一个起始点x0。
目的:可靠的计算无限制条件连续性最佳化问题(4-1)的一个局部最佳解。
步骤一、从一个起始点x0开始,针对无限制条件连续性最佳化问题(4-1),运用一个有效的局部搜寻法。
步骤二、如果局部搜寻算法收敛到一个局部最佳解,则停止执行;否则执行下一步骤。
步骤三、用x0当做起始条件,对非线性动态系统(5-7)在几个时间步距(time-steps)处进行积分,获得最后一点为终端点。以终端点当作起始点,执行步骤一。
5.2计算出口点(Exit Point)的方法
从一个起始点开始(一个已知无限制条件连续性最佳化问题(4-1)局部最佳解xs,也就是非线性动态系统(5-7)的稳定平衡点),运用非线性动态系统(5-7),来找寻无限制条件连续性最佳化问题(4-1)的出口点,称之为出口点搜寻法,如下表示:
给予:一个已知局部最佳解xs,预定的搜寻路径,及相关的非线性动态系统(5-7)。
目的:由预定的搜寻路径及动态系统(5-7)的稳定平衡点xs,计算所对应的出口点。
从已知的局部最佳解xs开始,沿着预定的搜寻路径移动,直到连续性目标函数(4-1)达到(第一)局部最大值的点上,则此点为出口点。
本发明另外提出一个计算出口点的方法:从xs开始,延着搜寻路径移动,计算搜寻路径的导数和非线性动态系统(5-7)向量场在每个时间点的内积值,当内积值正负符号变更时(由正到负),则表示已寻找到出口点在[t1,t2]间。然后运用在t1或t2时的搜寻路径的所得到的点来近似出口点。
5.3计算动态分解点(dynamical decomposition point)的方法
从一个起始点开始(一个已知无限制条件连续性最佳化问题(4-1)局部最佳解xs,也就是非线性动态系统(5-7)的稳定平衡点),运用非线性动态系统(5-7),来找寻非限制连续最佳化问题(4-1)的动态分解点,称之为动态分解点(DDP)搜寻法,如下表示:
给予:一个最佳化问题(4-1)的已知局部最佳解xs,一条预定的搜寻路径,及相关的非线性动态系统(5-7)。
目的:由预定的搜寻路径及动态系统(5-7)的稳定平衡点xs,计算出所对应的动态分解点。
步骤一、从已知的局部最佳解xs开始,沿着一条预定的搜寻路径t(xs)移动,侦测到出口点,此点位于动态系统(5-7)稳定平衡点(也就是局部最佳解xs)的准稳定边界上(quasi-stability boundary),设出口点为xex。
步骤二、从xex开始,应用下述步骤找寻最小距离点(minimum distancepoint),简称MDP:
(i)以出口点xex为起始条件,对非线性系统(5-7)在几个时间步距(time-steps)处进行积分;设终端点为目前出口点(current exit point)。
(ii)连接轨迹上的目前出口点和局部的最佳解(也就是稳定平衡点)成一直线。沿着此直线从稳定平衡点找寻目标函数(4-1)的(第一)局部最大的点,视其为修正出口点xex,并以此点代替目前出口点。指定这个点为出口点xex。
(iii)重复执行(i)及(ii),直到在(ii)中所获得的出口点,其向量场平均值(norm of vector field)(5-7)是小于一个临界值(threshold),也就是数值‖Fu(xex)‖≤ε。那么这点被视为最小距离点(MDP)。
步骤三、以MDP xd 0为起始点,求解系统(5-7)其非线性代数方程式FU(x)=0。设其解为xddp,则xddp是针对于动态系统(6-11)局部最佳解xs和搜寻路径t(xs)的动态分解点。
5.4搜寻另一个局部最佳解的基于出口点(EP-based)的方法
针对最佳化问题(4-1)而言,我们发明从一个已知的局部最佳解xs开始来搜寻到另一个局部最佳解的方法,称之基于出口点(EP-based)的方法。
给予:一个最佳化问题(4-1),其已知的局部最佳解xs。
目的:搜寻到最佳化问题(4-1)的另一个局部最佳解。
步骤一、从一个已知的局部最佳解xs开始,计算非线性动态系统(5-7)的出口点xex。
步骤二、设x0=xs+(1+ε)(xex-xs)其中ε为一极小值。
步骤三、从x0开始,对非线性系统(5-7)进行积分以获得一条轨迹且求得接口点(interface point)xinf。在此接口点运用一个有效的混合式局部搜寻法来找局部最佳解,其效果是会优于用轨迹来求解局部最佳解。
步骤四、从此接口点xinf开始,运用步骤三所选的有效混合式局部搜寻法来搜寻到一个毗连的局部最佳解。
5.5搜寻另一个局部最佳解的基于动态分解点(DDP-based)的方法
在最佳化问题(4-1)中,我们发明一个基于动态分解点(DDP-based)的方法,从一个已知局部最佳解来搜寻到另一个局部最佳解的方法,如下表示:
给予:一个最佳化问题(4-1)其已知的局部最佳解xs及一条先定的搜寻路线。
目的:搜寻到最佳化问题(4-1)的另一个局部最佳解。
步骤一、从一个已知的局部最佳解xs开始,沿着搜寻路径来计算非线性系统(5-7)的动态分解点。如动态分解点xddp。
步骤二、设x0=xs+(1+ε)(xddp-xs),其中如表示式存在ε为一极小值。
步骤三、从x0开始,对非线性系统(5-7)进行积分以获得一条轨迹且求得接口点(interface point)xinf。在此接口点运用一个有效的混合式局部搜寻法来找局部最佳解,其效果是会优于用轨迹来求解局部最佳解。
步骤四、从此接口点xinf开始,运用步骤三所选的有效混合式局部搜寻法来搜寻到一个毗连的局部最佳解。
5.6搜寻所有阶层一(tier-one)的局部最佳解的动态方法
在说明此方法前,我们先定义说明在最佳化问题(4-1)(相对于非线性动态系统(5-7))中,对一个已知的局部最佳解,所谓的阶层一(tier-one)局部最佳解及阶层N(tier-N)局部最佳解。
阶层一(tier-one)局部最佳解:如果非线性动态系统(5-7)的局部最佳解xs0其稳定区域的范围(closure)与局部最佳解xs1其稳定区域的范围(closure)相交,则我们称最佳化问题(4-1)局部最佳解xs1是局部最佳解xs0的阶层一(tier-one)局部最佳解。
阶层N(tier-N)局部最佳解:一个最佳化问题(4-1)的局部最佳解xsn,如果满足下述二条件,则我们称xsn是此已知局部最佳解xs0的阶层N(tier-N N>1)局部最佳解。
(i)xsn既不是局部最佳解xs0阶层-(N-2)的局部最佳解也不是阶层-(N-1)的局部最佳解。
(ii)局部最佳解xs0的阶层-(N-1)局部最佳解集合,其中某一个局部最佳解,是局部最佳解xsn的阶层一(tier-one)局部最佳解。
局部最佳解xs0的阶层-0局部最佳解是其本身xs0。
对最佳化问题(4-2),(4-3)及(4-4),所谓阶层-一(tier-one)局部最佳解及阶层-N(tier-N)局部最佳解的定义均相似。
对最佳化问题(4-1),我们发明二个方法(从一个已知的局部最佳解)来搜寻到所有阶层一(tier-one)的局部最佳解。第一个是基于出口点(EP-based)的方法,第二个是基于动态分解点(DDP-based)的方法。
基于出口点(EP-based)的方法
给予:一个无限制条件连续性最佳化问题(4-1),其已知的局部最佳解xs 0。
目的:搜寻最佳化问题(4-1)中,相对于局部最佳解xs 0的所有阶层一(tier-one)局部最佳解。
步骤一:设定所有阶层一(tier-one)局部最佳解集合Vs={φ},以及定义一组xs 0的搜寻路径Si,i=1,2,...,m.设i=1。
步骤二:从一个已知的局部最佳解xs 0开始,沿着搜寻路径Si移动,寻找局部最佳解。
(i)运用EP-based方法来寻找另一个局部最佳解。如局部最佳解被找到,以xs i表示继续下一步;否则执行(iii)。
(ii)检查xs i是否曾被找到(xs i∈Vs),如果尚未曾被找到过则设
(iii)设i=i+1。
(iv)重复执行步骤(i)到步骤(iii),直到i>m。
步骤三:输出xs 0所有阶层一(tier-one)的局部最佳解Vs。
基于动态分解点(DDP-based)的方法
给予:一个无限制条件连续性最佳化问题(4-1),其已知的局部最佳解xs 0。
目的:搜寻最佳化问题(4-1)中,相对于局部最佳解xs 0的所有的阶层一(tier-one)局部最佳解。
步骤一:设定动态分解点集合Vddp={φ},所有阶层一(tier-one)的局部最佳解集合Vs={φ}。
步骤二:定义一组xs 0的搜寻路径Si,i=1,2,...,mj.设i=1。
步骤三:从一个已知的局部最佳解xs 0开始,沿着预定的搜寻路径Si移动,寻找局部最佳解。
(i)运用动态分解点的方法来寻找非线性系统(5-7)的动态分解点。如动态分解点被找到,以xddp,i表示继续下一步;否则执行(vi)。
(ii)检查xddp,i是否曾被找到(xddp,i∈Vddp),如果曾被找到过则执行(vi),否则设Vddp=Vddp∪{xddp,i}继续执行(iii)。
(iii)设
其中如表示式存在ε为一极小值。
(iv)从x0,i开始,对非线性系统(5-7)进行积分以获得一条轨迹且求得接口点xinf,i。在此(接口)点运用一个有效的混合式局部搜寻法来找局部最佳解,其效果是会优于用轨迹来求解局部最佳解。
(v)从此界面点xinf,i开始,运用步骤(iv)所选的有效混合式局部搜寻法来搜寻对应xddp,i的一个毗连的局部最佳解xs i,并设
(vi)设i=i+1。
(v)重复执行步骤(i)到步骤(vi),直到i>mj。
步骤四:输出xs 0所有阶层一(tier-one)的局部最佳解Vs。
5.7搜寻到所有的局部最佳解的方法
对最佳化问题(4-1),我们发明二个方法(从一个已知的局部最佳解)来搜寻到所有的局部最佳解。基于出口点(EP-based)的方法,第二个是基于动态分解点(DDP-based)的方法。
基于出口点(EP-based)的方法
给予:一个连续性最佳化问题(4-1)的起始点x0(可以是任何点)。
目的:(i)搜寻到连续性最佳化问题(4-1)的所有的局部最佳解。
(ii)搜寻连续性最佳化问题(4-1)的全局最佳解。
步骤一:以起始点x0开始应用一个有效的(混合式)搜寻方法,来寻找一个局部最佳解xs 0。
步骤二:设j=0,初始化局部最佳解集合
阶层j(tier-j)的局部最佳解集合
步骤三:设阶层j+1的局部最佳解集合
步骤四:对在Vnew j中的每一个局部最佳解xs j,寻找它所有阶层-1的局部最佳解。
(i)针对于xs j,定义一组搜寻路径Si j i=1,2...,mj,设i=1。
(ii)从一个已知的局部最佳解xs j开始,运用基于出口点(EP-based)的方法寻找另一个局部最佳解。如局部最佳解被找到,以xs,j i表示并继续下一步;否则执行步骤(iv)。
(iii)检查xs,j i是否以前被找过,即xs,j i∈Vs,如果它尚未被找过,设 及
(iv)设i=i+1。
(v)重复执行(ii)到(iv),直到i>mj。
步骤五:检查最新计算的局部最佳解集合Vnew j+1,如果是空集合,执行步骤六;否则设j=j+1,并执行步骤三。
步骤六:输出所有的局部最佳解集合Vs,藉由比较Vs集合中的所有局部最佳解所对应的个别目标函数值,选择其中一个具有最小值的最佳解。输出此点为全局最佳解。
基于动态分解点(DDP-based)的方法
给予:一个连续性最佳化问题(4-1)的起始点x0(可以是任何点)。
目的:(i)搜寻到连续性最佳化问题(4-1)的所有的局部最佳解。
(ii)在连续性最佳化问题(4-1)的全局最佳解。
步骤一:以起始点x0开始应用一个有效的(混合式)搜寻方法,来寻找一个局部最佳解xs 0。
步骤二:设j=0,初始化局部最佳解集合
阶层j(tier-j)的局部最佳解集合
及动态分解点集合Vddp={φ}。
步骤三:设阶层j+1的局部最佳解集合
步骤四:对在Vnew j中的每一个局部最佳解xs j,寻找它所有的局部最佳解。
(i)定义xs j的一组搜寻路径Si j i=1,2...,mj,设i=1。
(ii)对xs j开始的每条搜寻路径Si j,运用找寻动态分解点的方法寻找非线性系统(5-7)的动态分解点。如动态分解点被找到,以xddp,i j表示继续下一步;否则执行(viii)。
(iii)检查xddp,i j是否曾被找到(xddp,i j∈Vddp),如果曾被找到过则执行(viii),否则设
(iv)设
其中(如表示式存在)ε为一极小值。
(v)从x0,i j开始,对非线性系统(5-7)进行积分以获得一条轨迹且求得接口点xinf,i j。在此接口点运用一个有效的混合式局部搜寻法来找局部最佳解,其效果是会优于用轨迹来求解局部最佳解。
(vi)从此界面点xinf,i j开始,运用步骤(v)所选的有效混合式局部搜寻法来搜寻一个毗连的局部最佳解xs,j i。
(vii)检查xs,j i是否以前被找过,即xs,j i∈Vs,如果它尚未被找过,设 及
(viii)设i=i+1。
(ix)重复执行(ii)到(vii),直到i>mj。
步骤五:检查最新计算的局部最佳解集合Vnew j+1,如果是空集合,执行步骤六;否则设j=j+1,并执行步骤三。
步骤六:输出所有的局部最佳解集合Vs,藉由比较Vs集合中的所有局部最佳解所对应的个别目标函数值,选择其中一个具有最小值的最佳解,输出此点为全局最佳解。
6.解决无限制条件离散性最佳化问题的动态方法
我们系在此说明本发明如何解决无限制条件离散性最佳化问题(4-3)的动态方法。
搜寻问题(4-3)的全局最佳解是非常困难的工作,这工作常常地只搜寻到一个解,此解是在邻域(neighborhood)中最好的。本发明需要定义什么是邻域。邻域函数N(y)(neighborhood function)是一个映射(N∶S→2s),对每一个解(solution)y,所行成的集合N(y)。此集合在某种程度上是靠近y的。N(y)集合被称y的邻域。如果对所有的x∈N(x*),UC(x)≥UC(x*),则我们称x*为邻域N(x*)的局部最小解(局部最佳解)。
许多具有如(4-3)形式的离散性最佳化问题是NP-hard的。通常人们认为NP-hard问题是不能在多项式限定的计算时间内最佳解决的。对于如(4-3)形式的离散性最佳化问题有三种解决方法。第一种是枚举法,它能保证找到最佳解,但必须以巨大的计算量为代价的。第二种方法使用一种多项式时间的近似算法来找到一个接近最佳的解。最后一种方法则求助于某些启发式技术或称为局部搜寻或局部改进的反复改进技术,它对解的质量或运行时间没有先验保证。
局部搜寻法是一个常被用来解决许多离散性最佳化问题的方法。由于所要解决问题的大小或不了解问题的结构可能会让列举法(enumerative methods)难以实际应用在离散性最佳化问题。另一方面,多项式时间的近似算法(polynomial-time approximaton algorithms),除了执行效能有所限制外,有可能会产生不好的解。而局部搜寻法系在合理的时间内可对特定之问题获得合理、或高质量的解。一个局部搜寻法(local search algorithms)的基本型态,我们称之反复改进(iterative improvement),其从某些起始点开始,搜寻其邻域中cost function值较小的解。如果解被搜寻到的话,将取代目前解并持续搜寻;否则目前解是局部最佳解并停止局部搜寻算法。
接下来我们提出并说明解决离散性最佳化问题(4-3)的局部搜寻算法,其基础型态方法,称为反复改进(iterative improvement)方法。
局部反复改进(局部搜寻)算法(Iterative local Improvement(Local search)
Algorithm)
步骤一:初始:选一个始起点x1和设定循环计次数k=1。
步骤二:改进:考虑局部修正集合(local improvementset){x∈N(xk)∶C(x)<C(xk)},N(xk)是环绕在xk的邻域。如果N(xk)是空集合,停止并设xk当作邻域N(xk)的局部最佳解;否则选择N(xk)邻域中的一员视为xk+1,设k=k+1,重复此步骤。
针对一个局部搜寻算法,有二个问题需要解决。
(i)邻域N(x)的定义。
(ii)从集合{x∈N(xk)∶C(x)<C(xk)}中,选择xk+1的机制。
为获得高质量的局部最佳解,找寻有效的邻域函数是局部搜寻算法的一大挑战。目前一般方法,仍缺少如何设定一有效邻域函数的规则。对于同一问题,可能存有许多不同的邻域函数,对不同定义的邻域,仍可能产生许多不同的结果(纵然运用相同的局部搜寻算法)。一个好的邻域函数设计常常需要依据问题本身的的离散结构。显然,为了解决问题(i),一个合适的离散邻域必须足够大以包含当前解的一些离散变量;同时又必须足够小以便能够利用可行的计算量来搜寻。为了简化符号表示,我们假定所有变量满足0-1限制条件。
●单位邻域:给定一个解xk,xk的单位邻域通过每次补足一个xk的分量来形成,即:
●K-变化邻域:K-变化邻域包括了单位邻域,它允许每次补足最多k个解分量。具体就是,
●分段交换邻域:分段交换邻域每次以一种互补的形式交换两个二值分量。
●K-交换邻域:K-交换邻域每次以一种互补的形式交换至多k个二值分量。
为实现多样性,在搜寻过程中邻域函数可以被转换。
本发明中,我们采用下列三种邻域的定义:
直接(immediate)邻域:点x′被视为x的一个直接邻域,若且唯若x′和x的差距(difference)可用向量e1=[u0,u1,...,un]表示,其中仅有一个ui为1,其余为0。因此点x和它的直接邻域x′的差别有1的差距发生。
单向延伸(one-way extended)邻域(OWEN):点x′被视为x的单向延伸邻域,若且唯若x′和x的差距(也就是x-x′或x′-x)可用向量e1=[u0,u1,...,un]表示,式中ui可为1或0。
完全(full)邻域:点x′被视为x的一个完全的邻域,若且唯若x′和x的差距可用向量e1=[u0,u1,...,un]表示,式中ui可为0,1或-1。
对所有的直接(Immediate)邻域集合,某点有最小的目标函数值,我们说此点是在离散空间S中直接邻域的局部最佳解。对所有的单向延伸(one-wayextended)邻域集合,某点有最小的目标函数值,我们说此点是在离散空间S中单向延伸邻域的局部最佳解。对所有的完全(full)邻域,某点有最小的目标函数值,我们说此点是在离散空间S中完全邻域的局部最佳解。以下事实是上述定义的推论:
事实1:如果点x*是关于其单向延伸邻域的一个局部最佳解,则它是关于其直接邻域的一个局部最佳解。
事实2:如果点x*是关于其完全邻域的一个局部最佳解,则它是关于其直接邻域以的一个局部最佳解以及关于其单向邻域以的一个局部最佳解。
事实3:对无限制条件离散性最佳化问题(4-3),C(x)的全局最佳结必定是关于其完全邻域的一个局部最佳解。
对无限制条件离散性最佳化问题(4-3),我们所谓邻域是指直接(immediate)邻域;局部最佳解是针对直接(Immediate)邻域所得到的。
为解决局部搜寻算法的问题(ii),存有二个求得xk+1的一般性局部反复改进算法(即在步骤二的选择规则)。
最佳邻域搜寻方法(Best neighborhood search method)
最佳邻域搜寻方法,总是选择一个邻域中目标函数有最大下降的xk+1点。这个方法是运用确定性方式来搜寻到局部最佳解。
较佳邻域搜寻方法(Better neighborhood search method)
除了前述选择邻域中最大下降者为邻域点xk+1外,我们的较佳邻域搜寻法是选取邻域中的第一个相遇点xk+1,且此点目标函数值是下降的。显然的,这个较佳邻域搜寻法是快速的;然而依据邻域中所有点被评估的顺序,这种局部搜寻法不能产生唯一解。显然地,较佳邻域搜寻法本质上是随机的。
在过去的三十多年内,大量的局部搜寻算法被发展出来并被运用于广泛的离散性优化问题。这些方法中的许多是针对于特定类型的离散性最优化问题的。同时,它们中的大部分只能有效地找到局部最佳解,而不是全局最佳解。在搜寻过程中,这些方法通常会陷入一个局部最佳解而不能移动到另一个局部最佳解。为弥合这种缺陷,并同时保持在邻域搜寻的框架内,一些修正业已提出,但是并未取得很大成功。对局部搜寻的一个直接的拓展就是使用不同的起始解执行多次局部搜寻法,并以其中最好的解作为最终解。但这种多起点方法,仍未见有较大的成功。
反复改进的局部搜寻法的缺点促成了大量更加复杂的用于寻找更佳解的局部搜寻算法的发展。这些局部搜寻法通过引入一些机制来允许搜索过程逃离局部最佳解。这当中的“逃离”机制使用特定的搜寻方案,以允许目标值退化的邻域,并使逃离局部最佳解成为可能。
然而,许多研究已经发现这些复杂的局部搜寻算法,与其它算法比较,需要大量的计算量并且通常不能找到全局最佳解。
本发明中,我们发展一个新的系统方法,它是以确定性方法搜寻到一般离散性最佳化问题所有的局部最佳解。针对解决无限制条件离散性最佳化问题(4.3),我们发展二个动态方法:
●一个为解决目标函数是封闭模式的无限制条件离散性最佳化问题。
●另一个为解决目标函数是黑盒模式的无限制条件离散性最佳化问题。
依据离散性动态方式与连续性动态方式此二种方式;本发明发展许多不同的动态方法。除此,为搜寻全局最佳解,本发明并发展几个有效的方法来解决下面两个重要且具挑战性的问题:
(i)该如何有效地脱离一个局部最佳解,并移向另外一个局部最佳解;和
(ii)该如何避免再次重复搜寻已知(已找过)的最佳解。
6.1基于离散性的动态方式(Discrete-based Dynamical Approach)
在下文中,我们发展一个离散性动态方式来解决无限制条件离散性最佳化问题(4-3)。
为解决无限制条件离散性最佳化问题(4-3),我们考虑相关的非线性离散动态系统;它以一组微分方程的型式来描述,
xk+1=f(xk) (6-5)
其中x∈S离散的状态空间(state space)。方程式(6-5)可视为一个映射(map)或交互循环(iteration)。我们视xk+1系由xk经由映射公式所对映到的。方程式(6-5)的解,由x0∈S称为一条系统轨迹(system trajectory)。在离散动态系统(6-5)中,如一点x*∈S且x*=f(x*),则此点是一个固定点(fixed point)。如任何系统轨迹能保持于固定点的邻域中(选择起始点x0尽量接近固定点),则称此固定点是稳定固定点(stable fixed point)。
我们接下对非线性离散动态系统(它的轨迹可找出所有的局部最佳解),提出下述充分条件。
(LD1)-非线性动态系统(6-5)的轨迹是收敛的,而且收敛至其中一个固定点;及
(LD2)-沿着任何离散动态系统(6-5)的轨迹,离散性最佳化问题的目标函数值是递减的。
(LD3)-离散性最佳化问题(4-3)的每一个局部最佳解是系统(6-5)的一个稳定固定点,反之亦然。
离散性最佳化问题(4-3)的所有局部最佳解,可以经由离散动态系统(6-5)的某些轨迹来有系统的计算获得。从这些局部最佳解,我们可轻易求解全局最佳解。
6.1.1混合式局部搜寻方法(Hybrid Local Search Method)
一个混合式基于离散性(discrete-based)的局部搜寻法(从一个起始点开始来找寻离散最佳化问题(4-3)的局部最佳解),如下表示:
给予:一个起始点x0。
目的:可靠的计算出一局部最佳解。
步骤一、从一个起始点x0开始,针对离散性最佳化问题(4-3),运用一个有效的局部反复修正算法(iterative improvement)。
步骤二、如果局部搜寻算法收敛到一个局部最佳解,停止执行;否则到下一个步骤执行。
步骤三、使用最佳邻域搜寻法(Best neighborhood search method),从x0开始,持续搜寻几个步骤后,记录最后一点为终端点。以终端点当作起始点,执行步骤一。
6.1.2计算出口点的方法
我们接下来说明如何在离散性最佳化问题(4-3)中,从已知的局部最佳解xs开始,沿着搜寻路径计算出口点。我们注意到搜寻路径ψt(xs)经过xs,是一条由t变量参数化的曲线ψ0(xs)=xs,且搜寻路径ψt(xs)对所有的t而言,系位于搜寻空间(解的空间)中。
在离散性最佳化问题(4-3)中,从已知的局部最佳解开始,沿着搜寻路径计算出口点的方法称之基于离散性(discrete-based)的出口点搜寻法,如下表示:
给予:一个已知的局部最佳解xs,预定的搜寻路径,以及相关的离散动态系统(6-5)。
目的:预定的搜寻路径及系统(6-5)的一个局部最佳解(稳定固定点)xs,计算出另一个局部最佳解。
从已知的局部最佳解xs开始,沿着预定的搜寻路径移动,直到最佳化问题(4-3)目标函数达到第一局部最大值的点上,则此点为出口点。
6.1.3基于离散性动态分解点的方法
在最佳化问题(4-3)中,从已知的局部最佳解xs开始,我们发展计算动态分解点的方法称之为基于离散性动态分解点搜寻法,其xs点是相对位于系统(6-5)内预定的搜寻路径的稳定固定点上,如下表示:
给予:一个离散性最佳化问题(4-3),其已知的局部最佳解xs,及预定的搜寻路径。
目的:由预定的搜寻路径及离散动态系统(6-5),计算出相对应的动态分解点。
步骤一、从已知的局部最佳解xs开始,沿着预定的搜寻路径移动,侦测到出口点,将出口点设为xex。
步骤二、从xex开始,应用最佳邻域搜寻方法,向前移动xex一时间步骤到新点xc。
步骤三、执行下列的射线调整过程并计算DDP点:
(i)构成一条射线,连接xs、xc。
(ii)如向量(xs-xex)及(xc-xex)有表达式,则执行(ii)(a)。;否则执行取代(ii)(a)的另一步骤。
(a)计算向量(xs-xex)及(xc-xex)的夹角ε。如果ε接近0°或180°,则xex是动态分解点并停止过程:否则执行下一步骤。
(取代步骤(a)的步骤)修正搜寻路径使得现有的xex落于修正后的路径上,检查xex、xc与xs是否在同一修正后的路径上。如果是的话,xex是动态分解点并停止过程;否则执行下一步骤。
(iii)调整xc到射线上(从xs开始)最大目标函数值的点,设为x′c。如果x′c跟xex非常接近,则x′c是动态分解点并停止执行;否则执行下一步骤。
步骤四、把xc′当作出口点(xc′→xex),执行步骤二。
6.1.4搜寻另一个局部最佳解的基于出口点的方法
对最佳化问题(4-3),我们发明一个从一个已知的局部最佳解xs开始来搜寻到另一个局部最佳解的方法,称之为基于离散性、且以出口点为基础的方法,如下表示:
给予:一个最佳化问题(4-3)其已知的局部最佳解xs,及预定的搜寻路径。
目的:搜寻到最佳化问题(4-3)的另一个局部最佳解。
步骤一、从一个已知的局部最佳解xs开始,沿着预定的搜寻路径移动,运用基于离散性的方法计算非线性动态系统(6-5)的出口点。如出口点被找到,以xex表示继续下一步;否则停止执行。
步骤二、从找到的xex开始,沿着预定的搜寻路径(由xs开始)向前移动一步至x0(或以x0=xs+(1+ε)(xex-xs)表示,如表示式存在且ε为一极小值)。
步骤三、从x0开始,运用一个最佳邻域搜寻法求得接口点xinf。在此接口点运用一个有效的混合式局部搜寻法来找局部最佳解,其效果是会优于用最佳邻域搜寻法来求解局部最佳解。
步骤四、从此接口点xinf开始,运用步骤三所选的有效混合式局部最佳搜寻法来搜寻到一个毗连的局部最佳解。
6.1.5搜寻另一个局部最佳解的基于动态分解点的方法
在最佳化问题(4-3)中,我们发明从一个已知的局部最佳解来搜寻到另一个局部最佳解的方法,称之为基于离散性、且以基于动态分解点的方法,如下表示:
给予:一个最佳化问题(4-3)其已知的局部最佳解xs,及预定的搜寻路径。
目的:搜寻到最佳化问题(4-3)搜寻路径中的另一个局部最佳解。
步骤一、从一个已知的局部最佳解xs开始,沿着预定的搜寻路径移动,运用基于离散性的方法计算动态分解点。如动态分解点被找到,以xddp表示继续下一步;否则停止执行。
步骤二、从找到的DDP点开始,沿着预定的搜寻路径(由xs开始)向前移动一步至x0(或以x0=xs+(1+ε)(xddp-xs)表示,如表示式存在,且ε为一极小值)。
步骤三、从x0开始,运用一个最佳邻域搜寻法来求得接口点xinf。在此接口点运用一个有效的混合式局部搜寻法来找局部最佳解,其效果是会优于用最佳邻域搜寻法来求解局部最佳解。
步骤四、从此接口点xinf开始,运用步骤三所选的有效混合式局部最佳搜寻法来搜寻到一个毗连的局部最佳解。
6.1.6搜寻所有阶层一(tier-one)的局部最佳解的基于离散性的方法
在最佳化问题(4-3)中,我们发明从一个已知的局部最佳解来搜寻到所有阶层一(tier-one)的局部最佳解的方法。
给予:最佳化问题(4-3),一个已知的局部最佳解xs 0。
目的:搜寻到局部最佳解xs 0所有阶层一(tier-one)的局部最佳解。
步骤一:设定所有阶层一(tier-one)的局部最佳解集合
以及定义一组xs 0的搜寻路径Si,i=1,2,..,m.设i=1。
步骤二:从一个已知的局部最佳解xs 0开始,沿着预定的搜寻路径移动,运用基于离散性且以出口点为基础的方法(或基于离散性且以动态分解点为基础的方法)寻找最佳化问题(4-3)的一个局部最佳解(此解是相对位于非线性动态系统(6-5)的一个稳定固定点)。如局部最佳解被找到,以xs i表示继续下一步;否则执行步骤四。
步骤三:检查xs i是否曾被找到(xs i∈Vs),如果尚未曾被找到过则设
步骤四:设i=i+1。
步骤五:重复执行步骤二到步骤四,直到i>m。
步骤六:输出xs 0所有阶层一(tier-one)的局部最佳解Vs。
6.1.7搜寻所有局部最佳解的基于动态离散性的方法
在离散性最佳化问题(4-3)中,我们发明一个从一个已知的局部最佳解来搜寻到所有局部最佳解的方法。
给予:一个最佳化问题(4-3)的起始点x0(可以是任何点)。
目的:(i)搜寻到离散性最佳化问题(4-3)中的所有的局部最佳解。
(ii)搜寻离散性最佳化问题(4-3)中的全局最佳解。
步骤一:以起始点x0开始应用一个有效的(混合式)搜寻方法,来寻找一个局部最佳解xs 0。
步骤二:设j=0,局部最佳解集合
阶层j(tier-j)的局部最佳解集合
步骤三:设阶层j+1的局部最佳解集合
步骤四:对在Vnew j中的每一个局部最佳解xs j,寻找它所有阶层1的局部最佳解。
(i)定义xs j的一组搜寻路径Si j i=1,2...,mj,设i=1。
(ii)从一个已知的局部最佳解xs j开始,沿着预定的搜寻路径移动,运用基于离散性且以出口点为基础的方法(或基于离散性且以动态分解点为基础的方法)寻找最佳化问题(4-3)的一个局部最佳解(此解是相对位于非线性动态系统(6-5)的一个稳定固定点)。如局部最佳解被找到,以xs,j i表示继续下一步;否则执行步骤(iv)。
(iii)检查xs,j i是否以前被找过,即xs,j i∈Vs,如果它尚未被找过,设 及
(iv)设i=i+1。
(v)重复执行(ii)到(iv),直到i>mj。
步骤五:检查最新计算的局部最佳解集合Vnew j+1,如果是空集合,执行步骤六;否则设j=j+1,并执行步骤三。
步骤六:输出所有的局部最佳解集合Vs,藉由比较Vs集合中所对应的目标函数值,选择其中一个具有最小值的最佳解,输出此点为全局最佳解。
6.2基于连续性的动态方式
在下文中,我们发展一个基于连续性的动态方法来解决无限制条件离散性最佳化问题(4-3),其目标函数具有可分析式的封闭模式。这方法基本是先于一个等效的连续性最佳化问题空间中求解,然后如有必要再于离散性状态空间中求解。另对有黑盒模式的最佳化问题(4-3),使用以这种连续特性为基础的方法是有条件性的,在下文中我们将予以说明。
等效方法(Equivalent Approach)
我们首先将无限制条件离散性最佳化问题(4-3)的搜寻空间转换成欧氏空间(Euclidean space)中等效的连续性最佳化问题模式:
最小化UCeq(x) x∈Rn (6-6)
此处UCeq(x)是定义在欧氏空间(Euclidean space)Rn中的一个连续函数,n是状态空间S的自由度(degree of freedom),我们认为转换工作必须满足下列两指导方针:
(G1)最佳化问题(4-3)和等效最佳化问题(6-6)两者有共同的全局最佳解(即x∈S是UC(x)的全局最佳解,若且唯若x∈Rn是UCeq(x)的全局最佳解)。
(G2)最佳化问题(4-3)和等效的最佳化问题(6-6)两者尽可能有许多(as many as possible)共同的局部最佳解。
在转换后,我们能藉由解等效性(equivalent)非线性最佳化问题(6-6)的全局最佳解,来搜寻最佳化问题(4-3)的全局最佳解。因此,那些在一般非线性最佳化问题(6-6),求解局部最佳解及全局最佳解的技术,能被应用来解决离散性最佳化问题(4-3)。
在满足前述二指导方针的充分条件下,我们首先建构一个等效函数(equivalent functions),详述如下:
附加调节器的转换(Transformation by appending a modular)
等效的目标函数UCeq(x)可建构成:
此处
以及L是原目标函数UC(x)的Lipschitz常数。
该变换技术有助于将离散性优化问题(4-3)变换成连续性优化问题(6-7)。如果UC(x)是可微分的,则该变换具有在任意状态空间上可微分的优点。其计算过程容易且直接,同时对该变换的理论分析也是可能的。可以证明UCeq(x)是一个连续函数,并且UCeq(x)具有与原始问题(4-3)一样的全局最佳解。然而,该变换可能会引入新的不属于原始问题的局部最佳解。在通过计算变换后的问题(6-7)的局部最佳解来寻找全局最佳解的过程中,该缺点导致大量的额外计算负担。并且,该变换只能用于那类具有解析的闭合形式目标函数的离散性最优化问题(4-3)。
在本发明知此一实施例之中,我们另外发展出一个新的转换方式,它同样的满足指导方针(G1)和(G2)。
分段式线性转换(Piecewise Linear Transformation)
其转换如下:
此处dist(x,y)是x和y间的距离。在大部份的情形下,系以欧氏距离(Euclidean distance)表示,x=(x1,x2...,xn)∈Rn 表示大于或等于xi的最小整数,
表示小于或等于xi的最大整数。该变换具有下列显著特性。
特性1:Ceq(x)几乎处处连续。
引理1:给定一点x0以及它的单向邻域点x1。定义一个由单位开盒构成的连通区域,该单位开盒由(x0,x1)和两点x0及x1描述。则x0或x1是变换后的目标函数Ceq(x)在该连通区域上的最大点或最小点。
特性2:UCeq(x)的局部最佳解与原始问题(4-3)关于单向扩展邻域(OWEN)的局部最佳解相等。
特性3:UCeq(x)具有与原始优化问题(4-3)相同的全局最佳解。
上述得到的特性表明我们所发展的变换能够满足指导方针(G1)和(G2)。特性2说明变换后的问题具有的局部最佳解不比原始问题的多。实际上,变换后的问题的局部最佳解是原始问题关于单向扩展邻域,的局部最佳解,而不是关于直接邻域的。变换后的问题通常具有比原始问题(4-3)少的局部最佳解。这是一个显著的特点,它能通过忽略浅度的局部最佳解来降低用以搜寻全局最佳解所需的运算量。该变换为我们运用我们的基于DDP的方法来有效解决离散性问题提供了途径。特性3说明变换后的问题和原始问题具有相同的全局最佳解。在本发明中,转换方式系运用最佳化问题(4-3)中,其目标函数为可分析式的封闭模式。此转换方式也可运用在目标函数是黑盒模式的最佳化问题(4-3)中,只要于状态空间中任二点的距离是明确定义的。
延伸的方式(Extended Approach)
我们到目前为止是集中焦点在(经转换)基于连续性的动态方式。另外一个基于连续性的动态方式乃是保持目标函数不变,离散状态空间(即搜寻空间)直接延伸成为连续状态空间。此问题被称为延伸的连续性最佳化问题。
最小化UC(x) (6-9)
这目标函数UC∶Rn→R具有一个封闭模式的表示式,n是状态空间S中的自由度,此搜寻空间是连续性的。明显的原问题(4-3)的最佳解和延伸的问题(6-9)是有不同的,但彼此之间在实际问题中可能是不会相隔太远地。
经由第一阶段求解延伸性问题(6-9)后,我们可在第二阶段利用第一阶段所求得的近似解当成起始条件来求解原最佳化问题(4-3)。从这二状态程序所求得的解将会是原最佳化问题(4-3)的局部最佳解。
我们注意到最佳化问题(4-3),其离散性目标函数经由转换产生等效系统(6-6),是具有与最佳化问题(4-3)相同的解空间。对于在目标函数不变状态下,离散性最佳化问题(4-3)转换后所产生的延伸状态空间(也就是一连续的状态空间)(6-9),如同系统(6-6)可表达为:
最小化UC(x) (6-10)
此处UC∶Rn→R是一个封闭模式的目标函数。n是解的状态空间S中的自由度。此解的空间是连续的。
转换后的最佳化问题(6-10)是属于非限制条件连续性最佳化问题(4-1)中的一部份。针对最佳化问题(6-10),建构满足章节5(LC1)-(LC3)条件的非线性动态系统。我们可以下列一般通式表达:
我们将会发展动态方法用来系统地计算离散性最佳化问题(4-3)所有的局部最佳解,其运用连续性的方式来求解等效的最佳化问题(6-6)或延伸的最佳化问题(6-9),它们的一般通式表达如(6-10)。
6.2.1混合式局部搜寻方法
一个混合式的局部搜寻法,从一个起始点开始(在一个连续的空间中)来找寻无限制条件离散性最佳化问题(4-3)的局部最佳解,如下表示:
给予:一个起始点x0。
目的:可靠的搜寻无限制条件离散性最佳化问题(4-3)的一个局部最佳解。
步骤一、从一个起始点x0开始,针对无限制条件离散性最佳化问题(4-3),运用一个有效的局部搜寻法。
步骤二、如果局部搜寻算法收敛到一个局部最佳解,执行步骤四;否则设最后一点为终端点。以终端点当作起始点,执行下一步骤。
步骤三、用x0当做起始条件,对非线性系统(6.11)在几个时间步距处进行积分,获得最后一点为终端点。以终端点当作起始点,执行步骤一。
步骤四、(针对延伸的方式)将计算所得的连续性局部最佳解xs,产生m(=2)个最接近的可行点集合xs1′,...,xsm′。至此有二方案可供选择;一为选择最小值的点为局部最佳解并停止执行。或另用此可行点集合当作初值点,继续至步骤五执行。
步骤五:(针对延伸的方式)针对每个初值点运用最佳最好邻域搜寻方法来分别求得m个xs1,...,xsm个局部最佳解,从其中选择最小值的点为原问题(4-3)局部最佳解。
6.2.2计算出口点的基于连续性的方法
一个基于连续性的方法,运用连续性动态系统(6-11),从一个起始点开始(在一个连续的空间中)来找寻所对应的出口点,称之为出口点搜寻法,如下表示:
给予:离散性最佳化问题(4-3)的一个已知局部最佳解xs,预定的搜寻路径,以及相关的非线性连续性动态系统(6-11)。
目的:由预定的搜寻路径及系统(5-7)的稳定平衡点xs,计算出所对应动态系统(6-11)的出口点。
从已知的局部最佳解xs开始,沿着预定的搜寻路径移动,直到连续性目标函数(6-10)达到第一局部最大值的点上,则此点为出口点。
本发明另外提出一个计算出口点的方法:从xs开始,延着搜寻路径移动,计算搜寻路径的导数和非线性动态系统(6-11)向量场在每个时间点的内积值,当内积值正负符号变更时(由正到负),则表示已寻找到出口点在[t1,t2]间。然后运用在t1或t2时的搜寻路径的所得到的点来趋近出口点。
6.2.3计算动态分解点的方法
在最佳化问题(4-3)中,给予已知的局部最佳解xs,我们发展一个计算动态分解点的方法称之为基于连续性的动态分解点搜寻法,其xs点是相对位于动态系统(6-11)的稳定平衡点,如下表示:
步骤一、从已知的局部最佳解xs开始,沿着预定的搜寻路径t(xs)移动,侦测到出口点,此点位于动态系统(6-11)稳定平衡点(也就是局部最佳解xs)的准稳定边界上(quasi-stability boundary),设出口点为xex。
步骤二、从xex开始,应用下述步骤找寻最小距离点,简称MDP:
(i)以出口点xex为起始条件,对非线性系统(6-11)在几个时间步距(time-steps)处进行积分;设终端点为目前出口点(current exit point)。
(ii)连接轨迹上的目前出口点和局部的最佳解(也就是稳定平衡点)成一直线,沿着此直线从稳定平衡点找寻目标函数(6-10)的第一局部最大的点,视其为修正出口点xex,并以此点代替目前的点,指定这个点为出口点xex。
(iii)重复执行(i)及(ii),直到在(ii)中所获得的出口点,其向量场平均值(norm of vector field)(6-10)是小于一个临界值,也就是数值‖Fu(xex)‖≤ε。那么这点被视为最小距离点,简称MDP。
步骤三、以MDP xd 0为起始点,求解系统(6-11)其非线性代数方程式FU(x)=0。设其解为xddp,则xddp是针对于动态系统(6-11)的稳定平衡点xs和搜寻路径t(xs)的动态分解点。
6.2.4搜寻另一个局部最佳解的基于出口点的方法
从最佳化问题(4-3)中,已知的局部最佳解xs开始,我们发明一个从一个已知的局部最佳解来搜寻到另一个局部最佳解的方法,称之基于出口点的方法。
给予:一个最佳化问题(4-3),其已知的局部最佳解xs。
目的:搜寻到最佳化问题(4-3)的另一个局部最佳解。
步骤一、从一个已知的局部最佳解xs开始,计算非线性动态系统(6-11)的出口点xex。
步骤二、设x0=xs+(1+ε)(xex-xs)其中ε为一极小值。
步骤三、从x0开始,对非线性系统(6-11)进行积分以获得一条轨迹且求得接口点xinf。在此接口点运用一个有效的混合式局部搜寻法来找局部最佳解,其效果是会优于用轨迹来求解局部最佳解。
(取代步骤三的步骤)、将x0点调向新的点x′0(远离xs,但接近(xep-xs)的方向)。由x′0开始运用最佳邻域搜寻法,可获得一条系统轨迹且求得接口点xinf。在此接口点运用一个有效的混合式局部搜寻法,其结果是会优于最佳邻域搜寻法。
步骤四、从此接口点xinf开始,运用步骤三针对问题(4-3)所选的有效混合式局部搜寻法来搜寻到一个毗连的局部最佳解。
6.2.5搜寻另一个局部最佳解的基于动态分解点的方法
在最佳化问题(4-3)中,我们发明一个从一个已知的局部最佳解来搜寻到另一个局部最佳解的方法,如下表示:
给予:最佳化问题(4-3)一个其已知的局部最佳解xs,和一条给定的搜寻路径。
目的:搜寻到最佳化问题(4-3)另一个局部最佳解。
步骤一、从一个已知的局部最佳解xs开始并沿着给定搜寻路径,运用系统(6-11)来计算所对应动态分解点xddp。
步骤二、设x0=xs+(1+ε)(xddp-xs),其中(如表示式存在)ε为一极小值。
步骤三、从x0开始,对非线性系统(6-11)进行积分以获得一条轨迹且求得接口点xinf。在此接口点运用一个有效的混合式局部搜寻法来找局部最佳解,其效果是会优于用轨迹来求解局部最佳解。
(取代步骤三的步骤)、将x0点调向新的点x′0(远离xs,但接近(xddp-xs)的方向)。由x′0开始运用最佳邻域搜寻法,可获得一条系统轨迹并求得接口点xinf。在此接口点运用一个有效的混合式局部搜寻法,其结果是会优于最佳邻域搜寻法。
步骤四、从此接口点xinf开始,运用步骤三针对问题(4-3)所选的有效混合式局部搜寻法来搜寻到一个毗连的局部最佳解。
6.2.6以动态的方法来搜寻到所有阶层一(tier-one)的局部最佳解。
在最佳化问题(4-3)中,我们发展二个基于连续性的方法,(从一个已知的局部最佳解)来搜寻到所有阶层一(tier-one)局部最佳解的方法。第一个是基于连续性且以出口点为基础的方法(或基于离散性且以动态分解点为基础的方法
基于连续性且以出口点为基础的方法
给予:离散性最佳化问题(4-3)一个其已知的局部最佳解xs 0。
目的:搜寻到离散性最佳化问题(4-3)局部最佳解xs 0所有阶层一(tier-one)的局部最佳解。
步骤一:设定所有阶层一(tier-one)的局部最佳解集合
以及定义一组xs 0的搜寻路径Si,i=1,2,...,m.设i=1。
步骤二:从一个已知的局部最佳解xs 0开始,沿着给定的搜寻路径Si移动,寻找局部最佳解。
(i)运用系统(6-11)及基于出口点的方法来寻找另一个局部最佳解。如局部最佳解被找到,以xs i表示继续下一步;否则执行(iii)。
(ii)检查xs i是否曾被找到(xs i∈Vs),如果尚未曾被找到过则设
(iii)设i=i+1。
(iv)重复执行步骤(i)到步骤(iii),直到i>m。
步骤三:输出xs 0所有阶层一(tier-one)的局部最佳解Vs。
基于离散性且以动态分解点为基础的方法
给予:离散性最佳化问题(4-3)一个其已知的局部最佳解xs 0。
目的:搜寻到离散性最佳化问题(4-3)局部最佳解xs 0所有阶层一(tier-one)的局部最佳解。
步骤一:设定动态分解点集合Vddp={φ},所有阶层一(tier-one)的局部最佳解集合
步骤二:,定义一组xs 0的搜寻路径Si,i=1,2,...,m.设i=1。
步骤三:从一个已知的局部最佳解xs 0开始,沿着预定的搜寻路径Si移动,寻找局部最佳解。
(i)运用系统(6-11)及找寻动态分解点的方法来寻找动态分解点。如动态分解点被找到,以xddp,i表示继续下一步;否则执行(vi)。
(ii)检查xddp,i是否曾被找到(xddp,i∈Vddp),如果曾被找到过则执行(vi),否则设Vddp=Vddp∪{xddp,i}继续执行(iii)。
(iii)设x0,i=xs+(1+ε)(xddp,i-xs),其中(如表示式存在)ε为一极小值。
(iv)从x0,i开始,对非线性系统(6-11)进行积分以获得一条轨迹且求得接口点xinf,i。在此接口点运用一个有效的混合式局部搜寻法来找局部最佳解,其效果是会优于用轨迹来求解局部最佳解。
(取代步骤(iv)的步骤)将x0,i点调向新的点x′0,i(远离xs 0,但接近(xddp,i-xs 0)的方向)。由x′0,i开始运用最佳邻域搜寻法,可获得一条系统轨迹并求得接口点xinf。在此接口点运用一个有效的混合式局部搜寻法,其结果是会优于最佳邻域搜寻法。
(v)从此界面点xinf,i开始,运用步骤(iv)对问题(4-3)所选的有效混合式局部搜寻法来搜寻对应xddp,i的一个毗连的局部最佳解。
(vi)设i=i+1。
(vii)重复执行步骤(i)到步骤(vi),直到i>m。
步骤四:输出xs 0所有阶层一(tier-one)的局部最佳解Vs。
6.2.7搜寻到所有的局部最佳解的方法
在离散性最佳化问题(4-3)中,我们发明二个动态方法,(从一个已知的局部最佳解)来搜寻到所有的局部最佳解的方法。第一个是基于连续性,根据出口点的方法,第二个是基于连续性,根据动态分解点的方法。
基于连续性且以出口点为基础的方法
给予:一个最佳化问题(4-3)的起始点x0(可以是任何点)。
目的:(i)搜寻离散性最佳化问题(4-3)所有的局部最佳解。
(ii)搜寻离散性最佳化问题(4-3)的全局最佳解。
步骤一:以起始点x0开始应用一个有效的(混合式)搜寻方法,来寻找离散性最佳化问题(4-3)中的一个局部最佳解xs 0。
步骤二:设j=0,初始化局部最佳解集合
阶层j(tier-j)的局部最佳解集合
步骤三:设阶层j+1的局部最佳解集合
步骤四:对在Vnew j中的每一个局部最佳解xs j,寻找它所有的局部最佳解。
(i)定义xs j的一组搜寻路径Si j i=1,2...,mj,设i=1。
(ii)从一个已知的局部最佳解xs j开始,运用基于出口点的方法寻找另一个局部最佳解。如局部最佳解被找到,以xs,j i表示继续下一步;否则执行步骤(iv)。
(iii)检查xs,j i是否以前被找过,即xs,j i∈Vs,如果它尚未被找过,设 及
(iv)设i=i+1。
(v)重复执行(ii)到(iv),直到i>mj。
步骤五:检查最新计算的局部最佳解集合Vnew j+1,如果是空集合,执行步骤六;否则设j=j+1,并执行步骤三。
步骤六:输出所有的局部最佳解集合Vs。藉由比较Vs集合中所对应的个别目标函数值,选择其中一个有最小目标函数值的最佳解,输出此点为全局最佳解。
以动态分解点为基础的方法
给予:一个最佳化问题(4-3)的起始点x0(可以是任何点)。
目的:(i)搜寻到离散性最佳化问题(4-3)所有的局部最佳解。
(ii)搜寻离散性最佳化问题(4-3)中的全局最佳解。
步骤一:以起始点x0开始应用一个有效的混合式搜寻方法,来寻找离散性最佳化问题(4-3)的一个局部最佳解xs 0。
步骤二:设j=0,初始化局部最佳解集合
阶层j(tier-j)的局部最佳解集合
及动态分解点集合Vddp={φ}。
步骤三:设阶层j+1的局部最佳解集合
步骤四:对在Vnew j中的每一个局部最佳解xs j,寻找它所有的局部最佳解。
(i)定义xs j的一组搜寻路径Si j i=1,2...,mj,设i=1。
(ii)对从xs j开始的每条搜寻路径Si j,运用系统(6-11)及找寻动态分解点的有效方法寻找动态分解点。如动态分解点被找到,以xddp,i j表示继续下一步;否则执行(vii)。
(iii)检查xddp,i j是否曾被找到(xddp,i j∈Vddp),如果曾被找到过则执行(vi),否则设
继续执行(iv)。
(iv)设
其中(如表示式存在)ε为一极小值。
(v)从x0,i j开始,对非线性系统(6-11)进行积分以获得一条轨迹且求得接口点xinf,i。在此接口点运用一个有效的混合式局部搜寻法来找局部最佳解,其效果是会优于用轨迹来求解局部最佳解。
(替代步骤(v)的步骤)将x0,i j点调向新的点x′0,i j(远离xs j,但接近(xddp,i j-xs j)的方向)。由x′0,i j开始运用最佳邻域搜寻法可获得一条系统轨迹并求得接口点xinf。在此接口点运用一个有效的混合式局部搜寻法,其结果是会优于最佳邻域搜寻法。
(vi)从此界面点xinf,i j开始,运用步骤(v)对问题(4-3)所选的有效混合式局部搜寻法来搜寻一个毗连的局部最佳解xs,j i。
(vii)检查xs,j i是否以前被找过,即xs,j i∈Vs,如果它尚未被找过,设 及
(viii)设i=i+1。
(ix)重复执行(ii)到(vii),直到i>mj。
步骤五:检查最新计算的局部最佳解集合Vnew j+1,如果是空集合,执行步骤六;否则设j=j+1,并执行步骤三。
步骤六:输出所有的局部最佳解集合Vs,藉由比较Vs集合中所对应的个别目标函数值,选择其中一个具有最小目标函数值的最佳解,输出此点为全局最佳解。
7.解决有限制条件离散性最佳化问题的动态方法
下文系说明本发明解决在有限制条件下离散性最佳化问题(4-4)的动态方法。
解决有限制条件离散性最佳化问题(4-4)的困难是决定于目标函数C(x)的结构,解的空间S及可行解集合(feasible set)FS三者。
对于一个离散性最佳化问题(4-4),运用一个局部搜寻法(local searchalgorithms)试着将现行解xk∈FS移向围绕在xk的邻域集合N(xk)中一个较佳解,步骤说明如下:
步骤一:初始:选一个始起点x1和设定循环计次数k=1。
步骤二:修正:考虑局部修正集合{x∈FS∩N(xk)∶C(x)<C(xk)},N(xk)是环绕在xk的邻域。如果N(xk)是空集合,即停止并把xk当作邻域N(xk)的局部最佳解;否则选择N(xk)邻域的其中一员视为xk+1,设定k=k+1,重复此步骤。
针对一个局部搜寻算法,存有三个问题。
(i)N(x)邻域的定义。
(ii)从集合(x∈FS∩N(xk)∶C(x)<C(xk)}中,如何选择xk+1的机制。
(iii)如何找到步骤一的第一个起始可行解?
前二个问题是与无限制条件离散性最佳化问题(4-3)相似的。为处理限制条件的特性,最佳邻域搜寻方法被修正为有限制条件的最佳邻域搜寻方法,只是从可行邻域集合(a set of feasible neighbors此邻域是满足限制条件)中选择一个目标函数有最大下降的解为xk+1。同样地,较佳邻域搜寻方法被修正为有限制条件的较佳邻域搜寻方法,只是从可行邻域集合(a set of feasibleneighbors此邻域是满足限制条件)中选择第一个目标函数有下降的解为xk+1。因此运用有限制条件的最佳邻域搜寻方法或有限制条件的较佳邻域搜寻方法,我们可得到xk+1∈FS。
针对第三个问题,当完全不知任何可行解时,我们可采用下列步骤来找寻一个可行解:
步骤一:初始:选一个始起点x1并检查x1∈FS?:如是属于则停止执行,并用吾人所找到的可行解开始局部搜寻;否则设定循环计次数k=1。
步骤二:可行性的修正:考虑非可行性的修正集合{x∈N(sk)∶d(x)<d(xk)},函数d(x)是测量x解的非可行性(infeasibility)。如果N(xk)是空集合,停止执行并发出警告讯息说明无可行解。但如存在x*∈N(xk)及d(x*)=0则停止执行,且x*为一个可行解。否则选择N(xk)邻域的其中一员视为xk+1,设定k=k+1,重复此步骤。
限制条件下空间求解方式(Constrained solution-space approach)
为求解有限制条件离散性最佳化问题(4-4),我们发展数个动态方法,其依据限制条件下空间求解方式,详如下述三阶段:
阶段一:在一个可行单位元集合中求解出一个局部最佳解。
阶段二:在这可行单位元集合中求解出所有的局部最佳解。
阶段三:寻找另一个可行单位元。如果无法找到则停止执行,否则执行阶段二。
我们之所以称此为限制条件下空间求解方式,系因搜寻局部最佳解的工作是仅在解空间的可行单位元中进行。
在此我们为解决有限制条件离散性最佳化问题(4-5),发展一个基于离散性的动态方法,其目标函数C∶S→R可为封闭模式或黑盒模式,其限制函数向量(constraint function vector)G∶S→Rm是为封闭模式。这个基于离散性的动态方法,在阶段二我们发展出一个基于离散性的方法,来在可行单位元集合中求解出所有的局部最佳解。这动态方法,在阶段三我们发展出一个基于连续性的方式,来寻找出所有的可行单位元。
不失一般特性,我们考虑下述最佳化问题(含等式限制式):
最小化C(x) (7-1)
受到下列限制
hi(x)=0,i∈I={1,2,...,l} (7-2)
一般情形,下列的可行集合或称为可行单位元
为平滑流形(smooth manifold)。大体上,这集合M是非常复杂,包含不连合但路径连接的可行单位元;换句话说,可行区域M能被分解成几个不连合但路径连接的可行单位元,如
此处每个Mk都是路径连接的可行单位元。每个可行单位元可能包含了有限制条件最佳化问题(7-1)的几个局部最佳解。
在阶段二我们提出一基于离散性的动态方法来找寻位于每个可行单位元中的所有的局部最佳解。同样地这基于离散性的方法是可解决无限制条件离散性非线性最佳化问题(4-3)。其所运用的离散性动态系统如下:
xk+1=f(xk) (7-3)
其中系统(7-3)的解xk∈S空间是离散的。离散性动态系统满足第六章节中所述的(LD1)-(LD3)条件。在本发明中,我们系发展出一个基于离散性动态系统(7-3)的动态轨迹方法,用以有系统地搜寻最佳化问题(4-5)中某一个可行单位元所有的局部最佳解。
7.1找寻一个可行点的方法
在本发明中,我们引用一个动态轨迹为基础的方法,其被描述在发明人江晓东于2001年五月四日所申请的美国专利第09/849,213号”DYNAMICALMETHOD FOR OBTAINING GLOBAL OPTIMAL SOLUTION OF GENERALNONLINEAR PROGRAMMING PROBLEMS”中,该专利申请在此合并作为本案的参考。此方法是依据某些轨迹(trajectories)有系统地搜寻问题(7-2)中的所有可行单位元,轨迹型式如下:
来建置如此的非线性动态系统以达成目的,此系统必须满足下列二条件:
(g1)每个系统(7-4)的轨迹必须收敛,而且收敛到其中一个平衡流形;和
(g2)一个集合是此系统(7-4)的一个稳定平衡流形,若且唯若这集合是限制条件方程式(7-2)的一个可行单位元。
本发明举例说明一个满足条件(g1)及(g2)的非线性动态系统,用以找寻所有的可行单位元,叙述如下:
此处向量H(x)=(h1(x),h2(x),...,hm(x))T是定义此最佳化问题其可行区域的限制向量。
我们发明二个方法,来找寻一个可行点(feasible point)。第一个方法是以动态轨迹为基础(trajectory-based)的方法,第二个方法则是混合式局部搜寻(hybrid local search)方法。
动态轨迹为基础(trajectory-based)的方法
我们接着说明从一不可行点(infeasible point)找寻一个可行单位元的方法。
给予:一个不可行点x0(可以是任何点)。
目的:搜寻到满足限制条件方程式(7-3)的一个可行点。
从给定起始点x0开始,对动态系统(7-4)在几个时间步距处进行积分并找寻收敛的一点(它是位于稳定平衡流形),此点是(7-2)的可行点。
混合式局部搜寻(hybrid local search)方法
我们接着提出一个混合式的方法,此方法配合已轨迹为基础(trajectory-based)的方法(全局收敛特性)及一个局部搜寻法(快速特性),来找寻满足限制条件方程式(7-3)的一个可行点。
给予:一个不可行点x0(可以是任何点)。
目的:搜寻到满足限制条件方程式(7-3)的一个可行点。
步骤一:从给定起始点x0开始,运用一个有效的局部反复修正(局部搜寻)算法。如果它收敛(即如果它找到一个可行点),那么停止;否则执行步骤二。
步骤二:从给定起始点x0开始,对动态系统(7-4)在几个时间步距处进行积分而得到终点,如果它的轨迹收敛(即如果它找到一个可行点),那么停止;否则将此终点更新为新的起始点x0,执行步骤一。
7.2一个局部搜寻方法
接着我们说明从一不可行点(infeasible point)利用Lagrange-based方法找寻离散性最佳化问题(4-5)的一个局部最佳解。
藉由slack变数y,我们可将不等限制式转换成等式限制式,如下说明:
g(x,y)=G(x)+y2=0 (7-6)
一个Lagrangian函数如下:
L(x,λ)=c(x)+λTg(x,y) (7-7)
如(x*,λ*)是Lagrange函数(7-7)的马鞍点(saddle point),则x*是离散性最佳化问题(4-5)的一个局部最佳解。其中梯度运算差(a difference gradientoperator)ΔxL(x,λ)定义如下:
因此,ΔxL(x,λ)总是指向目标函数下降的方向,ΔxL(x,λ)移动x点至其邻域有较低L(x,λ)值的一点x′。如果此x′点不存在则ΔxL(x,λ)=0。
依据此定义,ΔxL(x,λ)可表示成:
我们注意到ΔxL(x,λ)不是唯一性,而是指向一个有较佳邻域的方向。我们可用greedy搜寻方向(最佳邻域搜寻方向)或梯度下降方向(gradient decentdirection)为ΔxL(x,λ)的方向。
然后我们设立一个离散性Lagrange-based修正规则:
xk+1=xk+ΔxL(xk,λk)
λk+1=λk+U(k) (7-9)
其中U(k)定义如下:
此处λi(K)是一个非负的调整因子(non-negative adjustment factor),用来驱动搜寻方向远离前一个不适者。举例说λi(K)可设为1。
slack变数y可设定如下:
接着我们用一个离散性Lagrange-based方法来搜寻有条件离散性最佳化问题(4-4)的一个局部最佳解。
给予:一个不可行点x0(可以是任何点)。
目的:搜寻到满足限制条件离散性最佳化问题(4-4)的一个局部最佳解。
步骤一:从给定起始点x0开始(可能不满足部份限制条件)。
步骤二:经由下述步骤找寻一个局部最佳解:
(i)设k=1。
(ii)计算(7-10)式的U(k)。如果x0在可行单位元中,则用有限制条件较佳邻域搜寻方向(constrained better neighborhood direction)及式(7-8)来计算ΔxL(x,λ);否则用原解空间的较佳邻域搜寻方向来计算ΔxL(x,λ)。
(iii)如果U(k)及ΔxL(x,λ)为非常小的值,则现存点x0为局部最佳解;否则修正x及λ并执行下一步。
(iv)设k=k+1。
(v)以预定的递回次数,重复执行步骤(ii)至步骤(iv)。
7.3混合式局部搜寻(hybrid local search)方法
一个混合式局部搜寻方法,从给定的可行起始点开始,来找寻限制条件离散性最佳化问题(4-5)的一个局部最佳解。
给予:一个可行点x0(位于可行单位元中)。
目的:搜寻到可行单位元中的一个可行点。
步骤一:从给定起始点x0开始,运用一个有效的局部反复修正(iterativeimprovement local search algorithms)算法,求解有限制条件离散性最佳化问题(4-5)。
步骤二:如果局部搜寻法收敛到一个局部最佳解,那么停止;否则将此终点更新为新的起始点x0,执行下一步骤。
步骤三:从给定起始点x0开始,用有限制条件最佳邻域搜寻法或有限制条件较佳邻域搜寻法执行搜寻几个时间步距而得到终点。将此终点更新为新的起始点,执行步骤一。
7.4计算可行出口点的方法
运用一个离散性动态系统(7-3),从一个已知局部最佳解开始,沿着预定的搜寻路径,来找寻有限制条件离散性最佳化问题(4-3)的可行性出口点,称之为基于离散性的可行出口点(也就是出口点满足所有限制条件)搜寻法,如下表示:
给予:一个已知局部最佳解xs,及一条预定的搜寻路径。
目的:计算出所对应的可行性出口点。
从已知的局部最佳解xs开始,沿着预定的搜寻路径移动,直到目标函数(4-5)达到第一局部最大值的点,此点为出口点。进行过程中随时检查是否违反限制条件,如是则停止执行。
7.5计算可行动态分解点的方法
在离散性最佳化问题(4-5)中,给予一个已知的局部最佳解xs及预定的搜寻路径,我们发展一个计算可行性动态分解点的方法,如下表示:
给予:最佳化问题(4-5)中的一个已知局部最佳解xs,一条预定的搜寻路径t(xs),以及所相关的离散性动态系统(7-3)。
目的:计算出所对应的可行性动态分解点。
步骤一、从已知的局部最佳解xs开始,沿着预定的搜寻路径t(xs)移动,侦测到离散性动态系统(7-3)的可行出口点(也就是出口点满足所有限制条件)。设出口点为xex。
步骤二、从xex开始,应用有限制条件的最佳邻域搜寻方法,向前移动xex一时间步骤到新点xc。
步骤三、执行下列的射线调整过程并计算动态分解点。
(i)构成一条射线,连接xs、xc。
(ii)如向量(xs-xex)及(xc-xex)可表达成表示式,则执行(ii)、(a);否则执行取代步骤(ii)、(a)的步骤。
(a)计算向量(xs-xex)及(xc-xex)的夹角ε。如果ε接近0°或180°,则xex是动态分解点并停止过程;否则执行(iii)。
(取代步骤(a)的步骤)修正搜寻路径使得现有的xex落于修正后的路径上,检查xex、xc与xs是否在同一修正后的路径上。如果是的话,xex是动态分解点(DDP)并停止过程;否则执行下一步骤。
(iii)调整xc到射线上(从xs开始)的目标函数最大值的点,设为x′c。如果x′c跟xex相同,则x′c是动态分解点并停止执行;否则执行下一步骤。
步骤四、把x′c当作出口点(x′c→xex),执行步骤二。
7.6搜寻另一个局部最佳解的基于出口点的方法
对离散性最佳化问题(4-5),我们发明从一个已知局部最佳解xs开始来搜寻到另一个局部最佳解的方法,称之基于出口点的方法。
给予:一个有限制条件离散性最佳化问题(4-5)其已知的局部最佳解xs及预定的搜寻路径。
目的:搜寻到所对应的新的一个阶层(new tier-one)的局部最佳解。
步骤一、从已知的局部最佳解xs开始,运用一个基于离散性的方法(与非线性动态系统(7-3)相关),计算可行性出口点xex。如可行性出口点无法找到则停止执行;否则执行下一步骤。
步骤二、从找到的xex开始,沿着预定的搜寻路径(由xs开始)向前移动一步至x0(或以x0=xs+(1+ε)(xex-xs)表示,其中如表示式存在,ε为一很小值。
步骤三、从x0开始,运用一个最佳邻域搜寻法可获得一条系统轨迹并求得接口点xinf。在此接口点运用一个有效的混合式局部搜寻法来求解最佳化问题(4-5),其结果会优于最佳邻域搜寻法。
步骤四、从此接口点xinf开始,运用步骤三所选有效的混合式局部最佳搜寻法来搜寻到一个毗连的局部最佳解。
7.7搜寻另一个局部最佳解的基于动态分解点的方法
对离散性最佳化问题(4-5),我们发明从一个已知局部最佳解xs开始来搜寻到另一个局部最佳解的方法,称之基于动态分解点的方法。
给予:一个有限制条件离散性最佳化问题(4-5)其已知的局部最佳解xs及预定的搜寻路径。
目的:搜寻到所对应的新的一个阶层(tier-one)的局部最佳解。
步骤一、从已知的局部最佳解xs开始沿着预定的搜寻路径,运用一个基于离散性的方法(与非线性动态系统(7-3)相关),来计算出可行动态分解点xddp。如可行动态分解点无法找到则停止执行;否则执行下一步骤。
步骤二、从找到的xddp开始,沿着修正后的搜寻路径(由xs开始)向前移动一步至x0(或以x0=xs+(1+ε)(xex-xs)表示,其中如表示式存在,ε为一极小值。
步骤三、从x0开始,运用一个最佳邻域搜寻法可获得一条系统轨迹并求得接口点xinf。在此接口点运用一个有效的混合式局部搜寻法来求解最佳化问题(4-5),其结果会优于最佳邻域搜寻法。
步骤四、从此接口点xinf开始,运用步骤三所选的有效性混合式局部最佳搜寻法来搜寻到一个毗连的局部最佳解。
7.8搜寻可行单位元中所有阶层一(tier-one)的局部最佳解方法。
我们发明一个基于动态离散性的方法,从一个已知的局部最佳解开始,来寻找可行单位元中所有阶层一(tier-one)的局部最佳解。
给予:一个离散性最佳化问题(4-3),其已知的局部最佳解xs 0。
目的:搜寻落于可行单位元中所有阶层一(tier-one)的局部最佳解。
步骤一:设定所有阶层一(tier-one)的局部最佳解集合
并定义一组xs 0的搜寻路径Si,i=1,2,...,m.设i=1。
步骤二:从一个已知的局部最佳解xs 0开始,沿着预定的搜寻路径Si移动,运用动态系统(7-3)及离散性基于出口点的方法(或基于动态分解点的方法)寻找另一个局部最佳解。如局部最佳解被找到,以xs i表示并继续下一步;否则执行步骤四。
步骤三:检查xs i是否曾被找到(xs i∈Vs),如果尚未曾被找到过则设
步骤四:设i=i+1。
步骤五:重复执行步骤二到步骤四,直到i>m。
7.9搜寻可行单位元中所有局部最佳解方法。
我们发明一个基于动态离散性的方法,从一个已知的局部最佳解开始,来搜寻离散性最佳化问题(4-5),落于可行单位元中所有的局部最佳解。
给予:一个有限制条件离散性最佳化问题(4-3),其已知的局部最佳解xs 0。
目的:搜寻包含xs 0可行单位元内所有的局部最佳解。
步骤一:以起始点x0开始应用一个有效的混合式搜寻方法,来寻找一个局部最佳解xs 0。
步骤二:设j=0,初始化局部最佳解集合
阶层j(tier-j)的局部最佳解集合
步骤三:设阶层j+1的局部最佳解集合
步骤四:对在Vnew j中的每一个局部最佳解xs j,寻找它所有阶层一(tier-one)的局部最佳解。
(i)定义xs j的一组搜寻路径Si j i=1,2...,mj,设i=1。
(ii)从已知的局部最佳解xs j开始,运用相关的离散性非线性动态系统(7-3)及基于出口点(或基于动态分解点)的方法来寻找另一个局部最佳解。如局部最佳解被找到,则以xs,j i表示并继续下一步;否则执行步骤(iv)。
(iii)检查xs,j i是否以前被找过,即xs,j i∈Vs,如果它尚未被找过,设 及
(iv)设i=i+1。
(v)重复执行(ii)到(iv),直到i>mj。
步骤五:检查最新计算的局部最佳解集合Vnew j+1,如果是空集合,执行步骤六;否则设j=j+1,并执行步骤三。
步骤六:输出所有的局部最佳解集合Vs(位于某可行单位元内),藉由比较Vs集合中所对应的个别目标函数值,选择其中一个具有最小目标函数值的最佳解,输出此点为全局最佳解。
7.10搜寻毗连可行单位元的方法
我们发明一个动态方法,从一个已知的可行单位元开始,来寻找毗连的可行单位元。
给予:一个初值的可行点x0。
目的:搜寻有限制条件离散性最佳化问题(4-5)落于毗连可行单位元中的另一个可行点。
步骤一:以起始点x0+ε×Si开始,其中ε为一极小值,将系统(7-4)延着逆时轨迹(reverse-time trajectory)积分,在需要时运用一个局部搜寻方法,找寻系统(7-4)不稳定平衡流形中的一点。如找到此点设为xd i,并执行下一步骤;否则停止执行。
步骤二:设定
ε是一个小的数目。
步骤三: 以起始点xp i开始,将系统(7-4)延着顺时轨迹(forward-timetrajectory)积分,并运用一个有效的混合式局部搜寻法,来定位一个分离的(isolated)可行单位元并找寻出其中一个可行点。
7.11搜寻到所有局部最佳解方法。
我们发明一个基于动态离散性的方法,从一个已知的局部最佳解开始,来寻找离散性最佳化问题(4-5)中所有的局部最佳解。如果所有的局部最佳解被找到,则全局最佳解也因此可获得;否则最佳解也可从已求得的局部最佳解中获得。
给予:一个初始点x0。
目的:(i)搜寻有限制条件离散性最佳化问题(4-5)所有的局部最佳解。
(ii)搜寻有限制条件离散性最佳化问题(4-5)的全局部最佳解。
步骤一:以起始点x0开始应用一个有效的局部搜寻方法,来寻找一个局部最佳解xs 0。
步骤二:设j=0,初始化局部最佳解集合
阶层0(tier-0)的可行单位元集合
步骤三:设阶层j+1的可行单位元集合
步骤四:对在V0 j中的每一个可行点x0 j,寻找包含x0 j可行单位元内所有局部最佳解集合,并寻找所有毗连的可行单位元。
(i)从一个已知的局部最佳解x0 j开始,来寻找最佳化问题(4-5)中,落于可行单位元内所有的局部最佳解。
(ii)定义x0 j的一组搜寻路径Si j i=1,2...,k。
(iii)对每一搜寻路径Si j,寻找一毗连的可行单位元步骤如下:
(a)设i=1。
(b)运用一个方法来找寻毗连可行单位元内的一点x0,i j。
(c)从x0,i j开始,运用一个有效混合式的局部搜寻法,求解局部最佳化解xs,i j。检查xs,i j是否以前被找过,即xs,i j∈Vs,如果它尚未被找过,设 及
(d)设i=i+1。
(e)重复执行(b)到(d),直到i>k。
步骤五:检查最新计算的可行点集合V0 j+1,如果是空集合,执行步骤六;否则设j=j+1,并执行步骤三。
步骤六:输出所有的局部最佳解集合Vs,藉由比较Vs集合中所对应的个别目标函数值,选择其中一个具有最小目标函数值的最佳解,输出此点为全局最佳解。
8.超大规模集成电路(VLSI)分割问题
一个大规模集成电路系统依复杂度可被分割为数个层次:(1)系统层次(system-level)分割,系统被分割成一群子系统,每个子系统能在一块印刷电路板(PCB)板内各自分别设计及制造;(2)基板层次(board-level)分割,一块印刷电路板(PCB)板分割成许多大规模集成电路(VLSI)芯片组;(3)芯片层次(chip-level)分割。在每个芯片分割成更小的子线路(sub-circuits)。在每一个层次中,分割的限制条件和目标函数的是不同的。本发明将会专注于芯片层次的分割。所得结果能被运用到其它层次分割,且具有相同结果。
我们将分割的问题用图学(graph)理论表达。一个超图(hypergraph)G=(V,E)代表一个分割问题。设V={v1,v2,...,vn}是一组顶点(vertices)集合,E={e1,e2,...,em}是一组超边线(hyperedges)集合。每个顶点代表一个组件。当组件间(对应于顶点)是相互连接时,有一条超边线(hyperedge)连接着顶点间。因此每条超边线(hyperedge)是顶点(vertices)集合的子集,也就是
换句话说,每条网络是以超边线(hyperedge)表示。每个组件的面积表示为a(vi),1≤i≤n。分割问题是将集合V分割成V1,V2,...,Vk,则
Vi∩Vj=φ,i≠j
分割也被称为切割(cut)。分割的度量可称为切割尺度(cut-size),是超边线(hyperedges)经过切割面的数目。设Cij是Vi和Vj分割集合间的切割尺度。每一个分割集合Vi有一面积
及终端点数(terminalcount)Count(Vi)。分割集合Vi拥有的最大及最小面积为Ai max及Ai min。设P={p1,p2,...,pm}为一组超路径(hyperpaths)。设H(pi)是超路径(hyperpaths)的数目,pi是一个切割(cut)。
在芯片层次(chip-level)分割问题中,限制条件和目标函数描述如下:
● 目标1是在分割之间交互连接(interconnections)最小化。减少交互连接不但减少延迟而且减少分割间的接口,使得个别独立设计和制造比较容易的。太多的交互连接将增加设计面积并使布局(placement)和布线(routing)的运算法则复杂化。使交互连接最小化目标,可陈述如下:
● 目标2是分割后产生最小延迟。电路的分割可能在分割数次之后建造一条重要路径(critical path),为强调此问题,我们设目标函数如下:
● 限制条件1是维持终端点的数目不超过预先设定的临限值Ti。这限制性陈述如下:
Count(Vi)<Ti. (8-3)
● 限制条件2是维持每个分割的面积于限定的界限内。芯片层次(chip-level)的分割问题中,这个限制是维持每个分割保持相对可比较的尺度。否则的话,在两分割问题中可能的结果,为一分割是空的而另一个分割含有问题所有的组件。这个限制在其它的分割层次(当实际大小事先设定)不是重要的。面积限制陈述如下:
分割问题是类属于没有封闭模式的目标函数。在分割两个特定的实例间,没有存在连续的空间可供描述。所以只有发展离散性不连续的解法。
我们已应用第6节所发展的一个基于不连续性的动态分解点搜寻方法来解分割问题。其混合式的局部最佳搜寻法中所运用的局部最佳解搜寻法是工业标准FM方法。我们已发展完成此方法并且已试验数个指标性问题(benchmark questions)。试验结果显示在表4,其由不同的起始点开始,在50次最小割集数目,45-55%面积平均分割条件及参着实际组件大小的限制下执行。模拟中也将工业标准FM方法做一结果比较。
表4.指标性问题的分割结果
| 指针电路 | 单元数目 | 从FM方法所获得的割集数目 | 动态分解点方法 | |
| 割集数目 | 改善率 | |||
| S1423 | 831 | 17 | 15 | 13% |
| S38584 | 22451 | 199 | 54 | 268% |
| S38417 | 25589 | 405 | 120 | 238% |
| S13207 | 9445 | 91 | 78 | 17% |
| S15850 | 11071 | 144 | 79 | 82% |
| S35932 | 19880 | 120 | 100 | 20% |
| C7552 | 2247 | 23 | 21 | 9.5% |
| S9234 | 6098 | 56 | 51 | 9.8% |
| S5378 | 3225 | 98 | 76 | 29% |
藉由用传统的FM方法配合我们的动态分解点方法,表4显示我们所求的解其质量有显著的改良。改良的范围从9.5%到268%,愈大的电路达到愈大的改良,小的电路有小的改良。总之,动态分解点方法明显的比FM方法好,在某些例子中,动态分解点方法甚至能与目前最领先的多层(multi-level)分割方法相匹敌。我们近期工作显示,藉由与多层(multi-level)分割方法,并配合我们动态分解点方法的混合式搜寻法,也能够显著的改良多层(multi-level)分割方法所得到的结果。
运用动态分解点方法的另一个改良结果是解的偏差比FM方法明显的小。这改良特性表示动态分解点方法比FM方法需要更少的执行程序就可得到好的解。
文献参考:
1.“Local Search in Combinatorial optimation”Edited by E.Aarts and J.K.Lenstra,Wiley,1997.
2.H.D. Chiang and L.Fekih-Ahmed,“quasistability Regions of NonlinearDynamical Systems:Theory”,IEEE Trans. On Circuits and Systems:IFundamental Theory and Applications,Vol Cas-43,August 1996,pp.627-635.
3.Hsiao-Dong Chiang and Chia-Chi Chu,“A Systematic Search Method forObtaining Multiple Local Optimal Solutions of Nonlinear ProgrammingProblems”,IEEE Trans.On Circuits and Systems:I Fundalmental Theory andapplications,Vol.43,No.2,Feb.1996,pp.99-109.
4.H.D. Chiang,M Hirsch and F.F,Wu,“Stability Regions of NonlinearAutonomous Dynamical Systems”,IEEE Trans.On Automatic Control Vol.AC-33,Jan.1988,pp.16-27.
Claims (58)
1.一种基于连续性的动态方法,此方法可解决一般无限制条件最佳化问题,此最佳化问题有一个目标函数及它的问题解空间是有限的,求解步骤如下:
a)构建一个非线性动态系统满足下列条件:此系统的每一个稳定平衡点是此最佳化问题的一个局部最佳解;
b)搜寻一般无限制条件最佳化问题的所有局部最佳解的方法,步骤如下:
i)以起始点开始;
ii)寻找一个局部最佳解;
iii)从步骤(b)、(ii)找到的局部最佳解开始,运用基于出口点或动态分解点的方法,逐层地寻找所有的局部最佳解集合,也就是寻找所建构非线性动态系统的稳定平衡点集合;
c)藉由比较步骤(b)、(iii)所搜寻到的稳定平衡点集合,比较所对应的个别目标函数值,选择其中一个具有最小值的最佳解,输出此点为全局最佳解。
2.根据权利要求1所述的方法,其特征在于,一般的无限制条件连续性最佳化问题形式如下:最小化UC(x),此处目标函数UC:Rn→R可为封闭模式或黑盒模式,目标函数UC(x)是一个有下界的函数,因此它的全局最佳解是存在的且局部最佳解的数量是有限的。
3.根据权利要求1所述的方法,其特征在于,一般的无限制条件连续性最佳化问题形式如下:最小化UC(x),此处目标函数UC:S→R可为封闭模式或黑盒模式,S是一个离散性的解空间,目标函数UC(x)是一个有下界的函数,因此它的全局最佳解是存在的且局部最佳解的数量是有限的。
4.根据权利要求1所述的方法,其特征在于,在步骤(a)中构建一个非线性动态系统 其中x∈Rn,n是最佳化问题解空间的大小,构建的动态系统满足下述性质:
(a)向量空间f(x)满足解的唯一性及存在性;
(b)非线性动态系统的轨迹必须是收敛的,而且收敛至其中一个平衡点;及
(c)最佳化问题的目标函数值,沿着非线性动态系统的轨迹是递减。
5.根据权利要求4所述的方法,其特征在于,对一个连续性最佳化问题,具有封闭模式的目标函数UC(x),在步骤(a)构建一个非线性动态系统
此处(UC):Rn→Rn是目标函数UC(x)的梯度向量。
6.根据权利要求4所述的方法,其特征在于,对一个连续性最佳化问题,具有黑盒模式的目标函数UC(x),在步骤(a)构建一个非线性动态系统 此处x第i个组件的导数,可以用目标函数UC(x)的单向差分近似值表示,ei是Cartesian第i个基底向量,h是一个非常小的数。
7.根据权利要求4所述的方法,其特征在于,对一个连续性最佳化问题,具有黑盒模式的目标函数UC(x),在步骤(a)构建一个非线性动态系统 此处x第i个组件的导数,可用目标函数UC(x)的中央差分近似值表示,ei是Cartesian第i个基底向量,h是一个非常小的数。
8.根据权利要求3所述的方法,其特征在于,对一个离散性的最佳化问题,在进行步骤(a)之前,将此离散性最佳化问题转换成一个连续性的最佳化问题。
9.根据权利要求8所述的方法,其特征在于,转换后的系统需满足下述两条件:
a)一个离散性最佳化问题的全局最佳解,与转换后连续性最佳化问题的全局最佳解,彼此是靠近的;
b)一个离散性最佳化问题的局部最佳解集合,与转换后连续性最佳化问题的局部最佳解集合,彼此是靠近的。
10.根据权利要求8所述的方法,其特征在于,该转换步骤中的转换方式如下: 此处
以及L是原目标函数UC(x)的Lipschitz常数,UCeq(x)是转换后的目标函数。
12.根据权利要求2所述的方法,其特征在于,对一个连续性的最佳化问题,在权利要求1中的步骤(b)、(ii)运用一个混合式局部搜寻方法,其搜寻步骤如下:
a)从一个起始点x0开始,针对最佳化问题,运用一个有效的局部搜寻算法;
b)如果局部搜寻算法收敛到一个局部最佳解xs,停止执行;否则到下一个步骤执行;
c)用x0当作起始点,对非线性系统进行积分几个时间步距,以所获得轨迹的最后一点为终端点;
d)以终端点当作新的起始点;
e)执行步骤(a)。
13.根据权利要求12所述的方法,其特征在于,步骤(a)运用的局部搜寻算法是一个业已存在的局部搜寻方法。
14.根据权利要求3所述的方法,其特征在于,在权利要求1的步骤(b)、(ii)中运用一个混合式局部搜寻方法,其搜寻步骤如下:
a)从一个起始点x0开始,针对最佳化问题,运用一个有效的局部搜寻算法;
b)如果局部搜寻算法收敛到一个局部最佳解xs,执行步骤(e);否则到下一个步骤执行;
c)用x0当作起始点,对非线性动态系统进行积分几个时间步距,以所获得的轨迹最后一点为终端点,以终端点当作新的起始点;
d)执行步骤(a);
e)将计算所得的连续性局部最佳解xs,产生m(≥2)个最接近的可行点集合,执行步骤e)、(i)或e)、(ii),选择最小目标函数值的点为局部最佳解并停止执行;用此可行点集合当作初值点,继续执行步骤(f);
f)针对每个初值点,运用最佳邻域搜寻方法来分别求得m个xs1,...,xsm局部最佳解;
g)从其中选择最小目标函数值的点为最佳化问题局部最佳解并停止执行。
15.根据权利要求14所述的方法,其特征在于,步骤(a)运用的局部搜寻算法是一个业已存在的局部搜寻方法。
16.根据权利要求1所述的方法,其特征在于,在步骤(b)、(iii)中运用一个基于出口点的方法来计算所有局部最佳解,其搜寻步骤如下:
a)由已知一个局部最佳解xs 0开始;
b)设j=0,初始化局部最佳解集合
阶层j(tier-j)的局部最佳解集合
c)设阶层j+1的局部最佳解集合
d)对在Vnew j中的每一个局部最佳解xs j,寻找它所有阶层1(tier-1)的局部最佳解,并记录新产生阶层1(tier-1)的局部最佳解集合于Vs及Vnew j+1;
e)检查最新计算的局部最佳解集合Vnew j+1,如果不是空集合设j=j+1,并执行步骤(c);
输出Vs为包含xs 0所有的局部最佳解集合。
17.根据权利要求16所述的方法,其特征在于,在步骤(d)中运用一个基于出口点的方法,给予一个已知局部最佳解,来计算所有阶层1的局部最佳解,其搜寻步骤如下:
a)由已知一个局部最佳解xs 0开始,初始化局部最佳解集合
阶层j+1的局部最佳解集合
b)针对xs 0,定义一组搜寻路径Si,i=1,2,...,m;
c)设i=1;及
d)沿着预定的搜寻路径Si移动,寻找局部最佳解,步骤如下:
i)寻找另一个局部最佳解;如局部最佳解被找到,以xs i来表示并继续步(ii);否则执行(iii);
ii)检查xs i是否曾被找到,
如果尚未被找到过则设
及
iii)设i=i+1;及
iv)重复执行步骤(i)到步骤(iii),直到i>m;
输出Vs为包含xs 0的局部最佳解集合。
18.根据权利要求17所述的方法,其特征在于,在步骤(d)、(i)中运用一个基于出口点的方法,给予一个已知局部最佳解,来计算另一个局部最佳解,其搜寻步骤如下:
a)从一个已知的局部最佳解xs开始并运用一条预定的搜寻路径;
b)沿着预定的搜寻路径,计算以xs为系统的稳定平衡点而构建的非线性动态系统的出口点xex(EP);
c)设x0=xs+(1+ε)(xex-xs),其中ε为一极小值;
d)从x0开始,对非线性系统进行积分以获得一条轨迹且求得接口点xinf,在此接口点运用一个有效的混合式局部搜寻法来找局部最佳解,其效果是会优于用轨迹来求解局部最佳解;
e)从此界面点xinf开始,运用步骤(d)所选的局部搜寻法来搜寻到一个毗连的局部最佳解。
19.根据权利要求18所述的方法,其特征在于,步骤(d)中运用的局部搜寻算法是一个业已存在的局部搜寻方法。
20.根据权利要求18所述的方法,其特征在于,步骤(b)针对预定的搜寻路径,来计算出口点,其步骤如下:
a)从已知的局部最佳解xs开始;及
b)沿着预定的搜寻路径,寻找目标函数值为第一个局部最大的点,视其为出口点。
21.根据权利要求18所述的方法,其特征在于,步骤(b)针对预定的搜寻路径,来计算出口点,其步骤如下:
i)从已知的局部最佳解xs开始;
ii)沿着预定的搜寻路径移动,计算搜寻路径的导数和非线性动态系统向量场在每个时间点的内积值;
iii)当内积值正负符号变更时,即由正到负,则表示已寻找到出口点在[t1,t2]间,然后运用在t1或t2时的搜寻路径的所得到的点来近似出口点。
22.根据权利要求18所述的方法,其特征在于,步骤(d)进行轨迹搜寻来求解局部最佳解,其中含有对非线性动态系统进行积分程序。
23.根据权利要求18所述的方法,其特征在于,当最佳化问题是离散性,在步骤(d)进行轨迹搜寻,其中含有将x0点调向新的点x0′,即远离xs,但接近(xep-xs)的方向,然后由x0′开始运用最佳邻域搜寻法。
24.根据权利要求1所述的方法,其特征在于,在步骤(b)、(iii)中运用一个动态分解点为基础的方法来计算所有局部最佳解,其搜寻步骤如下:
a)由已知一个局部最佳解xs 0开始;
b)设j=0,初始化局部最佳解集合
阶层j的局部最佳解集合
动态分解点集合Vddp={φ};
c)设阶层j+1的局部最佳解集合
d)对在Vnew j中的每一个局部最佳解xs j,寻找它所有阶层1的局部最佳解,并记录新产生阶层1的局部最佳解集合于Vs及Vnew j+1;
e)检查最新计算的局部最佳解集合Vnew j+1,如果不是空集合设j=j+1,并执行步骤(c);
输出集合Vs为包含xs 0的局部最佳解集合。
25.根据权利要求24所述的方法,其特征在于,在步骤(d)中,当给予一个已知局部最佳解xs 0,来计算所有阶层1局部最佳解,其搜寻步骤如下:
a)由一个已知局部最佳解xs 0开始,初始化局部最佳解集合Vs,阶层j的局部最佳解集合Vnew j,动态分解点集合Vddp及阶层j+1的局部最佳解集合Vnew j+1;
b)针对xs 0定义一组搜寻路径Si,i=1,2...,mj,设i=1;
c)对每一搜寻路径Si,寻找它所对应的局部最佳解,步骤如下:
i)沿着搜寻路径Si寻找动态分解点,如动态分解点xddp,i被找到,继续下一步;否则执行(vii);
ii)检查xddp,i是否曾被找到,xddp,i∈Vddp,如果曾被找到过则执行(vii);否则设Vddp=Vddp∪{xddp,i}继续执行下一步骤(iii);
iii)设
其中,如表示式存在,ε为一极小值;
iv)从x0,i开始,对非线性系统进行积分以获得一条轨迹且求得接口点xinf,i,在此接口点运用一个有效的混合式局部搜寻法来找局部最佳解,其效果是会优于用轨迹搜寻来求解局部最佳解;
v)从此界面点xinf,i开始,运用步骤(iv)所选的局部搜寻法来搜寻一个相对于xddp,i毗连的局部最佳解xs i;
vi)检查xs i是否以前被找过,即
如果它尚未被找过,设
及
vii)设i=i+1;及
viii)重复执行(i)到(vii),直到i>mj;
输出集合Vs为包含xs 0的局部最佳解集合。
26.根据权利要求25所述的方法,其特征在于,步骤(c)、(iv)进行轨迹搜寻来求解局部最佳解,其中含有对构建的非线性动态系统进行积分程序。
27.根据权利要求25所述的方法,其特征在于,最佳化问题是离散性的,步骤(c)、(iv)进行轨迹搜寻,其中将x0点调向新的点x0′,即远离xs,但接近(xep-xs)的方向,然后由x0′开始运用最佳邻域搜寻法。
28.根据权利要求25所述的方法,其特征在于,步骤(c)、(iv)运用的局部搜寻算法是一个业已存在的局部搜寻方法。
29.根据权利要求25所述的方法,其特征在于,在步骤(c)、(i)中,针对一条给定的搜寻路径,计算以xs为系统的稳定平衡点的非线性动态系统的动态出口点(DDP),其搜寻步骤如下:
a)从已知的局部最佳解xs开始,沿着预定的搜寻路径移动;
b)计算出口点,设出口点为xex;
c)从xex开始,应用下述步骤寻找最小距离点(MDP)xd 0;及
i)以出口点xex为起始条件,对非线性动态系统x=FU(x)在几个时间步距处进行积分;设终端点为目前出口点;
ii)连接轨迹上的目前出口点和局部的最佳解xs,也就是稳定平衡点,成一直线,沿着此直线从稳定平衡点寻找目标函数的第一局部最大的点,视其为修正出口点xex,并以此点代替目前的点,指定这个点为出口点xex;
iii)重复执行(i)及(ii),直到在(ii)中所获得的出口点的norm值是小于一个比较值;
iv)此出口点为最小距离点(MDP)xd 0;及
d)以MDPxd 0为起始点,求解非线性代数方程式FU(x)=0,设其解为xddp,则xddp是针对于动态系统稳定平衡点xs和搜寻路径的动态分解点。
30.一个基于离散性的动态方法,此方法可解决一般离散性最佳化问题,此最佳化问题有一个目标函数及它的问题解空间是有限的,其步骤如下:
a)构建一个离散性非线性动态系统满足下列条件:此系统的每一个稳定固定点是此最佳化问题的一个局部最佳解;
b)搜寻一般的离散性最佳化问题所有的局部最佳解,步骤如下:
i)以起始点x0开始;
ii)寻找一个局部最佳解;
iii)从步骤(b)、(ii)中所搜寻到的局部最佳解开始,寻找所有局部最佳解集合,也就是所构建离散性非线性动态系统的稳定固定点集合;
c)藉由比较步骤(b)、(iii)稳定固定点集合中所对应的个别目标函数值,选择其中一个具有最小值的最佳解,输出此点为全局最佳解。
31.根据权利要求30所述的方法,其特征在于,一般离散性最佳化问题的形式如下:最小化UC(x),此处目标函数UC:S→R可为封闭模式或黑盒模式,其中S是一个离散解的空间,目标函数UC(x)是一个有下限的函数,因此它的全局最佳解是存在的且局部最佳解的数量是有限的。
32.根据权利要求30所述的方法,其特征在于,一般离散性最佳化问题的形式如下:最小化C(x)且受限于G(x)≤0,此处目标函数C:S→R可为封闭模式或黑盒模式,S是一个离散性的解空间,且限制函数向量G:S→Rm为封闭模式,目标函数C(x)是一个有下限的函数,因此在可行区域中它的全局最佳解是存在的且局部最佳解的数量是有限的。
33.根据权利要求30所述的方法,其特征在于,步骤(a)构建一个离散性非线性动态系统xk+1=f(xk),其中x∈S,S是最佳化问题的解空间,所构建的离散性非线性动态系统满足下述性质:
a)所构建的离散性非线性动态系统的轨迹是存在且唯一的;及
b)所构建的离散性非线性动态系统的轨迹必须是收敛的,而且收敛至其中一个固定点;及,离散性最佳化问题的目标函数值,沿着离散性非线性动态系统的轨迹是递减的。
34.根据权利要求30所述的方法,其特征在于,针对离散性最佳化问题,在步骤(a)、(ii)中,运用一个混合式局部搜寻法寻找一个局部最佳解,其搜寻步骤如下:
a)从给定起始点x0开始,运用一个有效的局部反复修正算法,求解有限制条件离散性最佳化问题;
b)如果局部搜寻算法收敛到一个局部最佳解,那么停止;否则到下一个步骤执行;
c)使用最佳邻域搜寻法,从x0开始执行搜寻几个时间步距而得到终点;
d)将此终点更新为新的起始点,执行步骤(a)。
35.根据权利要求34所述的方法,其特征在于,步骤(a)运用的局部搜寻算法是一个业已存在的局部搜寻方法。
36.根据权利要求30所述的方法,其特征在于,当最佳化问题是无限制条件情况下,步骤(b)、(iii)搜寻所有局部最佳解集合,其搜寻步骤如下:
a)由已知一个局部最佳解xs 0开始;
b)设j=0,初始化局部最佳解集合
阶层j的局部最佳解集合
c)设阶层j+1的局部最佳解集合
d)对在Vnew j中的每一个局部最佳解xs j,寻找它所有阶层1的局部最佳解,并记录新产生阶层1的局部最佳解集合于Vs及Vnew j+1;
e)检查最新计算的局部最佳解集合Vnew j+1,如果不是空集合设j=j+1,并执行步骤(c);
输出Vs为包含xs 0所有的局部最佳解集合。
37.根据权利要求36所述的方法,其特征在于,步骤(d)中,当给予一个已知局部最佳解xs 0,寻找所有阶层1的局部最佳解,其搜寻步骤如下:
a)由已知一个局部最佳解xs 0开始,初始化局部最佳解集合Vs,及阶层j+1的局部最佳解集合Vnew j+1,给定xs 0的一组搜寻路径Si,i=1,2...,mj,设i=1;
b)对每一搜寻路径Si,运用一个基于出口点(EP)或动态分解点(DDP)的搜寻方法,来寻找它所对应毗连的另一个局部最佳解;
c)检查xs i是否以前被找过,即
如果它尚未被找过,设
及
d)设i=i+1;及
e)重复执行(b)到(d),直到i>m;
输出Vs为包含xs 0的局部最佳解集合。
38.根据权利要求37所述的方法,其特征在于,在步骤(b)运用一个基于出口点的方法,给予一个已知局部最佳解,来计算另一个局部最佳解,其搜寻步骤如下:
a)从一个已知的局部最佳解xs开始,运用一条预定的搜寻路径;
b)沿着预定的搜寻路径,计算出口点xex(EP);
c)如果出口点不能被找到,则停止执行;否则进行下一步;
d)从出口点xex开始,(i)沿着预定的路径向前一步,得到新的一点x0,(ii)设x0=xs+(1+ε)(xex-xs),其中ε为一极小值;
e)从x0开始,使用最佳邻域搜寻法,求得一个接口点xinf,在此点开始运用一个局部搜寻法,其结果是会优于最佳邻域搜寻法;
f)从此界面点xinf开始,运用步骤(e)所选的局部搜寻法来搜寻到一个毗连的局部最佳解。
39.根据权利要求38所述的方法,其特征在于,步骤(e)运用的局部搜寻算法是一个业已存在的局部搜寻方法。
40.根据权利要求38所述的方法,其特征在于,在步骤(b)针对预定的路径,计算出口点,其步骤如下:
i)从已知的局部最佳解xs开始;及
ii)沿着预定的搜寻路径找寻最佳化问题的目标函数值为第一个局部最大的点,视其为出口点。
41.根据权利要求37所述的方法,其特征在于,在步骤(b)运用一个基于动态分解点的方法,给予一个已知局部最佳解,来计算另一个局部最佳解,其搜寻步骤如下:
a)从一个已知的局部最佳解xs开始,运用一条预定的搜寻路径;
b)沿着预定的搜寻路径,计算动态分解点xddp(DDP);
c)如果动态分解点不能被找到,则停止执行;否则进行下一步;
d)从动态分解点xddp开始,(i)沿着修正后的路径向前一步调整出口点xex,得到远离xs的一新的点x0,(ii)设x0=xs+(1+ε)(xddp-xs),其中ε为一很小值;
e)从x0开始,使用最佳邻域搜寻法,求得一个接口点xinf,在此点运用一个局部搜寻法,其结果是会优于最佳邻域搜寻法;
f)从此界面点xinf开始,运用步骤(e)所选的局部搜寻法来搜寻到一个毗连的局部最佳解。
42.根据权利要求41所述的方法,其特征在于,步骤(e)运用的局部搜寻算法是一个业已存在的局部搜寻方法。
43.根据权利要求41所述的方法,其特征在于,在步骤(b),针对一条给定的路径,计算动态出口点(DDP),其搜寻步骤如下:
a)从已知的局部最佳解xs开始,沿着预定的搜寻路径移动;
b)计算出口点,将出口点设为xex;
c)如出口点无法找到,则停止执行;
d)从xex开始,应用最佳邻域搜寻方法,向前移动xex一时间步骤到新点xc;
e)执行下列的射线调整过程并计算DDP点:
i)构成一条射线,连接xs、xc;
ii)如向量(xs-xex)及(xc-xex)可表达成表示式,则计算向量(xs-xex)及(xc-xex)之夹角ε,如果ε接近0°或180°,则xex是动态分解点并停止过程;否则执行步骤(e)(iv);
iii)如向量(xs-xex)及(xc-xex)不可表达成表示式,则修正搜寻路径使得现有之xex落于修正后的路径上,检查xex、xc与xs是否在同一修正后的路径上,如果是的话,xex是动态分解点并停止过程;
iv)调整xc到射线上,从xs开始,最大目标函数值之点,设为xc′;
v)如果xc′跟xex非常接近,则xc′是动态分解点并停止执行;否则执行步骤(f);
f)把xc′当作出口点xc′→xex,执行步骤(d)。
44.根据权利要求32所述的方法,当限制条件为封闭模式的离散性最佳化问题,在步骤(a)前建构一个系统,以利找寻所有的可行单位元,此所建构的连续性非线性动态系统满足条件:
a)每个基于连续性非线性动态系统的轨迹必须是收敛,而且收敛到其中一个平衡流形;和
b)当一个集合是连续性非线性动态系统的一个稳定平衡流形,若且唯若这集合是此有限制条件离散性最佳化问题的一个可行单位元。
45.根据权利要求32所述的方法,当处理限制条件为封闭模式的离散性最佳化问题,在权利要求30所述的步骤(b)(ii)计算一个局部最佳解,其步骤如下:
a)从给定起始点x0开始,可能不满足部份限制条件;
b)经由下述步骤,找寻一个局部最佳解;
i)设k=1;
ii)计算U(k)
此处λi(K)是一个非负的调整因子,用来驱动搜寻方向远离前一个不适者;
iii)如果x0在可行单位元中,则用有限制条件较佳邻域搜寻方向,及
来计算ΔxL(x,λ);否则用原解空间的较佳邻域搜寻方向来计算ΔxL(x,λ),其中L(x,λ)为Lagrange函数;
iv)如果U(k)及ΔxL(x,λ)为非常小的值,则至步骤(c);否则依
xk+1=xk+ΔxL(xk,λk)
λk+1=λk+U(k) 修正x及λ并执行下一步;
V)设k=k+1,以预定之递回次数,重复执行步骤(ii)至步骤(iv);
c)如步骤(b)的搜寻是收敛的,则现存点x0为局部最佳解。
46.根据权利要求32所述的方法,在权利要求30所述的步骤(b)(ii)从一个不可行点开始运用一个局部优化方法计算一个局部最佳解。
47.根据权利要求44所述的方法,当处理限制条件为封闭模式的离散性最佳化问题,在权利要求30所述的步骤(b)(iii)计算所有局部最佳解,其步骤如下:
a)以一个已知局部最佳解xs 0开始;
b)设j=0,初始化局部最佳解集合
阶层0(tier-0)的可行单位元集合
c)设阶层j+1的可行单位元集合
d)对在V0 j中的每一个可行点x0 j,寻找包含x0 j可行单位元内所有局部最佳解集合,并寻找所有毗连的可行单位元:
i)从一个已知的局部最佳解x0 j开始,来寻找最佳化问题中,落于可行单位元内所有的局部最佳解;
ii)针对x0 j定义一组搜寻路径Si j i=1,2...,k;
iii)对每一搜寻路径Si j,寻找一毗连的可行单位元步骤如下:
1)设i=1;
2)找寻毗连可行单位元内的一点x0,i j;
3)从x0,i j开始,运用一个局部搜寻法,求解局部最佳化解xs,i j,检查xs,i j是否以前被找过,即
如果它尚未被找过,设
及
4)设i=i+1;及
5)重复执行(d)(iii)(2)到(d)(iii)(4),直到i>k;
e)检查最新计算的可行点集合V0 j+1,如果不是空集合,则设j=j+1;重复执行步骤(c)到步骤(d);否则输出Vs为所有局部最佳解的集合。
48.根据权利要求47所述的方法,其特征在于,在步骤(d)(iii)(2)寻找毗连的可行单位元内的一点,其步骤如下:
a)以起始点x0+ε×Si开始,其中ε为一极小値,将连续性非线性动态系统延着逆时轨迹积分来找寻系统不稳定平衡流形中的一点,如找到此点设为xd i,并执行下一步骤;否则停止执行;
b)设定
ε是一个小的数目;
c)以起始点xp i开始运用下列的步骤来寻找一个分离的可行单位元并找寻出其中一个可行点x0 i:
i)用x0当做起始条件,对所建构的连续性非线性系统在几个时间步距处进行积分,获得最后一点为终端点的轨迹;
ii)如果轨迹收敛到一个可行点,则停止执行;
iii)否则运用反复改进局部搜寻法;
iv)如果局部搜寻法收敛到一个可行点,则停止执行;
v)以终端点当作起始点x0,执行步骤(c)(i)。
49.根据权利要求47所述的方法,其特征在于,在步骤(d)(iii)(3)运用一个混合式局部搜寻方法,找寻位于一个可行单位元内的局部最佳解,其搜寻步骤如下:
a)从一个起始点x0开始,针对离散性最佳化问题,运用一个反复改进局部搜寻算法;
b)如果局部搜寻算法收敛到一个局部最佳解,则停止执行;
c)使用最佳邻域搜寻法或较佳邻域搜寻法,从x0开始,持续搜寻数个步骤后,记录最后一点为终端点;
d)以终端点当作起始点;及
e)执行步骤(a)。
50.根据权利要求49所述的方法,其特征在于,步骤(a)运用的局部搜寻算法是一个业已存在的局部搜寻方法。
51.根据权利要求47所述的方法,其特征在于,在步骤(d)(i)寻找位于一个可行单位元内的局部最佳解集合,其搜寻步骤如下:
a)由已知一个局部最佳解xs 0开始,Vs是已找到的局部最佳解的集合;
b)设j=0,初始化一个可行单位元内局部最佳解集合
阶层j的局部最佳解集合
c)设阶层j+1的局部最佳解集合
d)对在Vnew j中的每一个局部最佳解xs j,寻找包含xs j可行单位元内所有阶层1(tier-1)的局部最佳解。并记录新产生阶层1(tier-1)的局部最佳解集合于Vs,Vnew j+1及Vs c;
e)检查最新计算的局部最佳解集合Vnew j+1,如果不是空集合设j=j+1,并执行步骤(c);
输出Vs为包含xs 0所有的局部最佳解集合。
52.根据权利要求51所述的方法,其特征在于,在步骤(d)找寻位于阶层1的局部最佳解集合,其搜寻步骤如下:
a)由一个已知的局部最佳解xs 0开始,Vs是已找到的局部最佳解的集合,初始化一个可行单位元内局部最佳解集合Vs c,阶层j的局部最佳解集合Vnew j,对xs 0定义一组搜寻路径Si,i=1,2,...,m.设i=1;
b)从一个已知的局部最佳解xs 0开始,沿着预定的搜寻路径Si移动,运用基于出口点方法或动态分解点方法寻找另一个局部最佳解;
c)如局部最佳解被找到,以xs i表示并继续下一步;否则执行步骤(e);
d)检查xs i是否曾被找到
如果尚未曾被找到过则设
及
e)设i=i+1;
f)重复执行步骤(b)到步骤(e),直到i>m;
输出Vs为包含xs 0所有的局部最佳解集合。
53.根据权利要求52所述的方法,其特征在于,在步骤(b)运用一个基于出口点的方法,给予一个已知局部最佳解,来计算另一个局部最佳解,其搜寻步骤如下:
a)从一个已知的局部最佳解xs开始,并运用一条预定的搜寻路径;
b)沿着预定的搜寻路径,计算相对应的出口点xex(EP);如果出口点不能被找到,则停止执行;
c)从出口点xex开始,(i)延着预定的路径向前一步(远离xs),得到新的一点x0,(ii)设x0=xs+(1+ε)(xex-xs),其中ε为一极小值;
d)从x0开始,利用有限制条件的最佳邻域搜寻法,求得一个接口点,在此点运用一个有限制条件的局部搜寻法,其结果是会优于有限制条件的最佳邻域搜寻法;
e)从此界面点xinf开始,运用步骤(e)所选有限制条件的局部搜寻法来搜寻到一个毗连的局部最佳解。
54.根据权利要求53所述的方法,其特征在于,步骤(d)运用的局部搜寻算法是一个业已存在的局部搜寻方法。
55.根据权利要求53所述的方法,其特征在于,在步骤(b)针对预定的路径,计算出口点,其步骤如下:
i)从已知的局部最佳解xs开始,沿着预定的路径搜寻目标函数值为第一个的局部最大的点,视其为出口点;
ii)在过程中检查是否违反限制条件;如违反限制条件,则停止执行并说明出口点无法找到。
56.根据权利要求52所述的方法,其特征在于,在步骤(b)运用一个基于动态分解点(DDP)的方法,给予一个已知局部最佳解,来计算另一个局部最佳解,其步骤如下:
a)从一个已知的局部最佳解xs开始,并运用一条预定的搜寻路径;
b)沿着预定的路径计算所对应的动态分解点xddp(DDP);如果动态分解点不能被找到,则停止执行;
c)从动态分解点xddp开始,(i)沿着修正后调整出口点xex的路径向前一步,得到远离xs的一新点x0,(ii)设x0=xs+(1+ε)(xddp-xs),其中ε为一很小值;
d)从x0开始,使用有限制条件的最佳邻域搜寻法,求得一个接口点xinf,在此点运用一个局部搜寻法,其结果是会优于有限制条件的最佳邻域搜寻法;
e)从此界面点xinf开始,运用步骤(d)所选的有限制条件局部搜寻法来搜寻到一个毗连的局部最佳解。
57.根据权利要求56所述的方法,其特征在于,步骤(d)运用的局部搜寻算法是一个业已存在的局部搜寻方法。
58.根据权利要求56所述的方法,其特征在于,在步骤(b),针对一条给定的路径,计算动态出口点(DDP),其搜寻步骤如下:
a)从已知的局部最佳解xs开始,沿着预定的搜寻路径移动;
b)侦测到出口点,将出口点设为xex;在过程中检查是否违反限制条件或出口点无法找到;如是,则停止执行;
c)从xex开始,应用有限制条件的最佳邻域搜寻方法,向前移动xex一时间步骤到新点xc;
d)执行下列的射线调整过程并计算DDP点:
i)构成一条直线,连接xs、xc;
ii)如果向量(xs-xex)及(xc-xex)可表达成表示式,则计算向量(xs-xex)及(xc-xex)之夹角ε;如果ε接近0°或180°,则xex是动态分解点并停止过程;否则执行步骤(d)(iv);
iii)如果向量(xs-xex)及(xc-xex)不可表达成表示式,则修正搜寻路径使得现有的xex落于修正后的路径上,检查xex、xc与xs是否在同一修正后的路径上;如果是的话,xex是动态分解点并停止过程;
iv)调整xc到直线上,从xs开始第一个局部最大目标函数值的点,设为xc′;
v)如果xc′跟xex非常接近,则xc′是动态分解点并停止执行;否则执行步骤(e);
e)把xc′当作出口点,xc′→xex,执行步骤(d)。
Applications Claiming Priority (2)
| Application Number | Priority Date | Filing Date | Title |
|---|---|---|---|
| US10/153,070 | 2002-05-22 | ||
| US10/153,070 US7050953B2 (en) | 2002-05-22 | 2002-05-22 | Dynamical methods for solving large-scale discrete and continuous optimization problems |
Publications (1)
| Publication Number | Publication Date |
|---|---|
| CN1668996A true CN1668996A (zh) | 2005-09-14 |
Family
ID=29548593
Family Applications (1)
| Application Number | Title | Priority Date | Filing Date |
|---|---|---|---|
| CNA038170116A Pending CN1668996A (zh) | 2002-05-22 | 2003-05-21 | 解大型连续性或离散性最佳化问题的动态方法 |
Country Status (6)
| Country | Link |
|---|---|
| US (1) | US7050953B2 (zh) |
| JP (1) | JP2005527034A (zh) |
| CN (1) | CN1668996A (zh) |
| AU (1) | AU2003237905A1 (zh) |
| TW (1) | TWI261763B (zh) |
| WO (1) | WO2003100598A1 (zh) |
Cited By (5)
| Publication number | Priority date | Publication date | Assignee | Title |
|---|---|---|---|---|
| CN105095680A (zh) * | 2015-09-21 | 2015-11-25 | 武汉理工大学 | 基于微分测度随机相遇不确定性的搜救方法及系统 |
| CN106597856A (zh) * | 2016-12-29 | 2017-04-26 | 北京理工大学 | 基于网格搜索的双星系统空间轨道族搜索方法 |
| CN108228135A (zh) * | 2016-12-15 | 2018-06-29 | 上海寒武纪信息科技有限公司 | 一种运算多种超越函数的装置 |
| CN109345465A (zh) * | 2018-08-08 | 2019-02-15 | 西安电子科技大学 | 基于gpu的高分辨率图像实时增强方法 |
| CN112258515A (zh) * | 2020-12-24 | 2021-01-22 | 上海国微思尔芯技术股份有限公司 | 一种基于固定顶点的图分割方法 |
Families Citing this family (62)
| Publication number | Priority date | Publication date | Assignee | Title |
|---|---|---|---|---|
| US7277832B2 (en) * | 2001-05-04 | 2007-10-02 | Bigwood Technology, Inc. | Dynamical method for obtaining global optimal solution of general nonlinear programming problems |
| US7072723B2 (en) * | 2002-10-23 | 2006-07-04 | Clearsight Systems Inc. | Method and system for optimization of general problems |
| US8504396B2 (en) * | 2002-12-24 | 2013-08-06 | Sap Aktiengeselleschaft | Flexible maintenance planning |
| WO2005048018A2 (en) * | 2003-10-23 | 2005-05-26 | Clearsight Systems Inc. | Method for optimization using state functions |
| US7979242B2 (en) * | 2004-02-09 | 2011-07-12 | International Business Machines Corporation | Method and structure for providing optimal design of toleranced parts in manufacturing |
| US8189002B1 (en) * | 2004-10-29 | 2012-05-29 | PME IP Australia Pty, Ltd. | Method and apparatus for visualizing three-dimensional and higher-dimensional image data sets |
| US20060173728A1 (en) * | 2005-01-21 | 2006-08-03 | Lianjun An | Adaptive product configuration model |
| US20060253517A1 (en) * | 2005-04-15 | 2006-11-09 | Argentar David R | Using binary array representations of sequences to eliminate redundant patterns in discovered patterns of symbols |
| EP1961639A1 (en) * | 2007-02-22 | 2008-08-27 | Nederlandse Organisatie voor toegepast- natuurwetenschappelijk onderzoek TNO | Vehicle driving assistance |
| US8392529B2 (en) | 2007-08-27 | 2013-03-05 | Pme Ip Australia Pty Ltd | Fast file server methods and systems |
| US9019287B2 (en) | 2007-11-23 | 2015-04-28 | Pme Ip Australia Pty Ltd | Client-server visualization system with hybrid data processing |
| US9904969B1 (en) | 2007-11-23 | 2018-02-27 | PME IP Pty Ltd | Multi-user multi-GPU render server apparatus and methods |
| WO2009067680A1 (en) | 2007-11-23 | 2009-05-28 | Mercury Computer Systems, Inc. | Automatic image segmentation methods and apparartus |
| US10311541B2 (en) | 2007-11-23 | 2019-06-04 | PME IP Pty Ltd | Multi-user multi-GPU render server apparatus and methods |
| US8319781B2 (en) | 2007-11-23 | 2012-11-27 | Pme Ip Australia Pty Ltd | Multi-user multi-GPU render server apparatus and methods |
| US7668707B2 (en) * | 2007-11-28 | 2010-02-23 | Landmark Graphics Corporation | Systems and methods for the determination of active constraints in a network using slack variables and plurality of slack variable multipliers |
| CA2703072C (en) | 2007-12-13 | 2016-01-26 | Exxonmobil Upstream Research Company | Iterative reservoir surveillance |
| JP5358668B2 (ja) * | 2008-03-26 | 2013-12-04 | 東京電力株式会社 | 電力システムの安定平衡点算出装置 |
| EP2269173A4 (en) * | 2008-04-22 | 2017-01-04 | Exxonmobil Upstream Research Company | Functional-based knowledge analysis in a 2d and 3d visual environment |
| US8892407B2 (en) | 2008-10-01 | 2014-11-18 | Exxonmobil Upstream Research Company | Robust well trajectory planning |
| TWI399659B (zh) * | 2009-06-25 | 2013-06-21 | Univ Nat Chiao Tung | Designed for Chip Design and Chip Products Designed for Chip Packaging and Board Design |
| CN102741854B (zh) | 2009-10-23 | 2015-08-19 | 埃克森美孚上游研究公司 | 利用梯度信息进行优化的方法 |
| EP2531694B1 (en) | 2010-02-03 | 2018-06-06 | Exxonmobil Upstream Research Company | Method for using dynamic target region for well path/drill center optimization |
| WO2012004742A1 (en) * | 2010-07-09 | 2012-01-12 | Koninklijke Philips Electronics N.V. | Automatic point-wise validation of respiratory motion estimation |
| US9593558B2 (en) | 2010-08-24 | 2017-03-14 | Exxonmobil Upstream Research Company | System and method for planning a well path |
| AU2011356658B2 (en) | 2011-01-26 | 2017-04-06 | Exxonmobil Upstream Research Company | Method of reservoir compartment analysis using topological structure in 3D earth model |
| EP2678802A4 (en) | 2011-02-21 | 2017-12-13 | Exxonmobil Upstream Research Company | Reservoir connectivity analysis in a 3d earth model |
| US9223594B2 (en) | 2011-07-01 | 2015-12-29 | Exxonmobil Upstream Research Company | Plug-in installer framework |
| US20130018700A1 (en) * | 2011-07-14 | 2013-01-17 | International Business Machines Corporation | Optimizing product portfolios under customer choice |
| WO2013169429A1 (en) | 2012-05-08 | 2013-11-14 | Exxonmobile Upstream Research Company | Canvas control for 3d data volume processing |
| US20140257767A1 (en) * | 2013-03-09 | 2014-09-11 | Bigwood Technology, Inc. | PSO-Guided Trust-Tech Methods for Global Unconstrained Optimization |
| US11244495B2 (en) | 2013-03-15 | 2022-02-08 | PME IP Pty Ltd | Method and system for rule based display of sets of images using image content derived parameters |
| US10070839B2 (en) | 2013-03-15 | 2018-09-11 | PME IP Pty Ltd | Apparatus and system for rule based visualization of digital breast tomosynthesis and other volumetric images |
| US10540803B2 (en) | 2013-03-15 | 2020-01-21 | PME IP Pty Ltd | Method and system for rule-based display of sets of images |
| US10317857B2 (en) * | 2013-03-15 | 2019-06-11 | Rockwell Automation Technologies, Inc. | Sequential deterministic optimization based control system and method |
| US8976190B1 (en) | 2013-03-15 | 2015-03-10 | Pme Ip Australia Pty Ltd | Method and system for rule based display of sets of images |
| US9400491B2 (en) * | 2013-03-15 | 2016-07-26 | Rockwell Automation Technologies, Inc. | Stabilized deteministic optimization based control system and method |
| US9509802B1 (en) | 2013-03-15 | 2016-11-29 | PME IP Pty Ltd | Method and system FPOR transferring data to improve responsiveness when sending large data sets |
| US9448546B2 (en) | 2013-03-15 | 2016-09-20 | Rockwell Automation Technologies, Inc. | Deterministic optimization based control system and method for linear and non-linear systems |
| US11183292B2 (en) | 2013-03-15 | 2021-11-23 | PME IP Pty Ltd | Method and system for rule-based anonymized display and data export |
| CA2907728C (en) | 2013-06-10 | 2021-04-27 | Exxonmobil Upstream Research Company | Interactively planning a well site |
| US9152611B2 (en) | 2013-07-30 | 2015-10-06 | Bigwood Technology, Inc. | Trust-tech enhanced methods for solving mixed-integer optimization problems |
| US9864098B2 (en) | 2013-09-30 | 2018-01-09 | Exxonmobil Upstream Research Company | Method and system of interactive drill center and well planning evaluation and optimization |
| WO2015199779A2 (en) | 2014-03-31 | 2015-12-30 | Peterson Elmor L | Flexible vector-processing algorithms for numerically solving extreme-scale, linear and non-linear, predictive and prescriptive, problems in science and engineering, on parallel-processing super computers |
| US9836697B2 (en) * | 2014-10-06 | 2017-12-05 | International Business Machines Corporation | Determining variable optimal policy for an MDP paradigm |
| US11599672B2 (en) | 2015-07-31 | 2023-03-07 | PME IP Pty Ltd | Method and apparatus for anonymized display and data export |
| US9984478B2 (en) | 2015-07-28 | 2018-05-29 | PME IP Pty Ltd | Apparatus and method for visualizing digital breast tomosynthesis and other volumetric images |
| US10909679B2 (en) | 2017-09-24 | 2021-02-02 | PME IP Pty Ltd | Method and system for rule based display of sets of images using image content derived parameters |
| JP6886112B2 (ja) | 2017-10-04 | 2021-06-16 | 富士通株式会社 | 学習プログラム、学習装置及び学習方法 |
| US10884721B2 (en) * | 2018-05-08 | 2021-01-05 | Autodesk, Inc. | Branch objects for dependent optimization problems |
| JP7156666B2 (ja) * | 2018-06-19 | 2022-10-19 | Necソリューションイノベータ株式会社 | パラメータ探索装置、パラメータ探索方法、及びプログラム |
| CN109408939B (zh) * | 2018-10-18 | 2022-11-29 | 燕山大学 | 一种兼顾应力和位移约束的薄板结构加强筋分布优化的改进方法 |
| US10713055B2 (en) | 2018-10-29 | 2020-07-14 | International Business Machines Corporation | Parallelization of numeric optimizers |
| US11507787B2 (en) | 2018-12-12 | 2022-11-22 | International Business Machines Corporation | Model agnostic contrastive explanations for structured data |
| TWI753329B (zh) | 2019-12-06 | 2022-01-21 | 財團法人工業技術研究院 | 具風險評估之最佳取樣參數搜尋系統、方法與圖案化使用者介面 |
| GB2592890A (en) * | 2019-12-18 | 2021-09-15 | Kalibrate Tech Limited | Discrete Optimisation |
| CN111241692B (zh) * | 2020-01-16 | 2022-11-08 | 南京航空航天大学 | 一种用于轮胎魔术公式的参数辨识方法 |
| CN111652412B (zh) * | 2020-05-20 | 2022-07-05 | 华中科技大学 | 一种应用于置换流水车间的邻域搜索调度方法及装置 |
| CN112859912B (zh) * | 2021-01-11 | 2022-06-21 | 中国人民解放军国防科技大学 | 中继充电模式下无人机路径规划的自适应优化方法与系统 |
| CN112883493B (zh) * | 2021-03-16 | 2023-04-11 | 中国人民解放军国防科技大学 | 一种基于迭代空间映射的无人机在线协同空域冲突消解方法 |
| CN113283194B (zh) * | 2021-05-31 | 2022-08-02 | 深圳大学 | 获取天然气系统最小状态气流量的节点级分散方法 |
| CN114911270A (zh) * | 2022-06-20 | 2022-08-16 | 南京信息工程大学 | 一种基于并行自适应蚁群算法的无人机覆盖路径规划方法 |
Family Cites Families (8)
| Publication number | Priority date | Publication date | Assignee | Title |
|---|---|---|---|---|
| US2002A (en) * | 1841-03-12 | Tor and planter for plowing | ||
| JP2779736B2 (ja) * | 1992-08-03 | 1998-07-23 | 株式会社日立製作所 | 最適化装置およびそれを利用した工程計画作成装置 |
| US6076030A (en) * | 1998-10-14 | 2000-06-13 | Carnegie Mellon University | Learning system and method for optimizing control of autonomous earthmoving machinery |
| US6490572B2 (en) * | 1998-05-15 | 2002-12-03 | International Business Machines Corporation | Optimization prediction for industrial processes |
| US6826549B1 (en) * | 1999-11-04 | 2004-11-30 | Mitsubishi Electric Research Laboratories, Inc. | Interactive heuristic search and visualization for solving combinatorial optimization problems |
| US6606529B1 (en) * | 2000-06-09 | 2003-08-12 | Frontier Technologies, Inc. | Complex scheduling method and device |
| US6961685B2 (en) | 2000-09-19 | 2005-11-01 | Sy Bon K | Probability model selection using information-theoretic optimization criterion |
| US7277832B2 (en) | 2001-05-04 | 2007-10-02 | Bigwood Technology, Inc. | Dynamical method for obtaining global optimal solution of general nonlinear programming problems |
-
2002
- 2002-05-22 US US10/153,070 patent/US7050953B2/en not_active Expired - Fee Related
- 2002-09-20 TW TW091121697A patent/TWI261763B/zh not_active IP Right Cessation
-
2003
- 2003-05-21 WO PCT/US2003/016039 patent/WO2003100598A1/en active Application Filing
- 2003-05-21 CN CNA038170116A patent/CN1668996A/zh active Pending
- 2003-05-21 AU AU2003237905A patent/AU2003237905A1/en not_active Abandoned
- 2003-05-21 JP JP2004507985A patent/JP2005527034A/ja active Pending
Cited By (8)
| Publication number | Priority date | Publication date | Assignee | Title |
|---|---|---|---|---|
| CN105095680A (zh) * | 2015-09-21 | 2015-11-25 | 武汉理工大学 | 基于微分测度随机相遇不确定性的搜救方法及系统 |
| CN105095680B (zh) * | 2015-09-21 | 2018-01-23 | 武汉理工大学 | 基于微分测度随机相遇不确定性的搜救方法及系统 |
| CN108228135A (zh) * | 2016-12-15 | 2018-06-29 | 上海寒武纪信息科技有限公司 | 一种运算多种超越函数的装置 |
| CN108228135B (zh) * | 2016-12-15 | 2021-09-07 | 上海寒武纪信息科技有限公司 | 一种运算多种超越函数的装置 |
| CN106597856A (zh) * | 2016-12-29 | 2017-04-26 | 北京理工大学 | 基于网格搜索的双星系统空间轨道族搜索方法 |
| CN109345465A (zh) * | 2018-08-08 | 2019-02-15 | 西安电子科技大学 | 基于gpu的高分辨率图像实时增强方法 |
| CN109345465B (zh) * | 2018-08-08 | 2023-04-07 | 西安电子科技大学 | 基于gpu的高分辨率图像实时增强方法 |
| CN112258515A (zh) * | 2020-12-24 | 2021-01-22 | 上海国微思尔芯技术股份有限公司 | 一种基于固定顶点的图分割方法 |
Also Published As
| Publication number | Publication date |
|---|---|
| AU2003237905A1 (en) | 2003-12-12 |
| WO2003100598A1 (en) | 2003-12-04 |
| TWI261763B (en) | 2006-09-11 |
| US7050953B2 (en) | 2006-05-23 |
| JP2005527034A (ja) | 2005-09-08 |
| US20030220772A1 (en) | 2003-11-27 |
Similar Documents
| Publication | Publication Date | Title |
|---|---|---|
| CN1668996A (zh) | 解大型连续性或离散性最佳化问题的动态方法 | |
| CN1186714C (zh) | 高基除法器及方法 | |
| CN1673965A (zh) | 实时可调度性确定方法和实时系统 | |
| CN1875345A (zh) | 在编译过程中表示和检查程序组件的一致性的可扩展类型系统 | |
| CN1568396A (zh) | 第2级涡轮喷嘴翼面 | |
| CN1763743A (zh) | 图表上的自动标签放置系统和方法 | |
| CN1897556A (zh) | 信息处理设备、信息处理方法和信息处理程序 | |
| CN1647139A (zh) | 数据变换装置和数据变换方法 | |
| CN1576516A (zh) | 涡轮叶片的翼面形状 | |
| CN1760804A (zh) | 信息处理设备,信息处理方法,及计算机程序 | |
| CN1580500A (zh) | 涡轮喷嘴的翼面形状 | |
| CN1950850A (zh) | 图像处理设备和方法、记录介质和程序 | |
| CN1860441A (zh) | 用于可重新配置环境中的高效高性能数据操作元件 | |
| CN1801183A (zh) | 信息处理装置和方法以及程序 | |
| CN1510593A (zh) | 编排系统、编排程序和编排方法 | |
| CN1580499A (zh) | 周围冷却的涡轮机叶片的翼面冷却孔位置、形式及结构 | |
| CN1592905A (zh) | 自动产生数据库查询的系统和方法 | |
| CN1766886A (zh) | 用于数据管理和/或转换的数据结构、数据库系统及方法 | |
| CN1783075A (zh) | 用于显示网络数据的方法、设备、处理器配置 | |
| CN1530855A (zh) | 布局系统和布局程序以及布局方法 | |
| CN1258729C (zh) | 基于虚拟模块的大规模混合模式布图方法 | |
| CN101038672A (zh) | 一种图像跟踪方法及系统 | |
| CN101044450A (zh) | 处理器 | |
| CN101078994A (zh) | 编译器装置、编译器方法和编译器程序 | |
| CN1624698A (zh) | 高阶合成方法和高阶合成装置 |
Legal Events
| Date | Code | Title | Description |
|---|---|---|---|
| C06 | Publication | ||
| PB01 | Publication | ||
| C10 | Entry into substantive examination | ||
| SE01 | Entry into force of request for substantive examination | ||
| C02 | Deemed withdrawal of patent application after publication (patent law 2001) | ||
| WD01 | Invention patent application deemed withdrawn after publication |