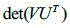CN115984442B - Method for generating surface 3D texture through feature array - Google Patents
Method for generating surface 3D texture through feature array Download PDFInfo
- Publication number
- CN115984442B CN115984442B CN202310265275.7A CN202310265275A CN115984442B CN 115984442 B CN115984442 B CN 115984442B CN 202310265275 A CN202310265275 A CN 202310265275A CN 115984442 B CN115984442 B CN 115984442B
- Authority
- CN
- China
- Prior art keywords
- grid
- points
- edge
- point
- intersection
- Prior art date
- Legal status (The legal status is an assumption and is not a legal conclusion. Google has not performed a legal analysis and makes no representation as to the accuracy of the status listed.)
- Active
Links
- 238000000034 method Methods 0.000 title claims abstract description 55
- 238000013519 translation Methods 0.000 claims abstract description 5
- 238000013507 mapping Methods 0.000 claims description 26
- 239000011159 matrix material Substances 0.000 claims description 21
- 238000000354 decomposition reaction Methods 0.000 claims description 3
- 238000009958 sewing Methods 0.000 claims description 2
- 230000000694 effects Effects 0.000 abstract description 4
- 230000007547 defect Effects 0.000 abstract 1
- 238000010586 diagram Methods 0.000 description 8
- 230000009466 transformation Effects 0.000 description 4
- 238000003491 array Methods 0.000 description 3
- 238000012545 processing Methods 0.000 description 3
- 238000003780 insertion Methods 0.000 description 2
- 230000037431 insertion Effects 0.000 description 2
- 230000009286 beneficial effect Effects 0.000 description 1
- 230000008859 change Effects 0.000 description 1
- 238000012986 modification Methods 0.000 description 1
- 230000004048 modification Effects 0.000 description 1
- 230000008569 process Effects 0.000 description 1
- 238000006467 substitution reaction Methods 0.000 description 1
- 238000000844 transformation Methods 0.000 description 1
Images
Classifications
-
- Y—GENERAL TAGGING OF NEW TECHNOLOGICAL DEVELOPMENTS; GENERAL TAGGING OF CROSS-SECTIONAL TECHNOLOGIES SPANNING OVER SEVERAL SECTIONS OF THE IPC; TECHNICAL SUBJECTS COVERED BY FORMER USPC CROSS-REFERENCE ART COLLECTIONS [XRACs] AND DIGESTS
- Y02—TECHNOLOGIES OR APPLICATIONS FOR MITIGATION OR ADAPTATION AGAINST CLIMATE CHANGE
- Y02T—CLIMATE CHANGE MITIGATION TECHNOLOGIES RELATED TO TRANSPORTATION
- Y02T90/00—Enabling technologies or technologies with a potential or indirect contribution to GHG emissions mitigation
Landscapes
- Image Generation (AREA)
Abstract
The invention discloses a method for generating a surface 3D texture through a feature array, which is used for generating regular 3D texture features on the surface of a triangular mesh to play a role in skid resistance and attractive appearance. The invention uses the edge contour of the characteristic grid as a basic graph, and after scaling and array, the basic graph is intersected with the uv unfolding graph of the selected area of the main grid, the intersection result is mapped back to the main grid to obtain a plurality of polygonal areas, then triangular patches in each area are deleted to form holes, and then the edge contour of the characteristic grid is matched with the corresponding holes through scaling, rotation and translation of the characteristic grid, and the integrated grid is formed after stitching. When the feature grid is small, the effect of 3D texture can be achieved. Compared with the defects that the traditional method depends on a bitmap, generates a compact grid and only supports 2.5 dimensions, the grid density of the method depends on the characteristic grid, the data volume is greatly reduced, and the quasi-3-dimensional characteristic is supported.
Description
Technical Field
The invention belongs to the field of graphic processing, and particularly relates to a method for generating a surface 3D texture through a feature array.
Background
In order to generate 3D texture features, two methods exist, one of which is to extract height information from a 2D texture image and map the height information into a three-dimensional space through parameterization, and the grid generated by the method is rich in detail, generally needs to encrypt the grid, so that the data volume is huge, or the grid needs to be simplified in extra time; second, such methods can only generate 2.5-dimensional features, and cannot generate quasi-3-dimensional features.
Another 3D texture is more regular, mainly repeating basic features. Theoretically, this feature requires fewer triangular patches to be expressed, but still requires a 2D image to be expressed, and cannot generate a more complex spatial structure.
Therefore, in order to overcome the shortcomings of the two methods, a method for generating a surface 3D texture with a complex spatial structure is needed, the processing speed is high, and the generated model data volume is small.
Disclosure of Invention
The invention aims to provide a method for generating a surface 3D texture through a feature array, which has the advantages of small data volume, support of a quasi 3D feature structure and high processing speed.
In order to achieve the technical purpose, the invention adopts the following technical scheme:
a method of generating a 3D texture of a surface by an array of features, comprising the steps of:
(a) Establishing a main model, namely a topological connection relation of a main grid M, by adopting a half-side structure, and calculating unit normal directions of all triangles f;
(b) Creating a sub-grid N on the surface of the main grid M according to the vertexes and the triangles f in the area, constructing a mapping relation R, mapping the vertexes in the sub-grid N on the corresponding vertexes in the main grid M one by one and recording, identifying the boundary of the sub-grid N, and expanding the sub-grid N to a uv plane through a parameterization method to form a parameterized grid;
(c) Marking the edge contour of the bottom surface of the feature grid as a polygon Pi, then arranging the polygon Pi according to a set mode and intervals to completely cover the parameterized grid area of the sub-grid N, and reserving the polygon completely in the parameterized grid area to form a set { S };
(d) Intersecting the polygons Pi in the set { S } with the parameterized grid, mapping the intersection points to the main grid M, inserting new vertexes at the intersection point positions on the main grid, mapping the polygons in the set { S } to the main grid to obtain a series of closed areas surrounded by half edges, recording as { Loop }, and inserting new edges according to the area boundaries;
(e) Triangularizing the surfaces of more than 3 sides in the main grid M, deleting triangles f in each closed area in the { Loop }, and obtaining a series of holes;
(f) And scaling the feature grid according to the size of the hole, rotating and translating the feature grid, adjusting the edge points of the feature grid to the corresponding points on the hole, and sewing the main grid M and each transformed feature grid into a whole for Ji Kongwei.
The edge contour of the characteristic grid is taken as a basic graph, after scaling and array, the basic graph is intersected with a uv unfolding graph of a selected area of the main grid, an intersection result is mapped back to the main grid to obtain a plurality of polygonal areas, triangular patches in each area are deleted to form holes, and then the edge contour of the characteristic grid is matched with the corresponding holes through scaling, rotation and translation of the characteristic grid, and the integrated grid is formed after stitching. When the feature grid is small, the effect of 3D texture can be achieved.
Further, in the step (d), the specific method for intersecting the polygon Pi with the parameterized mesh is as follows: for any polygon Pi in the set { S }, starting from the sequence number 0, finding a vertex P0 completely inside the triangle f, and starting from the vertex P0, calculating a series of intersection points of Pi and the parameterized grid, wherein the coordinates pt of the intersection points are recorded, the half h0 of the intersection points is recorded, the ratio t of the distance from the intersection point to the starting point of the half to the length of the half is recorded, after the intersection points are inserted, the half of the point is divided into two parts, the starting point of the h0 is unchanged, the ending point points pt, the total length is shortened, and the rest part forms a new half h1, and o1 is the opposite half of the h 1.
The main grid M or the sub-grid N thereof is curved in space, and needs to be flattened on a uv plane through parameterization, so that the parameterized grid can be intersected with a plane pattern formed by the edge contours of the characteristic grid.
The polygons Pi intersect the parameterized grid, and different intersection information needs to be recorded according to whether the intersection points are inside or on the sides of the triangle, so that mapping back to the corresponding positions of the main grid M is facilitated.
Further, in step (d), the vertices of the polygon Pi are also treated as intersections, and when the vertices are completely inside the triangle f, t= -1, h0 takes the half-edge h pointed by the triangle f; when the vertex is on the triangle f side, the vertex is judged to be on the grid side.
Vertices of the polygon Pi are also treated as intersections for recording the shape of the polygon Pi.
Further, in the step (d), the specific method for mapping the polygons in the set { S } to the main mesh is as follows: according to the mapping relation R, mapping intersection point information from the parameterized grid of the sub-grid N back to the main grid M, namely mapping back the end points of the edges, and then calculating the intersection point coordinates of the mapping edges according to the proportion value t of the intersection points; for points in the triangle f, calculating the barycenter coordinates on the parameterized grid of the sub-grid N, and then calculating the coordinates of the corresponding points in the main grid M by using the barycenter coordinates; at the same time, the half h0 where the intersection point is located is also pointed to the corresponding half in the main grid M.
For the intersection points on the parameterized grid, mapping to a main grid M according to the proportion value t of the intersection points; for points within triangle f, it is mapped to the main mesh M according to its centroid coordinates.
Further, in the step (d), a series of closed areas surrounded by half edges are obtained by the following specific methods: classifying intersection points with t value not being-1 according to the edge, if any intersection point exists on any one edge, recording that two half edges of the edge are respectively he0 and he1, taking he0 as a reference, and when the half edge with the intersection point is he1, replacing the corresponding t with 1.0-t; the intersections on the edge are ordered from big to small according to the t value, then the intersections are sequentially inserted into the half-edge he0, and h0 and o1 in the intersection information are updated at the same time.
After the intersection points are inserted, the half sides of the closed area can be formed for recording, and the closed area can correspond to the bottom edge outline of the feature grid.
Further, in the step (d), the specific method of inserting new edges according to these region boundaries is as follows: dividing a polygon set { S } into two types { S1} and { S2}, wherein the values of t of the intersections of the polygons in { S2} and the N parameterized grids of the sub-grids are all-1 or the vertices are judged to be on the grid edges, the { S1} is the part except for { S2} in { S }, finding out all intersection serial numbers of t not equal to-1 for the intersections of any polygon in the set { S1}, and inserting edges into the triangular grids for any two serial numbers i and j adjacent to each other according to the situation:
when i and j are on the same side, the o1 of the intersection point i and the o1 of the intersection point j are on the same side, at the moment, a new edge ji is inserted according to h0 of the intersection point j and the o1 of the intersection point i, wherein a half newH pointing to i from j points to an original surface f0, the opposite half of newH points to a newly created surface f1, then points i1, i2, i3 and i4 are sequentially inserted into the half newH, and the starting point of newH is unchanged and the end point is contracted towards j when one point is inserted;
when i and j are not on the same edge, a new edge ij is inserted according to o1 of an intersection point i and h0 of the intersection point j, wherein a half newH pointing to j from i points to an original surface f0, the opposite side newH points to a newly created surface f1, then points i3, i2 and i1 are sequentially inserted on the half newH, and the starting point of the newH is unchanged and the end point is contracted towards i when one point is inserted.
And inserting edges into the triangular grids according to the condition aiming at whether the intersection points of i and j are on the same edge or not, so as to obtain polygons corresponding to the edge contours of the feature grids on the main grids.
Further, in the step (e), the specific method of surface triangularization of more than 3 sides in the main grid M is as follows: for the polygon Pi in the set { S2}, find the plane F0 where it is located, add F0 into the set { F }, then find the polygon set { Poly }, which is completely inside, for any one of the planes Fi in { F }, determine the normal n of the plane Fi by backtracking, then rotate Fi and { Poly } to make the normal n parallel to +Z, set the rotation matrix as R, thus make Fi and { Poly } on the same horizontal plane, regard the edge where Fi is located as the area boundary, triangulate with the edge where { Poly } islocated as the constraint edge, then rotate the internal point of the area back according to the triangularization result, the rotation matrix is R -1 And inserted into the main mesh M, and the triangle f in the region is added to the main mesh M.
And rotating the space plane area to be triangulated to a horizontal position, and after plane triangulating is completed, rotating back through inverse transformation, so as to realize triangulating of the space area on the main grid M.
Further, in step (e), recording half sides advancing along polygons intersecting the grid sides to form a closed loop; recording half sides corresponding to all polygons in the set { Poly }, and forming a closed loop; placing the closed loops in a set { Loop }, all halves on each closed Loop pointing to contiguous triangles within the area enclosed by the closed loops; meshing the surface with the edge number larger than 3 in the main mesh to form a series of triangles; for any closed Loop L in the set { Loop }, a triangle in the area surrounded by L is found and deleted, forming a series of holes, denoted as { H }.
The triangle in the closed loop L needs to be deleted to create a hole corresponding to the bottom edge profile of the feature grid.
Further, in the step (f), the specific method for aligning the hole sites is as follows: calculating the characteristic size of any hole in the set { H }, such as the perimeter of the hole, calculating the perimeter of a polygon P formed by the edges of the characteristic grids, scaling the characteristic grids to ensure that the perimeter of the polygon P is equal to the perimeter of the hole, subdividing the edge polygons of the characteristic grids to ensure that the number of top points is the same as the number of top points on the hole and corresponds to each other according to the length proportion, and then rotating and translating the characteristic grids to ensure that the polygons on the characteristic grids are aligned with the hole.
Further, in step (f), the apertures on the main mesh M are aligned with the corner points of the polygon P formed by the edges of the feature mesh, and the mesh is aligned by minimizing the sum of squares of the point-to-distance, minimizing the following function:wherein p is i And q i The method comprises the steps that points on the edges of a characteristic grid and matching points on the edges of holes of a main grid M are respectively, R and t are respectively an integral rotation matrix and an integral translation vector, and the values of the points are unequal for each hole on the main grid M; to minimize f (R, t), R and t are as follows: />Wherein->,/>,/>For VU T Is an orthogonal matrix from the covariance matrix s=xy -T Singular value decomposition ∈>Wherein the matrix x= [ X ] 1 x 2 … x n ]Matrix y= [ Y ] 1 y 2 … y n ],And->,/>,/>The method comprises the steps of carrying out a first treatment on the surface of the For any point p on the feature grid i Calculating p i =Rp i And +t, through the transformation, the distance between the point on the edge of the characteristic grid and the matching point on the corresponding hole of the main grid M is minimum in the least square sense, but the point does not completely coincide, and the coordinates of the edge point of the characteristic grid are replaced by the coordinates of the matching point on the corresponding hole of the main grid M.
The openings in the main mesh M are generally not in the same plane, but the polygons formed by the edges of the feature mesh are in the same plane, so that the points on the edges of the feature mesh need to be properly adjusted to match the openings in the main mesh M.
By adopting the technical scheme, the invention has the following beneficial effects:
1. the polygons formed by the edge contours of the feature grids are used as basic patterns to be arrayed, a 3D texture library can be built only by preparing corresponding feature grid models, the feature grid files are far smaller than the bitmap, and finally the generated model files with 3D texture effects are relatively smaller.
2. The feature grid edge points are matched with the corresponding points of the holes on the main grid, the feature grid can be matched to the aligned holes only by one calculation, and the calculation speed is high.
3. The traditional bitmap-based method is only one high field, the invention can use a quasi-3-dimensional feature grid, and the feature grid can have a complex spatial structure.
Drawings
The invention is further described below with reference to the accompanying drawings.
FIG. 1 is a flow chart of a method of generating a 3D texture of a surface by an array of features.
Fig. 2 is a schematic diagram showing the change of intersection information before and after intersection points are inserted by intersecting sides of the polygon Pi with the parameterized mesh.
FIG. 3 is a schematic diagram of a polygon array intersecting a parameterized grid.
Fig. 4 is a schematic diagram of vertices of a polygon Pi on a mesh side.
Fig. 5 is a schematic illustration of the insertion of an intersection point on one side of a polygon Pi.
Fig. 6 is a schematic diagram of intersection points i and j of two adjacent t values, which are not-1, in the intersection points of the polygon Pi and the parameterized grid on the same edge.
FIG. 7 is a schematic diagram of points of intersection i, j, where two adjacent t values are not-1, among the points of intersection of the polygon Pi and the parameterized mesh, on different sides.
FIG. 8 is a schematic diagram of a triangle f0 broken up by an array of polygons, the triangle f0 excluding the area resulting from the intersection with each polygon, and the area being triangulated.
Fig. 9 is a schematic illustration of a pyramid-shaped, top-balled feature grid with non-fully aligned openings after scaling.
Fig. 10 is a schematic illustration of a bottom-opening pyramid-shaped feature grid aligned with openings in a curved surface.
FIG. 11 is a schematic diagram of vertex position changes after feature mesh scaling, edge subdivision, and point matching.
FIG. 12 is an array of pyramid and truncated pyramid feature grids generated on a handle surface and cylinder using the method of the present invention.
Fig. 13 shows a honeycomb array formed by two adjacent rows of intersecting sided hexagons in a staggered arrangement.
Fig. 14 is a circumferential array of two sets of four-pointed star shapes that are progressively enlarged in the radial direction.
Fig. 15 is a rectangular array of basic cells consisting of two differently shaped polygons.
Detailed Description
A method of generating a 3D texture of a surface by an array of features as shown in fig. 1, comprising the steps of:
(a) Establishing a main model, namely a topological connection relation of a main grid M, by adopting a half-side structure, and calculating unit normal directions of all triangles f;
(b) Selecting a region on the surface of a main grid M, creating a sub-grid N according to vertexes and triangles f in the region, constructing a mapping relation R, mapping vertexes in the sub-grid N onto corresponding vertexes in the main grid M one by one, recording, identifying the boundary of the sub-grid N, and expanding the sub-grid N to a uv plane by a parameterization method;
(c) Marking the edge contour of the bottom surface of the feature grid as a polygon Pi, then arranging the polygon Pi according to a set mode and intervals to completely cover the parameterized grid area of the sub-grid N, and reserving the polygon completely in the parameterized grid area to form a set { S };
(d) As shown in fig. 2, for any polygon Pi in the set { S }, starting from sequence number 0, a vertex P0 is found that is completely inside triangle f, and starting from P0, a series of intersections of Pi and the parameterized mesh are calculated, where the coordinates pt of the intersection are recorded, the half h0 where the intersection is located, and the ratio t of the distance of the intersection from the half starting point to the half length. If the polygon vertex is inside the triangle, such as P0, the value of t takes a value of-1. If the polygon vertex is on the triangle side, then the vertex is judged to be on the grid side. These two types of points are referred to as "feature points". After the intersection point is inserted, the half side where the point is divided into two parts, the starting point of h0 is unchanged, the end point points to point pt, the total length is shortened, the rest part forms a new half side h1, and o1 is the opposite half side of h 1. In FIG. 2, the t value of the 1 st intersection pt is 0.5, the 2 nd intersectionptA kind of electronic devicetThe value is0.25With the 2 nd intersection pointptRelated informationh0、h1、o1Are shown in bold italics to distinguish homonymic information associated with the 1 st intersection pt.
As shown in fig. 3, the parameterized grid has only two triangles (represented by thick solid lines) and the set S is made up of a series of squares (represented by thin solid lines), each of which intersects the parameterized grid at 4 points, with the remaining squares being entirely inside one of the triangles except the square that intersects the diagonal line.
The vertex of the polygon Pi is also treated as an intersection point, when the vertex is in a certain triangle f, let t= -1, h0 take half h pointed by f, and f can be found through h; when the vertex is on the side of a triangle, as shown in fig. 4, the next line segment of the polygon Pi may continue to enter the next adjacent triangle, or may turn back, as shown in fig. 4, the end points of the line segments i1-i2 and i4-i5 on the plane f0 are all on the grid side, so that the intersection point is determined as the end point of the current line segment, the next line segment i2-i3 enters the adjacent plane f1, and the line segments i5-i6 turn back to the plane f0, where the intersection points i2 and i5 are calculated only 1 time.
According to the mapping relation R, mapping intersection point information from the sub-grid N parameterized grid back to the main grid M, namely mapping back the end points of the edges, and then calculating the intersection point coordinates of the mapping edges according to the proportion value t of the intersection points; for points in the triangle f, calculating the barycenter coordinates on the parameterized grid of the sub-grid N, and then calculating the coordinates of the corresponding points in the main grid M by using the barycenter coordinates; at the same time, the half h0 where the intersection point is located is also pointed to the corresponding half in the main grid M.
The specific method for obtaining a series of closed areas surrounded by half edges is as follows: classifying the intersection points with t value not being-1 according to the edge (a certain half edge and the opposite half edge belong to the same edge), so that the intersection points on one edge can be known; if any one side has an intersection point, marking two half sides of the side as he0 and he1 respectively, taking he0 as a reference, and when the half side where the intersection point is located is he1, replacing the corresponding t with 1.0-t; the intersections on the edge are ordered from big to small according to the value of t, then the intersections are sequentially inserted into the half he0 (in the process, the starting point of he0 is unchanged, the end point points to the newly inserted point each time, the length is continuously reduced), and h0 and o1 in the intersection information are updated.
Taking fig. 5 as an example, h0 of the intersection points a and C is he0, h0 of the intersection points B and D is he1, t values of the intersection points B and D need to be 1.0-t, then, the intersection points are arranged from large to small according to t to obtain a sequence D, C, B, A, the points D, C, B, A are sequentially inserted on the half edge he0, finally, h0 of the intersection point a is he1, h0 of the intersection point B is o3, h0 of the intersection point C is the opposite half edge of o3, h0 of the intersection point D is o1, o1 of 4 points is calculated, and the opposite half edge of the next half edge of each h0 is taken, for example, o1 of the intersection point D is the opposite half edge of o2 in fig. 5. The specific method for inserting new edges according to the boundaries of the areas is as follows: dividing a polygon set { S } into two types { S1} and { S2}, wherein the values of t of the intersections of the polygons in { S2} and the N parameterized grids of the sub-grids are all-1 or are judged to be the end points of the current line segments, the { S1} is a part except for { S2} in { S }, finding out all intersection serial numbers of t not equal to-1 for the intersections of any polygon in the set { S1}, and inserting edges into the triangular grids for any two serial numbers i and j adjacent to each other according to the situation:
as shown in FIG. 6, when i andjo1 at the intersection i and the intersection when on the same sidejA kind of electronic deviceo1On the same side, at this time, according to the intersection pointjA kind of electronic deviceh0O1 insertion new edge with intersection iji, wherein is fromjThe half newH pointing to i points to the original surface f0, the opposite half of newH points to the newly created surface f1, then points i1, i2, i3 and i4 are sequentially inserted into the half newH, and the starting point of newH is unchanged and the end point is toward each pointjAnd (5) shrinkage. In FIG. 6, andjrelated toh0、o1Bold italics are used to distinguish the homonymic information associated with i.
As shown in FIG. 7, when i and j are not on the same side, o1 and the intersection point according to the intersection point ijA kind of electronic deviceh0Inserting new edge ijWherein from i point tojThe half newH of the new line points to the original surface f0, the opposite half of the newH points to the newly created surface f1, then points i3, i2 and i1 are sequentially inserted into the half newH, the starting point of the newH is unchanged when a point is inserted, and the end point is contracted towards i. In FIG. 7, andjrelated toh0、o1Bold italics are used to distinguish the homonymic information associated with i.
(e) For the polygon Pi in the set { S2}, find the plane F0 where it is located, add F0 into the set { F }, then find the polygon set { Poly }, which is completely inside, for any one of the planes Fi in { F }, determine the normal n of the plane Fi by backtracking, then rotate Fi and { Poly } to make the normal n parallel to +Z, set the rotation matrix as R, thus make Fi and { Poly } on the same horizontal plane, regard the edge where Fi is located as the area boundary, triangulate with the edge where { Poly } islocated as the constraint edge, then rotate the internal point of the area back according to the triangularization result, the rotation matrix is R -1 And inserted into the main mesh M, and the triangle f in the region is added to the main mesh M. Taking fig. 8 as an example, the original triangle area f0 is split into 10 faces of new f0 (corresponding to Fi) and f1 to f9,the new f0 is shown in the middle sub-graph of FIG. 8, which contains a polygon Poly_i completely inside f0, which is the only element that constitutes the set of { Poly }. The right hand sub-graph of fig. 8 shows the triangularization result with the new f0 as the region boundary and poly_i as the constraint edge.
Recording the advancing half sides along the polygons intersected with the grid sides to form a closed loop; recording half sides corresponding to the polygons in the set { Poly }, and forming a closed loop (e.g., v0-v1-v2-v3 in FIG. 8); placing the closed loops in a set { Loop }, all halves on each closed Loop pointing to contiguous triangles within the area enclosed by the closed loops; meshing the surface with the edge number larger than 3 in the main mesh to form a series of triangles; for any closed Loop L in the set { Loop }, a triangle in the area surrounded by L is found and deleted, forming a series of holes, denoted as { H }.
(f) Calculating the characteristic size of any hole in the set { H }, such as the perimeter of the hole, calculating the perimeter of a polygon P formed by the edges of the characteristic grids, scaling the characteristic grids to ensure that the perimeter of the polygon P is equal to the perimeter of the hole, subdividing the edge polygons of the characteristic grids to ensure that the number of top points is the same as the number of top points on the hole and corresponds to each other according to the length proportion, and then rotating and translating the characteristic grids to ensure that the polygons on the characteristic grids are aligned with the hole.
The graph below in fig. 9 shows the scaled but not fully aligned case, the alignment method is as follows:
first, the correspondence relation between feature points is determined, as shown in fig. 10, and large and small squares indicated by thick solid lines respectively correspond to the openings on the main mesh M and the polygons P formed by the edges of the feature meshes. The 4 corner points of the large square have been marked as "feature points" in the previous step, assuming that these points are aligned one-to-one with the 4 adjacent corner points in the small square;
secondly, in order to make the small square perfectly matched, the corresponding points need to be inserted into the small square so that the points of the small square are identical and the positions of the small square are in one-to-one correspondence with each other, as shown by the arrow in the right sub-graph of fig. 10.
In addition, the openings on the main grid M are not generally on the same plane, but the polygons formed by the edges of the feature grid are on the same plane, so that the points on the edges of the feature grid need to be properly adjusted to match the openings on the main grid M.
FIG. 11 is a diagram of feature grid edge subdivision and point matching, where the left side feature grid is scaled, translated, rotated, top edge contour subdivided, and matched to holes to obtain the right side grid. The top edge profile is originally square on the same plane, and after the holes are matched, the space closed broken line is changed.
The apertures on the main mesh M are aligned with the corner points of the polygon P made up of the edges of the feature mesh, the mesh is aligned by minimizing the sum of the squares of the distances of the points, minimizing the following function:wherein p is i And q i The method comprises the steps that points on the edges of a characteristic grid and matching points on the edges of holes of a main grid M are respectively, R and t are respectively an integral rotation matrix and an integral translation vector, and the values of the points are unequal for each hole on the main grid M; to minimize f (R, t), R and t are as follows: />Wherein->,/>,/>For VU T Is an orthogonal matrix from the covariance matrix s=xy -T Singular value decomposition ∈>Wherein the matrix x= [ X ] 1 x 2 … x n ]Matrix y= [ Y ] 1 y 2 … y n ],/>And->,,/>The method comprises the steps of carrying out a first treatment on the surface of the For any point p on the feature grid i Calculating p i =Rp i And +t, through the transformation, the distance between the point on the edge of the characteristic grid and the matching point on the corresponding hole of the main grid M is minimum in the least square sense, but the point does not completely coincide, and the coordinates of the edge point of the characteristic grid are replaced by the coordinates of the matching point on the corresponding hole of the main grid M.
Finally, the three-dimensional model M is stitched together with the feature grid around each hole to form a unified whole.
The method of the invention is used for generating the feature grid array of the pyramid and the pyramid with the ball at the top end on the surface of the main model of the cube.
In addition to generating the feature array on a plane, the feature grid array may be generated on any curved surface as well as on a cylindrical surface. Fig. 12 illustrates the generation of pyramid and truncated pyramid feature grid arrays on a handle using the method of the present invention. Wherein the top feature size is not necessarily a result of parametric distortion.
Second, the feature grid may comprise a very complex spatial structure, an array of feature grids, with 4 struts meeting at the top and a circular hole in the middle of the top, a quasi-three dimensional structure that is distinguished from 2.5 dimensions.
Again, the edge profile of the feature grid is not limited to a quadrilateral, a five-pointed star array generated in a localized area of the surface, wherein the edge profile of the feature grid is a concave decagon.
In addition, the embodiment of fig. 12 employs a rectangular array, but the pattern of the array is not limited, and other arrays or mathematical transformations are possible, as well as combinations of a plurality of different feature grid arrays, such as those shown in fig. 13-15.
The above is only a specific embodiment of the present invention, but the technical features of the present invention are not limited thereto. Any simple changes, equivalent substitutions or modifications made on the basis of the present invention to solve the substantially same technical problems and achieve the substantially same technical effects are encompassed within the scope of the present invention.
Claims (10)
1. A method of generating a 3D texture of a surface by an array of features, comprising the steps of:
(a) Establishing a main model, namely a topological connection relation of a main grid M, by adopting a half-side structure, and calculating unit normal directions of all triangles f;
(b) Creating a sub-grid N in a region selected by the surface of the main grid M according to vertexes and triangles f in the region, constructing a mapping relation R, mapping vertexes in the sub-grid N onto corresponding vertexes in the main grid M one by one and recording, identifying boundaries of the sub-grid N, and expanding the sub-grid N to a uv plane through a parameterization method to form a parameterized grid;
(c) Marking the edge contour of the bottom surface of the feature grid as a polygon Pi, then arranging the polygon Pi according to a set mode and intervals to completely cover the parameterized grid area of the sub-grid N, and reserving the polygon completely in the parameterized grid area to form a set { S };
(d) Intersecting the polygons Pi in the set { S } with the parameterized grid, mapping the intersection points to the main grid M, inserting new vertexes at the intersection point positions on the main grid, mapping the polygons in the set { S } to the main grid to obtain a series of closed areas surrounded by half edges, recording as { Loop }, and inserting new edges according to the area boundaries;
(e) Triangularizing the surfaces of more than 3 sides in the main grid M, deleting triangles f in each closed area in the { Loop }, and obtaining a series of holes;
(f) And scaling the feature grid according to the size of the hole, rotating and translating the feature grid, adjusting the edge points of the feature grid to the corresponding points on the hole, and sewing the main grid M and each transformed feature grid into a whole for Ji Kongwei.
2. A method of generating a 3D texture of a surface by an array of features as claimed in claim 1, wherein: in step (d), the specific method for intersecting the polygon Pi with the parameterized mesh is as follows: for any polygon Pi in the set { S }, starting from the sequence number 0, finding a vertex P0 completely inside the triangle f, and starting from the vertex P0, calculating a series of intersection points of Pi and the parameterized grid, wherein the coordinates pt of the intersection points are recorded, the half h0 of the intersection points is recorded, the ratio t of the distance from the intersection point to the starting point of the half to the length of the half is recorded, after the intersection points are inserted, the half of the intersection points is divided into two parts, the starting point of the h0 is unchanged, the end point points pt and the total length are shortened, and the rest part forms a new half h1, and o1 is the opposite half of the h 1.
3. A method of generating a 3D texture of a surface by an array of features as claimed in claim 2, wherein: in step (d), the vertices of the polygon Pi are also treated as intersections, and when the vertices are completely inside the triangle f, t= -1, h0 takes the half-edge h pointed by the triangle f; when the vertex is on the triangle f side, the vertex is judged to be on the grid side.
4. A method of generating a 3D texture of a surface by an array of features as claimed in claim 2, wherein: in step (d), the specific method for mapping the polygons Pi in the set { S } to the main mesh M is: according to the mapping relation R, mapping intersection point information from the parameterized grid of the sub-grid N back to the main grid M, namely mapping back the end points of the edges, and then calculating the intersection point coordinates of the mapping edges according to the proportion value t of the intersection points; for points in the triangle f, calculating the barycenter coordinates on the parameterized grid of the sub-grid N, and then calculating the coordinates of the corresponding points in the main grid M by using the barycenter coordinates; at the same time, the half h0 where the intersection point is located is also pointed to the corresponding half in the main grid M.
5. A method of generating a 3D texture of a surface by an array of features as claimed in claim 4, wherein: in step (d), a series of closed areas surrounded by half edges are obtained by the following specific methods: classifying intersection points with t value not being-1 according to the edge, if any intersection point exists on any one edge, recording that two half edges of the edge are respectively he0 and he1, taking he0 as a reference, and when the half edge with the intersection point is he1, replacing the corresponding t with 1.0-t; the intersections on the edge are ordered from big to small according to the t value, then the intersections are sequentially inserted into the half-edge he0, and h0 and o1 in the intersection information are updated at the same time.
6. A method of generating a 3D texture of a surface by an array of features as claimed in claim 5, wherein: in step (d), the specific method for inserting new edges according to the boundaries of the areas is as follows: dividing a polygon set { S } into two types { S1} and { S2}, wherein the values of t of the intersections of the polygons in { S2} and the N parameterized grids of the sub-grids are all-1 or the vertices are judged to be on the grid edges, the { S1} is the part except for { S2} in { S }, finding out all intersection serial numbers of t not equal to-1 for the intersections of any polygon in the set { S1}, and inserting edges into the triangular grids for any two serial numbers i and j adjacent to each other according to the situation:
when i and j are on the same side, the o1 of the intersection point i and the o1 of the intersection point j are on the same side, at the moment, a new edge ji is inserted according to h0 of the intersection point j and the o1 of the intersection point i, wherein a half newH pointing to i from j points to an original surface f0, the opposite half of newH points to a newly created surface f1, then points i1, i2, i3 and i4 are sequentially inserted into the half newH, and the starting point of newH is unchanged and the end point is contracted towards j when one point is inserted;
when i and j are not on the same edge, a new edge ij is inserted according to o1 of an intersection point i and h0 of the intersection point j, wherein a half newH pointing to j from i points to an original surface f0, the opposite side newH points to a newly created surface f1, then points i3, i2 and i1 are sequentially inserted into the half pointed by newH, and the starting point of newH is unchanged and the end point is contracted towards i when one point is inserted.
7. A method of generating a 3D texture of a surface by an array of features as claimed in claim 6, wherein: in step (e), the specific method of surface triangularization of more than 3 edges in the main mesh M is: for the polygon Pi in the set { S2}, find the plane f0 where it is locatedAdding F0 into a set { F }, then finding a polygon set { Poly }, which is completely inside any one of planes Fi in { F }, determining a normal n of the planes Fi by backtracking, rotating Fi and { Poly } to enable the normal n to be parallel to +Z, setting a rotation matrix as R, so that Fi and { Poly } are on the same horizontal plane, triangulating by taking the edge where Fi is located as a region boundary and the edge where { Poly } is located as a constraint edge, and rotating back the internal points of the region according to the triangularization result, wherein the rotation matrix is R -1 And inserted into the main mesh M, and the triangle f in the region is added to the main mesh M.
8. A method of generating a 3D texture of a surface by an array of features as claimed in claim 7, wherein: in step (e), recording half sides advancing along polygons intersecting the grid sides to form a closed loop; recording half sides corresponding to all polygons in the set { Poly }, and forming a closed loop; placing the closed loops in a set { Loop }, all halves on each closed Loop pointing to contiguous triangles within the area enclosed by the closed loops; meshing the surface with the edge number larger than 3 in the main mesh to form a series of triangles; for any closed Loop L in the set { Loop }, a triangle in the area surrounded by L is found and deleted, forming a series of holes, denoted as { H }.
9. A method of generating a 3D texture of a surface by an array of features as claimed in claim 8, wherein: in the step (f), the specific method for aligning the hole sites is as follows: calculating the characteristic size of any hole in the set { H }, calculating the perimeter of a polygon P formed by the edges of the characteristic grids, scaling the characteristic grids to ensure that the perimeter of the polygon P is equal to the perimeter of the hole, subdividing the edge polygons of the characteristic grids to ensure that the number of top points is the same as the number of top points on the hole and corresponds to each other according to the length proportion, and then rotating and translating the characteristic grids to ensure that the polygons on the characteristic grids are aligned with the hole.
10. A method of generating a 3D texture of a surface by an array of features as claimed in claim 9, whereinThe method comprises the following steps: in step (f), the apertures on the main mesh M are aligned with the corner points of the polygon P formed by the edges of the feature mesh, and the mesh is aligned by minimizing the sum of the squares of the distances of the points, minimizing the following functions:wherein p is i And q i The method comprises the steps that points on the edges of a characteristic grid and matching points on the edges of holes of a main grid M are respectively, R and t are respectively an integral rotation matrix and an integral translation vector, and the values of the points are unequal for each hole on the main grid M; to minimize f (R, t), R and t are as follows:wherein->,/>,/>For VU T Is an orthogonal matrix from the covariance matrix s=xy -T Singular value decomposition ∈>Wherein the matrix x= [ X ] 1 x 2 … x n ]Matrix y= [ Y ] 1 y 2 … y n ],/>And->,I=1, 2, …, n; for any point p on the feature grid i Calculating p i =Rp i +t, transformed by this method, tThe distance between the point on the edge of the feature grid and the matching point on the corresponding hole of the main grid M is the smallest in the least square sense, but the point does not completely coincide, and the coordinates of the edge point of the feature grid are replaced by the coordinates of the matching point on the corresponding hole of the main grid M.
Priority Applications (1)
| Application Number | Priority Date | Filing Date | Title |
|---|---|---|---|
| CN202310265275.7A CN115984442B (en) | 2023-03-20 | 2023-03-20 | Method for generating surface 3D texture through feature array |
Applications Claiming Priority (1)
| Application Number | Priority Date | Filing Date | Title |
|---|---|---|---|
| CN202310265275.7A CN115984442B (en) | 2023-03-20 | 2023-03-20 | Method for generating surface 3D texture through feature array |
Publications (2)
| Publication Number | Publication Date |
|---|---|
| CN115984442A CN115984442A (en) | 2023-04-18 |
| CN115984442B true CN115984442B (en) | 2023-06-23 |
Family
ID=85958191
Family Applications (1)
| Application Number | Title | Priority Date | Filing Date |
|---|---|---|---|
| CN202310265275.7A Active CN115984442B (en) | 2023-03-20 | 2023-03-20 | Method for generating surface 3D texture through feature array |
Country Status (1)
| Country | Link |
|---|---|
| CN (1) | CN115984442B (en) |
Citations (1)
| Publication number | Priority date | Publication date | Assignee | Title |
|---|---|---|---|---|
| CN114840926A (en) * | 2022-04-27 | 2022-08-02 | 哈尔滨工业大学 | Method for generating three-dimensional finite element grid with complex tire patterns |
Family Cites Families (8)
| Publication number | Priority date | Publication date | Assignee | Title |
|---|---|---|---|---|
| US7065242B2 (en) * | 2000-03-28 | 2006-06-20 | Viewpoint Corporation | System and method of three-dimensional image capture and modeling |
| US7358969B2 (en) * | 2004-09-27 | 2008-04-15 | International Business Machines Corporation | Method and system for partitioning the surface of a three dimentional digital object model in order to map a texture |
| US9472019B2 (en) * | 2010-06-30 | 2016-10-18 | Primal Space Systems, Inc. | System and method of from-region visibility determination and delta-PVS based content streaming using conservative linearized umbral event surfaces |
| CN102306396B (en) * | 2011-09-15 | 2013-09-25 | 山东大学 | Three-dimensional entity model surface finite element mesh automatic generation method |
| US9196089B2 (en) * | 2012-05-17 | 2015-11-24 | Disney Enterprises, Inc. | Techniques for processing reconstructed three-dimensional image data |
| CN107909650A (en) * | 2017-10-23 | 2018-04-13 | 浙江大学 | One kind is based on surface fitting and geodesic complex free curved surface Meshing Method |
| CN108682043A (en) * | 2018-02-08 | 2018-10-19 | 大连理工大学 | A kind of complex-curved measure planning method based on parameter mapping |
| US10810783B2 (en) * | 2018-04-03 | 2020-10-20 | Vangogh Imaging, Inc. | Dynamic real-time texture alignment for 3D models |
-
2023
- 2023-03-20 CN CN202310265275.7A patent/CN115984442B/en active Active
Patent Citations (1)
| Publication number | Priority date | Publication date | Assignee | Title |
|---|---|---|---|---|
| CN114840926A (en) * | 2022-04-27 | 2022-08-02 | 哈尔滨工业大学 | Method for generating three-dimensional finite element grid with complex tire patterns |
Also Published As
| Publication number | Publication date |
|---|---|
| CN115984442A (en) | 2023-04-18 |
Similar Documents
| Publication | Publication Date | Title |
|---|---|---|
| Gregory et al. | Interactive surface decomposition for polyhedral morphing | |
| CN109377561A (en) | A kind of digital-to-analogue surface mesh generation method based on conformal geometry | |
| CN107330903B (en) | Skeleton extraction method of human point cloud model | |
| CN110610478B (en) | Medical image three-dimensional reconstruction method based on neighborhood topology | |
| CN109584357A (en) | Three-dimensional modeling method, device, system and storage medium based on more contour lines | |
| CN106709171B (en) | A kind of decalcomania generation method based on repeat pattern discovery | |
| CN108230452B (en) | Model hole filling method based on texture synthesis | |
| US6462740B1 (en) | System for in-scene cloth modification | |
| Athanasiadis et al. | Feature-based 3D morphing based on geometrically constrained spherical parameterization | |
| Chowdhury et al. | Garment ideation: Iterative view-aware sketch-based garment modeling | |
| CN115984442B (en) | Method for generating surface 3D texture through feature array | |
| Miao et al. | An end-to-end shape-preserving point completion network | |
| Yoo | Three-dimensional morphing of similar shapes using a template mesh | |
| Amiri et al. | Connectivity maps for subdivision surfaces | |
| Madaras et al. | Skeleton texture mapping | |
| CN114494637B (en) | Sandstone three-dimensional real model reconstruction method based on structural matrix | |
| An et al. | Self-adaptive polygon mesh reconstruction based on ball-pivoting algorithm | |
| Coeurjolly et al. | Reversible discrete volume polyhedrization using marching cubes simplification | |
| Coeurjolly et al. | Digital surface regularization with guarantees | |
| CN109523626B (en) | Method and device for converting 3D model into yarn-level model capable of being manufactured in braiding mode | |
| Ramachandran et al. | Joint planar parameterization of segmented parts and cage deformation for dense correspondence | |
| CN116451328B (en) | Design method for large rockery based on landscape architecture | |
| Zhang et al. | Detection and filling of pseudo-hole in complex curved surface objects | |
| CN109801367A (en) | A kind of grid model feature edit method based on compression manifold mode | |
| Shi et al. | Research on the Method for Smoothing Surface of 3D Model Reconstructed based on Octree |
Legal Events
| Date | Code | Title | Description |
|---|---|---|---|
| PB01 | Publication | ||
| PB01 | Publication | ||
| SE01 | Entry into force of request for substantive examination | ||
| SE01 | Entry into force of request for substantive examination | ||
| GR01 | Patent grant | ||
| GR01 | Patent grant | ||
| CP03 | Change of name, title or address | ||
| CP03 | Change of name, title or address |
Address after: B-F3 Standard Factory Building, No. 518 Xianyuan Road, Wucheng District, Jinhua City, Zhejiang Province Patentee after: Zhejiang Shanzhu Group Co.,Ltd. Country or region after: China Address before: B-F3 Standard Factory Building, No. 518 Xianyuan Road, Wucheng District, Jinhua City, Zhejiang Province Patentee before: ZHEJIANG FLASHFORGE 3D TECHNOLOGY Co.,Ltd. Country or region before: China |