CN115526956A - Pattern migration method - Google Patents
Pattern migration method Download PDFInfo
- Publication number
- CN115526956A CN115526956A CN202211121413.6A CN202211121413A CN115526956A CN 115526956 A CN115526956 A CN 115526956A CN 202211121413 A CN202211121413 A CN 202211121413A CN 115526956 A CN115526956 A CN 115526956A
- Authority
- CN
- China
- Prior art keywords
- arc
- polygon
- circular arc
- fitting
- tangent
- Prior art date
- Legal status (The legal status is an assumption and is not a legal conclusion. Google has not performed a legal analysis and makes no representation as to the accuracy of the status listed.)
- Pending
Links
- 238000000034 method Methods 0.000 title claims abstract description 20
- 230000005012 migration Effects 0.000 title abstract description 14
- 238000013508 migration Methods 0.000 title abstract description 14
- 238000004364 calculation method Methods 0.000 claims abstract description 19
- 230000001154 acute effect Effects 0.000 description 4
- 238000013461 design Methods 0.000 description 4
- 208000019300 CLIPPERS Diseases 0.000 description 1
- 230000004075 alteration Effects 0.000 description 1
- 208000021930 chronic lymphocytic inflammation with pontine perivascular enhancement responsive to steroids Diseases 0.000 description 1
- 238000011960 computer-aided design Methods 0.000 description 1
- 230000007547 defect Effects 0.000 description 1
- 238000010586 diagram Methods 0.000 description 1
- 230000000694 effects Effects 0.000 description 1
- 230000001788 irregular Effects 0.000 description 1
- 239000011159 matrix material Substances 0.000 description 1
- 238000012986 modification Methods 0.000 description 1
- 230000004048 modification Effects 0.000 description 1
- 230000008569 process Effects 0.000 description 1
- 238000006467 substitution reaction Methods 0.000 description 1
- 230000007704 transition Effects 0.000 description 1
- 238000013519 translation Methods 0.000 description 1
Images
Classifications
-
- G—PHYSICS
- G06—COMPUTING; CALCULATING OR COUNTING
- G06T—IMAGE DATA PROCESSING OR GENERATION, IN GENERAL
- G06T11/00—2D [Two Dimensional] image generation
- G06T11/20—Drawing from basic elements, e.g. lines or circles
- G06T11/203—Drawing of straight lines or curves
Landscapes
- Physics & Mathematics (AREA)
- General Physics & Mathematics (AREA)
- Engineering & Computer Science (AREA)
- Theoretical Computer Science (AREA)
- Image Analysis (AREA)
Abstract
The invention discloses a graph migration method, which comprises the following steps: s1, fitting an arc in a first polygon with the arc by using a straight line segment, and connecting the fitted arc with the straight line segment in the first polygon with the arc to form a second polygon with a straight line; s2, performing offset calculation on the linear polygon to form a third offset polygon; s3, offsetting the circular arc in the first polygon to form a notch ring; and S4, carrying out parallel operation on the notch ring and the third polygon. The method can be applied to the accurate calculation of the graph migration operation in the EDA field, and can be used for popularizing the application range of the original accurate migration operation from the straight-line simple polygon to the simple polygon with the circular arc, so that the migration calculation range is larger, and the precision control is better.
Description
Technical Field
The invention relates to the field of electronic design automation and computer aided design, in particular to a deviation method of a polygon with an arc.
Background
The graphic migration technique is to input an arbitrary legal polygon (e.g. a closed simple polygon) and a migration distance parameter d, so as to obtain a new polygon, and to make the distance between the polygon after migration and the polygon before migration always be greater than or equal to the given migration distance parameter d.
Graph migration technology is a very important part in the field of electronic design automation (EDA for short), for example, design rule check DRC (DRC for short) check needs to check the distance between different modules so as to satisfy the constraint of minimum distance; once a module fails to satisfy the minimum distance constraint, the module is pushed, i.e., some or even all of the current module is subtracted, so as to satisfy the minimum distance constraint. The pattern shifting technique can ensure that as few portions as possible are subtracted to obtain the optimal reduced size.
The shifting of the graph is based on translating each edge in the shifting direction to generate a shifted polygon. After the simplex translation, the edges cannot be connected to form a complete polygon, and a new edge is usually connected by using arc transition to obtain a polygon with an arc; or by prolonging the translated edges, new intersection points between the edges are solved, and the new intersection points are connected into a complete polygon after the size of the included angle is controlled. For example, the chip design software Allegro Package design (APD for short) of Cadence company translates all the edges by an outward expansion distance d in the normal direction, and then for an outward convex included angle, the translated edges are extended to obtain an intersection point so as to obtain a new end point; and for the included angle of the inner concave, the intersection point can be directly solved through the translated line segment. After the above operation, a preliminary extended polygon may be obtained, and then the APD performs an acute angle trim control (acute angle control) on the obtained polygon, that is, for all acute angles of the polygon, when the distance between two sides of the acute angle exceeds a preset threshold, the current distance is connected in a self-defined manner, but the extended distance cannot be guaranteed to be constant d.
At present, the graphic computation library CGAL has been made into theoretically accurate polygon equidistant offsets based on Minkowski sum. Given the graph A, B ∈ R 2 And the Minkowski sum is defined as:i.e. input as 2 polygons, then draw all edges of one polygon based on their all end points as centers, and then remove the excess edges to form the resulting polygon. The offset based on Minkowski sum is an accurate version offset which is made by taking an input polygon as a basic polygon and a circle with an external expansion distance d as a radius as an addition graph; since all edges of the graphic operation library CGAL need to guarantee the characteristics of rational numbers (or rational algebraic numbers) and direct deviation of circular arcs can directly destroy the rational characteristics, the graphic operation library CGAL only supports the deviation operation of a common straight-line polygon at present and does not support the deviation of a polygon with a circular arc; similarly, the graphics library clipper itself only supports normal polygons, and does not accept circular arc polygons as an offset input.
Disclosure of Invention
The invention aims to overcome the defects of the existing graph migration technology and provides an accurate migration method of a polygonal graph with an arc. Not only can support the deviation of the polygon with the circular arc, but also the deviation circular arc can also ensure the accurate result.
In order to achieve the above objects and other objects, the present invention is achieved by the following technical solutions: a pattern shifting method, comprising the steps of:
step S1, fitting arcs in a first polygon by using straight-line segments to form fitting arcs, and connecting the fitting arcs with the straight-line segments in the first polygon to form a second polygon;
s2, performing offset calculation on the second polygon to form a third polygon after offset;
s3, offsetting the circular arc in the first polygon to form a notch ring;
and S4, carrying out phase-parallel operation on the notch ring and the third polygon.
In the step S1, fitting the circular arc in the polygon with the circular arc includes the following steps:
step S11, judging whether the arc is in a convex shape;
if the result of the step S11 is yes, executing the step S12 to select a plurality of end points on the circular arc, and connecting the end points to fit the circular arc to form a fitting circular arc;
if the result of the step S11 is negative, the step S13 is executed to select a plurality of end points on the circular arc, tangent lines which pass through the end points and are tangent to the circular arc are made, and the intersection points of the tangent lines are connected to fit the circular arc to form a fitting circular arc.
In the step S2, the arc is convex, and the offset calculation of the formed fitting arc includes a step of making a complete circle with the end point as a center and the offset distance as a radius on each end point of the fitting arc, where two adjacent circle tangents are offset edges.
In the step S2, the arc is in a non-convex shape, and the deviation calculation of the formed fitting arc includes the steps of finding a starting point of a connecting line on a whole circle with the end point as the center of the circle on each end point of the fitting arc, making a tangent line of the whole circle passing through the starting point, wherein the tangent line is tangent to the starting point with the whole circle, and the tangent line is parallel to a connecting edge of the center of the whole circle; extending the tangent until it intersects the next tangent at which the above steps are so repeated; the above steps are continued for all other end points until a collection of edges and full circles is obtained.
The present invention also provides a system comprising, at least one processor; and
a computer-readable storage medium storing instructions that, when executed by the at least one processor, cause the system to:
a computer-readable storage medium storing instructions that, when executed by the at least one processor, cause the system to:
fitting the circular arc in the first polygon, and connecting the fitted circular arc with the straight line segment in the first polygon to form a second polygon;
performing offset calculation on the second polygon to form a third polygon after offset;
shifting the circular arc in the first polygon to form a notch ring;
and carrying out parallel operation on the notch ring and the third polygon.
The fitting of the circular arc in the polygon with the circular arc comprises the following operation instructions:
judging whether the arc is in a convex shape;
as a result, selecting a plurality of end points on the circular arc, and connecting the end points to fit the circular arc to form a fitted circular arc;
if not, selecting a plurality of end points on the circular arc, making tangent lines which pass through the end points and are tangent to the circular arc, and connecting the intersection points of the tangent lines to fit the circular arc to form a fitted circular arc.
The arc is in a convex shape, the offset calculation of the formed fitting arc comprises the following operation instructions, a full circle with the end points as the circle center and the offset distance as the radius is made on each end point of the fitting arc, and the tangent lines of two adjacent circles are the edges after the offset.
The arc is in a non-convex shape, and the formed deviation calculation of the fitting arc comprises an operation instruction, wherein a connecting line initial point is found on a whole circle taking the end point as the circle center on each end point of the fitting arc, a tangent line of the whole circle is made through the initial point, the tangent line and the whole circle are tangent to the initial point, and the tangent line is parallel to the connecting edge of the circle center of the whole circle; extending the tangent until it intersects the next tangent at which the above steps are so repeated; the above steps are continued for all other end points until a collection of edges and full circles is obtained.
Compared with the prior art, the method has the advantages that all arcs are fitted to form a common polygon, the fitted arcs are recorded to generate a corresponding offset notch ring, the common polygon is subjected to parallel operation with the offset notch ring after an offset algorithm is adopted to obtain a final graph, and meanwhile, the final graph is also a Minkowski sum accurate value, so that the application range of the original accurate offset operation is popularized from a straight-line simple polygon to a simple polygon with arcs, the offset calculation range is larger, and the accuracy control is better.
The present invention will be described in further detail with reference to the accompanying drawings.
Drawings
FIG. 1 is a flowchart illustrating the steps of a method for pattern shifting according to the present invention.
FIG. 2 is a flow chart of the method steps for fitting arcs in a polygon with arcs of a circle according to the present invention.
FIG. 3 is a graph showing the deviation of the arc in the convex state according to the present invention.
FIG. 4 is a graph showing the deviation of the circular arc of the present invention in a non-convex state.
FIG. 5 is a comparison chart of the operation results of step S1 and step S3 according to an embodiment of the present invention.
FIG. 6 is a comparison chart of the operation results of step S2 according to an embodiment of the present invention.
FIG. 7 is a comparison chart of the operation results of step S4 according to an embodiment of the present invention.
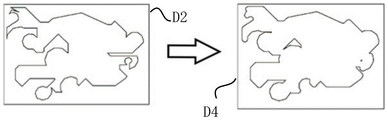
FIG. 8 is a diagram showing a comparison between the first polygon D1 with circular arc and the shifted circular arc polygon D6 according to the present invention.
Detailed Description
As shown in fig. 1, the method for shifting a pattern, which is a polygonal pattern with circular arcs, comprises the following steps:
step S1: and fitting the circular arc of the first polygon in the graph by using a straight line segment, and connecting the fitted circular arc with the straight line segment in the polygon with the circular arc to form a second polygon. Referring to fig. 5, the first polygon D1 with arcs includes 11 arcs, such as arcs L11-L111, and the arcs are fitted to form fitting arcs L12-L112, the fitting arcs L12-L112 are connected to straight segments of the polygon D1 with arcs to form a second polygon D2, and the second polygon D2 is a linear polygon.
As shown in fig. 2, step S1 specifically includes: step S11 judges whether the arc is convex. The judgment is mainly seen from the inside of the graph, referring to fig. 5, in the first polygon D1, the arc L11 is convex relative to the inside of the first polygon D1. The circular arc L61 is not convex.
If the result of step S11 is yes, step S12 is executed to select several end points on the arc, and connect the end points to fit the arc, so as to form a fitted arc.
As shown in fig. 3, a plurality of end points, for example, an end point P11, an end point P21, etc., are selected on the arc L11, and the end points are connected to fit the arc, so as to form a fitted arc L11', and the arc L12 represents a position where the polygon should exist after being shifted; the fitting circular arc L12' and the circular arc L12 are in an inscribed relation.
If the radius of the arc L11 is R and the offset distance is d, in an ideal state, for the convex arc L11, the radius of the arc L12 after being offset should be R + d.
If the result of the step S11 is negative, the step S13 is executed to select a plurality of end points on the circular arc, tangent lines which pass through the end points and are tangent to the circular arc are made, and the intersection points of the tangent lines are connected to fit the circular arc to form a fitting circular arc.
As shown in fig. 4, a plurality of end points, such as an end point P11 and an end point P21, are selected from the arc L61, tangent lines that pass through the end points and are tangent to the arc are made, and the intersection points of the tangent lines are connected to form a fitting arc L61', and the arc L62 represents a position where the polygon should exist after being shifted; the fitting circular arc L62' is in circumscribed relation with the circular arc L62.
The radius of the shifted arc L62 should be R-d.
A connecting line initial point is searched on a whole circle which takes the end point as the center of the circle and is made at each end point of the fitting circular arc L61', a tangent line of the whole circle is made through the initial point, the tangent line and the whole circle are tangent to the initial point, and the tangent line is parallel to a connecting edge of the center of the whole circle; extending the tangent line until it intersects the next tangent line at which the above steps are repeated; the above steps are continued for all other end points until a collection of edges and full circles is obtained, such as the fitted arc L62' in fig. 4.
Setting the end points of all tangent edges in the process as event points, storing the event points into a priority queue with the x coordinate from small to large, and calculating a new intersection point by using a scanning line algorithm;
the scan line algorithm is a common algorithm for scanning and converting polygons, fully utilizes the coherence between adjacent pixels, converts a vertex representation method of a geometric figure in a computer into a dot matrix representation method, avoids point-by-point judgment and repeated intersection calculation, and achieves the purposes of reducing the calculation amount and improving the algorithm efficiency.
Legal edges are thus added to the resulting graph, and other illegal edges are removed to produce the final resulting graph.
The legal edge refers to a tangent point, an arc around the tangent point and a tangent line after square deviation, wherein an original arc end point is taken as a circle center, and a circle with the radius of d is taken as an illegal edge; after the legal edge is added into the result graph, the circle taking the original arc end point as the center of the circle is removed, and the rest graph is the final result graph.
And S2, performing offset calculation on the second polygon to form a third polygon after offset.
Referring to fig. 6, the second polygon D2 is shifted to form a shifted third polygon D4. The offset algorithm uses, for example, a minkowski algorithm, the offset third polygon D4 carrying a circular arc.
And S3, offsetting the circular arcs in the polygon with the circular arcs to form a notch circular ring.
Referring to fig. 5, the first polygon D1 is shifted to form a gap ring D3.
All the circular arcs L11-L111 are connected with the circle centers and the circular arc end points (namely the intersection points of the original fitting line segments) and extend the line segments so as to intersect the circular arcs which are supposed to be formed after the deviation, the two newly intersected intersection points are respectively connected with the end points of the original circular arcs, and the original circular arcs and the circular arcs formed after the deviation are connected at the same time, namely the positions of the original circular arcs are upwardly deviated by a distance d, so that a plurality of circular rings L13-L113 are generated, and the shapes are reserved.
The above-mentioned upward shift d of the original circular arc position is merely a simple example. In a specific graph, the arc shape is not specified, more irregular graphs formed by arcs and line segments cannot be directly shifted up and down in software.
S4, carrying out parallel operation on the notch ring and the third polygon; therefore, the final offset graph and the notch ring generate sawtooth edges due to fitting of arcs, and finally a complete version of the offset arc polygon is formed. As shown in fig. 7, the third polygon D4 and the notched ring D3 are operated in parallel to finally form a complete version of the shifted circular arc polygon D6. Please refer to fig. 8 for better showing the offset effect.
Although embodiments of the present invention have been shown and described, it will be appreciated by those skilled in the art that changes, modifications, substitutions and alterations can be made in these embodiments without departing from the principles and spirit of the invention, the scope of which is defined in the appended claims and their equivalents.
Claims (8)
1. A pattern shifting method, comprising the steps of:
step S1, fitting an arc in a first polygon by using a straight line segment to form a fitting arc, and connecting the fitting arc with the straight line segment in the first polygon to form a second polygon;
s2, performing offset calculation on the second polygon to form an offset third polygon;
s3, offsetting the circular arc in the first polygon to form a notch ring;
and S4, carrying out parallel operation on the notch ring and the third polygon.
2. The pattern shifting method according to claim 1, wherein the step S1 of fitting the circular arcs in the polygon with circular arcs comprises the following steps:
step S11, judging whether the arc is in a convex shape;
if the result of the step S11 is yes, executing the step S12 to select a plurality of end points on the circular arc, and connecting the end points to fit the circular arc to form a fitting circular arc;
if the result of the step S11 is negative, the step S13 is executed to select a plurality of end points on the circular arc, tangent lines which pass through the end points and are tangent to the circular arc are made, and the intersection points of the tangent lines are connected to fit the circular arc to form a fitting circular arc.
3. The pattern shifting method according to claim 2, wherein in the step S2, the arc is convex, and the shift calculation of the fitting arc is performed, and the step S includes a step of making a complete circle with the end point as a center and the shift distance as a radius at each end point of the fitting arc, and tangent lines of two adjacent circles are shifted edges.
4. A pattern shifting method according to claim 3, wherein in step S2, the arc is non-convex and the shift calculation of the fitting arc is performed, comprising the steps of finding a starting point of a connecting line on a whole circle with the end points as the center of the circle at each end point of the fitting arc, drawing a tangent line of the whole circle passing through the starting point, the tangent line being tangent to the starting point and the tangent line being parallel to the connecting edge of the center of the whole circle; extending the tangent line until it intersects the next tangent line at which the above steps are repeated; the above steps are continued for all other end points until a collection of edges and full circles is obtained.
5. A system comprising, at least one processor; and
a computer-readable storage medium storing instructions that, when executed by the at least one processor, cause the system to:
fitting the circular arc in the first polygon, and connecting the fitted circular arc with the straight line segment in the first polygon to form a second polygon;
performing offset calculation on the second polygon to form a third polygon after offset;
shifting the circular arc in the first polygon to form a notch ring;
and carrying out parallel operation on the notch ring and the third polygon.
6. The system of claim 5, wherein fitting the circular arcs in the polygon with circular arcs comprises the following operations:
judging whether the arc is in a convex shape;
as a result, selecting a plurality of end points on the circular arc, and connecting the end points to fit the circular arc to form a fitted circular arc;
if not, selecting a plurality of end points on the circular arc, making tangent lines which pass through the end points and are tangent to the circular arc, and connecting the intersection points of the tangent lines to fit the circular arc to form a fitted circular arc.
7. The system of claim 6, wherein the arc is convex, and the calculation of the offset of the fitting arc comprises an operation instruction to make a complete circle with the end points as the center and the offset distance as the radius at each end point of the fitting arc, and the tangent lines of two adjacent circles are the edges after the offset.
8. The system of claim 7, wherein the arc is non-convex, and the deviation calculation of the fitting arc is performed by finding a starting point of a connecting line on a whole circle with the end point as a center on each end point of the fitting arc, and drawing a tangent line of the whole circle passing through the starting point, wherein the tangent line is tangent to the starting point and is parallel to a connecting edge of the center of the whole circle; extending the tangent line until it intersects the next tangent line at which the above steps are repeated; the above steps are continued for all other end points until a collection of edges and full circles is obtained.
Priority Applications (1)
| Application Number | Priority Date | Filing Date | Title |
|---|---|---|---|
| CN202211121413.6A CN115526956A (en) | 2022-09-15 | 2022-09-15 | Pattern migration method |
Applications Claiming Priority (1)
| Application Number | Priority Date | Filing Date | Title |
|---|---|---|---|
| CN202211121413.6A CN115526956A (en) | 2022-09-15 | 2022-09-15 | Pattern migration method |
Publications (1)
| Publication Number | Publication Date |
|---|---|
| CN115526956A true CN115526956A (en) | 2022-12-27 |
Family
ID=84698475
Family Applications (1)
| Application Number | Title | Priority Date | Filing Date |
|---|---|---|---|
| CN202211121413.6A Pending CN115526956A (en) | 2022-09-15 | 2022-09-15 | Pattern migration method |
Country Status (1)
| Country | Link |
|---|---|
| CN (1) | CN115526956A (en) |
Citations (4)
| Publication number | Priority date | Publication date | Assignee | Title |
|---|---|---|---|---|
| US20020035720A1 (en) * | 2000-09-19 | 2002-03-21 | Tamotsu Kitamura | Wiring editing method, for semiconductor package, capable of easily editing offset of wiring pattern |
| CN103970033A (en) * | 2014-05-20 | 2014-08-06 | 河海大学常州校区 | Method for realizing robot solid modeling and blade laser detection simulation on basis of MATLAB |
| CN109887052A (en) * | 2019-01-29 | 2019-06-14 | 广联达科技股份有限公司 | A kind of planar polygons offset method |
| US10627713B1 (en) * | 2018-10-19 | 2020-04-21 | Cadence Design Systems, Inc. | Checking minimum width, minimum distance and maximum curvature of planar region boundaries defined by arbitrary parametric curves |
-
2022
- 2022-09-15 CN CN202211121413.6A patent/CN115526956A/en active Pending
Patent Citations (4)
| Publication number | Priority date | Publication date | Assignee | Title |
|---|---|---|---|---|
| US20020035720A1 (en) * | 2000-09-19 | 2002-03-21 | Tamotsu Kitamura | Wiring editing method, for semiconductor package, capable of easily editing offset of wiring pattern |
| CN103970033A (en) * | 2014-05-20 | 2014-08-06 | 河海大学常州校区 | Method for realizing robot solid modeling and blade laser detection simulation on basis of MATLAB |
| US10627713B1 (en) * | 2018-10-19 | 2020-04-21 | Cadence Design Systems, Inc. | Checking minimum width, minimum distance and maximum curvature of planar region boundaries defined by arbitrary parametric curves |
| CN109887052A (en) * | 2019-01-29 | 2019-06-14 | 广联达科技股份有限公司 | A kind of planar polygons offset method |
Non-Patent Citations (2)
| Title |
|---|
| 潘意杰;陈晔;: "双重图形技术的优化设计", 机电工程, no. 12, 20 December 2008 (2008-12-20) * |
| 赵汝岩, 于胜春, 颜仙荣: "曲线偏移算法在CAD软件中的应用", 计算机工程与设计, no. 02, 28 February 2005 (2005-02-28) * |
Similar Documents
| Publication | Publication Date | Title |
|---|---|---|
| US6850239B2 (en) | 3-D character data generating device and a 3-D graphics data generating device | |
| US20070080966A1 (en) | Appropriately rendering a graphical object when a corresponding outline has exact or inexact control points | |
| JP2008299627A (en) | Information processing method and apparatus, program, storage medium | |
| CN114266800B (en) | Method and system for generating multiple rectangular bounding boxes of plane graph | |
| CN110689492B (en) | Image edge smoothing method and device | |
| US9922623B2 (en) | Emboldening of outline fonts | |
| JP4378208B2 (en) | Information processing apparatus and information processing method | |
| EP1600895A1 (en) | Rendering a graphical object when a corresponding outline lacks control points | |
| CN115526956A (en) | Pattern migration method | |
| US9779528B2 (en) | Text realization | |
| CN116843861A (en) | Three-dimensional model simplification method | |
| US7292249B2 (en) | Appropriately rendering a graphical object when a corresponding outline has excessive control points | |
| CN115222579A (en) | Method, device and medium for scanning and converting dot matrix data | |
| CN115619915A (en) | Three-dimensional model mapping method and device, storage medium and electronic equipment | |
| CN115359502A (en) | Image processing method, device, equipment and storage medium | |
| CN110658783B (en) | Solving method and system for feasible region of five-axis machining cutter shaft | |
| JP2005079392A (en) | Method for generating image drawing data | |
| CN110348163B (en) | Fitting method for continuous tangent circular arc of tire pattern boundary | |
| CN114119708A (en) | Method and device for generating tree structure, computing equipment and storage medium | |
| US7120887B2 (en) | Cloned and original circuit shape merging | |
| CN110599598A (en) | Method and device for unifying heterogeneous data | |
| JP2021033375A (en) | Apparatus for editing three-dimensional shape data and program for editing three-dimensional shape data | |
| West et al. | Multistage combined ellipse and line detection | |
| CN110032718B (en) | Table conversion method, system and storage medium | |
| CN114820441B (en) | Method and system for extracting numerical control machining path from bitmap |
Legal Events
| Date | Code | Title | Description |
|---|---|---|---|
| PB01 | Publication | ||
| PB01 | Publication | ||
| SE01 | Entry into force of request for substantive examination | ||
| SE01 | Entry into force of request for substantive examination |