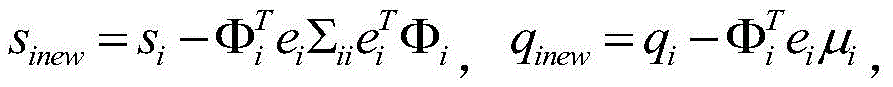CN115086116B - DCT and DWT-based sparse Bayesian power line channel and impulse noise joint estimation method - Google Patents
DCT and DWT-based sparse Bayesian power line channel and impulse noise joint estimation method Download PDFInfo
- Publication number
- CN115086116B CN115086116B CN202210666573.2A CN202210666573A CN115086116B CN 115086116 B CN115086116 B CN 115086116B CN 202210666573 A CN202210666573 A CN 202210666573A CN 115086116 B CN115086116 B CN 115086116B
- Authority
- CN
- China
- Prior art keywords
- vector
- matrix
- dct
- dwt
- power line
- Prior art date
- Legal status (The legal status is an assumption and is not a legal conclusion. Google has not performed a legal analysis and makes no representation as to the accuracy of the status listed.)
- Active
Links
- 238000000034 method Methods 0.000 title claims abstract description 37
- 239000013598 vector Substances 0.000 claims abstract description 77
- 239000011159 matrix material Substances 0.000 claims abstract description 66
- 230000004044 response Effects 0.000 claims abstract description 31
- 238000000638 solvent extraction Methods 0.000 claims abstract description 3
- 230000005540 biological transmission Effects 0.000 claims description 5
- 238000005259 measurement Methods 0.000 claims description 3
- 230000008569 process Effects 0.000 claims description 3
- 238000004891 communication Methods 0.000 abstract description 6
- 230000008901 benefit Effects 0.000 description 6
- 230000006870 function Effects 0.000 description 5
- 238000007792 addition Methods 0.000 description 3
- 230000006835 compression Effects 0.000 description 2
- 238000007906 compression Methods 0.000 description 2
- 238000000354 decomposition reaction Methods 0.000 description 2
- 230000000694 effects Effects 0.000 description 2
- 230000009286 beneficial effect Effects 0.000 description 1
- 230000007547 defect Effects 0.000 description 1
- 238000010586 diagram Methods 0.000 description 1
- 238000005516 engineering process Methods 0.000 description 1
- 238000012986 modification Methods 0.000 description 1
- 230000004048 modification Effects 0.000 description 1
- 238000011084 recovery Methods 0.000 description 1
- 238000011160 research Methods 0.000 description 1
- 238000005070 sampling Methods 0.000 description 1
- 238000004088 simulation Methods 0.000 description 1
- 238000001228 spectrum Methods 0.000 description 1
Images
Classifications
-
- H—ELECTRICITY
- H04—ELECTRIC COMMUNICATION TECHNIQUE
- H04L—TRANSMISSION OF DIGITAL INFORMATION, e.g. TELEGRAPHIC COMMUNICATION
- H04L25/00—Baseband systems
- H04L25/02—Details ; arrangements for supplying electrical power along data transmission lines
- H04L25/0202—Channel estimation
- H04L25/024—Channel estimation channel estimation algorithms
- H04L25/0242—Channel estimation channel estimation algorithms using matrix methods
-
- G—PHYSICS
- G06—COMPUTING; CALCULATING OR COUNTING
- G06F—ELECTRIC DIGITAL DATA PROCESSING
- G06F17/00—Digital computing or data processing equipment or methods, specially adapted for specific functions
- G06F17/10—Complex mathematical operations
- G06F17/14—Fourier, Walsh or analogous domain transformations, e.g. Laplace, Hilbert, Karhunen-Loeve, transforms
-
- G—PHYSICS
- G06—COMPUTING; CALCULATING OR COUNTING
- G06F—ELECTRIC DIGITAL DATA PROCESSING
- G06F17/00—Digital computing or data processing equipment or methods, specially adapted for specific functions
- G06F17/10—Complex mathematical operations
- G06F17/14—Fourier, Walsh or analogous domain transformations, e.g. Laplace, Hilbert, Karhunen-Loeve, transforms
- G06F17/147—Discrete orthonormal transforms, e.g. discrete cosine transform, discrete sine transform, and variations therefrom, e.g. modified discrete cosine transform, integer transforms approximating the discrete cosine transform
-
- G—PHYSICS
- G06—COMPUTING; CALCULATING OR COUNTING
- G06F—ELECTRIC DIGITAL DATA PROCESSING
- G06F17/00—Digital computing or data processing equipment or methods, specially adapted for specific functions
- G06F17/10—Complex mathematical operations
- G06F17/14—Fourier, Walsh or analogous domain transformations, e.g. Laplace, Hilbert, Karhunen-Loeve, transforms
- G06F17/148—Wavelet transforms
-
- G—PHYSICS
- G06—COMPUTING; CALCULATING OR COUNTING
- G06F—ELECTRIC DIGITAL DATA PROCESSING
- G06F17/00—Digital computing or data processing equipment or methods, specially adapted for specific functions
- G06F17/10—Complex mathematical operations
- G06F17/16—Matrix or vector computation, e.g. matrix-matrix or matrix-vector multiplication, matrix factorization
-
- H—ELECTRICITY
- H04—ELECTRIC COMMUNICATION TECHNIQUE
- H04B—TRANSMISSION
- H04B3/00—Line transmission systems
- H04B3/54—Systems for transmission via power distribution lines
- H04B3/542—Systems for transmission via power distribution lines the information being in digital form
-
- Y—GENERAL TAGGING OF NEW TECHNOLOGICAL DEVELOPMENTS; GENERAL TAGGING OF CROSS-SECTIONAL TECHNOLOGIES SPANNING OVER SEVERAL SECTIONS OF THE IPC; TECHNICAL SUBJECTS COVERED BY FORMER USPC CROSS-REFERENCE ART COLLECTIONS [XRACs] AND DIGESTS
- Y02—TECHNOLOGIES OR APPLICATIONS FOR MITIGATION OR ADAPTATION AGAINST CLIMATE CHANGE
- Y02D—CLIMATE CHANGE MITIGATION TECHNOLOGIES IN INFORMATION AND COMMUNICATION TECHNOLOGIES [ICT], I.E. INFORMATION AND COMMUNICATION TECHNOLOGIES AIMING AT THE REDUCTION OF THEIR OWN ENERGY USE
- Y02D30/00—Reducing energy consumption in communication networks
- Y02D30/70—Reducing energy consumption in communication networks in wireless communication networks
Landscapes
- Engineering & Computer Science (AREA)
- Physics & Mathematics (AREA)
- Mathematical Physics (AREA)
- General Physics & Mathematics (AREA)
- Data Mining & Analysis (AREA)
- Theoretical Computer Science (AREA)
- Mathematical Analysis (AREA)
- Pure & Applied Mathematics (AREA)
- Computational Mathematics (AREA)
- Mathematical Optimization (AREA)
- Databases & Information Systems (AREA)
- Software Systems (AREA)
- General Engineering & Computer Science (AREA)
- Algebra (AREA)
- Power Engineering (AREA)
- Computer Networks & Wireless Communication (AREA)
- Signal Processing (AREA)
- Discrete Mathematics (AREA)
- Computing Systems (AREA)
- Noise Elimination (AREA)
Abstract
The invention relates to a sparse Bayesian power line channel and impulse noise joint estimation method based on DCT and DWT, which belongs to the technical field of power line communication and comprises the following steps: converting a frequency domain signal received by a power line receiving end into a vector matrix form, extracting pilot frequency in the received signal, and constructing an observation matrix and an observation vector by combining with a DWT and a DCT; uniformly partitioning an observation matrix; initializing a model; starting with an empty model, and assuming that all signal blocks are not added into the model, performing block addition to obtain a sparse solution vector; taking the front ng row of the sparse solution vector to perform DCT and DWT to obtain a channel impulse response vector estimated value, and performing FFT (fast Fourier transform) on the channel impulse response vector estimated value to obtain a channel frequency response vector with the length of N; the ng-ng+N rows of the obtained sparse solution vector are time domain impulse noise estimation vectors, so that the frequency domain symbol with impulse noise removed is obtained.
Description
Technical Field
The invention belongs to the technical field of power line communication, and relates to a sparse Bayesian power line channel and impulse noise joint estimation method based on DCT and DWT
Background
Power Line Communication (PLC) is a communication method for transmitting information by using an existing power grid. Compared with other communication technologies, the method has the advantages of low cost, wide range, stable operation and the like, so that international standards such as PLC G3, PRIME, home Plug and IEEE P1901 have been proposed. However, since the power line channel environment is complicated, the composition and variation of Noise are complicated, and especially Impulse Noise (IN) deteriorates the performance of the conventional channel estimation technique. Thus, accurate CSI acquisition for PLC systems with IN is critical.
Traditional estimation methods such as least squares algorithms do not take noise effects into account, resulting in poor MSE performance and require a large number of pilots for channel estimation, but result in low band utilization due to the pilots not containing any useful information also occupying the frequency band during transmission. Similarly, the channel estimation scheme based on DFT interpolation improves estimation performance by setting a threshold value in the time domain to remove noise, but the threshold is difficult to determine due to the complex and variable power line channel environments.
Compressed sensing techniques indicate that signal sparsity can be exploited and that the original signal can be effectively recovered with a small number of observations, which means that accurate channel state information can be obtained by using a small number of pilots. There have been related studies on joint estimation of impulse noise and channels for power line communication systems using compressed sensing techniques. But it assumes that the PLC impulse response has sparse characteristics, directly applying CS theory to the time domain PLC channel model. A large number of researches show that the PLC channel has no sparse characteristic in the time domain or the frequency domain, which means that a method for sparse representation of the impulse response of the PLC channel can obtain poor performance. In addition, the tail zero padding of the channel impulse response is studied, so that the channel impulse response vector after zero padding can be approximately considered as a sparse vector, and a Bayesian algorithm is applied to perform channel estimation, but the complexity of the method is greatly improved along with the increase of the length of an OFDM symbol.
Disclosure of Invention
In view of the above, the present invention aims to provide a sparse bayesian power line channel and impulse noise joint estimation method based on discrete wavelet sparse transform (DCT) and discrete cosine transform (DWT).
In order to achieve the above purpose, the present invention provides the following technical solutions:
a sparse Bayesian power line channel and impulse noise joint estimation method based on DCT and DWT comprises the following steps:
s1: converting a frequency domain signal received by a power line receiving end into a vector matrix form;
s2: extracting pilot frequency in the received signal;
s3: combining with DWT and DCT, constructing an observation matrix and an observation vector by the extracted pilot frequency symbol based on the compressed sensing model;
s4: uniformly partitioning an observation matrix;
s5: initializing a compressed sensing estimation model of power line impulse noise and a channel;
s6: starting with an empty model, and performing block addition on the assumption that all signal blocks are not added into the model; each iteration calculates covariance matrix, block correlation and correlation structure matrix, updates model parameters, and rebuilds covariance matrix according to the correlation structure matrix until all covariance matrices are obtained;
s7: after the preset condition is met, the circulation of S6 is ended, and a sparse solution vector is obtained;
s8: taking the front ng row of the sparse solution vector obtained in the step S7 to perform DCT and DWT to obtain a channel impulse response vector estimated value, and performing FFT (fast Fourier transform) of zero padding to obtain a channel frequency response vector with the length of N;
s9: the ng-ng+N rows of the obtained sparse solution vector are time domain impulse noise estimation vectors, so that the frequency domain symbol with impulse noise removed is obtained.
Further, in step S1, the frequency domain signal received by the power line receiving end is converted into a vector matrix form
Y=diag(X)H+Fi+G (1)
Wherein X= [ X ] 1 ,X 2 ,...X N ] T For transmitting symbol vectors in the frequency domain, the OFDM frequency domain symbol vector has a length of N, H= [ H ] 1 ,H 2 ,...,H N ]For the channel frequency response vector, F is an N-dimensional fourier transform matrix, i represents time domain impulse noise, where g=fg represents frequency domain background noise, gaussian white noise, and G represents background noise.
Further, in step S2, the set of positions where pilots are inserted in the transmission signal is defined as P, and (·) P is a submatrix formed by the corresponding rows or elements of the index in the set P, and equation (1) is transformed into:
Y P =diag(X P )H p +F p i+G p (2)。
further, in step S3, in combination with the time domain sparse characteristic of the impulse noise, the compressed sensing estimation model of the power line impulse noise and the channel is:
wherein F is p,ng Is a fourier matrix of p×ng, ng is guard interval length, DCT ng*ng ,DWT ng*ng Is a matrix of ng dimension; in the formula, the ng 1-dimensional vector h is expressed as:
h=DCT*a (5)
h=DWT*b (6)
the formulae (3) and (4) are expressed as:
Y p =ΦX+G p (7)
where Φ is the observation matrix.
Further, in step S4, the observation matrix Φ is uniformly segmented Φ= [ Φ ] 1 ,Φ 2 ,...Φ m ]The block length is 8, the OFDM length is 1024, the ng length is 256, comb-shaped pilot frequencies are arranged and are evenly distributed, and the number is 64.
Further, the initializing in step S5 considers the signal-to-noise ratio SNR<20dB of the total number of the slots, set β = 0.1Y p || 2 , η=10 -4 M means that the observation vector is divided into m blocks of data, corresponding to m blocks of observation matrices,Φ i i.e. the observation matrix corresponding to the ith block, there are m such block observation matrices in total, eta is the algorithm exit condition, beta refers to the noise variance, and in the algorithm process, iterative computation is needed, s i ,q i Is a defined intermediate variable used to calculate the cost function.
Further, in step S6, starting with the null model, it is assumed that all signal blocks X i None of the blocks are added into the model, and the blocks are added; the set of bases in the model at the K-th iteration is a k Each iteration proceeds through the following steps:
s61: calculating covariance matrixCalculating block correlation gamma i =1/d i Tr(A i ) Wherein d is i Is matrix A i Tr represents the trace of the matrix. Calculating a correlation structure matrix B i =A i /r i Reconstruction, reconstructionWherein r is i Representing the variance of the i-th block. Until all A is obtained i And according to the cost function l=log|c|+y T C -1 y, where y represents the measurement vector input by the algorithm, i.e. the OFDM frequency domain symbol at the input pilot, c=β -1 I+ΦΓΦ T I represents an identity matrix, and Γ is a matrix formed by covariance matrices of the observation block matrix. Calculate->And to obtain +.sup.maximum ΔL (i)>An index of the observation block matrix that maximizes Δl (i);
Further, the method comprises the steps of, in step S7 satisfy [ gamma ] new - γ|/|γ| < η, skipping out of the loop of S6, yielding a sparse solution vector x=μ;
in step S9, the ng-ng+N lines of the obtained sparse solution vector are time domain impulse noise estimation vectorsThe frequency domain symbol from which impulse noise can be removed is +.>
Further, in step S62, Σμs is updated using the BSBL-FM algorithm i q i The method specifically comprises the following steps:
(1)the current block is added to the model and μ new =μ-βΣΦ T Φ i μ i ,Wherein Σ is a =-βΣΦ T Φ i Σ ii ,Wherein e i =β(Φ i -βΦΣΦ T Φ i ) Wherein e is i =β(Φ i -βΦΣΦ T Φ i ) μ is the mean vector of the probability distribution to which the output random vector is subject, Σ is the covariance vector of the probability distribution to which the output vector is subject, μ new Refer to the iteratively updated mean vector, Σ, in the algorithm new Refers to iteratively updated covariance vectors in algorithm, μ i Then is the i-th value in the mean vector, Σ a Defined as intermediate variables only, in order to represent Σ new Update procedure s inew ,q inew Representing updated s i ,q i To calculate a new cost function. e, e i Only algorithmsThe deduced intermediate variable has no physical meaning and conveniently represents q inew Is a new procedure of Sigma ii Is the covariance matrix corresponding to the ith block data for iteratively updating s i ;
(2)And->The block is deleted from the model and mu new =μ+ΔΣβΦ T y,Σ new =Σ+ΔΣ, wherein ΔΣ= - Σ i Σ ii -1 Σ i ,
The invention has the beneficial effects that: the invention provides a sparse Bayesian power line channel and impulse noise joint estimation method based on DCT and DWT, which aims at the defect that channel impulse response does not directly have sparse characteristics, and provides a DCT and DWT-based secondary compression method for sparse representation of the channel impulse response, so that the dimension of a required observation matrix is reduced, and better reconstruction performance can be obtained. In addition, in view of the compressed sensing algorithm of the BSBL-FM, only a small amount of observation values are needed to effectively recover the original signal and the advantage of better re-estimation performance, the BSBL-FM algorithm is applied to channel estimation. Compared with the traditional estimation method, the channel estimation based on sparse Bayes can obtain an accurate estimation value through a small amount of pilot frequency, and the spectrum utilization rate is improved.
Additional advantages, objects, and features of the invention will be set forth in part in the description which follows and in part will become apparent to those having ordinary skill in the art upon examination of the following or may be learned from practice of the invention. The objects and other advantages of the invention may be realized and obtained by means of the instrumentalities and combinations particularly pointed out in the specification.
Drawings
For the purpose of making the objects, technical solutions and advantages of the present invention more apparent, the present invention will be described in the following preferred detail with reference to the accompanying drawings, in which:
FIG. 1 is a flow chart of the overall scheme of the present invention;
FIG. 2 is a graph of channel frequency response referenced by the present invention;
fig. 3 is a diagram of the channel impulse response referred to in the present invention;
fig. 4 is a graph of the channel impulse response within ng referenced by the present invention;
fig. 5 is a graph of MSE performance versus the present invention.
Detailed Description
Other advantages and effects of the present invention will become apparent to those skilled in the art from the following disclosure, which describes the embodiments of the present invention with reference to specific examples. The invention may be practiced or carried out in other embodiments that depart from the specific details, and the details of the present description may be modified or varied from the spirit and scope of the present invention. It should be noted that the illustrations provided in the following embodiments merely illustrate the basic idea of the present invention by way of illustration, and the following embodiments and features in the embodiments may be combined with each other without conflict.
Wherein the drawings are for illustrative purposes only and are shown in schematic, non-physical, and not intended to limit the invention; for the purpose of better illustrating embodiments of the invention, certain elements of the drawings may be omitted, enlarged or reduced and do not represent the size of the actual product; it will be appreciated by those skilled in the art that certain well-known structures in the drawings and descriptions thereof may be omitted.
The same or similar reference numbers in the drawings of embodiments of the invention correspond to the same or similar components; in the description of the present invention, it should be understood that, if there are terms such as "upper", "lower", "left", "right", "front", "rear", etc., that indicate an azimuth or a positional relationship based on the azimuth or the positional relationship shown in the drawings, it is only for convenience of describing the present invention and simplifying the description, but not for indicating or suggesting that the referred device or element must have a specific azimuth, be constructed and operated in a specific azimuth, so that the terms describing the positional relationship in the drawings are merely for exemplary illustration and should not be construed as limiting the present invention, and that the specific meaning of the above terms may be understood by those of ordinary skill in the art according to the specific circumstances.
The invention provides a sparse Bayesian power line channel and impulse noise joint estimation method based on DCT and DWT, which is shown in figure 1 and comprises the following steps:
the OFDM frequency domain symbol vector length is n=1024, ng is the guard interval length, here set to N/4=256. The block length is 8, comb-shaped pilots are arranged and evenly distributed, and the number is 64.
S1, converting a frequency domain signal received by a power line receiving end into a vector matrix form;
wherein X= [ X ] 1 ,X 2 ,...X N ] T For transmitting symbol vectors in the frequency domain, h= [ H ] 1 ,H 2 ,...,H N ]For the channel frequency response vector, F is an N-dimensional fourier transform matrix, i, g represent the time domain impulse noise and background noise respectively,representing the hadamard product. />
Equation (1) can be written as a matrix-vector product of the following:
Y=diag(X)H+Fi+G (2)
where g=fg represents the frequency domain background noise, still gaussian white noise.
S2, extracting pilot frequency in a received signal;
defining a set of positions of inserting pilots in a transmission signal as P, wherein (-) P is a submatrix formed by corresponding lines or elements of indexes in the set P, and the formula (2) is converted into:
Y P =diag(X P )H p +F p i+G p (3)
s3, combining with the DWT, and constructing a measurement matrix and an observation vector by DCT on the extracted pilot frequency symbol based on the compressed sensing model;
the power line frequency response does not have sparse characteristics, and if the channel impulse response is assumed to have sparsity, the equation (2) can be expressed as:
Y P =diag(X P )F p,ng h+F p i+G p (4)
f in the formula p,ng Is a fourier matrix of P x ng, h is a vector of ng x 1 dimension. Considering the DCT, the energy compression characteristic of DWT, the h-sparsity in equation (4) is expressed as:
h=DCT*a (5)
h=DWT*b (6)
then correspondingly equation 4 can be expressed as:
Y P =diag(X P )F p,ng DCT ng*ng a+F p i+G p (7)
Y P =diag(X P )F p,ng DWT ng*ng b+F p i+G p (8)
where DCT, DWT is a matrix of ng dimension. The DCT matrix here is formed by the DCT of matlab
The function results, the DWT matrix, were obtained from the discrete wavelet transform matlab program written by the authors.
Combining the time domain sparse characteristic of impulse noise, the compressed sensing estimation model of the impulse noise of the power line and the channel is as follows:
the two formulas above can be expressed as:
Y p =ΦX+G p (11)
s4, uniformly dividing the observation matrix phi into blocks phi= [ phi ] 1 ,Φ 2 ,...Φ m ]The block length is 8;
s5, initializing, considering signal-to-noise ratio SNR<20dB of the total number of the slots, set β = 0.1Y p || 2 , η=10 -4 ;
S6, starting with the null model, assuming all signal blocks X i None are added to the model, and block additions are made. The set of bases in the model at the K-th such iteration is a k . Each iteration: 1. calculating covariance matrixCalculating block correlation gamma i =1/d i Tr(A i ) Where di is the dimension of the matrix Ai, here 8, the correlation structure matrix B is calculated i =A i /r i Rebuilding->Until all A is obtained i . And according to the cost function l=log|c|+y T C -1 y, wherein c=β -1 I+ΦΓΦ T Calculate->And to obtain +.sup.maximum ΔL (i)>2. According to->Whether or not it belongs to a k Updating Σμs i q i :
(1)The current block is added to the model and μ new =μ-βΣΦ T Φ i μ i ,Wherein Σ is a =-βΣΦ T Φ i Σ ii ,Wherein e i =β(Φ i -βΦΣΦ T Φ i )
(2)And->The block is deleted from the model and mu new =μ+ΔΣβΦ T y,Σ new =Σ+ΔΣ,Wherein ΔΣ= - Σ i Σ ii -1 Σ i 。
S7, when meeting the specification of gamma new - γ|/|γ| < η, skipping out of the loop of S6, yielding a sparse solution vector x=μ;
s8, taking the front ng row DCT and DWT of the sparse solution vector obtained in S7 to obtain a channel impulse response vector estimated value, and carrying out zero-filling FFT on the channel impulse response vector estimated value to obtain a channel frequency response vector with the length of N
S9, the ng-ng+N rows of the obtained sparse solution vector are time domain impulse noise estimation vectorsThe frequency domain symbol from which impulse noise can be removed is +.>
If the original signal X is known to be sparse or capable of sparse representation (the signal is sufficiently sparse in some transform domain), the difficulty of solving the under-determined equation can be greatly reduced. Thus, the accurate recovery of the original signal is possible on the premise of signal sparsity, and the premise of sparsity of the original signal is also a necessary condition for reconstructing the CS signal.
In compressed sensing based signal reconstruction, discrete wavelet sparse transforms (DWTs) and Discrete Cosine Transforms (DCTs) are typically used as sparse decomposition bases for signals. However, the addition of DCT and DWT to compressed sensing model in PLC channel environment has not been studied to obtain better performance. In addition, it is also studied to apply DCT transform to reduce the energy of high frequency of the channel frequency response of PLC so that the energy is more concentrated at low frequency, which means that the energy of the channel impulse response can be more concentrated by DWT, DCT transform, i.e. with sparse characteristics. In the signal reconstruction model based on compressed sensing under the PLC channel environment, discrete wavelet sparse transform (DWT) and Discrete Cosine Transform (DCT) are used as sparse decomposition bases of channel impulse response vectors, the DWT is applied, the DCT performs sparse representation on the channel impulse response, and compressed sensing is applied to estimate the channel and impulse noise. DCT, DWT has dimensions of ng only, so that the dimension of the overall observation matrix phi is p ng, and the data volume required to be stored is greatly reduced compared with zero-filling schemes.
According to the zimermann channel model, the characteristic of the power line reference channel time-frequency domain is simulated, OFDM symbols are 1024 subcarriers, subcarrier intervals are 24.414KHz, sampling frequency of 25MHz is adopted, OFDM time domain length is about 40us, ng length is about 10us, and the generated power line channel transmission characteristic frequency domain amplitude-frequency response and time impact response are shown in figures 2, 3 and 4.
Based on the power line channel impulse response obtained by simulation, constructing an observation vector as a frequency domain symbol Y at the pilot frequency of the receiving end P The sum observation matrix is phi, and the power line channel is interfered by background noise, so that the signal to noise ratio is continuously increased and changed from 0dB to 20 dB. As shown in fig. 5, compared with the compressed sensing channel estimation without the sparsification process, the MSE performance of the sparse bayesian power line channel and impulse noise joint estimation method based on the DCT is improved by 2dB, and the MSE performance of the sparse bayesian power line channel and impulse noise joint estimation method based on the DWT is improved by 3 dB. The dimension of the memory matrix is reduced by 1/4 compared to the zero-padded compressed sensing channel estimation scheme.
Finally, it is noted that the above embodiments are only for illustrating the technical solution of the present invention and not for limiting the same, and although the present invention has been described in detail with reference to the preferred embodiments, it should be understood by those skilled in the art that modifications and equivalents may be made thereto without departing from the spirit and scope of the present invention, which is intended to be covered by the claims of the present invention.
Claims (6)
1. A sparse Bayesian power line channel and impulse noise joint estimation method based on DCT and DWT is characterized in that: the method comprises the following steps:
s1: converting a frequency domain signal received by a power line receiving end into a vector matrix form;
s2: extracting pilot frequency in the received signal;
s3: combining with DWT and DCT, constructing an observation matrix and an observation vector by the extracted pilot frequency symbol based on the compressed sensing model;
s4: uniformly partitioning an observation matrix;
s5: initializing a compressed sensing estimation model of power line impulse noise and a channel;
s6: starting with an empty model, and performing block addition on the assumption that all signal blocks are not added into the model; each iteration calculates covariance matrix, block correlation and correlation structure matrix, updates model parameters, and rebuilds covariance matrix according to the correlation structure matrix until all covariance matrices are obtained;
s7: after the preset condition is met, the circulation of S6 is ended, and a sparse solution vector is obtained;
s8: taking the front ng row of the sparse solution vector obtained in the step S7 to perform DCT and DWT to obtain a channel impulse response vector estimated value, and performing FFT (fast Fourier transform) of zero padding to obtain a channel frequency response vector with the length of N;
s9: the ng to (ng+N) rows of the obtained sparse solution vector are time domain impulse noise estimation vectors, so that frequency domain symbols with impulse noise removed are obtained;
in step S1, the frequency domain signal received by the power line receiving end is converted into a vector matrix form
Y=diag(X)H+Fi+G (1)
Wherein X= [ X ] 1 ,X 2 ,...X N ] T For transmitting symbol vectors in the frequency domain, the OFDM frequency domain symbol vector has a length of N, H= [ H ] 1 ,H 2 ,...,H N ]For the channel frequency response vector, F is an N-dimensional fourier transform matrix, i represents time domain impulse noise, where g=fg represents frequency domain background noise, gaussian white noise, and G represents background noise;
in step S2, the set of positions where pilots are inserted in the transmission signal is defined as P, (·) P is a submatrix formed by the corresponding rows or elements of the index in the set P, and equation (1) is transformed into:
Y P =diag(X P )H p +F p i+G p (2)
in step S3, in combination with the time domain sparse characteristic of the impulse noise, the compressed sensing estimation model of the power line impulse noise and the channel is:
wherein F is p,ng Is a fourier matrix of p×ng, ng is guard interval length, DCT ng*ng ,DWT ng*ng Is a matrix of ng dimension; in the formula, the ng 1-dimensional vector h is expressed as:
h=DCT*a (5)
h=DWT*b (6)
the formulae (3) and (4) are expressed as:
Y p =ΦX+G p (7)
where Φ is the observation matrix.
2. The sparse bayesian power line channel and impulse noise joint estimation method based on DCT and DWT according to claim 1, characterized by: in step S4, the observation matrix Φ is uniformly segmented Φ= [ Φ ] 1 ,Φ 2 ,...Φ m ]The block length is 8, the OFDM length is 1024, the ng length is 256, comb-shaped pilot frequencies are arranged and are evenly distributed, and the number is 64.
3. The sparse bayesian power line channel and impulse noise joint estimation method based on DCT and DWT according to claim 2, characterized by: the initialization in step S5 takes into account the signal-to-noise ratio SNR<20dB of the total number of the slots, set β = 0.1Y p || 2 ,η=10 -4 M represents dividing the observation vector into m blocks of data, corresponding to m blocks of observation matrix, Φ i Representing an observation matrix corresponding to the ith block, wherein eta is an algorithm exit condition, beta refers to noise variance, iterative computation is needed in the algorithm process, and s i ,q i Is a defined intermediate variable used to calculate the cost function.
4. A sparse bayesian power line channel and impulse noise joint estimation method based on DCT and DWT according to claim 3, characterized by: in step S6, starting with the null model, assume all signal blocks X i None of the blocks are added into the model, and the blocks are added; the set of bases in the model at the K-th iteration is a k Each iteration proceeds through the following steps:
s61: calculating covariance matrixCalculating block correlation gamma i =1/d i Tr(A i ) Wherein d is i Is matrix A i Tr represents the trace of the matrix; calculating a correlation structure matrix B i =A i /r i Rebuilding->Wherein r is i Representing the variance of the ith block; until all A is obtained i And according to the cost function l=log|c|+y T C -1 y, calculateAnd to obtain +.sup.maximum ΔL (i)>An index of the observation block matrix that maximizes Δl (i); where y represents the measurement vector input by the algorithm, i.e., the OFDM frequency domain symbol at the input pilot; wherein c=β -1 I+ΦΓΦ T Wherein I represents an identity matrix, Γ is a matrix constituted by a covariance matrix of the observation block matrix;
5. The sparse bayesian power line channel and impulse noise joint estimation method based on DCT and DWT according to claim 4, characterized by: in step S7 satisfy [ gamma ] new - γ|/|γ| < η, skipping out of the loop of S6, yielding a sparse solution vector x=μ;
6. The sparse bayesian power line channel and impulse noise joint estimation method based on DCT and DWT according to claim 4, characterized by: in step S62, Σμs is updated using the BSBL-FM algorithm i q i The method specifically comprises the following steps:
(1)the current block is added to the model and μ new =μ-βΣΦ T Φ i μ i ,Wherein Σ is a =-βΣΦ T Φ i Σ ii ,Wherein e i =β(Φ i -βΦΣΦ T Φ i ),μ new Refer to iteratively updated mean vectors, Σ, in an algorithm new Refers to iteratively updated covariance vectors in algorithm, μ i Then is the i-th value in the mean vector, Σ a Is an intermediate variable defined to represent Σ new Update procedure s inew ,q inew Representing updated s i ,q i For calculating a new cost function; e, e i Is an intermediate variable derived by algorithm, and conveniently represents q inew Is a new procedure of Sigma ii Is the covariance matrix corresponding to the ith block data for iteratively updating s i ;
Priority Applications (1)
| Application Number | Priority Date | Filing Date | Title |
|---|---|---|---|
| CN202210666573.2A CN115086116B (en) | 2022-06-13 | 2022-06-13 | DCT and DWT-based sparse Bayesian power line channel and impulse noise joint estimation method |
Applications Claiming Priority (1)
| Application Number | Priority Date | Filing Date | Title |
|---|---|---|---|
| CN202210666573.2A CN115086116B (en) | 2022-06-13 | 2022-06-13 | DCT and DWT-based sparse Bayesian power line channel and impulse noise joint estimation method |
Publications (2)
| Publication Number | Publication Date |
|---|---|
| CN115086116A CN115086116A (en) | 2022-09-20 |
| CN115086116B true CN115086116B (en) | 2023-05-26 |
Family
ID=83250671
Family Applications (1)
| Application Number | Title | Priority Date | Filing Date |
|---|---|---|---|
| CN202210666573.2A Active CN115086116B (en) | 2022-06-13 | 2022-06-13 | DCT and DWT-based sparse Bayesian power line channel and impulse noise joint estimation method |
Country Status (1)
| Country | Link |
|---|---|
| CN (1) | CN115086116B (en) |
Citations (8)
| Publication number | Priority date | Publication date | Assignee | Title |
|---|---|---|---|---|
| CN104598971A (en) * | 2015-01-15 | 2015-05-06 | 宁波大学 | Radial basis function neural network based unit impulse response function extraction method |
| EP2945387A1 (en) * | 2014-05-13 | 2015-11-18 | Alcatel Lucent | Method and apparatus for encoding and decoding video |
| CN107634922A (en) * | 2017-09-22 | 2018-01-26 | 南开大学 | Compressed sensing time-domain channel estimating method based on wavelet transformation modulating system |
| CN110649953A (en) * | 2019-08-19 | 2020-01-03 | 江苏大学 | Channel estimation method based on variational Bayesian learning under condition of impulse noise |
| CN112003801A (en) * | 2020-08-25 | 2020-11-27 | 广东电网有限责任公司计量中心 | Channel impulse response and impulse noise joint estimation method, system and equipment |
| CN113055317A (en) * | 2021-03-12 | 2021-06-29 | 哈尔滨工程大学 | Orthogonal matching tracking channel estimation method for underwater sound OFDM system |
| CN113935246A (en) * | 2021-10-29 | 2022-01-14 | 闽南师范大学 | Signal robust sparse time-frequency analysis method, terminal equipment and storage medium |
| CN114492499A (en) * | 2021-11-24 | 2022-05-13 | 宜宾学院 | Pulse noise suppression method based on WD-PowerICA algorithm |
Family Cites Families (1)
| Publication number | Priority date | Publication date | Assignee | Title |
|---|---|---|---|---|
| US9154263B1 (en) * | 2014-03-31 | 2015-10-06 | King Fahd University Of Petroleum And Minerals | Evaluation of compressed sensing in UWB systems with NBI |
-
2022
- 2022-06-13 CN CN202210666573.2A patent/CN115086116B/en active Active
Patent Citations (8)
| Publication number | Priority date | Publication date | Assignee | Title |
|---|---|---|---|---|
| EP2945387A1 (en) * | 2014-05-13 | 2015-11-18 | Alcatel Lucent | Method and apparatus for encoding and decoding video |
| CN104598971A (en) * | 2015-01-15 | 2015-05-06 | 宁波大学 | Radial basis function neural network based unit impulse response function extraction method |
| CN107634922A (en) * | 2017-09-22 | 2018-01-26 | 南开大学 | Compressed sensing time-domain channel estimating method based on wavelet transformation modulating system |
| CN110649953A (en) * | 2019-08-19 | 2020-01-03 | 江苏大学 | Channel estimation method based on variational Bayesian learning under condition of impulse noise |
| CN112003801A (en) * | 2020-08-25 | 2020-11-27 | 广东电网有限责任公司计量中心 | Channel impulse response and impulse noise joint estimation method, system and equipment |
| CN113055317A (en) * | 2021-03-12 | 2021-06-29 | 哈尔滨工程大学 | Orthogonal matching tracking channel estimation method for underwater sound OFDM system |
| CN113935246A (en) * | 2021-10-29 | 2022-01-14 | 闽南师范大学 | Signal robust sparse time-frequency analysis method, terminal equipment and storage medium |
| CN114492499A (en) * | 2021-11-24 | 2022-05-13 | 宜宾学院 | Pulse noise suppression method based on WD-PowerICA algorithm |
Non-Patent Citations (3)
| Title |
|---|
| "Impulsive Noise Removal from Gray-Scale Video Sequences via Adaptive Thresholding";Sahar Sadrizadeh等;《IEEE》;全文 * |
| "基于稀疏贝叶斯学习的电力线载波通信接收机设计";吕新荣等;《电信科学》;全文 * |
| "大规模MIMO下贝叶斯压缩感知信道估计方法";黄俊伟等;《光通信研究》;全文 * |
Also Published As
| Publication number | Publication date |
|---|---|
| CN115086116A (en) | 2022-09-20 |
Similar Documents
| Publication | Publication Date | Title |
|---|---|---|
| CN108322409B (en) | Sparse OFDM channel estimation method based on generalized orthogonal matching pursuit algorithm | |
| CN106506042B (en) | Based on L1/2The electric line communication system impulse noise suppression method of norm regularization | |
| CN113242191B (en) | Improved time sequence multiple sparse Bayesian learning underwater acoustic channel estimation method | |
| CN104486267B (en) | SC FDE channel estimation methods based on Wavelet Denoising Method under a kind of short wave channel | |
| CN111865843B (en) | Large-scale MIMO-OFDM system mixed message transmission channel estimation method | |
| CN108599820A (en) | The extensive mimo system channel estimation methods of matching pursuit algorithm are sampled based on block structure self-adapting compressing | |
| CN106027445A (en) | Channel estimation method for sparse property of underwater acoustic block structure | |
| CN109688074B (en) | Channel estimation method of OFDM system based on compressed sensing | |
| CN113381951A (en) | MFTN joint channel estimation and equalization method under time-frequency conversion selective fading channel | |
| CN115412416B (en) | Low-complexity OTFS signal detection method for high-speed moving scene | |
| CN109729035A (en) | A kind of impulse noise suppression method in orthogonal frequency division multiplexi communication system | |
| CN104539562A (en) | MIMO-OFDM wideband HF channel estimation method | |
| CN112003801A (en) | Channel impulse response and impulse noise joint estimation method, system and equipment | |
| CN104079520A (en) | Impulse interference inhibition method of OFDM system | |
| CN115086116B (en) | DCT and DWT-based sparse Bayesian power line channel and impulse noise joint estimation method | |
| CN116055261B (en) | OTFS channel estimation method based on model-driven deep learning | |
| CN114268346B (en) | Power line carrier communication compressed sensing channel estimation method under non-Gaussian noise | |
| CN113055318B (en) | Channel estimation method | |
| CN116388800A (en) | Pulse noise suppression method based on fast Bayes matching pursuit | |
| CN114244675B (en) | MIMO-OFDM system channel estimation method based on deep learning | |
| US9318232B2 (en) | Matrix spectral factorization for data compression, filtering, wireless communications, and radar systems | |
| CN111082837A (en) | Recursive compressed sensing-based impulse noise suppression method for power line communication system | |
| CN113014341A (en) | Estimation method for nonideal sparse channel | |
| CN111212002A (en) | Blind identification method of ocean underwater sound OFDM channel based on subspace algorithm | |
| CN116094876B (en) | Channel estimation method of orthogonal time-frequency-space system based on asymmetric architecture |
Legal Events
| Date | Code | Title | Description |
|---|---|---|---|
| PB01 | Publication | ||
| PB01 | Publication | ||
| SE01 | Entry into force of request for substantive examination | ||
| SE01 | Entry into force of request for substantive examination | ||
| GR01 | Patent grant | ||
| GR01 | Patent grant |