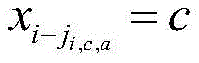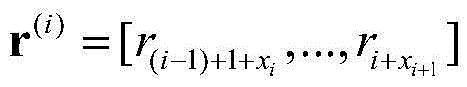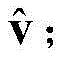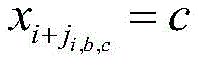CN111510166A - Method for processing symbol insertion and deletion in 4DPPM detection - Google Patents

Method for processing symbol insertion and deletion in 4DPPM detection Download PDF

Info

Publication number
CN111510166A
CN111510166A CN202010367683.XA CN202010367683A CN111510166A CN 111510166 A CN111510166 A CN 111510166A CN 202010367683 A CN202010367683 A CN 202010367683A CN 111510166 A CN111510166 A CN 111510166A
Authority
CN
China
Prior art keywords
sequence
symbol
drift
hidden markov
markov model
Prior art date
Legal status (The legal status is an assumption and is not a legal conclusion. Google has not performed a legal analysis and makes no representation as to the accuracy of the status listed.)
Pending
Application number
CN202010367683.XA
Other languages
Chinese (zh)
Inventor
陈为刚
张鹏
王丽霞
韩昌彩
杨晋生
Current Assignee (The listed assignees may be inaccurate. Google has not performed a legal analysis and makes no representation or warranty as to the accuracy of the list.)
Tianjin University
Original Assignee
Tianjin University
Priority date (The priority date is an assumption and is not a legal conclusion. Google has not performed a legal analysis and makes no representation as to the accuracy of the date listed.)
Filing date
Publication date
Application filed by Tianjin University filed Critical Tianjin University
Priority to CN202010367683.XA priority Critical patent/CN111510166A/en
Publication of CN111510166A publication Critical patent/CN111510166A/en
Pending legal-status Critical Current

Links

Images

Classifications

    • H—ELECTRICITY
    • H03—ELECTRONIC CIRCUITRY
    • H03M—CODING; DECODING; CODE CONVERSION IN GENERAL
    • H03M13/00—Coding, decoding or code conversion, for error detection or error correction; Coding theory basic assumptions; Coding bounds; Error probability evaluation methods; Channel models; Simulation or testing of codes
    • H03M13/29—Coding, decoding or code conversion, for error detection or error correction; Coding theory basic assumptions; Coding bounds; Error probability evaluation methods; Channel models; Simulation or testing of codes combining two or more codes or code structures, e.g. product codes, generalised product codes, concatenated codes, inner and outer codes
    • H—ELECTRICITY
    • H04—ELECTRIC COMMUNICATION TECHNIQUE
    • H04L—TRANSMISSION OF DIGITAL INFORMATION, e.g. TELEGRAPHIC COMMUNICATION
    • H04L1/00—Arrangements for detecting or preventing errors in the information received
    • H04L1/004—Arrangements for detecting or preventing errors in the information received by using forward error control
    • H04L1/0056—Systems characterized by the type of code used
    • H04L1/0061—Error detection codes
    • H04L1/0063—Single parity check
    • H—ELECTRICITY
    • H04—ELECTRIC COMMUNICATION TECHNIQUE
    • H04L—TRANSMISSION OF DIGITAL INFORMATION, e.g. TELEGRAPHIC COMMUNICATION
    • H04L1/00—Arrangements for detecting or preventing errors in the information received
    • H04L1/004—Arrangements for detecting or preventing errors in the information received by using forward error control
    • H04L1/0056—Systems characterized by the type of code used
    • H04L1/0064—Concatenated codes

Landscapes

  • Engineering & Computer Science (AREA)
  • Computer Networks & Wireless Communication (AREA)
  • Signal Processing (AREA)
  • Physics & Mathematics (AREA)
  • Probability & Statistics with Applications (AREA)
  • Theoretical Computer Science (AREA)
  • Error Detection And Correction (AREA)

Abstract

A method for processing symbol insertion and deletion in 4DPPM detection includes inserting watermark sequence into binary L DPC code coded by information sequence to generate cascade code, converting cascade code into 4DPPM symbol sequence and modulating it into 4DPPM chip sequence, sending it, demodulating received chip sequence to be received symbol sequence at receiving end, decoding received symbol sequence by first and second decoders, setting hidden Markov model based on known watermark sequence and equivalent information source and channel model at first decoder, obtaining maximum possible drift quantity of each symbol by recursive calculation of branch measurement and transfer position difference of hidden Markov model to determine position of each symbol and obtain estimated value of code word, correcting residual substitute error by second decoder to obtain decoded code word by using estimated value of code word.

Description

Method for processing symbol insertion and deletion in 4DPPM detection
Technical Field
The invention relates to the field of digital communication coding, in particular to a method for processing symbol insertion and deletion in 4DPPM detection.
Background
the Pulse Position Modulation (PPM) is a technology that can achieve high power utilization, and is therefore widely used in many types of communication systems, for example, the Infrared data Association (IrDA) has established 4-PPM as the standard modulation technique for 4-Mb/s serial data links, the United states National Aeronautical and Space Administration (NASA) has proposed that PPM technology be used in free space optical communication systems, PPM-like modulation methods can also be used in pulse-based ultra-wideband communication systems, etc. Differential Pulse Position Modulation (DPPM) is a derivative modulation method of PPM, DPPM can achieve higher power and spectrum utilization compared to PPM, however, as the length of a symbol sequence transmitting information in DPPM can be varied, chip flipping by additive white noise (AWGN) can cause damage to the corresponding symbol boundary, while causing subsequent symbols to deviate from the original position, which can cause severe insertion, segmentation and substitution errors, resulting in transmission failures.
the present invention relates to a method for correcting insertion and erasure errors in wireless infrared communications, and more particularly, to a method for correcting insertion and erasure errors in wireless infrared communications, which includes inserting a Marker (Marker) code into DPPM transmission chips, and correcting the insertion and erasure errors in wireless infrared communications.
Disclosure of Invention
The invention provides a method for processing symbol insertion and deletion in 4DPPM detection, which can solve insertion, deletion and substitution errors in 4DPPM symbol-by-symbol detection to solve the technical problems in the prior art.
A method for processing symbol insertion and deletion in 4DPPM detection includes inserting watermark sequence regularly into binary L DPC code coded by information sequence at transmitting end of communication channel to generate cascade code, converting cascade code into 4DPPM symbol sequence and modulating it into 4DPPM chip sequence, demodulating received chip sequence into received symbol sequence at receiving end of communication channel, decoding received symbol sequence by first-stage decoder and second-stage decoder in sequence, setting hidden Markov model based on known watermark sequence and equivalent information source and channel model at first-stage decoder, calculating forward measurement and backward measurement recursively by branch measurement and transfer position difference of hidden Markov model to obtain maximum possible shift quantity of each symbol, determining position of each symbol by maximum possible shift quantity and obtaining estimated value of code word, using error correcting code word estimated value by second-stage decoder to correct residual substitute error to obtain final decoded code word.
Furthermore, the insertion, deletion and substitution situations are deduced according to the known watermark sequence bits and the receiving symbols related to the known watermark sequence bits, a state transition grid diagram is established according to all the possible insertion, deletion and substitution situations of equivalent information source and equivalent channel models, and a hidden Markov model is established according to the chip flipping probability and the state transition grid diagram under different signal-to-noise ratios of the insertion/deletion/substitution channels.
Further, the method for establishing the hidden Markov model comprises the following steps:
Step A-1, defining the symbol drift amount x of the ith time iTo slave the transmission of a symbol t 0To the symbol t to be transmitted iThe number of insertions minus the number of erasures present between them shifts the symbol by an amount { x } iAs hidden state of hidden Markov model, let symbol maximum drift amount be x maxThen x iIs X { -X { [ MEANS of solving the problems of the prior art { ] -A + [ means + ] -A max,...,-1,0,1,...,xmax}；
Step A-2, setting the received symbol sequence r after channel transmission as r ═ r (0)r(1)...r(N-1)Consisting of subsequences
Figure BDA0002477062410000021
Composition, r is used as an observable vector of a hidden Markov model, and the state is from x i-1→xiIs transferred to the starter sequence r (i)The transmission of (1);
Step A-3, demapping the received symbol sequence r into bit pairs (u) ivi) Obtaining a corresponding receiving watermark sequence u and a corresponding receiving code word v; deducing insertion deletion and substitution situations by comparing watermark sequence bits and received symbols at a transmitting end;
Step A-4, establishing a hidden Markov model state transition grid diagram according to all transmission situations of equivalent information sources and channel models, and enabling each node in the grid diagram to correspond to the drift amount x of the ith position i。
Further, in the hidden markov model, a drift state x of a position i is set iB, shifting the drift state of the corresponding previous position to be a; let Q i,a,bA branch metric representing the received symbol sequence at the ith position, let j i,a,bRepresents a transfer position difference of the ith position; drifting state x for position i during state transition iB, the drift state a of the previous position corresponding to the transition has a plurality of different situations, and the branch metric Q is calculated according to different situations respectively i,a,bRecording the transfer position Difference j i,a,b。
Further, let w iRepresenting the ith code word bit in the known watermark sequence w; let r i+bA value representing the i + b th symbol in the received symbol sequence; let P fRepresenting chip flipping probability; drift state x for position i iB, multiple cases of shifting the drift state a of the corresponding previous position, and the corresponding branch metric Q i,a,bA difference j in transfer position i,a,bThe calculation methods of (a) are respectively as follows:
(1) If a is b, two transmission cases are corresponded: correct transmission and substitution, for the correct transmission case, corresponding to the transfer path i-1 → i, i.e. x i-1＝a，xiB, branch metric Q i,a,bAnd a difference j in transfer position i,a,bThe calculation formula of (2) is as follows:
Figure BDA0002477062410000031
ji,a,b＝i-(i-1)＝1，
For the alternative case, the corresponding transition path is i-2 → i, i.e., x i-2＝a，xiB, branch metric Q i,a,bAnd a difference j in transfer position i,a,bThe calculation formula of (2) is as follows:
Figure BDA0002477062410000032
ji,a,b＝i-(i-2)＝2；
(2) If a is b +2, the transition path corresponds to the abridged case { (001) → 3, (010) → 3, (100) → 3}, and i-3 → i, that is, x i-3＝a，xiB, branch metric Q i,a,bAnd a difference j in transfer position i,a,bThe calculation formula of (2) is as follows:
Qi,a,b＝Pf 2(1-Pf)2，(wi-2wi-1wi)＝000，ri+b＝(3)，
ji,a,b＝i-(i-3)＝3；
(3) If a is b +1, then pair Abridged case { (00) → 1, (01) → 2, (10) → 2, (02) → 3, (11) → 3, (20) → 3}, and the transition path is i-2 → i, i.e., x i-2＝a，xiB, branch metric Q i,a,bAnd a difference j in transfer position i,a,bThe calculation formula of (2) is as follows:
Figure BDA0002477062410000041
ji,a,b＝i-(i-3)＝3；
(4) If a ═ b-1, the transition path is i-1 → i, i.e., x → (00), 2 → (01), 2 → (10), 3 → (02), 3 → (11), 3 → (20) }, corresponding to the insertion situation, {1 → (00), 2 → (01), 2 → (10), 3 → (02), 3 → (20) } i-1＝a，xiB, branch metric Q i,a,bAnd a difference j in transfer position i,a,bThe calculation formula of (2) is as follows:
Figure BDA0002477062410000042
ji,a,b＝i-(i-1)＝1；
(5) If a ═ b-2, the transition path is i-1 → i, i.e., x → (000), 3 → (001), 3 → (010), 3 → (100) }, corresponding to the insertion case {2 → (000), 3 → (001), 3 → (010), 3 → (100) } i-1＝a，xiB, branch metric Q i,a,bAnd a difference j in transfer position i,a,bThe calculation formula of (2) is as follows:
Qi,a,b＝Pf 2(1-Pf)2,wi＝1,(ri-2+bri-1+bri+b)＝(000)or(001)or(010)or(100)，
ji,a,b＝i-(i-1)＝1。
Further, the method for obtaining the codeword estimation value by the first-stage decoder comprises the following steps:
Step B-1, in the hidden Markov model, defining the forward measurement as the drift amount x at the position i iProbability of receiving the first (i-1+ a) symbols of r, with F i(a) Represents a forward metric, F i(a) The calculation formula is as follows:
Figure BDA0002477062410000043
In the formula
Figure BDA0002477062410000044
Representing positions i-j i,c,aThe amount of drift of
Figure BDA0002477062410000045
The forward measure of the time of day,
Figure BDA0002477062410000046
Represents the ith-j i,c,aPosition receiving symbol sequence
Figure BDA0002477062410000047
A branch metric of (d);
Defining a backward metric as a given state x iWhen b, the tail sequence of r (r) is output i+b,..) using B i(b) Represents a backward measure, B i(b) The calculation formula is as follows:
Figure BDA0002477062410000051
In the formula
Figure BDA0002477062410000052
Indicates position i + j i,b,cThe amount of drift of
Figure BDA0002477062410000053
The backward measure of the time of flight,
Figure BDA0002477062410000054
Indicating the sequence of received symbols at the ith position
Figure BDA0002477062410000055
A branch metric of (d);
Step B-2, based on the forward metric F obtained by calculation i(a) And backward metric B i(b) Setting the maximum possible drift amount as
Figure BDA0002477062410000056
Calculating the maximum possible drift amount for each symbol
Figure BDA0002477062410000057
The calculation formula is as follows:
Figure BDA0002477062410000058
Step B-3, using the drift amount since the maximum possible drift amount of each symbol is identical to the maximum possible drift amount of its codeword bits
Figure BDA0002477062410000059
Inferring received codeword bits v iTo the received codeword bit v iCorrecting, and recording the corrected code word bits as
Figure BDA00024770624100000510
Figure BDA00024770624100000511
Further, the watermark sequence is a binary pseudo-random sequence.
The invention has the advantages and positive effects that: the invention provides a processing method for symbol insertion and truncation errors caused by symbol-by-symbol detection aiming at an efficient algorithm in 4DPPM detection. Different from the traditional processing method, the invention adopts a two-stage decoder, wherein the first-stage decoder establishes a hidden Markov model based on a known watermark sequence and an equivalent source and channel model to estimate insertion and deletion errors of a received symbol, and a hard decision forward-backward algorithm is adopted to output a code word estimation value. The second-level decoder adopts an outer decoder to execute the error correction decoding by the error correction code algorithm in the prior art and correct the residual substitute errors to obtain the final decoded code word. The method can process insertion and deletion errors in the transmission process. The method can effectively correct the insertion, deletion and substitution errors in the 4DPPM transmission, and compared with a decoding scheme which uses a dynamic programming algorithm and a Viterbi algorithm as an internal decoding algorithm, the decoding scheme provided by the invention improves the performance of correcting the insertion, deletion and substitution errors in the 4DPPM transmission.
Drawings
FIG. 1 is a workflow block diagram of the present invention;
FIG. 2 is a state transition trellis diagram of a hidden Markov model of the present invention;
FIG. 3 is a schematic diagram of an operational principle of the present invention;
FIG. 4 is a graph illustrating a comparison of 4DPPM transmission performance using different inner decoding algorithms;
FIG. 5 is a diagram illustrating a comparison of 4DPPM transmission performance using L DPC codes of different code lengths in a coding scheme;
FIG. 6 is a diagram of chip flipping error rate and symbol insertion/puncturing/substitution error rate for different SNR;
FIG. 7 is a graph comparing the average number of erroneous bits per frame in Hamming distance after processing by using the Viterbi inner decoder and the inner decoder of the present invention.
Detailed Description
For further understanding of the contents, features and effects of the present invention, the following embodiments are enumerated in conjunction with the accompanying drawings, and the following detailed description is given:
referring to fig. 1 to 7, a method for processing symbol insertion and deletion in 4DPPM detection includes, at a transmitting end of a communication channel, regularly inserting a watermark sequence into a binary L DPC code encoded by an information sequence to generate a concatenated code, converting the concatenated code into a 4DPPM symbol sequence and modulating the 4DPPM symbol sequence into a 4DPPM chip sequence, and transmitting the 4DPPM chip sequence, demodulating the received chip sequence into a received symbol sequence at a receiving end of the communication channel, and sequentially decoding the received symbol sequence by a first decoder and a second decoder, wherein the first decoder is provided with a hidden markov model established based on a known watermark sequence and an equivalent source and a channel model, and recursively calculates a forward metric and a backward metric from a branch metric and a transition position difference of the hidden markov model to obtain a maximum possible shift amount of each symbol, and determines a position of each symbol from the maximum possible shift amount to obtain a codeword estimation value, and the second decoder uses the codeword estimation value to correct remaining alternative errors to obtain a final decoded codeword.
In the invention, the first-level decoder is also called an inner decoder; the second level decoder is also called an outer decoder.
L DPC is explained as low density parity check.
The 4DPPM chinese notation is quaternary differential pulse position modulation.
The position difference is the distance between each position and the previous position to which it was transferred.
Preferably, the insertion, deletion and substitution situations can be deduced from the known watermark sequence bits and the received symbols associated with the known watermark sequence bits, a state transition grid diagram can be established corresponding to all the possible insertion, deletion and substitution situations of the equivalent source and equivalent channel models, and the hidden markov model can be established according to the chip flipping probability and the state transition grid diagram under different signal-to-noise ratios of the insertion/deletion/substitution channels.
Preferably, the method of building the hidden markov model may comprise the steps of:
Step A-1, defining the symbol drift amount x at the ith time iTo slave the transmission of a symbol t 0To the symbol t to be transmitted iThe number of insertions minus the number of erasures that exist between them can shift the symbols by an amount { x } iAs the hidden state of the hidden Markov model, the maximum drift amount of the sign can be set as x maxThen x iIs X { -X { [ MEANS of solving the problems of the prior art { ] -A + [ means + ] -A max,...,-1,0,1,...,xmax}；
In step a-2, the received symbol sequence r after channel transmission may be set to r ═ r (0)r(1)...r(N-1)It may be composed of subsequences
Figure BDA0002477062410000071
Composition, r can be used as an observable vector of a hidden Markov model State from x i-1→xiIs transferred to the starter sequence r (i)The transmission of (1);
Step A-3, the received symbol sequence r may be demapped into bit pairs (u) ivi) Obtaining a corresponding receiving watermark sequence u and a corresponding receiving code word v; the insertion deletion and substitution situations can be deduced by comparing watermark sequence bits and received symbols at a transmitting end;
Step A-4, a hidden Markov model state transition grid diagram can be established according to all transmission situations of equivalent information sources and channel models, so that each node in the grid diagram corresponds to the drift amount x of the ith position i。
Preferably, in the hidden Markov model, the drift state x of the possible location i is set iB, shifting the drift state of the corresponding previous position to be a; let Q i,a,bThe branch metric representing the received symbol sequence at the ith position may be set to j i,a,bRepresents a transfer position difference of the ith position; drifting state x for position i during state transition iB, the drift state a of the previous position corresponding to the transition has a plurality of different situations, and the branch metric Q can be calculated respectively corresponding to different situations i,a,bRecording the difference j of the transfer position i,a,b。
Preferably, w may be set iRepresenting the ith code word bit in the known watermark sequence w; can be provided with r i+bA value representing the i + b th symbol in the received symbol sequence; can be provided with P fRepresenting chip flipping probability; drift state x for position i iB, multiple cases of shifting the drift state a of the corresponding previous position, and the corresponding branch metric Q i,a,bA difference j in transfer position i,a,bThe calculation methods of (a) can be respectively as follows:
(1) If a is b, two transmission cases are corresponded: correct transmission and substitution, for the correct transmission case, corresponding to the transfer path i-1 → i, i.e. x i-1＝a，xiB, branch metric Q i,a,bAnd a difference j in transfer position i,a,bThe calculation formula of (2) is as follows:
Figure BDA0002477062410000072
ji,a,b＝i-(i-1)＝1，
For the alternative case, the corresponding transition path is i-2 → i, i.e., x i-2＝a，xiB, branch metric Q i,a,bAnd a difference j in transfer position i,a,bThe calculation formula of (2) is as follows:
Figure BDA0002477062410000081
ji,a,b＝i-(i-2)＝2；
(2) If a is b +2, the transition path corresponds to the abridged case { (001) → 3, (010) → 3, (100) → 3}, and i-3 → i, that is, x i-3＝a，xiB, branch metric Q i,a,bAnd a difference j in transfer position i,a,bThe calculation formula of (2) is as follows:
Qi,a,b＝Pf 2(1-Pf)2，(wi-2wi-1wi)＝000，ri+b＝(3)，
ji,a,b＝i-(i-3)＝3；
(3) If a + b +1, the transition path corresponds to the abridged case { (00) → 1, (01) → 2, (10) → 2, (02) → 3, (11) → 3, (20) → 3}, and i-2 → i, that is, x i-2＝a，xiB, branch metric Q i,a,bAnd a difference j in transfer position i,a,bThe calculation formula of (2) is as follows:
Figure BDA0002477062410000082
ji,a,b＝i-(i-3)＝3；
(4) If a ═ b-1, the transition path is i-1 → i, i.e., x → (00), 2 → (01), 2 → (10), 3 → (02), 3 → (11), 3 → (20) }, corresponding to the insertion situation, {1 → (00), 2 → (01), 2 → (10), 3 → (02), 3 → (20) } i-1＝a，xiB, branch metric Q i,a,bAnd a difference j in transfer position i,a,bThe calculation formula of (2) is as follows:
Figure BDA0002477062410000083
ji,a,b＝i-(i-1)＝1；
(5) If a ═ b-2, the transition path is i-1 → i, i.e., x → (000), 3 → (001), 3 → (010), 3 → (100) }, corresponding to the insertion case {2 → (000), 3 → (001), 3 → (010), 3 → (100) } i-1＝a，xiB, branch metric Q i,a,bAnd a difference j in transfer position i,a,bThe calculation formula of (2) is as follows:
Qi,a,b＝Pf 2(1-Pf)2,wi＝1,(ri-2+bri-1+bri+b)＝(000)or(001)or(010)or(100)，
ji,a,b＝i-(i-1)＝1。
Preferably, the method for obtaining the codeword estimation value by the first-stage decoder comprises the following steps:
Step B-1, in the hidden Markov model, the forward metric can be defined as the drift amount x at position i iThe probability that a and the first (i-1+ a) symbols of r are received, F may be used i(a) Represents a forward metric, F i(a) The calculation formula may be:
In the formula
Figure BDA0002477062410000092
Representing positions i-j i,c,aThe amount of drift of
Figure BDA0002477062410000093
The forward measure of the time of day,
Figure BDA0002477062410000094
Represents the ith-j i,c,aPosition receiving symbol sequence
Figure BDA0002477062410000095
A branch metric of (d);
The forward metric at position i is based on the position i transition correspondence If the drift amount of the position i is a, the value of the drift amount c of the previous position corresponding to the position i transfer can be { a-2, a-1, a, a +1, a +2}, according to the difference between the value c and the value a, the corresponding transfer position difference can be obtained by contrasting the built hidden Markov model, and j is used for calculating the corresponding transfer position difference i,c,aRepresents i-j i,c,aI.e. the coordinates of the corresponding previous position are transferred for position i.
A backward metric may be defined for a given state x iWhen b, the tail sequence of r (r) is output i+b,..), available as B i(b) Represents a backward measure, B i(b) The calculation formula may be:
Figure BDA0002477062410000096
In the formula
Figure BDA0002477062410000097
Indicates position i + j i,b,cThe amount of drift of
Figure BDA0002477062410000098
The backward measure of the time of flight,
Figure BDA0002477062410000099
Indicating the sequence of received symbols at the ith position
Figure BDA00024770624100000910
A branch metric of (d);
The backward measurement of the position i is obtained by calculation according to the backward measurement of the next position corresponding to the position i transfer, if the drift amount of the position i is b, the value of the drift amount c of the next position corresponding to the position i transfer can be { b-2, b-1, b, b +1, b +2}, the corresponding transfer position difference can be obtained according to a hidden Markov model established by comparing the difference between the b value and the c value, and j is used for obtaining the corresponding transfer position difference i,b,cDenotes, i + j i,b,cI.e. the coordinates of the corresponding subsequent position are transferred for position i.
Step B-2, forward metrics F which can be obtained on the basis of calculation i(a) And backward metric B i(b) Setting the maximum possible drift amount as
Figure BDA00024770624100000911
Calculating the maximum possible drift amount for each symbol
Figure BDA00024770624100000912
The calculation formula is as follows:
Figure BDA0002477062410000101
In step B-3, since the maximum possible drift amount of each symbol is identical to the maximum possible drift amount of its codeword bits, the drift amount can be used
Figure BDA0002477062410000102
Inferring received codeword bits v iTo the received codeword bit v iCorrecting, and recording the corrected code word bits as
Figure BDA0002477062410000103
Figure BDA0002477062410000104
The watermark sequence may be a binary pseudorandom sequence.
The working process and working principle of the present invention will be further described below with reference to an embodiment of the present invention, wherein each expression in the embodiment is defined as above.
a method for processing symbol insertion and puncturing in 4DPPM detection, mainly taking an example of a concatenated watermark code with a length of 1152 bits, which is constructed by a predetermined pseudorandom sequence with a length of 576 bits and an L DPC code with a length of 576 bits, a code rate of R0.67 and a code rate of R0.5, as shown in fig. 3, includes the following steps:
(1) the transmitting end encodes the information sequence b into a binary L DPC code d with the length of 576 bits, and regularly inserts a watermark sequence w with the length of 576 bits, namely a binary pseudo-random sequence, into the code word d to generate Concatenated code [ w ] 0d0,w1d1,...,wN-1dN-1]The length of the concatenated code is 1152 bits, and bit pairs (w) are sequentially formed idi) According to the mapping rules { (00) → '0', (01) → '1', (10) → '2', (11) → '3' }, the 4DPPM symbol x is converted into iGenerating a symbol sequence x with the length of 576 bits, modulating the symbol sequence x into a 4DPPM chip sequence c according to rules { '0' → (1), '1' → (01), '2' → (001), '3' → (0001) }, transmitting the chip sequence c through a channel to cause chip flipping to obtain a received chip sequence z, and recovering the received chip sequence into a received symbol sequence r with the length of 576 bits by using a 4DPPM symbol-by-symbol detection method;
(2) The first-stage decoder establishes a hidden Markov process model based on the watermark sequence and the equivalent information source and channel model, determines the hidden state and the observable vector of the hidden Markov model, and establishes a hidden Markov model state transition grid diagram according to all transmission situations of the equivalent information source and the channel model;
(2.1) defining the symbol drift amount x at the ith time iTo slave the transmission of a symbol t 0To the symbol t to be transmitted iThe number of insertions minus the number of erasures present between them shifts the symbol by an amount { x } iAs hidden state of hidden Markov model, limiting maximum symbol drift amount to 10 to reduce calculation amount of proposed inner decoding algorithm, so x iThe value set of (a) is X { -10., -, 1,0, 1., 10 };
(2.2) the received symbol sequence r after channel transmission is r ═ r (0)r(1)...r(N-1)From a subsequence
Figure BDA0002477062410000111
Composition, r is used as an observable vector of a hidden Markov model, and the state is from x i-1→xiIs transferred to the starter sequence r (i)The transmission of (1);
(2.3) demapping the received symbol sequence r into bit pairs (u) → (0) → (00), (1) → (01), (2) → (10), (3) → (11) } according to a rule { (0) → (01), (2) → (10) } ivi) Obtaining a corresponding received watermark sequence u and receiving A codeword v;
(2.4) establishing a hidden Markov model state transition grid graph according to all transmission situations of equivalent information sources and channel models, wherein each node in the grid graph corresponds to the drift amount x of the ith position iGiven a drift state of x for position i-1 i-1Drift state x of position i when a ia possible value of b is b ∈ { a, a +1, a +2}, given the drift state of i-2 is x i-2Drift state x of position i when a ia possible value of b is b ∈ { a-1, a }, given the drift state of i-3 is x i-3Drift state x of position i when a ia possible value of b is b ∈ { a-2}, and during the state transition process, the variable j is used i,a,bRecording the position difference, j, corresponding to the transition of the ith position i,a,b∈{1,2,3}。
(3) Based on the built hidden Markov process model, the chip flipping probability of the generalized insertion/deletion/substitution (IDS) channel under different signal-to-noise ratios is utilized to compare the known watermark bit with the associated received symbol, and the drift state x of the position i is subjected to the possible situations of all insertion, deletion and substitution in consideration of the equivalent source and equivalent channel models iB, there are 5 different cases to transfer the drift state a of the corresponding previous position, initializing the branch metric Q i,a,bRecording the difference j of the transfer position i,a,b(ii) a Can be provided with w iRepresenting the ith code word bit in the known watermark sequence w; can be provided with r i+bA value representing the i + b th symbol in the received symbol sequence; can be provided with P fRepresenting chip flipping probability; branch metrics Q in 5 different cases i,a,bAnd a difference j in transfer position i,a,bThe calculation method can be as follows:
(3.1) if a ═ b, then two transmission scenarios are corresponded: correct transmission and substitution, for the correct transmission case, corresponding to the transfer path i-1 → i, i.e. x i-1＝a，xiB, the branch metric calculation formula is:
Figure BDA0002477062410000112
ji,a,b＝i-(i-1)＝1，
For the alternative case, the corresponding transition path is i-2 → i, i.e., x i-2＝a，xiB, the branch metric calculation formula is:
Figure BDA0002477062410000121
ji,a,b＝i-(i-2)＝2；
(3.2) if a + b +2, the transition path is i-3 → i, i.e. x, corresponding to the deletion condition { (001) → 3, (010) → 3, (100) → 3}, and the transition path is i-3 → i i-3＝a，xiB, the branch metric calculation formula is:
Qi,a,b＝Pf 2(1-Pf)2，(wi-2wi-1wi)＝000，ri+b＝(3)，
ji,a,b＝i-(i-3)＝3；
(3.3) if a + b +1, the transition path corresponds to the deletion case { (00) → 1, (01) → 2, (10) → 2, (02) → 3, (11) → 3, (20) → 3}, and the transition path is i-2 → i, that is, x { (00) → 1) } and the transition path is x { (01) → 2 { (02) → 3) } 3 i-2＝a，xiB, the branch metric calculation formula is:
Figure BDA0002477062410000122
ji,a,b＝i-(i-3)＝3；
(3.4) if a ═ b-1, the transition path is i-1 → i, i.e., x, corresponding to the insertion case {1 → (00), 2 → (01), 2 → (10), 3 → (02), 3 → (11), 3 → (20) }, the transition path being i-1 → i i-1＝a，xiB, the branch metric calculation formula is:
Figure BDA0002477062410000123
ji,a,b＝i-(i-1)＝1；
(3.5) if a ═ b-2, then the transition path is i-1 → i, i.e., x → (000), 3 → (001), 3 → (010), 3 → (100) }, corresponding to the insertion case {2 → (000), 3 → (001), 3 → (010), 3 → (100) } i-1＝a，xiB, branch metric calculation The formula is as follows:
Qi,a,b＝Pf 2(1-Pf)2,wi＝1,(ri-2+bri-1+bri+b)＝(000)or(001)or(010)or(100)，ji,a,b＝i-(i-1)＝1。
(4) Branch metrics Q using hidden Markov models i,a,bAnd a difference j in transfer position i,a,bRecursively calculating a forward metric F i(a) And backward metric B i(b) Then calculating the maximum possible drift amount of each symbol
Figure BDA0002477062410000131
Using the maximum possible drift
Figure BDA0002477062410000132
Deducing the position of each symbol to obtain the estimated value of code word
Figure BDA0002477062410000133
(4.1) Using the received symbol sequence branch metric Q computed in the hidden Markov model i,a,bAnd recorded transfer position difference j i,a,bRecursively calculating a forward metric F i(a) And backward metric B i(b)。
Forward metrics
Figure BDA0002477062410000134
Denotes the amount of drift at position i as x iProbability of receiving the first (i-1+ a) symbols of r, F i(a) The calculation formula is as follows:
Figure BDA0002477062410000135
Backward measure
Figure BDA0002477062410000136
Representing a given state x iWhen b, the tail sequence of r (r) is output i+b,..), B i(b) The calculation formula is as follows:
Figure BDA0002477062410000137
(4.2) forward metrics F based on the calculation i(a) And backward metric B i(b) Calculating the maximum possible drift amount of each symbol
Figure BDA0002477062410000138
Figure BDA0002477062410000139
(4.3) since the maximum possible amount of drift per symbol coincides with the maximum possible amount of drift for its codeword bits, the amount of drift is used
Figure BDA00024770624100001310
Inferring received codeword bits v iTo the received codeword bit v iCorrecting, and recording the corrected code word bits as
Figure BDA00024770624100001311
Figure BDA00024770624100001312
(5) Outer decoder using codeword estimation
Figure BDA00024770624100001313
And executing a BP decoding algorithm of a logarithm domain, setting the iteration times as 20 times, and correcting the residual substitution errors to obtain a decoded code word.
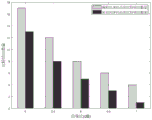
Under an Additive White Gaussian Noise (AWGN) channel, the method for processing symbol insertion and deletion in 4DPPM detection provided by the present invention is subjected to performance simulation, and the frame error rate performance of an internal decoding algorithm under different signal-to-noise ratios is compared with the frame error rate performance of a proposed hidden markov model-based hard decision forward-backward algorithm and a dynamic programming algorithm respectively adopted by the internal decoding algorithm. Referring to fig. 4, simulation results show that the decoding algorithm proposed by the present invention can significantly improve the error correction performance of insertion, truncation and substitution errors in 4DPPM transmission.
further, in order to illustrate the applicability of the decoding scheme provided by the invention to long codes with more insertion and deletion errors, an L DPC code with a code length of 24576 bits and a code rate of 0.67 is used to construct a concatenated watermark code with a length of 24576 × 2 bits with a predetermined pseudo-random sequence with a length of 24576 bits, the frame error rate performance of the concatenated watermark code with two different lengths of the inner decoding algorithm under different signal-to-noise ratios is compared by respectively adopting a Viterbi algorithm and a hidden Markov model-based hard decision forward-backward algorithm, and referring to FIG. 5, a simulation result shows that under the same code rate, a grouping decoding mode is adopted, the long code has more excellent error correction performance for insertion, deletion and substitution errors in 4DPPM transmission.
Using L DPC code with code length of 576 bits and code rate of 0.67 to analyze error characteristics of generalized IDS channel and compare the number of residual substitution errors of proposed hard decision forward and backward algorithm and Viterbi algorithm, referring to FIG. 6, to calculate a hard decision forward and backward algorithm based on hidden Markov model, the chip flipping probability P is estimated using the chip flipping error rate at different SNR fThe chip flipping of the generalized IDS channel is caused by the AWGN channel and the 4DPPM symbol soft demodulation method, so that the resulting symbol insertion, deletion, and substitution errors can be measured by edit distance, and fig. 6 gives the error rate at which the chip flipping and symbol insertion/deletion/substitution occur through the generalized IDS channel. Referring to fig. 7, which shows the average of the number of erroneous bits per frame over the hamming distance after both intra-decoding, it can be observed that the insertion and erasure errors have been corrected or converted into a small number of residual replacement errors by the intra-decoder. In addition, compared with the Viterbi algorithm, the hard decision forward and backward algorithm based on the hidden Markov model has better synchronization performance, and when the SNR is 5dB, the algorithm has better synchronization performance The residual error rate can be reduced to 2.25%, and reliable guarantee is provided for an outer decoder.
Those skilled in the art will appreciate that the drawings are only schematic illustrations of preferred embodiments, and the above-mentioned serial numbers of the embodiments of the present invention are only for description and do not represent the merits of the embodiments.
The above description is only for the purpose of illustrating the preferred embodiments of the present invention and is not to be construed as limiting the invention, and any modifications, equivalents and improvements made within the spirit of the present invention are intended to be included within the scope of the present invention. The above-mentioned embodiments are only for illustrating the technical ideas and features of the present invention, and the purpose thereof is to enable those skilled in the art to understand the contents of the present invention and to carry out the same, and the present invention shall not be limited to the embodiments, i.e. the equivalent changes or modifications made within the spirit of the present invention shall fall within the scope of the present invention.

Claims (7)

1. A method for processing symbol insertion and deletion in 4DPPM detection is characterized in that a watermark sequence is regularly inserted into a binary L DPC code coded by an information sequence at a communication channel sending end to generate a cascade code, the cascade code is converted into a 4DPPM symbol sequence and modulated into a 4DPPM chip sequence to be sent, the received chip sequence is demodulated into a received symbol sequence at a communication channel receiving end, the received symbol sequence is decoded by a first-stage decoder and a second-stage decoder in sequence, wherein the first-stage decoder is provided with a hidden Markov model established based on a known watermark sequence and an equivalent information source and a channel model, forward measurement and backward measurement are recursively calculated by branch measurement and a transfer position difference of the hidden Markov model to obtain the maximum possible drift amount of each symbol, the position of each symbol is determined by the maximum possible drift amount and a codeword estimation value is obtained, and the second-stage decoder adopts an error correction code algorithm to correct residual substitute errors by the codeword estimation value to obtain a final decoded codeword.
2. The method as claimed in claim 1, wherein the interpolation, puncturing and substitution situations are inferred from known watermark sequence bits and their associated received symbols, a state transition trellis diagram is established corresponding to all possible interpolation, puncturing and substitution situations of equivalent source and equivalent channel models, and the hidden markov model is established according to the chip flipping probability and the state transition trellis diagram under different snr of the interpolated/punctured/substituted channel.
3. The method for processing symbol insertion and puncturing in 4DPPM detection as recited in claim 2, wherein the method for establishing the hidden markov model comprises the steps of:
Step A-1, defining the symbol drift amount x of the ith time iTo slave the transmission of a symbol t 0To the symbol t to be transmitted iThe number of insertions minus the number of erasures present between them shifts the symbol by an amount { x } iAs hidden state of hidden Markov model, let symbol maximum drift amount be x maxThen x iIs X { -X { [ MEANS of solving the problems of the prior art { ] -A + [ means + ] -A max,...,-1,0,1,...,xmax}；
Step A-2, setting the received symbol sequence r after channel transmission as r ═ r (0)r(1)...r(N-1)Consisting of subsequences
Figure FDA0002477062400000011
Composition, r is used as an observable vector of a hidden Markov model, and the state is from x i-1→xiIs transferred to the starter sequence r (i)The transmission of (1);
Step A-3, demapping the received symbol sequence r into bit pairs (u) ivi) Obtaining a corresponding receiving watermark sequence u and a corresponding receiving code word v; deducing insertion deletion and substitution situations by comparing watermark sequence bits and received symbols at a transmitting end;
Step A-4, establishing a hidden Markov model state transition grid diagram according to all transmission situations of equivalent information sources and channel models, and enabling each node in the grid diagram to correspond to the drift amount x of the ith position i。
4. The method of claim 3, wherein a drift state x of a position i is set in a hidden Markov model iB, shifting the drift state of the corresponding previous position to be a; let Q i,a,bA branch metric representing the received symbol sequence at the ith position, let j i,a,bRepresents a transfer position difference of the ith position; drifting state x for position i during state transition iB, the drift state a of the previous position corresponding to the transition has a plurality of different situations, and the branch metric Q is calculated according to different situations respectively i,a,bRecording the difference j of the transfer position i,a,b。
5. The method of claim 4, wherein w is set as iRepresenting the ith code word bit in the known watermark sequence w; let r i+bA value representing the i + b th symbol in the received symbol sequence; let P fRepresenting chip flipping probability; drift state x for position i iB, multiple cases of shifting the drift state a of the corresponding previous position, and the corresponding branch metric Q i,a,bA difference j in transfer position i,a,bThe calculation methods of (a) are respectively as follows:
(1) If a is b, two transmission cases are corresponded: correct transmission and substitution, for the correct transmission case, corresponding to the transfer path i-1 → i, i.e. x i-1＝a，xiB, branch metric Q i,a,bAnd a difference j in transfer position i,a,bThe calculation formula of (2) is as follows:
Figure FDA0002477062400000021
ji,a,b＝i-(i-1)＝1，
For the alternative case, the corresponding transition path is i-2 → i, i.e., x i-2＝a，xiB, branch metric Q i,a,bAnd a difference j in transfer position i,a,bThe calculation formula of (2) is as follows:
Figure FDA0002477062400000022
ji,a,b＝i-(i-2)＝2；
(2) If a is b +2, the transition path corresponds to the abridged case { (001) → 3, (010) → 3, (100) → 3}, and i-3 → i, that is, x i-3＝a，xiB, branch metric Q i,a,bAnd a difference j in transfer position i,a,bThe calculation formula of (2) is as follows:
Qi,a,b＝Pf 2(1-Pf)2，(wi-2wi-1wi)＝000，ri+b＝(3)，
ji,a,b＝i-(i-3)＝3；
(3) If a + b +1, the transition path corresponds to the abridged case { (00) → 1, (01) → 2, (10) → 2, (02) → 3, (11) → 3, (20) → 3}, and i-2 → i, that is, x i-2＝a，xiB, branch metric Q i,a,bAnd a difference j in transfer position i,a,bThe calculation formula of (2) is as follows:
Figure FDA0002477062400000031
ji,a,b＝i-(i-3)＝3；
(4) If a ═ b-1, the transition path is i-1 → i, i.e., x → (00), 2 → (01), 2 → (10), 3 → (02), 3 → (11), 3 → (20) }, corresponding to the insertion situation, {1 → (00), 2 → (01), 2 → (10), 3 → (02), 3 → (20) } i-1＝a，xiB, branch metric Q i,a,bAnd a difference j in transfer position i,a,bThe calculation formula of (2) is as follows:
Figure FDA0002477062400000032
ji,a,b＝i-(i-1)＝1；
(5) If a ═ b-2, the transition path is i-1 → i, i.e., x → (000), 3 → (001), 3 → (010), 3 → (100) }, corresponding to the insertion case {2 → (000), 3 → (001), 3 → (010), 3 → (100) } i-1＝a，xiB, branch metric Q i,a,bAnd a difference j in transfer position i,a,bIs calculated by Comprises the following steps:
Qi,a,b＝Pf 2(1-Pf)2,wi＝1,(ri-2+bri-1+bri+b)＝(000)or(001)or(010)or(100)，
ji,a,b＝i-(i-1)＝1。
6. The method of claim 4, wherein the method for obtaining codeword estimates by the first stage decoder comprises the steps of:
Step B-1, in the hidden Markov model, defining the forward measurement as the drift amount x at the position i iProbability of receiving the first (i-1+ a) symbols of r, with F i(a) Represents a forward metric, F i(a) The calculation formula is as follows:
Figure FDA0002477062400000033
In the formula
Figure FDA0002477062400000041
Representing positions i-j i,c,aThe amount of drift of
Figure FDA0002477062400000042
The forward measure of the time of day,
Figure FDA0002477062400000043
Represents the ith-j i,c,aPosition receiving symbol sequence
Figure FDA0002477062400000044
A branch metric of (d);
Defining a backward metric as a given state x iWhen b, the tail sequence of r (r) is output i+b,..) using B i(b) Represents a backward measure, B i(b) The calculation formula is as follows:
Figure FDA0002477062400000045
In the formula
Figure FDA0002477062400000046
Indicates position i + j i,b,cThe amount of drift of
Figure FDA0002477062400000047
The backward measure of the time of flight,
Figure FDA0002477062400000048
Indicating the sequence of received symbols at the ith position
Figure FDA0002477062400000049
A branch metric of (d);
Step B-2, based on the forward metric F obtained by calculation i(a) And backward metric B i(b) Setting the maximum possible drift amount as
Figure FDA00024770624000000410
Calculating the maximum possible drift amount for each symbol
Figure FDA00024770624000000411
The calculation formula is as follows:
Figure FDA00024770624000000412
Step B-3, using the drift amount since the maximum possible drift amount of each symbol is identical to the maximum possible drift amount of its codeword bits
Figure FDA00024770624000000413
Inferring received codeword bits v iTo the received codeword bit v iCorrecting, and recording the corrected code word bits as
Figure FDA00024770624000000414
Figure FDA00024770624000000415
7. The method of claim 1, wherein the watermark sequence is a binary pseudo-random sequence.
CN202010367683.XA 2020-04-30 2020-04-30 Method for processing symbol insertion and deletion in 4DPPM detection Pending CN111510166A (en)

Priority Applications (1)

Application Number Priority Date Filing Date Title
CN202010367683.XA CN111510166A (en) 2020-04-30 2020-04-30 Method for processing symbol insertion and deletion in 4DPPM detection

Applications Claiming Priority (1)

Application Number Priority Date Filing Date Title
CN202010367683.XA CN111510166A (en) 2020-04-30 2020-04-30 Method for processing symbol insertion and deletion in 4DPPM detection

Publications (1)

Publication Number Publication Date
CN111510166A true CN111510166A (en) 2020-08-07

Family

ID=71864933

Family Applications (1)

Application Number Title Priority Date Filing Date
CN202010367683.XA Pending CN111510166A (en) 2020-04-30 2020-04-30 Method for processing symbol insertion and deletion in 4DPPM detection

Country Status (1)

Country Link
CN (1) CN111510166A (en)

Cited By (2)

* Cited by examiner, † Cited by third party
Publication number Priority date Publication date Assignee Title
CN113595561A (en) * 2021-07-14 2021-11-02 深圳宏芯宇电子股份有限公司 Hybrid decoding method, storage device controller and storage system
CN114629755A (en) * 2022-05-16 2022-06-14 睿迪纳(南京)电子科技有限公司 Modulation method, demodulation method and frequency offset compensation and high-speed demodulation circuit thereof

Citations (3)

* Cited by examiner, † Cited by third party
Publication number Priority date Publication date Assignee Title
DE102013215126A1 (en) * 2013-08-01 2015-02-05 Deutsches Zentrum für Luft- und Raumfahrt e.V. Method for transmitting data from a sender to a receiver
CN106712901A (en) * 2016-12-02 2017-05-24 天津大学 Hard decision-directed forward and backward estimation method under symbol insertion and deletion channel
CN106788458A (en) * 2016-12-02 2017-05-31 天津大学 To method of estimation before and after being oriented to the hard decision for substituting mistake towards insertion abreviation

Patent Citations (3)

* Cited by examiner, † Cited by third party
Publication number Priority date Publication date Assignee Title
DE102013215126A1 (en) * 2013-08-01 2015-02-05 Deutsches Zentrum für Luft- und Raumfahrt e.V. Method for transmitting data from a sender to a receiver
CN106712901A (en) * 2016-12-02 2017-05-24 天津大学 Hard decision-directed forward and backward estimation method under symbol insertion and deletion channel
CN106788458A (en) * 2016-12-02 2017-05-31 天津大学 To method of estimation before and after being oriented to the hard decision for substituting mistake towards insertion abreviation

Non-Patent Citations (1)

* Cited by examiner, † Cited by third party
Title
WEIGANG CH EN ETAL.: "Correcting Insertions/Deletions in DPPM Using Hidden Markov Model", 《IEEE》 *

Cited By (3)

* Cited by examiner, † Cited by third party
Publication number Priority date Publication date Assignee Title
CN113595561A (en) * 2021-07-14 2021-11-02 深圳宏芯宇电子股份有限公司 Hybrid decoding method, storage device controller and storage system
CN114629755A (en) * 2022-05-16 2022-06-14 睿迪纳(南京)电子科技有限公司 Modulation method, demodulation method and frequency offset compensation and high-speed demodulation circuit thereof
CN114629755B (en) * 2022-05-16 2022-09-20 睿迪纳(南京)电子科技有限公司 Modulation method, demodulation method and frequency offset compensation and high-speed demodulation circuit thereof

Similar Documents

Publication Publication Date Title
US8397148B2 (en) Low complexity decoding algorithm for tail-biting convolutional codes
CN108462558B (en) Method and device for decoding polarization code SCL and electronic equipment
US5757821A (en) Method and apparatus for detecting communication signals having unequal error protection
WO2001043293A1 (en) Reduced search symbol estimation algorithm
US9184769B2 (en) Decoding method and decoder
CN106712901B (en) The front and back that a kind of insertion of symbol is oriented to hard decision under abreviation channel is to estimation method
CN106656208A (en) Concatenated code method of symbol-level hard decision iteration decoding correcting synchronization errors
CN111510166A (en) Method for processing symbol insertion and deletion in 4DPPM detection
CN106656209B (en) Cascade code method for correcting synchronous errors by adopting iterative decoding
CN108134612B (en) Iterative decoding method for correcting synchronous and substitute error cascade code
Prévost et al. CRC-assisted error correction in a trellis coded system with bit stuffing
CN111313908B (en) Irregular watermark encoding and decoding method for correcting non-binary insertion/deletion
CN105406877B (en) A kind of interpretation method of short code long circulating code
CN106788458B (en) Hard decision-oriented forward and backward estimation method for insertion deletion and substitution errors
CN107959650B (en) Blind frame synchronization method for low-bit-rate BCH (broadcast channel) code
CN106534037B (en) A kind of soft demodulating method of high order modulation signal
CN108055106B (en) Recognition method for code word boundary based on RM code partial decoding auxiliary differential detection
Chen et al. Correcting insertions/deletions in DPPM using hidden Markov model
CN112929131B (en) Mark code transmission method based on weighted editing distance
CN114337691B (en) Soft decoding method for Zipper code based on Chase-Pyndiah algorithm
CN108809335B (en) Decoding method and device
CN115549692A (en) Low-complexity forward-backward decoding method based on weighted editing distance
CN110995282A (en) Forward/backward decoding method with completely overlapped paths
JP3816752B2 (en) Code synchronization determination device
CN117155742A (en) Signal processing method, device, equipment, system and medium

Legal Events

Date Code Title Description
PB01 Publication
PB01 Publication
SE01 Entry into force of request for substantive examination
SE01 Entry into force of request for substantive examination
WD01 Invention patent application deemed withdrawn after publication

Application publication date: 20200807

WD01 Invention patent application deemed withdrawn after publication