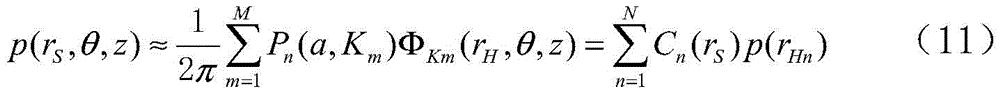CN109211399B - 一种锥面声源统计近场声全息方法 - Google Patents
一种锥面声源统计近场声全息方法 Download PDFInfo
- Publication number
- CN109211399B CN109211399B CN201811211082.9A CN201811211082A CN109211399B CN 109211399 B CN109211399 B CN 109211399B CN 201811211082 A CN201811211082 A CN 201811211082A CN 109211399 B CN109211399 B CN 109211399B
- Authority
- CN
- China
- Prior art keywords
- conical
- sound pressure
- sound
- field
- holographic
- Prior art date
- Legal status (The legal status is an assumption and is not a legal conclusion. Google has not performed a legal analysis and makes no representation as to the accuracy of the status listed.)
- Active
Links
Images
Classifications
-
- G—PHYSICS
- G01—MEASURING; TESTING
- G01H—MEASUREMENT OF MECHANICAL VIBRATIONS OR ULTRASONIC, SONIC OR INFRASONIC WAVES
- G01H17/00—Measuring mechanical vibrations or ultrasonic, sonic or infrasonic waves, not provided for in the preceding groups
Landscapes
- Physics & Mathematics (AREA)
- General Physics & Mathematics (AREA)
- Measurement Of Mechanical Vibrations Or Ultrasonic Waves (AREA)
- Holo Graphy (AREA)
Abstract
本发明公开了一种锥面声源统计近场声全息方法,利用与壳体结构装备共形的测量面获取全息声压数据,在统计最优柱面近场声全息理论方法的基础上,通过柱面‑锥面坐标变换,直接通过空间域全息面上复声压的线性叠加来计算锥形壳体结构装备辐射声场,填补了近场声全息技术在锥面声源中的应用空白,展示了其在低频噪声分析中的有效性,适用于锥形壳体结构水下兵器,从而为锥形壳体结构装备的声隐身性能评估提供了理论基础,具有重要的理论意义及工程应用价值。适用于主要处于低频振动噪声的锥形壳体结构装备的辐射声场重构,将锥形壳体结构装备辐射声场以可视化的方式显示出来,从而可以直观看出辐射声场的大小及分布情况。
Description
技术领域
本发明属于机械结构声辐射信号处理领域,特别涉及一种锥面声源统计 近场声全息方法。
背景技术
作为海军作战装备,水下航行器的续航力大,机动性强,独立作战能力 强,但其产生的噪声波在海水中可传递至数百海里,易被地方探测,严重削 弱了其声隐身性能,降低了其作战性能。因此,提高其声隐身性能是保证其 安全性和作战能力关键。目前,首要解决的技术问题是获得水下航行器辐射 声场,以实现对其隐身性能的精确评估。但对于内部声源繁多、传播路径复 杂的水下航行器壳体装备,难以对其声隐身性能进行精确评估。当前,普遍 利用装备有高精度固定式测量分析系统的水声试验场测试评估水下航行器声 隐身性能,然而,水声试验场选址要求极高、技术复杂且成本高昂。
近场声全息(Nearfield Acoustic Holography,NAH)是一种非常有效 的噪声源识别、定位与声场可视化方法,是通过近场测试获取足够多低空间 频率传播波和高空间频率倏逝波成分重建出分辨率不受分析波长限制的高精 度全息图像和丰富空间声场信息。然而传统NAH是通过空间二维傅立叶变换 来实现解卷积运算得到重建面声压,在全息计算过程中会带来窗效应和卷绕 误差,因而要求测试孔径面积至少为声源面积两倍,对于大尺寸锥形壳体结 构装备,满足NAH要求的精确测试很难实现。除此,在水下航行器低速航行时,机械设备振动噪声为主要噪声,其声源位于锥形结构,然而在目前的NAH 研究中,还未出现锥面声源辐射声场重构的研究。
发明内容
本发明的目的在于提供一种锥面声源统计近场声全息方法,以克服现有 技术的不足。
为达到上述目的,本发明采用如下技术方案:
一种锥面声源统计近场声全息方法,包括以下步骤:
步骤1),获取待测锥形结构外侧全息声压数据;
步骤2),通过柱面-锥面坐标变换,构造适用于锥面声源的单元面波;
步骤3),利用Nyguist采样定理选择声波波数矢量,选取的单元面波包 含锥形面所有全息声压数据;
步骤4),采用标准Tikhonov正则化方法,使用基于后验准则的广义交 叉验证(GCV)选取正则化参数;
步骤5),利用步骤4)标准Tikhonov正则化结合GCV方法求取叠加系数 矩阵;
步骤6),将锥形壳体结构装备表面声压表示为共形测量面声压的线性叠 加,获得锥形壳体结构装备辐射声场。
进一步的,使用与锥形壳体结构装备表面共形的测量面,布置声压传感 器,获取高效的全息声压数据。
进一步的,使用传声器测量声场全息声压数据,采用锥面统计最优近场 声全息算法采集全息声压数据。
进一步的,步骤2)中,通过柱面-锥面坐标变换,采用分离变量法求解 Helmholtz方程,得到空间任意点处的复声压,其过程如下:
首先,得到稳态声波场Helmholtz方程在柱面坐标系下的行波解为
在柱面坐标系下,令Pn(r,n,kz)为p(r,θ,z)的二维傅氏变换,为
同时给出其傅氏反变换为
令上式r=a得,
由(1)(2)(3)(4)式可解得:
式中,Pn(a,kz)为p(a,θ,z)的二维傅氏变换。
进一步的,由波数矢量K=(n,kz)确定的柱面上的空间频率域单元柱面波 为:
将积分运算离散化,则全息面和重建面上的复声压表示为:
进一步的,锥面测量结构时,锥角β保持不变,将式(6)中的柱面不变 量r用锥面锥角β表示,式(6)可变为如下形式:
再将式(7)在锥面下为:
重建锥面上任意点rS=(rS,θ,z)处波数矢量为Km的单元面波由全息面上所 有点rHn=(rH,θn,zn)处波数矢量为Km的单元面波叠加而得到,即:
式中,rHn=(rH,θn,zn)(n=1,2,…,N)为全息锥面上N个声压测量点,M为重 建锥面和全息锥面上复声压所包含的单元面波数目,Cn(rS)为叠加系数;
根据上述原理,可得:
式中,p(rs,θ,z)和p(rHn)分别为重建锥面和全息锥面上各点声压;
再由式(8),确定的M个线性方程所构成的方程组:
其中M≥N,则方程组可以表示为:
α(rS)=ACn(rS) (15)
其中M根据柱面SONAH理论中确定波数矢量的方法来确定;
通过正则化来抑制小幅度倏逝波的影响,得上式的正则化解为:
Cn(rS)=(AHA+λ2I)-1AHα(rS) (16)
式中,AH为矩阵A的共轭转置矩阵,λ为正则化参数,起滤波作用,I为 单位对角阵。
进一步的,利用标准Tikhonov正则化结合基于后验准则的广义交叉验证 选取正则化参数,确定λ使GCV目标函数达到极小,其中GCV函数定义为:
其中,trace()表示方阵的迹,即方阵的对角线各个元素的和,σi为 矩阵A的特征值。
进一步的,利用正则化去除测量误差的方法,结合公式(12)、(13)和(14), 求取叠加系数C(rS)=(A+A+λ2)A+b;
利用权利要求5)中求取的叠加系数C(rS)和在全息面上测得的各点声压 p(rHn),将锥形壳体结构装备表面各点声压表示为共形测量面声压的线性叠 加,即p(rS)=C(rS)p(rHn),获得锥形壳体结构装备辐射声场。
与现有技术相比,本发明具有以下有益的技术效果:
本发明公开了一种锥面声源统计近场声全息方法,利用与壳体结构装备 共形的测量面获取全息声压数据,在统计最优柱面近场声全息理论方法的基 础上,通过柱面-锥面坐标变换,直接通过空间域全息面上复声压的线性叠加 来计算锥形壳体结构装备辐射声场,填补了近场声全息技术在锥面声源中的 应用空白。本方法充分展示了其在低频噪声分析中的有效性,适用于锥形壳 体结构水下兵器,从而为锥形壳体结构装备的声隐身性能评估提供了理论基 础,具有重要的理论意义及工程应用价值。适用于主要处于低频振动噪声的 锥形壳体结构装备的辐射声场重构,将锥形壳体结构装备辐射声场以可视化 的方式显示出来,从而可以直观看出辐射声场的大小及分布情况。
本发明在统计最优柱面近场声全息及技术的基础上,通过柱面-锥面坐 标变换,直接通过空间域中全息面上复声压的叠加来计算重建面上的复声压, 不但从原理上解决了NAH带来的窗效应和卷绕误差。
采用本发明提供的方法测量声场信息时,除了记录传播波成分外,还能 记录高空间频率且随传播距离按指数规律衰减的倏逝波成分,获得了丰富的 声场信息,提高了重构精度。
本发明提供的方法对锥形壳体结构装备辐射声场进行重构,适用于锥形 结构水下兵器,能够实现锥形壳体结构装备辐射声场重构,为其声隐身性能 评估提供了理论基础。
本发明锥面声源统计最优近场声全息可以很好地解决以上问题,适用于 锥形结构水下兵器,可实现锥形壳体结构装备辐射声场的重构。
附图说明
图1为本发明全息测量面加噪声理论声压图;
图2为本发明锥形壳体结构装备表面理论声压图;
图3为本发明锥形壳体结构装备表面重建声压图;
图4为本发明θ=0母线上声压分布曲线;
图5为本发明不同测量距离下θ=0母线上声压分布曲线;
图6为本发明全息测量面加噪声理论声压图;
图7为本发明锥形壳体结构装备表面理论声压图;
图8为本发明锥形壳体结构装备表面重建声压图;
图9为本发明θ=0母线上声压分布曲线;
图10为本发明不同正则化参数选取方法的重构误差曲线。
图11为本发明锥面近场声全息测量结构示意图。
图12为本发明锥面近场声全息测量结构测量面正视图。
具体实施方式
下面结合附图对本发明做进一步详细描述:
如图1至图10所示,一种锥面声源统计近场声全息方法,包括以下步骤:
步骤1),获取待测锥形结构外侧全息声压数据;
步骤2),通过柱面-锥面坐标变换,构造适用于锥面声源的单元面波;
步骤3),利用Nyguist采样定理选择声波波数矢量,选取的单元面波包 含锥形面所有全息声压数据;
步骤4),采用标准Tikhonov正则化方法,使用基于后验准则的广义交 叉验证(GCV)选取正则化参数;
步骤5),利用步骤4)标准Tikhonov正则化结合GCV方法求取叠加系数 矩阵;
步骤6),将锥形壳体结构装备表面声压表示为共形测量面声压的线性叠 加,获得锥形壳体结构装备辐射声场。
本发明为模拟锥形、类锥形壳体结构装备,采用轴向为1.2m、大截面半 径为0.3m,小截面半径为0.12m的锥形壳体为研究对象;使用与锥形壳体结 构装备表面共形的测量面,选择合理的测量参数,布置声压传感器,获取高 效的全息声压数据;
步骤1)中,使用传声器测量声场全息声压数据:
采用锥面统计最优近场声全息算法采集全息声压数据:
在统计最优柱面近场声全息技术基础上,通过柱面-锥面坐标变换,采用 分离变量法求解Helmholtz方程,仅考虑向外发散传播的声波,得到空间任 意点处的复声压。其实现过程如下:
首先,得到稳态声波场Helmholtz方程在柱面坐标系下的行波解为
在柱面坐标系下,令Pn(r,n,kz)为p(r,θ,z)的二维傅氏变换,为
同时给出其傅氏反变换为
令上式r=a得,
由(1)(2)(3)(4)式可解得:
式中,Pn(a,kz)为p(a,θ,z)的二维傅氏变换。
由波数矢量K=(n,kz)确定的柱面上的空间频率域单元柱面波为:
将积分运算离散化,则全息面和重建面上的复声压表示为:
在柱面SONAH技术中,单元柱面波表达式(6)中,对于一确定的圆柱测 量面,其半径r是确定的,包围声源的圆柱面半径a也是确定的,两者都不随 圆柱面轴向位置的变化而变化。然而对于锥面声源,其半径大小是随轴向距 离位置的变化而变化,但同样地,考虑到一固定的锥面,无论是锥面测量面 还是包含声源的圆锥面,其锥角的大小是固定不变的。锥面近场声全息测量 方案如图11所示,最外层圆锥面为全息测量面,测量面沿锥面母线的长度为 L,上表面半径为rs所在的圆锥面为重建面,声源都包含在上表面半径为ra 所在的圆锥面内。
测量面正视图如图12所示,在整个锥面上,锥角β保持不变,源面位于 图中虚线位置。故可将式(6)中的柱面不变量r用锥面锥角β表示,式(6) 可变为如下形式:
再将式(7)在锥面下为:
同样,根据波场的叠加原理可知:重建面上任意点处任意波数矢量的单 元柱面波,只能由全息面上所有点处相同波数矢量的单元柱面波叠加而成, 则重建锥面上任意点rS=(rS,θ,z)处波数矢量为Km的单元面波都可以由全息面 上所有点rHn=(rH,θn,zn)处波(在这里rHn=zn×tanβ+rh1)数矢量为Km的单元面 波叠加而得到,即:
式中,rHn=(rH,θn,zn)(n=1,2,…,N)为全息锥面上N个声压测量点,M为重 建锥面和全息锥面上复声压所包含的单元面波数目,Cn(rS)为叠加系数;
根据上述原理,可得:
式中,p(rs,θ,z)和p(rHn)分别为重建锥面和全息锥面上各点声压。
再由式(8),确定的M个线性方程所构成的方程组:
其中M≥N,则方程组可以表示为:
α(rS)=ACn(rS) (15)
其中M根据柱面SONAH理论中确定波数矢量的方法来确定;
通过正则化来抑制小幅度倏逝波的影响,得上式的正则化解为:
Cn(rS)=(AHA+λ2I)-1AHα(rS) (16)
式中,AH为矩阵A的共轭转置矩阵,λ为正则化参数,起滤波作用,I为 单位对角阵。以上在统计最优柱面近场声全息理论的基础上推倒了基于声压 重构的锥面统计最优近场声全息技术的基本公式。
进一步地,利用标准Tikhonov正则化结合基于后验准则的广义交叉验证 (GCV)选取正则化参数,抑制噪声、随机误差等引起的测量误差;该方法求 解正则化参数是指:确定λ使GCV目标函数达到极小,其中GCV函数定义为:
其中,trace()表示方阵的迹,即方阵的对角线各个元素的和,σi为 矩阵A的特征值。GCV函数的分子项为正则化解的残差,这一项在许多正则 化方法中均很容易计算。
根据权利要求4所述的算法及权利要求5的正则化去除测量误差的方法, 结合公式(12)、(13)和(14),求取叠加系数C(rS)=(A+A+λ2)A+b。
利用权利要求5)中求取的叠加系数C(rS)和在全息面上测得的各点声压 p(rHn),将锥形壳体结构装备表面各点声压表示为共形测量面声压的线性叠 加,即p(rS)=C(rS)p(rHn),获得锥形壳体结构装备辐射声场。
为验证所提出锥面声源统计最优近场声全息对锥形壳体结构装备辐射声 场重构的有效性,以轴向长度为1.2m、锥面大截面半径为0.30m,小截面半 径为0.12m的锥形面模拟锥形壳体结构装备;在壳体内部使用半径逐渐增大 的脉动球紧密排列,振动频率为f,半径由0.01m以0.02m为间隔增大到 0.15m,位于0.1m≤z≤1.12m处。
采用全息测量面与壳体结构装备表面共形的测量方案。全息锥面大截面 半径为0.38m,小截面半径为0.20m,传声器在轴向的间隔为0.1m,周向间 隔为30°,重构距离为0.08m,重构面锥形水下兵器结构表面。
在全息测量面施加信噪比为40的随机噪声,在不同声源频率时,得到全 息测量面加噪声理论声压如图1和图6所示,图1中f=300Hz,图6中f=150Hz, 图2和图7为不同频率下锥形壳体结构装备表面理论声压图,图2中f=300Hz, 图7中f=150Hz。利用锥面声源统计最优近场声全息方法对锥形壳体结构装 备辐射声场进行重构,直接通过空间域全息面测量上复声压的线性叠加来计 算壳体结构装备辐射声场,得到不同频率声源辐射声场分布图如图3和图8 所示,图3中f=300Hz,图8中f=150Hz。在测量距离为d=0.08m和0.04m时,得到不同声源频率下θ=0母线上声压分布曲线图如图4和图9所示,图4中f=300Hz,d=0.08m,图9中f=150Hz,d=0.04m,可见,锥面SONAH可以 实现对锥面声源空间声场的重建,重建声场的计算值和理论值在各点都有较 好的吻合。在d=0.05m和0.1m两个不同的测量距离下得到θ=0母线上声压分 布曲线如图5所示,图5中f=300Hz,当重建距离变小时,其所得到的重建 值与理论值的吻合程度越好。图10为分别采用不同正则化参数选取方法,得到在不同频率(从200Hz以100Hz为步长变化到1500Hz)下重构的总体相对 误差曲线,可以看到,基于后验准则的GCV参数选取方法的重建效果要好于 基于先验知识的Hald准则方法。而且GCV方法在实际应用中无需预先知道测 量信号的误差水平,因此实用性更好。
在现有的近场声全息技术中,还没有将NAH技术应用于锥面声源,因而 对于锥形结构水下兵器辐射空间声场重构问题还尚未解决。本发明方法利用 统计最优近场声全息技术实现了锥面声源辐射声场的重构,展示了其在低频 噪声分析中的有效性,适用于锥形壳体结构水下兵器,从而为锥形壳体结构 装备的声隐身性能评估提供了理论基础,具有重要的理论意义及工程应用价 值。
Claims (5)
1.一种锥面声源统计近场声全息方法,其特征在于,包括以下步骤:
步骤1),获取待测锥形结构外侧全息声压数据;
步骤2),通过柱面-锥面坐标变换,构造适用于锥面声源的单元面波;具体的:通过柱面-锥面坐标变换,采用分离变量法求解Helmholtz方程,得到空间任意点处的复声压,其过程如下:
首先,得到稳态声波场Helmholtz方程在柱面坐标系下的行波解为
在柱面坐标系下,令Pn(r,n,kz)为p(r,θ,z)的二维傅氏变换,为
同时给出其傅氏反变换为
令上式r=a得,
由(1)(2)(3)(4)式可解得:
式中,Pn(a,kz)为p(a,θ,z)的二维傅氏变换;
由波数矢量K=(n,kz)确定的柱面上的空间频率域单元柱面波为:
将积分运算离散化,则全息面和重建面上的复声压表示为:
锥面测量结构时,锥角β保持不变,将式(6)中的柱面不变量r用锥面锥角β表示,式(6)可变为如下形式:
再将式(7)在锥面下为:
重建锥面上任意点rS=(rS,θ,z)处波数矢量为Km的单元面波由全息面上所有点rHn=(rH,θn,zn)处波数矢量为Km的单元面波叠加而得到,即:
式中,rHn=(rH,θn,zn)为全息锥面上N个声压测量点,n=1,2,3…,N,M为重建锥面和全息锥面上复声压所包含的单元面波数目,Cn(rS)为叠加系数;
根据上式(7)-式(10)可得:
式中,p(rs,θ,z)和p(rHn)分别为重建锥面和全息锥面上各点声压;
再由式(8),确定的M个线性方程所构成的方程组:
其中M≥N,则方程组可以表示为:
α(rS)=ACn(rS) (15)
其中M根据柱面SONAH理论中确定波数矢量的方法来确定;
通过正则化来抑制小幅度倏逝波的影响,得上式的正则化解为:
Cn(rS)=(AHA+λ2I)-1AHα(rS) (16)
式中,AH为矩阵A的共轭转置矩阵,λ为正则化参数,起滤波作用,I为单位对角阵;
步骤3),利用Nyguist采样定理选择声波波数矢量,选取的单元面波包含锥形面所有全息声压数据;
步骤4),采用标准Tikhonov正则化方法,使用基于后验准则的广义交叉验证(GCV)选取正则化参数;
步骤5),利用步骤4)标准Tikhonov正则化结合GCV方法求取叠加系数矩阵;
步骤6),将锥形壳体结构装备表面声压表示为共形测量面声压的线性叠加,获得锥形壳体结构装备辐射声场。
2.根据权利要求1所述的一种锥面声源统计近场声全息方法,其特征在于,使用与锥形壳体结构装备表面共形的测量面,布置声压传感器,获取高效的全息声压数据。
3.根据权利要求2所述的一种锥面声源统计近场声全息方法,其特征在于,使用传声器测量声场全息声压数据,采用锥面统计最优近场声全息算法采集全息声压数据。
5.根据权利要求1所述的一种锥面声源统计近场声全息方法,其特征在于,利用正则化去除测量误差的方法,结合公式(12)、(13)和(14),求取叠加系数C(rS)=(A+A+λ2)A+b;
利用求取的叠加系数C(rS)和在全息面上测得的各点声压p(rHn),将锥形壳体结构装备表面各点声压表示为共形测量面声压的线性叠加,即p(rS)=C(rS)p(rHn),获得锥形壳体结构装备辐射声场。
Priority Applications (1)
| Application Number | Priority Date | Filing Date | Title |
|---|---|---|---|
| CN201811211082.9A CN109211399B (zh) | 2018-10-17 | 2018-10-17 | 一种锥面声源统计近场声全息方法 |
Applications Claiming Priority (1)
| Application Number | Priority Date | Filing Date | Title |
|---|---|---|---|
| CN201811211082.9A CN109211399B (zh) | 2018-10-17 | 2018-10-17 | 一种锥面声源统计近场声全息方法 |
Publications (2)
| Publication Number | Publication Date |
|---|---|
| CN109211399A CN109211399A (zh) | 2019-01-15 |
| CN109211399B true CN109211399B (zh) | 2020-07-28 |
Family
ID=64980844
Family Applications (1)
| Application Number | Title | Priority Date | Filing Date |
|---|---|---|---|
| CN201811211082.9A Active CN109211399B (zh) | 2018-10-17 | 2018-10-17 | 一种锥面声源统计近场声全息方法 |
Country Status (1)
| Country | Link |
|---|---|
| CN (1) | CN109211399B (zh) |
Families Citing this family (5)
| Publication number | Priority date | Publication date | Assignee | Title |
|---|---|---|---|---|
| CN111707354B (zh) * | 2020-05-29 | 2021-07-13 | 西安交通大学 | 一种基于平面测试的圆柱壳体声场分步组合重构方法 |
| CN111707353B (zh) * | 2020-05-29 | 2021-11-09 | 西安交通大学 | 一种基于近场声全息技术的回转曲面声场重建方法 |
| CN111624865B (zh) * | 2020-06-04 | 2021-11-02 | 四川大学 | 基于光程限制函数的柱面全息去遮挡方法 |
| CN113591303A (zh) * | 2021-07-29 | 2021-11-02 | 广东电网有限责任公司 | 一种噪声预测方法及系统 |
| CN114252148B (zh) * | 2021-12-31 | 2022-12-06 | 中国人民解放军海军工程大学 | 一种基于长椭球波叠加的声场重建方法 |
Citations (7)
| Publication number | Priority date | Publication date | Assignee | Title |
|---|---|---|---|---|
| GB1263093A (en) * | 1968-03-06 | 1972-02-09 | Holotron Corp | Improvements in and relating to ultrasonic imaging techniques |
| CN101344428A (zh) * | 2008-07-22 | 2009-01-14 | 鸿远亚太科技(北京)有限公司 | 声场的全空间变换方法 |
| CN101556187A (zh) * | 2009-05-07 | 2009-10-14 | 广东美的电器股份有限公司 | 空调器噪声源可视化识别的统计最优近场声全息法及其操作方法 |
| CN102141431A (zh) * | 2010-02-01 | 2011-08-03 | 鸿远亚太科技(北京)有限公司 | 双层介质空间中的声场测量与变换方法 |
| CN103743469A (zh) * | 2013-12-11 | 2014-04-23 | 西安交通大学 | 压电水声换能器声辐射模态测量方法及系统 |
| CN106358129A (zh) * | 2016-08-29 | 2017-01-25 | 陈立康 | 一种全息立体扬声器 |
| CN108629081A (zh) * | 2018-04-02 | 2018-10-09 | 西安交通大学 | 基于统计最优近场声全息的壳体装备表面声场重构方法 |
-
2018
- 2018-10-17 CN CN201811211082.9A patent/CN109211399B/zh active Active
Patent Citations (7)
| Publication number | Priority date | Publication date | Assignee | Title |
|---|---|---|---|---|
| GB1263093A (en) * | 1968-03-06 | 1972-02-09 | Holotron Corp | Improvements in and relating to ultrasonic imaging techniques |
| CN101344428A (zh) * | 2008-07-22 | 2009-01-14 | 鸿远亚太科技(北京)有限公司 | 声场的全空间变换方法 |
| CN101556187A (zh) * | 2009-05-07 | 2009-10-14 | 广东美的电器股份有限公司 | 空调器噪声源可视化识别的统计最优近场声全息法及其操作方法 |
| CN102141431A (zh) * | 2010-02-01 | 2011-08-03 | 鸿远亚太科技(北京)有限公司 | 双层介质空间中的声场测量与变换方法 |
| CN103743469A (zh) * | 2013-12-11 | 2014-04-23 | 西安交通大学 | 压电水声换能器声辐射模态测量方法及系统 |
| CN106358129A (zh) * | 2016-08-29 | 2017-01-25 | 陈立康 | 一种全息立体扬声器 |
| CN108629081A (zh) * | 2018-04-02 | 2018-10-09 | 西安交通大学 | 基于统计最优近场声全息的壳体装备表面声场重构方法 |
Non-Patent Citations (2)
| Title |
|---|
| Near-field acoustic holography in conical coordinates;Tracianne Neilsen etc.;<Acoustical Society of America>;20090821;第2-7页 * |
| 统计最优柱面近场声全息;李卫兵 等;《机械工程学报》;20050430;第41卷(第4期);第123-127页 * |
Also Published As
| Publication number | Publication date |
|---|---|
| CN109211399A (zh) | 2019-01-15 |
Similar Documents
| Publication | Publication Date | Title |
|---|---|---|
| CN109211399B (zh) | 一种锥面声源统计近场声全息方法 | |
| JP5496192B2 (ja) | 音響場を再構成するための方法 | |
| US8077540B2 (en) | System and method for determining vector acoustic intensity external to a spherical array of transducers and an acoustically reflective spherical surface | |
| CN107478325B (zh) | 一种非稳态平面声源的自由场还原方法 | |
| JP2011527422A (ja) | 音場の再構成 | |
| Pereira | Acoustic imaging in enclosed spaces | |
| JP6386556B2 (ja) | 広周波数帯域音響ホログラフィ | |
| EP2856183B1 (en) | Systems and methods for detecting transient acoustic signals | |
| CN109764956B (zh) | 一种基于组合优化正则化方法的近场声全息方法 | |
| CN102226837A (zh) | 适用于圆柱形障板条件下矢量圆阵声压振速联合测向方法 | |
| CN112926231B (zh) | 一种基于等效源法的有限空间中近场声全息测量方法 | |
| Shuai et al. | Research on acoustic fault diagnosis of bearings based on spatial filtering and time-frequency domain filtering | |
| CN108629081A (zh) | 基于统计最优近场声全息的壳体装备表面声场重构方法 | |
| GB2521681A (en) | Underwater leak detection apparatus, underwater leak detection system and method of detecting an underwater leak of a fluid | |
| CN109798975A (zh) | 一种采用声压和质点加速度测量的非稳态平面声源的自由场实时还原方法 | |
| CN117233266A (zh) | 一种基于循环神经网络的全波形反演导波层析成像方法 | |
| CN114252148B (zh) | 一种基于长椭球波叠加的声场重建方法 | |
| EP2690461A1 (en) | Method for estimating the water speed of an acoustic node | |
| Hou et al. | A review for the noise source identification methods based microphone array | |
| CN116952356A (zh) | 基于浅海环境水下声全息技术的近场辐射噪声测量方法 | |
| Lobréau et al. | Hemispherical double-layer time reversal imaging in reverberant and noisy environments at audible frequencies | |
| CN111505568B (zh) | 基于差分优化的四面体阵目标方位估计方法 | |
| Li et al. | Functional generalized inverse beamforming based on the double-layer microphone array applied to separate the sound sources | |
| Oudompheng et al. | Passive synthetic aperture array to improve noise mapping of a moving ship | |
| Zhang et al. | Source localization in reverberation environment based on improved equivalent sound source near-field acoustic holography algorithm |
Legal Events
| Date | Code | Title | Description |
|---|---|---|---|
| PB01 | Publication | ||
| PB01 | Publication | ||
| SE01 | Entry into force of request for substantive examination | ||
| SE01 | Entry into force of request for substantive examination | ||
| GR01 | Patent grant | ||
| GR01 | Patent grant |