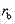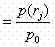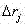CN103617334A - Method for checking strength of absorber valve block under any non-uniform pressure - Google Patents

Method for checking strength of absorber valve block under any non-uniform pressure Download PDF

Info

Publication number
CN103617334A
CN103617334A CN201310693240.XA CN201310693240A CN103617334A CN 103617334 A CN103617334 A CN 103617334A CN 201310693240 A CN201310693240 A CN 201310693240A CN 103617334 A CN103617334 A CN 103617334A
Authority
CN
China
Prior art keywords
valve plate
radius
uniform pressure
checking
damper
Prior art date
Legal status (The legal status is an assumption and is not a legal conclusion. Google has not performed a legal analysis and makes no representation as to the accuracy of the status listed.)
Granted
Application number
CN201310693240.XA
Other languages
Chinese (zh)
Other versions
CN103617334B (en
Inventor
周长城
程正午
高炳凯
Current Assignee (The listed assignees may be inaccurate. Google has not performed a legal analysis and makes no representation or warranty as to the accuracy of the list.)
Shandong University of Technology
Original Assignee
Shandong University of Technology
Priority date (The priority date is an assumption and is not a legal conclusion. Google has not performed a legal analysis and makes no representation as to the accuracy of the date listed.)
Filing date
Publication date
Application filed by Shandong University of Technology filed Critical Shandong University of Technology
Priority to CN201310693240.XA priority Critical patent/CN103617334B/en
Publication of CN103617334A publication Critical patent/CN103617334A/en
Application granted granted Critical
Publication of CN103617334B publication Critical patent/CN103617334B/en
Expired - Fee Related legal-status Critical Current
Anticipated expiration legal-status Critical

Links

Images

Landscapes

  • Testing Of Devices, Machine Parts, Or Other Structures Thereof (AREA)
  • Investigating Strength Of Materials By Application Of Mechanical Stress (AREA)

Abstract

The invention relates to a method for checking the strength of an absorber valve block under any non-uniform pressure and belongs to the technical field of absorbers. The method is characterized in that the annular absorber valve block is divided into a plurality of micro ring units in a non-uniform pressure mechanical model, the maximum stress coefficient of the absorber valve block under any non-uniform pressure is acquired through maximum stress coefficient superposition calculation under micro ring pressure, and therefore stress strength calculation and checking of the absorber valve block under any non-uniform pressure can be achieved. Living example calculation and ANSYS emulation proof indicate that the maximum stress calculation and strength checking method, for the design and strength checking of an absorber and an overlapped valve block, of the absorber valve block under any non-uniform pressure is accurate and reliable. Meanwhile, by means of the method, the design level, quality and performance of an absorber can be improved, design and test costs can be reduced, and the requirement for the design life of the absorber can be met on the premise that characteristic design requirements are met.

Description

Method for checking strength of damper valve plate under any non-uniform pressure
Technical Field
The invention relates to a shock absorber, in particular to a method for checking the strength of a shock absorber valve plate under any non-uniform pressure.
Background
The pressure borne by the damper valve plate is actually non-uniformly distributed and even may be irregularly distributed, however, at present, no accurate and reliable analytical calculation method is provided for strength checking of the damper valve plate under the non-uniform pressure at home and abroad, the maximum stress of the damper valve plate is mostly approximately calculated according to the average pressure, and because the maximum stress value of the damper valve plate obtained by calculating according to the average pressure has a certain difference with the actual value, the requirements of CAD design and strength checking of the damper and the superposed valve plate are difficult to meet. With the rapid development of the automobile industry and the continuous improvement of the vehicle running speed, higher requirements are put forward on the design of the shock absorber, and in order to realize the modern CAD design of the shock absorber and the superposed valve plate, an accurate stress intensity calculation and checking method of the shock absorber valve plate under any non-uniform pressure must be established so as to meet the requirements of the precise design and the intensity checking of the shock absorber and the superposed valve plate, so that the design of the shock absorber and the superposed valve plate is more accurate and reliable, and the design level, the performance and the service life of the shock absorber are improved.
Disclosure of Invention
Aiming at the defects in the prior art, the invention aims to provide an accurate and reliable strength checking method of the damper valve plate under any non-uniform pressure.
In order to solve the technical problem, the strength checking method of the absorber valve plate under any non-uniform pressure provided by the invention is characterized in that a mechanical model of the absorber valve plate under any non-uniform pressure is shown in figure 1, and the implementation steps of the technical scheme are as follows:
(1) is determined at a radiusr j Micro-ring pressure proportionality coefficient of
Figure 438406DEST_PATH_IMAGE001
：
According to given non-uniform pressurep(r) And has a maximum value ofp 0Inner circle radius of annular valve plate of shock absorberr aAnd the radius of the outer circler bThe annular valve sheet is divided into (N-1) micro-rings at any radius ri
Figure 48379DEST_PATH_IMAGE002
Inner circle radius of micro ring=r j Outer radius of circle
Figure 393702DEST_PATH_IMAGE004
，（j=1,2，…，N-1) determining the radiusr j Micro-ring pressure proportionality coefficient ofIt can be expressed as:
Figure 554742DEST_PATH_IMAGE001
Figure 189117DEST_PATH_IMAGE005
：
(2) determining maximum stress coefficient of damper valve plate
Figure 662824DEST_PATH_IMAGE006
：
According to the radius of the inner circle of the valve plateRadius of outer circle
Figure 583692DEST_PATH_IMAGE008
Modulus of elasticityEPoisson ratioμAt a radius ofr j Micro ring
Figure 338153DEST_PATH_IMAGE009
（j=1,2，…，N-1) inner circle radius
Figure 717182DEST_PATH_IMAGE010
=r j Outer radius of circle
Figure 173571DEST_PATH_IMAGE011
Radius in step (1)r j Micro-ring pressure proportionality coefficient of
Figure 210928DEST_PATH_IMAGE012
Determining the maximum stress intensity coefficient of the damper valve plate
Figure 69163DEST_PATH_IMAGE006
Namely:
Figure 415830DEST_PATH_IMAGE013
,
in the formula,
Figure 107318DEST_PATH_IMAGE014
,
Figure 400896DEST_PATH_IMAGE015
；
Figure 113637DEST_PATH_IMAGE016
，
Figure 100048DEST_PATH_IMAGE017
；
Figure 281762DEST_PATH_IMAGE018
Figure 910189DEST_PATH_IMAGE019
；
Figure 477437DEST_PATH_IMAGE020
；
Figure 385481DEST_PATH_IMAGE021
；
Figure 303758DEST_PATH_IMAGE022
Figure 939139DEST_PATH_IMAGE023
；
Figure 626472DEST_PATH_IMAGE024
，
Figure 705418DEST_PATH_IMAGE025
;
(3) maximum stress of damper valve plate
Figure 845412DEST_PATH_IMAGE026
And (3) calculating:
according to the thickness of the valve platehMaximum value of non-uniform pressurep 0And the maximum stress intensity coefficient in step (2)
Figure 550063DEST_PATH_IMAGE006
Maximum stress on valve plate
Figure 560744DEST_PATH_IMAGE026
The calculation is carried out, namely:
；
(4) checking the stress intensity of the damper valve plate:
according to allowable stress of damper valve plate
Figure 434952DEST_PATH_IMAGE028
And in step (3)
Figure 943294DEST_PATH_IMAGE026
And checking the stress intensity, namely: if it is not
Figure 605219DEST_PATH_IMAGE029
Figure 744077DEST_PATH_IMAGE028
The valve plate of the damper does not meet the requirement of stress intensity; if it is not
Figure 609396DEST_PATH_IMAGE030
Figure 390270DEST_PATH_IMAGE028
Then decreaseThe valve plate of the vibration device can meet the requirement of stress intensity.
Compared with the prior art, the invention has the advantages that:
the pressure borne by the annular throttle valve plate of the shock absorber is actually non-uniformly distributed and even can be irregularly distributed, however, at present, no accurate and reliable method is provided for checking the stress intensity of the shock absorber valve plate under the non-uniformly distributed pressure at home and abroad, the maximum stress of the shock absorber valve plate is mostly calculated according to the uniformly distributed pressure, and because the stress value of the valve plate obtained by calculation has a certain difference with the actual value, the requirements of CAD design and intensity checking of the shock absorber and the superposed valve plate are difficult to meet. The invention discloses a method for checking the stress intensity of a damper valve plate under any non-uniform pressure, which divides an annular damper valve plate into a plurality of micro-ring units in a non-uniform pressure mechanical model, determines the pressure coefficient of the micro-ring, and obtains the maximum stress coefficient of the damper valve plate through the superposition operation of the maximum stress coefficient under the pressure of the micro-ring
Figure 906702DEST_PATH_IMAGE006
So as to obtain the maximum non-uniform pressure according to the thickness of the valve platep 0Maximum stress coefficient
Figure 216460DEST_PATH_IMAGE006
By using
Figure 818343DEST_PATH_IMAGE031
The stress intensity check of the damper valve plate under any non-uniform pressure can be realized. Compared with ANSYS simulation verification results, the established method for checking the stress intensity of the absorber valve plate under any non-uniform pressure is accurate, and a reliable method for checking the stress intensity of the absorber valve plate under any non-uniform pressure is provided for the accurate design and intensity check of the absorber superposed valve plate; the method can improve the design level, quality and performance of the shock absorber, reduce the design and test cost of the shock absorber, and meet the requirement on the design life of the shock absorber on the premise of ensuring the characteristic design requirement of the shock absorber.
For a better understanding of the invention, reference is made to the following further description taken in conjunction with the accompanying drawings.
FIG. 1 is a mechanical model of a damper valve plate under any non-uniform pressure;
FIG. 2 is a flow chart of intensity checking of a damper valve plate under any non-uniform pressure;
FIG. 3 is the non-uniform pressure proportionality coefficient of the damper valve plate according to the first embodimentk pr A curve;
FIG. 4 is a simulated cloud of the maximum stress of the valve plate of the damper under the non-uniform pressure in the first embodiment;
FIG. 5 is the non-uniform pressure proportionality coefficient of the valve plate of the damper in the second embodimentk pr A curve;
FIG. 6 is a simulated cloud of the maximum stress of the valve plate of the damper in the second embodiment under the non-uniform pressure;
FIG. 7 is a non-uniform pressure proportionality coefficient of a valve plate of the damper in the third embodimentk pr A curve;
FIG. 8 is a simulated cloud of the maximum stress of the valve plate of the shock absorber in the third embodiment under the non-uniform pressure;
FIG. 9 is a proportional coefficient of non-uniform pressure of a valve plate of the damper according to the fourth embodimentk pr A curve;
FIG. 10 is a simulated cloud diagram of the maximum stress of the valve plate of the damper under the non-uniform pressure in the fourth embodiment.
Detailed description of the preferred embodiments
The present invention will be described in further detail by way of examples.
The first embodiment is as follows: radius of inner circle of certain damper valve plate
Figure 153641DEST_PATH_IMAGE032
=5.0mm, radius of the outer circle=8.5mm, modulus of elasticityE=2.0
Figure 5239DEST_PATH_IMAGE033
And poisson's ratioμ=0.3, maximum allowable stress
Figure 828838DEST_PATH_IMAGE028
=2000MPa, thicknessh=0.3mm, valve port radiusr o=8.0mm at radius [5.0,8.0 ]]Uniform pressure is applied to mm sectionp 0At [8.0,8.5 ] =3.0MPa]Applying linear non-uniform pressure on mm sectionp(r)=
Figure 217094DEST_PATH_IMAGE034
And (MPa) checking the stress intensity of the damper valve plate.
The strength checking method of the absorber valve plate provided by the embodiment of the invention under any non-uniform pressure has the strength checking calculation flow as shown in figure 2, and the specific checking steps are as follows:
(1) determining the radius of the valve plater j Micro-ring pressure proportionality coefficient ofk pj ：
According to non-uniform pressurep(r)=
Figure 193272DEST_PATH_IMAGE034
MPa and maximum value thereofp 0=3.0MPa, inner circle radius of damper valve plate
Figure 375991DEST_PATH_IMAGE032
=5.0mm, radius of the outer circle
Figure 421308DEST_PATH_IMAGE008
=8.5mm, and the radius interval [ 2 ]
Figure 347676DEST_PATH_IMAGE035
]Are divided into 70 parts and the micro-ring spacing
Figure 427627DEST_PATH_IMAGE009
=0.05mm，（j=1,2, 3, …, 70), then at the radiusr j Inner circle radius of micro ring
Figure 806349DEST_PATH_IMAGE010
=r j Outer radius of circle，（j=1,2, …, 70), determined at a radiusr j Micro-ring pressure proportionality coefficient of
Figure 537861DEST_PATH_IMAGE012
Namely:
Figure 737899DEST_PATH_IMAGE012
Figure 528000DEST_PATH_IMAGE037
；
calculated micro-ring pressure proportionality coefficient
Figure 16750DEST_PATH_IMAGE001
As shown in fig. 3;
(2) determining maximum stress coefficient of damper valve plate
Figure 301232DEST_PATH_IMAGE006
：
According to the inner radius of the damper valve plate
Figure 355776DEST_PATH_IMAGE032
=5.0mm, radius of the outer circle
Figure 51199DEST_PATH_IMAGE008
=8.5mm, modulus of elasticityE=2.0
Figure 823983DEST_PATH_IMAGE033
And poisson's ratioμ=0.3, radiusr j Micro ring
Figure 364686DEST_PATH_IMAGE009
（jInner circle radius of =1,2, …, 70)
Figure 24469DEST_PATH_IMAGE010
=r j Outer radius of circle
Figure 156373DEST_PATH_IMAGE036
Micro-ring pressure scaling factor in step (1)
Figure 619715DEST_PATH_IMAGE012
Determining the maximum stress coefficient of the damper valve plate
Figure 495267DEST_PATH_IMAGE006
I.e. by
Figure 524403DEST_PATH_IMAGE038
=36.697mm2,
In the formula,
Figure 312362DEST_PATH_IMAGE039
=41.288 mm2,
Figure 528579DEST_PATH_IMAGE040
=12.386 mm2;
Figure 942243DEST_PATH_IMAGE041
，
Figure 825885DEST_PATH_IMAGE042
；
Figure 502854DEST_PATH_IMAGE018
Figure 750909DEST_PATH_IMAGE019
；
；
；
Figure 819862DEST_PATH_IMAGE022
；
(3) maximum stress of damper valve plate
Figure 500559DEST_PATH_IMAGE026
And (3) calculating:
according to the thickness of the valve plateh=0.3mm, maximum non-uniform pressurep 0=3.0MPa, and maximum stress factor in step (2)Maximum stress to valve sheetThe calculation is carried out, namely:
=1223.2MPa；
according to the inner circle radius of the valve plate of the shock absorberr a5.0mm, outer circle radiusr b8.5mm thickh0.3mm, elastic modelE200GPa, Poisson's ratioμSetting up simulation model with ANSYS as 0.3, and dividing grid unit as 0.1mm at radius [5.0,8.0 ]]Applying uniform pressure on mm sectionp 0=3.0MP, at radius [8.0,8.5]Applying linear non-uniform pressure on mm sectionp(r)=
Figure 631140DEST_PATH_IMAGE034
MPa, simulating a stress cloud chart of the obtained damper valve plate, as shown in figure 4; as can be seen from fig. 4, the maximum stress of the absorber valve plate under the non-uniform pressure obtained by ANSYS simulation is 1190MPa, the deviation from 1223.2MPa calculated by the method is 33.2MPa, and the relative deviation is only 2.71%, which indicates that the calculation method of the maximum stress of the absorber valve plate under any non-uniform pressure is correct, and provides an accurate maximum stress calculation and strength check method of the absorber valve plate under any non-uniform pressure for the split design and stress strength check of the absorber valve plate;
(4) checking the stress intensity of the damper valve plate:
according to allowable stress of damper valve plate
Figure 343881DEST_PATH_IMAGE028
=2000MPa, and in step (3)
Figure 81024DEST_PATH_IMAGE026
=1223.2MPa, it is known
Figure 980847DEST_PATH_IMAGE030
Figure 78116DEST_PATH_IMAGE028
Namely, the damper valve plate can meet the requirement of stress intensity.
Example two: thickness of certain damper valve plateh=0.3mm, radius of inner circle
Figure 645364DEST_PATH_IMAGE032
=5.0mm, radius of the outer circle=8.5mm, modulus of elasticityE=2.0And poisson's ratioμ=0.3, maximum allowable stress
Figure 575907DEST_PATH_IMAGE028
=2000MPa, in
Figure 263241DEST_PATH_IMAGE032
,
Figure 591454DEST_PATH_IMAGE008
]Secondary non-uniform pressure is applied in the range
Figure 200290DEST_PATH_IMAGE043
And (MPa) checking the stress intensity of the damper valve plate.
The checking step of the first embodiment is adopted, namely:
(1) determining the radius of the valve plater j Micro-ring pressure proportionality coefficient ofk pj ：
Root of herbaceous plantAccording to non-uniform pressure
Figure 639361DEST_PATH_IMAGE043
MPa and maximum value thereofp 0=3.0MPa, inner circle radius of damper valve plate
Figure 929004DEST_PATH_IMAGE032
=5.0mm, radius of the outer circle
Figure 428118DEST_PATH_IMAGE008
=8.5mm, and the radius interval [ 2 ]
Figure 524250DEST_PATH_IMAGE044
]Are divided into 70 parts and the micro-ring spacing
Figure 767013DEST_PATH_IMAGE009
=0.05mm，（j=1,2, 3, …, 70), radiusr j Inner circle radius of micro ring
Figure 428938DEST_PATH_IMAGE010
=r j Outer radius of circle
Figure 567796DEST_PATH_IMAGE036
，（j=1,2, …, 70), determined at a radiusr j Micro-ring pressure proportionality coefficient of
Figure 698694DEST_PATH_IMAGE012
Namely:
Figure 213989DEST_PATH_IMAGE045
；
calculated micro-ring pressure proportionality coefficientk pj As shown in fig. 5;
(2) determining maximum stress coefficient of damper valve plate
Figure 730421DEST_PATH_IMAGE006
：
According to the inner radius of the damper valve plate=5.0mm, radius of the outer circle
Figure 658374DEST_PATH_IMAGE008
=8.5mm, modulus of elasticityE=2.0
Figure 711780DEST_PATH_IMAGE033
And poisson's ratioμ=0.3 at radiusr j Micro ring
Figure 82719DEST_PATH_IMAGE009
（jInner circle radius of =1,2, …, 70)
Figure 94537DEST_PATH_IMAGE010
=r j Outer radius of circleMicro-ring pressure scaling factor in step (1)Determining the maximum stress coefficient of the damper valve plate
Figure 16991DEST_PATH_IMAGE006
Namely:
Figure 199710DEST_PATH_IMAGE046
= 20.658mm2,
in the formula,
Figure 979448DEST_PATH_IMAGE047
= 23.242mm2,
Figure 905815DEST_PATH_IMAGE048
= 6.9727mm2;
wherein,
Figure 251346DEST_PATH_IMAGE049
andthe same as in the first embodiment;
(3) maximum stress of damper valve plate
Figure 619803DEST_PATH_IMAGE026
And (3) calculating:
according to the thickness of the valve plateh=0.3mm, maximum non-uniform pressurep 0=3.0MPa, and maximum stress intensity coefficient in step (2)
Figure 349862DEST_PATH_IMAGE006
Maximum stress to damper valve plateThe calculation is carried out, namely:
Figure 543263DEST_PATH_IMAGE027
=688.61MPa；
according to the inner circle radius of the valve plate of the shock absorberr a5.0mm, outer circle radiusr b8.5mm thickh0.3mm, elastic modelE200GPa, Poisson's ratioμThe simulation model is built by using ANSYS (American society for research and plant research) with the unit of grid division of 0.1mm at the radius of [5.0,8.5 ]]Applying secondary non-uniform pressure on mm section
Figure 828750DEST_PATH_IMAGE043
MPa, simulating a stress cloud chart of the obtained damper valve plate, as shown in figure 6; it can be known that the maximum stress of the absorber valve plate under the non-uniform pressure obtained by ANSYS simulation is 670MPa, the deviation from 688.61 calculated by the method is 18.61MPa, and the relative deviation is only 2.70%, which indicates that the calculation method of the maximum stress of the absorber valve plate under any non-uniform pressure is correct;
(4) checking the stress intensity of the damper valve plate:
according to allowable stress of damper valve plate
Figure 113232DEST_PATH_IMAGE028
=2000MPa, and in step (3)
Figure 167776DEST_PATH_IMAGE026
=688.61MPa, it is known
Figure 332041DEST_PATH_IMAGE030
Figure 104825DEST_PATH_IMAGE028
Namely, the damper valve plate can meet the requirement of stress intensity.
Example three: the structural parameters and the material characteristic parameters of a certain damper valve plate are the same as those of the first embodiment, namely the thicknessh=0.3mm, radius of inner circle
Figure 176686DEST_PATH_IMAGE032
=5.0mm, radius of the outer circle
Figure 836469DEST_PATH_IMAGE008
=8.5mm, modulus of elasticityE=2.0
Figure 437214DEST_PATH_IMAGE033
Poisson ratioμ=0.3, maximum allowable stress
Figure 431715DEST_PATH_IMAGE028
=2000MPa, in
Figure 307267DEST_PATH_IMAGE032
,
Figure 70824DEST_PATH_IMAGE008
]Applying a sinusoidal non-uniform pressure within a range
Figure 124362DEST_PATH_IMAGE051
And (MPa) checking the stress intensity of the damper valve plate.
The checking step of the first embodiment is adopted, namely:
(1) determining the radius of the valve plater j Micro-ring pressure proportionality coefficient of：
According to non-uniform pressure
Figure 488664DEST_PATH_IMAGE051
MPa and maximum value thereofp 0=3.5MPa, inner circle radius of damper valve plate=5.0mm, radius of the outer circle
Figure 846013DEST_PATH_IMAGE008
=8.5mm, and the radius interval [ 2 ]]Are divided into 70 parts and the micro-ring spacing
Figure 260824DEST_PATH_IMAGE009
=0.05mm，（j=1,2, 3, …, 70), radiusr j Inner circle radius of micro ring
Figure 998973DEST_PATH_IMAGE003
=r j Outer radius of circle
Figure 112422DEST_PATH_IMAGE004
，（j=1,2, …, 70), determining the radius of the valve sheetr j Micro-ring pressure proportionality coefficient of
Figure 568811DEST_PATH_IMAGE001
Namely:
Figure 324278DEST_PATH_IMAGE052
；
calculated micro-ring pressure proportionality coefficientk pj As shown in fig. 7;
(2) determining maximum stress coefficient of damper valve plate：
According to the inner radius of the damper valve plate
Figure 952016DEST_PATH_IMAGE032
=5.0mm, radius of the outer circle=8.5mm, modulus of elasticityE=2.0
Figure 454859DEST_PATH_IMAGE033
And poisson's ratioμ=0.3 at radiusr j Micro ring
Figure 636442DEST_PATH_IMAGE009
（jInner circle radius of =1,2, …, 70)=r j Outer radius of circleMicro-ring pressure scaling factor in step (1)
Figure 636256DEST_PATH_IMAGE001
Determining the maximum stress coefficient of the damper valve plateNamely:
= 40.183mm2,
in the formula,
Figure 747934DEST_PATH_IMAGE014
= 45.21mm2, = 13.563mm2;
wherein,
Figure 86960DEST_PATH_IMAGE049
and
Figure 884014DEST_PATH_IMAGE050
the same as in the first embodiment;
(3) maximum stress of damper valve plate
Figure 24009DEST_PATH_IMAGE026
And (3) calculating:
according to the thickness of the valve plateh=0.3mm, maximum non-uniform pressurep 0=3.5MPa, and maximum stress intensity coefficient in step (2)
Figure 463080DEST_PATH_IMAGE006
=40.183mm2Maximum stress to damper valve plate
Figure 752723DEST_PATH_IMAGE026
The calculation is carried out, namely:
Figure 720679DEST_PATH_IMAGE027
=1562.7MPa；
according to the inner circle radius of the valve plate of the shock absorberr a5.0mm, outer circle radiusr b8.5mm thickh0.3mm, elastic modelE200GPa, Poisson's ratioμThe simulation model is built by using ANSYS (American society for research and plant research) with the unit of grid division of 0.1mm at the radius of [5.0,8.5 ]]Applying sinusoidal non-uniform pressure on mm section
Figure 347969DEST_PATH_IMAGE051
MPa, simulating a stress cloud chart of the obtained damper valve plate, as shown in figure 8; it can be known that the maximum stress of the absorber valve plate under the non-uniform pressure obtained by ANSYS simulation is 1550MPa, the deviation from 1562.7MPa calculated by the method is 12.7MPa, and the relative deviation is only 0.81%, which indicates that the calculation method of the maximum stress of the absorber valve plate under any non-uniform pressure is correct;
(4) checking the stress intensity of the damper valve plate:
according to allowable stress of damper valve plate
Figure 590732DEST_PATH_IMAGE028
=2000MPa, and in step (3)
Figure 455920DEST_PATH_IMAGE026
=1562.7MPa, it is known
Figure 991254DEST_PATH_IMAGE028
Namely, the damper valve plate can meet the requirement of stress intensity.
Example four: the material property parameter of a certain damper valve plate is the same as that of the first embodiment, namely the radius of the inner circle
Figure 37708DEST_PATH_IMAGE032
=5.0mm, radius of the outer circle
Figure 757402DEST_PATH_IMAGE008
=10.0mm, thicknessh=0.25mm, modulus of elasticityE=2.0
Figure 598319DEST_PATH_IMAGE033
Poisson ratioμ=0.3, maximum allowable stress
Figure 200202DEST_PATH_IMAGE028
=2000MPa, in
Figure 535499DEST_PATH_IMAGE032
,
Figure 375279DEST_PATH_IMAGE008
]Applying a sinusoidal non-uniform pressure within a rangeAnd (MPa) checking the stress intensity of the damper valve plate.
The checking step of the first embodiment is adopted, namely:
(1) determining the radius of the valve plater j Micro-ring pressure proportionality coefficient ofk pj ：
According to non-uniform pressure
Figure 476276DEST_PATH_IMAGE054
MPa and maximum value thereofp 0=3.5MPa, inner circle radius of damper valve plate=5.0mm, radius of the outer circle
Figure 293240DEST_PATH_IMAGE008
=10.0mm, and the radius interval [ 2 ]]Are divided into 100 parts and the micro-ring spacing
Figure 803167DEST_PATH_IMAGE009
=0.05mm，（j=1,2, 3, …, 100) at radiusr j Inner circle radius of micro ring
Figure 729534DEST_PATH_IMAGE003
=r j Outer radius of circle
Figure 75065DEST_PATH_IMAGE004
，（j=1,2, …, 100), determining the radius of the valve sheetr j Micro-ring pressure proportionality coefficient of
Figure 176489DEST_PATH_IMAGE001
Namely:
Figure 974680DEST_PATH_IMAGE055
；
calculated micro-ring pressure proportionality coefficientk pj As shown in fig. 9;
(2) determining maximum stress coefficient of damper valve plate
Figure 173581DEST_PATH_IMAGE006
：
According to the inner radius of the damper valve plate=5.0mm, radius of the outer circle
Figure 180031DEST_PATH_IMAGE008
=10.0mm, modulus of elasticityE=2.0
Figure 465519DEST_PATH_IMAGE033
And poisson's ratioμ=0.3 at radiusr j Micro ring
Figure 733689DEST_PATH_IMAGE009
（jInner circle radius of =1,2, …, 100)
Figure 257074DEST_PATH_IMAGE010
=r j Outer radius of circle
Figure 218077DEST_PATH_IMAGE036
Micro-ring pressure scaling factor in step (1)k pj Determining the maximum stress coefficient of the damper valve plate
Figure 741593DEST_PATH_IMAGE006
Namely:
= 81.263mm2；
in the formula,
Figure 722505DEST_PATH_IMAGE047
= 91.428mm2,
Figure 57671DEST_PATH_IMAGE056
= 13.563mm2；
Figure 317751DEST_PATH_IMAGE041
，
Figure 678457DEST_PATH_IMAGE042
；
Figure 707592DEST_PATH_IMAGE018
Figure 10398DEST_PATH_IMAGE019
；
Figure 492195DEST_PATH_IMAGE020
；
Figure 374700DEST_PATH_IMAGE021
；
Figure 479852DEST_PATH_IMAGE023
；
(3) maximum stress of damper valve plate
Figure 448945DEST_PATH_IMAGE026
And (3) calculating:
according to the thickness of the valve plateh=0.25mm, maximum non-uniform pressurep 0=3.5MPa, and maximum stress intensity coefficient in step (2)
Figure 400720DEST_PATH_IMAGE006
= 81.263mm2Maximum stress to valve sheet
Figure 155181DEST_PATH_IMAGE026
The calculation is carried out, namely:
Figure 799789DEST_PATH_IMAGE057
=4550.7MPa；
according to the inner radius of the damper valve plate=5.0mm, radius of the outer circle
Figure 480486DEST_PATH_IMAGE008
=10.0mm, thicknessh=0.25mm, modulus of elasticityE=2.0
Figure 73141DEST_PATH_IMAGE033
Poisson ratioμ=0.3, establishing a simulation model by using ANSYS, wherein the unit of grid division is 0.1mm and the radius is [5.0,10 ]]Applying sinusoidal non-uniform pressure on mm section
Figure 170541DEST_PATH_IMAGE054
MPa, simulating a stress cloud chart of the obtained damper valve plate, as shown in figure 10; it can be known that the maximum stress of the absorber valve plate under the nonuniform pressure obtained by ANSYS simulation is 4420MPa, the deviation from 4550.7MPa obtained by calculation by the method is 130.7MPa, and the relative deviation is only 2.87%, which indicates that the calculation method of the maximum stress of the absorber valve plate under any nonuniform pressure is correct;
(4) checking the stress intensity of the damper valve plate:
according to allowable stress of damper valve plate
Figure 114227DEST_PATH_IMAGE028
=2000MPa, and in step (3)
Figure 673384DEST_PATH_IMAGE026
=4550.7MPa, it is known
Figure 857689DEST_PATH_IMAGE028
Namely, the damper valve plate cannot meet the requirement of stress intensity.

Claims (1)

1. The method for checking the strength of the absorber valve plate under any non-uniform pressure comprises the following specific steps:
(1) is determined at a radiusr j Micro-ring pressure proportionality coefficient of：
According to given non-uniform pressurep(r) And has a maximum value ofp 0Inner circle radius of annular valve plate of shock absorberr aAnd the radius of the outer circler bThe annular valve sheet is divided into (N-1) micro-rings at any radius ri
Figure 201310693240X100001DEST_PATH_IMAGE002
Inner circle radius of micro ring=r j Outer radius of circle
Figure 201310693240X100001DEST_PATH_IMAGE004
，（j=1,2，…，N-1) determining the radiusr j Micro-ring pressure proportionality coefficient ofIt can be expressed as:
Figure 884899DEST_PATH_IMAGE001
Figure 699272DEST_PATH_IMAGE005
；
(2) determining maximum stress coefficient of damper valve plate
Figure 201310693240X100001DEST_PATH_IMAGE006
：
According to the radius of the inner circle of the valve plate
Figure 584051DEST_PATH_IMAGE007
Radius of outer circle
Figure 201310693240X100001DEST_PATH_IMAGE008
Modulus of elasticityEPoisson ratioμAt a radius ofr j Micro ring
Figure 224986DEST_PATH_IMAGE009
（j=1,2，…，N-1) inner circle radius=r j Outer radius of circleRadius in step (1)r j Micro-ring pressure proportionality coefficient of
Figure 201310693240X100001DEST_PATH_IMAGE012
Determining the maximum stress intensity coefficient of the damper valve plate
Figure 303153DEST_PATH_IMAGE006
Namely:
Figure 296517DEST_PATH_IMAGE013
,
in the formula,
Figure 201310693240X100001DEST_PATH_IMAGE014
,
Figure 926212DEST_PATH_IMAGE015
；
Figure 201310693240X100001DEST_PATH_IMAGE016
，
Figure 725541DEST_PATH_IMAGE017
；
Figure 201310693240X100001DEST_PATH_IMAGE018
Figure 560511DEST_PATH_IMAGE019
；
Figure 201310693240X100001DEST_PATH_IMAGE020
；
；
Figure 169663DEST_PATH_IMAGE023
；
Figure 201310693240X100001DEST_PATH_IMAGE024
，
Figure 756371DEST_PATH_IMAGE025
;
(3) maximum stress of damper valve plate
Figure 201310693240X100001DEST_PATH_IMAGE026
And (3) calculating:
according to the thickness of the valve platehMaximum value of non-uniform pressurep 0And the maximum stress intensity coefficient in step (2)Maximum stress on valve plateThe calculation is carried out, namely:
Figure 339297DEST_PATH_IMAGE027
；
(4) checking the stress intensity of the damper valve plate:
according to allowable stress of damper valve plateAnd in step (3)And checking the stress intensity, namely: if it is not
Figure 289990DEST_PATH_IMAGE029
Figure 123954DEST_PATH_IMAGE028
The valve plate of the damper does not meet the requirement of stress intensity; if it is not
Figure 201310693240X100001DEST_PATH_IMAGE030
Figure 887641DEST_PATH_IMAGE028
And the valve plate of the damper can meet the requirement of stress intensity.
CN201310693240.XA 2013-12-18 2013-12-18 Strength check methods under vibroshock valve block meaning in office non-uniform distributed pressure Expired - Fee Related CN103617334B (en)

Priority Applications (1)

Application Number Priority Date Filing Date Title
CN201310693240.XA CN103617334B (en) 2013-12-18 2013-12-18 Strength check methods under vibroshock valve block meaning in office non-uniform distributed pressure

Applications Claiming Priority (1)

Application Number Priority Date Filing Date Title
CN201310693240.XA CN103617334B (en) 2013-12-18 2013-12-18 Strength check methods under vibroshock valve block meaning in office non-uniform distributed pressure

Publications (2)

Publication Number Publication Date
CN103617334A true CN103617334A (en) 2014-03-05
CN103617334B CN103617334B (en) 2016-08-24

Family

ID=50168037

Family Applications (1)

Application Number Title Priority Date Filing Date
CN201310693240.XA Expired - Fee Related CN103617334B (en) 2013-12-18 2013-12-18 Strength check methods under vibroshock valve block meaning in office non-uniform distributed pressure

Country Status (1)

Country Link
CN (1) CN103617334B (en)

Cited By (2)

* Cited by examiner, † Cited by third party
Publication number Priority date Publication date Assignee Title
CN105138806A (en) * 2015-10-08 2015-12-09 山东理工大学 Method for checking intensity of unequal-thickness annular valve plate of hydro-pneumatic spring
CN109063263A (en) * 2018-07-03 2018-12-21 哈尔滨电气股份有限公司 A kind of tower body skirt and lower head junction lower head strength check methods

Citations (4)

* Cited by examiner, † Cited by third party
Publication number Priority date Publication date Assignee Title
EP1837548A1 (en) * 2006-03-23 2007-09-26 Continental Aktiengesellschaft Pneumatic spring and damping unit with decompression bellows
CN103148148A (en) * 2013-03-08 2013-06-12 山东理工大学 Method for checking strength of rebound sandwich valve sheet of shock absorber
CN103150434A (en) * 2013-03-08 2013-06-12 山东理工大学 Method for calculating combined stress of annular valve sheet of shock absorber
CN103161871A (en) * 2013-04-03 2013-06-19 山东理工大学 Intensity checking method of overlaying valve plates of compression valve of vehicle buffer

Patent Citations (4)

* Cited by examiner, † Cited by third party
Publication number Priority date Publication date Assignee Title
EP1837548A1 (en) * 2006-03-23 2007-09-26 Continental Aktiengesellschaft Pneumatic spring and damping unit with decompression bellows
CN103148148A (en) * 2013-03-08 2013-06-12 山东理工大学 Method for checking strength of rebound sandwich valve sheet of shock absorber
CN103150434A (en) * 2013-03-08 2013-06-12 山东理工大学 Method for calculating combined stress of annular valve sheet of shock absorber
CN103161871A (en) * 2013-04-03 2013-06-19 山东理工大学 Intensity checking method of overlaying valve plates of compression valve of vehicle buffer

Cited By (4)

* Cited by examiner, † Cited by third party
Publication number Priority date Publication date Assignee Title
CN105138806A (en) * 2015-10-08 2015-12-09 山东理工大学 Method for checking intensity of unequal-thickness annular valve plate of hydro-pneumatic spring
CN105138806B (en) * 2015-10-08 2018-01-16 山东理工大学 The strength check methods of hydro-pneumatic spring not uniform thickness annular valve block
CN109063263A (en) * 2018-07-03 2018-12-21 哈尔滨电气股份有限公司 A kind of tower body skirt and lower head junction lower head strength check methods
CN109063263B (en) * 2018-07-03 2023-10-13 哈尔滨电气股份有限公司 Method for checking strength of lower seal head at joint of tower skirt and lower seal head

Also Published As

Publication number Publication date
CN103617334B (en) 2016-08-24

Similar Documents

Publication Publication Date Title
CN105740591A (en) Method for verifying strength of each leaf of end contact type few-leaf oblique main and auxiliary springs
CN103294919B (en) Vibration damper circular sandwich valve plate determines the method for radial stress under non-uniform distributed pressure
CN103106312A (en) Calculation method for vibration absorber isodesmic annular superposed valve plate deformation
CN105138806B (en) The strength check methods of hydro-pneumatic spring not uniform thickness annular valve block
CN103116683A (en) Superposition computing method for deformation of absorber annular valve sheet under unevenly distributed pressure
CN103617334A (en) Method for checking strength of absorber valve block under any non-uniform pressure
CN103106349A (en) Method for calculating radial stress of annular valve plate of vibration absorber
CN103150434A (en) Method for calculating combined stress of annular valve sheet of shock absorber
CN103678832A (en) Method for calculating composite stress of non-equal structure superposed valve plates of vehicle shock absorber
CN103148148B (en) Method for checking strength of rebound sandwich valve sheet of shock absorber
CN103246789A (en) Computing method of deformation of annular sandwich valve plates of vibration absorber under non-uniform pressure
CN103246791B (en) The computing method of vibration damper circular sandwich valve plate circumferential stress under non-uniform distributed pressure
CN103632012A (en) Method for calculating combined stress of valve plate of shock absorber under arbitrary axisymmetric and non-uniform pressure
CN103177158A (en) Computing method for circumferential stress of equivalent structure circular sandwich valve plate of absorber
CN103632011A (en) Method for calculating deformation of valve plate of shock absorber under arbitrary axisymmetric and non-uniform pressure
CN103150478B (en) The computing method of absorber annular valve sheet circumferential stress under non-uniform distributed pressure
CN105279319B (en) The computational methods of hydro-pneumatic spring not uniform thickness annular valve block Maximum circumferential stress
CN103150479B (en) The computing method of absorber annular valve sheet radial stress under non-uniform distributed pressure
CN103324824A (en) Computing method for equivalent thickness of hydraulic buffer isomorphic annular sandwich valve plates
CN103177157A (en) Computing method for radial stress of equivalent structure circular sandwich valve plate of absorber
CN103617374A (en) Method for calculating circumferential stress of annular absorber valve block under any non-uniform pressure
CN103617335A (en) Method for calculating radial stress of annular absorber valve block under any non-uniform pressure
CN103246790B (en) The computing method of vibration damper circular sandwich valve plate compound stress under non-uniform distributed pressure
CN103678833A (en) Method for calculating radial stress of non-equal structure superposed valve plates of vehicle shock absorber
CN105160136B (en) The computational methods of hydro-pneumatic spring not uniform thickness annular valve block maximum radial stress

Legal Events

Date Code Title Description
PB01 Publication
PB01 Publication
C10 Entry into substantive examination
SE01 Entry into force of request for substantive examination
C14 Grant of patent or utility model
GR01 Patent grant
CF01 Termination of patent right due to non-payment of annual fee

Granted publication date: 20160824

Termination date: 20191218

CF01 Termination of patent right due to non-payment of annual fee