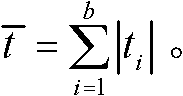The initial prestress distribution of a kind of rope bar tension structure is confirmed method
Technical field
The invention discloses a kind of initial prestress distribution of rope bar tension structure and confirm method, belong to the architectural design and the structural design field of space structure based on gradient method optimization.
Background technology
Rope bar tension structure is that elementary cell is formed by drag-line and depression bar, and it is that inside configuration exists from stress mode and mechanism displacement with the maximum difference of general traditional structure.If structure can provide rigidity through applying prestress, though there is the infinitely small mechanism of single order in inside configuration, but still can bear certain load as traditional structure.Before not applying prestress, structure self rigidity can't be kept shape, and system is in relaxation state, and the prestress that only applies a certain size could be shaped and bearing load; And its prestressed size and distribution directly affect the stress performance of structure, have only the prestress size in the structure reasonable with distribution, and structure just can have the good mechanical performance.Therefore finding the solution the initial prestress distribution of rope bar tension structure is the key issue that at first need solve.
In a three-dimensional cable-rod structure, suppose that free node i links to each other with node j, k, (i, j), its internal force is f in the unit of connected node i, j
Ij, length is l
Ij(i, k), its internal force is f in the unit of connected node i, k
Ik, length is l
IkThe external load that acts on node i is p
i, its component in x, y, three directions of z is p
Ix, p
Iy, p
IzCable-strut system can be expressed as at the balance equation at node i place:
Suppose a given space articulated structure system, its rod member number is b, and the node number is N, and the constraint number is k, and then the unconfinement displacement number of structural system is n=3 * N-k.The balance equation of this structural system is:
Af=P
Wherein A is n * b matrix, is called balancing matrix; F is a force vector in the b dimension rod member; P is a n dimension nodal force vector.
According to matrix theory, establishing the A rank of matrix is r, then can carry out svd to the A matrix:
S in the formula
Rr=diag{S
11, S
22..., S
RrBe called the singular value of matrix A, and S is arranged
11>=S
22>=...>=S
Rr>0; Matrix U and V can be expressed as respectively: [u
1, u
2..., u
r, m
1..., m
m] and [w
1, w
2..., w
r, t
1..., t
s], then m=n-r is a mechanism displacement mode number, s=b-r is from stress mode number.
Current most of rope bar tension structure is looked in the power method, does not consider the ability of structure bearing load, and civil engineering structure all is used for bearing load, thus the rigidity that the prestress distribution of trying to achieve like this possibly cause structure very a little less than.
Summary of the invention
Confirm that in order to overcome existing initial prestress distribution method do not consider the shortcoming of the rigidity of structure, the present invention utilizes optimization method to seek the initial prestress distribution form that can guarantee that construction geometry is stable, rigidity is maximum, prestress distribution is even and satisfy conditions such as drag-line is drawn, depression bar pressurized.
For solving the problems of the technologies described above, the technical scheme that the present invention adopts is:
The initial prestress distribution of a kind of rope bar tension structure is confirmed method, comprises following steps:
The first step, give the geometry and the topological relation of standing wire bar tension structure, its rod member number is b, and the node number is N, and the constraint number is k, and then the unconfinement displacement number of structural system is n=3 * N-k, and calculates its balancing matrix:
Af=P
Wherein A is n * b matrix, is called balancing matrix; F is a force vector in the b dimension rod member; P is a n dimension nodal force vector;
Second step, calculate rope bar tension structure from stress mode number:
S in the formula
Rr=diag{S
11, S
22..., S
RrBe called the singular value of matrix A, and S is arranged
11>=S
22>=...>=S
Rr>0; Matrix U and V can be expressed as respectively: [u
1, u
2..., u
r, m
1..., m
m] and [w
1, w
2..., w
r, t
1..., t
s], then m=n-r is a mechanism displacement mode number, s=b-r is from stress mode number;
When asked when stress mode is counted s and is 1, if this satisfies Suo Shoula from stress mode, the condition of bar pressurized is exactly desired initial prestress distribution; If do not satisfy this condition, need to give again the geometry or the topological relation of fixed structure; When counting s from stress mode greater than 1 the time, then general pre-stressed state T is the linear combination of s independence from stress mode, promptly
T=α
1T
1+α
2T
2+...+α
sT
s
In the formula: T
iFor system i rank independent of the stress modal vector; α
iBe combination coefficient, seek combination coefficient α with optimization method
i
The 3rd goes on foot, confirms the objective function in the optimization method,
Wherein, w
1Be minimal eigenvalue weight coefficient, w
2Be feasibility condition weight coefficient, w
3Be total prestress size weight coefficient, w
4Be total prestress distribution homogeneity weight coefficient, δ is the given big or small limit value condition of total prestress, and ε is given internal force deviation limit value, min (λ
Min) be the rigidity maximal condition of rope bar tension structure,
Be the internal force demand condition of rod member,
Be the homogeneity of prestress distribution,
Be the feasibility condition of structure, λ
MinBe the minimal characteristic root of rope bar tension structure geometric stiffness matrix quadratic form, t
iI element in the vector T also is the internal force of i root rod member,
Mean value for all rod member internal force is expressed as:
When rod member is drag-line, funtc
iBe expressed as:
When rod member is depression bar, funts
iBe expressed as:
The 4th goes on foot, produces at random the c group from stress mode combination coefficient; Thereby can obtain c initial prestress distribution; Utilize gradient method to be optimized, thereby obtain the final initial prestress distribution of c group, relatively c organizes the corresponding stiffness matrix quadratic form minimal characteristic root of final initial prestress distribution then; Getting the maximum data of stiffness matrix quadratic form minimal characteristic root is net result, and the value of c is the integer greater than 100;
Whether the rope bar tension structure of the 5th step, the judgement initial prestress distribution of getting satisfies stability condition; Whether judge by positive definite through its tangent stiffness matrix K for stability of structure; If structure is stable, and then the quadratic form of tangent stiffness matrix is a positive definite under arbitrarily little displacement modes d:
d
TKd>0
If satisfy stability condition, the output result; If do not satisfy stability condition, carried out for the 4th step again.
The invention has the beneficial effects as follows that the present invention is maximum with system stiffness, prestress distribution is even and drag-line is drawn, depression bar is drawn is objective function, utilize optimization method to seek from stress mode combination coefficient.The initial prestress distribution of the rope bar tension structure that the present invention confirms has been considered the ability of structure bearing load, and under the certain situation of the total prestress size of structure, rigidity is maximum.In addition, prestress distribution all has superiority at aspects such as structure Design, construction even maintenances uniformly.So the prestress distribution that the present invention confirms has identical cross section with making with class A of geometric unitA, so promptly can save starting material and convenient construction, the more important thing is that the safety margin that makes with class A of geometric unitA is identical.Because restrictive condition of the present invention is less, be fit to the confirming of prestress level of various cable-strut systems.
Description of drawings
Below in conjunction with accompanying drawing and embodiment to further explain of the present invention:
Fig. 1 is a calculation flow chart of the present invention.
Fig. 2 is rope bar tension structure node serial number figure.
Fig. 3 is rope bar tension structure rod member numbering figure.
Fig. 4 is different comparison synoptic diagram from stress modal vector combination coefficient initial value Optimization result.
Embodiment
Confirm that the initial prestress distribution of rope bar tension structure comprises following steps:
(1) gives the geometry and the topological relation of standing wire bar tension structure, and calculate its balancing matrix;
(2) calculate rope bar tension structure from stress mode number.When asked when stress mode is counted s and is 1, if this satisfies Suo Shoula from stress mode, the condition of bar pressurized is exactly desired initial prestress distribution; If do not satisfy this condition, need to give again the geometry or the topological relation of fixed structure.The present invention is primarily aimed at from stress mode and counts s greater than 1 situation, and then general pre-stressed state T is the linear combination of s independence from stress mode, promptly
T=α
1T
1+α
2T
2+...+α
sT
s
In the formula: T
iFor system i rank independent of the stress modal vector; α
iBe combination coefficient.Generally can seek combination coefficient α with optimization method
i
(3) confirm objective function in the optimization method,
Wherein, w
1Be minimal eigenvalue weight coefficient, w
2Be feasibility condition weight coefficient, w
3Be total prestress size weight coefficient, w
4Be total prestress distribution homogeneity weight coefficient, δ is the given big or small limit value condition of total prestress, and ε is given internal force deviation limit value.The implication of other parameter of objective function is following:
(a) rigidity is maximum
The tangent stiffness matrix K of structure can be divided into geometric stiffness matrix K
GWith the material stiffness matrix K
E, then to displacement modes d arbitrarily, the quadratic form Q of stiffness matrix can be expressed as:
Q=d
TKd=d
TK
Ed+d
TK
Gd
And general rope bar tension structure all is indeterminate structure, if the d in the following formula is displacement modes matrix M (matrix M is the last m row of matrix U), then K
EM=0.The quadratic form of its stiffness matrix can be written as:
Q=M
TK
GM
The minimal eigenvalue λ of the Q that provides according to formula 7
MinCan judge the size of the rigidity of structure.λ
MinBig more, then the rigidity of structure is big more.Therefore, if hope that the rigidity of structure under the situation that the material and the external load of system are confirmed is maximum, prestress distribution should make the minimal eigenvalue λ of Q
MinMaximum.So the rigidity maximum of rope bar tension structure can be expressed as:
min(-λ
min)
It is pointed out that total prestress size that structure is used needs control; Otherwise, if prestress distribution is all amplified k doubly, then the quadratic form characteristic of correspondence value of stiffness matrix is also amplified k doubly.Like this, seek biggest characteristic value λ
MinJust become and sought maximum k.This joint is that the internal force quadratic sum through given all rod members limits overall prestress size, and formula specific as follows is expressed as:
T wherein
iBeing i element in the vector T, also is the internal force of i root rod member.So the internal force of rod member need satisfy:
(b) homogeneity of prestress distribution
Prestress distribution all has superiority at aspects such as structure Design, construction even maintenances uniformly.For example, prestress distribution has identical cross section with making with class A of geometric unitA uniformly, so promptly can save starting material and convenient construction, the more important thing is that the safety margin that makes with class A of geometric unitA is identical.Here, through controlling each element force deviation, specifically try to achieve by following formula:
Wherein:
thus the homogeneity of prestress distribution can be expressed as:
(c) feasibility condition
Because the drag-line of cable-rod structure can only be drawn, depression bar can only pressurized, so need when confirming prestress distribution, consider the prestressed positive and negative attribute of rod member.If preceding b
1The root rod member is a drag-line, back b
2The root rod member is a depression bar, and this paper judges through following program whether the rod member in the structure satisfies feasibility condition.When rod member was drag-line, function was:
When rod member was depression bar, function was:
Then the objective function of the feasibility condition of structure is:
(4) produce the c group at random from stress mode combination coefficient; Thereby can obtain c initial prestress distribution; Utilize gradient method to be optimized; Thereby obtain the final initial prestress distribution of c group, relatively c organizes the corresponding stiffness matrix quadratic form minimal characteristic root of final initial prestress distribution then, and getting the maximum data of stiffness matrix quadratic form minimal characteristic root is net result.The value of c is the integer greater than 100.
Whether the rope bar tension structure of (5) judging the initial prestress distribution of getting satisfies stability condition.Stability of structure can whether positive definite be judged through its tangent stiffness matrix K.If structure is stable, and then the quadratic form of tangent stiffness matrix is a positive definite under arbitrarily little displacement modes d:
d
TKd>0
If satisfy stability condition, the output result; If do not satisfy stability condition, carried out for the 4th step again.
Utilize flow process establishment corresponding program shown in Figure 1, the concrete example specific embodiments of the invention of structure is made more detailed explanation:
One strop of cable dome structure setting, rod member is counted b=49, and wherein depression bar is 9, and drag-line is 40, and unrestrained joint is 18, the restraint joint number is 8.Its node coordinate is seen table 1, and this structure has 6 from stress mode, sees table 2.Its node and rod member numbering are seen Fig. 2 and Fig. 3.Confirm binding occurrence δ=30 of internal force quadratic sum, internal force deviation limit value ε=0.001.Because initial mode Vector Groups syzygy number has certain influence to the final optimization pass result, so program takes to search 100, chooses the maximum data of stiffness matrix quadratic form minimal characteristic root and is optimum result.100 groups of result datas more as shown in Figure 4.The minimal characteristic root that obtains best stiffness matrix quadratic form is 1.0994.
The independence of utilizing optimization method to obtain the best from stress modal vector combination coefficient is: { 2.2929-0.2352-0.03614.1286,0.0147-2.7641}
TThe force density of the rod member that obtains after the optimization distributes and sees Table 3.
Table 1 cable dome structure node coordinate
Table 2 cable dome structure from stress mode
Table 3 cable dome structure Optimization result